1. Introduction
Globally, cement manufacturing industries are encountering challenges to minimize the energy resources [
1] and carbon footprints [
2]. In cement industries, the production of cement clinker is an energy-intense process [
3], and its thermal specific energy consumption as high as 734 KCal/Kg on average. It makes clinker production incur the majority of the plant’s operating cost. Hence, the primary objective of the cement plants is to optimize the process of clinker production, which can significantly reduce the energy consumption and improves the cement quality [
4]. Rotary kiln is the major equipment responsible for the production of cement clinker. In the kiln, limestone suitably blended with clay and other materials are fed as raw material and uniformly heated to a high temperature (1300 °C) for clinker production. The quality of the cement clinker majorly depends on the raw material quality and the optimal heating process.
Continuous operation, longer time constants, uncertainty of raw material characteristics, and complex dynamics are the significant challenges that have to be addressed to optimize the kiln operations [
5]. The control objectives of a rotary kiln are to minimize the fuel consumption for heating, to maximize the clinker production and to increase the cement quality [
6]. These objective exhibit stronger interdependencies and also depends on uncertain input parameters such as quality of raw materials, and thermal regulation inside the kiln. These complexities necessitate a proper trade-off to achieve optimal operation of the rotary kiln at a desired production rate with better cement quality. Thus, the control of cement kiln is a complex and on-going research problem involving expert knowledge with intelligent approaches.
Model predictive controller (MPC) emerges as a promising tool to handle the challenges associated with the control of the kiln process. MPCs’ ability to handle multi-input–multi-output (MIMO) process with large time delay [
7] and non-minimum-phase process makes it widely adopted for various industrial processes. They are found to be successfully deployed for control of ball mill grinding [
8]. MPCs’ are competent in handling uncertain disturbances and plant-model mismatch. MPC’s capability to handle constraints of both manipulated and controlled variables makes them suited for practical applications in cement industries. Literature reports on the usage of linear and non-linear MPCs for the various manufacturing process. Though, nonlinear MPC is effective in handling the nonlinear process in cement industries, [
9] computational cost limits its usage in practical applications. Hence, the proposed study is carried out with linear MPC with the MIMO model for control of the rotary kiln process.
The control performance of MPC predominantly depends on the accuracy of the model describing the plant behavior and other controller parameters [
10]. These plant models can be represented by conventional mathematical approaches like transfer function, state-space, and ARMA (Autoregressive-moving-average). Machine learning technique based models like neural networks and fuzzy systems are also used to model the plant behavior. MPC controller parameters include horizons and weights given to each metric used in its cost function. Prediction and control horizons are used to determine the number of future samples to be predicted and the number of control signals to be applied to the plant model, respectively. A higher prediction horizon is capable of predicting the complete behavior of the plant and can effectively optimize the control input at the cost of higher computational intensity. On the other hand, a lesser prediction horizon reduces the computational complexity but fails to predict the plant output. Also, these horizon values are plant-specific and depend on the type of disturbance the plant encounters [
11]. Hence, there is a need for tuning methods to determine these horizon values based on the plant and their disturbance dynamics.
Generally, MPC is a multi-objective optimization problem, and its cost function is formulated as a summation of various performance metrics like squared tracking error, rate change of manipulation, magnitude of input, and outputs. These metrics are highly correlated, and the minimization of all these metrics is infeasible [
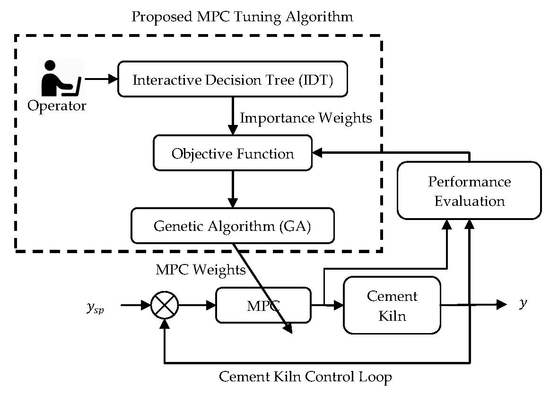
12]. To overcome this problem, MPC weights are introduced to determine the importance given to each of these performance metrics. Accurate tuning of these weights that can minimize the overall cost function with reliable controller performance is a challenging and ongoing research problem. Lack of unified procedure and plant/disturbance specific nature of these weights are additional challenges that increase the complexity. It demands a significant amount of manual overhead in tuning these weights for change in plant behavior or disturbance. Hence, there is a need for an intelligent automated tuning procedure that can track the change of plant behavior and tunes the MPC weights on demand, which is addressed in this paper.
Major contributions of this work include (i) design of MPC for rotary kiln using state-space model. (ii) Formulation of single objective function for genetic algorithm (GA) using interactive decision tree (IDT). (iii) Use of GA for tuning MPC weights in specific to disturbance dynamics. (iv) Performance analysis and comparison with multi-objective GA under various scenarios of cement kiln operations.
The remaining sections of this article are organized as follows;
Section 2 describes the related work reported in the literature for MPC weight tuning, which describes the importance of this research problem from industrial perspective. The operations of rotary kiln in the cement manufacturing process, and the state-space model used for MPC are described in
Section 3. The design of MPC and the role of MPC weights in the cost function are illustrated in
Section 4.
Section 5 presents the MPC design methodology and
Section 6 describes the proposed MPC tuning procedure using GA with IDT algorithm.
Section 7 illustrates the performance analysis of the proposed MPC tuning technique under various disturbance scenarios and discussion on the choice of MPC parameters for every scenario.
Section 8 concludes the work with future direction.
2. Related Work
Over recent years significant research has been carried out to determine MPC weights. Both online and offline weight tuning methods are widely investigated in the literature [
13]. Online weight tuning methods vary the MPC weights during the plant run-time. These techniques are applied for minimizing run-time factors such as instantaneous error, overshoots, and transient response [
14]. On the other hand, offline tuning methods provide a constant weight to complete one cycle of plant operation. The overall performance is evaluated in terms of steady-state error, integral squared error (ISE), integral absolute error (IAE), and integral time absolute error (ITAE). Then, the weights are tuned and tested to minimize these error metrics. Though online tuning provides the flexibility of changing the weights during run-time, it may lack to evaluate the overall performance of the MPC. Offline tuning is preferred in control systems where overall performance needs to be improved. Thus, the proposed work aims to tune the MPC weights offline to improve the overall performance in the presence of disturbances.
Empirical relations described by the plant model are fundamentally used for the selection of weights. Investigation of general guidelines for the selection of weighting factors for the cost function has also been reported [
15]. However, its performance degrades when there are uncertainties in plant parameters and plant-model mismatch. With a fixed sampling interval and horizon values, optimization-based weight tuning procedures found to have improved performance as compared with the trial and error approach [
16]. Controller matching [
17] is one of the widely used techniques to determine these weight parameters. It involves tuning of MPC parameters to match its performance with a standard pre-defined controller. It makes the MPC behave similar to the standard controller and exhibits asymptotic stability. Usage of IAE in tracking for online tuning of MPC weights [
18] is presented. Need for an accurate model, standard controller, and continuity in cost functions (existence of derivative) are some of the challenges in MPC weight tuning using conventional approaches.
Optimization techniques emerge as an alternative solution to overcome these limitations. Constraint least-square optimization technique has been investigated to tune the MPC weights for achieving [
19] reliable performance. Conventional gradient descent [
20] approach has also been investigated to determine the optimal set of MPC parameters based on process repeatability and pre-defined time-domain specifications. Formulation of the cost function, which has to be minimized to determine the MPC parameters, is a complex process, and several attempts have been reported in the literature [
21,
22,
23]. Customization of this cost function and selection of optimization techniques have brought in a wider variant of MPC tuning strategies. The cost functions are formulated as per the available plant knowledge and also using the economic aspects. Maximization of comfort and energy saving [
21] are achieved by weight tuning in building thermal/heating, ventilation, and air conditioning (HVAC) [
22] control system. Minimization of energy consumption in various domestic appliances like the water heater, air conditioner, and refrigerator had been addressed by weight adjustment in the MPC. Production maximization with reduced energy consumption [
23] had been achieved by tuning MPC weights in the distillation column. With the variant of cost functions reported in the literature, the proposed work also aims to formulate the cost function to improve the MPC performance amidst structured and unstructured disturbances in the cement kiln.
GA-based multi-objective optimization technique had been developed to tune the MPC weights and prediction horizon that minimize the cost function related to the steady-state and transient filter performance is reported in [
24]. GA-based weight tuning approach is reported to provide a faster convergence as compared with the iterative weighted tuning approach. Particle swarm optimization (PSO)-based weight optimization had also been implemented in MPC control to minimize the multi-objective cost function at [
25] in both disturbance rejection and set point tracking scenario. The automatic estimation of MPC weight factor coefficients by PSO algorithm in nonlinear MPC (NMPC) is also proposed in the literature [
26,
27]. Other optimization techniques like lexicographic optimization, compromise optimization, and normal boundary intersection method have also been adopted for tuning of weight to minimize the cost function in MPC [
23,
28,
29]. Hence, in the proposed work, a combination of GA with IDT is used to tune the MPC weights. GA is capable of providing an evolutionary approach, and IDT is used to capture the available expert knowledge along with the requirements [
30], which makes the proposed technique a reliable tuning procedure for the industrial process like cement kiln.
3. Process Description
Cement is a soft, grey, and powdered material used widely in construction. It majorly involves (i) raw material preparation, (ii) pyro processing, (iii) milling, and (iv) packing, as illustrated in
Figure 1. Limestone and clay are transported from quarry to the crusher. The crusher grinds the limestone to produce a raw-meal. The blender tends to smooth the crushed material and re-circulate the larger particles back to the crusher. Other additives (silica, alumina, magnesia, and iron ore) from the silos and the raw meal are loaded to the raw-mill and ground. The product from the raw mill is fed to the cyclone separator for the separation of larger particles. Before feeding the rotary kiln, a calciner is used to pre-heat the raw meal to 900 °C. The rotary kiln heats the raw meal uniformly to reach a temperature of 1500 °C. The uniformity and precision of heating determine the quality of clinker produced by the rotary kiln. The produced clinker is fed to the cement mill for grinding, and cement is manufactured. Finally, the cement is packed and ready for delivery.
The proposed work mainly focuses on the rotary kiln, which is predominantly responsible for the overall quality and production of cement. Rotary kiln is used in the pyro-processing stage, where calcium carbonate reacts with silica-bearing minerals to form a mixture of calcium silicates. The kiln is made up of steel plate lined with firebricks and inclined at a slope of (1–4°) to facilitate smooth material movement, as in
Figure 2. It is slowly rotated on its axis at a range of 30 to 250 revolutions per hour to ensure uniform heating and distribution of raw meal. The raw meal and fuel are fed at the elevated and bottom-end, respectively. The raw-meal is burned at a high temperature (1450 °C) and cooled down to 100 °C at grate cooler to produce clinker.
Modeling of Cement Kiln
This section describes the modeling of the rotary kiln system, which can be used for MPC design. The operation of cement kiln depends on several variables, and it is modeled as a multivariable process. Feed and fuel flowrates are manipulated under constant and rotational speed to achieve uniform heating and are considered as model inputs. The kiln torque required to maintain the rotational speed depends on the mass of raw-meal present in it. It is measured in terms of current (A) required by the electric drive to satisfy the torque requirement. The temperature at the burning zone of the rotary kiln has a direct impact on the quality of cement and can be regulated by the feed and fuel flowrates. Thus, in the proposed work, the rotary kiln is modeled as a MIMO system with two inputs (feed and fuel flowrates) and two outputs (kiln torque and burning zone temperature (BZT)).
Complex interactions across various parameters of kiln limit the usage of the first principle method to design an accurate model. Hence, a data-driven modeling technique has been employed to determine the model of the cement kiln. A cement kiln is emulated using the industrial emulator software, and data are acquired with variations around its operating point. This input–output data from the emulated cement kiln is pre-processed for noise and offset removal. Various modeling techniques have been investigated to estimate the model from the kiln input–output data, as described in [
32]. Linear models such as transfer function, state-space, ARX (autoregressive-exogenous-input), and ARMAX (autoregressive-moving-average with exogenous inputs) are investigated. The model order and the number of delay samples are chosen using Hankel singular value, which describes the energy of the state variables [
33]. The number of state variables having higher energy is determined as the order of the model. From the analysis, it is observed that cement kiln is accurately modeled with the fourth-order state-space model. It exhibits a fit percentage of 72.5% and 97.6% for torque and BZT, respectively, as reported in [
32]. The fit percentage (
) is determined by using the predicted (
) and the actual output (
) from the model and plant, respectively, as in Equation (1). Thus, the proposed work uses this state-space model for MPC design and further analysis.
4. Design of MPC
MPC is an optimal multivariable optimization controller that has been widely used in process industries. In the proposed work, the kiln is modeled as a fourth-order system with four state vectors
. Feed (
and fuel (
flowrates are considered as control inputs (
. The output matrix
is defined by two of the possible measurements, namely torque (
and BZT (
.
corresponds to the state, input, and output matrix, which govern the dynamics of the kiln. The state-space model of the kiln described in Equations (2) and (3) is used to predict the future behavior of the cement kiln. Kalman filter-based state observer [
34] is used to predict the states of the cement kiln. It uses the state observer parameters (
) and the noise covariance matrices like process noise covariance, measurement noise covariance, and input noise covariance to determine the Kalman gain. This gain is used to fuse the prediction and measurement to assess state of the kiln accurately. Then, the estimated states are employed to determine the future error, and a cost function is formulated using this error along with the rate change of inputs. An online optimizer is used to estimate the control input that can minimize the cost function. Finally, the control input is implemented on the kiln to regulate both the torque and BZT. Practical limitations of the control variables and plant behavior are fed as constraints in minimizing the cost function, as illustrated in
Figure 3.
MPC works on the principles of the receding horizon approach [
35]. The future behavior of the kiln is estimated using the state-space model and past outputs. It is predicted for a finite number of samples described by the prediction horizon (
P). Higher samples of prediction horizon often predict the complete behavior of kiln but at the cost of higher computational load. On the other hand, a lower prediction horizon may be inefficient to predict the kiln behavior and makes the MPC more aggressive. There is a need for optimal determination of the prediction horizon for efficient control. The control horizon (
M) describes the set of control inputs determined to minimize the cost function over the finite number of samples. This control horizon cannot outrun the prediction horizon to retain feasibility conditions (
M<P) [
36]. The choice of control horizon depends on the prediction horizon and the closed-loop response of the kiln. Once the control inputs corresponding to a minimal cost function are determined, the first sample of control input is implemented, as illustrated in
Figure 4.
4.1. Formulation of MPC Cost Function
The MPC cost function is formulated with two objectives, namely tracking error, rate change of inputs as in Equation (4). The cost function corresponding to the tracking error () is formulated using the squared difference between the reference/setpoint () and predicted plant behavior ( for a finite duration indicated by the prediction horizon . The scaling problem associated with a multivariable system is addressed by the use of scaling variable (). This scaling variable is determined by the nominal operating point, which is estimated from the input and output data pair used for modeling. It makes the output variables of different scales to be normalized into a uniform scale. The importance of tracking error of the individual output variable ( over the prediction horizon () is determined by the error weights () as in Equation (5).
Similar to tracking error, the cost function for rate change of input is also formulated as in Equation (6). The rate change in inputs is determined by the difference between the present and past control action over the finite control horizon
duration. The scale factors (
) and input weights (
) are used to provide normalization and importance, respectively. Conventionally, the scale factor for the input variables is identified using the nominal operating range of the process variables. In the proposed work, the rotary kiln is modeled as MIMO with two inputs (
) and two outputs (
). The nominal values of the input and output variables are identified from the mean values of the data used during modeling of the cement kiln process.
4.2. Role of MPC Weights
Weights provide the importance of each of the control objectives in the cost function. In the proposed work, the MPC weights are comprised of two weighting vectors, namely output weight (
) and rate weight (
). These vectors define the importance of each control objectives across variables (
) and horizons (
). A higher value of output weights (
) drives the MPC to manipulate the process that leads to improved tracking response. This improvement is realized at the cost of intense manipulation of control signals, which may demand more energy. On contrast, a reduction in output weight may lead to increased tracking error. The rate weight governs the incremental change of the control input/energy usage [
37]. An increase in the rate weight optimizes the energy usage by at the cost of significant tracking error. Thus, there is a need for procedures to determine optimal weight parameters, which can minimize the tracking error with reduced energy utilization.
5. MPC Weight Tuning Using GA
GA is a stochastic optimization technique inspired by the process of natural selection. It can provide inheritance from the preceding generation and also offers out-of-the-box solutions through mutation. Heuristic and iterative nature of GA makes it an optimal tool to determine the weights for MPC. GA involves the five steps, namely (i) initialization of population, (ii) evaluation of fitness function, (iii) selection of optimal population, (iv) crossover, and (v) mutation as described in
Figure 5.
The population for GA is initialized with the set of individuals. Each of these individuals represents the possible solution within the constraint search space. An objective function is formulated to determine the performance of the system for individuals. Successful individuals producing higher performances are chosen for the next generation. The number of individuals chosen is fixed and pre-defined by population size. Higher population size may yield an increased resolution in the given search space and also can bring in near-optimal solutions at higher computational cost. Lesser population size degrades the resolution and reduces the computational load. Hence, a trade-off is needed on the choice of population size. Next, these selected individuals are made to crossover to produce a new generation. This new generation has characteristics inherent from their parent’s population. Also, mutation allows the new generation to have some external influenced characteristics. This makes GA to overcome local minima problem and attain a global optimization.
In this work, each individual of the population is composed of the weights given to the MPC cost function. They are characterized by the set of output and input rate weights with search space constrained by using upper and lower bounds as in Equation (7).
6. Interactive Decision Tree Algorithm
The weights or importance given to these metrics used in GA objective function is determined by using the IDT approach. The decision tree provides a decision support tool [
38] for the selection of weights that can improve the objective function. It prompts for the operator response to determine the improvements in the performance metrics. The response-based interaction reduces the manual overhead and also has the potential to capture expert knowledge [
39]. Thus, the integration of expert knowledge with GA can guarantee convergence and provide optimal MPC tuning.
Initially, the weights for individual metrics (
) in the objective function are distributed uniformly as in Equation (14). The MPC weights are tuned using this objective function. The objective of the GA is to determine the MPC weights that minimize the fitness function with uniform weighted metrics. The performance improvement in these metrics for GA determined MPC weights are evaluated as in Equation (15) and compared with the default MPC weights (
). The algorithm interacts with the operator to determine the weakly improved metrics (
). If all the metrics are improved to the satisfactory level of the operator, then the operator selects none of the metrics (
) and will terminate the algorithm. Weight corresponding to the identified weakly improved metric (
) is increased by a smaller increment (
) as in Equation (16), and weights of the other metrics (
) are decremented equally in accordance to Equation (17) without loss of generality. GA-based MPC weight tuning is performed for this new set of fitness weights, and performance improvement is determined. The operator feedback is acquired to determine the need for further improvement in the identified metrics. If the metrics need further improvement, then the weights are incremented by a factor (
). Once a satisfying improvement is achieved, the weight for the identified metrics is fixed, and the remaining weights are distributed in the same procedure to the subsequent weakly improved metrics, as illustrated in
Figure 6.
7. Results and Discussion
The performance of the proposed tuning technique is evaluated in various scenarios that predominantly occur in cement kiln operations. Single objective function formulated in terms of tracking error and energy utilization is used in GA to determine the MPC weights. IDT is used to tune the importance weight of these performance metrics to achieve the optimal improvement in them. The distribution of importance weight, along with their performance improvement at the initial and final step of IDT, is presented. At the initial step, all the performance metrics are weighted equally, and IDT is capable of distributing the weights to achieve optimal performance at the final step.
The performance of the proposed IDT-based single-objective GA (SoGA) is compared with the conventional multi-objective GA (MoGA). Unlike the proposed SoGA, MoGA does not combine individual metrics. It provides a Pareto front [
33] of the MPC weights, which represents the boundary traced between the feasible and infeasible solution space. It describes the dependencies of the metrics (tracking error and energy utilization) and also provides an insight on possible minimization of them. The optimal MPC weight from the Pareto front is determined by using the utopia point. The utopia point is determined by the possible minimal values of all the metrics, and this may fall in the infeasible solution space. It is projected over the Pareto front surface to determine the feasible MPC weight that minimizes the cost. The implementation of SoGA and MoGA are made identical with the parameters described in
Table 1 to compare their performance on MPC tuning in various control scenarios.
7.1. Tuning Scenarios
MPC weights are predominantly specific to plant dynamics and the nature of disturbances the plant encounters. It demands re-tuning of weights for the given scenario of the plant [
40,
41]. Also, MPC weight tuning is a non-convex optimization problem with model behavior and disturbance nature as influential parameters. Hence, in the proposed work, MPC weights are tuned in five different scenarios that predominantly occur in the cement kiln process. One tracking and four disturbance rejection scenarios are considered in this study. The tracking performance includes tuning of MPC weights that facilitates optimal tracking of the step change in set point with reduced energy consumption. Pulse and Gaussian nature of noise are considered in disturbance rejection scenarios. A pulse form of disturbance occurs in the kiln when an accidental increase in fuel or change in feed quality is encountered. Hence, a pulse form of input disturbance is considered as one of the weight tuning scenarios. Any industrial process suffers unstructured random disturbances. Gaussian noise rejection is identified as another scenario to account for such random disturbance, as listed in
Table 2.
7.1.1. Set Point Tracking (SPT) Scenario
A step-change in the reference is made to observe the tracking behavior of the MPC, whose weights are tuned using the proposed methodology. The percentage improvement in performance metrics with GA tuned weights are evaluated in comparison with the default MPC weights and are listed in
Table 3. It is observed that the SoGA with equal importance (i.e., at initial iteration) of all the performance metrics is capable of providing improvements. Further, improvement is achieved using the IDT-based importance weighting function. The weakly improved performance metrics (
) is identified, and its importance is raised to observe further improvement. The operator can interactively terminate the increasing importance, and the attention can be moved to the next weaker performance metrics (
. Finally, the iteration is terminated with consent from the operator identifying significant improvements in all the performance metrics.
Compared to SoGA with equal importance (at initial iteration), IDT-defined importance weights are capable of providing better performance in set point tracking scenario (at final iteration). SoGA-based MPC has significantly improved the rise time of torque and reduced the overshoot in BZT, as illustrated in
Figure 7. It can prevent the burn-over of raw materials and preserves the cement quality. The fuel consumption is also reduced (
Figure 8), as indicated by the
, which is one of the primary requirements in cement kiln operations. Further, the performance of the proposed IDT-based SoGA method is compared with the existing MoGA. It is observed that the SoGA is capable of providing MPC weights that can produce better performance in set-point tracking scenarios.
7.1.2. Measured Pulse Disturbance (MPD) Scenario
Accidental increases in feed and manual overrun of fuel input are inevitable in cement kiln operation. The change of raw material quality varies the thermal specificity, which may lead to variations in the thermal behavior of the cement kiln. To emulate this scenario, a pulse form of input disturbance is provided in both the manipulating input and the MPC performance is analyzed. A remarkable improvement in energy loss function is observed with the SoGA-based weight tuning as compared with the default MPC weights. The weight for the change in fuel flow rate is increased and provides the MPC to look ahead at the elevated flow rate because of the disturbance. It reduces the energy supplied from MPC as the required energy is already available with the disturbance. It also leads to improved rejection of disturbances in BZT, which is an influential parameter of the fuel flowrate. The importance weights are tuned to improve the disturbance rejection behavior using the proposed IDT. The rejection performance of the torque is improved at a minimal compromise on BZT. The overall performance of the SoGA-MPC is compared with MoGA and illustrated in
Table 4.
Though SoGA slightly provides a degraded performance in rejecting the disturbance at torque, optimal energy usage is guaranteed as compared to the existing MoGA. Thus, the energy-intense nature of cement kiln makes the operator choose the SoGA-based weights to achieve optimal operation.
Figure 9 illustrates the transient response of the cement kiln under disturbance. A pulse form of disturbance is introduced in both the manipulating inputs, as in
Figure 10. It is observed that the MPC tuned with the proposed technique (SoGA-MPC) can minimize the overshoot in BZT and recover from the disturbance. The fuel consumption is also significantly reduced with the same feed flowrate, which is capable of maintaining the production rate.
7.1.3. Measured Gaussian Disturbance (MGD) Scenario
Industrial processes are always subjected to stochastic and unstructured disturbances. Input disturbances in the form of Gaussian noise are given to the cement kiln, and the MPC performance is analyzed. Significant degradation in energy utilization is observed when the MPC weights are tuned using SoGA with equal importance (at initial iteration). However, the proposed IDT rescues the SoGA with appropriate importance adjustments and produces performance improvement in all the metrics at the final iteration as described in
Table 5. The energy loss functions are recovered from degradation (
−98.7785) to a significant improvement (
45.9010). This trend is also reflected in MoGA-based weight tuning method, and degradation of the energy loss functions for improvement in IAE is observed.
Figure 11 and
Figure 12 illustrate the transient behavior of cement kiln under Gaussian disturbance. It is observed that the proposed SoGA-MPC is capable of suppressing the stochastic variations caused by the Gaussian disturbance. Thus, the SoGA-MPC appears to be a preferred method as it provides overall improvements with optimal energy utilization.
7.1.4. Unmeasured Pulse Disturbance (UMP) Scenario
Most of the cement industries have semi-automatic control of the kiln process. Operators are also deployed to monitor and control the process in conjunction with MPC. It makes the accidental increase in feed, and fuels are common incidents that occur in the cement kiln process. Lack of input sensors makes these variations not measurable and the MPC is unaware of this input changes. The variations in kiln inputs generated by the operators go unmeasured because of the unavailability of input sensors for MPC. This sudden unknown drift in manipulation variables makes the MPC produce offset (steady-state error) and degrades the cement quality to a greater extent. The offset can be eliminated by using an integrator system as an input disturbance model [
34], which accumulates the offset and increases the magnitude of prediction error. This higher prediction error enables a more significant control action to compensate for the unmeasured disturbances. Also, the proposed work uses IAE as a cost function. The IAE evaluates the overall performance of the MPC in the complete run-time. It makes offset as a significant factor that deteriorates the IAE, and the MPC weights are tuned by prioritizing offset elimination. Thus, the proposed work determines MPC weights that enable offset-free disturbance rejection. Hence, the proposed weight tuning procedure is also subjected to UMP scenarios, and its performance is evaluated.
Being unmeasured disturbances, MPC can sense this disturbance only after it is reflected in the process parameters. The performance of the SoGA at initial iteration (with uniform importance weights) and MoGA is identical to the default MPC weights. It makes no significant improvements to be observed in SoGA- and MoGA-tuned MPC. However, the energy utilization is improved with the proposed IDT-based SoGA at a minimal degradation in torque performance. MoGA-MPC fails to provide improvements in performance metrics because of the unmeasured disturbances. This behavior is also observed in transient response, as illustrated in
Figure 13 and
Figure 14. The sluggish nature of disturbance rejection observed in this scenario is improved by using the disturbance model. The gain of the integrated type disturbance model is increased to improve the transient response. It is observed that the MPC tends to reject the disturbance faster but at higher peak overshoot in torque response. A significant improvement in disturbance rejection performance is observed in BZT with higher energy utilization (Fuel flowrate). Thus, the proposed IDT-based SoGA can provide optimal energy utilization and go incompliance with the overall control objective of the cement kiln process as illustrated in
Table 6.
7.1.5. Unmeasured Gaussian Disturbance (UMG) Scenario
Gaussian noise of pre-defined variance is added to the feed and fuel flow rate, and the performance of the proposed technique is investigated. The unmeasured input disturbances are sensed only with the variations in the output parameters. It results in excess utilization of energy to achieve improvement in the output parameters (torque and BZT) during the initial iteration of SoGA. The use of IDT for SoGA provides importance to energy utilization, and a significant improvement is achieved without compromising the IAE of output parameters. This behavior is also observed in the case of MoGA, which provides degraded energy performance to provide improvements in IAE as in
Table 7. The elevation caused in BZT because of Gaussian noise is suppressed using the proposed SoGA-MPC, which can maintain the cement quality amidst disturbances (
Figure 15). The fuel and feed flowrate are significantly reduced at every instant of the sample, as illustrated in
Figure 16, which is a major control objective of the cement kiln process.
A comparative analysis of performance metrics for MPC with default weights, SoGA-tuned weights, and MoGA-tuned weights is presented in
Table 8. A negative sign in energy loss function indicates the amount of energy saved, i.e., energy utilization below the nominal value. Higher negative values indicate an improved energy saving, and positive values indicate excessive energy used above the nominal value. Minimal value of IAE indicates a reduced deviation of toque and BZT from their set points. It is observed that the proposed SoGA-MPC is capable of providing improved performance in SPT and MDP scenarios. During MDG scenario, energy utilization has been improved at the cost of degraded tracking performance. Identical performance is observed between SoGA, and MoGA during UMP scenarios. The proposed SoGA-MPC reduces a significant amount of energy during UMG scenario. Also, the average performance improvements obtained using SoGA and MoGA in contrast with the default MPC weights are analyzed as in
Figure 17. It is observed that the proposed SoGA is capable of providing performance improvement for all the test scenarios, whereas the MoGA performance degrades in the case of MDP scenario (indicated by a negative value in % performance improvement). Thus, the proposed IDT-based SoGA is capable of achieving energy-optimized performance. It is mainly due to the incorporation of the operator’s knowledge by interactions and the use of scenario-specific tuning procedures.
8. Conclusions
Weights of the MPC play a vital role in determining the optimal control of the cement kiln process. These weights can change the operating mode, and facilitate MPC to provide adequate control for the given scenario.GA has been employed for tuning the MPC weights under various scenarios in which the cement kiln is operated. Single objective function incorporating the tracking error and energy utilization metrics is formulated to facilitate GA for tuning weights. The importance given to each of these performance metrics is determined by using IDT with the operator’s interaction. The operator’s knowledge is extracted in the form of a decision to change the importance specific to the control scenarios. Thus, the proposed tuning procedure uses an operator driven stochastic optimization technique, which can provide faster convergence with satisfied controller performance.
Five scenarios testing the tracking and disturbance rejection performance are considered in this study. The results illustrate a significant reduction of fuel flow rate by 64% with GA-tuned MPC weights for the tracking problem. Measured disturbances can provide knowledge about the disturbance to the MPC, and the controller can react to these disturbances before they affect the process. The proposed tuning procedure is capable of determining the MPC weights to minimize its control action, which is reflected by a reduction in energy utilization. In unmeasured disturbance scenarios, MPC senses the disturbances using its measurements only. It hinders the GA to bring in overall improvements in all the performance metrics. However, IDT can facilitate to understand the operator’s choice to minimize the energy at the cost of tracking error. Though use of integrator type disturbance model facilitates offset-free disturbance rejection, usage of other types of disturbance model needs to be investigated.
Finally, the proposed SoGA with IDT is compared with the MoGA-based weight tuning procedure. The comparison illustrates better performance with the proposed design by 23.74% on average of all the test scenarios. The proposed MPC tuning procedure can be applied for other industrial processes, which demands the incorporation of the operator’s knowledge. Further, an inference system can be designed to recommend MPC weights by observing the control scenarios of the cement kiln process. Implementation of artificial intelligence techniques to understand the control scenarios is the future scope of the proposed work.