Colloids at Fluid Interfaces
Abstract
1. Introduction
2. Driving the Assembly: Interfacial Tension and Contact Angle
2.1. Interfacial Tension
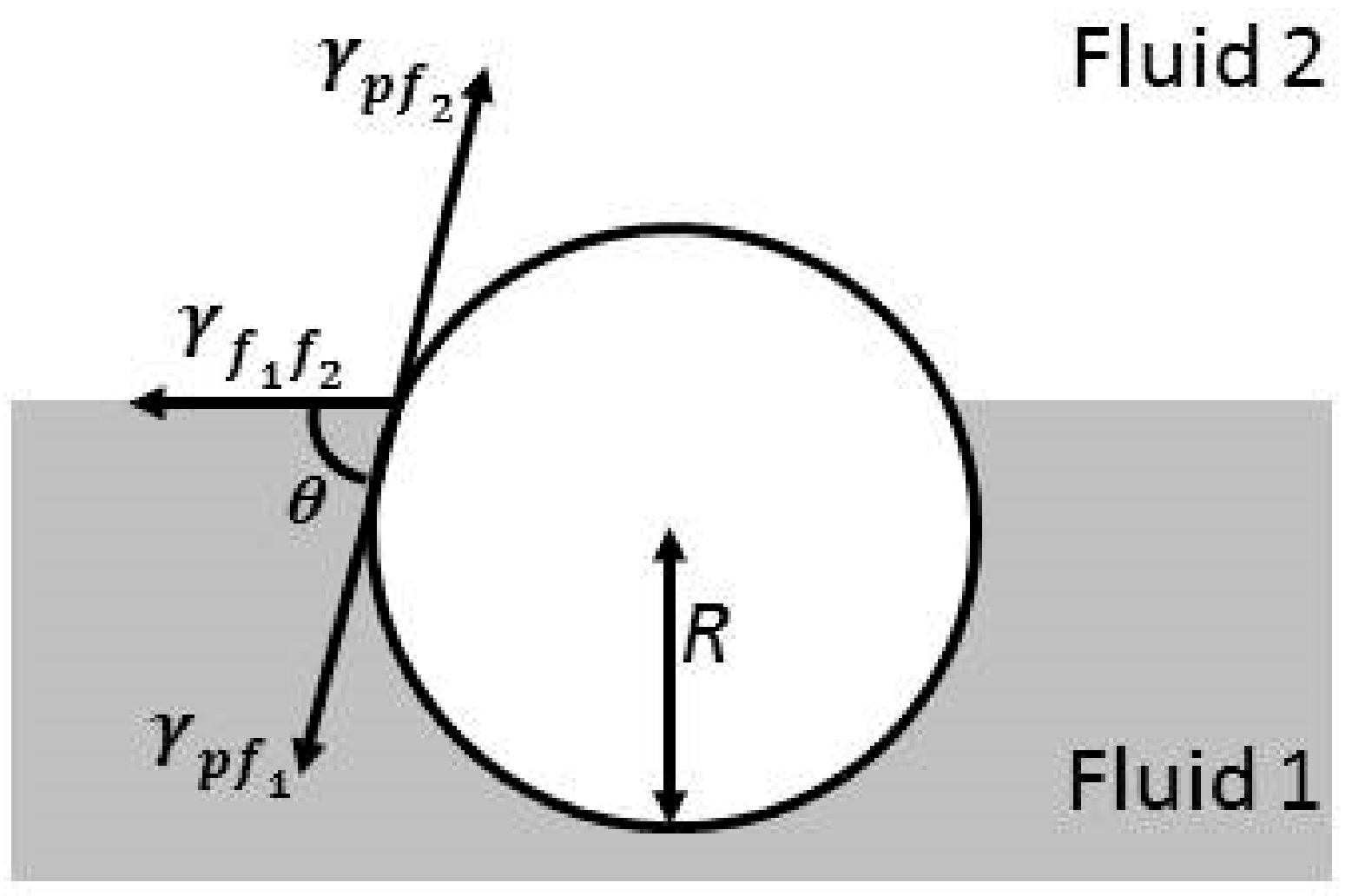
2.2. Contact Angle and Wetting
2.3. Organization of Colloids at Interfaces
3. Interactions between Colloids Trapped at Fluid Interfaces
3.1. Direct Interactions
3.2. External Interactions
4. Dynamics of Colloids Trapped at Fluid Interfaces
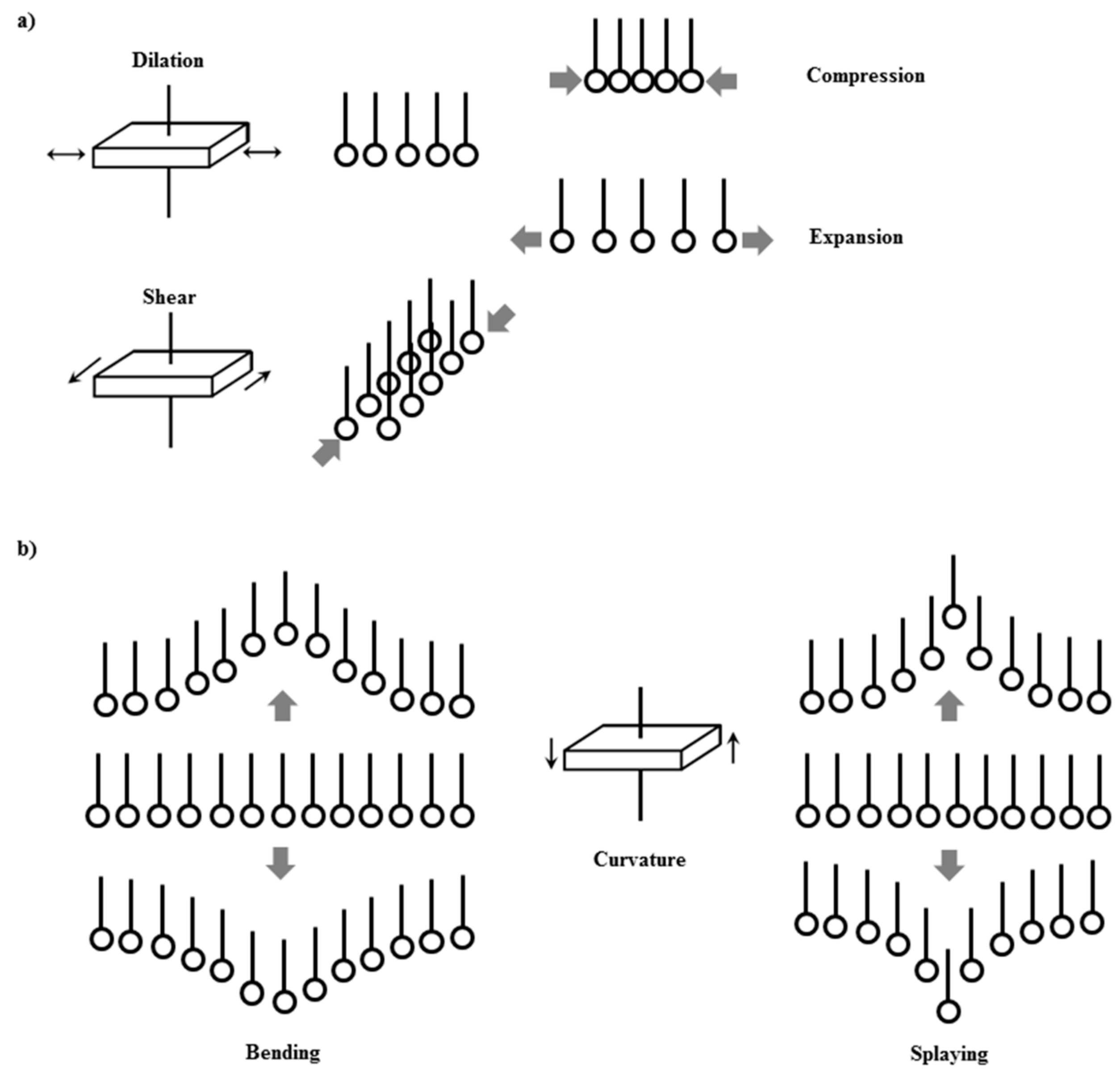
5. Rheological Behavior of Particles Attached at Fluid Interfaces
5.1. Dilational Rheology
5.2. Shear Rheology
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, S.; Russel, T.P. Nanoparticle Assembly at Liquid–Liquid Interfaces: From the Nanoscale to Mesoscale. Adv. Mater. 2018, 30, 1800714. [Google Scholar] [CrossRef] [PubMed]
- Forth, J.; Kim, P.Y.; Xie, G.; Liu, X.; Helms, B.A.; Russel, T.P. Building Reconfigurable Devices Using Complex Liquid-Fluid Interfaces. Adv. Mater. 2019, 31, 1806370. [Google Scholar] [CrossRef] [PubMed]
- Garbin, V. Colloidal particles: Surfactants with a difference. Phys. Today 2013, 66, 67–68. [Google Scholar] [CrossRef]
- Binks, B.P. Particles as surfactants—Similarities and differences. Curr. Opin. Colloid Interface Sci. 2002, 7, 21–41. [Google Scholar] [CrossRef]
- Luengo, G.S.; Galliano, A.; Dubief, C. Aqueous Lubrication in Cosmetic. In Aqueous Lubrication. Natural and Biomimetic Approaches; Spencer, N.D., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2014; pp. 103–144. [Google Scholar]
- Llamas, S.; Guzmán, E.; Ortega, F.; Baghdadli, N.; Cazeneuve, C.; Rubio, R.G.; Luengo, G.S. Adsorption of polyelectrolytes and polyelectrolytes-surfactant mixtures at surfaces: A physico-chemical approach to a cosmetic challenge. Adv. Colloid Interface Sci. 2015, 222, 461–487. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.F.; Wennerström, H. The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet; Wiley-VCH: Hoboken, NJ, USA, 1994. [Google Scholar]
- Morrison, I.D.; Ross, S. Colloidal Dispersions: Suspensions, Emulsions, and Foams; Wiley-Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Santini, E.; Guzmán, E.; Ferrari, M.; Liggieri, L. Emulsions stabilized by the interaction of silica nanoparticles and palmitic acid at the water–hexane interface. Colloids Surf. A 2014, 460, 333–341. [Google Scholar] [CrossRef]
- Maestro, A.; Rio, E.; Drenckhan, W.; Langevin, D.; Salonen, A. Foams stabilised by mixtures of nanoparticles and oppositely charged surfactants: Relationship between bubble shrinkage and foam coarsening. Soft Matter 2014, 10, 6975–6983. [Google Scholar] [CrossRef]
- Arriaga, L.R.; Drenckhan, W.; Salonen, A.; Rodrigues, J.A.; Íñiguez-Palomares, R.; Rio, E.; Langevin, D. On the long-term stability of foams stabilised by mixtures of nano-particles and oppositely charged short chain surfactants. Soft Matter 2012, 8, 11085–11097. [Google Scholar] [CrossRef]
- Santini, E.; Ravera, F.; Ferrari, M.; Alfè, M.; Ciajolo, A.; Liggieri, L. Interfacial properties of carbon particulate-laden liquid interfaces and stability of related foams and emulsions. Colloids Surf. A 2010, 365, 189–198. [Google Scholar] [CrossRef]
- Santini, E.; Guzmán, E.; Ravera, F.; Ciajolo, A.; Alfè, M.; Liggieri, L.; Ferrari, M. Soot particles at the aqueous interface and effects on foams stability. Colloids Surf. A 2012, 413, 216–223. [Google Scholar] [CrossRef]
- Carter, B.O.; Wang, W.; Bray, C.L.; Adams, D.J.; Cooper, A.I. Methane Storage in Dry Water Gas Hydrates. J. Am. Chem. Soc. 2008, 130, 11608–11609. [Google Scholar]
- Nguyen, A.; Schulze, H.J. Colloidal Science of Flotation; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Asuri, P.; Karajanagi, S.S.; Dordick, J.S.; Kane, R.S. Directed Assembly of Carbon Nanotubes at Liquid−Liquid Interfaces: Nanoscale Conveyors for Interfacial Biocatalysis. J. Am. Chem. Soc. 2006, 128, 1046–1047. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.S.; Varadaraj, R. Colloid and interface science in the oil industry. Curr. Opin. Colloid Interface Sci. 1999, 1, 535–539. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H.; Bao, G. Physical Principles of Nanoparticle Cellular Endocytosis. ACS Nano 2015, 9, 8655–8671. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E. Lung surfactant-particles at fluid interfaces for toxicity assessments. Curr. Opin. Colloid Interface Sci. 2019, 39, 24–39. [Google Scholar] [CrossRef]
- Hinman, S.S.; McKeating, K.S.; Cheng, Q. Surface Plasmon Resonance: Material and Interface Design for Universal Accessibility. Anal. Chem. 2018, 90, 19–39. [Google Scholar] [CrossRef]
- Brilson, L.J. An Essential Guide to Electronic Material Surfaces and Interfaces; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Hari Babu Vasili, H.B.; Gamino, M.; Gàzquez, J.; Sánchez, F.; Valvidares, M.; Gargiani, P.; Pellegrin, E.; Fontcuberta, J. Magnetoresistance in Hybrid Pt/CoFe2O4 Bilayers Controlled by Competing Spin Accumulation and Interfacial Chemical Reconstruction. ACS Appl. Mater. Interfaces 2018, 10, 12031–12041. [Google Scholar] [CrossRef]
- Ballauf, M. Self-assembly creates 2D materials. Science 2016, 352, 656–657. [Google Scholar] [CrossRef]
- Maestro, A.; Santini, E.; Guzmán, E. Physico-chemical foundations of particle-laden fluid interfaces. Eur. Phys. J. E 2018, 41, 97. [Google Scholar] [CrossRef]
- Maestro, A.; Santini, E.; Zabiegaj, D.; Llamas, S.; Ravera, F.; Liggieri, L.; Ortega, F.; Rubio, R.G.; Guzman, E. Particle and Particle-Surfactant Mixtures at Fluid Interfaces: Assembly, Morphology, and Rheological Description. Adv. Condens. Matter Phys. 2015, 2015, 917516. [Google Scholar] [CrossRef]
- Garbin, V. Collapse mechanisms and extreme deformation of particle-laden interfaces. Curr. Opin. Colloid Interface Sci. 2019, 39, 202–211. [Google Scholar] [CrossRef]
- Garbin, V.; Crocker, J.C.; Stebe, K.J. Nanoparticles at fluid interfaces: Exploiting capping ligands to control adsorption, stability and dynamics. J. Colloid Interface Sci. 2012, 387, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E.; Llamas, S.; Maestro, A.; Fernández-Peña, L.; Akanno, A.; Miller, R.; Ortega, F.; Rubio, R.G. Polymer–surfactant systems in bulk and at fluid interfaces. Adv. Colloid Interface Sci. 2016, 233, 38–64. [Google Scholar] [CrossRef] [PubMed]
- Maestro, A.; Guzmán, E.; Santini, E. Interfacial Rheology of Particle-Laden Interfaces and Its Role in the Stabilization of Dispersed Systems. In Rheology: Principles, Applications and Environmental Impacts; Karpushkin, E., Ed.; Nova Science Publisher, Inc.: New York, NJ, USA, 2015; pp. 1–26. [Google Scholar]
- Mendoza, A.J.; Guzmán, E.; Martínez-Pedrero, F.; Ritacco, H.; Rubio, R.G.; Ortega, F.; Starov, V.M.; Miller, R. Particle laden fluid interfaces: Dynamics and interfacial rheology. Adv. Colloid Interface Sci. 2014, 206, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Maestro, A.; Guzmán, E.; Ortega, F.; Rubio, R.G. Contact angle of micro- and nanoparticles at fluid interfaces. Curr. Opin. Colloid Interface Sci. 2014, 19, 355–367. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E.; Liggieri, L.; Ravera, F.; Loglio, G.; Maestro, A.; Rubio, R.G.; Krägel, J.; Grigoriev, D.; Miller, R. Particle-Surfactant Interaction at Liquid Interfaces. In Colloid and Interface Chemistry for Nanotechnology; Kralchevsky, P., Miller, R., Ravera, F., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 77–109. [Google Scholar]
- Maestro, A. Tailoring the interfacial assembly of colloidal particles by engineering the mechanical properties of the interface. Curr. Opin. Colloid Interface Sci. 2019, 39, 232–250. [Google Scholar] [CrossRef]
- Thijssen, J.H.J.; Vermant, J. Interfacial rheology of model particles at liquid interfaces and its relation to (bicontinuous) Pickering emulsions. J. Phys. Condens. Matter 2017, 30, 02300. [Google Scholar] [CrossRef]
- Dasgupta, S.; Auth, T.; Gompper, G. Nano- and microparticles at fluid and biological interfaces. J. Phys. Condens. Matter 2017, 29, 373003. [Google Scholar] [CrossRef]
- Varga, I.; Campbell, R.A. General Physical Description of the Behavior of Oppositely Charged Polyelectrolyte/Surfactant Mixtures at the Air/Water Interface. Langmuir 2017, 33, 5915–5924. [Google Scholar] [CrossRef]
- Fernandez-Rodriguez, M.A.; Chen, L.; Deming, C.P.; Rodriguez-Valverde, M.A.; Chen, S.; Cabrerizo-Vilchez, M.A.; Hidalgo-Alvarez, R. A simple strategy to improve the interfacial activity of true Janus gold nanoparticles: A shorter hydrophilic capping ligand. Soft Matter 2016, 12, 31–34. [Google Scholar] [CrossRef]
- Fernandez-Rodriguez, M.A.; Ramos, J.; Isa, L.; Rodriguez-Valverde, M.A.; Cabrerizo-Vilchez, M.A.; Hidalgo-Alvarez, R. Interfacial Activity and Contact Angle of Homogeneous, Functionalized, and Janus Nanoparticles at the Water/Decane Interface. Langmuir 2015, 31, 8818–8823. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Rodriguez, M.A.; Song, Y.; Rodríguez-Valverde, M.Á.; Chen, S.; Cabrerizo-Vilchez, M.A.; Hidalgo-Alvarez, R. Comparison of the Interfacial Activity between Homogeneous and Janus Gold Nanoparticles by Pendant Drop Tensiometry. Langmuir 2014, 30, 1799–1804. [Google Scholar] [CrossRef] [PubMed]
- Noskov, B.A.; Bykov, A.G. Dilational rheology of monolayers of nano- and micropaticles at the liquid-fluid interfaces. Curr. Opin. Colloid Interface Sci. 2018, 37, 1–12. [Google Scholar] [CrossRef]
- Yazhgur, P.A.; Noskov, B.A.; Liggieri, L.; Lin, S.Y.; Loglio, G.; Miller, R.; Ravera, F. Dynamic properties of mixed nanoparticle/surfactant adsorption layers. Soft Matter 2013, 9, 3305–3314. [Google Scholar] [CrossRef]
- Maestro, A.; Guzmán, E.; Santini, E.; Ravera, F.; Liggieri, L.; Ortega, F.; Rubio, R.G. Wettability of silica nanoparticle–surfactant nanocomposite interfacial layers. Soft Matter 2012, 8, 837–843. [Google Scholar] [CrossRef]
- Santini, E.; Guzmán, E.; Ravera, F.; Ferrari, M.; Liggieri, L. Properties and structure of interfacial layers formed by hydrophilic silica dispersions and palmitic acid. Phys. Chem. Chem. Phys. 2012, 14, 607–615. [Google Scholar] [CrossRef]
- Liggieri, L.; Santini, E.; Guzmán, E.; Maestro, A.; Ravera, F. Wide-frequency dilational rheology investigation of mixed silica nanoparticle–CTAB interfacial layers. Soft Matter 2011, 7, 7699–7709. [Google Scholar] [CrossRef]
- Zabiegaj, D.; Santini, E.; Guzmán, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Carbon Soot-Ionic Surfactant Mixed Layers at Water/Air Interfaces. J. Nanosci. Nanotechnol. 2015, 15, 3618–3625. [Google Scholar] [CrossRef]
- Zabiegaj, D.; Santini, E.; Guzmán, E.; Ferrari, M.; Liggieri, L.; Buscaglia, V.; Buscaglia, M.T.; Battilana, G.; Ravera, F. Nanoparticle laden interfacial layers and application to foams and solid foams. Colloids Surf. A 2013, 438, 132–140. [Google Scholar] [CrossRef]
- Llamas, S.; Mendoza, A.J.; Guzmán, E.; Ortega, F.; Rubio, R.G. Salt effects on the air/solution interfacial properties of PEO-containing copolymers: Equilibrium, adsorption kinetics and surface rheological behavior. J. Colloid Interface Sci. 2013, 400, 49–58. [Google Scholar] [CrossRef]
- Llamas, S.; Fernández-Peña, L.; Akanno, A.; Guzmán, E.; Ortega, V.; Ortega, F.; Csaky, A.G.; Campbell, R.A.; Rubio, R.G. Towards understanding the behavior of polyelectrolyte–surfactant mixtures at the water/vapor interface closer to technologically-relevant conditions. Phys. Chem. Chem. Phys. 2018, 20, 1395–1407. [Google Scholar] [CrossRef] [PubMed]
- Akanno, A.; Guzmán, E.; Fernández-Peña, L.; Llamas, S.; Ortega, F.; Rubio, R.G. Equilibration of a Polycation–Anionic Surfactant Mixture at the Water/Vapor Interface. Langmuir 2018, 34, 7455–7464. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.; Aksenenko, E.V.; Fainerman, V.B. Dynamic interfacial tension of surfactant solutions. Adv. Colloid Interface Sci. 2017, 247, 115–129. [Google Scholar] [CrossRef] [PubMed]
- Akanno, A.; Guzmán, E.; Ortega, L.F.-P.F.; Rubio, R.G. Surfactant-Like Behavior for the Adsorption of Mixtures of a Polycation and Two Different Zwitterionic Surfactants at theWater/Vapor Interface. Molecules 2019, 24, 3442. [Google Scholar] [CrossRef] [PubMed]
- Fainerman, V.B.; Kovalchuk, V.I.; Lucassen-Reynders, E.H.; Grigoriev, D.O.; Ferri, J.K.; Leser, M.E.; Michel, M.; Miller, R.; Mohwald, H. Surface-Pressure Isotherms of Monolayers Formed by Microsize and Nanosize Particles. Langmuir 2006, 22, 1701–1705. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.; Fainerman, V.B.; Kovalchuk, V.I.; Grigoriev, D.O.; Leser, M.E.; Michel, M. Composite interfacial layers containing micro-size and nano-size particles. Adv. Colloid Interface Sci. 2006, 128–130, 17–26. [Google Scholar] [CrossRef]
- Miller, R.; Fainerman, V.B.; Makievski, A.V.; Kragel, J.; Grigoriev, D.O.; Kazakov, V.N.; Sinyachenko, O.V. Dynamics of protein and mixed proteinr/surfactant adsorption layers at the water/fluid interface. Adv. Colloid Interface Sci. 2000, 86, 39–82. [Google Scholar] [CrossRef]
- Groot, R.; Stoyanov, S. Equation of state of surface-adsorbing colloids. Soft Matter 2011, 6, 1682–1692. [Google Scholar] [CrossRef]
- Mulero, A. (Ed.) Theory and Simulation of Hard-Sphere Fluids and Related System; Springer: Berlin, Germany, 2008. [Google Scholar]
- Deshmukh, O.S.; Maestro, A.; Duits, M.H.G.; van den Ende, D.; Stuart, M.C.; Mugele, F. Equation of state and adsorption dynamics of soft microgel particles at an air–water interface. Soft Matter 2014, 10, 7045–7050. [Google Scholar] [CrossRef]
- Levine, S.; Bowen, B.D.; Partridge, S.J. Stabilization of emulsions by fine particles I. Partitioning of particles between continuous phase and oil/water interface. Colloids Surf. 1989, 38, 325–344. [Google Scholar] [CrossRef]
- Zang, D.Y.; Rio, E.; Delon, G.; Langevin, D.; Wei, B.; Binks, B.P. Influence of the contact angle of silica nanoparticles at the air–water interface on the mechanical properties of the layers composed of these particles. Mol. Phys. 2011, 109, 1057–1066. [Google Scholar] [CrossRef]
- Stocco, A.; Rio, E.; Binks, B.P.; Langevin, D. Aqueous foams stabilized solely by particles. Soft Matter 2011, 7, 1260–1267. [Google Scholar] [CrossRef]
- Herzig, E.M.; White, K.A.; Schofield, A.B.; Poon, W.C.K.; Clegg, P.S. Bicontinuous emulsions stabilized solely by colloidal particles. Nat. Mater. 2007, 6, 966–971. [Google Scholar] [CrossRef] [PubMed]
- Danov, K.D.; Krachevsky, P.A. Capillary forces between particles at a liquid interface: General theoretical approach and interactions between capillary multipoles. Adv. Colloid Interface Sci. 2010, 154, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Zanini, M.; Isa, L. Particle contact angles at fluid interfaces: Pushing the boundary beyond hard uniform spherical colloids. J. Phys. Condens. Matter 2016, 28, 313002. [Google Scholar] [CrossRef]
- Fletcher, P.D.I.; Holt, B.L. Controlled Silanization of Silica Nanoparticles to Stabilize Foams, Climbing Films, and Liquid Marbles. Langmuir 2011, 27, 12869–12876. [Google Scholar] [CrossRef]
- Petcu, C.; Purcar, V.; Spătaru, C.-I.; Alexandrescu, E.; Şomoghi, R.; Trică, B.; Niţu, S.G.; Panaitescu, D.M.; Donescu, D.; Jecu, M.-L. The Influence of New Hydrophobic Silica Nanoparticles on the Surface Properties of the Films Obtained from Bilayer Hybrids. Nanomaterials 2017, 7, 47. [Google Scholar] [CrossRef]
- Guzmán, E.; Ortega, F.; Baghdadli, N.; Cazeneuve, C.; Luengo, G.S.; Rubio, R.G. Adsorption of Conditioning Polymers on Solid Substrates with Different Charge Density. ACS Appl. Mater. Interfaces 2011, 3, 3181–3188. [Google Scholar] [CrossRef]
- Maestro, A.; Bonales, L.J.; Ritacco, H.; Rubio, R.G.; Ortega, F. Effect of the spreading solvent on the three-phase contact angle of microparticles attached at fluid interfaces. Phys. Chem. Chem. Phys. 2010, 12, 14115–14120. [Google Scholar] [CrossRef]
- Bresme, F.; Oettel, M. Nanoparticles at fluid interfaces. J. Phys. Condens. Matter 2007, 19, 413101. [Google Scholar] [CrossRef]
- Bonales, L.J.; Rubio, J.E.F.; Ritacco, H.; Vega, C.; Rubio, R.G.; Ortega, F. Freezing Transition and Interaction Potential in Monolayers of Microparticles at Fluid Interfaces. Langmuir 2011, 27, 3391–3400. [Google Scholar] [CrossRef] [PubMed]
- Parolini, L.; Law, A.D.; Maestro, A.; Martin, D.; Buzza, A.; Cicuta, P. Interaction between colloidal particles on an oil–water interface in dilute and dense phases. J. Phys. Condens. Matter 2015, 27, 194119. [Google Scholar] [CrossRef] [PubMed]
- Zang, D.; Stocco, A.; Langevin, D.; Wei, B.; Binks, B.P. An ellipsometry study of silica nanoparticle layers at the water surface. Phys. Chem. Chem. Phys. 2009, 11, 9522–9529. [Google Scholar] [CrossRef] [PubMed]
- Santini, E.; Krägel, J.; Ravera, F.; Liggieri, L.; Miller, R. Study of the monolayer structure and wettability properties of silica nanoparticles and CTAB using the Langmuir trough technique. Colloids Surf. A 2011, 382, 186–191. [Google Scholar] [CrossRef]
- Bykov, A.G.; Noskov, B.A.; Loglio, G.; Lyadinskaya, V.V.; Miller, R. Dilational surface elasticity of spread monolayers of polystyrene microparticles. Soft Matter 2014, 10, 6499–6505. [Google Scholar] [CrossRef]
- Noskov, B.A.; Yazhgur, P.A.; Liggieri, L.; Lin, S.-Y.; Loglio, G.; Miller, R.; Ravera, F. Dilational rheology of spread and adsorbed layers of silica nanoparticles at the liquid-gas interface. Colloid J. 2014, 76, 127–138. [Google Scholar] [CrossRef]
- Bykov, A.G.; Loglio, G.; Miller, R.; Noskov, B.A. Dilational surface elasticity of monolayers of charged polystyrene nano- and microparticles at liquid/fluid interfaces. Colloids Surf. A 2015, 485, 42–48. [Google Scholar] [CrossRef]
- Bonales, L.J.; Martínez-Pedrero, F.; Rubio, M.A.; Rubio, R.G.; Ortega, F. Phase Behavior of Dense Colloidal Binary Monolayers. Langmuir 2012, 28, 16555–16566. [Google Scholar] [CrossRef]
- Girotto, M.; dos Santos, A.P.; Levin, Y. Interaction of Charged Colloidal Particles at the Air–Water Interface. J. Phys. Chem. B 2016, 120, 5817–5822. [Google Scholar] [CrossRef]
- Bresme, F.; Lehle, H.; Oettel, M. Solvent-mediated interactions between nanoparticles at fluid interfaces. J. Chem. Phys. 2009, 130, 214711. [Google Scholar] [CrossRef]
- Oettel, M.; Dietrich, S. Colloidal Interactions at Fluid Interfaces. Langmuir 2008, 24, 1425–1441. [Google Scholar] [CrossRef] [PubMed]
- Pieranski, P. Two-Dimensional Interfacial Colloidal Crystals. Phys. Rev. Lett. 1980, 45, 569–572. [Google Scholar] [CrossRef]
- Hurd, A.J. The electrostatic interaction between interfacial colloidal particles. J. Phys. A Math. Gen. 1985, 18, L1055–L1060. [Google Scholar] [CrossRef]
- Masschaele, K.; Park, B.J.; Furst, E.M.; Fransaer, J.; Vermant, J. Finite Ion-Size Effects Dominate the Interaction between Charged Colloidal Particles at an Oil-Water Interface. Phys. Rev. Lett. 2010, 105, 048303. [Google Scholar] [CrossRef] [PubMed]
- Jun Park, B.; Vermant, J.; Furst, E.M. Heterogeneity of the electrostatic repulsion between colloids at the oil–water interface. Soft Matter 2010, 6, 5327–5333. [Google Scholar] [CrossRef]
- Birdi, K.S. (Ed.) Handbook of Surface and Colloid Chemistry; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Maestro, A.; Jones, D.; Sánchez de Rojas Candela, C.; Guzman, E.; Duits, M.H.G.; Cicuta, P. Tuning Interfacial Properties and Processes by Controlling the Rheology and Structure of Poly(N-isopropylacrylamide) Particles at Air/Water Interfaces. Langmuir 2018, 34, 7067–7076. [Google Scholar] [CrossRef]
- Maestro, A.; Guzmán, E.; Chuliá, R.; Ortega, F.; Rubio, R.; Miller, R. Fluid to soft-glass transition in a quasi-2D system: Thermodynamic and rheological evidences for a Langmuir monolayer. Phys. Chem. Chem. Phys. 2011, 13, 9534–9549. [Google Scholar] [CrossRef]
- Tabor, R.F.; Grieser, F.; Dagastine, R.R.; Chan, D.Y.C. The hydrophobic force: Measurements and methods. Phys. Chem. Chem. Phys. 2014, 16, 18065–18075. [Google Scholar] [CrossRef]
- Wickman, H.H.; Korley, J.N. Colloid crystal self-organization and dynamics at the air/water interface. Nature 1998, 393, 445–447. [Google Scholar] [CrossRef]
- Orsi, D.; Rimoldi, T.; Guzmán, E.; Liggieri, L.; Ravera, F.; Ruta, B.; Cristofolini, L. Hydrophobic Silica Nanoparticles Induce Gel Phases in Phospholipid Monolayers. Langmuir 2016, 32, 4868–4876. [Google Scholar] [CrossRef]
- Orsi, D.; Guzmán, E.; Liggieri, L.; Ravera, F.; Ruta, B.; Chushkin, Y.; Rimoldi, T.; Cristofolini, L. 2D dynamical arrest transition in a mixed nanoparticle-phospholipid layer studied in real and momentum spaces. Sci. Rep. 2015, 5, 17930. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E.; Orsi, D.; Cristofolini, L.; Liggieri, L.; Ravera, F. Two-Dimensional DPPC Based Emulsion-like Structures Stabilized by Silica Nanoparticles. Langmuir 2014, 30, 11504–11512. [Google Scholar] [CrossRef]
- Loudet, J.-C.; Alsayed, A.M.; Zhang, J.; Yodh, A.G. Capillary Interactions Between Anisotropic Colloidal Particles. Phys. Rev. Lett. 2005, 94, 018301. [Google Scholar] [CrossRef] [PubMed]
- Uppapalli, S.; Zhao, H. The influence of particle size and residual charge on electrostatic interactions between charged colloidal particles at an oil–water interface. Soft Matter 2014, 10, 4555–4560. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Rodriguez, M.A.; Binks, B.P.; Rodriguez-Valverde, M.A.; Cabrerizo-Vilchez, M.A.; Hidalgo-Alvarez, R. Particles adsorbed at various non-aqueous liquid-liquid interfaces. Adv. Colloid Interface Sci. 2017, 247, 208–222. [Google Scholar] [CrossRef]
- Montes Ruiz-Cabello, F.J.; Moazzami-Gudarzi, M.; Elzbieciak-Wodka, M.; Maroni, P.; Labbez, C.; Borkovec, M.; Trefalt, G. Long-ranged and soft interactions between charged colloidal particles induced by multivalent coions. Soft Matter 2015, 11, 1562–1571. [Google Scholar] [CrossRef]
- Botto, L.; Lewandowski, E.P.; Cavallaro, M.; Stebe, K.J. Capillary interactions between anisotropic particles. Soft Matter 2012, 8, 9957–9971. [Google Scholar] [CrossRef]
- Grzelczak, M.; Vermant, J.; Furst, E.M.; Liz-Marzán, L.M. Directed Self-Assembly of Nanoparticles. ACS Nano 2010, 4, 3591–3605. [Google Scholar] [CrossRef]
- Giner-Casares, J.J.; Reguera, J. Directed self-assembly of inorganic nanoparticles at air/liquid interfaces. Nanoscale 2016, 8, 16589–16595. [Google Scholar] [CrossRef]
- Dörr, A.; Hardt, S.; Masoud, H.; Stone, H.A. Drag and diffusion coefficients of a spherical particle attached to a fluid–fluid interface. J. Fluid Mech. 2016, 790, 607–618. [Google Scholar] [CrossRef]
- Erni, P. Deformation modes of complex fluid interfaces. Soft Matter 2011, 7, 7586–7600. [Google Scholar] [CrossRef]
- Maestro, A.; Zaccone, A. Nonaffine deformation and tunable yielding of colloidal assemblies at the air–water interface. Nanoscale 2017, 9, 18343–18351. [Google Scholar] [CrossRef] [PubMed]
- Maestro, A.; Deshmukh, O.S.; Mugele, F.; Langevin, D. Interfacial Assembly of Surfactant-Decorated Nanoparticles: On the Rheological Description of a Colloidal 2D Glass. Langmuir 2015, 31, 6289–6297. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Pedrero, F.; Benet, J.; Rubio, J.E.F.; Sanz, E.; Rubio, R.G.; Ortega, F. Field-induced sublimation in perfect two-dimensional colloidal crystals. Phys. Rev. E 2014, 89, 012306. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, O.S.; van den Ende, D.; Stuart, M.C.; Mugele, F.; Duits, M.H.G. Hard and soft colloids at fluid interfaces: Adsorption, interactions, assembly & rheology. Adv. Colloid Interface Sci. 2015, 222, 215–227. [Google Scholar] [CrossRef] [PubMed]
- Dhont, J.K.G. An Introduction to Dynamics of Colloids; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Bähler, P.T.; Zanini, M.; Morgese, G.; Benetti, E.M.; Isa, L. Immobilization of Colloidal Monolayers at Fluid–Fluid Interfaces. Gels 2016, 2, 19. [Google Scholar] [CrossRef] [PubMed]
- Cristofolini, L.; Orsi, D.; Isa, L. Characterization of the dynamics of interfaces and of interface-dominated systems via spectroscopy and microscopy techniques. Curr. Opin. Colloid Interface Sci. 2018, 37, 13–32. [Google Scholar] [CrossRef]
- Boniello, G.; Blanc, C.; Fedorenko, D.; Medfai, M.; Mbarek, N.B.; In, M.; Gross, M.; Stocco, A.; Nobili, M. Brownian diffusion of a partially wetted colloid. Nat. Mat. 2015, 14, 908–911. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, W.; Fischer, T.M.; Weitz, D.A.; Tong, P. Short-time self-diffusion of nearly hard spheres at an oil-water interface. J. Fluid Mech. 2009, 618, 243–261. [Google Scholar] [CrossRef]
- Cipelletti, L.; Bissig, H.; Trappe, V.; Ballesta, P.; Mazoyer, S. Time-resolved correlation: A new tool for studying temporally heterogeneous dynamics. J. Phys. Condens. Matter 2002, 15, S257–S262. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Dynamic light scattering by non-ergodic media. Physica A 1989, 157, 705–741. [Google Scholar] [CrossRef]
- Mazoyer, S.; Ebert, F.; Maret, G.; Keim, P. Correlation between dynamical heterogeneities, structure and potential-energy distribution in a 2D amorphous solid. Eur. Phys. J. E 2011, 34, 101. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bellour, M.; Skouri, M.; Munch, J.P.; Hébraud, P. Brownian motion of particles embedded in a solution of giant micelles. Eur. Phys. J. E 2002, 8, 431–436. [Google Scholar] [CrossRef] [PubMed]
- Keim, P.; Maret, G.; Herz, U.; von Grünberg, H.H. Harmonic Lattice Behavior of Two-Dimensional Colloidal Crystals. Phys. Rev. Lett. 2004, 92, 215504. [Google Scholar] [CrossRef] [PubMed]
- Liggieri, L.; Miller, R. (Eds.) Interfacial Rheology; Brill: Leiden, The Netherlands, 2010. [Google Scholar]
- Tajuelo, J.; Guzmán, E.; Ortega, F.; Rubio, R.G.; Rubio, M.A. Phase Diagram of Fatty Acid Langmuir Monolayers from Rheological Measurements. Langmuir 2017, 33, 4280–4290. [Google Scholar] [CrossRef] [PubMed]
- Llamas, S.; Guzmán, E.; Akanno, A.; Fernández-Peña, L.; Ortega, F.; Campbell, R.A.; Miller, R.; Rubio, R.G. Study of the Liquid/Vapor Interfacial Properties of Concentrated Polyelectrolyte–Surfactant Mixtures Using Surface Tensiometry and Neutron Reflectometry: Equilibrium, Adsorption Kinetics, and Dilational Rheology. J. Phys. Chem. C 2018, 122, 4419–4427. [Google Scholar] [CrossRef]
- Guzmán, E.; Fernández-Peña, L.; Akanno, A.; Llamas, S.; Ortega, F.; G Rubio, R. Two Different Scenarios for the Equilibration of Polycation—Anionic Solutions at Water–Vapor Interfaces. Coatings 2019, 9, 438. [Google Scholar] [CrossRef]
- Guzman, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Effect of the Incorporation of Nanosized Titanium Dioxide on the Interfacial Properties of 1,2-Dipalmitoyl-sn-glycerol-3-phosphocholine Langmuir Monolayers. Langmuir 2017, 33, 10715–10725. [Google Scholar] [CrossRef]
- Guzman, E.; Santini, E.; Zabiegaj, D.; Ferrari, M.; Liggieri, L.; Ravera, F. Interaction of Carbon Black Particles and Dipalmitoylphosphatidylcholine at the Water/Air Interface: Thermodynamics and Rheology. J. Phys. Chem. C 2015, 119, 26937–26947. [Google Scholar] [CrossRef]
- Guzman, E.; Ferrari, M.; Santini, E.; Liggieri, L.; Ravera, F. Effect of silica nanoparticles on the interfacial properties of a canonical lipid mixture. Colloids Surf. B 2015, 136, 971–980. [Google Scholar] [CrossRef]
- Guzman, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Interfacial Properties of Mixed DPPC-Hydrophobic Fumed Silica Nanoparticle Layers. J. Phys. Chem. C 2015, 119, 21024–21034. [Google Scholar] [CrossRef]
- Guzman, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Mixed DPPC-cholesterol Langmuir monolayers in presence of hydrophilic silica nanoparticles. Colloids Surf. B 2013, 105, 284–293. [Google Scholar] [CrossRef] [PubMed]
- Guzman, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. DPPC-DOPC Langmuir monolayers modified by hydrophilic silica nanoparticles: Phase behaviour, structure and rheology. Colloids Surf. A 2012, 413, 174–183. [Google Scholar] [CrossRef]
- Guzman, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Influence of silica nanoparticles on phase behavior and structural properties of DPPC-Palmitic acid Langmuir monolayers. Colloids Surf. A 2012, 413, 280–287. [Google Scholar] [CrossRef]
- Guzman, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Influence of silica nanoparticles on dilational rheology of DPPC-palmitic acid Langmuir monolayers. Soft Matter 2012, 8, 3938–3948. [Google Scholar] [CrossRef]
- Guzman, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Effect of Hydrophilic and Hydrophobic Nanoparticles on the Surface Pressure Response of DPPC Monolayers. J. Phys. Chem. C 2011, 115, 21715–21722. [Google Scholar] [CrossRef]
- Sanchez-Arribas, N.; Guzman, E.; Lucia, A.; Toloza, A.C.; Velarde, M.G.; Ortega, F.; Rubio, R.G. Environmentally friendly platforms for encapsulation of an essential oil: Fabrication, characterization and application in pests control. Colloids Surf. A 2018, 555, 473–481. [Google Scholar] [CrossRef]
- Ryazantsev, Y.S.; Velarde, M.G.; Guzman, E.; Rubio, R.G.; Ortega, F.; Montoya, J.-J. On the autonomous motion of active drops or bubbles. J. Colloid Interface Sci. 2018, 527, 180–186. [Google Scholar] [CrossRef]
- Ryazantsev, Y.S.; Velarde, M.G.; Rubio, R.G.; Guzman, E.; Ortega, F.; Lopez, P. Thermo- and soluto-capillarity: Passive and active drops. Adv. Colloid Interface Sci. 2017, 247, 52–80. [Google Scholar] [CrossRef]
- Noskov, B.A. Fast adsorption at the liquid-gas interface. Adv. Colloid Interface Sci. 1996, 69, 63–129. [Google Scholar] [CrossRef]
- Bykov, A.G.; Guzmán, E.; Rubio, R.G.; Krycki, M.M.; Milyaeva, O.Y.; Noskov, B.A. Influence of temperature on dynamic surface properties of spread DPPC monolayers in a broad range of surface pressures. Chem. Phys. Lipids 2019, 225, 104812. [Google Scholar] [CrossRef]
- Ravera, F.; Santini, E.; Loglio, G.; Ferrari, M.; Liggieri, L. Effect of Nanoparticles on the Interfacial Properties of Liquid/Liquid and Liquid/Air Surface Layers. J. Phys. Chem. B 2006, 110, 19543–19551. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Liggieri, L.; Loglio, G.; Santini, E.; Zanobini, A. Liquid–liquid interfacial properties of mixed nanoparticle–surfactant systems. Colloids Surf. A 2008, 323, 99–108. [Google Scholar] [CrossRef]
- Kotsmar, C.; Pradines, V.; Alahverdjieva, V.S.; Aksenenko, E.V.; Fainerman, V.B.; Kovalchuk, V.I.; Krägel, J.; Leser, M.E.; Noskov, B.A.; Miller, R. Thermodynamics, adsorption kinetics and rheology of mixed protein–surfactant interfacial layers. Adv. Colloid Interface Sci. 2009, 150, 41–54. [Google Scholar] [CrossRef] [PubMed]
- Safouane, M.; Langevin, D.; Binks, B.P. Effect of Particle Hydrophobicity on the Properties of Silica Particle Layers at the Air−Water Interface. Langmuir 2007, 23, 11546–11553. [Google Scholar] [CrossRef] [PubMed]
- Zahn, K.; Wille, A.; Maret, G.; Sengupta, S.; Nielaba, P. Elastic Properties of 2D Colloidal Crystals from Video Microscopy. Phys. Rev. Lett. 2003, 90, 155506. [Google Scholar] [CrossRef]
- Zang, D.Y.; Rio, E.; Langevin, D.; Wei, B.; Binks, B.P. Viscoelastic properties of silica nanoparticle monolayers at the air-water interface. Eur. Phys. J. E 2010, 31, 125–134. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kawaguchi, M. Surface dilational moduli of latex-particle monolayers spread at air–water interface. J. Colloid Interface Sci. 2013, 390, 147–150. [Google Scholar] [CrossRef]
- del Río, O.I.; Kwok, D.Y.; Wu, R.; Alvarez, J.M.; Neumann, A.W. Contact angle measurements by axisymmetric drop shape analysis and an automated polynomial fit program1This paper represents, in part, the PhD theses of D.Y. Kwok and O.I. del Río.1. Colloids Surf. A 1998, 143, 197–210. [Google Scholar] [CrossRef]
- Cicuta, P.; Stancik, E.J.; Fuller, G.G. Shearing or Compressing a Soft Glass in 2D: Time-Concentration Superposition. Phys. Rev. Lett. 2003, 90, 236101. [Google Scholar] [CrossRef]
- Trappe, V.; Weitz, D.A. Scaling of the Viscoelasticity of Weakly Attractive Particles. Phys. Rev. Lett. 2000, 85, 449–452. [Google Scholar] [CrossRef] [PubMed]
- Reynaert, S.; Moldenaers, P.; Vermant, J. Interfacial rheology of stable and weakly aggregated two-dimensional suspensions. Phys. Chem. Chem. Phys. 2007, 9, 6463–6475. [Google Scholar] [CrossRef] [PubMed]
- Imperiali, L.; Liao, K.-H.; Clasen, C.; Fransaer, J.; Macosko, C.W.; Vermant, J. Interfacial Rheology and Structure of Tiled Graphene Oxide Sheets. Langmuir 2012, 28, 7990–8000. [Google Scholar] [CrossRef] [PubMed]
- Barman, S.; Christopher, G.F. Simultaneous Interfacial Rheology and Microstructure Measurement of Densely Aggregated Particle Laden Interfaces Using a Modified Double Wall Ring Interfacial Rheometer. Langmuir 2014, 30, 9752–9760. [Google Scholar] [CrossRef] [PubMed]
- Madivala, B.; Fransaer, J.; Vermant, J. Self-Assembly and Rheology of Ellipsoidal Particles at Interfaces. Langmuir 2009, 25, 2718–2728. [Google Scholar] [CrossRef]
- Brown, E.; Zhang, H.; Forman, N.A.; Maynor, B.W.; Betts, D.E.; DeSimone, J.M.; Jaeger, H.M. Shear thickening and jamming in densely packed suspensions of different particle shapes. Phys. Rev. E 2011, 84, 031408. [Google Scholar] [CrossRef]
- Wilson, H.J.; Davis, R.H. Shear stress of a monolayer of rough spheres. J. Fluid Mech. 2002, 452, 425–441. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maestro, A.; Guzmán, E. Colloids at Fluid Interfaces. Processes 2019, 7, 942. https://doi.org/10.3390/pr7120942
Maestro A, Guzmán E. Colloids at Fluid Interfaces. Processes. 2019; 7(12):942. https://doi.org/10.3390/pr7120942
Chicago/Turabian StyleMaestro, Armando, and Eduardo Guzmán. 2019. "Colloids at Fluid Interfaces" Processes 7, no. 12: 942. https://doi.org/10.3390/pr7120942
APA StyleMaestro, A., & Guzmán, E. (2019). Colloids at Fluid Interfaces. Processes, 7(12), 942. https://doi.org/10.3390/pr7120942





