Incremental Parameter Estimation under Rank-Deficient Measurement Conditions
Abstract
:1. Introduction
2. Notation and Symbols
3. Methods
3.1. System Representation and Extents
3.1.1. Dynamic Model in Terms of Numbers of Moles
3.1.2. Dynamic Model in Terms of Extents
3.2. Labeling Extents
3.2.1. Definitions
- The rth extent is labeled sensed if the measurements are affected by through the measurement Equation (7), that is, if has at least one non-zero element.
- The rth extent is labeled observable if (i) it is sensed ( not null); and (ii) the change in the measurements caused by a change in can be unambiguously attributed to the change in that extent, that is, is independent of all other column vectors in .
3.2.2. Labeling Procedure
- (a)
- Label the extents corresponding to zero columns in as non-sensed and use the vector to identify their positions in . Label the remaining extents as sensed and use the vector to identify their positions in .
- (b)
- Find all rows in with a single non-zero element and find the column positions of these non-zero elements. Label the extents corresponding to these column positions as observable and use the vector to identify their positions in . These extents are observable because one can compute a unique value based on the available information (measurements, extent-based measurement matrix, and initial conditions).
- (c)
- Label the extents that are sensed but not observable as ambiguous. These extents are ambiguous because one cannot compute a unique value based on the available information. The vector is used to identify their positions in .
3.2.3. Practical Cases
- Full-rank extent-based measurement matrix (). This occurs when there are at least as many measurements as reactions () and the matrix is full column rank. As a result, , , and . This is the most frequently studied case, e.g., in [5,6,7]. This case enables computing unique values for the R extents by means of a linear transformation [5], thus allowing the estimation of kinetic parameters for each reaction rate model individually.
- Rank-deficient measurement matrix (). If , for example because there are fewer measurements than reactions (), it is no longer possible to compute all R extents from M measurements without additional information such as an established kinetic model. One can distinguish two situations within this case:
- (a)
- No ambiguity (). In this case, and . As shown in [8], it is possible in this case to implement efficient parameter estimation by identifying subsystems of the complete model that include a subset of the kinetic rate laws and their parameters.
- (b)
- Ambiguity present (). This situation results in . For this case, no generally applicable method for incremental parameter estimation is available until now.
3.3. Observable and Unobservable Extent Directions
3.3.1. Factorization of
- is obtained by selecting the non-zero rows in ,
- is the matrix composed of the columns of corresponding to the column positions of the first non-zero elements in the rows of .
3.3.2. Definition of Observable and Unobservable Extent Directions
3.4. Observable Extents and Extent Directions
3.5. Unobservable Extents and Extent Directions
3.6. System Partitioning
- The size of each parameter subset should be as small as possible.
- The estimates in the jth parameter subset can be computed without consideration of any other parameter subset , .
- Each parameter in appears in at most one of the parameter subsets .
3.6.1. Step 1—Model Reformulation
- (a)
- Express as a function of andThe vector is now replaced with the right-hand side of (26). As a result, the above system becomes:
- (b)
- State augmentation
- (c)
- Interpolation of the observable extents and extent directionsTo increase the efficiency of system partitioning, it is useful to account for the fact that the observable extents and extent directions can be expressed in terms of measurements. However, since the observable extents and extent directions are only known at H discrete measurement points, their values always need to be obtained via interpolation. In this work, we apply piece-wise linear interpolation as follows:with which the system (32) and (33) becomes:
3.6.2. Step 2—Graph-Based System Partitioning
- (a)
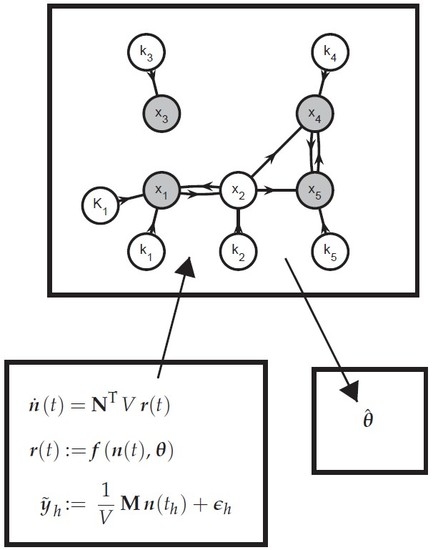
- Create a graphOne creates a directed graph with a vertex for every state variable in and every parameter in . Hence, this graph has vertices. A directed arc is added from vertex v to vertex w if the vth element of appears in the right-hand side of the wth equation in (35) and (36) (, ). This graph represents the information flow for simulating (35) and (36). Additional arcs and vertices may be added to describe the influence of known inputs and the links between extents and measured variables. For system partitioning, this is however unnecessary and omitted for clarity.
- (b)
- Extents predicted from measurements or simulationThe simultaneous approach uses a complete model of the reaction system to predict the extents (or concentrations) via simulation. If one wants to partition the reaction system into small groups of reactions, only the extents belonging to a given group can be generated via the simulation of that group. The other extents that enter the rate laws must be provided by the user as quantities known from measurements.That information can be included in the graph by annotating the various arcs. The arcs that originate at a vertex corresponding to an observable extent or an observable extent direction are labeled observation arcs, considering that observable extent or an observable extent direction can be replaced with their measured values (34). They are visualized as dashed-line arrows. The remaining arcs are labeled simulation arcs and visualized as solid-line arrows. The observation arcs represent the idea that the elements of can be regarded as known inputs for simulating (35) and (36).
- (c)
- Subgraph selectionIdentify the J subgraphs consisting of arcs and vertices in on directed paths that (i) lead to a vertex representing an observable extent or an observable extent direction; and (ii) consist of simulation arcs only. The selected vertices represent an -dimensional vector of extents , a -dimensional vector of directions , and a -dimensional vector of parameters . The positions of in are given by the vector so that:and the selection matrices and are defined so that:
- (d)
- Add observation arcs and verticesFor every graph , add (i) the observation arcs that have a target vertex belonging to and (ii) the source vertices of the added observation arcs. These added source vertices represent the minimal subset of interpolants in (34) that are required to simulate and and are referred to as . This means that the graph now represents all information required to simulate the observable extents and the observable extent directions . Accordingly, one can rewrite the jth equation subsystem as:
3.7. Parameter Estimation Methods
3.7.1. Simultaneous Parameter Estimation
3.7.2. Incremental Parameter Estimation
- (a)
- Modification A: Removing correlation terms. Let and define the -dimensional vector of observable extents and extent directions . This vector includes all observable extents , whose positions in are given by the vector , and all observable extent directions in Subsystem j. We further define the matrix so that:The -dimensional vector is then defined by selecting the elements of as:where the vector gives the positions of in . Now define the residuals associated with subsystem j:This way, the objective function defined above can be reformulated as:and can subsequently approximated with :with . This first modification results in:
- (b)
- Modification B: Separation of problem into J smaller problems . An approximation to problem is now obtained by optimizing each of the J terms in (54) separately and simulating the values of with (43) and (44). We refer to each problem as :Problemsubject toThe most important feature of problems , is that each of them involves only a small number of parameters . Please note that the approximation of problem by this set of problems is perfect in the special case where the right-hand sides (56) do not involve interpolated extents, that is, if the vectors () are empty. Another error, named Type B approximation error, is introduced when this is not the case.
3.8. Implementation
4. Results
4.1. Simulation Study
4.1.1. Reaction System
4.1.2. Dynamic Model in Terms of Numbers of Moles
4.1.3. Scenario A
- non-sensed extent, ,
- observable extents, ,
- ambiguous extents, ,
4.1.4. Scenario B
- non-sensed extents, ,
- observable extents, ,
- ambiguous extents.
4.1.5. Scenario C
- non-sensed extents, .
- observable extents, .
- ambiguous extents.
4.1.6. Scenario D
- non-sensed extents,
- observable extents,
- ambiguous extents, .
4.1.7. Scenario E
- non-sensed extents,
- observable extents, ,
- ambiguous extents.
4.2. Experimental Study
- non-sensed extents,
- observable extents, ,
- ambiguous extents, ,
5. Discussion
5.1. Generalized Framework for Extent Computation
5.2. Optimal System Partitioning
5.3. New Opportunities
- (a)
- Identifiability analysis. While not a core objective of this work, it has been shown that the graph partitioning method can help identify unidentifiable parameters. Given that this labeling is based on a model reformulation and does not depend on the temporal resolution or quality of the collected measurements, it follows that the method identifies structurally unidentifiable parameters. Unlike other methods [27], the proposed approach does not require symbolic differentiation. It remains to be explored whether this can also be used to positively identify structurally identifiable parameters. For a discussion on the evaluation and use of indicators of structural and practical parameter identifiability we refer to [28].
- (b)
- Soft-sensing. The appearance of observable directions among the ambiguous extents is closely related to the concepts of observability and detectability in the context of state estimation [29]. Note however that the observability labels in this work are based on the stoichiometric balances and measurement equations alone, thus excluding the dynamic model. At the same time, it is suspected that the extents corresponding to vertices that are not on directed paths to vertices representing observable extents or extent directions can be labeled as structurally unobservable, again observing that the exact timing and quality of the measurements does not play any role in this labeling. Similarly to the identifiability analysis discussed above, such an approach would not rely on symbolic differentiation. Whether this can be used to unambiguously determine observability and detectability for all model states remains to be studied.
- (c)
- Experimental design. The labeling of extents and directions as observable or unobservable suggests that experimental design may be used to optimize the selection of measured variables. A method to do so has been applied in [30] to enumerate all Pareto-optimal flow sensor layouts in wastewater treatment plants. In [31], symbolic computation enabled the identification of optimal experimental designs. Similar approaches could be applied as a measurement selection method for metabolic flux analysis and the monitoring of complex systems.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rieger, L.; Gillot, S.; Langergraber, G.; Ohtsuki, T.; Shaw, A.; Takács, I.; Winkler, S. Guidelines for Using Activated Sludge Models. IWA Task Group on Good Modelling Practice. IWA Scientific and Technical Report; IWA Publishing: London, UK, 2012. [Google Scholar]
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Bhatt, N.; Amrhein, M.; Bonvin, D. Incremental identification of reaction and mass-transfer kinetics using the concept of extents. Ind. Eng. Chem. Res. 2011, 50, 12960–12974. [Google Scholar] [CrossRef]
- Bhatt, N.; Kerimoglu, N.; Amrhein, M.; Marquardt, W.; Bonvin, D. Incremental identification of reaction systems—A comparison between rate-based and extent-based approaches. Chem. Eng. Sci. 2012, 83, 24–38. [Google Scholar] [CrossRef]
- Rodrigues, D.; Srinivasan, S.; Billeter, J.; Bonvin, D. Variant and invariant states for chemical reaction systems. Comput. Chem. Eng. 2015, 73, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Masˇić, A.; Srinivasan, S.; Billeter, J.; Bonvin, D.; Villez, K. Identification of biokinetic models using the concept of extents. Environ. Sci. Technol. 2017, 51, 7520–7531. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, S.; Billeter, J.; Narasimhan, S.; Bonvin, D. Data reconciliation for chemical reaction systems using vessel extents and shape constraints. Comput. Chem. Eng. 2017, 101, 44–58. [Google Scholar] [CrossRef]
- Masˇić, A.; Billeter, J.; Bonvin, D.; Villez, K. Extent computation under rank-deficient conditions. IFAC-PapersOnLine 2017, 50, 3929–3934. [Google Scholar] [CrossRef] [Green Version]
- Kretsovalis, A.; Mah, R.S.H. Observability and redundancy classification in multicomponent process networks. AIChE J. 1987, 33, 70–82. [Google Scholar] [CrossRef]
- Crowe, C.M. Observability and redundancy of process data for steady state reconciliation. Chem. Eng. Sci. 1989, 44, 2909–2917. [Google Scholar] [CrossRef]
- Fuguitt, R.E.; Hawkins, J.E. Rate of the thermal isomerization of α-Pinene in the liquid phase1. J. Am. Chem. Soc. 1947, 69, 319–322. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; MacGregor, J.F.; Erjavec, J. Some problems associated with the analysis of multiresponse data. Technometrics 1973, 15, 33–51. [Google Scholar] [CrossRef]
- Tjoa, I.B.; Biegler, L.T. Simultaneous solution and optimization strategies for parameter estimation of differential-algebraic equation systems. Ind. Eng. Chem. Res. 1991, 30, 376–385. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, M.; Egea, J.A.; Banga, J.R. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinform. 2006, 2006, 483. [Google Scholar]
- Brunel, N.J.; Clairon, Q. A tracking approach to parameter estimation in linear ordinary differential equations. Electr. J. Stat. 2015, 9, 2903–2949. [Google Scholar] [CrossRef] [Green Version]
- Dattner, I.; Gugushvili, S. Application of one-step method to parameter estimation in ODE models. Stat. Neerl. 2018, 72, 126–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonvin, D.; Rippin, D.W.T. Target factor analysis for the identification of stoichiometric models. Chem. Eng. Sci. 1990, 45, 3417–3426. [Google Scholar] [CrossRef]
- Sahlodin, A.M.; Chachuat, B. Convex/concave relaxations of parametric ODEs using Taylor models. Comput. Chem. Eng. 2011, 35, 844–857. [Google Scholar] [CrossRef]
- Masˇić, A.; Udert, K.; Villez, K. Global parameter optimization for biokinetic modeling of simple batch experiments. Environ. Model. Softw. 2016, 85, 356–373. [Google Scholar] [CrossRef]
- Rodrigues, D.; Billeter, J.; Bonvin, D. Maximum-likelihood estimation of kinetic parameters via the extent-based incremental approach. Comput. Chem. Eng. 2018. [Google Scholar] [CrossRef]
- Billeter, J.; Rodrigues, D.; Srinivasan, S.; Amrhein, M.; Bonvin, D. On decoupling rate processes in chemical reaction systems—Methods and applications. Comput. Chem. Eng. 2017, 114, 296–305. [Google Scholar] [CrossRef]
- Srinivasan, S.; Billeter, J.; Bonvin, D. Identification of multiphase reaction systems with instantaneous equilibria. Ind. Eng. Chem. Res. 2016, 29, 8034–8045. [Google Scholar] [CrossRef]
- Rodrigues, D.; Billeter, J.; Bonvin, D. Generalization of the concept of extents to distributed reaction systems. Chem. Eng. Sci. 2017, 171, 558–575. [Google Scholar] [CrossRef]
- Aldroubi, A.; Sekmen, A. Reduced row echelon form and non-linear approximation for subspace segmentation and high-dimensional data clustering. Appl. Comput. Harmon. Anal. 2014, 37, 271–287. [Google Scholar] [CrossRef]
- Vidal, R. Subspace clustering. IEEE Signal Process. Mag. 2011, 28, 52–68. [Google Scholar] [CrossRef]
- Billeter, J.; Bonvin, D.; Villez, K. Extent-Based Model Identication under Incomplete Observability Conditions; Technical Report No. 6, v3.0; Eawag: Dübendorf, Switzerland, 2018. [Google Scholar]
- Petersen, B.; Gernaey, K.; Devisscher, M.; Dochain, D.; Vanrolleghem, P.A. A simplified method to assess structurally identifiable parameters in Monod-based activated sludge models. Water Res. 2003, 37, 2893–2904. [Google Scholar] [CrossRef]
- Bonvin, D.; Georgakis, C.; Pantelides, C.C.; Barolo, M.; Grover, M.A.; Rodrigues, D.; Schneider, R.; Dochain, D. Linking models and experiments. Ind. Eng. Chem. Res. 2016, 55, 6891–6903. [Google Scholar] [CrossRef]
- Sontag, E.D. Mathematical Control Theory: Deterministic Finite Dimensional Systems; Springer Science & Business Media: Berlin, Germany, 2013; Volume 6. [Google Scholar]
- Villez, K.; Vanrolleghem, P.A.; Corominas, L. Optimal flow sensor placement on wastewater treatment plants. Water Res. 2016, 101, 75–83. [Google Scholar] [CrossRef]
- Billeter, J.; Neuhold, Y.M.; Hungerbuehler, K. Systematic prediction of linear dependencies in the concentration profiles and implications on the kinetic hard-modelling of spectroscopic data. Chemom. Intell. Lab. Syst. 2009, 95, 170–187. [Google Scholar] [CrossRef] [Green Version]












| Symbol | Description | Dimensions |
|---|---|---|
| Measurement error at time | ||
| Kinetic parameters (in subsystem j) | ||
| , | Selection matrix | , |
| Number of observable extent directions (in system j, interpolated in system j) | ||
| Number of unobservable extent directions | ||
| Number of extents and observable extent directions | ||
| Measurement error variance-covariance matrix | ||
| Time (integrand) | ||
| Estimation error variance-covariance matrix | ||
| Extents and observable extent directions | ||
| Observable extent directions (in subsystem j) | ||
| Observable extents and extent directions (in subsystem j) | ||
| Computed observable extents and extent directions (in subsystem j) | ||
| Interpolated observable extents and extent directions (in subsystem j) | ||
| Unobservable extent directions | ||
| Unobservable extents and extent directions | ||
| Number of observable extents and extent directions (in subsystem j) | ||
| Indices of ambiguous extents | ||
| Reduced row echelon form of | ||
| Model prediction residuals at (in subsystem j) | ||
| Indices of computed extents and extent directions simulated by subsystem j | ||
| Information flow graph (for subsystem j) | ||
| Rate expressions (in subsystem j) | ||
| Extent-based measurement matrix | ||
| Measurement matrix for the observable extent directions/observable extents and extent directions | ||
| H | Number of measurements | |
| h | Measurement sample index | |
| i | Subsystem index | |
| J | Number of subsystems | |
| Indices of extents in subsystem j | ||
| j | Subsystem index | |
| Species-based measurement matrix | ||
| M | Number of measurement samples | |
| Stoichiometric matrix | ||
| Extent and extent direction-based stoichiometric matrices | A/ | |
| Indices of non-sensed extents | ||
| Number of moles (at time ) | ||
| Indices of observable extents (in subsystem j) | ||
| Projection matrix | ||
| Objective function | ||
| Number of reactions (in subsystem j, ambiguous/non-sensed/ observable/observable in subsystem j/interpolated in subsystem j/sensed) | ||
| Reaction rates | ||
| r | Reaction index | |
| S | Number of species | |
| Indices of sensed extents | ||
| T () | Number of parameters (in subsystem j) | |
| Time (of measurement sample h) | ||
| , | Mixing matrix | |
| Direction matrix for observable/unobservable direction directions | ||
| V | Reactor volume | |
| Weight matrix (for subsystem j) | ||
| Extents (in subsystem j, of reaction r) | ||
| Noise-free measurements (at time , ) | ||
| Measurements in sample h |
| Name | Unit | True Value | ||||
|---|---|---|---|---|---|---|
| WRMSR | − |
| Name | Unit | ||||
|---|---|---|---|---|---|
| 0.213 | 0.214 | 0.213 | |||
| 0.107 | 0.106 | 0.107 | |||
| 0.074 | 0.074 | 0.074 | |||
| 0.989 | 1.037 | 0.989 | |||
| 0.144 | 0.148 | 0.144 | |||
| WRMSR | − |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villez, K.; Billeter, J.; Bonvin, D. Incremental Parameter Estimation under Rank-Deficient Measurement Conditions. Processes 2019, 7, 75. https://doi.org/10.3390/pr7020075
Villez K, Billeter J, Bonvin D. Incremental Parameter Estimation under Rank-Deficient Measurement Conditions. Processes. 2019; 7(2):75. https://doi.org/10.3390/pr7020075
Chicago/Turabian StyleVillez, Kris, Julien Billeter, and Dominique Bonvin. 2019. "Incremental Parameter Estimation under Rank-Deficient Measurement Conditions" Processes 7, no. 2: 75. https://doi.org/10.3390/pr7020075
APA StyleVillez, K., Billeter, J., & Bonvin, D. (2019). Incremental Parameter Estimation under Rank-Deficient Measurement Conditions. Processes, 7(2), 75. https://doi.org/10.3390/pr7020075