Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency
Abstract
:1. Introduction
2. Materials and Methods
2.1. Air-Core-Liquid-Ring Atomizers
2.2. Spray Test Rig
2.3. Droplet Size Measurement
2.4. Calculations and Statistical Analysis
3. Results and Discussion
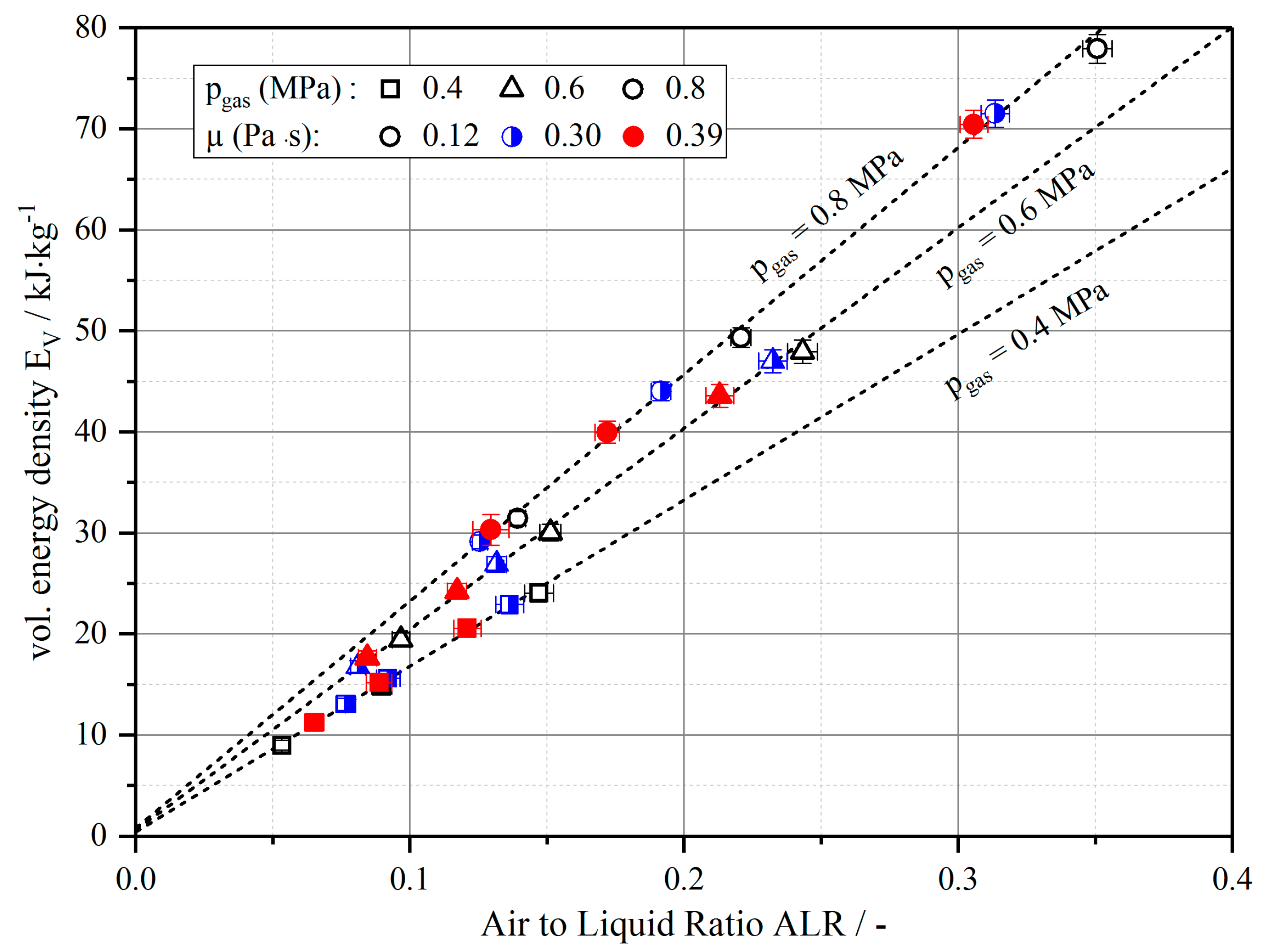
3.1. Correlation between Volumetric Energy Density (EV) and Air-to-Liquid Ratio (ALR) of Applied Processing Conditions
3.2. Droplet Sizes in Dependency of EV and ALR
3.3. Influence of Atomizer Scale Up on Atomization Efficiency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lefebvre, A.H. Atomization and Sprays; Hemisphere Pub. Corp: Philadelphia, PA, USA, 1989; ISBN 0-89116-603-3. [Google Scholar]
- Ashgriz, N. (Ed.) Handbook of Atomization and Sprays; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-7263-7. [Google Scholar]
- Masters, K. Spray Drying in Practice; SprayDryConsult International ApS: Charlottenlund, Denmark, 2002; ISBN 87-986606-08-3. [Google Scholar]
- Mujumdar, A.S. (Ed.) Handbook of Industrial Drying, 4th ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Bayvel, L.P.; Orzechowski, Z. Liquid Atomization; Taylor & Francis: Washington, DC, USA, 1993; ISBN 9780891169598. [Google Scholar]
- Lefebvre, A.H. Airblast Atomization. Prog. Energy Combust. Sci. 1980, 6, 233–261. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Energy Considerations in Twin-Fluid Atomization. J. Eng. Power-Trans. ASME 1992, 114, 89–96. [Google Scholar] [CrossRef]
- Karnawat, J.; Kushari, A. Controlled atomization using a twin-fluid swirl atomizer. Exp. Fluids 2006, 41, 649–663. [Google Scholar] [CrossRef]
- Omer, K.; Ashgriz, N. Spray Nozzles. In Handbook of Atomization and Sprays; Ashgriz, N., Ed.; Springer: New York, NY, USA, 2011; pp. 497–597. ISBN 978-1-4419-7263-7. [Google Scholar]
- Rizk, N.K.; Lefebvre, A.H. The Influence of Liquid-Film Thickness on Airblast Atomization. J. Eng. Power-Trans. ASME 1980, 102, 706–710. [Google Scholar] [CrossRef]
- Rizkalla, A.A.; Lefebvre, A.H. The Influence of Air and Liquid Properties on Airblast Atomization. J. Fluids Eng. 1975, 97, 316–320. [Google Scholar] [CrossRef]
- Jasuja, A.K. Atomization of Crude and Residual Fuel Oils. J. Eng. Power 1979, 101, 250–258. [Google Scholar] [CrossRef]
- Harari, R.; Sher, E. Optimization of a plain jet atomizer. At. Sprays 1997, 7, 97–113. [Google Scholar] [CrossRef]
- Mulhem, B.; Schulte, G.; Fritsching, U. Solid–liquid separation in suspension atomization. Chem. Eng. Sci. 2006, 61, 2582–2589. [Google Scholar] [CrossRef]
- Mlkvik, M.; Stähle, P.; Schuchmann, H.P.; Gaukel, V.; Jedelsky, J.; Jicha, M. Twin-fluid atomization of viscous liquids: The effect of atomizer construction on breakup process, spray stability and droplet size. Int. J. Multiph. Flow 2015, 19–31. [Google Scholar] [CrossRef]
- Buckner, H.J.; Sojka, P.E. Effervescent Atomization of High-Viscosity Fluids: Part I. Newtonian Liquids. At. Sprays 1991, 1, 239–252. [Google Scholar] [CrossRef]
- Jedelsky, J.; Jicha, M.; Slama, J.; Otahal, J. Development of an Effervescent Atomizer for Industrial Burners. Energy Fuels 2009, 23, 6121–6130. [Google Scholar] [CrossRef]
- Stähle, P.; Gaukel, V.; Schuchmann, H.P. Investigation on the Applicability of the Effervescent Atomizer in Spray Drying of Foods: Influence of Liquid Viscosity on Nozzle Internal Two-Phase Flow and Spray Characteristics. J. Food Process Eng. 2015, 38, 474–487. [Google Scholar] [CrossRef]
- Schröder, J.; Kraus, S.; Rocha, B.B.; Gaukel, V.; Schuchmann, H.P. Characterization of gelatinized corn starch suspensions and resulting drop size distributions after effervescent atomization. J. Food Eng. 2011, 105, 656–662. [Google Scholar] [CrossRef]
- Sovani, S.D.; Sojka, P.E.; Lefebvre, A.H. Effervescent atomization. Prog. Energy Combust. Sci. 2001, 27, 483–521. [Google Scholar] [CrossRef]
- Mlkvik, M.; Stähle, P.; Gaukel, V.; Zaremba, M.; Jedelský, J.; Jícha, M.; Dančová, P.; Vít, T. Performance of Twin-Fluid Atomizers for Atomization of Viscous Solutions. EPJ Web Conf. 2015, 92, 2052. [Google Scholar] [CrossRef] [Green Version]
- Zaremba, M.; Weiß, L.; Malý, M.; Wensing, M.; Jedelský, J.; Jícha, M. Low-pressure twin-fluid atomization: Effect of mixing process on spray formation. Int. J. Multiph. Flow 2017, 89, 277–289. [Google Scholar] [CrossRef]
- Zaremba, M.; Kozák, J.; Malý, M.; Weiß, L.; Rudolf, P.; Jedelský, J.; Jícha, M. An experimental analysis of the spraying processes in improved design of effervescent atomizer. Int. J. Multiph. Flow 2018, 103, 1–15. [Google Scholar] [CrossRef]
- Chin, J.S. Effervescent atomization and internal mixing air assist atomization. Int. J. Turbo Jet Engines 1995, 12, 119–127. [Google Scholar] [CrossRef]
- Shepard, T.G. Bubble Size Effect on Effervescent Atomization. Ph.D. Dissertation, University of Minnesota, Minneapolis, MN, USA, 2011. [Google Scholar]
- Stähle, P.; Gaukel, V.; Schuchmann, H.P. Influence of feed viscosity on the two-phase flow inside the exit orifice of an effervescent atomizer and on resulting spray characteristics. Food Res. Int. 2015, 77, 55–62. [Google Scholar] [CrossRef]
- Stähle, P.; Gaukel, V.; Schuchmann, H.P. Comparison of an Effervescent Nozzle and a Proposed Air-Core-Liquid-Ring (ACLR) Nozzle for Atomization of Viscous Food Liquids at Low Air Consumption. J. Food Process Eng. 2017, 40. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, S.Y. Dependence of spraying performance on the internal flow pattern in effervescent atomizers. At. Sprays 2001, 11, 735–756. [Google Scholar]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Spray performance and steadiness of an effervescent atomizer and an air-core-liquid-ring atomizer for application in spray drying processes of highly concentrated feeds. Chem. Eng. Process.-Process Intensif. 2018, 96–102. [Google Scholar] [CrossRef]
- Karbstein, H.P.; Schubert, H. Developments in the Continuous Mechanical Production of O/W-Macro-Emulsions. Chem. Eng. Process. 1995, 34, 205–211. [Google Scholar] [CrossRef]
- Schuchmann, H.P.; Köhler, K.; Emin, M.A.; Schubert, H. Food Process Engineering Research and Innovation in a Fast Changing World: Paradigms/Case Studies. In Advances in Food Process Engineering Research and Applications; Yanniotis, S., Taoukis, P., Stoforos, N.G., Eds.; Springer: Boston, MA, USA, 2013; pp. 41–59. ISBN 978-1-4614-7905-5. [Google Scholar]
- Stähle, P.; Schuchmann, H.P.; Gaukel, V. Performance and Efficiency of Pressure-Swirl and Twin-Fluid Nozzles Spraying Food Liquids with Varying Viscosity. J. Food Process Eng. 2017, 40. [Google Scholar] [CrossRef]
- Walzel, P. Efficiency of the energy transformation at spray systems. In Proceedings of the 11th ILASS 1997, Florence, Italy, 9–11 July 1997. [Google Scholar]
- Kleinhans, A.; Georgieva, K.; Wagner, M.; Gaukel, V.; Schuchmann, H.P. On the characterization of spray unsteadiness and its influence on oil drop breakup during effervescent atomization. Chem. Eng. Process. Process Intensif. 2016, 104, 212–218. [Google Scholar] [CrossRef]
- Kleinhans, A.; Hornfischer, B.; Gaukel, V.; Schuchmann, H.P. Influence of viscosity ratio and initial oil drop size on the oil drop breakup during effervescent atomization. Chem. Eng. Process. Process Intensif. 2016, 109, 149–157. [Google Scholar] [CrossRef]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Pneumatic atomization: Beam steering correction in laser diffraction measurements of spray droplet size distributions. Appl. Sci. 2018, 8, 1738. [Google Scholar] [CrossRef]
- Konstantinov, D.; Marsh, R.; Bowen, P.J.; Crayford, A. Effervescent atomization for industrial energy-technology review. At. Sprays 2010, 20, 525–552. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Twin-fluid atomization: Factors influencing mean drop size. At. Sprays 1992, 2, 101–119. [Google Scholar] [CrossRef]



| cMD (% d.b.) | µ (Pa·s) | ur(µ) (%) | σ (N·m−1) | ur(σ) (%) | ρ (kg·m−3) | ur(ρ) (%) | RI (-) | ur(RI) (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 0.12 | 9.79 | 0.073 | 0.02 | 1175 | 0.02 | 1.40 | 0.07 |
| 45 | 0.30 | 5.83 | 0.074 | 0.06 | 1206 | 0.03 | 1.41 | 0.06 |
| 47 | 0.39 | 3.79 | 0.074 | 0.05 | 1218 | 0.06 | 1.42 | 0.04 |
| Dimension | Atomizer 1 | Atomizer 2 |
|---|---|---|
| A | 1.5 mm | 1.5 mm |
| B | 2.4 mm | 2.4 mm |
| C | 1.5 mm | 2.5 mm |
| D | 1.5 mm | 3 mm |
| Atomizer 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| cMD | µ | pgas | QL | Qgas | ur(Qgas) | ALR | ur(ALR) | EV | ur(EV) |
| (% d.b.) | (Pa∙s) | (Mpa) | (L·h−1) | (Nm3·h−1) | (%) | (-) | (%) | (kJ·L−1) | (%) |
| 0.4 | 21 | 2.9 | 2.01 | 0.15 | 3.57 | 24.1 | 3.72 | ||
| 30 | 2.5 | 2.34 | 0.09 | 4.08 | 14.8 | 4.15 | |||
| 40 | 1.9 | 2.99 | 0.05 | 5.40 | 9.0 | 5.30 | |||
| 21 | 4.7 | 2.13 | 0.24 | 2.22 | 47.9 | 2.45 | |||
| 40 | 0.12 | 0.6 | 30 | 4.1 | 1.40 | 0.15 | 2.55 | 30.0 | 2.72 |
| 40 | 3.5 | 2.86 | 0.10 | 3.37 | 19.4 | 3.44 | |||
| 21 | 6.8 | 2.55 | 0.35 | 1.52 | 77.9 | 1.81 | |||
| 0.8 | 30 | 6.0 | 0.96 | 0.22 | 1.68 | 49.3 | 1.93 | ||
| 40 | 5.1 | 1.96 | 0.14 | 1.99 | 31.4 | 2.18 | |||
| 21 | 2.7 | 0.00 | 0.14 | 3.72 | 22.9 | 3.86 | |||
| 0.4 | 25 | 2.1 | 2.71 | 0.09 | 4.69 | 15.6 | 4.73 | ||
| 30 | 2.2 | 2.66 | 0.08 | 4.62 | 13.0 | 4.64 | |||
| 21 | 4.6 | 1.26 | 0.23 | 2.21 | 47.0 | 2.44 | |||
| 45 | 0.30 | 0.6 | 30 | 3.7 | 1.55 | 0.13 | 2.69 | 26.9 | 2.84 |
| 40 | 3.0 | 1.90 | 0.08 | 3.31 | 16.8 | 3.37 | |||
| 21 | 6.2 | 2.48 | 0.31 | 1.65 | 71.5 | 1.92 | |||
| 0.8 | 30 | 5.5 | 2.11 | 0.19 | 1.85 | 44.0 | 2.07 | ||
| 40 | 4.7 | 1.24 | 0.13 | 2.15 | 29.1 | 2.31 | |||
| 21 | 2.4 | 2.37 | 0.12 | 4.13 | 20.6 | 4.23 | |||
| 0.4 | 23 | 1.9 | 2.99 | 0.09 | 5.18 | 15.2 | 5.19 | ||
| 30 | 1.9 | 3.09 | 0.07 | 5.37 | 11.3 | 5.32 | |||
| 21 | 4.2 | 1.36 | 0.21 | 2.38 | 43.6 | 2.59 | |||
| 47 | 0.39 | 0.6 | 30 | 3.4 | 0.00 | 0.12 | 3.01 | 24.2 | 3.13 |
| 40 | 3.1 | 3.23 | 0.08 | 3.87 | 17.6 | 3.88 | |||
| 21 | 6.1 | 0.95 | 0.31 | 1.67 | 70.5 | 1.93 | |||
| 0.8 | 30 | 5.0 | 0.00 | 0.17 | 2.62 | 40.0 | 2.75 | ||
| 40 | 4.9 | 2.04 | 0.13 | 5.04 | 30.3 | 5.04 | |||
| Atomizer 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| cMD | µ | pgas | SMD = c × ALR−b | SMD = c × EV−b | ||||
| (% d.b.) | (Pa∙s) | (Mpa) | b | c | R2 | b | c | R2 |
| 40 | 0.12 | 0.4 | 0.685 | 11.3 | 0.96 | 0.706 | 396 | 0.96 |
| 0.6 | 0.776 | 11.2 | 0.90 | 0.793 | 720 | 0.90 | ||
| 0.8 | 0.506 | 15.9 | 0.99 | 0,514 | 254 | 0.99 | ||
| total | 0.634 | 12.9 | 0.96 | 0.321 | 163 | 0.80 | ||
| 45 | 0.30 | 0.4 | 0.597 | 16.2 | 0.80 | 0.611 | 361 | 0.80 |
| 0.6 | 0.695 | 13.4 | 0.97 | 0.711 | 573 | 0.97 | ||
| 0.8 | 0.805 | 12.4 | 0.93 | 0.821 | 1048 | 0.93 | ||
| total | 0.706 | 13.2 | 0.96 | 0.680 | 514 | 0.92 | ||
| 47 | 0.39 | 0.4 | 0.968 | 7.1 | 0.80 | 0.994 | 1107 | 0.80 |
| 0.6 | 0.516 | 20.8 | 0.99 | 0.528 | 339 | 0.99 | ||
| 0.8 | 0.378 | 26.2 | 0.99 | 0.384 | 210 | 0.99 | ||
| total | 0.413 | 24.7 | 0.90 | 0.531 | 265 | 0.97 | ||
| Atomizer 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| cMD | µ | pgas | QL | ur(QL) | Qgas | ur(Qgas) | ALR | ur(ALR) | EV | ur(EV) |
| (% d.b.) | (Pa∙s) | (Mpa) | (L·h−1) | (%) | (Nm3·h−1) | (%) | (-) | (%) | (kJ·L−1) | (%) |
| 40 | 0.12 | 0.4 | 100 | 0.21 | 13.2 | 2.00 | 0.14 | 1.85 | 24.1 | 2.01 |
| 120 | 0.82 | 12.0 | 7.36 | 0.11 | 8.05 | 18.6 | 8.36 | |||
| 141 | 0.48 | 11.7 | 3.08 | 0.09 | 2.78 | 15.5 | 2.71 | |||
| 0.6 | 100 | 0.63 | 19.6 | 0.88 | 0.22 | 0.92 | 43.3 | 0.92 | ||
| 120 | 0.05 | 18.9 | 0.03 | 0.17 | 0.07 | 34.9 | 0.07 | |||
| 140 | 0.68 | 18.4 | 1.13 | 0.14 | 1.76 | 29.2 | 1.89 | |||
| 0.8 | 100 | 0.66 | 24.0 | 0.24 | 0.26 | 0.87 | 58.4 | 0.91 | ||
| 120 | 0.46 | 23.5 | 0.65 | 0.22 | 0.90 | 48.2 | 0.91 | |||
| 140 | 0.22 | 22.9 | 0.25 | 0.18 | 0.47 | 40.8 | 0.46 | |||
| (a) | |||||||||
| cMD | µ | Atomizer | dexit orifice | SMD = c × ALR−b | SMD = c × EV−b | ||||
| (% d.b.) | (Pa∙s) | - | (mm) | b | c | R2 | b | c | R2 |
| 40 | 0.12 | 1 | 1.5 | 0.634 | 12.9 | 0.96 | 0.531 | 266 | 0.97 |
| 2 | 3.0 | 0.544 | 25.3 | 0.78 | 0.420 | 293 | 0.80 | ||
| (b) | |||||||||
| cMD | µ | Atomizer | dexit orifice | x90,3 = c·× ALR−b | x90,3 = c × EV−b | ||||
| (% d.b.) | (Pa∙s) | - | (mm) | b | c | R2 | b | c | R2 |
| 40 | 0.12 | 1 | 1.5 | 0.387 | 105.6 | 0.94 | 0.334 | 680.7 | 0.95 |
| 2 | 3.0 | 0.615 | 91.2 | 0.90 | 0.485 | 1502.6 | 0.95 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency. Processes 2019, 7, 139. https://doi.org/10.3390/pr7030139
Wittner MO, Karbstein HP, Gaukel V. Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency. Processes. 2019; 7(3):139. https://doi.org/10.3390/pr7030139
Chicago/Turabian StyleWittner, Marc O., Heike P. Karbstein, and Volker Gaukel. 2019. "Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency" Processes 7, no. 3: 139. https://doi.org/10.3390/pr7030139
APA StyleWittner, M. O., Karbstein, H. P., & Gaukel, V. (2019). Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency. Processes, 7(3), 139. https://doi.org/10.3390/pr7030139





