Accelerating Biologics Manufacturing by Upstream Process Modelling
Abstract
:1. Introduction
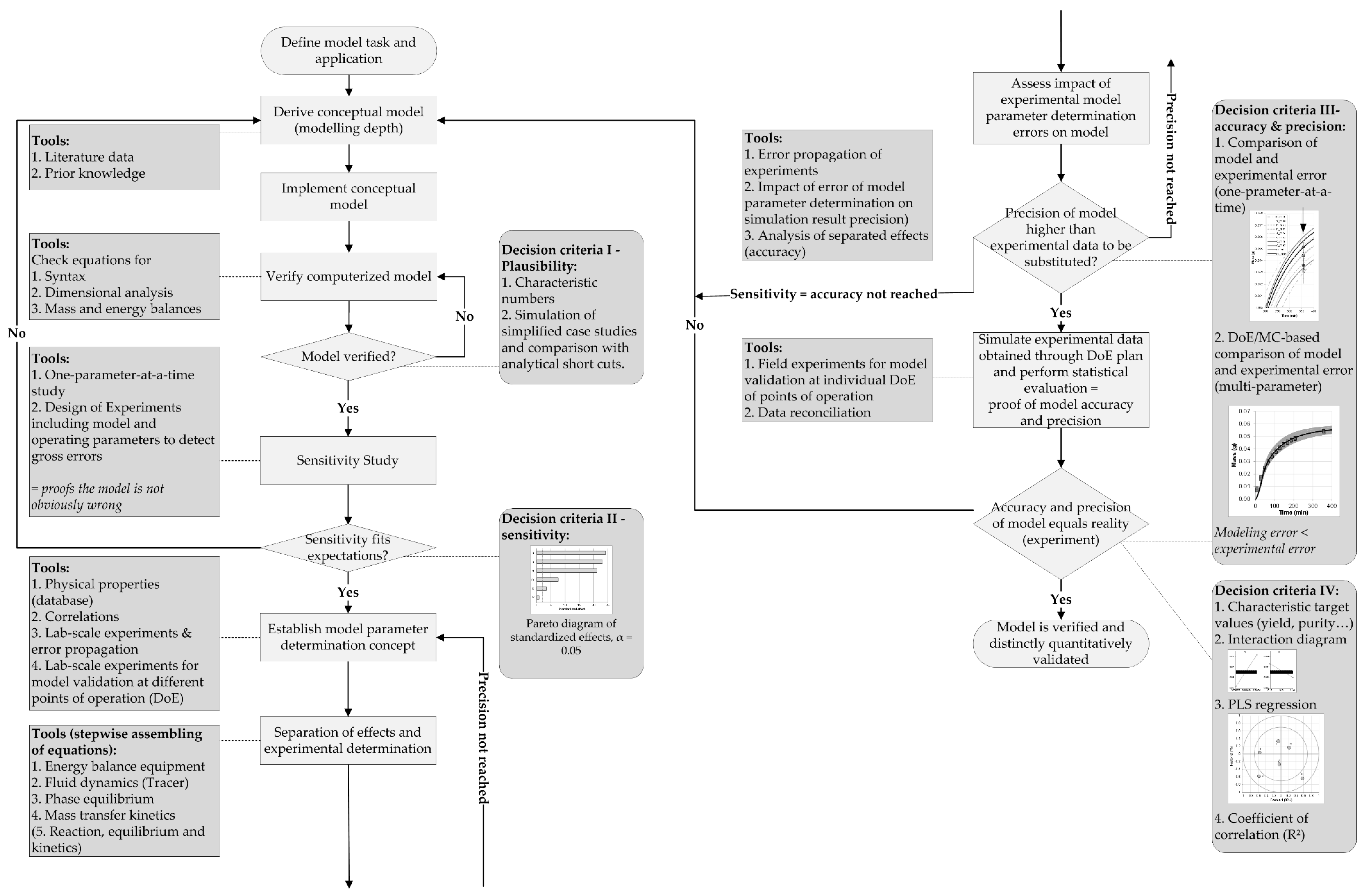
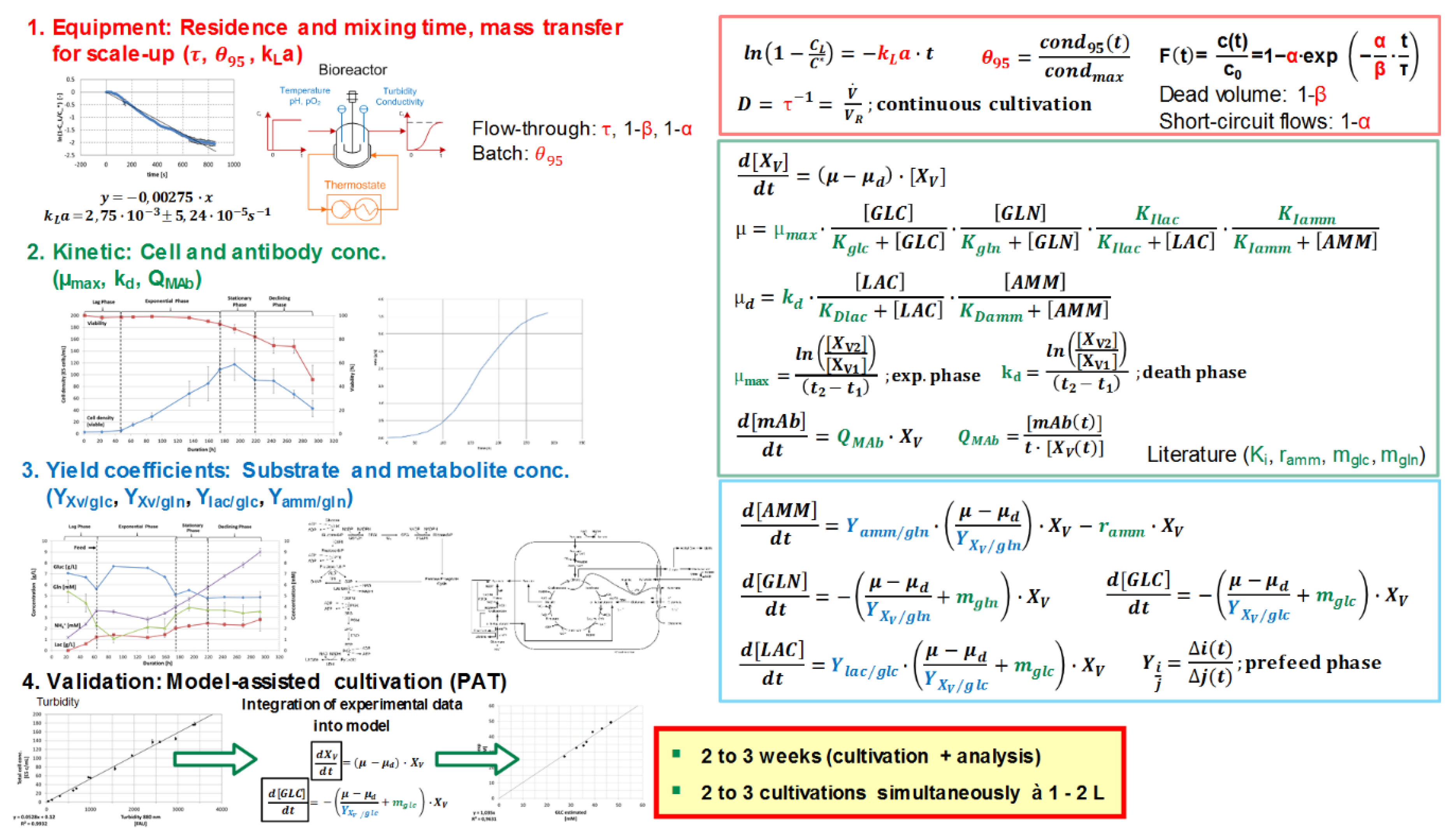
2. Materials and Methods
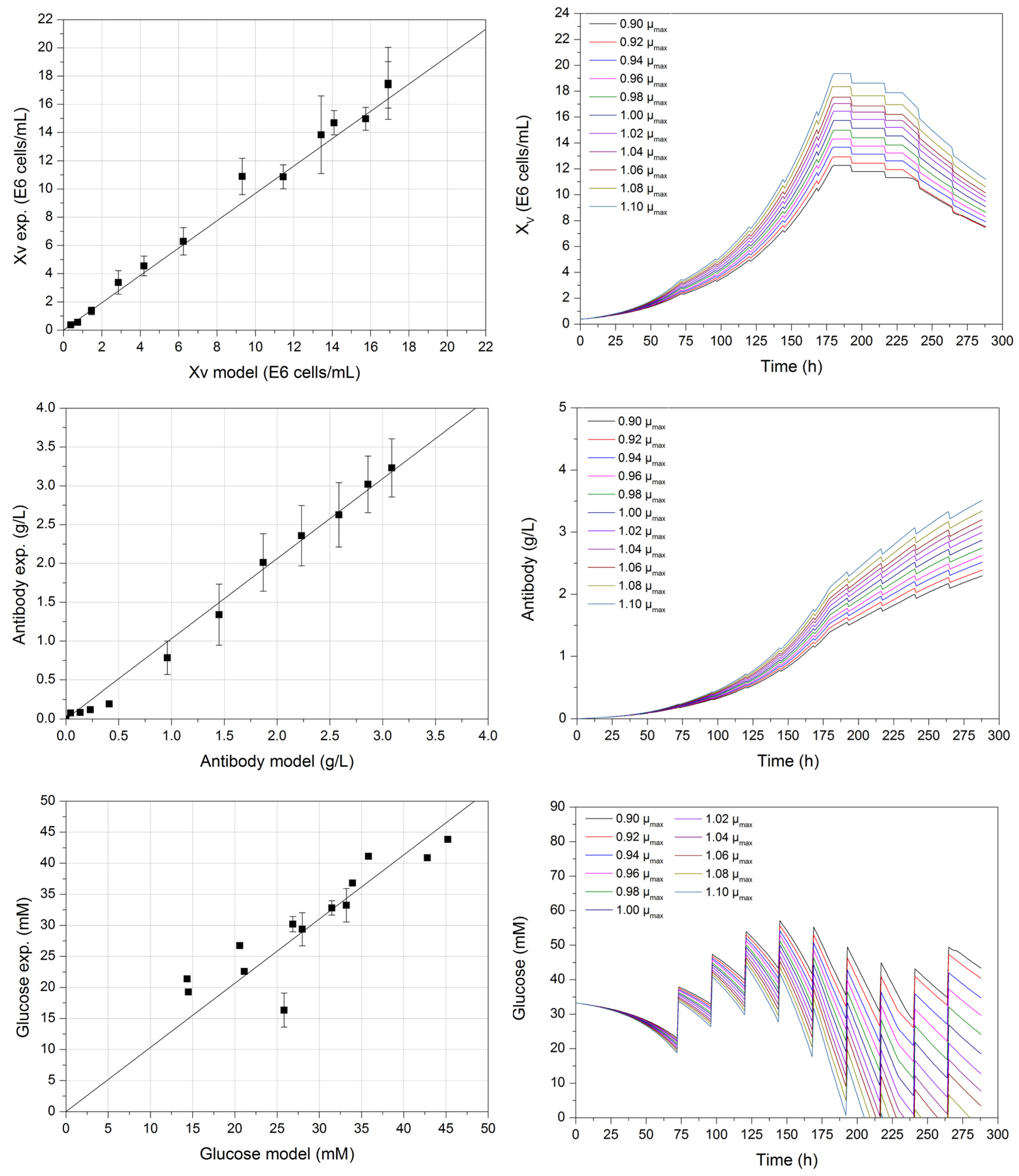
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hinz, D.C. Process analytical technologies in the pharmaceutical industry: The FDA’s PAT initiative. Anal. Bioanal. Chem. 2006, 384, 1036–1042. [Google Scholar] [CrossRef]
- Kornecki, M.; Schmidt, A.; Strube, J. Pat as Key-Enabling Technology for Qbd in Pharmaceutical Manufacturing—A Conceptual Review on Upstream and Downstream Processing. Chem. Today 2018, 36, 44–48. [Google Scholar]
- Krull, I.S.; Rakesh, M.; Anurag, S.R. Tools for Enabling Process Analytical Technology Applications in Biotechnology. BioPharm. Int. 2012. Available online: http://www.biopharminternational.com/tools-enabling-process-analytical-technology-applications-biotechnology-0?id=&pageID=1&sk=&date= (accessed on 20 March 2019).
- Sommerfeld, S.; Strube, J. Challenges in biotechnology production—Generic processes and process optimization for monoclonal antibodies. Chem. Eng. Process. Process Intensif. 2005, 44, 1123–1137. [Google Scholar] [CrossRef]
- Bechmann, J.; Rudolph, F.; Gebert, L.; Schaub, J.; Greulich, B.; Dieterle, M.; Bradl, H. Process parameters impacting product quality. BMC Proc. 2015, 9, O7. [Google Scholar] [CrossRef]
- FDA. Guidance for Industry. PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance. Available online: https://www.fda.gov/downloads/drugs/guidances/ucm070305.pdf (accessed on 19 February 2018).
- FDA; CDER; CBER; USDHHS. Pharmaceutical Development Q8(R2). 2009. Available online: https://www.ich.org/fileadmin/Public_Web_Site/ICH_Products/Guidelines/Quality/Q8_R1/Step4/Q8_R2_Guideline.pdf (accessed on 19 February 2018).
- Oyeleye, O.; Ogundeji, S.T.; Ola, S.I.; Omitogun, O.G. Basics of animal cell culture: Foundation for modern science. BMBR 2016, 11, 6–16. [Google Scholar] [CrossRef]
- Präve, P. (Ed.) Handbook of Biotechnology, 4th ed.; Oldenbourg: Munich, Germany, 1994. [Google Scholar]
- Musmann, C.; Joeris, K.; Markert, S.; Solle, D.; Scheper, T. Spectroscopic methods and their applicability for high-throughput characterization of mammalian cell cultures in automated cell culture systems. Eng. Life Sci. 2016, 16, 405–416. [Google Scholar] [CrossRef]
- Kornecki, M.; Strube, J. Process Analytical Technology for Advanced Process Control in Biologics Manufacturing with the Aid of Macroscopic Kinetic Modeling. Bioengineering 2018, 5, 25. [Google Scholar] [CrossRef] [PubMed]
- Uhlenbrock, L.; Sixt, M.; Strube, J. Quality-by-Design (QbD) process evaluation for phytopharmaceuticals on the example of 10-deacetylbaccatin III from yew. Resour. Eff. Technol. 2017, 3, 137–143. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Schmidt, A.; Mestmäcker, F.; Mouellef, M.; Huter, M.; Uhlenbrock, L.; Kornecki, M.; Lohmann, L.; Ditz, R.; Strube, J. Accelerating Biologics Manufacturing by Modelling OR: Is approval under the QbD- and PAT-approach demanded by authorities still appropriate without a digital-twin? Processes 2019, 7, 94. [Google Scholar] [CrossRef]
- Ben Yahia, B.; Malphettes, L.; Heinzle, E. Macroscopic modeling of mammalian cell growth and metabolism. Appl. Microbiol. Biotechnol. 2015, 99, 7009–7024. [Google Scholar] [CrossRef]
- Goudar, C.T. Computer programs for modeling mammalian cell batch and fed-batch cultures using logistic equations. Cytotechnology 2012, 64, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Goudar, C.T.; Joeris, K.; Konstantinov, K.B.; Piret, J.M. Logistic equations effectively model mammalian cell batch and fed-batch kinetics by logically constraining the fit. Biotechnol. Prog. 2005, 21, 1109–1118. [Google Scholar] [CrossRef]
- Goudar, C.T.; Konstantinov, K.B.; Piret, J.M. Robust parameter estimation during logistic modeling of batch and fed-batch culture kinetics. Biotechnol. Prog. 2009, 25, 801–806. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.D.; Barford, J.P. An unstructured kinetic model of macromolecular metabolism in batch and fed-batch cultures of hybridoma cells producing monoclonal antibody. Biochem. Eng. J. 2000, 4, 153–168. [Google Scholar] [CrossRef]
- Sidoli, F.R.; Mantalaris, A.; Asprey, S.P. Modelling of Mammalian Cells and Cell Culture Processes. Cytotechnology 2004, 44, 27–46. [Google Scholar] [CrossRef]
- Hefzi, H.; Ang, K.S.; Hanscho, M.; Bordbar, A.; Ruckerbauer, D.; Lakshmanan, M.; Orellana, C.A.; Baycin-Hizal, D.; Huang, Y.; Ley, D.; et al. A Consensus Genome-scale Reconstruction of Chinese Hamster Ovary Cell Metabolism. Cell Syst. 2016, 3, 434–443. [Google Scholar] [CrossRef] [PubMed]
- Selişteanu, D.; Șendrescu, D.; Georgeanu, V.; Roman, M. Mammalian Cell Culture Process for Monoclonal Antibody Production: Nonlinear Modelling and Parameter Estimation. BioMed Res. Int. 2015, 2015. [Google Scholar] [CrossRef]
- Chen, N.; Bennett, M.H.; Kontoravdi, C. Analysis of Chinese hamster ovary cell metabolism through a combined computational and experimental approach. Cytotechnology 2014, 66, 945–966. [Google Scholar] [CrossRef] [PubMed]
- Nicolae, A.; Wahrheit, J.; Bahnemann, J.; Zeng, A.-P.; Heinzle, E. Non-stationary 13C metabolic flux analysis of Chinese hamster ovary cells in batch culture using extracellular labeling highlights metabolic reversibility and compartmentation. BMC Syst. Biol. 2014, 8, 50. [Google Scholar] [CrossRef]
- Wahrheit, J.; Nicolae, A.; Heinzle, E. Dynamics of growth and metabolism controlled by glutamine availability in Chinese hamster ovary cells. Appl. Microbiol. Biotechnol. 2014, 98, 1771–1783. [Google Scholar] [CrossRef] [PubMed]
- Borchers, S.; Freund, S.; Rath, A.; Streif, S.; Reichl, U.; Findeisen, R. Identification of growth phases and influencing factors in cultivations with AGE1.HN cells using set-based methods. PLoS ONE 2013, 8, e68124. [Google Scholar] [CrossRef] [PubMed]
- Ahn, W.S.; Antoniewicz, M.R. Parallel labeling experiments with 1,2-(13)Cglucose and U-(13)Cglutamine provide new insights into CHO cell metabolism. Metab. Eng. 2013, 15, 34–47. [Google Scholar] [CrossRef]
- Ghorbaniaghdam, A.; Henry, O.; Jolicoeur, M. A kinetic-metabolic model based on cell energetic state: Study of CHO cell behavior under Na-butyrate stimulation. Bioprocess Biosyst. Eng. 2013, 36, 469–487. [Google Scholar] [CrossRef] [PubMed]
- Martinez, V.S.; Dietmair, S.; Quek, L.-E.; Hodson, M.P.; Gray, P.; Nielsen, L.K. Flux balance analysis of CHO cells before and after a metabolic switch from lactate production to consumption. Biotechnol. Bioeng. 2013, 110, 660–666. [Google Scholar] [CrossRef] [PubMed]
- Templeton, N.; Dean, J.; Reddy, P.; Young, J.D. Peak antibody production is associated with increased oxidative metabolism in an industrially relevant fed-batch CHO cell culture. Biotechnol. Bioeng. 2013, 110, 2013–2024. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, F.; Vande Wouwer, A.; Jungers, R.M.; Bastin, G. Dynamic metabolic models of CHO cell cultures through minimal sets of elementary flux modes. J. Biotechnol. 2013, 164, 409–422. [Google Scholar] [CrossRef] [PubMed]
- Ahn, W.S.; Antoniewicz, M.R. Metabolic flux analysis of CHO cells at growth and non-growth phases using isotopic tracers and mass spectrometry. Metab. Eng. 2011, 13, 598–609. [Google Scholar] [CrossRef] [PubMed]
- Naderi, S.; Meshram, M.; Wei, C.; McConkey, B.; Ingalls, B.; Budman, H.; Scharer, J. Development of a mathematical model for evaluating the dynamics of normal and apoptotic Chinese hamster ovary cells. Biotechnol. Prog. 2011, 27, 1197–1205. [Google Scholar] [CrossRef]
- Nolan, R.P.; Lee, K. Dynamic model of CHO cell metabolism. Metab. Eng. 2011, 13, 108–124. [Google Scholar] [CrossRef]
- Xing, Z.; Bishop, N.; Leister, K.; Li, Z.J. Modeling kinetics of a large-scale fed-batch CHO cell culture by markov chain monte carlo method. Biotechnol. Prog. 2010, 26, 208–219. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Li, Z.; Chow, V.; Lee, S.S. Identifying inhibitory threshold values of repressing metabolites in CHO cell culture using multivariate analysis methods. Biotechnol. Prog. 2008, 24, 675–683. [Google Scholar] [CrossRef]
- Gao, J.; Gorenflo, V.M.; Scharer, J.M.; Budman, H.M. Dynamic metabolic modeling for a MAB bioprocess. Biotechnol. Prog. 2007, 23, 168–181. [Google Scholar] [CrossRef]
- Kontoravdi, C.; Asprey, S.P.; Pistikopoulos, E.N.; Mantalaris, A. Development of a dynamic model of monoclonal antibody production and glycosylation for product quality monitoring. Comput. Chem. Eng. 2007, 31, 392–400. [Google Scholar] [CrossRef]
- Teixeira, A.P.; Alves, C.; Alves, P.M.; Carrondo, M.J.T.; Oliveira, R. Hybrid elementary flux analysis/nonparametric modeling: Application for bioprocess control. BMC Bioinform. 2007, 8, 30. [Google Scholar] [CrossRef]
- Provost, A.; Bastin, G.; Agathos, S.N.; Schneider, Y.J. Metabolic design of macroscopic bioreaction models: Application to Chinese hamster ovary cells. Bioprocess Biosyst. Eng. 2006, 29, 349–366. [Google Scholar] [CrossRef]
- Oliveira, R. Combining first principles modelling and artificial neural networks: A general framework. Comput. Chem. Eng. 2004, 28, 755–766. [Google Scholar] [CrossRef]
- Vande Wouwer, A.; Renotte, C.; Bogaerts, P. Biological reaction modeling using radial basis function networks. Comput. Chem. Eng. 2004, 28, 2157–2164. [Google Scholar] [CrossRef]
- Sainz, J.; Pizarro, F.; Perez-Correa, J.R.; Agosin, E. Modeling of yeast metabolism and process dynamics in batch fermentation. Biotechnol. Bioeng. 2003, 81, 818–828. [Google Scholar] [CrossRef]
- Altamirano, C.; Illanes, A.; Casablancas, A.; Gamez, X.; Cairo, J.J.; Godia, C. Analysis of CHO cells metabolic redistribution in a glutamate-based defined medium in continuous culture. Biotechnol. Progress 2001, 17, 1032–1041. [Google Scholar] [CrossRef]
- Nyberg, G.B.; Balcarcel, R.R.; Follstad, B.D.; Stephanopoulos, G.; Wang, D.I.C. Metabolism of peptide amino acids by Chinese hamster ovary cells grown in a complex medium. Biotechnol. Bioeng. 1999, 62, 324–335. [Google Scholar] [CrossRef]
- Kornecki, M.; Mestmäcker, F.; Zobel-Roos, S.; Heikaus de Figueiredo, L.; Schlüter, H.; Strube, J. Host Cell Proteins in Biologics Manufacturing: The Good, the Bad, and the Ugly. Antibodies 2017, 6, 13. [Google Scholar] [CrossRef]
- Subramanian, G. (Ed.) Continuous Biomanufacturing//Continuous Biomanufacturing. Innovative Technologies and Methods; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]





| Year | Organism | Operational Mode | Input-Output Relation | Kinetic Model | Model Variables | Reference |
|---|---|---|---|---|---|---|
| 2016 | CHO | Batch | Genome-scale | Genome-scale metabolic network | >1700 genes | [20] |
| 2015 | Hybridoma 130-8F | Batch | Dynamical model | Monod | X, Glc, Gln, Asn, Asp, Lac, Pro, Ala, mAb, Glu, Amm | [21] |
| 2014 | CHO | Batch, Fed-Batch | MFA | Cell population dynamics and single cell model | Single cell model describes glucose metabolism in the cytosol. Cell growth model connects single cell model to extracellular environment and cell population behaviour | [22] |
| 2014 | CHO | Batch | 13C MFA | Monod type | Glycolysis; TCA cycle; anaplerotic reactions; synthesis of fatty acids, proteins, and carbohydrates for biomass production; amino acid production and degradation | [23] |
| 2014 | CHO | Batch, Fed-Batch | Dynamic MFA | Stoichiometric model | Glc, Lac, Pyr, Amm, Ala, Asn, Asp, Glu, Gln, Gly, Ser | [24] |
| 2013 | AGE1.HN | Batch | Expert reasoning | Mechanistic Monod type | X, Amm, Lac, Gln, mAb, Glc | [25] |
| 2013 | CHO, adherent | Fed-Batch | 13C MFA | Monod type | 79 reactions | [26] |
| 2013 | CHO cell line (ATCC, CRL9606) | Batch | MFA | Michaelis-Menten type kinetic | Glycolysis, pentose phosphate pathway, TCA cycle, glutaminolysis, and cell respiration | [27] |
| 2013 | CHO-XL99 | Batch | FBA + yield coefficients | Monod type | Glycolysis, TCA cycle, pentose phosphate pathway, biomass precursors (e.g., fatty acids, steroids, glycogen, and nucleotides) | [28] |
| 2013 | CHO | Fed-Batch | 13C MFA | Monod type | Glycolysis, TCA cycle, pentose phosphate pathway, multiple cataplerotic and anaplerotic reactions, and both catabolism and anabolism of amino acids | [29] |
| 2013 | CHO-320 | Batch | EFMs | Monod type | 19 EFM in exponential phase, 18 in stationary, 17 in death phase | [30] |
| 2011 | CHO-K1 | Fed-Batch | non-stationary 13C MFA | Monod type | 73 reactions and 77 metabolites | [31] |
| 2011 | CHO | Batch, Fed-Batch | MFA | Logistic type | 30 metabolites involved in 34 bioreactions | [32] |
| 2011 | CHO-K1 | Fed-Batch | dynamic MFA | Michaelis-Menten type kinetic | 24 metabolites and 34 reactions | [33] |
| 2010 | CHO | Fed-Batch | Expert reasoning | Monod | X, Amm, Lac, Gln, mAb, Glc | [34] |
| 2009 | CHO, BHK, Hybridoma | Batch, Fed-Batch | Nonlinear parameter estimation | Logistic | X, Amm, Lac, Gln, mAb, Glc | [17] |
| 2008 | CHO | Fed-Batch | PFA | Monod | X, Amm, Lac, Gln, Glc, CO2, mAb | [35] |
| 2007 | Hybridoma 130-8F | Batch | MFA + EFM | Monod | X, Glc, Glu, Ala, Pro, CO2, Asp, Asn, Amm, Lac, Gln, Pro, mAb | [36] |
| 2007 | Hybridoma 14-4-4S | Fed-Batch | Expert reasoning | Monod | X, Amm, Lac, Gln, Glc, mAb, Glycosylation | [37] |
| 2007 | BHK-21A | Fed-Batch | Metabolic network + EFM | Hybrid | X, Ala, Amm, Lac, Gln, Glc, mAb | [38] |
| 2006 | CHO | Batch | MFA | Michaelis-Menten type kinetic | 10 reactions for growth, 4 reactions for transition, 3 reactions for death | [39] |
| 2004 | Baker’s yeast | Fed-Batch | First principle + ANN | Hybrid | X, EtOH, Glc, Amm, O2, CO2 | [40] |
| 2004 | CHO | Batch | Neural network | Hybrid | X, Glc, Lac, Gln | [41] |
| 2003 | Yeast | Batch | Metabolic network | Monod type | X, EtOH, Glc, Glycerol, Amm | [42] |
| 2001 | CHO TF 70R | Continuous | MFA | Monod type | 48 metabolites and 43 reactions | [43] |
| 1999 | CHO | Continuous | MFA | Biochemical reaction network | 33 reactions | [44] |
| Parameter | Description | Value | Unit | Source |
|---|---|---|---|---|
| XV,initial | Starting viable cell concentration | 0.37 | E6 cells mL−1 | exp |
| GLCinitial | Starting glucose concentration | 33.24 | mM | exp |
| GLNinitial | Starting glutamine concentration | 6.0 | mM | exp |
| LACinitial | Starting lactate concentration | 0.42 | mM | exp |
| AMMinitial | Starting ammonium concentration | 0.91 | mM | exp |
| µmax | Maximum growth rate | 0.029 | h−1 | exp |
| kd | Maximum death rate | 0.0066 | h−1 | exp |
| YX/glc | Yield coefficient cell conc./glucose | 0.413 | E9 cells mmol−1 | exp |
| YX/gln | Yield coefficient cell conc./glutamine | 0.573 | E9 cells mmol−1 | exp |
| Ylac/glc | Yield coefficient lactate/glucose | 1.391 | mmol mmol−1 | exp |
| Yamm/gln | Yield coefficient ammonium/glutamine | 0.739 | mmol mmol−1 | exp |
| QmAb | Specific production rate | 2.25 | E-12 g cells−1 h−1 | exp |
| ramm | Ammonium removal rate | 6.3 | E-12 mmol cells−1 h−1 | Lit. |
| mglc | Glucose maintenance coefficient | 69.2 | E-12 mmol cells−1 h−1 | Lit. |
| a1 | Coefficient for mgln | 3.2 | E-12 mmol cells−1 h−1 | Lit. |
| a2 | Coefficient for mgln | 2.1 | mM | Lit. |
| Kglc | Monod constant glucose | 0.15 | mM | Lit. |
| Kgln | Monod constant glutamine | 0.04 | mM | Lit. |
| KIlac | Monod constant lactate for inhibition | 45.0 | mM | Lit. |
| KIamm | Monod constant ammonium for inhibition | 9.5 | mM | Lit. |
| KDlac | Monod constant lactate for death | 40.0 | mM | Lit. |
| KDamm | Monod constant ammonium for death | 4.0 | mM | Lit. |
| Parameter Set | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ..... |
|---|---|---|---|---|---|---|---|---|---|---|
| XV min (E6 cells/mL) | 0.37 | 0.32 | 0.42 | 0.36 | 0.38 | 0.40 | 0.34 | 0.32 | 0.37 | ..... |
| XV max (E6 cells/mL) | 17.01 | 10.60 | 24.17 | 20.13 | 19.74 | 15.06 | 19.50 | 19.84 | 19.28 | ..... |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kornecki, M.; Strube, J. Accelerating Biologics Manufacturing by Upstream Process Modelling. Processes 2019, 7, 166. https://doi.org/10.3390/pr7030166
Kornecki M, Strube J. Accelerating Biologics Manufacturing by Upstream Process Modelling. Processes. 2019; 7(3):166. https://doi.org/10.3390/pr7030166
Chicago/Turabian StyleKornecki, Martin, and Jochen Strube. 2019. "Accelerating Biologics Manufacturing by Upstream Process Modelling" Processes 7, no. 3: 166. https://doi.org/10.3390/pr7030166
APA StyleKornecki, M., & Strube, J. (2019). Accelerating Biologics Manufacturing by Upstream Process Modelling. Processes, 7(3), 166. https://doi.org/10.3390/pr7030166





