Enhancement Study of Ice Storage Performance in Circular Tank with Finned Tube

Abstract

Combined experimental and numerical studies are conducted to study ice storage performance of an ice storage tank with finned tube. Axially arranged fins on the refrigerant tube are applied to enhance the solidification. The evolution of the solid–liquid interface and the variation of temperature of the typical position is examined. The effect of natural convection is discussed in detail. In addition, the effects of refrigerant temperature and initial water temperature on the ice storage performance are analyzed. The results indicate that the ice storage performance is enhanced by the metal fins remarkably. The defection of poor heat transfer after ice is formed can be solved by applying fins in ice storage devices. Natural convection leads to unnecessary mixing of water with different temperatures, lessening the cooling energy stored and acting as a disadvantage during solidification. Decreasing the refrigerant temperature and initial water temperature is beneficial for ice storage.

1. Introduction

Latent heat storage through phase change materials is of great interest in a wide range of technical applications, including electronics cooling [1,2], microfluidics system [3], building energy conservation [4], biomedical engineering [5], space thermal control [6,7], solar energy utilization [8], and chemical process [9,10]. As a typical application, the ice storage technique stores cooling capacity through the solidification of water during the valley electricity demand period and releases the cooling capacity by melting the ice during the peak electricity demand period. Peak load shifting of the electrical grid [11,12] can be achieved through ice storage with low cost, which is of significance in maintaining the steady operation of the electrical grid. Hence, extensive efforts have been devoted to the study of ice storage processes. Conventionally, ice is formed outside a tube or coiler in which refrigerating medium is running. However, thermal resistance between the refrigerating medium and water increases with the thickness of ice due to the low heat transfer coefficient of ice. This poor heat transfer characteristic hinders the widespread use of the ice storage technique. Hence, a number of previous investigations [13,14] have been conducted to improve heat transfer performance, in which methods have included adding extensional structures [15], metal foam [16,17], rough surface structures or particles with high thermal conductivity [18].

Most attempts to explore the natural convection during ice storage processes with a finned tube are based on experimental results [19,20]. Jannesari and Abdollahi [21] studied the effect of a thin ring and annular fin on the improvement of ice formation. The ice formation rate was increased by 15% through the utilization of fins. Ismail and Lino [22] investigated the enhancement of heat transfer in phase change materials (PCM) with a radial finned tube. It was found that the temperature of the refrigerating medium affected the solidification process strongly. Further, the increment in the fin diameter accelerated the velocity at the interface, thus reducing solidification time. Rozenfeld et al. [23] designed a double-pipe heat storage device with helical fins, which shortens the melting time by up to approximately 66%. Four types of solidification of pure water, depending on the strength of natural convection, are reported by Kumar et al. [24]. The enhancement performance of circular and longitudinal fins outside a sleeve-tube is studied by Agyenim et al. [25]. Longitudinal fins proved to be better than circular fins.

Numerical approaches have also been conducted to investigate ice storage processes [26,27,28]. However, in most research, the flow of the liquid PCM or water was neglected and the effect of natural convection was not taken into account. Jia et al. [29] studied the cold storage of a spherical PCM capsule with fins using the enthalpy method. Ezan and Kalfa [30] numerically investigated the natural convection heat transfer of freezing water inside a square cavity without fins. However, numerical research on the natural convection during solidification in ice storage devices with a finned tube is still lacking [31].

In summary, fluid flow affects heat transfer during solidification, especially at the solid–liquid interface. Besides, the variation of the density of water is non-linear with temperature, which leads to more complicated behavior during solidification. The coupled effect of fins and natural convection on ice storage performance is of significance. Therefore, this article experimentally and numerically investigates the enhancement of ice storage performance in a circular tank by an axially finned tube, in an effort to identify the role of natural convection on ice storage performance. The evolution of the solid–liquid interface and the temperature variation along both the radial and circumferential direction in the water and in the fins, are analyzed. The effect of natural convection on the ice storage process is discussed in particular, based on detailed transit temperature distribution and ice storage ratio. In addition, the effects of temperature of the refrigerants and the initial temperature of the water are discussed.

2. Experimental and Numerical Methods

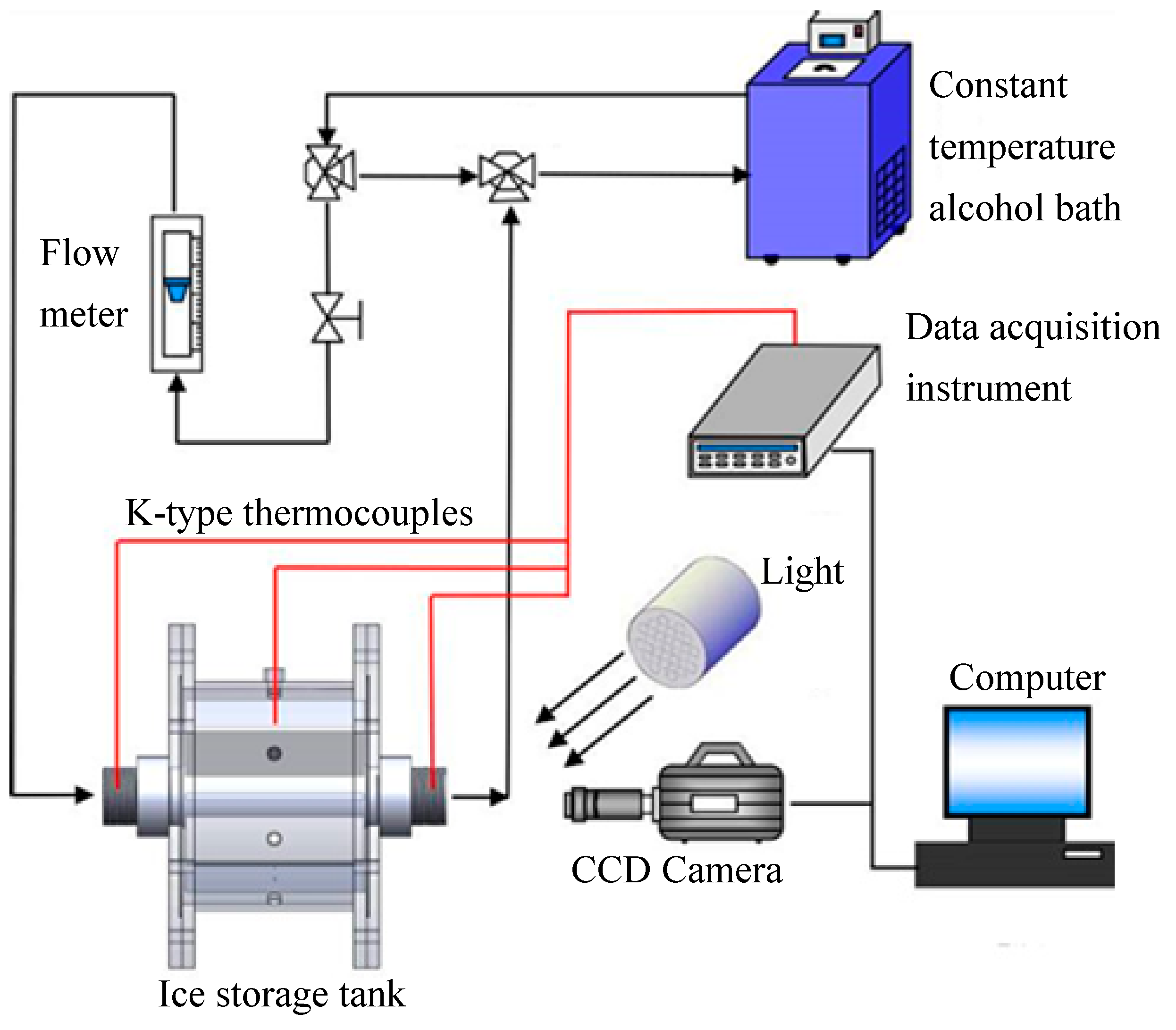
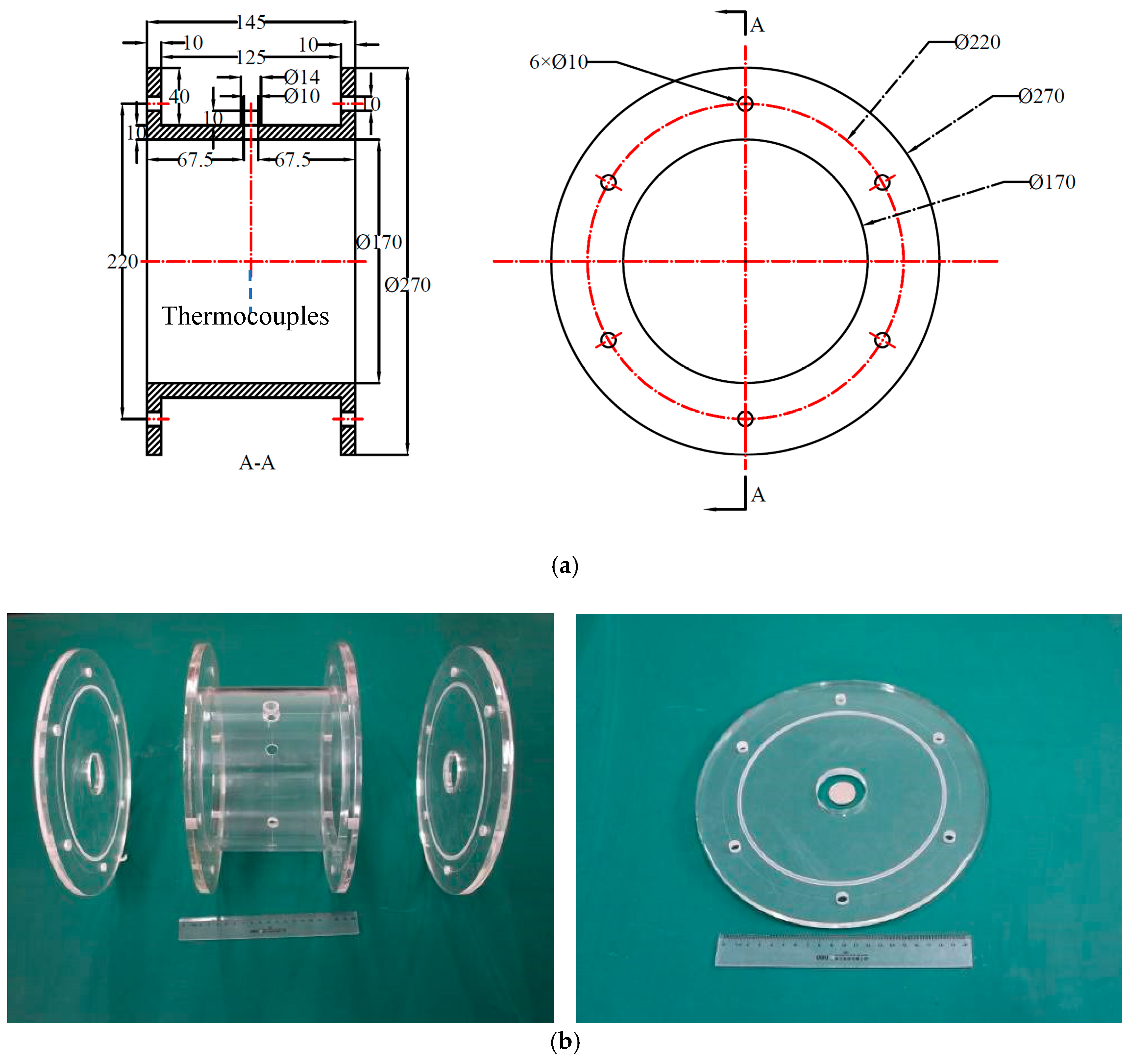
2.1. Ice Storage Performance Test System

A visualization experimental system was designed as shown in Figure 1, based on which the solid–liquid phase change process during ice storage in a circular tank was studied. The experimental system was comprised of a polymethyl methacrylate ice storage tank, an aluminum finned tube, a flow meter, a constant-temperature bath with working fluid of alcohol and glycol water solution as refrigerant, a light source, a data acquisition instrument (recording the temperature inside the ice storage tank), a computer and a CCD camera monitoring the solid–liquid phase change. The ice storage tank, with a height of 145 mm and inner diameter of 170 mm, was wrapped in foamed polyethylene and tin foil for thermal insulation (Figure 2). The aluminum tube, with eight 50 mm-length fins, was assembled inside the ice storage tank so that the working fluid was flowing inside the tube (Figure 3). During the experiment, the tank was filled with water. In order to measure the temperature of different locations inside the tank during the solid–liquid phase change process, thermocouples were arranged in the water and the fin of the tube through the preset holes, as shown in Figure 4. There were three sets of temperature measurement points in the water, and four sets of temperature measurement points in the fin of the tube. All of the thermocouples were at the same cross section. During the experiment, the temperatures of the refrigerant were −5 °C, −10 °C and −15 °C, and the flow rate was 30 mL/min, with initial water temperatures of 4 °C, 10 °C and 17 °C, respectively. The freezing temperature of glycol water solution is −53 °C while the specific heat is 2.4 kJ/(kg·°C).

2.2. Numerical Methods

To study the enhancement of ice storage performance by arranging external fines on the tube, a transit numerical model, taking natural convection into consideration, was developed based on the enthalpy–porosity method. To simplify the simulation, the following assumptions were made:

• Water is isotropic in both liquid and solid state, and the physical parameters of water are constant, except density;
• For the tube with fins, which is also isotropic, the values of the physical parameters are common;
• The effects of the volume and the supercooling during freezing are neglected, and the phase transition temperature is fixed;
• There is only laminar flow inside the tank;
• The fluid and solid are in local heat balance.

Instead of tracking the solid–liquid interface explicitly, a liquid fraction β was introduced to describe the distribution of the liquid and solid as

$$\beta =\{\begin{array}{ll}1& T\ge T_s\\ 0& T<T_s\end{array}$$

(1)

where T_s is the solidification temperature of water. The thermal capacity and thermal conductivity throughout the entire computational domain were calculated as

$$c=c_s+\beta (c_l-c_s)$$

(2)

$$\lambda ={\lambda }_s+\beta ({\lambda }_l-{\lambda }_s)$$

(3)

where the subscript s denotes solid and subscript l denotes liquid.

The mass conservation equation is expressed as

$$\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}=0$$

(4)

where $\rho$ is the density, t is the flow time, u is the velocity component along the x-axis and v is the velocity component along the y-axis.

The momentum equation along the x-axis is

$$\frac{\partial (\rho u)}{\partial t}+u\frac{\partial (\rho u)}{\partial x}+v\frac{\partial (\rho u)}{\partial y}=\frac{\partial }{\partial x}(u\frac{\partial u}{\partial x})+\frac{\partial }{\partial y}(u\frac{\partial u}{\partial y})-\frac{\partial p}{\partial x}+S_u$$

(5)

The momentum equation along the y-axis is

$$\frac{\partial (\rho v)}{\partial t}+u\frac{\partial (\rho v)}{\partial x}+v\frac{\partial (\rho v)}{\partial y}=\frac{\partial }{\partial x}(u\frac{\partial v}{\partial x})+\frac{\partial }{\partial y}(u\frac{\partial v}{\partial y})-\frac{\partial p}{\partial x}+S_v$$

(6)

where p is the pressure. The source terms in Equations (5) and (6) are

$$S_u=\frac{{(1-\beta )}^2}{{\beta }^3+\xi }{A}_{mush}u$$

(7)

$$S_v=\frac{{(1-\beta )}^2}{{\beta }^3+\xi }{A}_{mush}v+\frac{\rho g\delta (h-h_{ref})}{c}$$

(8)

where ξ is a computational constant that prevents 0 from occurring in the denominator, A_mush = 100,000 is the constant of the mushy zone, g is the gravitational acceleration, δ is the coefficient of thermal expansion, h is the enthalpy, h_ref is the reference enthalpy and c is the thermal capacity.

The energy equation is

$$S_h=\frac{\partial (\rho \Delta H)}{\partial t}$$

(9)

where the latent heat is calculated as

$$\Delta H=\{\begin{array}{cc}L,& T\ge T_m\\ 0,& T<T_m\end{array}$$

(10)

where L = 333,400 J/kg is the latent heat of water.

Natural convection is considered in this work, while the density of water is set to vary with temperature. Since the density of water reaches maximum at 4 °C, a non-linear function was adopted as [32,33,34,35]

$$\rho ={\rho }_{max}(1-\omega {\left|T-T_{max}\right|}^q)$$

(11)

where ρ_max = 999.972 kg/m³, ω = 9.297173 × 10⁻⁶·°C, q = 1.894816, T_max = 4.02935·°C. In the current mathematical model, the ice storage was assumed be a process of ice accumulation with little effect of frosting [36].

There is a thermal equilibrium between the water and the fins, which is given by

$$T_{fin,\Omega }=T_{w,\Omega }$$

(12)

$$-{\lambda }_{fin}({\frac{\partial T_{fin}}{\partial n}|}_{\Omega })=-{\lambda }_w({\frac{\partial T_w}{\partial n}|}_{\Omega })$$

(13)

where the subscript fin denotes the fins of the tube, subscript w denotes water, subscript Ω is the boundaries between the water and the fins, and n represents the normal direction of heat flux.

3. Results and Discussion

Based on the aforementioned visualization experiment and numerical model, both experimental and numerical studies on the ice formation in circular tank on the cooling tube with axially arranged fins were conducted, in an effort to clarify the involved natural convection and morphology development. In the current work, we performed repetitive experiments six times to attain reliable results.

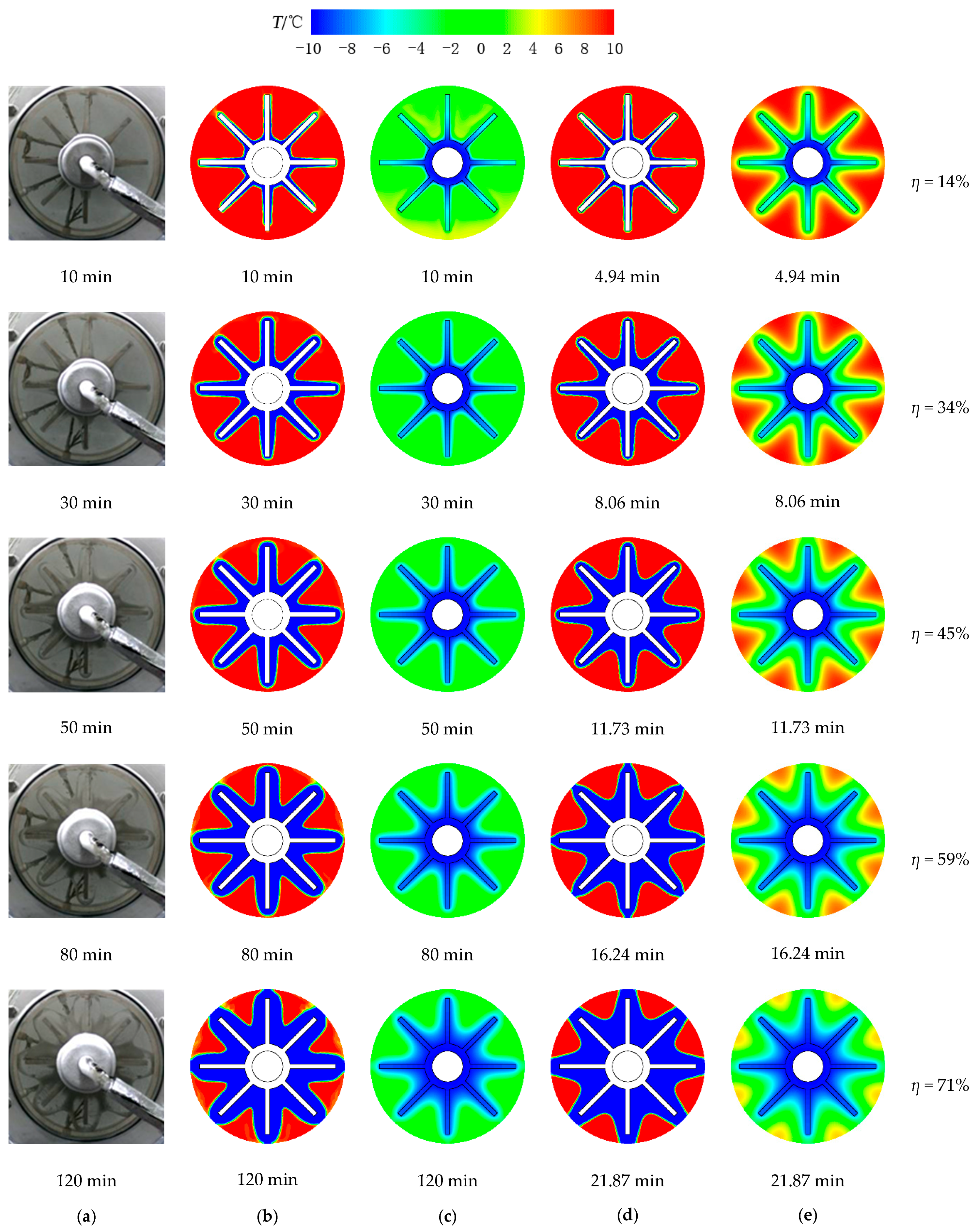
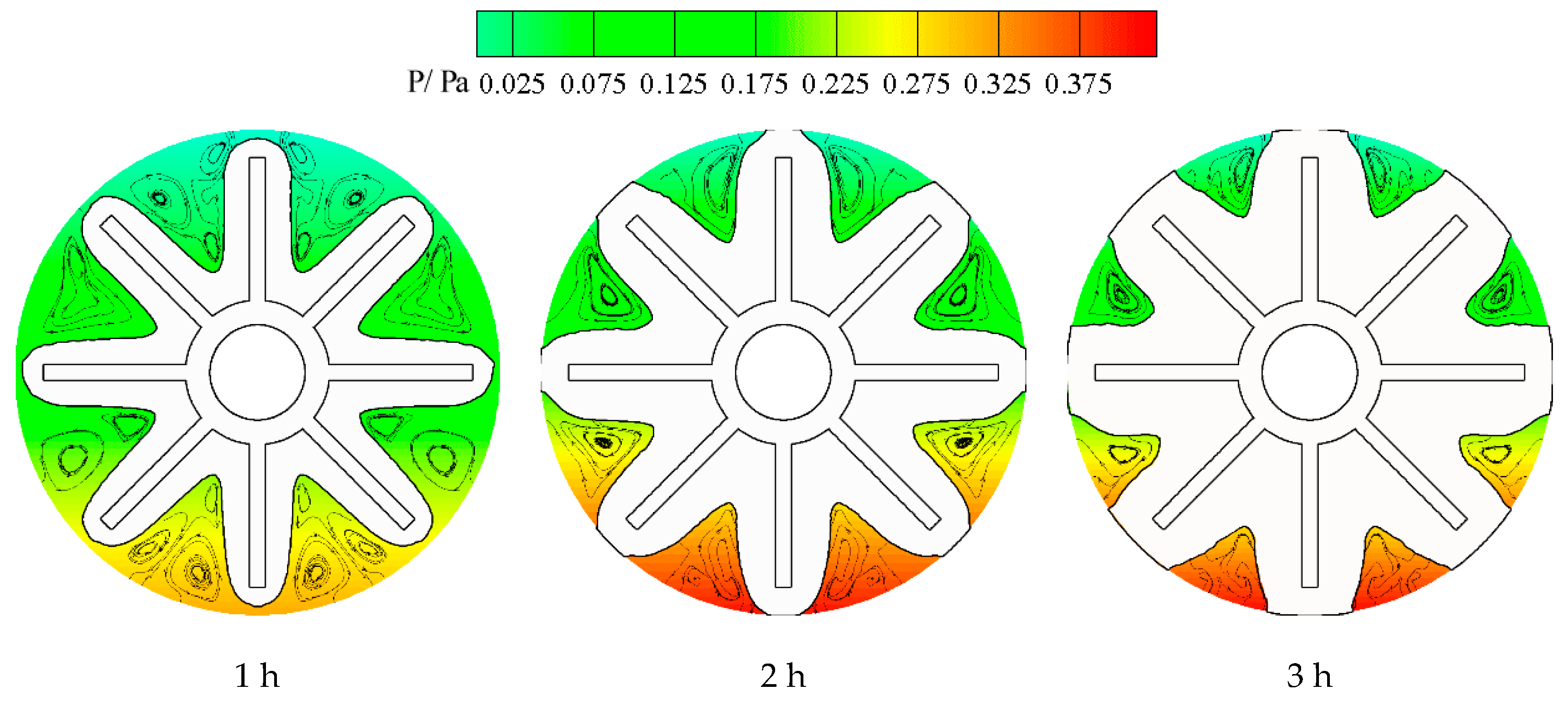
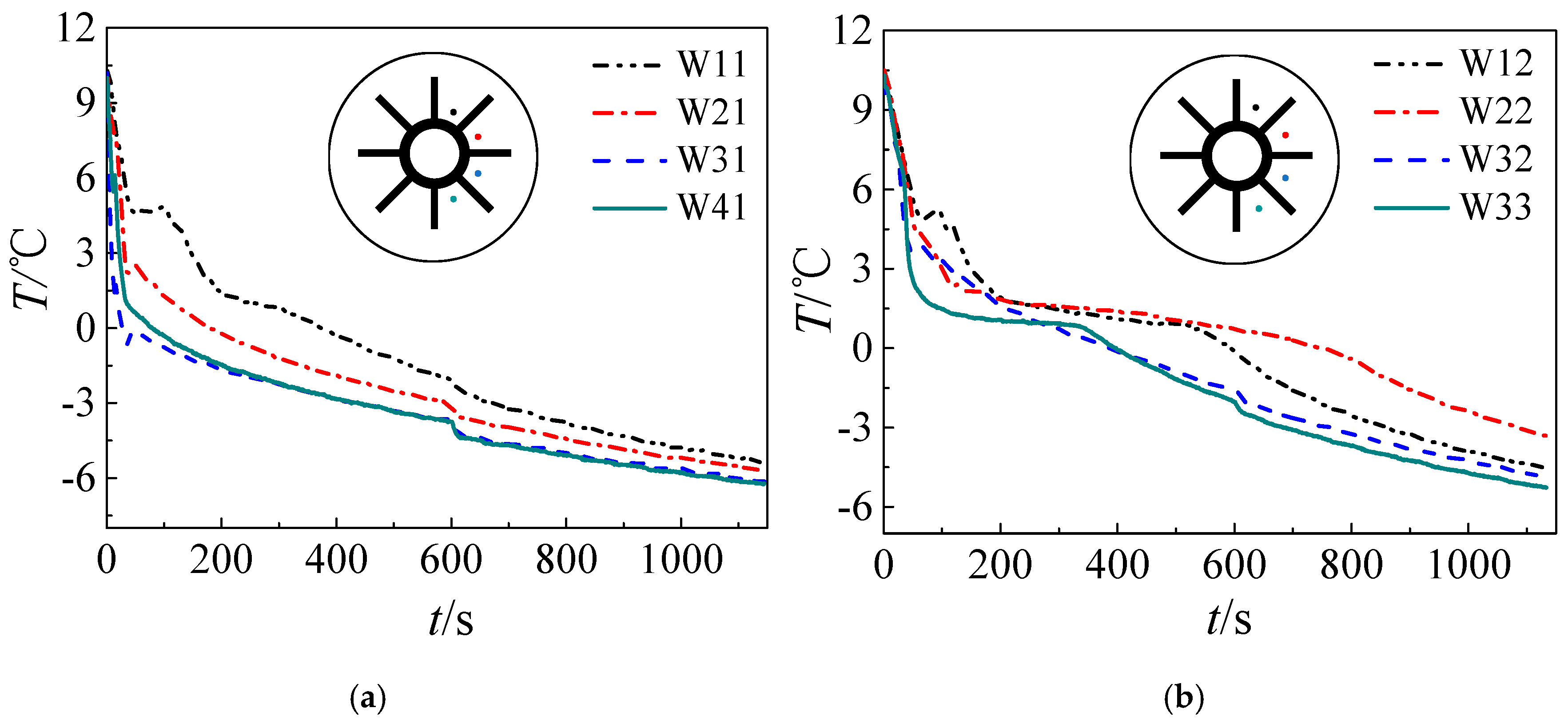
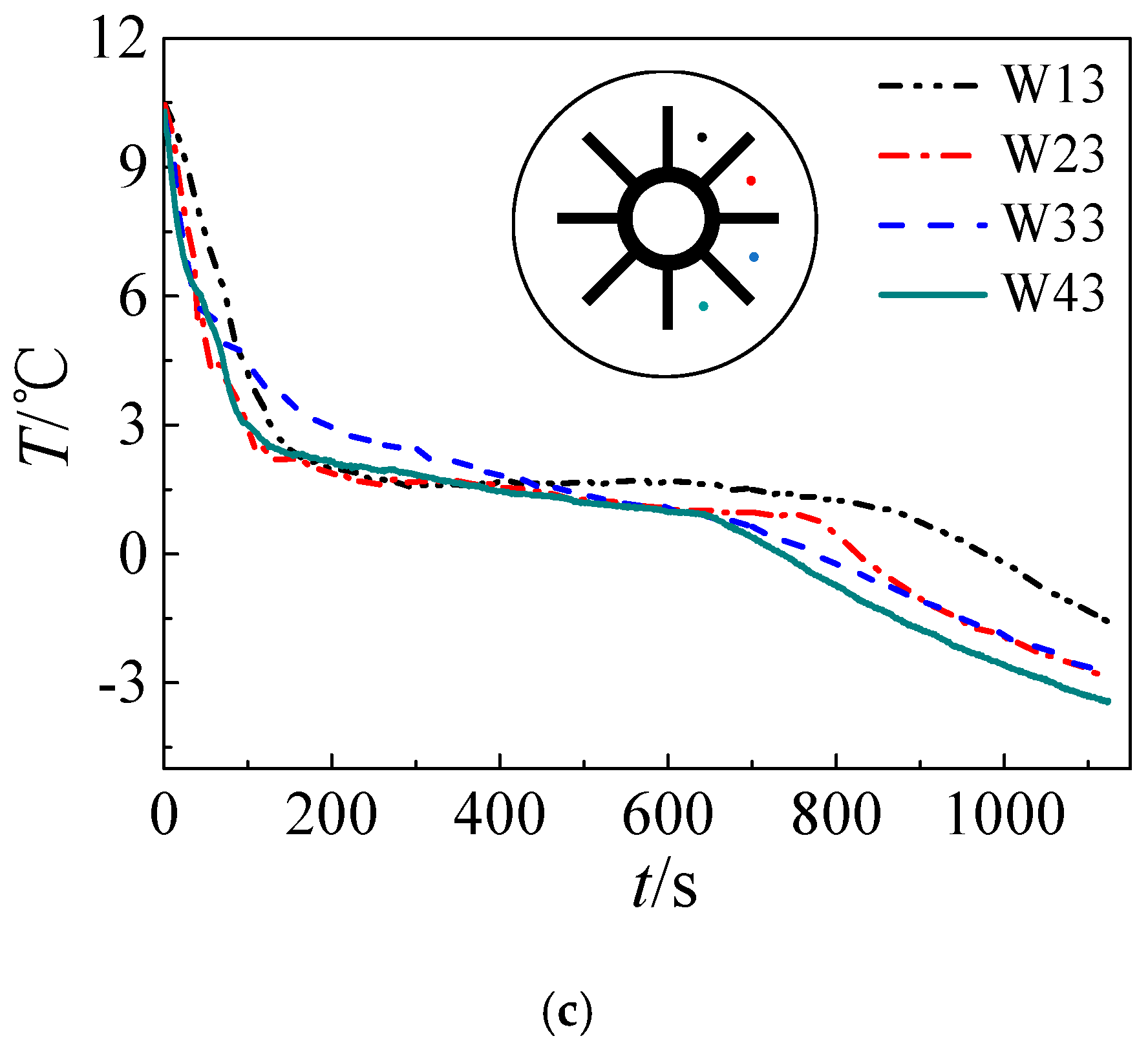
3.1. Solidification Process

To examine the evolution of the liquid–solid interface in the ice storage area, the morphologies of the ice during the ice storage process are shown in Figure 5a. The temperature of the refrigerants in this section was −10 °C and the initial temperature of the water was 10 °C. The interface reconstructed from numerical results is shown in Figure 5b (considering the effect of natural convection) and Figure 5d (neglecting natural convection). All the values used in the simulation were the same as the values in the experiments. The temperature of the inner surface of the tube was set to be constant at −10 °C and the initial temperature of the water was set to be 10 °C. The surface of the tank is set to be adiabatic. The initial pressure inside the tank was the same as the environment and the gauge pressure is 0 Pa. To further understand the heat transfer characteristics during solidification, the corresponding temperature contours and velocity vectors from numerical simulation are presented in Figure 5c,e. η is the relative ice storage ratio defined as the quality of ice divided by the total quality of water before solidification.

Evidently, the contour of the ice develops from the inner to the outer region of the tank along the fins and the shape of the ice layer resembles the shape of the fins. As can be seen from both the experimental snapshot and numerical reconstruction figures, the ice is formed on both surfaces of the tube fins at t = 10 min. This is attributed to the fast cooling effect brought by the fins and the temperature of the fins are much lower than the bulk region of water, as shown in Figure 5c. At the beginning of solidification, the thickness of the ice on the fins decreases slightly along the lengthwise direction of the fins due to the temperature gradient on the fins. The relative ice storage ratio increases with time, as shown in Figure 6. As solidification continues, the ice at the bottom of the fins connects at the adjacent fins, meaning that the ice at the bottom of the fins is thicker under the condition of no natural convection. When the cooling energy is distributed more evenly in the water, the ice layer has equivalent thickness along the fins under the influence of natural convection. The rate of solidification is at its maximum at the beginning of solidification, which can be ascribed to the high heat transfer temperature difference and low thermal resistance during this period. As the ice grows thicker and the water in the tank cools, the heat transfer temperature difference drops and the thermal resistance increases, leading to slowing down in the solidification process, as shown in Figure 6.

As soon as the temperature gradient develops in the water, natural convection occurs. It can be seen from the comparison between Figure 5b,d that the contours of the ice differ and solidification requires less time if there is no natural convection. The variation of ice thickness along the lengthwise direction of the fins is less obvious under the condition of natural convection due to the transfer of cooling energy by the flow of the water and because the temperature inside the tank is no longer longitudinally symmetrical. The temperature of water at the bottom of the sub-regions is also higher than that at the top. Consequently, solidification is faster at the top of fins than at the bottom, especially in the early stage. In addition, Figure 7 shows the natural convection in the tank. It can be seen that tank is divided into several sub-regions by the fins and some vortexes are observed in each sub-region with different profiles. Note that the number of vortexes decreases with time, suggesting that natural convection is suppressed by the increasing confinement in each sub-region with growing ice. In addition, vortexes are asymmetrical between the top and bottom of the tank due to uneven pressure distribution in the sub-regions caused by gravity. The numerical results indicate that, to store the same amount of ice, only about 20% of time is required in the system without natural convection. Decouple time is required for all the water to solidify under the influence of natural convection. This is mainly a result of the mixing of cold water around the fins and the warm water away from the fins. In particular, a large portion of the cooling energy is consumed to cool the bulk of the water through sensible heat at the beginning of the solidification. Only a small amount of cooling energy can be used to overcome the latent heat of the water around the fins and accomplish the solidification process. This can be verified by the temperature distribution inside the tank, as illustrated in Figure 5c,e. In the system without natural convection cooling energy can only be transferred through heat conduction. Hence the water near the shell of the tank was still warm even when the solidification process was over halfway complete (t = 16.24 min in Figure 5e). Water is cooler in the system with natural convection possessing smaller heat transfer difference.

In conclusion, natural convection causes the mixing of water and brings a disadvantage to the ice storage technique, especially in the system using materials with low viscosity. To reduce natural convection, materials with high viscosity and small density variation with temperature are recommended and fin structures can be designed to hinder the fluid flow.

To further understand the heat transfer affected by natural convection along the radial direction during solidification, experimental measurements of temperature variation of the points arranged radially in the tank are plotted in Figure 8. Note that the indexes of temperature points in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 are given in Figure 4 and can also be seen in the simplified schematic added in each inset. The points in Figure 8a,b are symmetric about the x-axis and the points in Figure 8a are higher than the points in Figure 8b. In both two different radial directions, the decrease in the temperature is rapid at the beginning and then gradually slows down. The temperature of the points closer to the tube such as point W21 is lower than those away from the tube such as point W24. However, due to the mixing behavior of fluids, temperature differences between the points at the outer rings (such as points W22, W23 and W24) are less obvious. Temperature fluctuations are observed in all points measured, resulting from the vortexes driven by natural convection. Besides, the temperature difference of the measuring points in Figure 8a is smaller than that in Figure 8b, indicating that heat transfer is intense in the upper part of the ice storage tank.

Caused by natural convection, water also flows in the circumferential direction during heat transfer. The evolution of the temperature of circumferentially arranged points with different distance from the tube is shown in Figure 9. Variation of the temperature for all the measuring points follows a similar tendency. However, the temperature of the points in the upper part of the ice storage tank is higher than those in the lower part due to natural convection. The temperature difference between the points closer to the tube is higher (Figure 9a) than those away from the tube (Figure 9c), indicating that the mixing behavior in the region away from the tube is stronger. This is due to the larger space for natural convection that the fluid flow is less confined.

Temperature distribution in the fins is similar in all three fins examined, as shown in Figure 10. At the beginning, the temperature drops rapidly due to the high temperature difference and heat transfer rate. This decrease slows down when solidification begins. The temperature of points close to the tube is the lowest, but the temperature difference of the fin along the radial direction is much smaller than that of the water due to the high thermal conductivity of the aluminum. Comparing Figure 8 and Figure 10, the temperature difference between the fins and water is still high at the top of the fins, indicating that heat transfer can be enhanced greatly by fins. Also, a slight temperature fluctuation in the fins is observed and this is caused by the heat transfer with water whose temperature is affected by natural convection.

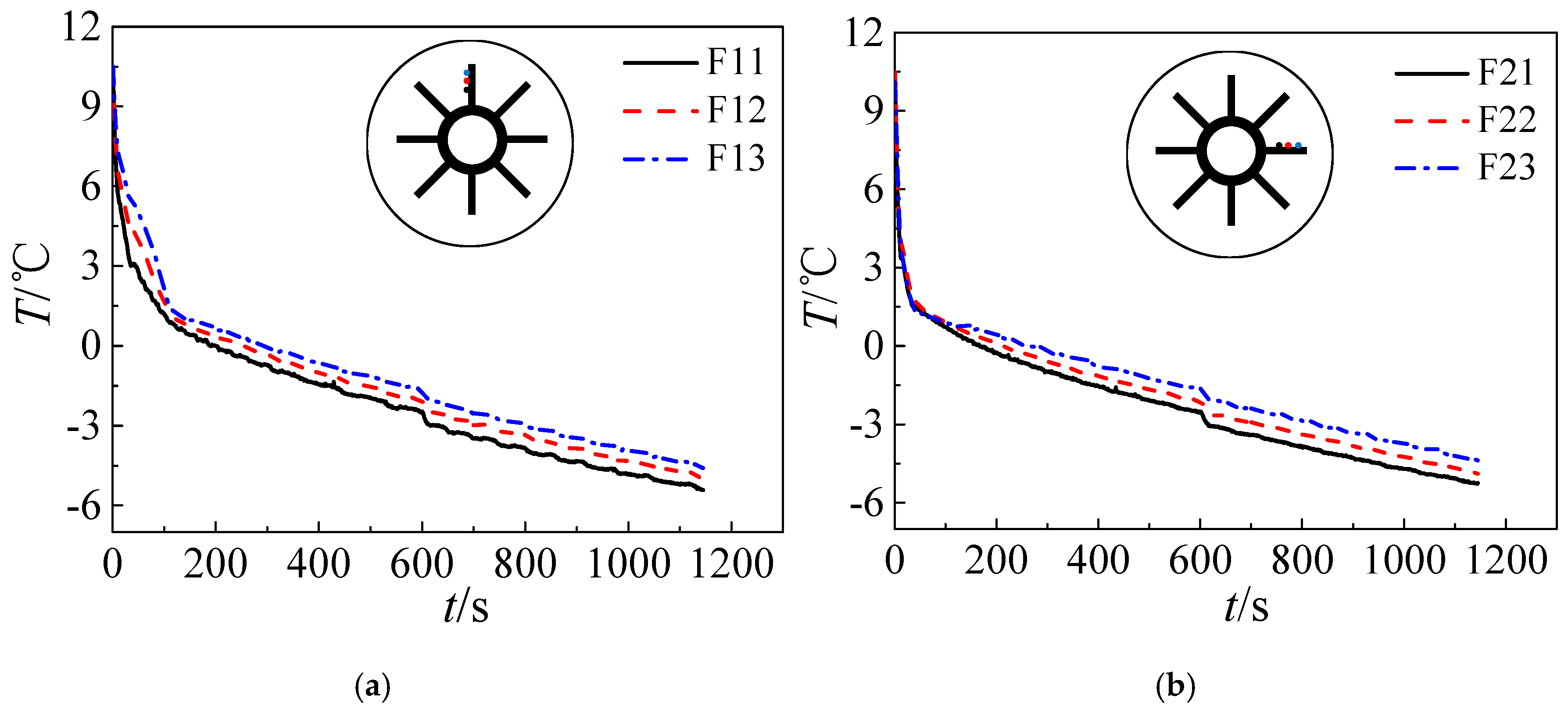
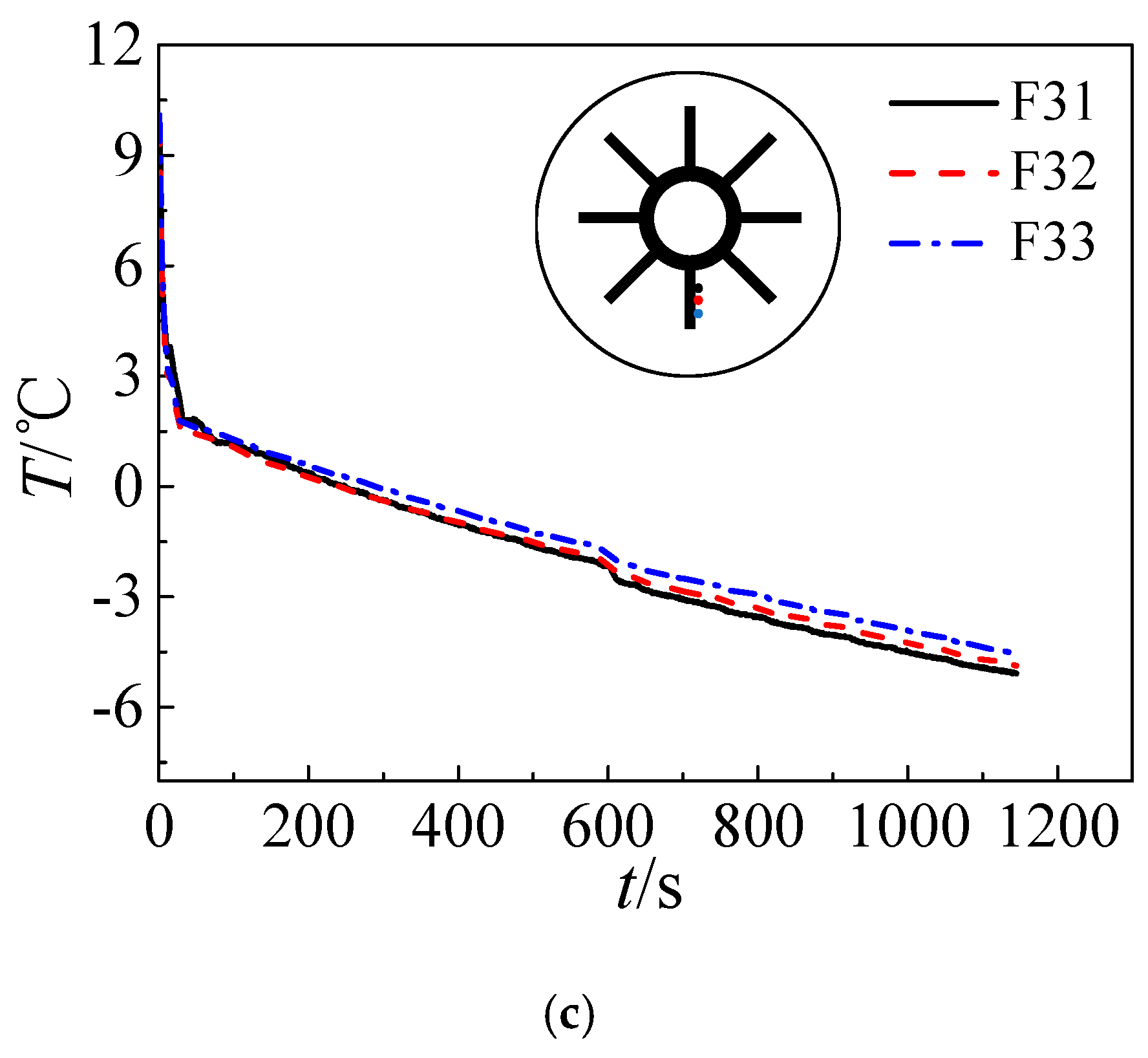
3.2. Effect of the Temperature of the Refrigerants

Table 1. Time evolution of liquid–solid interface during the ice storage process with different refrigerant temperatures.

Refrigerant Temperature	−5 °C	−10 °C	−15 °C
t = 10 min
t = 30 min
t = 50 min
t = 80 min
t = 120 min

shows the time evolution of liquid–solid interface during the ice storage processes with different temperature of the refrigerants. The decrease in the temperature of the refrigerants evidently accelerates the ice storage process. The volume of ice with the lower temperature of the refrigerant is greater. To analyze the effect of the refrigerant temperature quantitatively, Figure 11 gives the variation of the temperature in the freezing area. In all three conditions, the temperature drops rapidly due the large temperature difference and the enhancement of the heat transfer by the fins is intense during the pre-solidification phase. Following this, the ice gets thicker, which leads to a deterioration of heat transfer. Besides, a portion of the cooling energy is stored in the ice in the form of latent heat. The temperature decrease slows down soon after for all three refrigerant temperatures. During the solidification process, the temperature is stable. However, the solidification process is shortened by a lower refrigerant temperature. The temperature of the ice decreases with the refrigerant temperature, indicating that more cooling energy is stored in the form of sensible heat in ice in the system with low refrigerant temperature during the post-solidification phase. At the end of the ice storage process, temperature fluctuations can be ignored due to the weak natural convection with small liquid fraction.

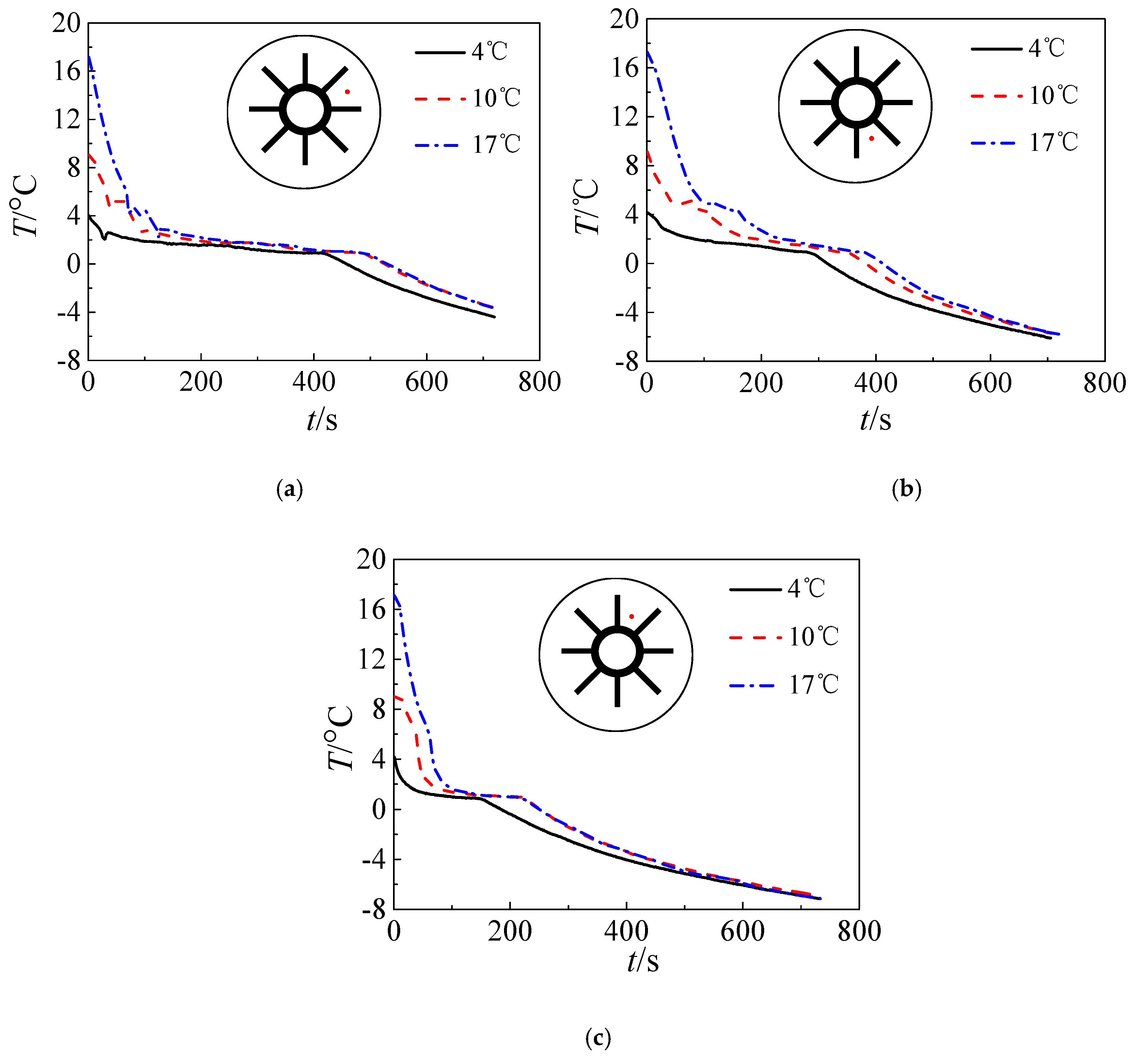
3.3. Effect of the Initial Temperature of the Water

Table 2. Time evolution of the liquid–solid interface during the ice storage process with different initial water temperatures.

Initial Temperature of the Water	4 °C	10 °C	17 °C
t = 10 min
t = 30 min
t = 50 min
t = 80 min
t = 120 min

shows the time evolution of the liquid–solid interface during the ice storage process with different initial temperatures of water. Comparing the contours of ice in Table 1 and Table 2, the influence of the initial temperature of the water is more evident than the effect of the refrigerant temperature in the pre-solidification phase. The volume of ice with a lower initial temperature of the water is much larger, indicating that the cooling of water before solidification consumes a large amount of cooling energy. As shown in Figure 12, the temperature drops rapidly in the system with high initial water temperature due to the large temperature difference between the water and refrigerant. Afterwards, the temperature is relatively stable due to the solidification. The duration of the stable period is similar in all three conditions tested; a slight difference is caused by the different strength of the natural convection.

Finally, the temperature of the same measuring point is independent with the initial temperature of the water, indicating that the effect of the initial temperature of the water is weak at the post-solidification phase.

4. Conclusions

The combined experimental and numerical studies were conducted to study ice storage performance of an ice storage tank with a finned tube. The evolution of the solid–liquid interface and the temperature variation in both the radial and circumferential directions in the water and in the fins are analyzed. The effect of natural convection on the ice storage process is discussed, with particular focus on the detailed transit of temperature distribution and ice storage ratio. In addition, via the comparison between the performances of the ice storage tank under different working conditions, the effects of the refrigerant temperature and initial water temperature on the ice storage performance are discussed. The main conclusions drawn are as follows:

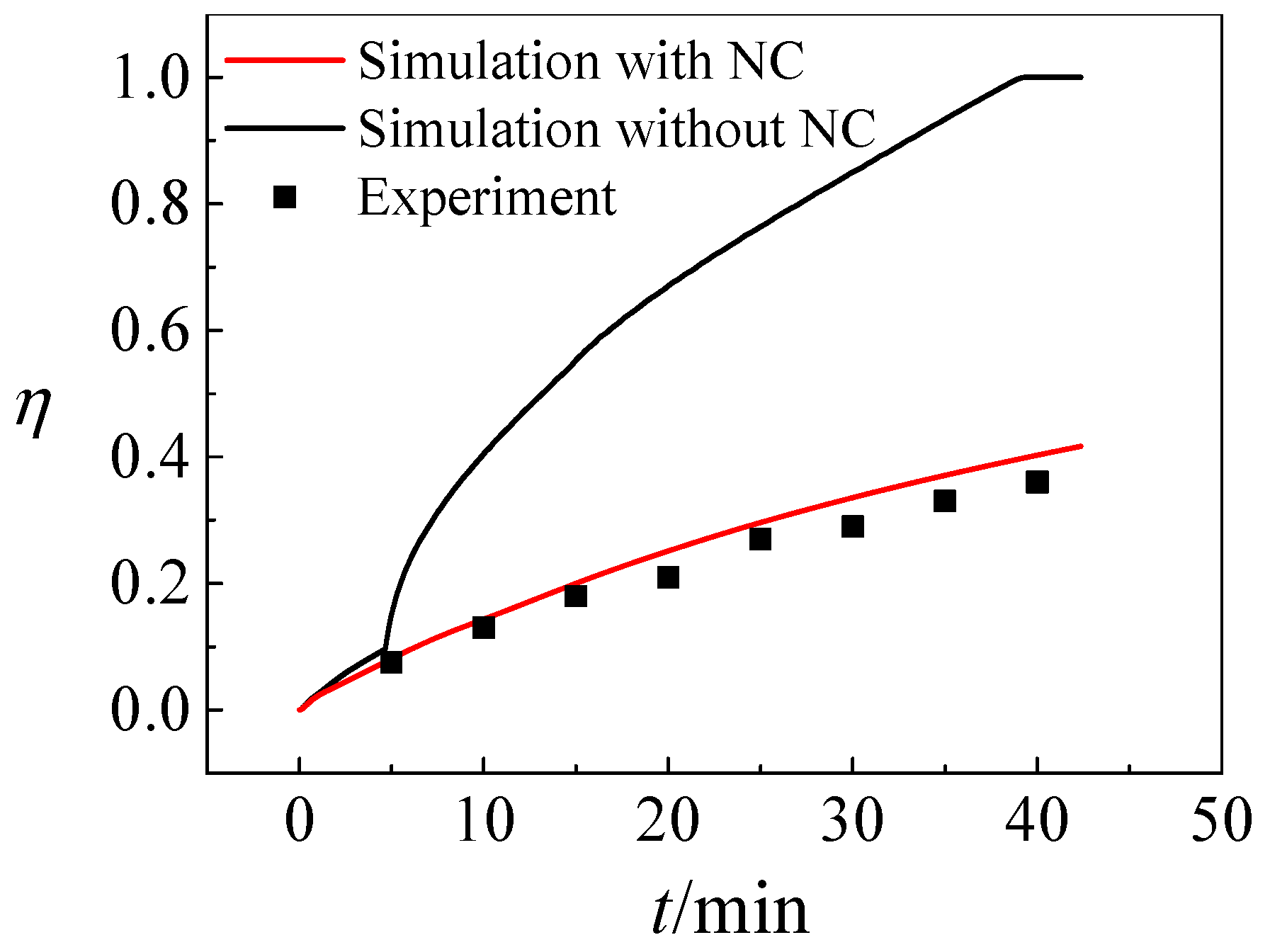
• Compared with solidification without natural convection, double the time or more is required to store the same amount of ice under the influence of natural convection. Decouple time is required for the device with natural convection to eventually solidify all the water.
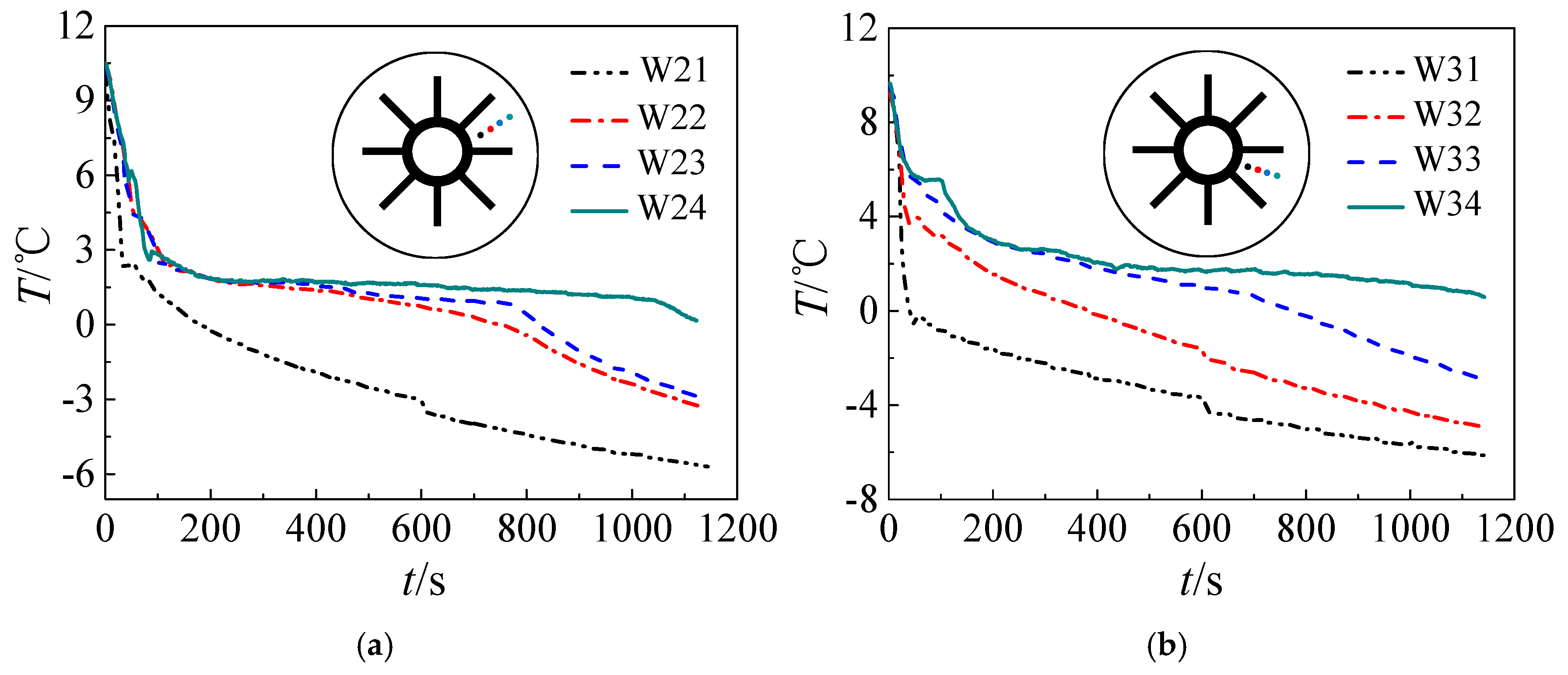
• Both numerical simulation and experimental results show that the freezing area is larger in the upper part of the tank and the temperature of the upper part is lower due to natural convection. Additionally, the liquid fraction and water area is large at the initial stage, during which natural convection is strong. Water with different temperature mixes that a large amount of cooling energy is consumed in cooling the water. The heat transfer temperature difference is reduced and less cooling energy can be occupied in solidification, indicating that natural convection is disadvantageous in ice storage systems.
• Variations of refrigerant temperature do not obviously affect the pre-solidification phase. However, the time required by solidification shortens with refrigerant temperature and more cooling energy can be stored in ice in the form of sensible heat in the post-solidification phase.
• The duration of the pre-solidification phase increases with increasing initial water temperature. However, the influence the initial water temperature on the temperature of the ice weakens with time.