Global Evolution Commended by Localized Search for Unconstrained Single Objective Optimization
Abstract
1. Introduction
2. Primary DE, DFP, and RJADE/TA
2.1. Primary DE
| Algorithm 1 Outlines of RJADE/TA Procedure. |
|
2.2. Reflected Adaptive Differential Evolution with Two External Archives (RJADE/TA)
2.3. Davidon–Fletcher–Powell (DFP) Method
3. Related Work
4. Developed Algorithm
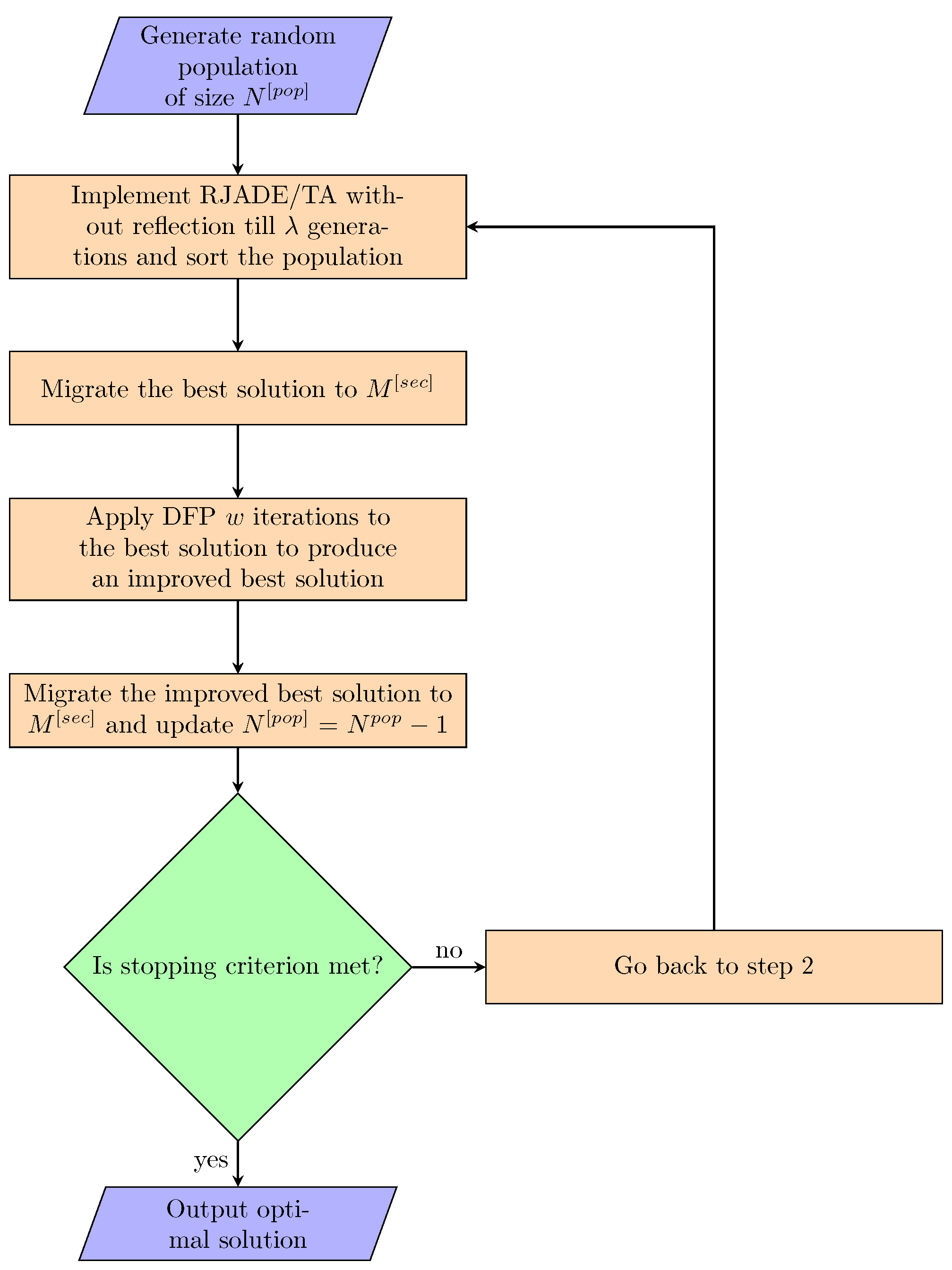
RJADE/TA-ADP-LS
| Algorithm 2 RJADE/TA-ADP-LS. |
|
5. Validation of Results
5.1. Global Search Algorithms in Comparison
5.1.1. RJADE/TA
5.1.2. RJADE/TA-LS
5.1.3. jDE
5.1.4. jDEsoo and jDErpo
5.2. Parameter Settings/Termination Criteria
5.3. Comparison of RJADE/TA-ADP-LS against Established Global Optimizers
5.4. Performance Evaluation of RJADE/TA-ADP-LS Versus RJADE/TA-LS
5.5. Analysis/Discussion of Various Parameters Used
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Price, K.V. Eliminating drift bias from the differential evolution algorithm. In Advances in Differential Evolution; Springer: Berlin, Germany, 2008; pp. 33–88. [Google Scholar]
- Xiong, N.; Molina, D.; Ortiz, M.L.; Herrera, F. A walk into metaheuristics for engineering optimization: principles, methods and recent trends. Int. J. Comput. Intell. Syst. 2015, 8, 606–636. [Google Scholar] [CrossRef]
- Storn, R.; Price, K.V. Differential Evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Storn, R. Differential evolution research—Trends and open questions. In Advances in Differential Evolution; Springer: Berlin, Germany, 2008; pp. 1–31. [Google Scholar]
- Engelbrecht, A.; Pampara, G. Binary Differential Evolution Strategies. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2007), Singapore, 25–28 September 2007; pp. 1942–1947. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R. A Discrete Binary Version of the Partical Swarm Algorithm. In Proceedings of the World Multiconference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4109. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A New Optimizer using Particle Swarm Theory. In Proceedings of the 6th International Symposium on Micromachine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Guest Editorial: Special Issue on Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 201–203. [Google Scholar] [CrossRef]
- Dorigo, M. Ant colony optimization. Scholarpedia 2007, 2, 1461. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M. Ant colony optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 36–39. [Google Scholar]
- Al-Salami, N.M. System evolving using ant colony optimization algorithm. J. Comput. Sci. 2009, 5, 380. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, K.; Li, G.; Wang, X.; Yang, S.; Ming, Z.; Huang, J.Z.; Lu, N. A smart artificial bee colony algorithm with distance-fitness-based neighbor search and its application. Future Gener. Comput. Syst. 2018, 89, 478–493. [Google Scholar] [CrossRef]
- Passino, K.M. Bacterial foraging optimization. Int. J. Swarm Intell. Res. (IJSIR) 2010, 1, 1–16. [Google Scholar] [CrossRef]
- Gazi, V.; Passino, K.M. Bacteria foraging optimization. In Swarm Stability and Optimization; Springer: Berlin, Germany, 2011; pp. 233–249. [Google Scholar]
- Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech Concurr. Comput. Prog. C3P Rep. 1989, 826, 1989. [Google Scholar]
- Fan, S.K.S.; Zahara, E. A hybrid Simplex Search and Partical Swarm optimization for unconstrained optimization. Eur. J. Oper. Res. 2007, 181, 527–548. [Google Scholar] [CrossRef]
- Yuen, S.Y.; Chow, C.K. A Genetic Algorithm that Adaptively Mutates and Never Revisits. IEEE Trans. Evol. Comput. 2009, 13, 454–472. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming II, Automatic Discovery Of Reusable Subprograms; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the IEEE World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. arXiv 2010, arXiv:1005.2908. [Google Scholar] [CrossRef]
- Larrañaga, P.; Lozano, J.A. Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation; Springer: Berlin, Germany, 2001; Volume 2. [Google Scholar]
- Zhang, Q.; Sun, J.; Tsang, E.; Ford, J. Hybrid estimation of distribution algorithm for global optimization. Eng. Comput. 2004, 21, 91–107. [Google Scholar] [CrossRef]
- Zhang, Q.; Muhlenbein, H. On the convergence of a class of estimation of distribution algorithms. IEEE Trans. Evol. Comput. 2004, 8, 127–136. [Google Scholar] [CrossRef]
- Lozano, J.A.; Larrañaga, P.; Inza, I.; Bengoetxea, E. Towards a New Evolutionary Computation: Advances on Estimation of Distribution Algorithms; Springer: Berlin, Germany, 2006; Volume 192. [Google Scholar]
- Hauschild, M.; Pelikan, M. An introduction and survey of estimation of distribution algorithms. Swarm Evol. Comput. 2011, 1, 111–128. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. Hybrid Grey Wolf Optimizer with Mutation Operator. In Soft Computing for Problem Solving; Springer: Berlin, Germany, 2019; pp. 961–968. [Google Scholar]
- Leon, M.; Xiong, N. Eager random search for differential evolution in continuous optimization. In Portuguese Conference on Artificial Intelligence; Springer: Berlin, Germany, 2015; pp. 286–291. [Google Scholar]
- Maučec, M.S.; Brest, J.; Bošković, B.; Kačič, Z. Improved Differential Evolution for Large-Scale Black-Box Optimization. IEEE Access 2018, 6, 29516–29531. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.; Wu, G.; Amaratunga, G.A. Parameter estimation of solar cells using datasheet information with the application of an adaptive differential evolution algorithm. Renew. Energy 2019, 132, 425–438. [Google Scholar] [CrossRef]
- Sacco, W.F.; Rios-Coelho, A.C. On Initial Populations of Differential Evolution for Practical Optimization Problems. In Computational Intelligence, Optimization and Inverse Problems with Applications in Engineering; Springer: Berlin, Germany, 2019; pp. 53–62. [Google Scholar]
- Wu, G.; Shen, X.; Li, H.; Chen, H.; Lin, A.; Suganthan, P. Ensemble of differential evolution variants. Inf. Sci. 2018, 423, 172–186. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N. An improved differential evolution algorithm using efficient adapted surrogate model for numerical optimization. Inf. Sci. 2018, 451, 326–347. [Google Scholar] [CrossRef]
- Al-Dabbagh, R.; Neri, F.; Idris, N.; Baba, M. Algorithm Design Issues in Adaptive Differential Evolution: Review and taxonomy. Swarm Evol. Comput. 2018, 43, 284–311. [Google Scholar] [CrossRef]
- Betzig, L.L. Despotism, Social Evolution, and Differential Reproduction; Routledge: Abingdon, UK, 2018. [Google Scholar]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2018, 44, 546–558. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P. Recent advances in differential evolution An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Cui, L.; Huang, Q.; Li, G.; Yang, S.; Ming, Z.; Wen, Z.; Lu, N.; Lu, J. Differential Evolution Algorithm with Tracking Mechanism and Backtracking Mechanism. IEEE Access 2018, 6, 44252–44267. [Google Scholar] [CrossRef]
- Cui, L.; Li, G.; Zhu, Z.; Ming, Z.; Wen, Z.; Lu, N. Differential evolution algorithm with dichotomy-based parameter space compression. Soft Comput. 2018, 23, 1–18. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.S.; Zheng, W. Differential evolution utilizing a handful top superior individuals with bionic bi-population structure for the enhancement of optimization performance. Enterpr. Inf. Syst. 2018, 1–22. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; Wiley: Hoboken, NJ, USA, 1987; pp. 80–87. [Google Scholar]
- Lozano, M.; Herrera, F.; Krasnogor, N.; Molina, D. Real-Coded Memetic Algorithms with Crossover Hill-Climbing. Evol. Comput. 2004, 12, 273–302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Khanum, R.A.; Jan, M.A.; Tairan, N.M.; Mashwani, W.K. Hybridization of Adaptive Differential Evolution with an Expensive Local Search Method. J. Optim. 2016, 1016, 1–14. [Google Scholar] [CrossRef]
- Davidon, W.C. Variable metric method for minimization. SIAM J. Optim. 1991, 1, 1–17. [Google Scholar] [CrossRef]
- Antoniou, A.; Lu, W.S. Practical Optimization: Algorithms and Engineering Applications; Springer: Berlin, Germany, 2007. [Google Scholar]
- Khanum, R.A.; Tairan, N.; Jan, M.A.; Mashwani, W.K.; Salhi, A. Reflected Adaptive Differential Evolution with Two External Archives for Large-Scale Global Optimization. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 675–683. [Google Scholar]
- Spedicato, E.; Luksan, L. Variable metric methods for unconstrained optimization and nonlinear least squares. J. Comput. Appl. Math. 2000, 124, 61–95. [Google Scholar]
- Mamat, M.; Dauda, M.; bin Mohamed, M.; Waziri, M.; Mohamad, F.; Abdullah, H. Derivative free Davidon-Fletcher-Powell (DFP) for solving symmetric systems of nonlinear equations. IOP Conf. Ser. Mater. Sci. Eng. 2018, 332, 012030. [Google Scholar] [CrossRef]
- Ali, M.; Pant, M.; Abraham, A. Simplex Differential Evolution. Acta Polytech. Hung. 2009, 6, 95–115. [Google Scholar]
- Khanum, R.A.; Jan, M.A.; Mashwani, W.K.; Tairan, N.M.; Khan, H.U.; Shah, H. On the hybridization of global and local search methods. J. Intell. Fuzzy Syst. 2018, 35, 3451–3464. [Google Scholar] [CrossRef]
- Leon, M.; Xiong, N. A New Differential Evolution Algorithm with Alopex-Based Local Search. In International Conference on Artificial Intelligence and Soft Computing; Springer: Berlin, Germany, 2016; pp. 420–431. [Google Scholar]
- Dai, Z.; Zhou, A.; Zhang, G.; Jiang, S. A differential evolution with an orthogonal local search. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2329–2336. [Google Scholar]
- Ortiz, M.L.; Xiong, N. Using random local search helps in avoiding local optimum in differential evolution. In Proceedings of the IASTED, Innsbruck, Austria, 17–19 February 2014; pp. 413–420. [Google Scholar]
- Khanum, R.A.; Zari, I.; Jan, M.A.; Mashwani, W.K. Reproductive nelder-mead algorithms for unconstrained optimization problems. Sci. Int. 2015, 28, 19–25. [Google Scholar]
- Zari, I.; Khanum, R.A.; Jan, M.A.; Mashwani, W.K. Hybrid (N)elder-mead algorithms for nonlinear numerical optimization. Sci. Int. 2015, 28, 153–159. [Google Scholar]
- Khanum, R.A.; Jan, M.A.; Mashwani, W.K.; Khan, H.U.; Hassan, S. RJADETA integrated with local search for continuous nonlinear optimization. Punjab Univ. J. Math. 2019, 51, 37–49. [Google Scholar]
- Brest, J.; Zamuda, A.; Fister, I.; Boskovic, B. Some Improvements of the Self-Adaptive jDE Algorithm. In Proceedings of the IEEE Symposium on Differential Evolution (SDE), Orlando, FL, USA, 9–12 December 2014; pp. 1–8. [Google Scholar]
- Brest, J.; Boskovic, B.; Zamuda, A.; Fister, I.; Mezura-Montes, E. Real Parameter Single Objective Optimization using self-adaptive differential evolution algorithm with more strategies. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013; pp. 377–383. [Google Scholar]
- Liang, J.; Qu, B.; Suganthan, P.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. 2013. Available online: http://al-roomi.org/multimedia/CEC_Database/CEC2013/RealParameterOptimizationCEC2013_RealParameterOptimization_TechnicalReport.pdf (accessed on 22 April 2019).


| First archive | Second archive | ||
| Primary population | Population size | ||
| Function evaluations | Maximum function evaluations | ||
| FEs of RJADE/TA | Gap between two successive updates of | ||
| Crossover probability | Mutation scaling factor | ||
| Set of successful crossover probabilities | Set of successful mutation factors | ||
| w | No. of iterations of DFP | r | Number of migrated solutions to |
| New candidate/solution at iteration y | Ever best candidate/solution at iteration y |
| Bench Marks | jDE | jDEsoo | jDErpo | RJADE/TA | RJADE/TA-ADP-LS |
|---|---|---|---|---|---|
| BMF1 | |||||
| BMF2 | |||||
| BMF3 | |||||
| BMF4 | |||||
| BMF5 | |||||
| BMF6 | |||||
| BMF7 | |||||
| BMF8 | |||||
| BMF9 | |||||
| BMF10 | |||||
| BMF11 | |||||
| BMF12 | |||||
| BMF13 | |||||
| BMF14 | |||||
| BMF15 | |||||
| BMF16 | |||||
| BMF17 | |||||
| BMF18 | |||||
| BMF19 | |||||
| BMF20 | |||||
| BMF21 | |||||
| BMF22 | |||||
| BMF23 | |||||
| BMF24 | |||||
| BMF25 | |||||
| BMF26 | |||||
| BMF27 | |||||
| BMF28 | |||||
| − | 17 | 17 | 14 | 13 | |
| + | 6 | 8 | 10 | 10 | |
| = | 5 | 3 | 4 | 5 |
| BMF1 | BMF2 | BMF3 | BMF4 | BMF5 | BMF6 | BMF7 | ||
|---|---|---|---|---|---|---|---|---|
| RJADE/TA-LS | ||||||||
| RJADE/TA-ADP-LS | Mean | |||||||
| BMF8 | BMF9 | BMF10 | BMF11 | BMF12 | BMF13 | BMF14 | ||
| RJADE/TA-LS | ||||||||
| RJADE/TA-ADP-LS | Mean | |||||||
| BMF15 | BMF16 | BMF17 | BMF18 | BMF19 | BMF20 | BMF21 | ||
| RJADE/TA-LS | ||||||||
| RJADE/TA-ADP-LS | Mean | |||||||
| BMF22 | BMF23 | BMF24 | BMF25 | BMF26 | BMF27 | BMF28 | ||
| RJADE/TA-LS | ||||||||
| RJADE/TA-ADP-LS | Mean |
| Algorithms | RJADE/TA-ADP-LS | RJADE/TA-LS |
|---|---|---|
| Number of Problems solved in total of 23 | 13 of 23 | 10 of 23 |
| % age | 57% | 43% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanum, R.A.; Jan, M.A.; Tairan, N.; Mashwani, W.K.; Sulaiman, M.; Khan, H.U.; Shah, H. Global Evolution Commended by Localized Search for Unconstrained Single Objective Optimization. Processes 2019, 7, 362. https://doi.org/10.3390/pr7060362
Khanum RA, Jan MA, Tairan N, Mashwani WK, Sulaiman M, Khan HU, Shah H. Global Evolution Commended by Localized Search for Unconstrained Single Objective Optimization. Processes. 2019; 7(6):362. https://doi.org/10.3390/pr7060362
Chicago/Turabian StyleKhanum, Rashida Adeeb, Muhammad Asif Jan, Nasser Tairan, Wali Khan Mashwani, Muhammad Sulaiman, Hidayat Ullah Khan, and Habib Shah. 2019. "Global Evolution Commended by Localized Search for Unconstrained Single Objective Optimization" Processes 7, no. 6: 362. https://doi.org/10.3390/pr7060362
APA StyleKhanum, R. A., Jan, M. A., Tairan, N., Mashwani, W. K., Sulaiman, M., Khan, H. U., & Shah, H. (2019). Global Evolution Commended by Localized Search for Unconstrained Single Objective Optimization. Processes, 7(6), 362. https://doi.org/10.3390/pr7060362






