A Computational Fluid Dynamics Approach for the Modeling of Gas Separation in Membrane Modules

Abstract

Natural gas demand has increased rapidly across the globe in the last decade, and it is set to play an important role in meeting future energy requirements. Natural gas is mainly produced from fossil fuel and is a side product of crude oil produced beneath the earth’s crust. Materials hazardous to the environment, like CO₂, H₂S, and C₂H₄, are present in raw natural gas. Therefore, purification of the gaseous mixture is required for use in different industrial applications. A comprehensive computational fluid dynamics (CFD) model was proposed to perform the separation of natural gas from other gases using membrane modules. The CFD technique was utilized to estimate gas flow variations in membrane modules for gas separation. CFD was applied to different membrane modules to study gas transport through the membrane and flux, and to separate the binary gas mixtures. The different parameters of membrane modules, like feed and permeate pressure, module length, and membrane thickness, have been investigated successfully. CFD allows changing the specifications of membrane modules to better configure the simulation results. It was concluded that in a membrane module with increasing feed pressure, the pressure gradient also increased, which resulted in higher flux, higher permeation, and maximum purity of the permeate. Due to the high purity of the gaseous product in the permeate, the concentration polarization effect was determined to be negligible. The results obtained from the proposed CFD approach were verified by comparing with the values available in the literature.

1. Introduction

Natural gas is considered one of the significant fossil fuels. It is found in subsurface reservoirs and mostly produced as a byproduct of oil production. The demand for natural gas has seen a considerable rise in recent years [1,2]. As per the reports of the U.S. Energy Information Administration (EIA), global natural gas consumption is increasing 4% annually. It is estimated that 10% of the world power sector depends on natural gas [3]. By 2040, power production and industrial usage are expected to be 73% dependent on natural gas. Natural gas consists of several chemical species, including methane (CH₄), ethane, propane, butane, water vapor, nitrogen, and acidic gases such as carbon dioxide (CO₂) and hydrogen sulfide (H₂S). The species comprising natural gas, like CO₂, N₂, water vapor, and H₂S, are considered impurities [4]. The different concentrations of impurities in natural gas is in the range 4–50%, depending on the reservoir. The presence of these impurities can significantly affect pipelines, in terms of corrosion, and raise health and safety concerns [5]. Therefore, typical pipeline specifications usually mandate that the concentration of carbon dioxide in natural gas not exceed 2–5 volume percent, making it necessary to treat natural gas and remove the impurities before it is transported. In recent years, the membrane separation process has been widely used because it is more economical compared to other methods [6].

Membrane gas separation can remove unnecessary species from a gas mixture. The membrane allows only the desired components of a mixture to pass through because of its selectivity [7]. It is a widely used process due to its reliability, separation performance, low maintenance, and easy operation [8]. Moreover, membrane technology is used for the separation of various fuel mixtures in different industries as a result of economic competitiveness and other current demanding situations related to competitive environments [9]. It has many applications in industrial sectors, hydrogen recovery from ammonia, hydrogen recovery in refineries, air separation for oxygen purification, sour gas treatment, and carbon dioxide removal from natural gas [10]. These processes are integrated with big industrial units to perform specific industrial operations. It is estimated that the use of membrane gas separation will increase substantially in 2020 [11]. It is an essential fact that the use of this technology will decrease the unit operation cost of gas separation and reduce the environmental hazards [12].

The different mathematical models for the separation of gaseous mixtures using a membrane were developed using altered assumptions [13]. Recently, it was found that the most commonly available commercial membrane modules for gas separation were hollow fiber and spiral wound membrane modules [14,15]. Many researchers have investigated flow behavior with different module arrangements for gas separation and desalination processes [16,17]. Alrehili’s study [18] showed the different arrangements of fibers with parallel feed channels that made a hybrid membrane module. The simulation results of the hybrid module gave better membrane flux for both spiral wound and hollow fiber membrane module configurations. Ahsan [19] applied computational fluid dynamics (CFD) modeling to gas separation using a finite difference method in polymeric membranes. Saeed [20] described laminar flow behavior in spacers with narrow channels, and mass transfer coefficient calculated with different wire spacing. Karode [21] determined that pressure dropped with bounding surfaces in a rectangular channel. The effect of shear stresses on both sides of the membrane was also observed.

Other researchers developed a mathematical algorithm for flow behavior and membrane surfaces, and investigated the concentration polarization phenomena in gas separation processes [22]. The transfer of CO₂ gas molecules through the membrane increased due to higher flux on the feed side, but rejected molecules of other gases that then accumulated on the membrane surface [23]. For this reason, concentration polarization occurs in membrane processes. Mourgues [24] showed the effect of concentration polarization on membrane separation processes for both counter-current and co-current patterns. The most important factors were analyzed based on feed pressure, permeability, and selectivity of the mixture.

Several researchers developed membrane processes to study the influence of concentration polarization on the feed side. Ahsan and Hussein [25], in their CFD model, studied energy transfer phenomena in the membrane using permeation flux. Coroneo [26] developed a three-dimensional single-tube membrane module to define flux, based on Sievert’s law, considering both membrane sides. Recently, a non-isothermal model was developed to evaluate the effect of temperature on permeance [27]. In another study, Chen [28] considered co-current and counter-current flow patterns of the membrane process at different operating conditions using COMSOL Multiphysics 4.0a software.

Another study looked at plug flow and perfect mixing channel, commonly used for modeling membrane gas separation, and reported the fluid behavior in permeate [29]. Flat sheet membrane modules were widely used to evaluate membrane performance. The incompressible Navier–Stokes model was used to improve the fluid chamber while the solid stress–strain model was used to enhance the mechanical performance of the module [30].

In this study, the CFD technique was used to solve the model equations. The permeability of the membrane was measured by introducing the species of interest into the feed gas. The effect of gas flow profiles on gas separation in the membrane modules is reported. A three-dimensional (3D) model was established using CFD simulation in COMSOL Multiphysics software. The geometry of the flat sheet and spiral wound membrane modules were determined, and co-current and counter-current models were used to find the flow profiles. The effect of molar flux on species transported en mass through the membrane was considered. The binary gas mixtures CO₂/CH₄ and CH₄/C₂H₆ were used for separation in the flat sheet and spiral wound membrane modules, respectively. The investigated parameters, permeability, feed pressure, permeate pressure, and feed gas concentration, were compared with the data available in the literature.

2. Numerical Methods

The CFD technique (COMSOL Multiphysics® 4.3, COMSOL, Inc., Burlington, MA, USA, 2012) is used in simulations looking at flow profiles in the membrane module. In this study, the flat sheet and spiral wound membrane modules were used for the simulations. The data used for the simulations were taken from the literature and are shown in

Table 1. Properties for membranes modules. Reproduced with permission from R. Qi, M.A. Henson, Separation and Purification Technology; published by Elsevier, 1998.

Parameters	Spiral Wound Membrane Module [31]	Flat Sheet Membrane Module [32]	Units
Feed Pressure	35$\times$105	106.7$\times$103	Pa
Permeate Pressure	1.05$\times$105	1.1$\times$103	Pa
Feed gas	0.20 CO2	0.395 CH4	Mole fraction
Permeance	1.48$\times$10−9	2$\times$10−7	mol/(m2·s·pa)
Selectivity	20	2.73
Module Diameter	0.3	6$\times$10−3	m
Module Length	1	0.8	m
Thickness	2.84$\times$10−3	15$\times$10−6	m

.

The numerical simulations were performed using the COMSOL Multiphysics^® package (COMSOL Multiphysics® 4.3, COMSOL, Inc., Burlington, MA, USA, 2012). The spiral wound and flat sheet membranes were developed with 3D axisymmetric geometry. Fick’s law of permeation was used for the main transport of diluted species through the membrane. The following assumptions were made [13].

2.1. Assumptions

• Steady-state and ideal gas conditions;
• Isothermal conditions;
• Solution–diffusion mechanism for permeation;
• Permeance not dependent on the concentration of gas or the feed pressure;
• No axial mixing of gaseous molecules;
• Constant pressure drop on the feed and permeate side.

2.2. Mathematical Modeling of Mass Transport

The model accounts for diffusion transport in a unit cell of the structure sketched in Figure 1. The unit cell is a small part of the membrane that is representative of the whole membrane. In this model, the initial flux in the membrane was studied, and corresponded to the largest difference in concentration between the two chambers on different sides of the membrane. The supporting structure in the membrane consisted of a mesh structure made up of a dense and rigid polymeric material. This system was used to classify the permeability properties of a membrane to certain species.

2.2.1. Convection and Diffusion Model

In the convection and diffusion model, the mass transport equation contained both phenomena. In chemical engineering, the convection and diffusion model is applicable for mass transport, which is described by Fick’s Law. In the 19th century, Fick gave the simplest definition of diffusion for mass transport. The mass flux of any species is directly proportional to the concentration gradient due to diffusion. The rate of change of concentration at a point in space is proportional to the second derivative of concentration with space;

$$\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{t}}{ + \mathrm{v}}_{\mathrm{x}}\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{x}}{ + \mathrm{v}}_{\mathrm{y}}\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{y}}{ + \mathrm{v}}_{\mathrm{z}}\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{z}}{ = \mathrm{D}}_{\mathrm{AB}}\left[\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{x}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{y}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{z}}\right]{+\mathrm{R}}_{\mathrm{a}}$$

(1)

Convective transport accounts for the bulk flow of fluid due to velocity v. This term v can be solved analytically or by solving the momentum equation with the mass balance equation. All these expressions include time (t), and spatial and velocity components are used for mass balance with convection. The v_x, v_y, and v_z are velocity fields in three dimensions. R_a describes the rate of reaction and it should be equal to zero as no reaction is involved in gas separation in membrane modules.

2.2.2. Diffusion Term

The chemical species is transferred from high to low regions due to diffusion, and becomes a mass transfer phenomenon with time and space. The chemical species is dissolved in a solvent or any gas mixture, for example as oxygen enrichment in the air. The evolution of species mass transfer depends on its concentration with respect to time and space. The gradient for diffusion occurs as a result of the motion of the molecules. Due to the kinetic energy of molecules, they can collide with each other in random directions. Then, flux ${\mathrm{N}}_{\mathrm{a}}$ for diffusion can be written as;

$${\mathrm{N}}_{\mathrm{a}}{=-\mathrm{D}}_{\mathrm{AB}}\left[\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{x}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{y}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{z}}\right]$$

(2)

where mass transfer occurs as a result of diffusion ${\mathrm{D}}_{\mathrm{AB}}.$

2.2.3. Membrane Model

The unit cell is a small part of the membrane module that demonstrates the whole membrane module. The steady-state diffusion equation, which shows mass transport in a model with diffusion, can be written as;

$${\mathrm{D}}_{\mathrm{AB}}\left[\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{x}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{y}}+\frac{{\partial }^2{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{z}}\right]=0$$

(3)

It can also be represented in terms of a nebula operator;

$$\mathrm{D}·{\nabla }^2{\mathrm{C}}_{\mathrm{a}}=0$$

(4)

where ${\mathrm{C}}_{\mathrm{a}}$ denotes concentration (mole/m³) and ${\mathrm{D}}_{\mathrm{AB}}$ is the diffusion coefficient of the diffusing species (m²/s). All boundaries are considered to be insulating

$${\mathrm{D}}_{\mathrm{AB}}\left[\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{x}}+\frac{\partial {\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{y}}+\frac{\partial \mathrm{Ca}}{\partial \mathrm{z}}\right]=0$$

(5)

$$\mathrm{D}\nabla {\mathrm{C}}_{\mathrm{a}}·\mathrm{n}=0$$

(6)

The two faces are applied as boundary conditions where the concentration of the two components is set from high to low. Boundary Condition 1 (B.C.1) is considered to be high concentrations on the feed side and Boundary Condition 2 (B.C.2) is represented on the reject side in low concentrations.

B.C.1

$${\mathrm{C}=\mathrm{C}}_0$$

(7)

B.C.2

$${\mathrm{C}=\mathrm{C}}_{0,1}$$

(8)

2.2.4. Membrane Flux

Diffusion through the membrane was represented in terms of the initial boundary condition ${\mathrm{C}}_0$ and the final boundary condition ${\mathrm{C}}_{0,1}$.

$${\mathrm{N}}_{\mathrm{a}}=\frac{\mathrm{D}}{\mathsf{\delta }}\left({\mathrm{C}}_0-{\mathrm{C}}_{0,1}\right)$$

(9)

where $\frac{\mathrm{D}}{\mathsf{\delta }}$ is a barrier with a corresponding thickness.

The permeability (P) of gas can be defined as a product of the diffusion coefficient (D) and solubility coefficient (S),

$$\mathrm{P}=\mathrm{D}·\mathrm{S}.$$

(10)

The relationship between partial pressure and concentration is defined as

$$\mathrm{C}=\mathrm{S}·\mathrm{p}.$$

(11)

The flux through the membrane can be presented in terms of permeability and partial pressure,

$${\mathrm{N}}_{\mathrm{a}}=\frac{\frac{\mathrm{P}}{\mathrm{S}}}{\mathsf{\delta }}\left(\mathrm{S}·\mathrm{pf}-\mathrm{S}·\mathrm{ph}\right)$$

(12)

where feed pressure $\mathrm{pf}$ and permeate pressure $\mathrm{ph}$ are used for calculating gradient across the membrane. Solubility is obtained using a ratio of the concentration gradient and partial pressure difference for the binary mixture. The solubility S can be calculated as

$$\mathrm{S}=\frac{\Delta \mathrm{p}}{\Delta \mathrm{C}}.$$

(13)

This membrane model was used to study gas separation in flat sheet and spiral wound membrane modules.

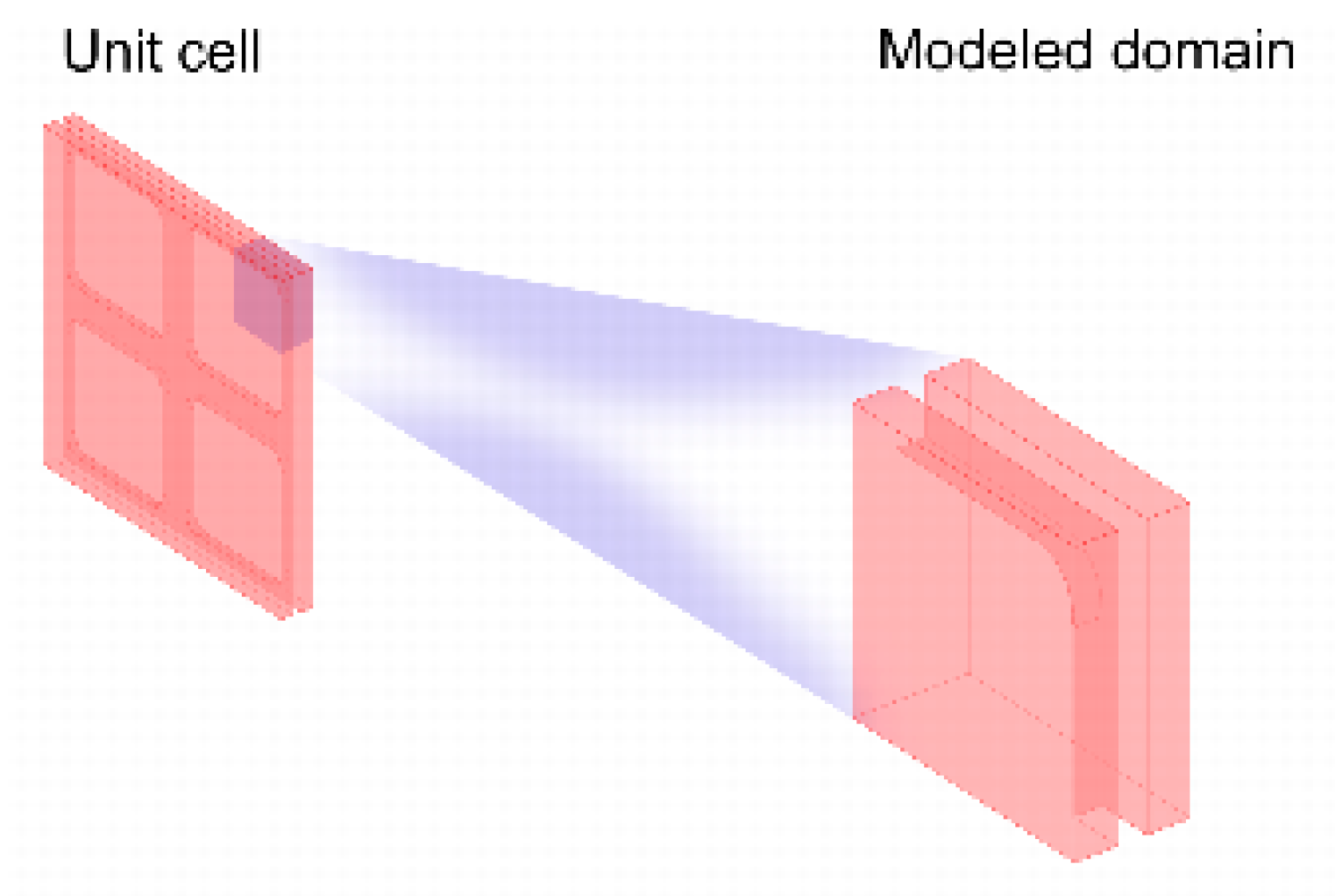
2.3. Geometry

A sketch of the geometries of flat sheet and spiral wound membrane modules is shown in Figure 2.

2.4. Meshing

The subdomains are often called elements or cells, and the collection of all elements or cells is called a mesh (Figure 3). In this process, a physics-controlled mesh was applied. An extremely fine grid element was used, while a further increase did not affect the model results. The mesh consisted of 1,324,604 domain elements, and 46,750 boundary elements, and 900 edge elements were used for the flat sheet membrane module. The mesh consisted of 3,257,454 domain elements, 413,420 boundary elements, and 3439 edge elements used for the spiral wound membrane module.

3. Results

CFD analysis was performed for the flat sheet and spiral wound membrane modules. The simulation was carried out using COMSOL Multiphysics software 5.2a. Fluxes of gases and concentration variations were found across the length of membrane modules. Various parameters like feed pressure, concentrations across the length of the module, permeability, and feed were considered in this study.

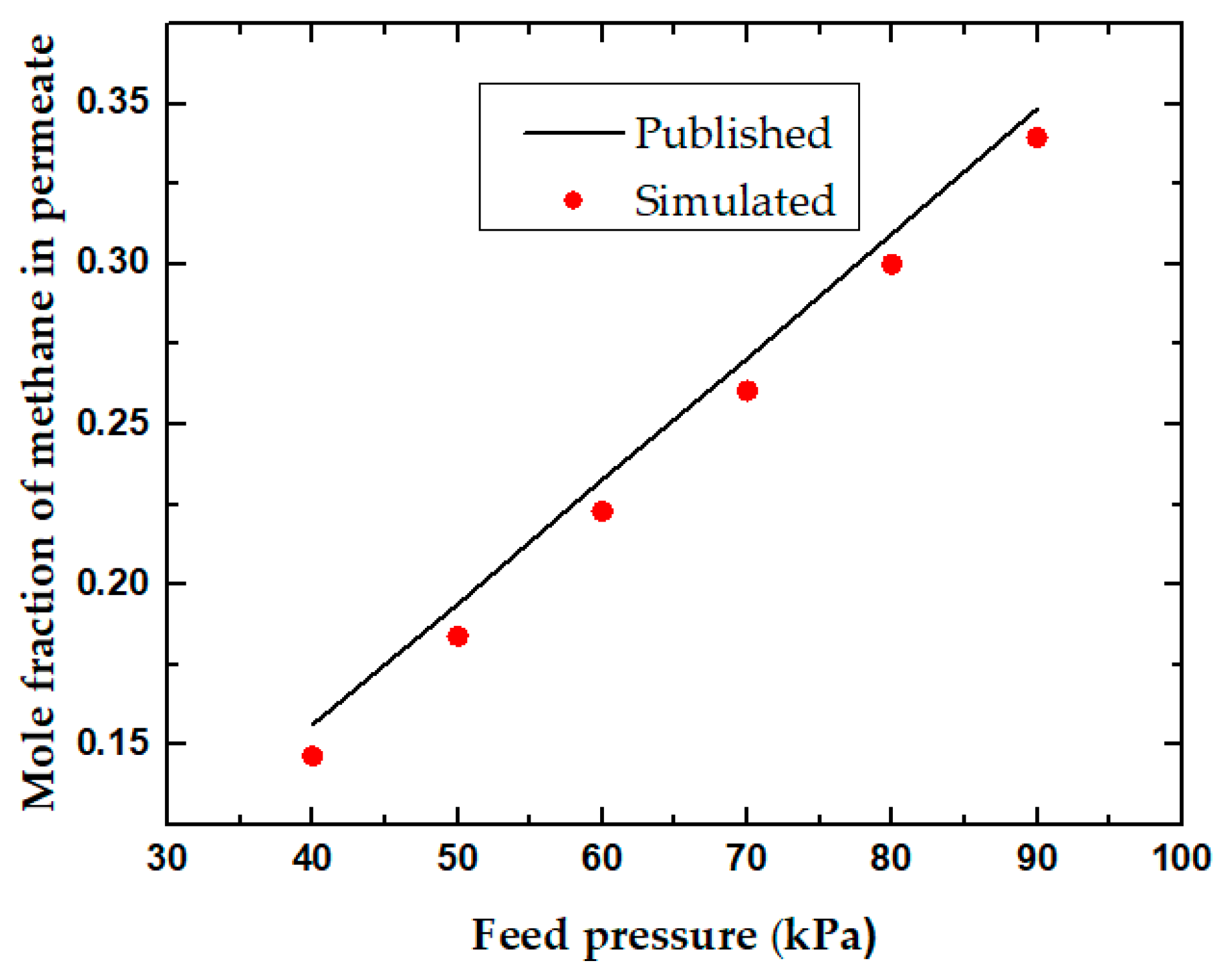
3.1. CH₄/C₂H₆ Separation

The flat sheet membrane module is usually used for pilot plant testing or lab scale testing. The separation of methane and ethane was considered for the flat sheet membrane module in this study. The simulation of a flat sheet membrane module was performed to check the concentration change on the reject and permeate sides. The feed gas entered the membrane module and the permeate collected at the bottom of the module. A cross-flow model with specific boundary conditions was used. The boundary conditions included a high feed concentration on the right side and low feed concentration on the left side. Figure 4a shows the concentration variation of CH₄ on the feed and permeate sides. The contour shows the concentration variation of gas on both sides of the membrane. The slice centration shows the gas variations in the center of the module. Figure 4b shows the differing concentration variation from the feed side to the permeate side. The gas moved through the flat sheet module and permeate collected at the bottom.

Figure 4c shows the concentration gradient of CH₄ present in the flat sheet membrane module. Streamlines were used for concentration gradient representation in Figure 4c. The lines moving from high to low and passing through the membrane represent the gas diffusion through the membrane. The membrane is located in the center of the module and the permeate is shown on the bottom surface. The results verified that a gradient was present, and that gas diffused through the membrane. The flux was calculated for the given parameters using COMSOL Multiphysics software. The contour in Figure 4d indicates the flux variations in the flat sheet membrane module. The color bar shows the flux magnitude in the module. The flux calculated in the module can be explained by Fick’s law.

3.2. CH₄/CO₂ Separation

The simulation of a spiral wound membrane module was presented to show the concentration of feed CO₂ on the reject and permeate sides. The feed gas entered the membrane module from the central tube and moved through to the end. The module shows that the concentration of CO₂ changed throughout Figure 5a. The high concentration was applied to the first wrapped sheet as a boundary condition, permeate collected in the permeate channel, and a low concentration was applied to the second plate of the membrane module.

The contour shows that the gas concentration varied along the membrane on the permeate and reject sides. Figure 5b shows the slice concentration of CO₂ in a spiral wound membrane module. The result shows the concentration variation in the center of the module. It verifies that the gas diffused through the membrane from the feed channel and collected in the permeate channel. Figure 5c shows the concentration gradient present in the spiral wound membrane module for CH₄/CO₂ separation. The arrows show that the gas passes through the membrane from the feed side to the permeate collector of the module. The results prove that a gradient was present, and that the gas diffused through the membrane. Figure 5d shows the diffusive flux magnitude in the spiral wound membrane module for CO₂. The diffusive flux magnitude in the membrane module was obtained using concentration and permeability parameters. The flux through the membrane was calculated in the gas separation process and depended on gas diffusion in the perm-selective membrane, due to the pressure and concentration gradient. It illustated that mass transport occurred through the membrane in the spiral wound membrane module.

3.3. Parametric Study of the Spiral Wound Membrane Module

Feed Pressure and Permeate Pressure

The membrane length was considered for the spiral wound membrane module, and the results were verified via the literature. Figure 6 shows that permeate pressure was a function of membrane length for different values. Basically, the permeate pressure was less than the feed pressure. Therefore, it was necessary to calculate the changes in permeate pressure according to length. Increasing the membrane module’s length decreased the permeate pressure because of the gradient changes throughout the module from the feed side to the reject side. Therefore, less mass transfer occurred as a result of less gradient in the module. It was observed that feed pressure had a reverse effect on permeate pressure. An increase in the feed pressure produced more gradient across the membrane, which resulted in higher mass transfer through the membrane. Figure 7 represents the feed pressure variation with methane recovery in the spiral wound module. The results show that higher amounts of methane permeate were obtained in the end because a high gradient was produced, and gas diffusion through the membrane was very high.

3.4. Parametric Study for the Flat Sheet Membrane Module

Feed Pressure and Length

It was observed that the permeate concentration changed along the length of the module. The more permeable components passed through the membrane while other components were left as rejects. The CH₄ gas was more suitable for permeation through the membrane. Figure 8 demonstrates that the mole fraction of CH₄ increased on the permeate side across the length of the module and decreased on the reject side, with respect to length. The ethane gas increased on the reject side because the permeation of ethane through the membrane was very low. Therefore, the maximum possible purity of the gas was achieved.

Figure 9 shows that increasing the feed pressure causes the gradient to increase. Due to high feed pressure, the permeation of components through the membrane increased when the driving force increased. Therefore, it was estimated that the higher the feed pressure the better the separation. This was also true for methane recovery on the permeate side because increasing feed pressure resulted in more pressure gradient and turbulence for mass transfer. Therefore, the gas passed through the membrane. The permeate values calculated by the numerical model for the spiral wound and flat sheet membrane modules are shown in

Table 2. Comparison of the model results with the published data for CH₄ (permeate) at different values of selectivity.

Spiral Wound Membrane Modules				Flat Sheet Membrane Module
Selectivity PA/PB	CH4 (Permeate)		Difference (%)	Selectivity PA/PB	CH4 (Permeate)		Difference (%)
	Published [31]	This Model			Published [32]	This Model
20	0.881	0.786	10.8	2	0.457	0.417	8.7
40	0.936	0.903	3.5	4	0.672	0.635	5.5
60	0.952	0.913	4.1	6	0.749	0.718	4.2
80	0.967	0.929	3.9	8	0.891	0.829	6.9

for comparison with published data. A maximum difference of 10.8% and 8.7% was found for the spiral wound and flat sheet membrane modules, respectively.

4. Discussion

Computational fluid dynamics simulations were used to study mass transport in spiral wound and flat sheet membrane modules. Three-dimensional geometrics were considered to analyze the membrane-based gas separation for the binary gas mixture. Counter-current and cross-flow membrane models were used to verify the results. The simple Fick’s law was used to explain mass flux transport of the binary gas mixture through the membrane. The membrane model was defined using COMSOL Multiphysics software for the separation of the binary mixture. The membrane model was applied as a thin diffusion barrier, which allowed certain species to pass through the membrane. The effect of molar flux for species in mass transport through a membrane was considered. In the present model, the different parameters were investigated to verify the models in the literature. Different gas mixtures, like CO₂/CH₄ and CH₄/C₂H₆, were investigated in different membrane modules.

A spiral wound membrane module was discussed for CH₄/CO₂ membrane separation. The module geometry consisted of three flat sheets that wrapped around a central tube. The membrane collector was present at the center of the feed and reject sides. The cross-flow model was applied to verify the literature results. In the spiral wound membrane module, the increase in membrane length showed a considerable decrease in concentration polarization. When the length of the membrane increased, an increase in the residual mole fraction was observed. An increase in the permeate purity was also observed, which indicated that the concentration polarization was negligible.

A flat sheet membrane module was considered for the separation of CH₄/C₂H₆. The model showed a variation of membrane results that have been discussed. This was novel work describing the flow profiles of gases in different membrane modules. The contour also showed the total flux, concentration gradient, and diffusive flux magnitude of different membrane modules. The investigated parameters were compared with published results. It was observed that in a flat sheet membrane module with increasing feed pressure, the pressure gradient also increased, which resulted in higher flux, higher permeation, and maximum purity of the permeate. The concentration polarization was observed to be negligible. Furthermore, with increasing module length in the flat sheet membrane module, a decrease in concentration polarization was observed because the increase in the module length resulted in more permeation of the desired component and an increase in permeate purity. In the spiral wound membrane module, increasing the membrane length resulted in a considerable decrease in concentration polarization. When the length of the membrane was increased, an increase in the residual mole fraction was observed. An increase in the permeate purity was also observed, which indicated that the concentration polarization was negligible.

5. Conclusions

The membrane modules were modeled using CFD to obtain the maximum possible value of the desired gas in the permeate. The effect of concentration polarization on gas separation performance was negligible. Different parameters were studied in the membrane modules, such as feed pressure, module length, permeate pressure, and feed concentration. Increasing feed pressure in the membrane modules caused the pressure gradient to increase. Therefore, maximum mass transfer occurred through the membrane. Moreover, the length was considered to show gas variation in the permeate. In the end, the contours of gas flow profiles in the membrane modules were successfully reported. Modeling predictions were compared with the published data and validated, and it was found that there was good agreement between them for the different values of selectivity. The comparison indicated that the membrane modules were very efficient in terms of the separation of the desired gas at a higher pressure gradient.