The Effect of Very Cohesive Ultra-Fine Particles in Mixtures on Compression, Consolidation, and Fluidization
Abstract
:1. Introduction
2. Experimental Apparatus, Materials, and Methodology
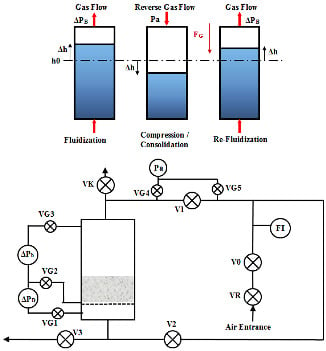
2.1. Experimental Apparatus
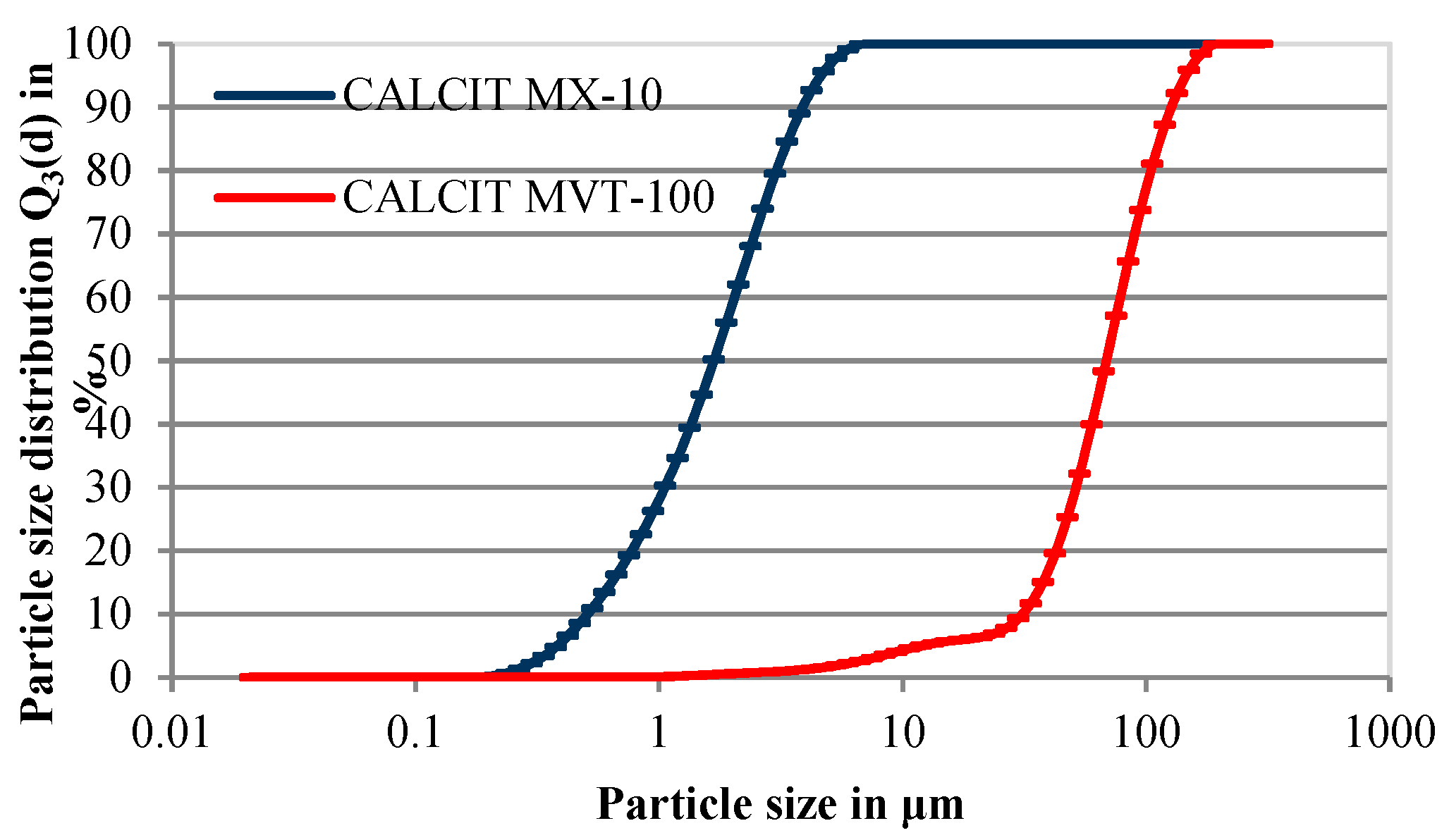
2.2. Powder Bed Materials
2.3. Experimental Methodology
3. Results and Discussion
3.1. Initial Fluidization Results
3.2. Compression Test Results
3.2.1. Effect of Applied Pressure on the Specific Volume Fraction of Particles
3.2.2. Effect of Applied Pressure on the Volume Fraction of Particles
3.2.3. Decompression Phase
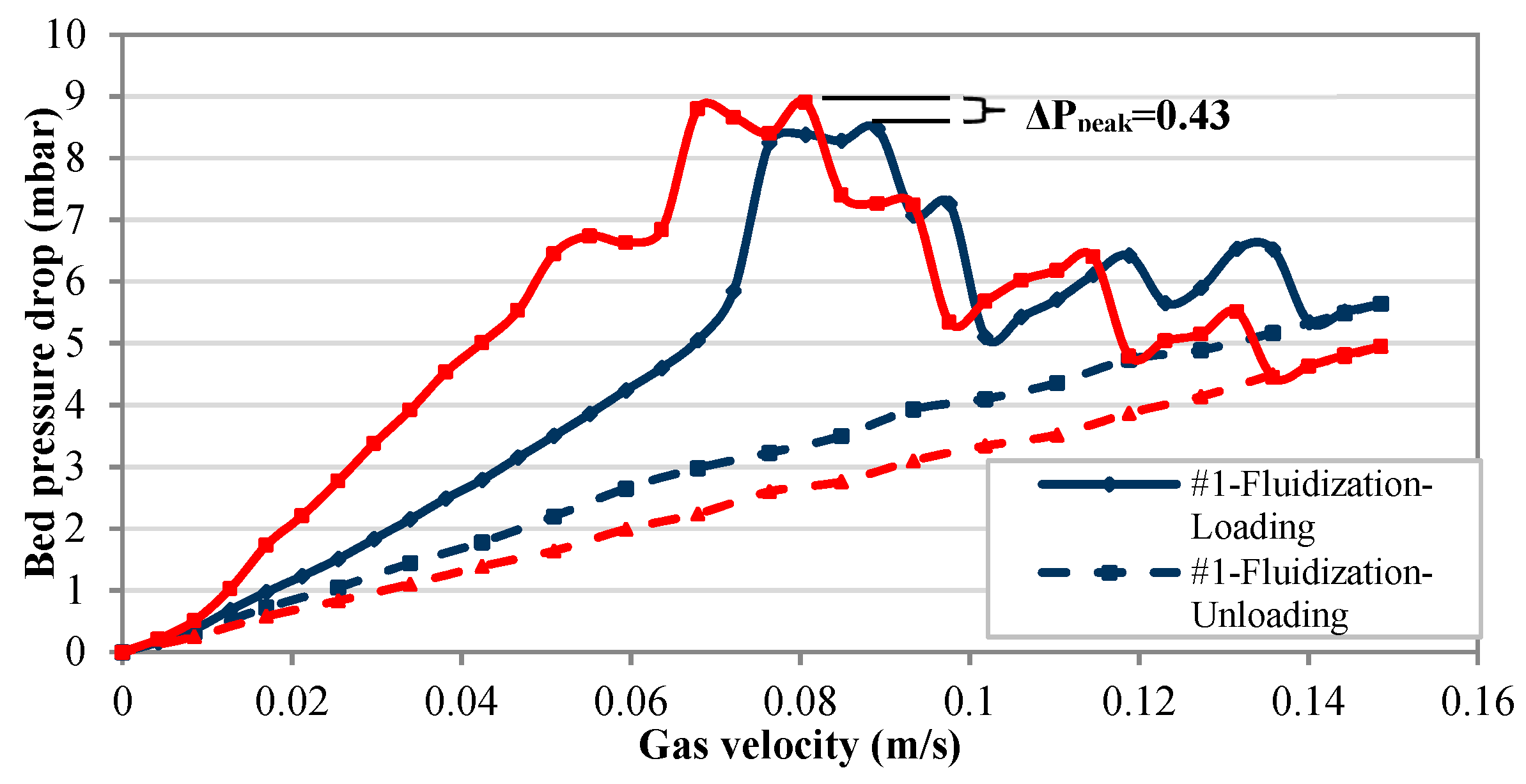
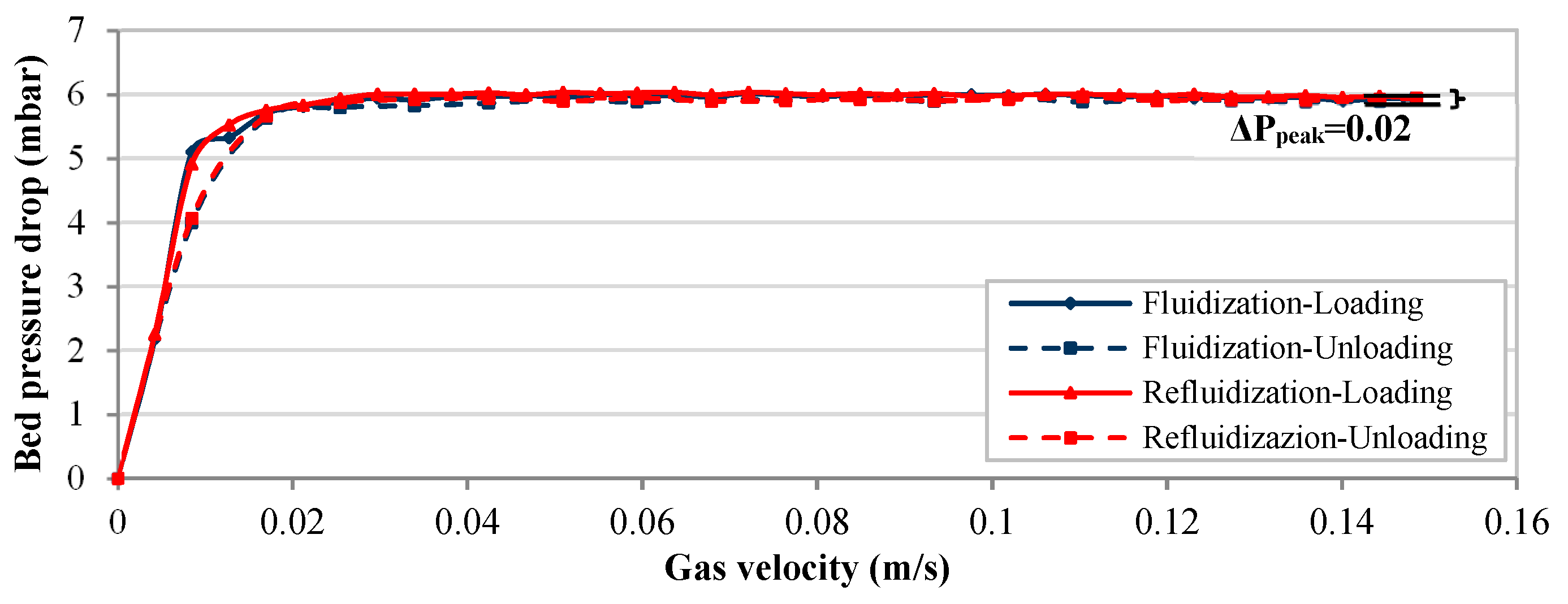
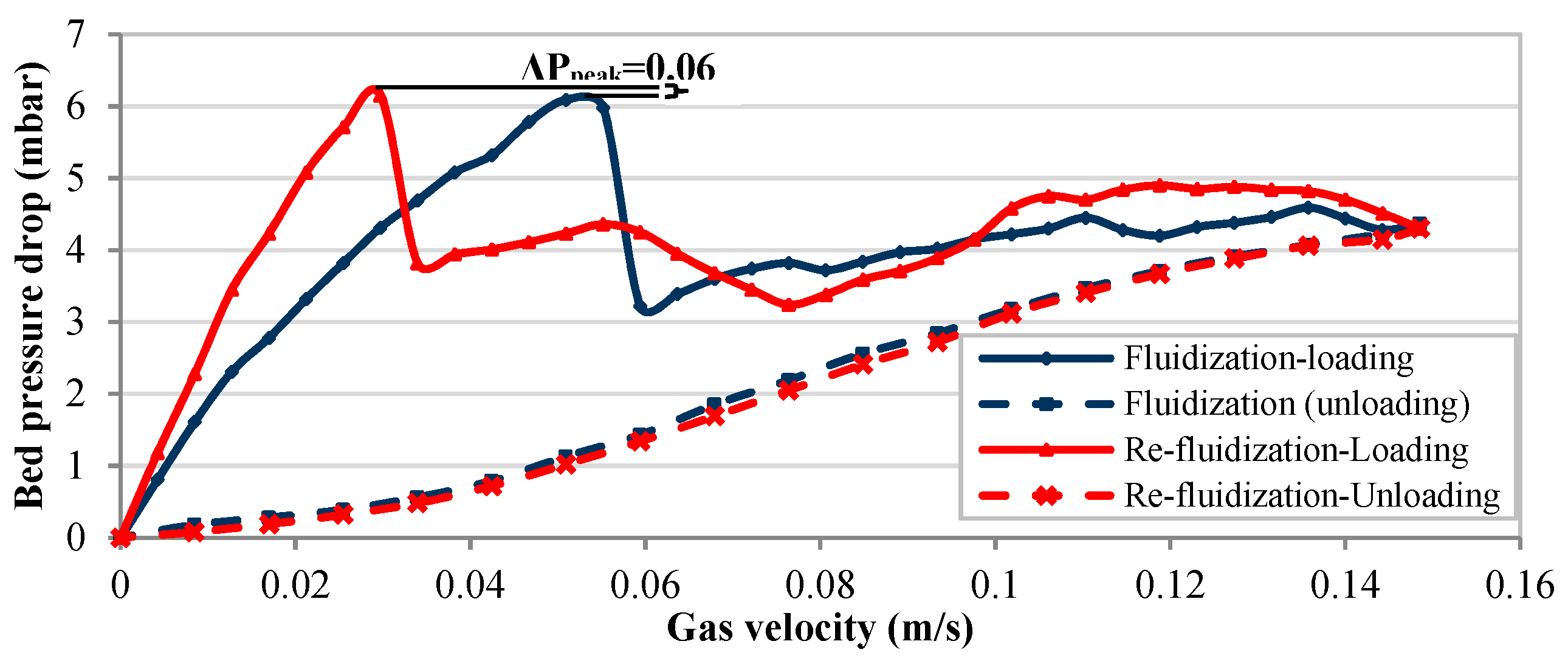
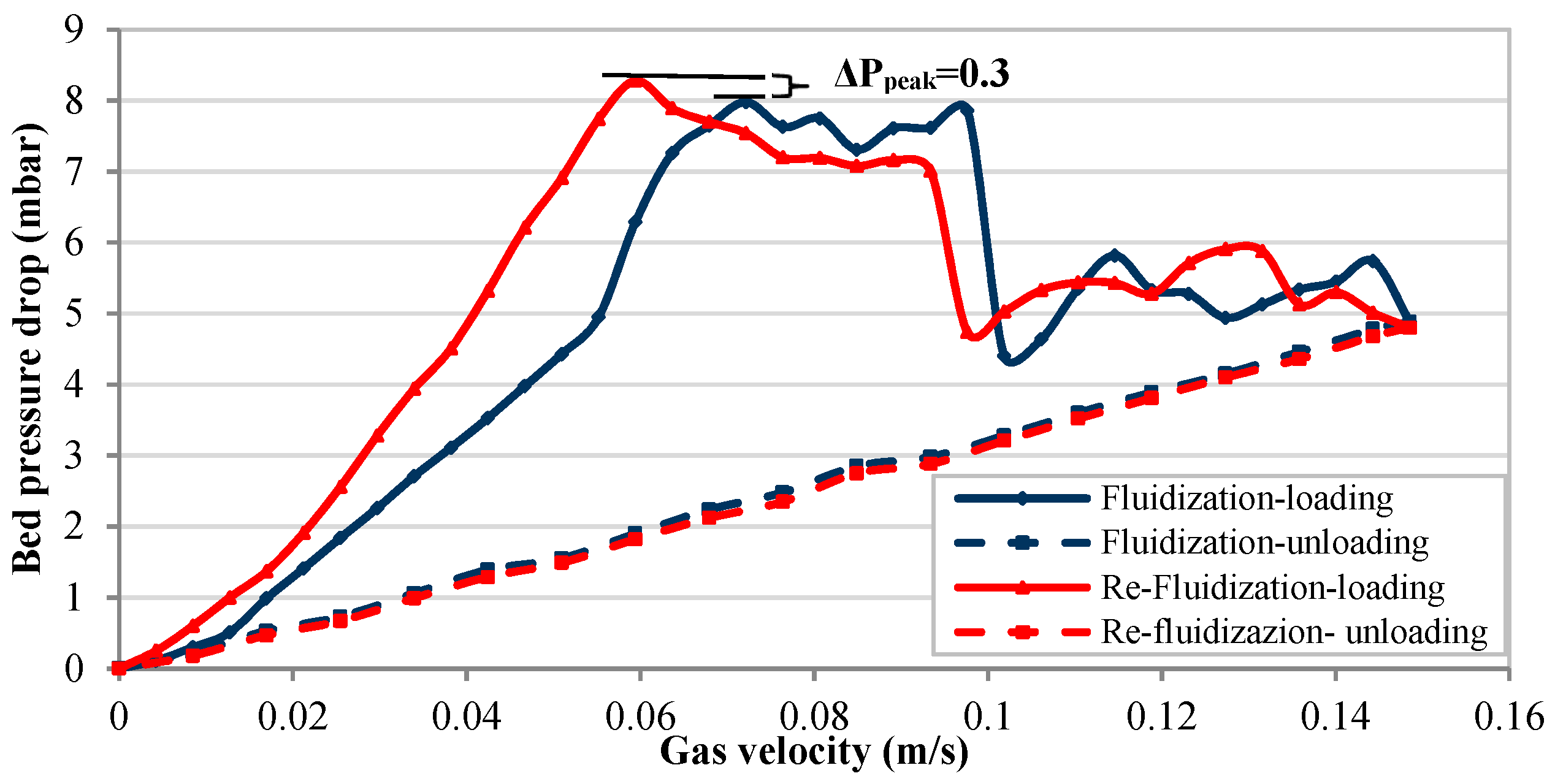
3.3. Re-Fluidization Tests
3.3.1. Re-Fluidization of Pure Materials (Macro-Scale)
3.3.2. Re-Fluidization of Different Mixtures of Fine and Ultra-Fine Particulate Materials (Macro-Scale)
3.3.3. Analysis of the Re-Fluidization Behavior in Micro-Scale
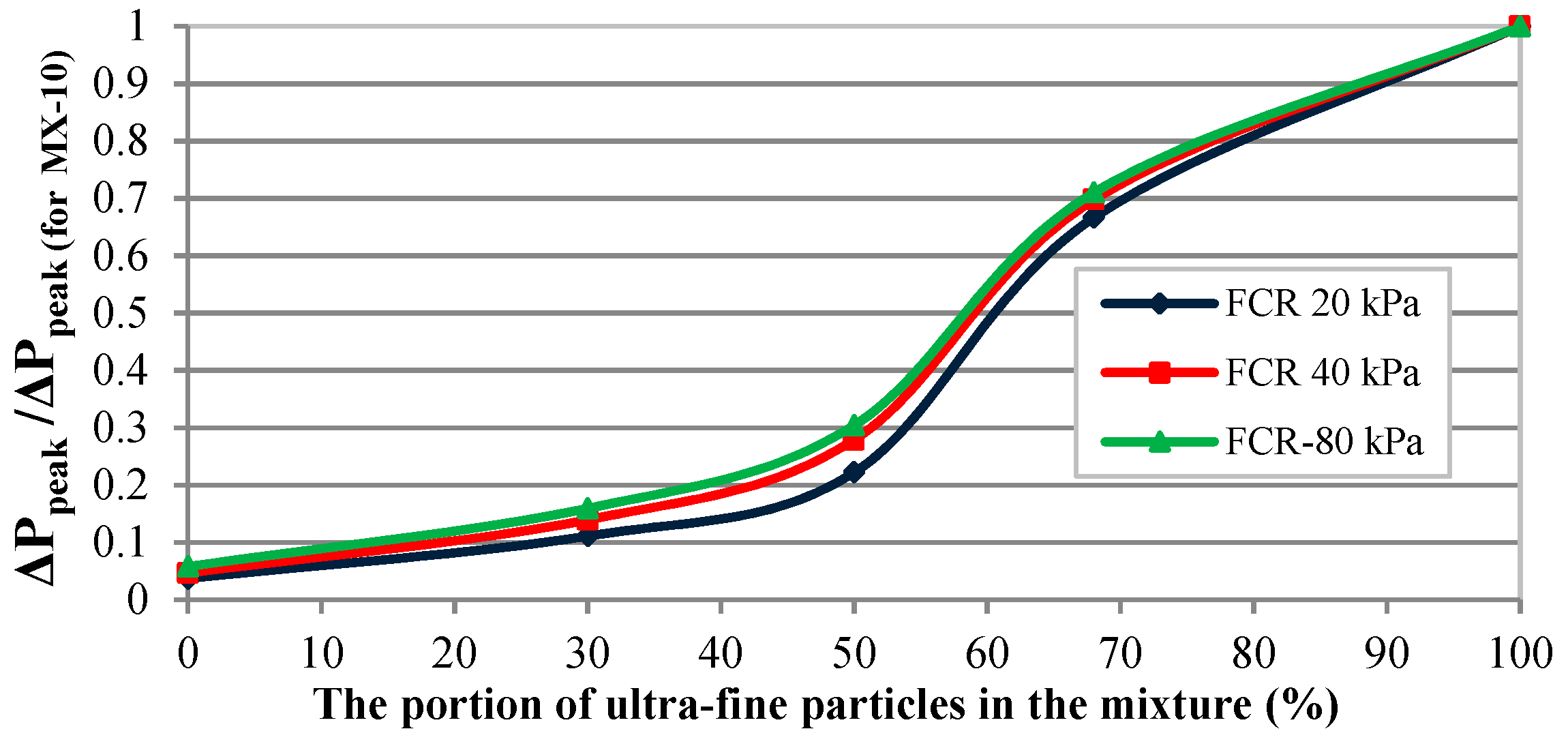
3.3.4. The Role of Ultra-Fine Powders in the Mixture on the Value and the Corresponding Superficial Gas Velocity of Peak Point
4. Summary and Conclusions
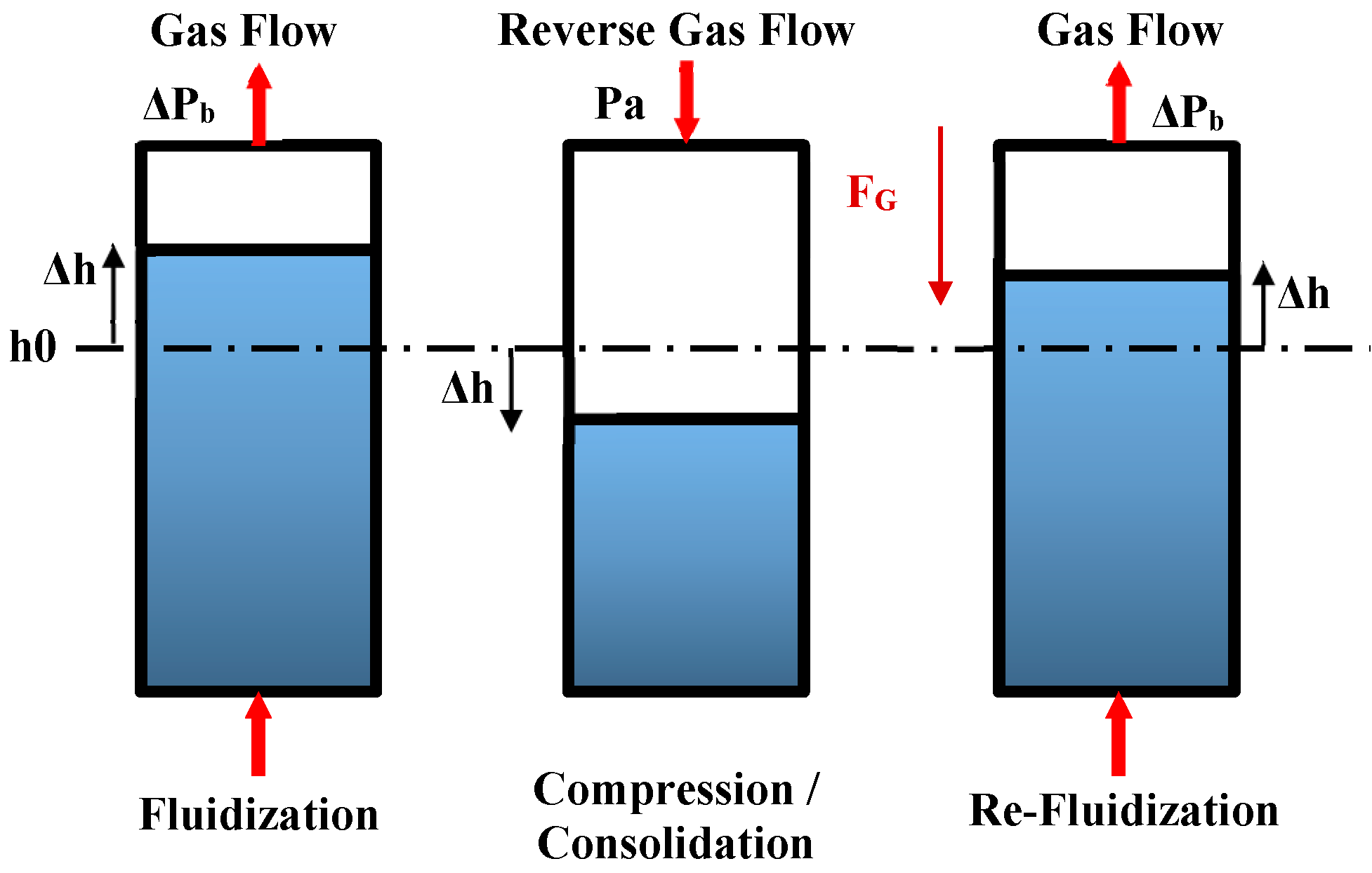
- Methodology: Systematic measurements of the compression and re-fluidization behavior were conducted for different mixtures of fine and ultra-fine material fractions. The first step of each experiment (initial fluidization) was performed to minimize the initial level of stresses in the bed, before compression. Then, a compression step was carried out, using three different pressure levels. Finally, re-fluidization was the last step of the experiment to evaluate the effect of compression on fluidization behavior of a compressed bed.
- Initial Fluidization: Concerning the initial fluidization, the fluidization of fine material is characterized by easy fluidization; only a slight hysteresis effect is visible. For each mixture containing ultra-fine powders, the fluidization is partial and includes cracks, channels, and the formation of agglomerates (due to inter-particle forces). Therefore, their fluidization is a non-reproducible and time-varying process. High fluctuations were observed in the bed pressure drop during the loading process. However, the fluidization unloading curve shows an almost linear behavior, denoting an approximately constant permeability.
- Compression: The results of the compression step show that the compression behavior follows the logarithmic law for all three pressures levels (20, 40, and 80 kPa). The compressibility index is almost the same for the low and intermediate pressure levels. However, for higher pressures, the compressibility index decreases strongly due to change in the compaction regime. Similarly, for the higher pressure, the slope of the particle volume fraction versus logarithmic display of dimensionless stress is noticeably different. The results of compression experiments further reveal that this slope does not depend on the size distribution of the mixtures but on the type of material itself.
- Re-fluidization: When analyzing the re-fluidization test results, history effects are observed leading to an increase in the bed pressure drop at peak point () between initial fluidization and re-fluidization of compressed bed. While the peak of the bed pressure drop increases, the superficial gas velocity corresponding to the peak point is smaller for re-fluidization after compression, compared to initial fluidization; consequently, the slope of the loading curve is much larger for re-fluidization. The opposite is observed for the unloading curves. When increasing the proportion of ultra-fine particles in the binary mixture, increases as well, particularly strongly in the intermediate range of 50% to 70% of ultra-fine particles, when the ultra-fine powders start to be dominant in the mixture.
- Future work: One of the most important processes in particle technology is the permeation of a fluid (air) in a particulate porous media. It could be more interesting if the porous media is a compressed and consolidated bed of a binary mixture. However, knowledge about this issue is limited. Therefore, investigating the permeation after compression and the effect of permeation on the re-fluidization of a binary mixture of fine and ultra-fine particles could be the next step of this study.
Author Contributions
Funding
Conflicts of Interest
Symbols and Notations
| Greek Symbols | |
| The void fraction of particle bed (-) | |
| The slope of particle volume fraction versus the dimensionless applied stress (-) | |
| The dynamic viscosity of the fluidizing gas (kg/m.s) | |
| The bulk density of particulate material (kg/m3) | |
| The density of the fluid or gas (kg/m3) | |
| The density of particle (kg/m3) | |
| Normal stress (kg/m.s2) | |
| Major principal normal stress | |
| Minor principal normal stress | |
| Isostatic tensile strength | |
| Applied compression stress | |
| Critical pressure (Empirical parameter) | |
| The dimensionless applied pressure () | |
| Average pressure (()/2) | |
| Shear stress (kg/m.s2) | |
| Particle volume fraction (-) | |
| The jammed particle volume fraction (-) | |
| Roman Symbols | |
| Bed cross-section area (m2) | |
| Granular Bond number (-) | |
| D | The fractal dimension of formed agglomerates (-) |
| Particle diameter (m) | |
| Mass-mean particle diameter (m) | |
| Size of new agglomerates (m) | |
| Sauter mean diameter (m) | |
| Bulk solid flowability (-) | |
| Gravity acceleration (m/s2) | |
| The height of the bed (m) | |
| The pressure drop across the bed (m) | |
| The ratio of size enlargement (-) | |
| Permeability (m2) | |
| Settled initial bed height (m) | |
| Compressibility index (-) | |
| P | Total Pressure (kg/m.s2) |
| Pa | Gage pressure within the apparatus (kg/m.s2) |
| Pwb | Total weight per cross-section area of the particle bed (kg/m.s2) |
| Bed pressure drop (kg/m.s2) | |
| The pressure drop of the gas distributor (kg/m.s2) | |
| The mean velocity of the fluid (m/s) | |
| The velocity of after disruption point (Peak point) (m/s) | |
| Superficial gas velocity (m/s) | |
| The volumetric flow rate of the fluid passing through a porous medium (m3/s) | |
References
- Grossmann, L.; Tomas, J.; Csöke, B. Compressibility and flow properties of a cohesive limestone powder in a medium pressure range. Granul. Matter 2004, 6, 103–109. [Google Scholar] [CrossRef]
- Gochioco, K. The Effect of Crystalline and Amorphous Lactose on Mechanical Properties of Roller Compaction Ribbon and Tablets. Master’s Thesis, University of Kansas, Lawrence, KS, USA, 2014. [Google Scholar]
- Faldu, B.; Zalavadiya, B. Compaction Behaviour: Force Distribution Through Powder Bed. Int. J. Pharm. Res. Dev. 2012, 4, 38–50. [Google Scholar]
- Darwin, G.H. On the Horizontal Thrust of a Mass of Sand. In Minutes of the Proceedings of the Institution of Civil Engineers; ICE Virtual Library: London, UK, 1883; Volume 71, pp. 350–378. [Google Scholar] [CrossRef]
- Castellanos, A. The relationship between attractive interparticle forces and bulk behaviour in dry and uncharged fine powders. Adv. Phys. 2005, 54, 263–276. [Google Scholar] [CrossRef]
- Tomas, J. Adhesion of ultrafine particles—A micromechanical approach. Chem. Eng. Sci. 2007, 62, 1997–2010. [Google Scholar] [CrossRef]
- Valverde, J.M.; Castellanos, A. Compaction of fine powders: From fluidized agglomerates to primary particles. Granul. Matter 2007, 9, 19–24. [Google Scholar] [CrossRef]
- Walker, E.E. The properties of powders. Part VI. The compressibility of powders. Trans. Faraday Soc. 1923, 19, 73–82. [Google Scholar] [CrossRef]
- Poquillon, D.; Lemaitre, J.; Baco-Carles, V.; Tailhades, P.; Lacaze, J. Cold compaction of iron powders-relations between powder morphology and mechanical properties-Part I: Powder preparation and compaction. Powder Technol. 2002, 126, 65–74. [Google Scholar] [CrossRef]
- Tomas, J. Energy Absorption at Particle Contact, Compression, and Shear Flow of Dry Ultrafine Powder. Part. Sci. Technol. 2009, 27, 337–351. [Google Scholar] [CrossRef]
- Tomas, J. The mechanics of dry, cohesive powders. Powder Handl. Process. 2003, 15, 296–314. [Google Scholar]
- Rumpf, H. Die Wissenschaft des Agglomerierens. Chemie Ing. Tech. - CIT 1974, 46, 1–11. [Google Scholar] [CrossRef]
- Geldart, D. Types of gas fluidization. Powder Technol. 1973, 7, 285–292. [Google Scholar] [CrossRef]
- Schulze, D. Powders and Bulk Solids; English Ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-73767-4. [Google Scholar]
- Kamranian Marnani, A.; Bück, A.; Antonyuk, S.; van Wachem, B.; Thévenin, D.; Tomas, J. The Effect of the Presence of Very Cohesive Geldart C Ultra-Fine Particles on the Fluidization of Geldart A Fine Particle Beds. Processes 2019, 7, 35. [Google Scholar] [CrossRef]
- Turki, D.; Fatah, N. Behavior and fluidization of the cohesive powders: Agglomerates sizes approach. Brazilian J. Chem. Eng. 2008, 25, 697–711. [Google Scholar] [CrossRef]
- Castellanos, A.; Valverde, J.M.; Quintanilla, M.A.S. Physics of compaction of fine cohesive particles. Phys. Rev. Lett. 2005, 94, 075501. [Google Scholar] [CrossRef] [PubMed]
- Valverde, J.M.; Quintanilla, M.A.S.; Castellanos, A. Jamming Threshold of Dry Fine Powders. Phys. Rev. Lett. 2004, 92, 258303. [Google Scholar] [CrossRef] [PubMed]
- Ajbar, A.; Alhumazi, K.; Asif, M. Improvement of the fluidizability of cohesive powders through mixing with small proportions of group A particles. Can. J. Chem. Eng. 2008, 83, 930–943. [Google Scholar] [CrossRef]
- Zhou, T.; Li, H. Effects of adding different size particles on fluidization of cohesive particles. Powder Technol. 1999, 102, 215–220. [Google Scholar] [CrossRef]
- Duan, H.; Liang, X.; Zhou, T.; Wang, J.; Tang, W. Fluidization of mixed SiO2 and ZnO nanoparticles by adding coarse particles. Powder Technol. 2014, 267, 315–321. [Google Scholar] [CrossRef]
- Song, L.; Zhou, T.; Yang, J. Fluidization behavior of nano-particles by adding coarse particles. Adv. Powder Technol. 2009, 20, 366–370. [Google Scholar] [CrossRef]
- Tomas, J.; Kache, G. Micro- and macromechanics of hopper discharge of ultrafine cohesive powder. Int. J. Chem. React. Eng. 2012, 10, 47–65. [Google Scholar] [CrossRef]
- Tomas, J. Micromechanics of Fine Particle Adhesion - Contact Models and Energy Absorption. In APM Proceedings; Russian Academy of Sciences Institute for Problems in Mechanical Engineering: St. Petersburg (Repino), Russia, 2008; pp. 652–667. [Google Scholar]
- Kamranian Marnani, A.; Idowu, R.; Bück, A.; Antonyuk, S.; Thévenin, D.; Tomas, J. Classification of ultra-fine adhesive particles at fine cohesive powders. In Proceedings of the 12th International Conference on Bulk Materials Storage, Handling and Transportation (ICBMH 2016), Darwin, Australia, 11–14 July 2016. [Google Scholar]
- Schulze, D. Flow properties of powders and bulk solids (fundamentals). Powder Technol. 2010, 65, 321–333. [Google Scholar]
- Hostler, S.R. Wave propagation in granular materials. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2005. [Google Scholar]
- Liu, C. Spatial patterns of sound propagation in sand. Phys. Rev. B 1994, 50, 782–794. [Google Scholar] [CrossRef] [PubMed]
- Geldart, D.; Harnby, N.; Wong, A.C. Fluidization of cohesive powders. Powder Technol. 1984, 37, 25–37. [Google Scholar] [CrossRef]
- Majmudar, T.S.; Sperl, M.; Luding, S.; Behringer, R.P. Jamming Transition in Granular Systems. Phys. Rev. Lett. 2007, 98, 058001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sederman, A.J.; Alexander, P.; Gladden, L.F. Structure of packed beds probed by Magnetic Resonance Imaging. Powder Technol. 2001, 117, 255–269. [Google Scholar] [CrossRef]
- Boutreux, T.; de Gennes, P.G. Compaction of granular mixtures: A free volume model. Phys. A Stat. Mech. Appl. 1997, 244, 59–67. [Google Scholar] [CrossRef]
- Richard, P.; Philippe, P.; Barbe, F.; Bourlès, S.; Thibault, X.; Bideau, D. Analysis by X-ray microtomography of a granular packing undergoing compaction. Phys. Rev. E 2003, 68, 02030. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, J. The Mechanics of Soils and Foundations, 2nd ed.; Taylor & Francis Group: New York, NY, USA, 2007; ISBN 9780415362566. [Google Scholar]
- Dwivedi, S.K. Analysis of Particle Deformation Mechanisms and Compact Expansion During Compaction on a high speed Rotary Tablet Press. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 1992. [Google Scholar]
- Khomane, K.S.; Bansal, A.K. Effect of particle size on in-die and out-of-die compaction behavior of ranitidine hydrochloride polymorphs. AAPS PharmSciTech 2013, 14, 1169–1177. [Google Scholar] [CrossRef] [PubMed]
- Tomas, J. Product design of cohesive powders - Mechanical properties, compression and flow behavior. Chem. Eng. Technol. 2004, 27, 605–618. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.; Harriot, P. Unit Operations of Chemical Engineering, 5th ed.; McGraw-Hill, Inc.: Singapore, 1993; Volume 7, ISBN 0070448442. [Google Scholar]
- Millán, J.M.V. Fluidization of Fine Powders; Particle Technology Series; Springer: Dordrecht, The Netherlands, 2013; Volume 18, ISBN 978-94-007-5586-4. [Google Scholar]
- Quintanilla, M.A.S.; Valverde, J.M.; Castellanos, A. The transitional behaviour of avalanches in cohesive granular materials. J. Stat. Mech. Theory Exp. 2006, P07015. [Google Scholar] [CrossRef]
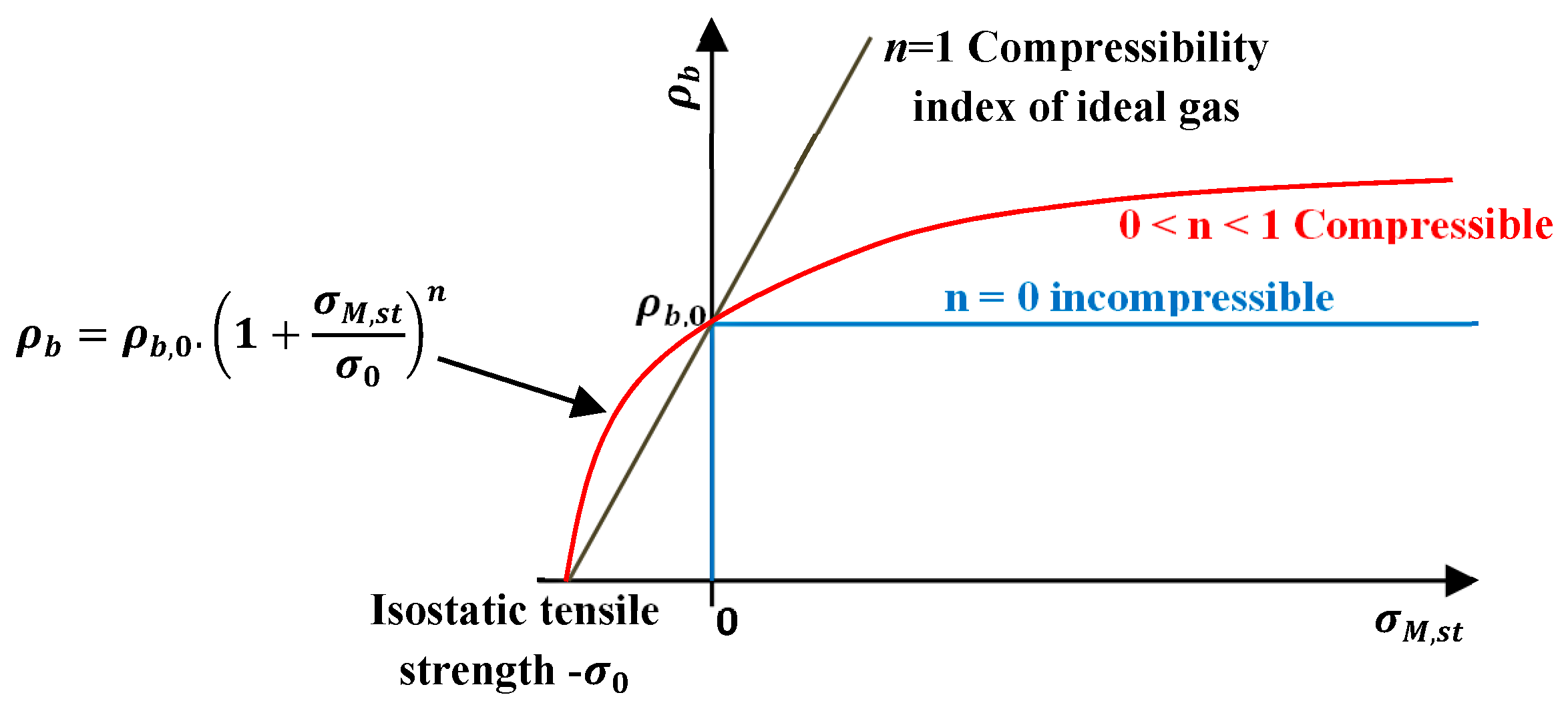



| Index n | Evaluation | Examples | Flowability |
|---|---|---|---|
| 0–0.01 | Incompressible | Gravel | Free flowing |
| 0.01–0.05 | Low compressibility | Fine sand | Free flowing |
| 0.05–0.1 | Compressible | Dry powder (Calcite) | Cohesive |
| 0.1–1 | Very compressible | Moist powder | Very cohesive |
| Particulate Material | |||||
|---|---|---|---|---|---|
| CALCIT MVT 100 | 73 | 38 | 1241 | 2700 | 11 |
| CALCIT MX 10 | 1.8 | 1.23 | 756 | 2700 | 1.37 |
| Sub-Step 1 | Sub-Step 2 | Sub-Step 3 | Sub-Step 4 | |
|---|---|---|---|---|
| Level 1 (Low) | 5 | 10 | 15 | 20 |
| Level 2 (Intermediate) | 10 | 20 | 30 | 40 |
| Level 3 (High) | 20 | 40 | 60 | 80 |
| Material Name | Pressure Level | n | |
|---|---|---|---|
| CALCIT MVT 100 (100% fine) | Low | 0.039 | 0.403 |
| Intermediate | 0.037 | 0.403 | |
| High | 0.030 | 0.408 | |
| 70–30% (fine–ultra-fine) | Low | 0.050 | 0.346 |
| Intermediate | 0.048 | 0.347 | |
| High | 0.041 | 0.350 | |
| 50–50% (fine–ultra-fine) | Low | 0.062 | 0.313 |
| Intermediate | 0.060 | 0.314 | |
| High | 0.048 | 0.318 | |
| 32–68% (fine–ultrafine) | Low | 0.090 | 0.256 |
| Intermediate | 0.085 | 0.256 | |
| High | 0.071 | 0.260 | |
| CALCIT MX 10 (100% ultra-fine) | Low | 0.110 | 0.231 |
| Intermediate | 0.104 | 0.232 | |
| High | 0.088 | 0.235 |
| Material Name | Pressure Level | |
|---|---|---|
| CALCIT MVT 100 (100% fine) | Low | 0.403 |
| Intermediate | 0.403 | |
| High | 0.408 | |
| 70–30% (fine–ultra-fine) | Low | 0.346 |
| Intermediate | 0.347 | |
| High | 0.350 | |
| 50–50% (fine–ultra-fine) | Low | 0.313 |
| Intermediate | 0.314 | |
| High | 0.318 | |
| 32–68% (fine–ultra-fine) | Low | 0.256 |
| Intermediate | 0.256 | |
| High | 0.260 | |
| CALCIT MX 10 (100% ultra-fine) | Low | 0.231 |
| Intermediate | 0.232 | |
| High | 0.235 |
| FCR Test | MVT 100 | MX 10 |
|---|---|---|
| Applied pressure (kPa) | (mbar) | |
| 20 | 0.01 ± 0.006 | 0.27 ± 0.025 |
| 40 | 0.02 ± 0.006 | 0.43 ± 0.035 |
| 80 | 0.04 ± 0.006 | 0.69 ± 0.035 |
| Mixture Ratio (% of Fine–% of Ultra-Fine) | |||
|---|---|---|---|
| Applied pressure during compression (kPa) | 70–30 | 50–50 | 32–68 |
| 20 | 0.03 ± 0.01 | 0.06 ± 0.01 | 0.18 ± 0.015 |
| 40 | 0.06 ± 0.012 | 0.12 ± 0.012 | 0.30 ± 0.015 |
| 80 | 0.11 ± 0.012 | 0.21 ± 0.015 | 0.49 ± 0.025 |
| MVT 100 | 30–70 | 50–50 | 68–32 | MX 10 | |
|---|---|---|---|---|---|
| FCR-Fluidization | 6.01 mbar at 0.0467 m/s | 6.09 mbar at 0.0509 m/s | 6.82 mbar at 0.0637 m/s | 7.98 mbar at 0.0722 m/s | 8.47 mbar at 0.0891 m/s |
| FCR-Refluidization | 6.03 mbar at 0.0255 m/s | 6.15 mbar at 0.0297 m/s | 6.94 mbar at 0.0382 m/s | 8.28 mbar at 0.0594 m/s | 8.90 mbar at 0.0806 m/s |
| MVT 100 (100% Fine) | Mixture Ratio (% of Fine–% of Ultra-Fine) | MX 10 (100% Ultra-Fine) | ||||
|---|---|---|---|---|---|---|
| 70–30 | 50–50 | 32–68 | ||||
| Fluidization (FCR) | Loading | 569 | 173 | 87 | 55 | 49 |
| Fluidization (FCR) | Unloading | 362 | 16 | 28 | 36 | 41 |
| Re-fluidization (FCR) | Loading | 583 | 259 | 125 | 78 | 73 |
| Re-fluidization (FCR) | Unloading | 359 | 13 | 22 | 28 | 33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamranian Marnani, A.; Bück, A.; Antonyuk, S.; van Wachem, B.; Thévenin, D.; Tomas, J. The Effect of Very Cohesive Ultra-Fine Particles in Mixtures on Compression, Consolidation, and Fluidization. Processes 2019, 7, 439. https://doi.org/10.3390/pr7070439
Kamranian Marnani A, Bück A, Antonyuk S, van Wachem B, Thévenin D, Tomas J. The Effect of Very Cohesive Ultra-Fine Particles in Mixtures on Compression, Consolidation, and Fluidization. Processes. 2019; 7(7):439. https://doi.org/10.3390/pr7070439
Chicago/Turabian StyleKamranian Marnani, Abbas, Andreas Bück, Sergiy Antonyuk, Berend van Wachem, Dominique Thévenin, and Jürgen Tomas. 2019. "The Effect of Very Cohesive Ultra-Fine Particles in Mixtures on Compression, Consolidation, and Fluidization" Processes 7, no. 7: 439. https://doi.org/10.3390/pr7070439
APA StyleKamranian Marnani, A., Bück, A., Antonyuk, S., van Wachem, B., Thévenin, D., & Tomas, J. (2019). The Effect of Very Cohesive Ultra-Fine Particles in Mixtures on Compression, Consolidation, and Fluidization. Processes, 7(7), 439. https://doi.org/10.3390/pr7070439