On the Three-Dimensional Structure of the Flow through Deterministic Lateral Displacement Devices and Its Effects on Particle Separation

Abstract

Experiments have shown that a suspension of particles of different dimensions pushed through a periodic lattice of micrometric obstacles can be sorted based on particle size. This label-free separation mechanism, referred to as Deterministic Lateral Displacement (DLD), has been explained hinging on the structure of the 2D solution of the Stokes flow through the patterned geometry, thus neglecting the influence of the no-slip conditions at the top and bottom walls of the channel hosting the obstacle lattice. We show that the no-slip conditions at these surfaces trigger the onset of off-plane velocity components, which impart full three-dimensional character to the flow. The impact of the 3D flow structure on particle transport is investigated by enforcing an excluded volume approach for modelling the interaction between the finite-sized particles and the solid surfaces. We find that the combined action of particle diffusion and of the off-plane velocity component causes the suspended particles to migrate towards the top and bottom walls of the channel. Preliminary results suggest that this effect makes the migration angle of the particles significantly different from that obtained by assuming a strictly two-dimensional structure for the flow of the suspending fluid.

1. Introduction

The inherently laminar regime characterizing momentum transport at microfluidic scales makes it possible to accurately design a priori device geometries and operating conditions able to perform specific tasks as regards the transport of chemical species or even of mesoscopic objects suspended in a carrier fluid. In single-phase mixtures, that is, when the suspended species are molecules and can be considered as point-sized, the interaction between convective and diffusive transport is typically exploited to improve the rate of homogenization of the concentration profiles within the mixture [1]. Here, the synergistic interaction between advection and diffusion occurs via the amplification of concentration gradients by cross-sectional velocity components (e.g., triggered by complex boundary geometries [2] as well as inertial [3], electro-osmotic [4], and magnetohydrodynamic effects [5] or a combination of the above [6]), which sustain the homogenizing action of the Fickian flux as the mixture flows downstream the device. Symmetrically, the outcome of tracer mixing experiments can be used to infer properties of the velocity profiles within the microfludic channels, especially as regards the occurrence of slip boundary conditions for the flow when the characteristic dimension of the cross-section falls below the micrometric scale [7,8].

An even richer physical phenomenology is observed when the size of the entities suspended in the carrier fluid increases from that of solubilized molecules to mesoscopic objects (henceforth referred to as particles), that is, when the flowing mixture is distinctly two-phase. In this case, microfluidics-assisted processes are typically used for separating and sorting the dispersed phase based on some physical feature of the particles (e.g., size, electric charge, shape and so on). In certain regimes, quantified by sufficiently large values of the particle Reynolds number ${\mathrm{Re}}_p=\rho \parallel \mathbf{u}-\mathbf{v}\parallel /\mu$ ($\rho$, $\mu$ and $\mathbf{u}$ being the density, viscosity and local velocity of the supending fluid, respectively, and $\mathbf{v}$ being the instantaneous particle velocity), the transport features of the embedded particles can be controlled exploiting their inertia, which makes them deviate from the streamlines of the underlying suspending flow [9,10]. At vanishing values of ${\mathrm{Re}}_p$, that is, in the the overdamped regime [11], particles tend to trace over the streamlines of the carrier flow and approaches alternative to inertial effects must be used to control their motion. These approaches are based on a tailored design of the solid surfaces of the device that exploits the mesoscopic character of the particle, that is, the fact that the particle size is not altogether negligible with respect to the smallest characteristic dimension of the channel geometry. Historically, the simplest example of wall effects for controlling the transport features of particles is provided by hydrodynamic chromatography (HDC), which was first proposed at the beginning of the 1970s [12], and thereafter used to perform the size-based separation of solutions suspending particles of different dimensions [13] and even macromolecules [14]. The HDC separation mechanisms has been explained through a simple one-way coupling, excluded volume model: The (supposedly spherical) particle is assumed to follow the flow streamline of the unperturbed single-phase Poiseuille flow computed at the particle center of mass. Besides, because of its finite size, the distance between the particle center and the channel walls must be greater or at most equal to the particle radius. Thus, adjacent to the channel walls, there is an annular volume (excluded volume) of thickness equal to the particle radius that is not accessible to the center of the particle. Owing to the no-slip condition of the suspending flow, this region is characterized by low velocity values, which vanish when approaching the solid walls. By this effect, bigger particles tend, on the average, to experience larger velocity values and move faster with respect to smaller ones. Specifically, an analytical expression of the average particle velocity versus particle size can be obtained based on the assumption that cross-sectional diffusion causes the center of the particle to visit all of the accessible positions with equal probability. By this property, the time-averaged particle velocity for an ensemble of realizations of Brownian trajectories can be computed as the spatial average of the flow velocity over the core channel cross-section that is accessible to the particle of prescribed size (ergodic property). Thus, by this approach, the average particle velocity increases with increasing particle size and approaches the average velocity of the flow at vanishing values of the particle radius [13].

A more recent and elegant use of the excluded volume effect to control particle motion is the so-called Deterministic Lateral Displacemenet (DLD) separation mechanism [15], which constitutes the focus object of this article. Here, the core of the device is represented by a channel with rectangular cross-section (typically very shallow) that is filled with a spatially periodic pattern of identical impermeable obstacles. The shape of the obstacles is generally cylindrical, even though different choices have been considered for reducing the hydraulic resistance and/or preventing clogging of the device by particle clustering [16,17]. Figure 1 shows the patterned geometry of a tilted array, specified by the lattice vectors ${\mathbf{e}}_1$ and ${\mathbf{e}}_2$, which define the elementary periodic cell of the system.

In what follows, it is assumed that $\parallel {\mathbf{e}}_1\parallel =\parallel {\mathbf{e}}_2\parallel =\ell$. The key point underpinning the separation mechanism is that the lattice is at an angle, say ${\theta }_l$, with respect to the lateral walls of the hosting channel. Specifically, ${\theta }_l$ can be defined as the smallest angle between the lattice vectors and the direction of the walls that confine the array laterally. The height, H, width, W and length, L, of the channel are in the order of few micrometers, millimeters and centimeters, respectively, whereas the characteristic length ℓ of the lattice vector(s) is of the same order as H, so that the number of repeated elementary cells within the device ranges from ${10}^5$ to ${10}^6$. DLD-based microseparators have been proven effective for a variety of biological/clinical applications, such as isolating blood cell subtypes [18], extracting circulating tumor cells [19,20,21,22], selecting large cells from a replicating population for tissue engineering [23], purifying human blood from parasites [24] and purification of fungal spores [25], enrichment of leukocites [26]. A further scale down of DLD devices has been recently attempted for separating suspended objects in the range of few tens of nanometers, thus shifting the domain of clinical applications of the technique from the cell size to that of viruses and exosomes [27] and even DNA strands [28].

The DLD device is filled with a buffer solution (acqueous, in the vast majority of cases) that is pushed through the lattice by a pressure drop, for example, provided by a syringe pump. Depending on the material used for manufacturing the device (PDMS is a common choice in view of its suitability for lithography-etching microfabrication techniques) the characteristic fluid velocity ranges from 10 $\mathsf{\mu }$m/s to order one mm/s, corresponding to an overall pressure drop over the entire channel length in the order of tens of KPa. The maximum allowed velocity is clearly slaved to the maximum pressure that can be withstood by the structure. Typically, characteristic lengths and velocities used in DLD are characterized by values of the Reynolds number well below unity, so that strictly creeping flow conditions can safely be assumed.

It has been experimentally observed [15] that a focused stream of suspended particles of various dimensions continuously introduced at some point upstream the periodic lattice separates into different streams, each containing particles of specified dimension and each characterized by its own average migration angle ${\theta }_P$. Figure 1 represents schematically the situation where the suspension is a mixture of particles of three different diameters, which have been labelled with different fluorescent markers. As the divided streams separate from each other while flowing through the structure, their width increases due to existence of Brownian (diffusive) components of particle motion that arise as a consequence of the thermal fluctuations of the molecules constituting the suspending fluid. The dispersion bandwidth is quantified by the variance, ${\sigma }_p$, of the scattered values of the individual displacements $x_p^i$ along the cross-sectional coordinate associated with particles one and the same size (Figure 1). Experimental results [28] show that the variance ${\sigma }_p$ can attain unexpectedly large values and that its extent is only weakly reduced when the flow rate through the device is increased.

By enforcing crude approximations as regards the fluid-particle and the obstacle-particle interactions, the basic mechanisms driving the size-based separation has been explained in a purely kinematic (i.e., diffusionless) setting, based on the structure of the unperturbed single-phase Stokes flow through the obstacle lattice. Here the particle is assumed to behave just as a point-sized tracer at its geometric center would. Thus, so long as the particle does not touch the obstacle surface, its center is expected to trace over the flow streamlines. At the particle-obstacle contact, the obstacle surface is assumed to annihilate the component of the particle displacement ortogonal to its surface leaving the tangential component unaltered (see Figure 2).

As a result, the particle glides around the obstacle surface and it detaches from it when the local velocity of the flow at its center is precisely tangent to the obstacle surface. In the case of spherical particles and cylindrical obstacles, the global trajectory of the particle center is a piecewise alternated collection of segments of flow streamlines and arcs of circumferences of radius equal the sum of the particle and of the obstacle radii. The classical picture put forward in the seminal article by Huang et al. [15], where the separation method was first proposed, is the case where the lattice angle stems from a rational number $\tan \left({\theta }_l\right)=1/N$ with $N>2$ integer. In this case, the flow through the unit periodic cell divides into N flux tubes, each carrying an equal fraction $1/N$ of the total flowrate. These flux tubes, which have been referred to as ’lanes,’ are identified by critical streamlines that originate from and terminate onto, the surface of (different) obstacles. For particles below a critical size, $R_{\mathrm{crit}}$ (see Figure 2), the steric exclusion by the obstacle is not enough to make the particle center change lane [29]. Thus the average direction of such particles will be the same as that pertaining to the flux tubes of the unperturbed flow. Because the flow is ultimately confined by the lateral channel walls, the particle deflection with respect to the wall direction equals zero. For particle bigger than the critical size, the particle radius is such that the particle center is forced to change lane at each obstacle collision, so that on the large scale, its average direction will be collinear with the lattice angle ${\theta }_l$. Thus, in this kinematic model, the response curve yielding the particle migration angle versus the particle size is a piecewise constant curve, jumping discontinuously from zero the the value ${\theta }_l$, the discontinuity being located at the critical particle radius, $R_{\mathrm{crit}}$. Multidirectional sorting modes, where mutiple critical radius value can be identified have also been predicted based on the lattice geometry in the case where the obstacle radius approaches zero [30]. Clearly, this purely kinematic model overlooks many relevant aspects of particle transport, which can be unambiguously identified in experiments, and that are ultimately related to the existence of fluctuating (i.e., diffusive) components of particle motion and approaches that include the effect of particle diffusion have also been proposed [31]. Among these approaches, an excluded-volume model inspired by that used in Hydrodynamic Chromatography, explicitly accounting for particle diffusion, has been put forward by one of these authors and co-authors in a series of recent articles [32,33,34,35,36] for tackling transport of finite-size particles in DLD devices. In all of these works, a two-dimensional setting was enforced, thus assuming that the effect of the top and bottom walls of the channel hosting the obstacle lattice could be neglected. In what follows, this assumption is relaxed and the whole three-dimensionality of the problem is considered, as regards both momentum transport of the suspending fluid and particle transport. We find that when the height of the channel is comparable to the size ℓ of the lattice vectors ${\mathbf{e}}_1$ and ${\mathbf{e}}_2$, new phenomena which cannot be captured in the 2D setting occur. We provide preliminary numerical evidence suggesting that these phenomena can have a sizeable impact on the particle migration angle ${\theta }_p$, whose predicted value in the 3D setting is in better agreement with the experimental observations with respect to that obtained from a 2D setting of the problem.

2. Transport Model and Numerical Approach

In this Section, the system geometry and the one-way coupling excluded-volume approach to particle transport described in the Introduction are discussed in the three-dimensional setting.

2.1. System Geometry

Figure 3a shows the planar structure of the obstacle lattice and the reference frames, $XY$ and $xy$, the first collinear with the channel axis, the second with those of the periodic lattice. The pressure drop causing the flow of the suspending fluid is parallel to the lateral walls of the device. The three-dimensional structure of the flow domain is depicted in Panel (b) of the same figure. The length, say ℓ, of the edge of the squared unit cell is henceforth assumed as the characteristic length for making the spatial coordinates dimensionless. The geometry of the system is then specified by the lattice angle, ${\theta }_l$, the dimensionless obstacle diameter, $d_{\mathrm{ob}}=D_{\mathrm{ob}}/\ell$ ($D_{\mathrm{ob}}$ being the dimensional diameter) and the cell aspect ratio, say $\alpha$, in the direction z orthogonal to the $xy$ plane.

2.2. Stokes Flow of the Suspending Fluid

By enforcing the one-way coupling approximation, the problem of determining the flow of the suspending fluid can considered as stand-alone. The flow is created by an overall pressure drop between the inlet and outlet sections of the channel hosting the obstacle lattice. Because the Reynolds number is well below unity in all of the practical implementations of the DLD device, the flow can safely be assumed in the creeping regime, and, as such, described by the solution of the steady Stokes problem,

$${\nabla }^2\mathbf{v}=\nabla p\left[\nabla ·\mathbf{v}=0\right]$$

(1)

equipped with the prescribed pressure drop through the structure and with no-slip impermeability condition onto all of the solid surfaces that confine the flow. Note that, in the 3D setting, these are composed by the obstacle boundaries and by the top and bottom walls of the channel, henceforth referred to as ’channel ceiling’ and ’floor,’ respectively. Equation (1) is made dimensionless by assuming a characteristic length L, a characteristic velocity U and a characteristic value for the pressure $P_{\mathrm{ref}}$. In what follows, L is taken equal to the length ℓ of the cell edge, $U=\sqrt{V_x^2+V_y^2+V_z^2}$, where $V_x,V_y,V_z$ represent the cell-averaged values of the components of the local fluid velocity and where $P_{\mathrm{ref}}=\mu U/\ell$, $\mu$ being the dynamic viscosity of the fluid. This last choice is suggested by the fact in the Stokes regime the viscous stress dominates over flow inertia, so that the typically used value $P_{\mathrm{ref}}=(1/2)\rho U^2$ (where $\rho$ is the density of the fluid) would make the pressure variable disappear from the momentum balance equation in the limit where the Reynolds number vanishes.

Because of the Stokes regime, the flow through the obstacle array inherits by the lattice geometry the same spatial periodicity properties. More specifically, the periodicity breakup due to the presence of the lateral walls of the channel swiftly fades away when moving at a distance of order two- to three cell lengths from the wall toward the channel core [36]. Note that, in the case where the device is composed of a small number of cells along the spanwise coordinate (i.e., orthogonally to the flow), tailored design strategies have been devised to obtain nevertheless a spatially periodic flow [37]. Thus, the Stokes problem can be conveniently approached by considering the unit periodic cell as a domain, and by imposing periodic boundary conditions for the velocity at opposite faces of this domain. In the local coordinate frame $xy$ collinear with the lattice, the average dimensionless pressure gradient accross the cell, say $\langle \nabla P\rangle$, can be represented by $\langle \nabla P\rangle =\left(\langle \partial P/\partial x,\rangle ,\langle \partial P/\partial y,\rangle ,\langle \partial P/\partial z\rangle \right)=(\cos {\theta }_l,\sin {\theta }_l,0)$ where the average is taken over the cell volume.

The above specified Stokes boundary value problem defined on the unit cell was solved by using a commercial finite-element solver, COMSOL Multiphysics 5.3 and a 3D unstructured mesh. A particular of the mesh and the structure of the velocity field is depicted in Figure 4. Because of the purely viscous momentum transport mechanism, the velocity profile does not develop the steep boundary layers observed in the inertial regimes, making it possible to obtain an accurate representation of the velocity field at relatively modest computational expenses. As can be observed from Figure 4, owing to the incompressible character of the flow, the maximum velocity is reached in the restricted gap between adjacent obstacles, where the cross-section available to the flow is minimal.

2.3. Excluded-Volume Approach for Particle Transport

In this section, a succinct description of the excluded-volume approach based on the concept of effective obstacle for tackling finite-size advecting diffusing particles is described. This approach constitutes the three-dimensional extension of an established method discussed in previous work for the 2D setting (see References [33,34,36]).

As regards the deterministic components of particle motion, that is, the Stokesian drag by the fluid surrounding the particle and the obstacle-particle interaction, the excluded-volume approach is the straightforward extension to the 3D case of the one-way coupling approach discussed in the Introduction. By this approach, so long as the center ${\mathbf{x}}_p$ of the (overdamped) particle is at a distance greater than or at most equal to, the particle radius from the solid surfaces within the channel, it is assumed that ${\mathbf{v}}_p=d{\mathbf{x}}_p/dt=\mathbf{v}\left({\mathbf{x}}_p\right)$ where $\mathbf{v}$ is the solution of the single-phase Stokes problem discussed above. At the boundaries of the excluded-volume domain, henceforth refereed to as ’effective boundaries’ and collectively denoted as $\partial {\Omega }_{\mathrm{eff}}$ (the subscript “eff” stands for “effective”), the normal component of the particle velocity directed towards the excluded-volume is annhilated, whereas the tangential component is preserved. Figure 5 provides an illustration of the effective transport domain for a finite-sized particle.

Note that, with respect to the 2D case, beyond the surface defining the boundary of the excluded-volume around the obstacles, the effective boundary also consists of the surfaces that delimit the excluded-volume at the top and bottom wall of the channel, which are next referred to as ’effective ceiling’ and ’effective floor.’ For a particle of finite size, the transport domain ${\Omega }_{\mathrm{eff}}$ available to the (center of) the particle is therefore strictly contained within the fluid-dynamic domain $\Omega$.

As suggested by the experiments, the presence of diffusional (Brownian) components of particle motion which result from the thermal fluctuations of the molecules constituting the suspending fluid must be considered. Under the assumption of isotropic character for the diffusion process, the motion of a generic particle within the lattice is modeled by the stochastic differential equation

$$d{\mathbf{x}}_p={\mathbf{v}}_p\left({\mathbf{x}}_p\right)dt+\sqrt{2/{\mathrm{Pe}}_p}d\mathbf{w}$$

(2)

where $d\mathbf{w}$ is the increment of vector-valued Wiener process in the time interval $dt$, possessing zero mean and variance equal to $\sqrt{dt}$ and where the particle Péclet number, ${\mathrm{Pe}}_p$, is defined as

$${\mathrm{Pe}}_p=\frac{U\ell }{{\mathcal{D}}_p}$$

(3)

In Equation (3), the bare particle diffusivity ${\mathcal{D}}_p$ is given by the Stokes-Einstein relation, ${\mathcal{D}}_p=k_{B}T/\left(6\pi r_p\mu \right)$, $k_B,T,r_p$ and $\mu$ being Boltzmann’s constant, the absolute temperature, the particle radius and the dynamic viscosity of the suspending fluid, respectively. By the excluded volme approach, the particle velocity ${\mathbf{v}}_p\left({\mathbf{x}}_p\right)$ appearing at the right hand side of Equation (2) is expressed by

$${\mathbf{v}}_p\left({\mathbf{x}}_p\right)=\left\{\begin{array}{ccc}\mathbf{v}\hfill & \mathrm{for}\mathrm{all}\hfill & {\mathbf{x}}_p\in {\Omega }_{\mathrm{eff}}\hfill \\ \mathbf{v}+\left(\mathbf{v}·\mathbf{n}\right)\mathbf{n}\hfill & \mathrm{for}\mathrm{all}\hfill & {\mathbf{x}}_p\in \partial {\Omega }_{\mathrm{eff}}\mathrm{whenever}\mathbf{v}·\mathbf{n}<0\hfill \end{array}\right.$$

(4)

In Equation (4), $\mathbf{n}$ denotes a unit vector normal to the boundary $\partial {\Omega }_{\mathrm{eff}}$ pointing towards the interior of ${\Omega }_{\mathrm{eff}}$.

To prevent the center of the particle entering the excluded volume regions, reflecting boundary conditions for the total displacement (i.e., convective plus diffusive) $d{\mathbf{x}}_p$ must be enforced at the effective boundaries.

Next, consider an ensemble of $N_p$ particles with initial positions ${\mathbf{x}}_p^{\left(i\right)}\left(0\right)$ ($i=1,2\cdots ,N_p$) that evolve under Equation (2). At any time t, the average particle velocity, say ${\mathbf{V}}_p\left(t\right)$, of the particle ensemble is defined as

$${\mathbf{V}}_p\left(t\right)=\frac{1}{N_p}\sum _{i=1}^{i=N_p}{\mathbf{v}}_p({\mathbf{x}}_p^{\left(i\right)}\left(t\right))$$

(5)

where ${\mathbf{x}}_p^{\left(i\right)}\left(t\right)$ is the position at time t of the of the particle located at ${\mathbf{x}}_p^{\left(i\right)}\left(0\right)$ at time $t=0$. As discussed in previous work (see References [34,36]), the ensemble-averaged velocity ${\mathbf{V}}_p\left(t\right)$ of a swarm of noisy particle trajectories governed by the stochastic process Equation (2) in the presence of the spatially-periodic field ${\mathbf{v}}_p$ in Equation (4) converges to a constant value ${\mathbf{V}}_p^{\infty }$,

$$\underset{t\to \infty }{lim}{\mathbf{V}}_p\left(t\right)={\mathbf{V}}_p^{\infty }$$

(6)

that is independent of the particle initial positions ${\mathbf{x}}_p^{\left(i\right)}\left(0\right)$. The angle between ${\mathbf{V}}_p^{\infty }$ and the average direction of the suspending flow (collinear to the lateral walls of the device channel) provides the excluded-volume model prediction of the experimentally determined average deflection angle, ${\theta }_p$ as defined by the position of the peak of fluorescence intensity depicted in Figure 1. By the Fokker-Planck theorem [38], the (dimensionless) Eulerian equivalent of a statistically significant number of particles that evolve uder the stochastic process expressed by Equation (2) is given by the advection-diffusion equation expressing the evolution of the particle number density $\varphi (\mathbf{x},t)$,

$$\frac{\partial \varphi }{\partial t}+\mathbf{v}·\nabla \varphi =\frac{1}{{\mathrm{Pe}}_p}{\nabla }^2\varphi$$

(7)

Note that, unlike the flow velocity, $\varphi (\mathbf{x},t)$ is not periodic. However, provided that only the information about the ensemble average velocity is sought, one can recast the Eulerian problem expressed by Equation (7) into a cell problem. This can be done by first observing that the Eulerian counterpart of the ensemble average in Equation (5) is given by

$${\mathbf{V}}_p\left(t\right)=\frac{1}{\mathrm{Vol}\left(\mathcal{D}\right)}{\int }_{\mathcal{D}}\left({\mathbf{v}}_p\left(\mathbf{x}\right)\varphi (\mathbf{x},t)-\frac{1}{{\mathrm{Pe}}_p}\nabla \varphi \right)d\mathcal{D}$$

(8)

where $\mathcal{D}$ is the entire lattice domain and $\mathrm{Vol}\left(\mathcal{D}\right)$ denotes its volume. By setting

$$C({\mathbf{x}}_c,t)=\sum _{l,m}\varphi ({\mathbf{x}}_c+l{\mathbf{e}}_1+m{\mathbf{e}}_2,t)$$

(9)

where ${\mathbf{x}}_c=x_c\mathbf{i}+y_c\mathbf{j}+z_c\mathbf{k}$, ($0\le x_c\le 1,0\le y_c\le 1,0\le z_c\le \alpha$) represents the local position vector with respect to the local coordinate system of an arbitrary periodic cell ${\Omega }_{\mathrm{eff}}$ (see Reference [34])

$${\mathbf{V}}_p\left(t\right)=\frac{1}{\mathrm{Vol}\left({\Omega }_{\mathrm{eff}}\right)}{\int }_{{\Omega }_{\mathrm{eff}}}\left({\mathbf{v}}_p\left({\mathbf{x}}_c\right)C({\mathbf{x}}_c,t)-\frac{1}{{\mathrm{Pe}}_p}\nabla C\right)d{\Omega }_{\mathrm{eff}}$$

(10)

$\mathrm{Vol}\left({\Omega }_{\mathrm{eff}}\right)$ being the volume of the effective transport domain. Here $C({\mathbf{x}}_c,t)$ (henceforth referred to as ’cumulative particle number density’) is the solution of

$$\frac{\partial C}{\partial t}+\mathbf{v}·{\nabla }_{c}C=\frac{1}{{\mathrm{Pe}}_p}{\nabla }_c^{2}C$$

(11)

equipped with periodic boundary conditions at the opposite vertical faces of the cell and with zero total flux condition at the effective boundary,

$$\mathbf{J}·\mathbf{n}{|}_{\partial {\Omega }_{\mathrm{eff}}}=0\mathbf{J}=C{\mathbf{v}}_p-(1/\mathrm{Pe}){\nabla }_{c}C$$

(12)

which constitute the straightforward 3D extension of the analogous conditions enforced in the 2D setting (see Reference [34] for details). The symbols ${\nabla }_c$ and ${\nabla }_c^2$ in Equations (11) and (12) denote the gradient and Laplacian operator in the local cell coordinate system. Because in what follows only the cumulative particle concentration will be used, we henceforth drop the subscript “c” so as to symplify the notation. Unlike the case of a point-size tracer, the normal component of the approaching velocity of a finite-size particle at the effective boundary is generically different from zero. Thus, the zero net flux condition expressed by Equation (12) implies that a gradient of the cumulative particle number density C must develop at those points of the effective boundary where the normal velocity component is opposedly oriented to the local vector $\mathbf{n}$ normal to the surface (i.e., at points where the approaching velocity would cause the center of the particle to enter the excluded-volume region). At fixed fluid dynamic conditions, it is expected that such concentration gradient will become steeper and steeper at increasing values of ${\mathrm{Pe}}_p$, as already observed in two-dimensional implementations of the excluded-volume approach (see, e.g., Reference [34]). For this reason, a tailored discretization of the effective transport domain ${\Omega }_{\mathrm{eff}}$, specifically constructed so as to capture the thin boundary layer developed by $C(\mathbf{x},t)$, must be enforced at those effective boundaries where the local fluid velocity possesses a sizeable normal component oriented towards the exterior of ${\Omega }_{\mathrm{eff}}$. Figure 6 shows the unstructured 3D mesh and the detail of the boundary layer near the surface of the effective cylinder surface.

In what follows, the modelling approach described above is used to determine the features of particle transport in the 3D geometry, with specific focus on the average migration angle, ${\theta }_p$, which primarily impacts upon separation performance of DLD-based microfluidic separators.

3. Results

Flow Structure and Hydraulic Resistance

Next, results showing the occurrence of 3D effects as regards the structure of the single-phase incompressible Stokes flow through the periodic obstacle array are discussed, showing that the velocity field $\mathbf{v}\left(\mathbf{x}\right)$ explicitly depends on the vertical coordinate z. We start by observing that in the presence of free-slip conditions at the cell floor and ceiling of the cell, a strictly two-dimensional flow would be obtained, where the off-plane velocity component $v_z$ is identically equal to zero, ${\mathbf{v}}_{2D}=(v_x(x,y),v_y(x,y),0)$. Conversely, 3D effects associated with non-vanishing values of the vertical velocity component at some internal region of the momentum transport domain $\Omega$ are to be expected whenever no-slip conditions at these surfaces are enforced. This occurrence can be directly inferred by the structure of the Stokes problem. To this end, let $\mathbf{v}={\mathbf{v}}_{\perp }+v_z\mathbf{k}$ and $\nabla ={\nabla }_{\perp }+{\partial }_z\mathbf{k}$, where ${\mathbf{v}}_{\perp }$ and ${\nabla }_{\perp }$ are the projections of $\mathbf{v}$ and $\nabla ={\partial }_x\mathbf{i}+{\partial }_y\mathbf{j}+{\partial }_z\mathbf{k}$ onto the $xy$ coordinate plane and where $\mathbf{k}$ is a unit vector normal to the $xy$ plane. The in-plane projection of the Stokes problem reads

$${\nabla }_{\perp }^2{\mathbf{v}}_{\perp }+{\partial }_{zz}^2{\mathbf{v}}_{\perp }={\nabla }_{\perp }P$$

(13)

where ${\nabla }_{\perp }^2=({\nabla }_{\perp }·{\nabla }_{\perp }$ ). The local momentum balance along the vertical (i.e., z) coordinate is instead given by

$${\nabla }_{\perp }^2{v}_z+{\partial }_{zz}^2{v}_z={\partial }_{z}P$$

(14)

Next, consider Equation (13). The presence of no-slip conditions at the top and bottom wall of the cell make the in-plane velocity ${\mathbf{v}}_{\perp }$ explicitly dependent on the z coordinate. Therefore the term ${\nabla }_{\perp }P$ must also depend on z. This implies that a fixed $\overline{x}$ and $\overline{y}$, the pressure $P(\overline{x},\overline{y},z)$ is not constant along the z coordinate. Thus, the term at the right hand side of Equation (14) does not vanish identically in the cell domain. But then, Equation (14) is a Poisson equation with a non-vanishing source term, which implies that its solution $v_z$ cannot be identically zero in $\Omega$. We also observe that, in principle, the presence of an off-plane velocity component that depends (nonlinearly) on the z coordinate breaks down the solenoidal character of the projection ${\mathbf{v}}_{\perp }$ with respect to the planar coordinates $xy$, that is, unlike the ${\mathbf{v}}_{2D}$ flow, ${\nabla }_{\perp }·{\mathbf{v}}_{\perp }\ne 0={\nabla }_{\perp }·{\mathbf{v}}_{2D}$, so that distorsion effects on the planar projection of the streamline structure of the 3D flow might arise with respect to the geometry of the 2D solution.

Figure 7 shows the occurrence of a fully 3D structure of the flow field for a cell geometry specified by an obstacle diameter $d_o=0.4$, an aspect ratio $\alpha =3/2$ and a lattice angle ${\theta }_l={\tan }^{-1}\left(0.28\right)$. As can be gathered, the absolute maximium and minimum is of order $10\%$ with respect to the average cell velocity U. One also notes that along the approaching average direction of the flow $(\cos \left({\theta }_l\right),\sin \left({\theta }_l\right),0)$ the off-plane velocity component tends to drive particles that do no belong to the symmetry plane $z=1/2$ towards the cell floor and ceiling. Specifically particles whose center falls in the region $z>\alpha /2$ of $\Omega$ are expected to be driven upward towards the cell ceiling, whereas particles occupying the lower half of the transport domain are pushed downward towards the cell floor.

A more quantitative illustration of the structure of the vertical velocity component can be gained from Figure 8a, which depicts the profiles of $v_z$ along a vertical line embedded in $\Omega$ for cell geometries characterized by the same obstacle diameter, $d_o=0.4$ and different values of the cell aspect ratio $\alpha$. The z variable is here rescaled to the aspect ratio $\alpha$ so that all of the profiles are defined onto the same interval. The maximum of $v_z$ displays a non-monotonic behavior when varying the cell aspect ratio, first increasing from $\alpha =3/4$ to $\alpha =1$, and then decreasing at larger $\alpha$ values. Note how at the highest values of the aspect ratio considered ($\alpha =4$, curve d) the velocity profile approaches zero in a large interval about the symmetry plane $z=\alpha /2$.

A global measure of the intensity of the off plane velocity is represented in Figure 8b through the scaled $L_2$ norm, $\parallel v_z\parallel$, of $v_z$ defined by

$$\parallel v_z\parallel ={\left(\frac{{\int }_{\Omega }{v}_z^{2}dxdydz}{{\int }_{\Omega }(v_x^2+v_y^2+v_z^2)dxdydz}\right)}^{1/2}$$

(15)

Figure 8b shows the the dependence of this quantity on $\alpha$ for different obstacle sizes. As can be seen, the relative intensity of the off-plane velocity component takes on values that are in the order of few percent with respect to the average velocity magnitude, with a maximum intensity reached at a value ${\alpha }_c$ of the aspect ratio $1<{\alpha }_c<2$, which depends on the obstacle diameter $d_o$. By this data, one could surmise that the 3D effect, quantified by the magnitude of the off plane component $v_z$, is modest and could be neglected. This idea is also supported by the negligible impact of the non-vanishing z-component of the velocity on the structure of the streamlines onto $xy$ planes $z=\mathrm{const}.$, as shown in Figure 9.

A similar observation was put forward by D’Avino [39], who compared the results of full 3D two-phase numerical simulations of a non-diffusing spherical particle suspended in a viscous (possibly shear-thinning) fluid through a DLD array of cylindrical obstacles with their 2D counterparts, concluding that the 2D setting provides an accurate description of the particle motion, when purely deterministic actions are taken into account.

In what follows, we provide numerical evidence showing that this conclusion is no longer correct whenever the particle is afforded diffusional components of motion alogside the deterministic actions. Specifically, in the excluded-volume model here considered, the presence of a non-vanishing particle diffusivity (however small) interacts with the weak off plane velocity component so as to alter significantly the steady-state profile of the cumulative particle concentration C with respect to that obtained in the 2D setting. More importantly, the 3D structure of the cumulative particle concentration has a sizeable effect on the particle average migration angle, which makes its value significantly different from that predicted by 2D simulations.

Before closing this Section, we briefly address the impact of the presence of the no-slip conditions enforced on the ceiling and flow of the elementary cell on the hydraulic resistance for an assigned pressure drop accross the cell. Figure 10 reports the dimensionless velocity, $U/(\Delta P\ell /\mu )$, scaled to the characteristic value of the pressure drop accross the cell $\Delta P$ versus $\alpha$ for different values of the (dimensionless) obstacle diameter, $d_{\mathrm{o}}$.

At low values of the aspect ratio, $\alpha$, the average velocity is dominated by the viscous friction at floor and ceiling surfaces of the cell in that the extent of the obstacle surface is immaterial with respect to that of the horizontal surfaces. At larger $\alpha$ values, the hydraulic resistance results as a bargain between the viscous friction at the obstacle and at the flat surfaces. At larger $\alpha$ values, the influence of the obstacle surface becomes more and more pronounced, whereas the momentum boundary layers ensuing from the floor and ceiling surfaces are completely separated from each other and attain a constant thickness which is independent of $\alpha$. Because the average of the velocity is taken over the cell volume which depends linearly on $\alpha$, the influence of these latter on the volume averaged velocity becomes less and less important as the aspect ratio increases. Eventually, the hydraulic resistance is governed by the laminar boundary layer at the obstacle surface, whose extent also depends also linearly on $\alpha$. As a result, the cell-averaged velocity saturates towards a constant value which is exactly what would be obtained in a 2D representation of the problem. The above observation has important practical implications. Generally, the geometry of the device should be chosen so as to ensure diluted conditions for the suspension, as concentrated particle conditions could lead to unpredictable behavior of particle dynamics, not to mention the possibility of clogging events. Furthermore, increasing $\alpha$ at fixed pressure drop also increases the total (dimensionless) volumetric flowrate $q_v$ through the cell. In this respect, the cell aspect ratio could be a viable operating parameter for obtaining at one time diluted conditions and high throughput. However, as $\alpha$ increases at fixed flowrate, the mechanical stability of the obstacles might be impaired, so that an optimal value for $\alpha$ might result from these oppositely directed effects. The data in Figure 10 suggest the the optimal aspect ratio, say ${\alpha }_c$, could be chosen in the range where the average velocity switches from a linear increase in $\alpha$ to the saturation regime, as a further increase of aspect ratio would have comparatively modest effects on $q_v$ while creating mechanical stability issues.

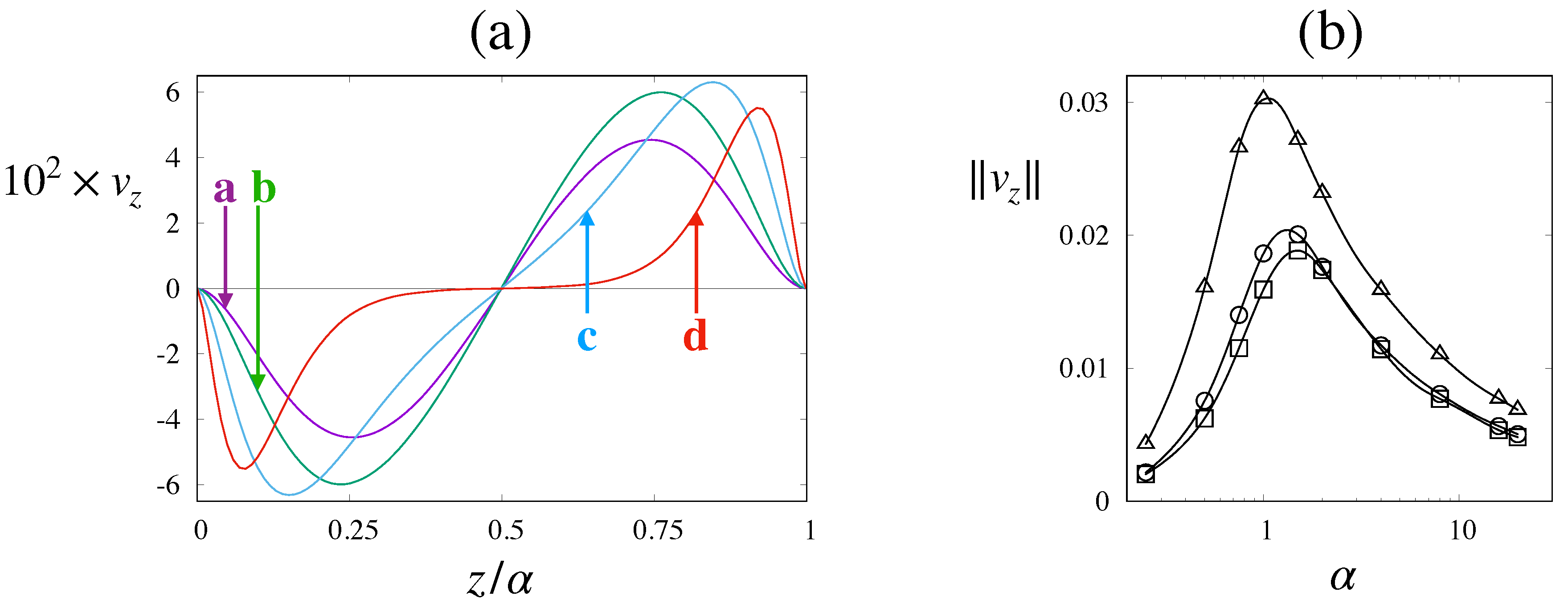
4. Particle Transport

Before discussing the transport features of particles evolving under the periodic Stokes flow according to the excluded-volume model, a preliminary observation is in place about the physical interpretation of the particle number density $\varphi$ in Equation (7), (and of the cumulative particle concentration C as defined by Equation (9)) in a context where the particle size is comparable to that of the periodic cell. Clearly, unlike the case of point-sized tracers, the finite size of the particle, together with the diluted suspension assumption, implies that the number of particles that can be embedded in a single periodic cell is not statistically significant (for large particle sizes this number may reduce to few units, depending on the geometry of the lattice). In this contex, the product $\varphi (\mathbf{x},t)dxdydz$ represents the probability of finding (the center of) a particle released a time $t=0$ at the origin of the coordinate system in a volume element centered at $\mathbf{x}$ at time t. Accordingly, the cumulative particle concentration $C(\mathbf{x},t)$ represents the probability of finding the particle at the relative cell position $\mathbf{x}$ at time t, regardless of the specific location of the cell within the periodic lattice. This much clarified, we next analyze the effects of the presence of a non-vanishing vertical component of the velocity on particle transport by using the excluded-volume model for particles that was described in Section 2.3. Let us then consider the features of the solution of Equation (11) subject to the boundary condition Equation (12). Because the cumulative particle concentration evolves in a closed domain (periodic boundary conditions are enforced at opposite vertical faces of the unit periodic cell) and owing to the presence of the dissipative Laplacian term, the evolving field $C(\mathbf{x},t)$ associated with a generic initial condition is expected to approach a steady-state solution $C_{ss}\left(\mathbf{x}\right)$ that solves $\mathbf{v}·\nabla C_{ss}=(1/\mathrm{Pe}){\nabla }^2{C}_{ss}$ with the same boundary conditions as those enforced for $C(\mathbf{x},t)$. When steady-sate conditions have been reached, macrotransport behavior for the particle ensemble settles in and the average particle velocity ${\mathbf{V}}_p\left(t\right)$ becomes a (vector-valued) constant ${\mathbf{V}}_p^{\infty }=(V_{p,x}^{\infty },V_{p,y}^{\infty },V_{p,z}^{\infty })$ which allows to obtain the average deflection angle of the particles of the assigned size as $\langle {\theta }_p\rangle ={\theta }_l-{\tan }^{-1}{V}_{p,y}^{\infty }/V_{p,x}^{\infty }$ (note that $V_{p,z}^{\infty }=0$ by symmetry of the boundary value problem). In order to investigate the approach to this condition, we next consider the evolution of the cumulative particle distribution starting from an initial condition where particles are evenly distributed within the effective transport domain ${\Omega }_{\mathrm{eff}}$. Panels-(a) through -(c) of Figure 11 show the time-evolution of $C(\mathbf{x},t)$ onto the surface of the effective obstacle (the horizontal axis is here the angular coordinate of the unfolded cylinder).

Given that the cumulative particle number density spans a very large interval of values, ${log}_{10}C$ is represented in place of C for visualization purposes. At short times (Figure 11a), all particles are pushed towards the effective obstacle surface by the main (planar) components of the flow. As a consequence, the field $C\left(\mathbf{x},t\right)$ onto the effective obstacle surface is essentially independent of the z coordinate and the average particle velocity as given in Equation (10) is not influenced by the three-dimensionality of the problem. However, as time goes by, the weak vertical components of the flow onto the effective cylinder make particles migrate towards the floor and ceiling of the cell as can be gathered by the data in Figure 11b. At steady-state (Figure 11c), the 3D structure of the particle concentration field is strongly dependent on the z coordinate. Note that the time-scale quantifying the transient evolution from an essentially two-dimensional to a full three-dimensional structure of the cumulative particle number density is of the order of few hundreds (dimensionless) time units, which physically correspond to a situation where particles cross an approximately equal number of obstacle rows downstream the injection point. As in typical implementations of the DLD technique, the obstacle array is composed of order ${10}^3$ obstacle rows, the migration phenomenon above described falls well within the space/time limits of the process. Panels-(d) through (i) of Figure 11 show the structure of $C(\mathbf{x},t\to \infty )$ at the symmetry plane $z=\alpha /2$ and at the ceiling of the effective transport domain $z=\alpha -r_p$. At short times (compare panels-(d) and (c)), the planar structure of the concentration field is similar, whereas at large times the symmetry plane becomes progressively devoid of particles. The impact of particle size and flowrate on this migration process can be appreciated by considering the cases shown in Figure 12 that shows for a particle size $r_p=0.025$ (equal to half of that considered in Figure 11) the structure of the steady-state cumulative particle concentration onto the effective obstacle surface, as well as the one-dimensional profiles onto selected circumferences therein contained at different values of the particle Péclet number. Because particles of different size suspended in one and the same flow possess different $\mathrm{Pe}$ values (in view of the fact that the bare particle diffusivity depends on particle size) a reference Péclet number, ${\mathrm{Pe}}_{\mathrm{ref}}=U\ell /{\mathcal{D}}_{\mathrm{ref}}$, where ${\mathcal{D}}_{\mathrm{ref}}=k_{B}T/\left(6\pi r_{p,\mathrm{ref}}\right)$ is next considered by targeting a reference particle size $r_{p,\mathrm{ref}}$. iAs reference value we choose $r_{p,\mathrm{ref}}=0.0625$, which correspond to particle of diameter equal to 1 $\mathsf{\mu }$m in the device geometry considered in Reference [15] with an average flow velocity U = 400 $\mathsf{\mu }$m/s.

At ${\mathrm{Pe}}_{\mathrm{ref}}={10}^3$, the oscillations about the average value (here set to unity, $\langle C\rangle =1$), result contained and almost no 3D effect can be observed. At ${\mathrm{Pe}}_{\mathrm{ref}}=3.5\times {10}^3$, deviations from the uniform concentration condition are more significant and so is the difference between the values of C onto the circumference at the symmetry plane and at the ceiling of the effective transport domain. For a quantitative comparison, Figure 13 reports the one-dimensional concentration profiles onto the same selected circumferences as those of Figure 12 for the particle size $r_p=0.05$ corresponding to the same ${\mathrm{Pe}}_{\mathrm{ref}}$ values.

Note how, at the higher value of the reference Péclet number, the concentration on the circumference at the symmetry plane is almost uniformly vanishing, whereas a peak value three orders of magnitude larger than the average concentration develops at the circumference resulting from the intersection between the effective obstacle and the cell ceiling.

Because the two fields are markedly different, (the difference increasing at increasing $\mathrm{Pe}$), sizeable effect can be expected as regards the average migration velocity ${\mathbf{V}}_p^{\infty }$ and, consequently, on the average particle migration angle ${\theta }_p$. In order to gain a quantitative appreciation of the 3D effect, we attempted the prediction of the average migration angle based on the 2D and the 3D representation of the problem for the particle size $r_p=0.05$ corresponding to a dimensional particle diameter of 0.8 $\mathsf{\mu }$m in the experiment reported in Reference [15]. As we found no indication of the channel depth or of the working temperature in the discussion of the experimental data in Reference [15], we fixed $\alpha =1$ for the cell aspect ratio, and assumed $T=300$ K as a working temperature to estimate the diffusion coefficient from the Stokes-Einstein relationship, so that the particle Péclet number could be fixed. Under these assumptions, the reference Péclet number corresponding to the experiment where the flowrate was fixed at $400\mathsf{\mu }{\mathrm{s}}^{-1}$ reported in Reference [15] can be estimated as ${\mathrm{Pe}}_{\mathrm{ref}}=7\times {10}^3$. With these estimated operating parameters, we computed the 2D and 3D prediction of the average migration angle ${\theta }_p$, obtaining ${\theta }_p^{2D}=4.953deg$ and ${\theta }_p^{3D}=3.339deg$, respectively, to be compared to the experimentally determined value ${\theta }_p^{ex}=3(\pm 0.1)deg$. Thus in this case, considering a full 3D setting of the problem allows to lower the relative error of the predicted value with respect to the experimental resul from $65\%$ to $13\%$. The above result should only be taken as an indication of possible improvements allowed by the 3D approach to the numerical prediction of particle transport features. In point of fact, the very steep boundary layer developed by the cumulative particle concentration for large particles at high values of the Péclet number demands that an independent validation of the numerical results stemming from the Eulerian approach to the particle number density be developed. This could be done, for example, by enforcing ensemble averages over a large number of particles governed by the Langevin equation equivalent to the Eulerian excluded-volume model.

5. Conclusions

Theoretical/numerical approaches to particle transport in Deterministic Lateral Displacement devices are largely based on a two-dimensional setting for modelling the flow structure of the suspending fluid. We find that the friction induced by the top and bottom walls of the channel hosting the obstacle lattice lends the flow a three-dimensional structure, characterized by the appearance of a non-vanishing component of the velocity along the direction orthogonal to these walls. The 3D effect depends on the aspect ratio, $\alpha$, of the periodic cell, as well as on the size of the obstacle, the maximum of the 3D perturbation to the two-dimensional solution being attained when $\alpha$ ranges in the interval $1\le \alpha \le 2$. Quantitatively, the magnitude of the off-plane velocity is relatively modest. In the geometries here considered, its maximum value is always found below 10 % of the average velocity, whereas its integral norm is of the order of few percents with respect to the norm of the total velocity. Accordingly, the distortion effect on the planar streamline geometry of the flow is also generally weak. Thus, transport models that only account for the deterministic components of particle motion are hardly influenced by the fact that solution for the flow problem is afforded a third dimension.

The situation is drastically different as soon as one considers that a Brownian component of motion for the micrometric sized particles must be superimposed to the deterministic drag of the fluid, if a realistic prediction of experimental results is sought. By enforcing a simple excluded-volume model, we find that the combined action of the weak off-plane component of the fluid velocity and the diffusional motion of the particle causes particles to migrate towards to top and bottom walls of the channel, thereby attaining a spatial distribution that is markedly different with respect to that predicted by the two-dimensional framing of the problem. Given that the average particle migration angle depends on the structure of the particle distribution, sizeable effect of the 3D flow structure on this quantity can be anticipated. By taking experimental data reported in the literature, we provide preliminary numerical evidence that the average deflection angle predicted by the 3D setting of the excluded volume model is sensitively different from its 2D counterpart, the first resulting in better agreement with experiments than the second. Given the large value of the particle Péclet number characterizing physically realistic implementations of DLD separation processes, the number of degrees of freedom needed for an accurate numerical solution of the particle transport equation in the Eulerian approach is also very large and requires that data be confirmed and validated either by tailored experiments or by Lagrangian stochastic approaches, which provide an altogether independent method for computing the average direction of the particle current. This analysis goes beyond the scope of the present article and will be object of future work.