Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation
Abstract
:1. Introduction
2. Robust Process Design
2.1. Probability-Based Robust Optimization
2.2. Imprecise Uncertainties
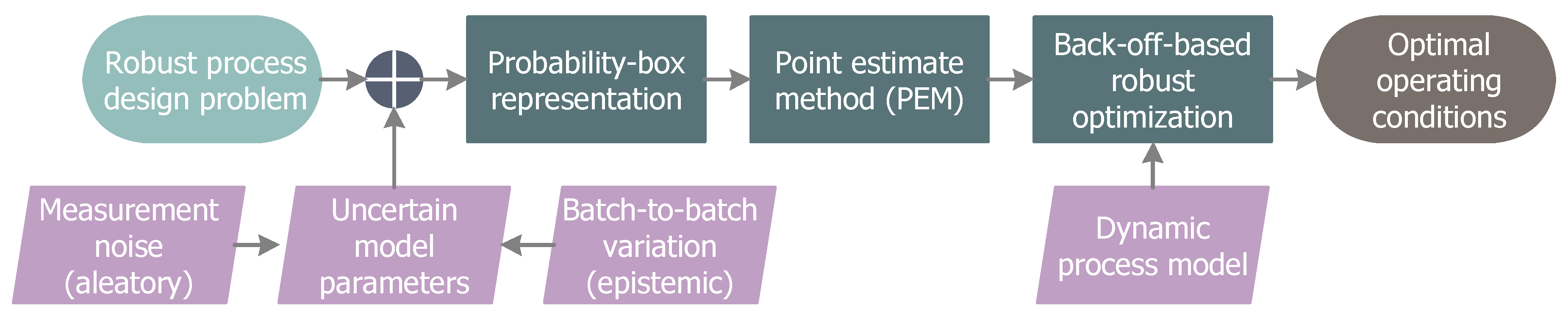
3. PEM-Based Back-Off Approach
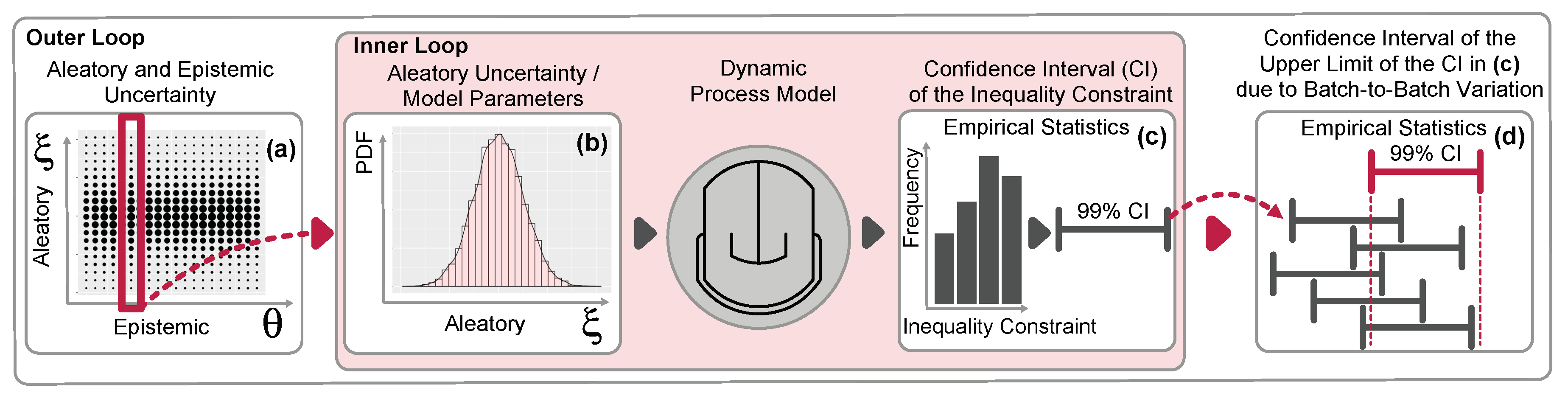
3.1. Point Estimate Method
3.2. Back-Off Realization
4. Case Study
4.1. Mathematical Model of the Primary Drying Process
4.2. Optimal Process Design Strategy
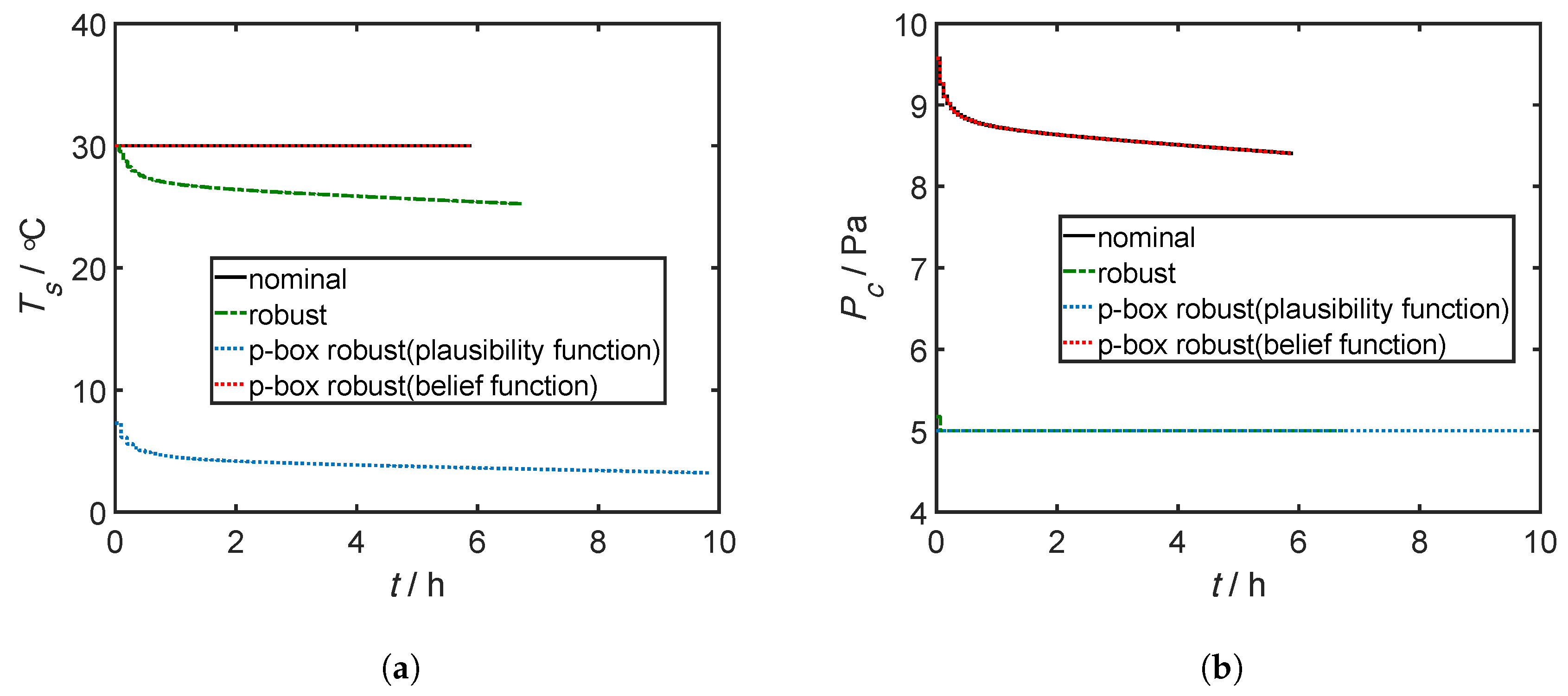
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FDA. Pharmaceutical CGMPs for the 21st Century—A Risk-based Approach; Final Report; U.S. Food and Drug Administration: Rockville, MD, USA, 2014.
- Gernaey, K.V.; Cervera-Padrell, A.E.; Woodley, J.M. A perspective on PSE in pharmaceutical process development and innovation. Comput. Chem. Eng. 2012, 42, 15–29. [Google Scholar] [CrossRef]
- Wang, Z.; Escotet-Espinoza, M.S.; Ierapetritou, M. Process analysis and optimization of continuous pharmaceutical manufacturing using flowsheet models. Comput. Chem. Eng. 2017, 107, 77–91. [Google Scholar] [CrossRef]
- Metta, N.; Verstraeten, M.; Ghijs, M.; Kumar, A.; Schafer, E.; Singh, R.; De Beer, T.; Nopens, I.; Cappuyns, P.; Van Assche, I.; et al. Model development and prediction of particle size distribution, density and friability of a comilling operation in a continuous pharmaceutical manufacturing process. Int. J. Pharm. 2018, 549, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Emenike, V.N.; Schenkendorf, R.; Krewer, U. A systematic reactor design approach for the synthesis of active pharmaceutical ingredients. Eur. J. Pharm. Biopharm. 2018, 126, 75–88. [Google Scholar] [CrossRef] [PubMed]
- Burmeister Getz, E.; Carroll, K.; Jones, B.; Benet, L. Batch-to-batch pharmacokinetic variability confounds current bioequivalence regulations: A dry powder inhaler randomized clinical trial. Clin. Pharmacol. Ther. 2016, 100, 223–231. [Google Scholar] [CrossRef] [PubMed]
- ICH Expert Working Group. Development and Manufacture of Drug Substances Q11; International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICE): Geneva, Switzerland, 2012. [Google Scholar]
- Djuris, J.; Djuric, Z. Modeling in the quality by design environment: Regulatory requirements and recommendations for design space and control strategy appointment. Int. J. Pharm. 2017, 30, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Telen, D.; Vallerio, M.; Cabianca, L.; Houska, B.; Van Impe, J.; Logist, F. Approximate robust optimization of nonlinear systems under parametric uncertainty and process noise. J. Process Control 2015, 33, 140–154. [Google Scholar] [CrossRef] [Green Version]
- Mortier, S.T.F.; Van Bockstal, P.J.; Corver, J.; Nopens, I.; Gernaey, K.V.; De Beer, T. Uncertainty analysis as essential step in the establishment of the dynamic Design Space of primary drying during freeze-drying. Eur. J. Pharm. Biopharm. 2016, 103, 71–83. [Google Scholar] [CrossRef]
- Maußer, J.; Freund, H. Optimization Under Uncertainty in Chemical Engineering: Comparative Evaluation of Unscented Transformation Methods and Cubature Rules. Chem. Eng. Sci. 2018, 183, 329–345. [Google Scholar] [CrossRef]
- Emenike, V.N.; Xiangzhong, X.; Schenkendorf, R.; Spiess, A.; Krewer, U. Robust dynamic optimization of enzyme-catalyzed carboligation: A point estimate-based back-off approach. Comput. Chem. Eng. 2018, 121, 232–247. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R. Stochastic back-off-based robust process design for continuous crystallization of ibuprofen. Comput. Chem. Eng. 2019, 124, 80–92. [Google Scholar] [CrossRef]
- Halemane, K.P.; Grossmann, I.E. Optimal process design under uncertainty. AIChE J. 1983, 29, 425–433. [Google Scholar] [CrossRef] [Green Version]
- Nagy, Z.; Braatz, R. Worst-case and distributional robustness analysis of finite-time control trajectories for nonlinear distributed parameter systems. IEEE Trans. Control Syst. Technol. 2003, 11, 694–704. [Google Scholar] [CrossRef] [Green Version]
- Grossmann, I.E.; Apap, R.M.; Calfa, B.A.; García-Herreros, P.; Zhang, Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty. Comput. Chem. Eng. 2016, 91, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Mockus, L.; Peterson, J.J.; Lainez, J.M.; Reklaitis, G.V. Batch-to-Batch Variation: A Key Component for Modeling Chemical Manufacturing Processes. Org. Process Res. Dev. 2014, 19, 908–914. [Google Scholar] [CrossRef]
- Lee, S.L.; O’Connor, T.F.; Yang, X.; Cruz, C.N.; Chatterjee, S.; Madurawe, R.D.; Moore, C.M.V.; Yu, L.X.; Woodcock, J. Modernizing Pharmaceutical Manufacturing: From Batch to Continuous Production. J. Pharm. Innov. 2015, 10, 191–199. [Google Scholar] [CrossRef]
- Hagsten, A.; Casper Larsen, C.; Møller Sonnergaard, J.; Rantanen, J.; Hovgaard, L. Identifying sources of batch to batch variation in processability. Powder Technol. 2008, 183, 213–219. [Google Scholar] [CrossRef]
- Xiong, H.; Yu, L.X.; Qu, H. Batch-to-batch quality consistency evaluation of botanical drug products using multivariate statistical analysis of the chromatographic fingerprint. AAPS PharmSciTech 2013, 14, 802–810. [Google Scholar] [CrossRef]
- Woodcock, J. The concept of pharmaceutical quality. Am. Pharm. Rev. 2004, 7, 10–15. [Google Scholar]
- Benet, L.Z.; Jayachandran, P.; Carroll, K.J.; Burmeister Getz, E. Batch-to-Batch and Within-Subject Variability: What Do We Know and How Do These Variabilities Affect Clinical Pharmacology and Bioequivalence? Clin. Pharmacol. Ther. 2019, 105, 326–328. [Google Scholar] [CrossRef]
- Mülhopt, S.; Diabaté, S.; Dilger, M.; Adelhelm, C.; Anderlohr, C.; Bergfeldt, T.; Gómez de la Torre, J.; Jiang, Y.; Valsami-Jones, E.; Langevin, D.; et al. Characterization of Nanoparticle Batch-To-Batch Variability. Nanomaterials 2018, 8, 311. [Google Scholar] [CrossRef] [PubMed]
- Nagy, Z.K. Model based robust control approach for batch crystallization product design. Comput. Chem. Eng. 2009, 33, 1685–1691. [Google Scholar] [CrossRef] [Green Version]
- Su, Q.; Chiu, M.S.; Braatz, R.D. Integrated B2B-NMPC control strategy for batch/semibatch crystallization processes. AIChE J. 2017, 63, 5007–5018. [Google Scholar] [CrossRef]
- Baudrit, C.; Dubois, D. Practical representations of incomplete probabilistic knowledge. Comput. Stat. Data Anal. 2006, 51, 86–108. [Google Scholar] [CrossRef] [Green Version]
- Beer, M.; Ferson, S.; Kreinovich, V. Do we have compatible concepts of epistemic uncertainty? Proceeedings of the 6th Asian-Pacific Symposium on Structural Reliability and its Applications (APSSRA6), Shanghai, China, 28–30 May 2016; pp. 1–10. [Google Scholar]
- Schöbi, R.; Sudret, B. Structural reliability analysis for p-boxes using multi-level meta-models. Probabilistic Eng. Mech. 2017, 48, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, D.D.; Olewnik, A. Computationally Efficient Imprecise Uncertainty Propagation. J. Mech. Des. 2013, 135, 051002. [Google Scholar] [CrossRef]
- Shang, C.; You, F. Distributionally robust optimization for planning and scheduling under uncertainty. Comput. Chem. Eng. 2018, 110, 53–68. [Google Scholar] [CrossRef]
- Ferson, S.; Troy Tucker, W. Sensitivity analysis using probability bounding. Reliab. Eng. Syst. Saf. 2006, 91, 1435–1442. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Uncertainty propagation of p-boxes using sparse polynomial chaos expansions. J. Comput. Phys. 2017, 339, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Bi, S.; Broggi, M.; Wei, P.; Beer, M. The Bhattacharyya distance: Enriching the P-box in stochastic sensitivity analysis. Mech. Syst. Signal Process. 2019, 129, 265–281. [Google Scholar] [CrossRef]
- Smith, R.C. Uncertainty quantification: Theory, Implementation, and Applications; siam: Philadelphia, PA, USA, 2013; Volume 12. [Google Scholar]
- Xie, X.; Schenkendorf, R.; Krewer, U. Toward a comprehensive and efficient robust optimization framework for (bio)chemical processes. Processes 2018, 6, 183. [Google Scholar] [CrossRef]
- Shi, J.; Biegler, L.T.; Hamdan, I.; Wassick, J. Optimization of grade transitions in polyethylene solution polymerization process under uncertainty. Comput. Chem. Eng. 2016, 95, 260–279. [Google Scholar] [CrossRef]
- Nimmegeers, P.; Telen, D.; Beetens, M.; Logist, F.; Impe, J.V. Parametric uncertainty propagation for robust dynamic optimization of biological networks. BMC Syst. Biol. 2016, 6929–6934. [Google Scholar]
- Paulson, J.A.; Mesbah, A. An efficient method for stochastic optimal control with joint chance constraints for nonlinear systems. Int. J. Robust Nonlinear Control 2017, 1–21. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Dias, L.S.; Ierapetritou, M.G. Optimal operation and control of intensified processes—Challenges and opportunities. Current Opin. Chem. Eng. 2019, 8–12. [Google Scholar] [CrossRef]
- Lerner, U.N. Hybrid Bayesian Networks for Reasoning about Complex Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Schenkendorf, R. A general framework for uncertainty propagation based on point estimate methods. In Proceedings of the Second European Conference of the Prognostics and Health Management Society, Nantes, France, 8–10 July 2014. [Google Scholar]
- Srinivasan, B.; Bonvin, D.; Visser, E.; Palanki, S. Dynamic optimization of batch processes: II. Role of measurements in handling uncertainty. Comput. Chem. Eng. 2003, 27, 27–44. [Google Scholar] [CrossRef]
- Fissore, D.; Pisano, R.; Barresi, A.A. Advanced approach to build the design space for the primary drying of a pharmaceutical freeze-drying process. J. Pharm. Sci. 2011, 100, 4922–4933. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R. Robust optimization of a pharmaceutical freeze-drying process under non-Gaussian parameter uncertainties. Chem. Eng. Sci. 2019, 207, 805–819. [Google Scholar] [CrossRef]
- Scutellà, B.; Passot, S.; Bourlés, E.; Fonseca, F.; Tréléa, I.C. How Vial Geometry Variability Influences Heat Transfer and Product Temperature During Freeze-Drying. J. Pharm. Sci. 2017, 106, 770–778. [Google Scholar] [CrossRef]
- Scutellà, B.; Bourlés, E.; Tordjman, C.; Fonseca, F.; Mayeresse, Y.; Trelea, I.C.; Passot, S. Can the desorption kinetics explain the residual moisture content heterogeneity observed in pharmaceuticals freeze-drying process? In Proceedings of the 6th European Drying Conference: EuroDrying 2017, Liège, Belgium, 19–21 June 2017. [Google Scholar]
- Scutellà, B.; Trelea, I.C.; Bourlés, E.; Fonseca, F.; Passot, S. Use of a multi-vial mathematical model to design freeze-drying cycles for pharmaceuticals at known risk of failure. In Proceedings of the 21th International Drying Symposium, Valencia, Spain, 18–21 September 2018; Universitat Politècnica València: Valencia, Spain, 2018; pp. 11–14. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A symbolic package for automatic differentiation and optimal control. In Recent Advances in Algorithmic Differentiation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 297–307. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]



| Parameters | Symbols | Unit | Nominal Value |
|---|---|---|---|
| cross-sectional area of product | m2 | ||
| outer cross-sectional area of the vial | m2 | ||
| m2 | |||
| dried product resistance | m/s | ||
| heat transfer coefficient | J/(m2sK) | 11.47 | |
| m | 0.00658 | ||
| kg/m3 | 919 | ||
| - | 0.97 | ||
| M | kg/mol | 0.018 | |
| k | - | 1.33 | |
| R | J/(Kmol) | 8.314 |
| Parameters | Distribution | Mean Value | Standard Deviation |
|---|---|---|---|
| Gaussian | [50,000, 80,000] | ||
| Gaussian |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Schenkendorf, R. Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation. Processes 2019, 7, 509. https://doi.org/10.3390/pr7080509
Xie X, Schenkendorf R. Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation. Processes. 2019; 7(8):509. https://doi.org/10.3390/pr7080509
Chicago/Turabian StyleXie, Xiangzhong, and René Schenkendorf. 2019. "Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation" Processes 7, no. 8: 509. https://doi.org/10.3390/pr7080509
APA StyleXie, X., & Schenkendorf, R. (2019). Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation. Processes, 7(8), 509. https://doi.org/10.3390/pr7080509







