Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata

Abstract

In this work, a closed-loop identification method based on a reinforcement learning algorithm is proposed for multiple-input multiple-output (MIMO) systems. This method could be an attractive alternative solution to the problem that the current frequency-domain identification algorithms are usually dependent on the attenuation factor. With this method, after continuously interacting with the environment, the optimal attenuation factor can be identified by the continuous action reinforcement learning automata (CARLA), and then the corresponding parameters could be estimated in the end. Moreover, the proposed method could be applied to time-varying systems online due to its online learning ability. The simulation results suggest that the presented approach can meet the requirement of identification accuracy in both square and non-square systems.

1. Introduction

With the rapid development of modern industry, it becomes increasingly difficult for the traditional model control methods to properly control complex process due to the uncertainty, time-delay, multivariable coupling, and constraints between input and output. It is a challenge for the traditional identification methods to obtain optimal results, particularly in multivariable systems, due to their complex structure, various parameters, and time-varying in industrial applications. Methods for the identification of multivariable systems go back to the 1960s, but most identification methods require the observation to be noise-free. This situation together with their heavy computational cost makes them difficult to be applied in practice [1]. In view of the above problems, many researchers proposed replacing the state space model with a polynomial matrix to describe the multivariable system. In 1975, Guidozi [2] proposed the equivalence relation between the observable canonical form of system state and the canonical form of an input–output difference equation, and established the mapping relation between the parameters of the state equation and the observed input–output data. Subsequently, some researchers proposed row subspace identification methods based on the Hankel matrix. In these methods, the first step is to obtain the augmented observability matrix (or state sequence) of the system, and then the parameter matrix of each subspace is calculated. The main representative methods include multivariable output error state space (MOESP) [3,4], numerical algorithms for subspace state-space system identification (N4SID) [5,6], and canonical variate analysis (CVA) [7,8]. At first, these methods of subspace identification were difficult to apply online, and were very computationally intensive in recursive decomposition. With the development of technology, they have been widely applied in industrial practice due to the advantage that they do not depend on any prior knowledge in the identification of the multivariable system. However, the objective of multivariate identification methods based on state space models is not to find the optimal solution, but the Pareto suboptimal solutions, so there is substantial room for improvement in the performance of these methods.

Methods for the identification of multivariable systems based on state space have large computational demand, take a long time, and it is difficult for them to achieve the global optimal solution. Therefore, many researchers have focused on identification methods based on the transfer function matrix or other models (i.e., to transform the state space model into a transfer function model through the Laplace transform). Researchers have proposed several methods for the transfer function $n$ matrix modeling of multivariable systems, such as the instrumental model method, the sub-sub model recursive method, the combined identification algorithm (CIA), the extended least squares method, and the multi-innovation recursive identification method, which have greatly promoted the direction of multivariable system identification based on the transfer function matrix model. With the instrumental model, the identification of the transfer function model can be decomposed into several sub-models, and it has attracted increasing attention. In [9], the least squares method was used to eliminate the bias in a multi-input single-output (MISO) system, but this method is still difficult to apply online, and it has harsh preconditions and assumptions. Ding et al. [10] proposed a bias-compensation-based recursive least-squares algorithm to solve the problem of the identification in non-stationary systems. On the basis of the nearest Kronecker product and low-rank approximation, Camelia et al. [11] proposed a low-complexity recursive least-squares (RLS) algorithm, which has good robustness against additive noise and good identification effect. The instrumental model [12] can solve the problem of the unknown information vector in the model. Du et al. [13] proposed a robust output error model identification method, and used the auxiliary model to estimate the noiseless output under random noise, which is suitable for the time-delay industrial process under load disturbance. In order to eliminate the interference of abnormal points in the observation, the multi-innovation concept was introduced to accelerate the convergence of the model [14]. Based on the sub-model (MISO), Li et al. [15] proposed a sequential excitation method for a multiple-input multiple-output (MIMO) system. With sequential excitation signals, the multiple-input multiple-output (MIMO) system could be decomposed into several equivalent single-input single-output (SISO) systems in an open-loop control.

In recent years, the open-loop step response test has been a common method in the field of system identification, and is simple to operate and easy to implement. However, there are still some issues: (1) Open-loop identification is usually not permitted in field systems. Considering the factors of safety and economy, the output of the controller is required within a limited range once the system is running. (2) The input signal is usually limited to a step-function signal, and the test time is limited to the transition time. It is often affected by external disturbance and the change of internal working conditions. Therefore, authors in [16,17,18,19] proposed frequency response estimation methods for the identification of the closed-loop system. However, the existing methods still have some limitations (e.g., the accuracy depends on the choice of attenuation factor). The value of the attenuation factor is usually given according to prior knowledge. Jin et al. [20] proposed an intelligent searching algorithm to obtain the range of the attenuation factor, and achieved good results. However, for large-scale complex systems, it is time-varying and the attenuation factor easily falls into local premature convergence.

Learning automata (LA) have potential applications in system control. Li et al. [21] proposed a coral reef algorithm based on LA for the coverage control problem of heterogeneous directional sensor networks. Mohammed et al. [22] developed a fuzzy maximum power point tracking controller using the information collected by LA through the learning process. Thus, a novel method based on a reinforcement learning algorithm, namely continuous action reinforcement learning automata (CARLA), is presented here to solve the issue mentioned above. After continuously interacting with the environment, an optimal attenuation factor can be achieved by CARLA, and then the system parameters of the system can be estimated. Moreover, the proposed method can be used online and applied to time-varying systems due to its online learning ability.

2. Materials and Methods

2.1. Background

Frequency response methods can be applied to the parameter estimation of open-loop and closed-loop systems, but their accuracy depends on the value of the attenuation factor, which is usually obtained from prior knowledge. Some researchers [20,23] proposed the use of heuristic search algorithms (e.g., particle swarm optimization (PSO) and its improved methods) to obtain the optimal value. However, it is difficult to solve the issue of the on-line identification of time-varying systems. An online adaptive learning method is required to find the optimal solution of the parameters within the contiguous space. To solve these problems, a frequency response estimation (FRE) method based on continuous action reinforcement learning automata (CARLA-FRE) is proposed in this paper.

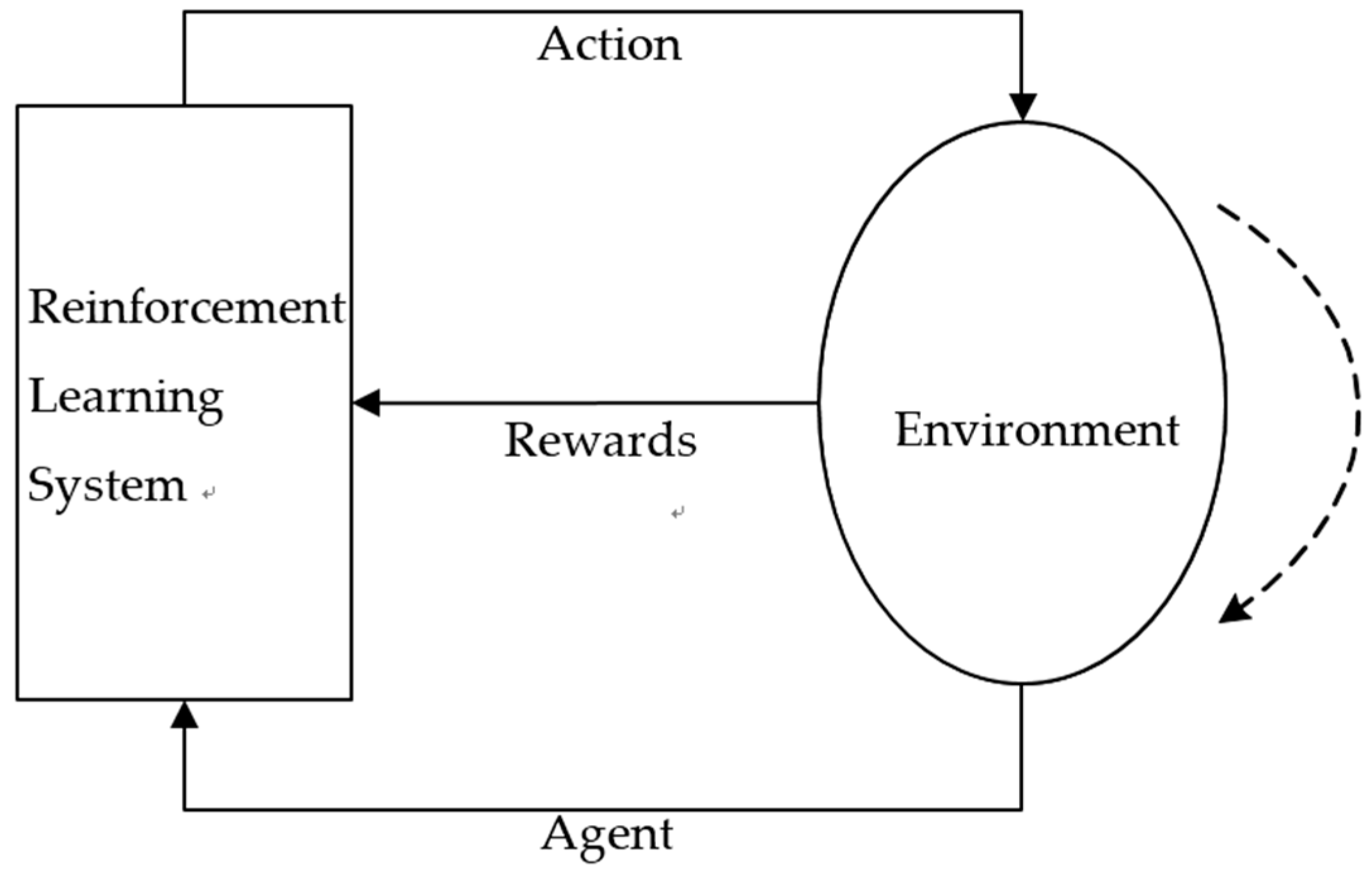
2.2. Basic Reinforcement Learning

As an important branch of machine learning, reinforcement learning (RL) [24] interacts with the environment actively and constantly, updates iterations based on feedback, and finally gives the optimal strategy. It contains the main elements of agent, state, action, and rewards, and its learning target is to obtain the optimal strategy to maximize the long-term cumulative rewards. As shown in Figure 1, the most important feature of reinforcement learning is the capability of autonomous and online learning without any prior knowledge and state transition probability. Firstly, the agent perceives the state of the environment and takes various exploratory actions according to the accumulative compensation. After taking the action, the environment undergoes a state transition and enters into a new state. At the same time, the behavior strategy is evaluated, and the feedback is returned to the learning system. After receiving the feedback of the reward or the punishment, the agent modifies its strategies continuously to meet the requirements of the environment, and the whole process is iteratively updated until the optimal strategy is obtained.

2.3. Continuous Action Reinforcement Learning Automata (CARLA)

The target of system identification is to obtain the appropriate attenuation factor, which is a problem of finding the optimal action. Because the action space is continuous, a continuous action reinforcement learning automata (CARLA) [25,26] is proposed in this paper. Compared with other algorithms, CARLA can use the probability density function to select behavior in continuous space with a stochastic or unknown system model. The system learns interactively with the environment in a trial-and-error manner, and gets better behavior strategies by strengthening signals, increasing the probability of the action by strategy iteration, and finally obtains the optimal parameters online [27,28,29,30].

For CARLA, each action $x$ is a mapping of a cumulative probability density function (CPDF), registered as $f\left(x\right)$. With reinforcement signal $\beta$, the density functions are updated many times, and the optimal decision variables with the maximum of the corresponding CPDF is obtained. During the process of the iteration, the reinforcement signal is determined by the evaluation function of the last iteration. Therefore, the whole process of learning and updating is always optimized in the direction of better results, and the ultimate goal is to achieve long-term rewards rather than one-step rewards, so as to ensure the global optimality. The learning process is as follows:

CARLA algorithm

1: Initialize the probability density function $f^0(x_{\mathrm{i}})$: establish the uniform distribution of CPDFs according to the range of the parameter;

2: Actions selection: select actions (or parameters) randomly based on the CPDF value;

3: System evaluation: take the action, substitute parameters into the system to obtain the responding curve, and calculate the fitness function $J(x_{\mathrm{i}})$;

4: Calculate the enhanced signal value $\beta$ according to the value of the fitness function;

5: Update each CPDF value according to the enhanced signal value;

6: Update behavior parameters: introduce the normal random number generator to update the action parameters at the next moment;

7: If the stopping condition has not been reached, return to step 2 until the convergence condition is met.

3. Frequency Response Estimation Based on CARLA (CARLA-FRE)

3.1. Frequency Response Estimation Based on CARLA (CARLA-FRE)

In order to improve learning efficiency of the algorithm, the threshold value of attenuation factor obtained in [31] is used as the initial region of CARLA (i.e., $x^i\in [x_{\min }^i,x_{\max }^i]$). Then, using the powerful interactive learning ability of CARLA, the optimal parameters can be obtained online to improve the accuracy and effectiveness of frequency response estimation. The learning process is shown in Figure 2, and the details of the algorithm are as follows:

(1) Selection of the test signal: The input functions with the characteristics of continuous second-order derivability can be used as the excitation signals of frequency response estimation. Therefore, there are many choices of test signal, including the step signal $r\left(t\right)=c$, the pulse signal $r(t)=1/\delta \left(t\right)$, the exponential attenuation signal $r\left(t\right)=e^{-kt}$, and the composite function $r\left(t\right)=t{e}^{-kt}$.

(2) Selection of the test mode: This includes open-loop identification and closed-loop identification, according to the process requirements and environmental conditions. If the system is asymptotically stable and the external disturbance is small or the disturbance signal is regular, it may be a good choice to adopt a simple open-loop testing mode. If the process requires high safety and stability, large shutdown loss, and sensitive to external disturbance, it will be necessary to choose the closed-loop approach.

(3) Selection of the model structure: The establishment of a system model includes structure selection and parameter identification. The former selects the model structure according to the characteristics of the process, including model order and time delay. The latter estimates model parameters on the basis of the model structure. This paper focuses on the problem of model parameter estimation.

Steps (1)–(3) can be regarded as the preparation stage of the test, which can seriously affect the accuracy of system identification.

(4) Analysis of system parameters: This part focuses on the frequency response estimation method. The mathematical expressions of the relationship between system parameters and input–output can be given by analyzing the transfer function of the system. Then, the frequency response of the expression can be obtained by substituting $s=a+jw$, where $a$ is the attenuation factor. With the appropriate attenuation factor $a$, the parameter estimation can be obtained. The traditional approach is to give the value of $a$ directly according to experiential knowledge, or using a heuristic searching algorithm. However, in practice, the system often has time-varying characteristics, and the attenuation factor usually falls into local premature convergence. Therefore, an online learning method is required to acquire appropriate parameters adaptively.

(5) Online optimization of attenuation factor based on CARLA:

a. Initialize the attenuation factor $a(0)$. According to the literature, the range of the attenuation factor can be set as $a\in [a_{\min },a_{\max }]$ in advance. For each iteration k, the action $a\left(k\right)$ can be selected according to the probability density function $f\left(a,k\right)$. In the beginning, the probability density function $f\left(a,k\right)$ can be initialized as in Formula (1):

$$f(x^i,0)=\{\begin{array}{c}\frac{1}{x_{\max }^i-x_{\min }^i},x^i\in \left[x_{\min }^i,x_{\max }^i\right]\\ 0,x^i\notin \left[x_{\min }^i,x_{\max }^i\right]\end{array}.$$

(1)

b. Select the attenuation factor. Select the attenuation factor $a$ according to the value of the probability distribution function (as Formulas (2) and (3))— the attenuation factor $a$ with the maximum value of probability distribution function $f\left(a,k\right)$ is the best.

$$F(x^i,k)={\displaystyle {\int }_0^{x^i}f(x^i,k)\mathrm{d}{x}^i}$$

(2)

$$x^{i*}=\arg \underset{x^i}{\max }F(x^i,k)$$

(3)

c. Calculate the cost function $J\left(a,k\right)$. According to the cost function, the cost function value under the current attenuation factor $a$ will be calculated as Formula (4). It is the integral square error (ISE) of the real output and the estimated output of the system.

$$J(X,k)={\displaystyle \int {(\Delta e)}^2\mathrm{d}t}$$

(4)

$$J(X,k)={\displaystyle \int {(\Delta e)}^2\mathrm{d}t}\approx {\displaystyle \sum _{T=1}^M{(Y_T-y_T)}^2}$$

(5)

d. Calculate the enhancement signal $\beta \left(k\right)$. By substituting the cost value $J\left(a,k\right)$, average cost value $J_{mean}$, and minimum cost value $J_{min}$ into Formula (6), the enhancement signal $\beta \left(k\right)$ can be calculated to measure the performance of the evaluation. The closer the value of $\beta \left(k\right)$ is to 1, the better the performance of the system under the attenuation factor. On the contrary, the closer the value of $\beta \left(k\right)$ is to 0, the worse the performance of the system under the attenuation factor.

$$\beta (k)=\min \left\{\max \left\{0,\frac{J_{\mathrm{mean}}-J(X,k)}{J_{\mathrm{mean}}-J_{\min }}\right\},1\right\}$$

(6)

e. Update the value of the probability density function corresponding to the current attenuation factor $a$. After the system takes action to change the environment, it will give feedback to this policy, and update the probability density function corresponding to the iteration action by strengthening the signal. The probability density function $f\left(a,k+1\right)$ corresponding to the selected attenuation factor can be updated according to Formula (7):

$$f(x^i,k+1)=\{\begin{array}{l}{\alpha }^k(f(x^i,k)+\beta (k)H(x^i,r)),x^i\in \left[x_{\min }^i,x_{\max }^i\right]\\ 0,x^i\notin \left[x_{\min }^i,x_{\max }^i\right]\end{array},$$

(7)

where $H(x^i,r))$ is the Gaussian nearest neighbor function, whose value represents the possibility of action change. The specific formula is as follows:

$$H(x^i,r))=\lambda \exp \left(-\frac{{(x^i-r)}^2}{2{\sigma }^2}\right),$$

(8)

$${\alpha }^k=\frac{1}{{\displaystyle {\int }_{x_{\min }^i}^{x_{\max }^i}\left(f(x^i,k)+\beta (k)H(x^i,r)\right)\mathrm{d}}{x}^i},$$

(9)

$$\lambda =\frac{g_h}{(x_{\max }^i-x_{\min }^i)},$$

(10)

$$\sigma =g_w(x_{\max }^i-x_{\min }^i),$$

(11)

where $g_h$ and $g_w$ represent the height and width of the Gaussian distribution function, respectively. They determine the speed and depth of the learning process, respectively. According to previous work [32], $g_w=0.02$ and $g_h=0.3$ are usually selected if the sample number is 500 in the calculation of the strengthened signal, $r$ is the action parameter, and $a$ is the normalized factor, which can keep the value of the probability density function within [0,1].

f. Update attenuation factor parameters. In order to solve the problem of large computations when updating the probability density function value and the probability distribution value in step $b$, this paper proposes an improved method as follows:

$$\alpha (k+1)=\{\begin{array}{l}\mathrm{norm}(\alpha (k),\omega e^{(1-\beta (k))}),\alpha (k)\in \left[{\alpha }_{\min },{\alpha }_{\max }\right]\\ \alpha (k),\alpha (k)\notin \left[{\alpha }_{\min },{\alpha }_{\max }\right]\end{array},$$

(12)

where $norm\left(\alpha (k),\omega e^{(1-\beta (k))}\right)$ is the normal-distribution random number simulator with $\alpha (k)$, $\omega e^{(1-\beta (k))}$, and $\omega$ as the average, standard deviation, and learning rate factor, respectively. It can be seen that the learning time of the improved algorithm is linear with the number of iterations. Compared with the previous method using the integral operation to calculate the value of the probability distribution function, the calculation and learning time of the improved algorithm are significantly reduced without any loss of learning performance.

g. Update the iterations to achieve the optimal attenuation factor $a$ which makes the estimated output as close as possible to the real output.

(6) Substitute the learned optimal attenuation factor into the mathematical expression in step (4) to obtain the parameter estimation. After obtaining the system estimation model, it can be applied to the internal model control.

3.2. The Applications of CARLA-FRE in MIMO Systems

In industrial applications, due to the complex structure, various parameters, and the coupling relationship between the loops of multivariable systems, the traditional identification methods are difficult to use effectively in multivariable systems. Li [15] proposed a multivariable system identification method based on sequential step signals. With the sequential step method, the multiple-input multiple-output (MIMO) system could be equivalently decomposed into several single-input single-output (SISO) systems. Then, the analytic expressions of model parameters of these sub-systems could be obtained by frequency response estimation. The simulation results reveal that the presented approach could match the requirements of identification accuracy both in square and non-square systems.

3.2.1. Closed-Loop Identification for Square Multivariate Systems

A multivariable square closed-loop control system $n\times n$ is depicted in Figure 3, where $G_s\left(s\right)$ is the controlled object, $G_c\left(s\right)$ is the distributed diagonal controller, $R$ is the system input vector, Y is the system output vector, E is the deviation vector, and U is the controller output vector.

$$R(s)={\left[r_1,\cdots ,r_n\right]}^T$$

(13)

$$Y(s)={\left[y_1,\cdots ,y_n\right]}^T$$

(14)

$$U(s)={\left[u_1,\cdots ,u_n\right]}^T$$

(15)

$$G_s(s)=\left[\begin{array}{cccc}{g}_{s_{11}}(s)& g_{s_{12}}(s)& \cdots & g_{s_{1n}}(s)\\ g_{s_{21}}(s)& g_{s_{22}}(s)& \cdots & g_{s_{2n}}(s)\\ ⋮& ⋮& \ddots & ⋮\\ g_{s_{n1}}(s)& g_{s_{n2}}(s)& \cdots & g_{s_{nn}}(s)\end{array}\right]$$

(16)

$$G_c(s)=\left[\begin{array}{cccc}{g}_{c1}(s)& 0& \cdots & 0\\ 0& g_{c2}(s)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & g_{cn}(s)\end{array}\right]$$

(17)

According to the above, it can be known that

$$Y=G_c{G}_s(R-Y).$$

(18)

So, we can get:

$$\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]=\left[\begin{array}{cccc}{g}_{c1}& 0& \cdots & 0\\ 0& g_{c2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & g_{cn}\end{array}\right]\left[\begin{array}{cccc}{g}_{s_{11}}& g_{s_{12}}& \cdots & g_{s_{1n}}\\ g_{s_{21}}& g_{s_{22}}& \cdots & g_{s_{2n}}\\ ⋮& ⋮& \ddots & ⋮\\ g_{s_{n1}}& g_{s_{n2}}& \cdots & g_{s_{nn}}\end{array}\right]\left[\begin{array}{c}{r}_1-y_1\\ r_2-y_2\\ ⋮\\ r_n-y_n\end{array}\right].$$

(19)

Then, the MIMO system can be equivalently decomposed into several SISO systems as follows:

$$\{\begin{array}{c}{y}_1=g_{c1}{g}_{s_{11}}(r_1-y_1)+\cdots +g_{cn}{g}_{s_{1n}}(r_n-y_n)\hfill \\ y_2=g_{c1}{g}_{s_{21}}(r_1-y_1)+\cdots +g_{cn}{g}_{s_{2n}}(r_n-y_n)\hfill \\ ⋮\\ y_n=g_{c1}{g}_{s_{n1}}(r_1-y_1)+\cdots +g_{cn}{g}_{s_{nn}}(r_n-y_n)\hfill \end{array}.$$

(20)

A method to simplify the identification process of closed-loop systems was proposed in the literature, in which the system deviation could be regarded as the input signal, that is, $r(t)$ could be replaced with $e(t)=r(t)-y(t)$ of the identification process, and the closed-loop system was equivalent to the open-loop system. Therefore, Formula (20) can be further expressed as Formula (21):

$$\{\begin{array}{c}{y}_1=g_{c1}{g}_{s_{11}}{e}_1+\cdots +g_{cn}{g}_{s_{1n}}{e}_n\hfill \\ y_2=g_{c1}{g}_{s_{21}}{e}_1+\cdots +g_{cn}{g}_{s_{2n}}{e}_n\hfill \\ ⋮\\ y_n=g_{c1}{g}_{s_{n1}}{e}_1+\cdots +g_{cn}{g}_{s_{nn}}{e}_n\hfill \end{array}.$$

(21)

Then, $n$ step excitation signals are applied to the system successively and $n$ groups of vector relationships can be obtained for each MISO system, depicted, for example, as Formula (22):

$$\{\begin{array}{c}{y}_i^1=g_{ci}{g}_{s_{i1}}{e}_1^1+\cdots +g_{ci}{g}_{s_{in}}{e}_n^1\hfill \\ y_i^2=g_{ci}{g}_{s_{i1}}{e}_1^2+\cdots +g_{ci}{g}_{s_{in}}{e}_n^2\hfill \\ ⋮\\ y_i^n=g_{ci}{g}_{s_{i1}}{e}_1^n+\cdots +g_{ci}{g}_{s_{in}}{e}_n^n\hfill \end{array},$$

(22)

where $r_i^j$ is the excitation signal of the input channel of the ith subsystem under the jth test, $y_i^j$ is the output signal of the output channel of the ith subsystem under the jth test, and then the deviation signal of the channel can be obtained, $e_i^j=r_i^j-y_i^j$, that is, the equivalent input signal in the identification process.

Therefore, the following expression can be obtained by matrix transformation:

$$\left[\begin{array}{c}{y}_i^1\\ y_i^2\\ ⋮\\ y_i^n\end{array}\right]=g_{ci}\left[\begin{array}{cccc}{e}_1^1& e_2^1& \cdots & e_n^1\\ e_1^2& e_2^2& \cdots & e_n^2\\ ⋮& ⋮& \ddots & ⋮\\ e_1^n& e_2^n& \cdots & e_n^n\end{array}\right]\left[\begin{array}{c}{g}_{s_{i1}}\\ g_{s_{i2}}\\ ⋮\\ g_{s_{in}}\end{array}\right]=\left[\begin{array}{cccc}{g}_{ci}{e}_1^1& g_{ci}{e}_2^1& \cdots & g_{ci}{e}_n^1\\ g_{ci}{e}_1^2& g_{ci}{e}_2^2& \cdots & g_{ci}{e}_n^2\\ ⋮& ⋮& \ddots & ⋮\\ g_{ci}{e}_1^n& g_{ci}{e}_2^n& \cdots & g_{ci}{e}_n^n\end{array}\right]\left[\begin{array}{c}{g}_{s_{i1}}\\ g_{s_{i2}}\\ ⋮\\ g_{s_{in}}\end{array}\right].$$

(23)

That is,

$$Y_i=F_i·G_{s_i},$$

(24)

where

$$Y_i={\left[\begin{array}{cccc}{y}_i^1& y_i^2& \cdots & y_i^n\end{array}\right]}^T,$$

(25)

$$F_i=\left[\begin{array}{cccc}{g}_{ci}{e}_1^1& g_{ci}{e}_2^1& \cdots & g_{ci}{e}_n^1\\ g_{ci}{e}_1^2& g_{ci}{e}_2^2& \cdots & g_{ci}{e}_n^2\\ ⋮& ⋮& \ddots & ⋮\\ g_{ci}{e}_1^n& g_{ci}{e}_2^n& \cdots & g_{ci}{e}_n^n\end{array}\right],$$

(26)

$$G_{i_s}={\left[\begin{array}{cccc}{g}_{s_{i1}}& g_{s_{i2}}& \cdots & g_{s_{in}}\end{array}\right]}^T.$$

(27)

Since the closed-loop system is asymptotically stable and the input signal is continuously differentiable, it can be proved that $F_i$ is a non-singular square matrix. So, Formula (28) can be further obtained according to Formula (24):

$$G_{s_i}=F_i{}^{-1}·Y_i=\frac{\mathrm{adj}(F_i)}{\det (F_i)}·Y_i,$$

(28)

where $F_i{}^{-1}$ is the inverse matrix of $F_i$, $\mathrm{adj}(·)$ is the adjoint matrix operator, and $\det (·)$ is the matrix determinant operator.

According to Formula (28), the MIMO system identification problem can first be decomposed into several MISO subsystem problems, and then further decomposed into SISO identification problems.

$$G_{s_{ij}}={\frac{{\displaystyle \sum _{k=1}^n{F}_{kj}^{*}{y}_i^k}}{\det (F_i)}}_i$$

(29)

$G_{s_{ij}}$ is the transfer function of the decomposed equivalent subsystem (SISO) of the MISO system, and $F_{kj}^{*}$ is the joint factor of the jth row of the $F$ matrix under the kth test.

For Formula (29), if the assumption that ${\overline{u}}_{ij}=\det (F_i)$, ${\overline{y}}_{ij}={\displaystyle \sum _{k=1}^n{F}_{kj}^{*}{y}_i^k}$, ${\overline{u}}_{ij}$, and ${\overline{y}}_{ij}$ can be regarded as the equivalent input and output of the SISO system identification problem, MISO can be further decomposed into several SISO identification problems. Considering that the presented CARLA-FRE is applicable for a variety of excitation signals, the parameters of the decomposed equivalent SISO system can be estimated using CARLA-FRE. Then, the identified SISO can be combined into a MIMO system according to Formulas (24) and (19) to complete the multivariable system identification.

3.2.2. Closed-Loop Identification for Non-Square Multivariate Systems

For multivariable non-square systems, due to the inconsistency between the input and output dimensions of the system, the inverse matrix of the equivalent matrix F does not exist, making the methods above difficult to apply directly. Based on the idea of the first method in [17], this paper adjusts the decentralized controller into a centralized controller, establishes an association between the input and output of each loop in the MIMO system, and then constructs a solvable matrix form. A multivariable non-square closed-loop control system of $m\times n,(m\ne n)$ is shown in Figure 4, where $G_s\left(s\right)$ is the controlled object, $G_c\left(s\right)$ is the central controller, R is the system input vector, Y is the system output vector, E is the deviation vector, and U is the controller output vector.

$$G_c(s)=\left[\begin{array}{cccc}{g}_{c_{11}}(s)& g_{c_{12}}(s)& \cdots & g_{c_{1n}}(s)\\ g_{c_{21}}(s)& g_{c_{22}}(s)& \cdots & g_{c_{2m}}(s)\\ ⋮& ⋮& \ddots & ⋮\\ g_{c_{n1}}(s)& g_{c_{n2}}(s)& \cdots & g_{c_{nm}}(s)\end{array}\right]$$

(30)

In a non-square system structure, $m$ times signals are applied to the input of the system in turn, and the system will output $n$ response signals at a time, that is, $m\times n(m\ne n)$ groups of equations are generated. The system can be decomposed and calculated according to Formulas (28) and (29), and the pseudo-inverse of the matrix is selected to replace it accordingly.

4. CARLA Algorithm Performance Verification

The continuous action reinforcement learning algorithm has strong online search and learning ability and can converge to the optimal value after full ergodic learning, without prior knowledge to set parameters. In order to test the identification ability of the CARLA algorithm, it was compared with the particle swarm optimization and the parallel diffuse algorithm (fireworks algorithm, FWA) by employing standard test functions. Here the Sphere, Rosenbrock, Griewank, Rastrigin, Ackley, and Schwefel’s problem 22 functions were selected to illustrate the applicability and performance of the CARLA algorithm.

(1) Sphere function:

$$f(x)={\displaystyle \sum _{i=1}^n{x}_i^2},$$

(31)

As can be shown in Figure 5.

The Sphere function has a unique global minimum value, which is obtained by the sum of squares when the minimum value is taken by independent variables with the same definition of domain.

(2) Rosenbrock function:

$$f(x)={\displaystyle \sum _{i=1}^{\mathrm{N}-1}\left[{(1-x_i)}^2+100{(x_{i+1}-x_i{}^2)}^2\right]}.$$

(32)

As shown in Figure 6, Rosenbrock’s global optimum lies in a smooth, narrow and parabolic valley. Due to the limited information, it is difficult to determine the search gradient and find the optimal solution. Therefore, it is often used to test the optimization performance of the non-convex function of the optimization algorithm, and the function can find the minimum value 0 at $x^{*}=(1,\cdots ,1)$.

(3) Griewank function:

$$\min f(x_i)={\displaystyle \sum _{i=1}^{\mathrm{N}}\frac{x_i{}^2}{4000}}-{\displaystyle \prod _{i=1}^N\cos (\frac{x_i}{\sqrt{i}})+1},$$

(33)

where $\left|x_i\right|\le 8$.

As shown in Figure 7, the Griewank function has many local minimum points, and the number is related to the dimension of variables. It can detect the ability of the algorithm to jump out of the local minimums and the global minimum value f(0) = 0, which is generally recognized as a difficult complex multimodal problem for the optimization algorithm.

(4) Rastrigin function:

$$\min f(x_i)={\displaystyle \sum _{i=1}^{\mathrm{D}}\left[x_i{}^2-10\cos (2\pi x_i)+10\right]},$$

(34)

where $x_i\in \left[-5.12,5.12\right]$.

As shown in Figure 8, the Rastrigin function is a multi-peak function, and there are about ${10}^{\mathrm{n}}$ local minimum points within the range of $\left\{x_i\in \left[-5.12,5.12\right], i=1,2\cdots n\right\}$. Similar to the Griewank function, it is also a typical nonlinear multi-modal function, and the peak shape features ups, downs, and jumps, so it is difficult to optimize and find the global optimal value.

(5) Ackley function:

$$f(\mathrm{X})=-20{\mathrm{e}}^{-\frac{1}{5}\sqrt{\frac{1}{\mathrm{n}}{\displaystyle \sum _{i=1}^{\mathrm{n}}{x}_i{}^2}}}-e^{\frac{1}{\mathrm{n}}{\displaystyle \sum _{i=1}^{\mathrm{n}}\cos (2\pi x_i)}}+20+e.$$

(35)

As shown in Figure 9, when the dimension of the Ackley function increases, its direction gradient and forward direction are various. This function can detect the global convergence speed of an algorithm. The function finds a minimum value 0 at $x^{*}=(0,\cdots ,0)$.

(6) Schwefel’s problem 22 function:

$$f(\mathrm{X})={\displaystyle \sum _{i=1}^{\mathrm{n}}\left|x_i\right|}+{\displaystyle \prod _{i=1}^n\left|x_i\right|},$$

(36)

where $\left|x_i\right|\le 10$.

As shown in Figure 10, Schwefel’s problem 22 function, proposed by Schwefel, is a continuous and smooth multimodal function which belongs to the classical test functions. When the independent variable approaches infinity, the function forms a large number of local extremum regions, and the global optimal value is located at the boundary of the definition domain. The function finds its minimum value 0 at $x^{*}=(0,\cdots ,0)$.

The parameter configuration is shown in

Table 1. Parameter configuration of the test functions.

Standard Function Type	Dimensionality	Sweet Spot	Optimal Fitness Value	Search Interval Settings
Sphere	30	[0,0,…,0]	0	(−100,100)
Rosenbrock	30	[1,1,…,1]	0	(−2.048,2.048)
Griewank	30	[0,0,…,0]	0	(−8,8)
Rastrigin	30	[0,0,…,0]	0	(−5.12,5.12)
Ackley	30	[0,0,…,0]	0	(−8,8)
Schwefel’s problem 22	30	[0,0,…,0]	0	(−10,10)

.

Particle swarm optimization (PSO), parallel diffuse algorithm (FWA), and continuous action reinforcement learning (CARLA) algorithms were respectively tested for the standard functions above. The results are shown in

Table 2. Parameter configuration of the test function. PSO: particle swarm optimization.

Standard Function Type	PSO		FWA		CARLA
	Mean Value	Standard Deviation	Mean Value	Standard Deviation	Mean Value	Standard Deviation
Sphere	0	0	0	0	0	0
Rosenbrock	66.59	204.29	12.16	12.82	8.91	10.22
Griewank	0	0.01	0	0	0	0
Rastrigin	6.77	7.70	0	0	0.01	0.21
Ackley	0.043	0.042	0	0	0	0
Schwefel’s problem 22	23.93	13.61	0	0	0	0

. FWA and CARLA algorithms had better search accuracy than the PSO algorithm, and both could accurately obtain function parameter estimation.

5. Simulation

5.1. Square Multivariate System: Wood-Berry Model

The Wood-Berry double distillation towel model is a classic multivariate model in industrial production. The identification of the Wood-Berry model has drawn the attention of academic and industrial researchers due to the complex characteristics of multi-parameters, large time-delay, and strong coupling relationships. Many works, including Li’s sequence identification method based on step response (frequency response estimation, FRE) [33,34], Cheng’s identification method based on heuristic search (NLG-particle swarm optimization, NPSO) algorithm [20], Cao’s intelligent search algorithm based on parallel diffuse type algorithm (modified fireworks explosion optimization algorithm-FRE, MFA-FRE) [23], etc., have acquired many achievements. In this paper, some comparative simulations between the presented CARLA-FRE and the methods above were carried out to estimate the parameters of the Wood-Berry model (see Figure 11).

The transfer function of the Wood-Berry model is:

$$G_s(s)=\left[\begin{array}{cc}\frac{12.8e^{-s}}{16.7s+1}& \frac{-18.9e^{-3s}}{21s+1}\\ \frac{6.6e^{-7s}}{10.9s+1}& \frac{-19.4e^{-3s}}{14.4s+1}\end{array}\right].$$

The sequential step signal is:

$$R=\left[\left[\begin{array}{c}{r}_1^1\\ r_2^1\end{array}\right],\left[\begin{array}{c}{r}_1^2\\ r_2^2\end{array}\right]\right]=\left[\left[\begin{array}{c}1\\ 2\end{array}\right],\left[\begin{array}{c}4\\ 2\end{array}\right]\right].$$

Four methods were used to respectively identify the mentioned multivariable closed-loop system, and the results are presented in

Table 3. Wood-Berry model identification results. (FRE: frequency response estimation; NPSO-FRE: NLG-particle swarm optimization-FRE; MFA-FRE: modified fireworks explosion optimization algorithm-FRE).

Wood-Berry	${\mathit{G}}_{11}(\mathit{s})$	${\mathit{G}}_{12}(\mathit{s})$	${\mathit{G}}_{21}(\mathit{s})$	${\mathit{G}}_{22}(\mathit{s})$
Actual model	$\frac{12.8e^{-s}}{16.7s+1}$	$\frac{-18.9e^{-3s}}{21s+1}$	$\frac{6.6e^{-7s}}{10.9s+1}$	$\frac{-19.4e^{-3s}}{14.4s+1}$
Method in [26] (FRE)	$\frac{12.7929e^{-1.0044s}}{16.6193s+1}$	$\frac{-18.9e^{-3.01s}}{21.001s+1}$	$\frac{6.5998e^{-6.9852s}}{10.9205s+1}$	$\frac{-19.3942e^{-3.006s}}{14.4339s+1}$
error (%)	0.98	0.34	0.40	0.47
Method in [20] (NPSO-FRE)	$\frac{12.7984e^{-1.0027s}}{16.6942s+1}$	$\frac{-18.8996e^{-3.0002s}}{20.9990s+1}$	$\frac{6.5996e^{-7.0005s}}{10.9001s+1}$	$\frac{-19.4000e^{-3.0007s}}{14.4001s+1}$
error (%)	0.32	0.014	0.015	0.024
Method in [23] (MFA-FRE)	$\frac{12.7979e^{-1.0025s}}{16.6910s+1}$	$\frac{-18.9001e^{-3.0001s}}{21.0001s+1}$	$\frac{6.6000e^{-7.0001s}}{10.8999s+1}$	$\frac{-19.4001e^{-3.0001s}}{14.4001s+1}$
error (%)	0.32	0.004	0.008	0.005
Method in this paper (CARLA-FRE)	$\frac{12.7981e^{-1.0014s}}{16.6901s+1}$	$\frac{-18.9002e^{-3.0003s}}{21.0004s+1}$	$\frac{6.6003e^{-7.0002s}}{10.9005s+1}$	$\frac{-19.3987e^{-3.0003s}}{14.4005s+1}$
error (%)	0.21	0.013	0.012	0.021

. It can be seen that several methods achieved high estimation accuracy in the parameter identification of the Wood-Berry model. In addition, the CARLA-FRE method proposed in this paper can be implemented online and adjusted automatically with the change of objects.

5.2. Non-Square Multivariate System: Shell Model

Multivariable non-square systems exist widely in industrial production, and this paper takes the Shell model of a standard non-square model [35] as an example to test the proposed method. The closed-loop control of the Shell model is shown in Figure 12:

Here, the model transfer function matrix is:

$$G_s(s)=\left[\begin{array}{ccc}\frac{4.05e^{-81s}}{50s+1}& \frac{1.77e^{-84s}}{60s+1}& \frac{5.88e^{-81s}}{50s+1}\\ \frac{5.39e^{-54s}}{50s+1}& \frac{5.72e^{-42s}}{60s+1}& \frac{6.9e^{-45s}}{40s+1}\end{array}\right].$$

The controller is the following formula:

$$G_{\mathrm{c}}=\left[\begin{array}{cc}4& 4\\ -1& -2\\ -0.6& -0.5\end{array}\right].$$

The sequential step signal is

$$R=\left[\begin{array}{ccc}\left[\begin{array}{c}{r}_1^1\\ r_2^1\\ r_3^1\end{array}\right]& \left[\begin{array}{c}{r}_1^2\\ r_2^2\\ r_3^2\end{array}\right]& \left[\begin{array}{c}{r}_1^3\\ r_2^3\\ r_3^3\end{array}\right]\end{array}\right].$$

Gaussian white noises with a noise-to-signal ratio (NSR) of 10% and 20% were applied to verify the effectiveness of the algorithm, and the results were compared with the MAF-FRE method, as shown in

Table 4. Identification results of the Shell model.

Actual Model	Noise 0%		Noise 20%
	MFA-FRE	CARLA-FRE	MFA-FRE	CARLA-FRE
$\frac{119e^{-5s}}{21.7s+1}$	$\frac{118.9998e^{-5.0174s}}{21.7255s+1}$	$\frac{118.9828e^{-5.0132s}}{21.7027s+1}$	$\frac{118.9987e^{-5.0479s}}{21.6557s+1}$	$\frac{118.9825e^{-5.0143s}}{21.7031s+1}$
error (%)	0.47	0.29	1.16	0.32
$\frac{40e^{-5s}}{337s+1}$	$\frac{39.9877e^{-5.0240s}}{336.1787s+1}$	$\frac{39.9862e^{-5.0179s}}{336.7018s+1}$	$\frac{40.1770e^{-4.7120s}}{338.3429s+1}$	$\frac{39.9783e^{-5.0258s}}{336.7251s+1}$
error (%)	0.75	0.39	6.45	0.65
$\frac{-21e^{-5s}}{10s+1}$	$\frac{-20.9072e^{-5.0085s}}{9.9200s+1}$	$\frac{-20.9563e^{-5.0037s}}{9.9677s+1}$	$\frac{-20.8994e^{-5.3567s}}{9.9907s+1}$	$\frac{-20.9273e^{-5.0042s}}{9.9381s+1}$
error (%)	1.41	0.61	7.71	1.05
$\frac{77e^{-5s}}{50s+1}$	$\frac{76.8300e^{-5.0102s}}{49.7549s+1}$	$\frac{76.9137e^{-5.0114s}}{49.9371s+1}$	$\frac{76.7488e^{-5.1236s}}{49.8870s+1}$	$\frac{76.9029e^{-5.0313s}}{49.9218s+1}$
error (%)	0.92	0.47	3.02	0.91
$\frac{76.7e^{-3s}}{28s+1}$	$\frac{76.6657e^{-2.9980s}}{28.0045s+1}$	$\frac{76.7128e^{-3.0026s}}{27.9438s+1}$	$\frac{76.4512e^{-2.9641s}}{27.8876s+1}$	$\frac{76.7241e^{-3.0129s}}{29.9039s+1}$
error (%)	0.52	0.31	2.31	0.81
$\frac{-50e^{-5s}}{10s+1}$	$\frac{-50.0989e^{-5.0012s}}{9.9980s+1}$	$\frac{-49.9611e^{-5.0043s}}{0.9837s+1}$	$\frac{-50.0425e^{-5.1011s}}{9.9356s+1}$	$\frac{-49.9217e^{-5.0183s}}{0.9731s+1}$
error (%)	0.24	0.25	2.75	0.79
$\frac{93e^{-5s}}{50s+1}$	$\frac{93.0011e^{-5.0112s}}{49.6576s+1}$	$\frac{93.0118e^{-5.0185s}}{49.8194s+1}$	$\frac{93.1022e^{-4.7869s}}{49.9881s+1}$	$\frac{93.0237e^{-5.0386s}}{49.7621s+1}$
error (%)	0.91	0.74	4.39	1.27
$\frac{-36.7e^{-5s}}{166s+1}$	$\frac{-36.7903e^{-5.0097s}}{166.1148s+1}$	$\frac{-36.7198e^{-5.0238s}}{165.9671s+1}$	$\frac{-36.7061e^{-4.8760s}}{165.6667s+1}$	$\frac{-36.7237e^{-5.0934s}}{165.7830s+1}$
error (%)	2.70	0.55	2.70	2.06
$\frac{-103.3e^{-4s}}{23s+1}$	$\frac{-103.2389e^{-4.0098s}}{23.0009s+1}$	$\frac{-103.2471e^{-4.0184s}}{22.9744s+1}$	$\frac{-103.3141e^{-4.0012s}}{23.0023s+1}$	$\frac{-103.2176e^{-4.0421s}}{22.8761s+1}$
error (%)	0.31	0.62	0.29	1.67

. It can be seen that both methods achieved high estimation accuracy in the parameter identification of the Shell model, and the CARLA-FRE method proposed in this paper could better adapt to changes in the external environment.

6. Conclusions

This paper proposed a frequency response estimation method based on a continuous action reinforcement learning machine. It could solve closed-loop identification problems of multivariable square systems and non-square systems. Some comparative simulations between the presented method and existing methods were carried out. The classic Wood-Berry model (square system) and the Shell model (non-square system) were chosen to test the algorithms. From the results, it was found that the proposed method could not only achieve good identification accuracy, but also had stronger online learning ability and anti-interference ability.