Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method
Abstract
:1. Introduction
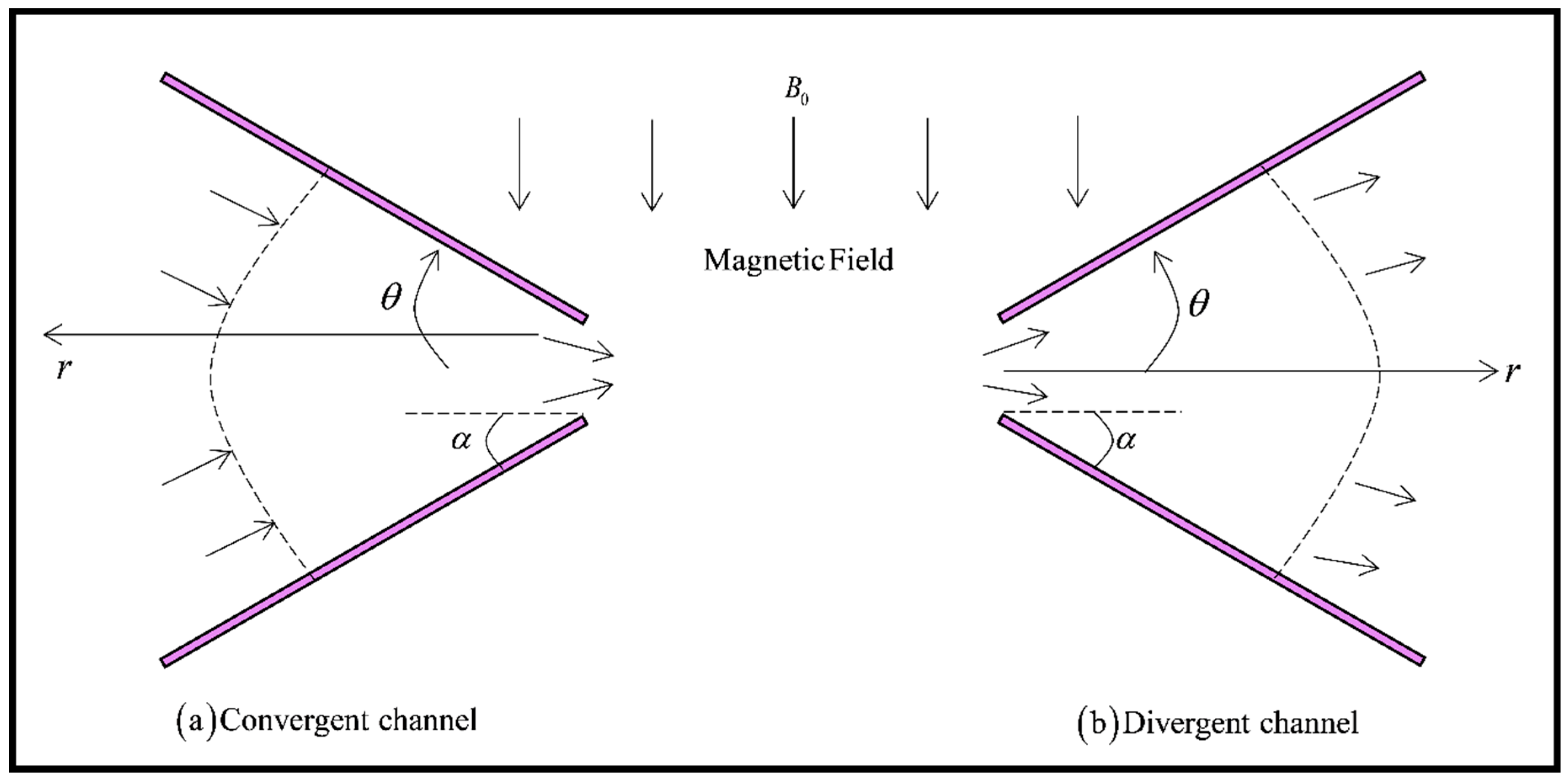
2. Mathematical Model
3. Solution by Using Spectral Homotopy Analysis Method
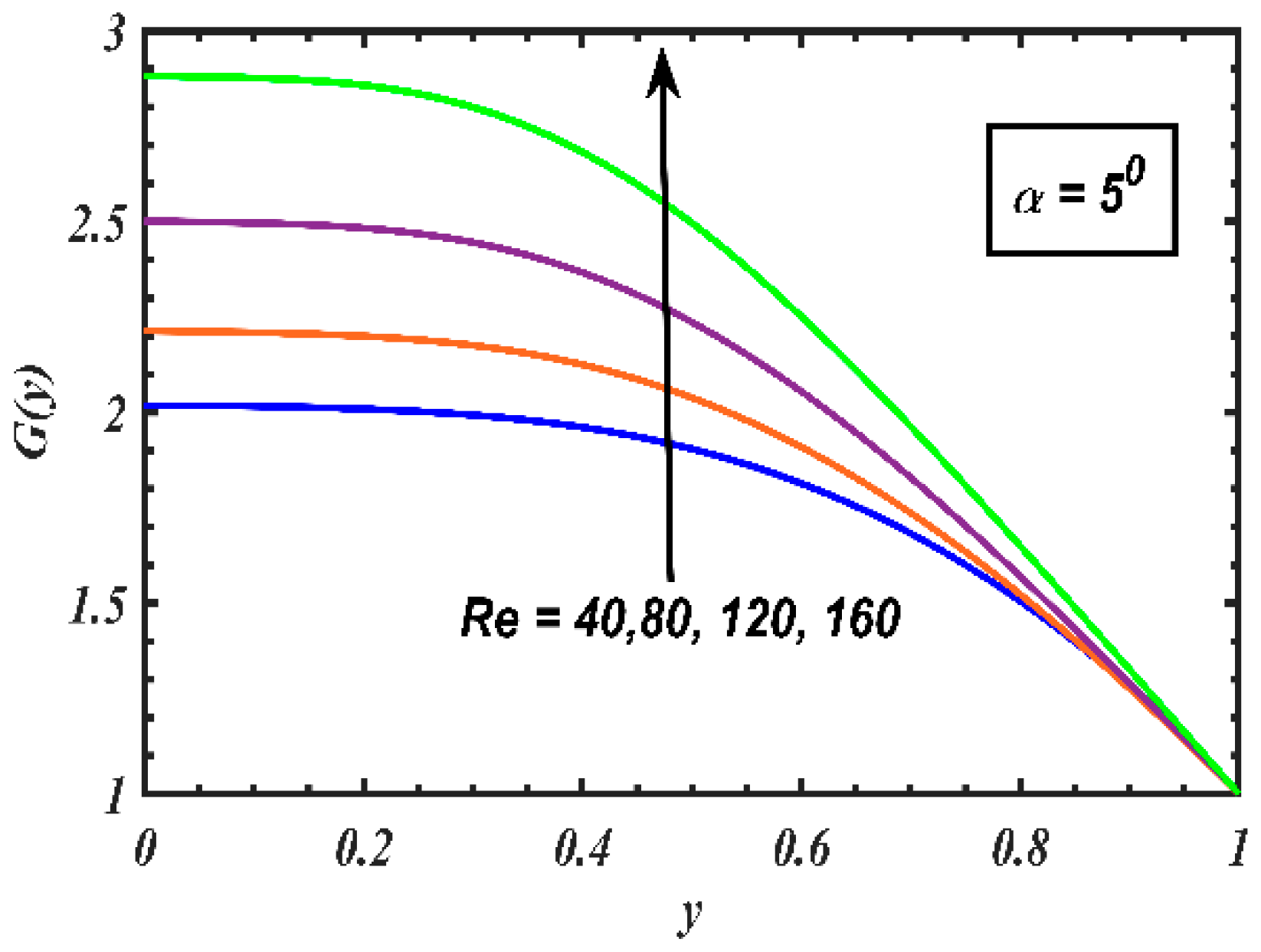
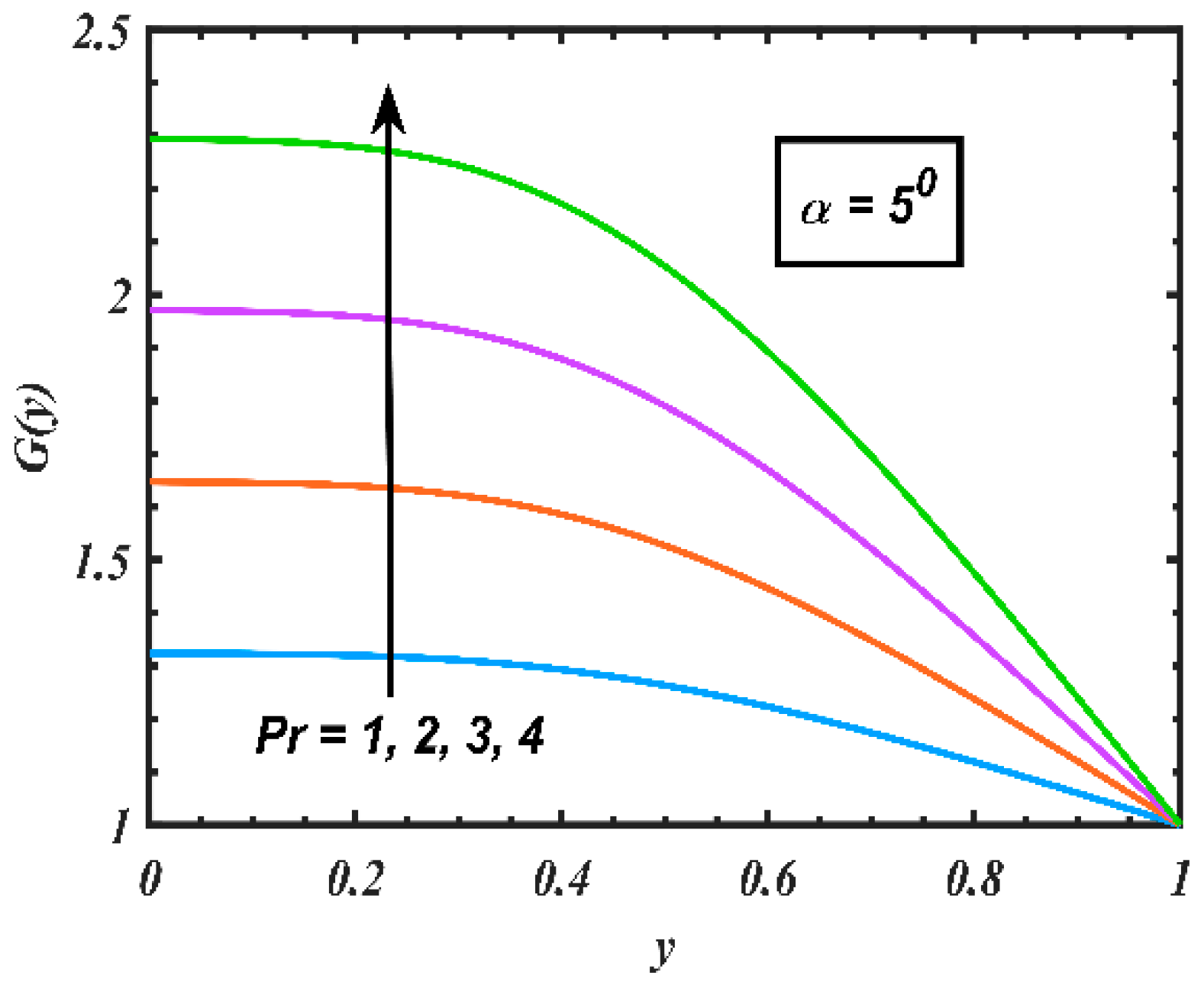
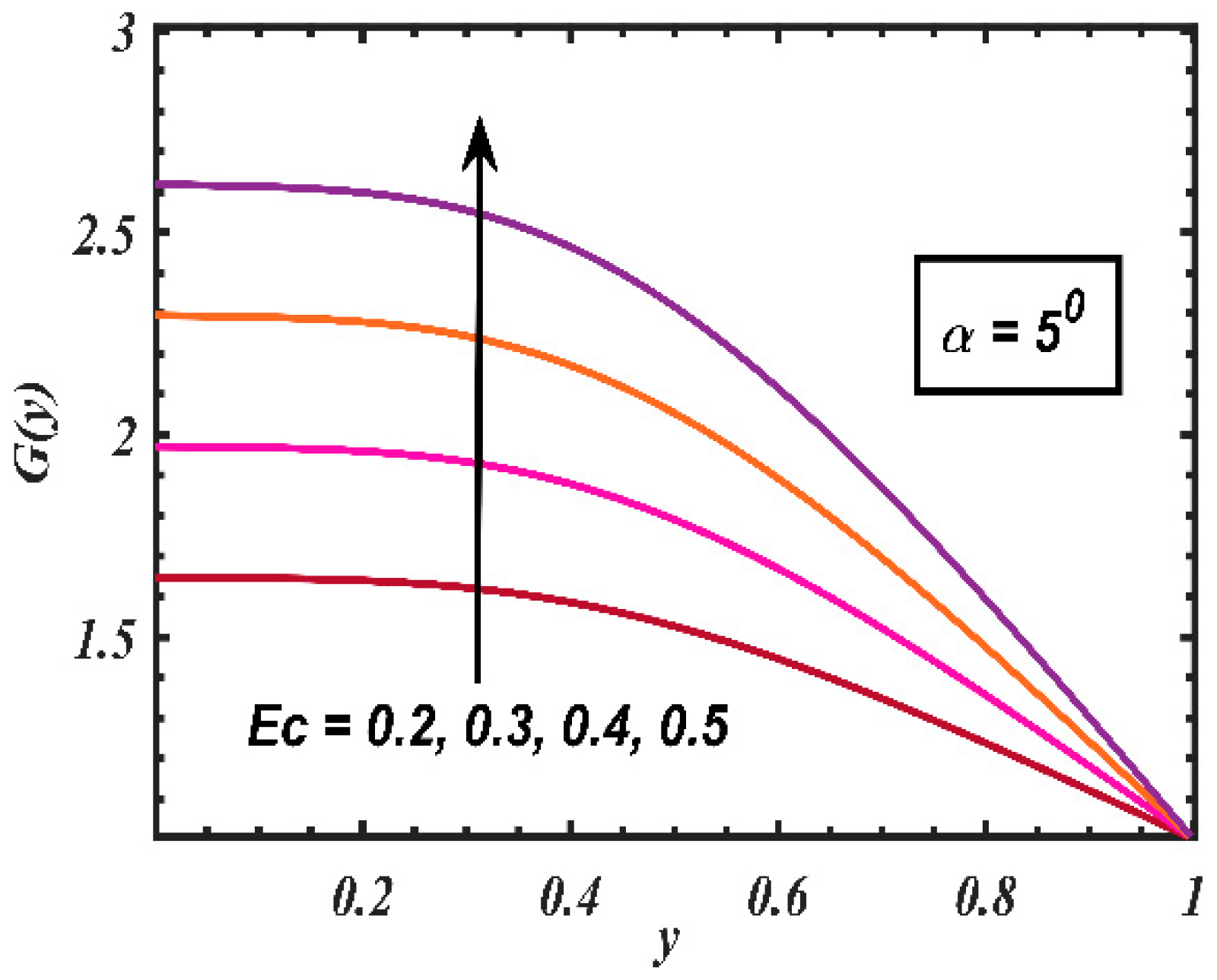
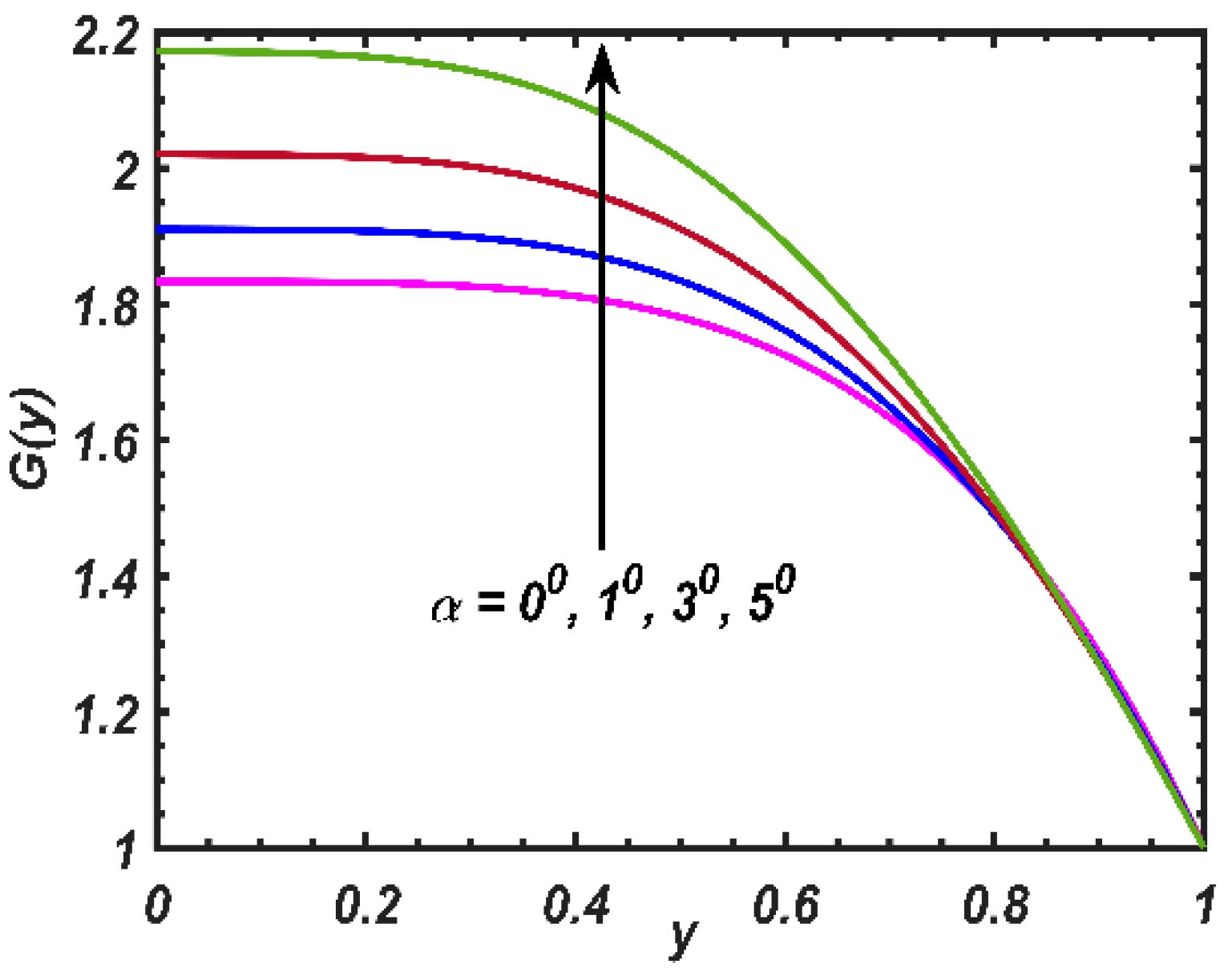
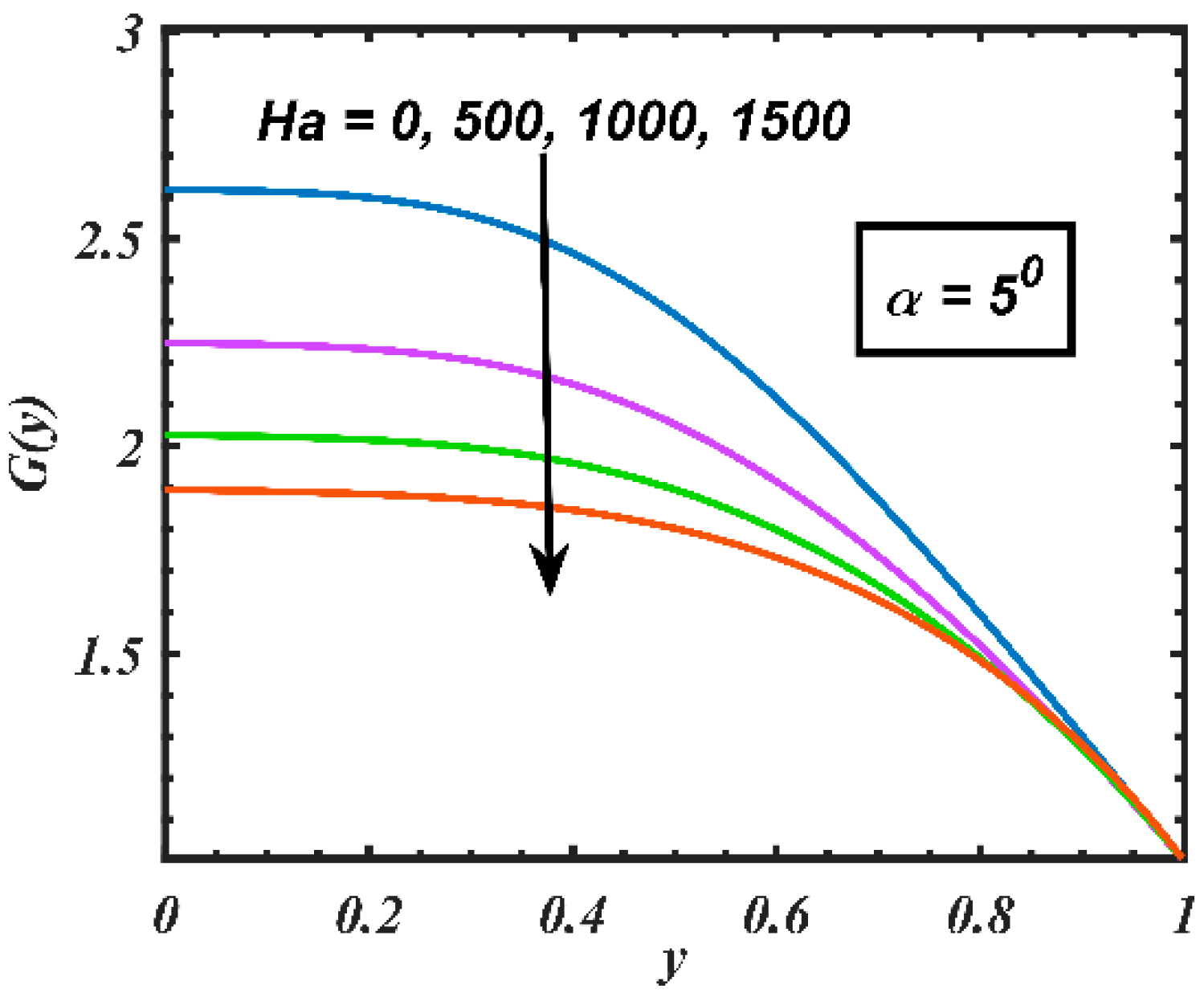
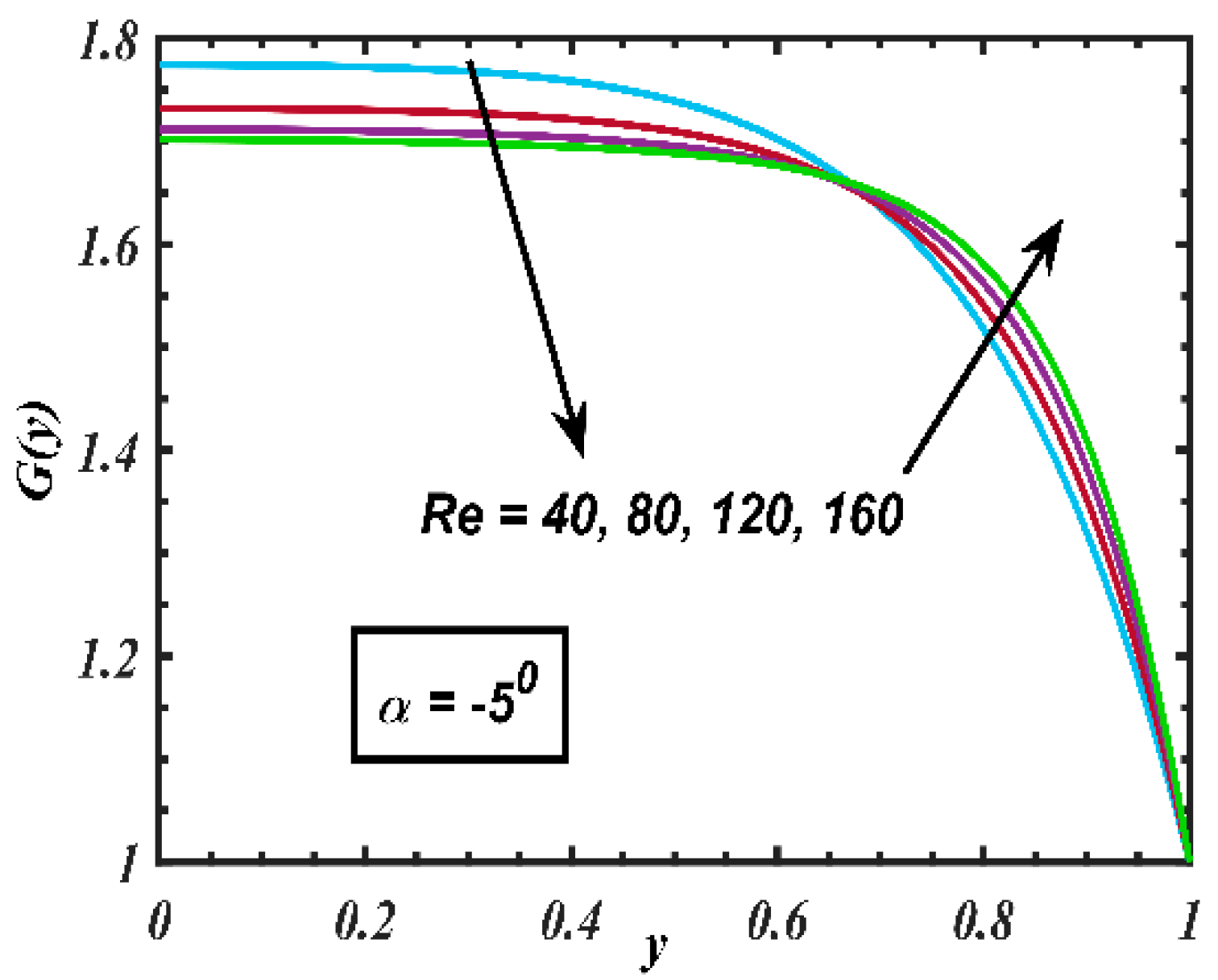
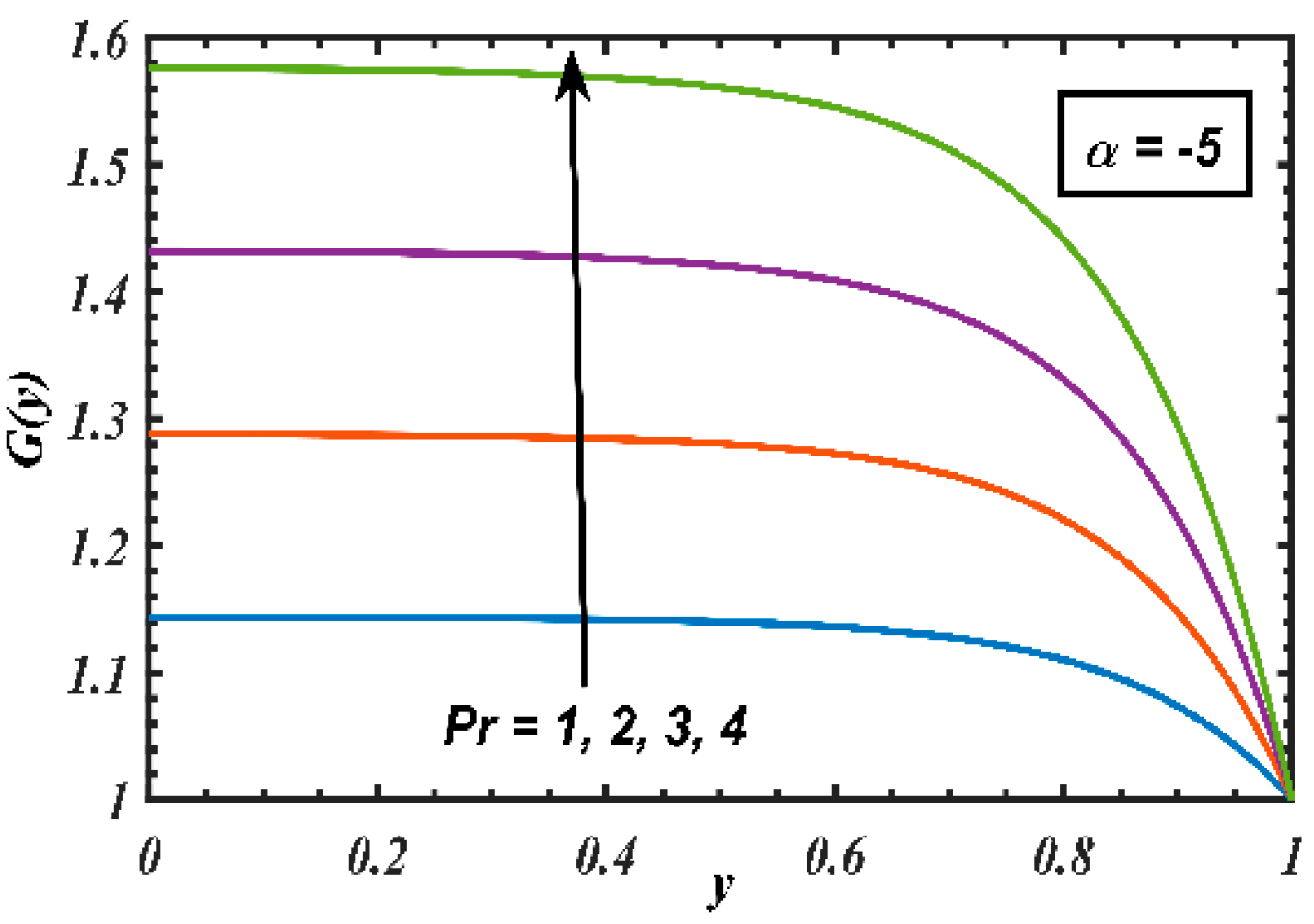
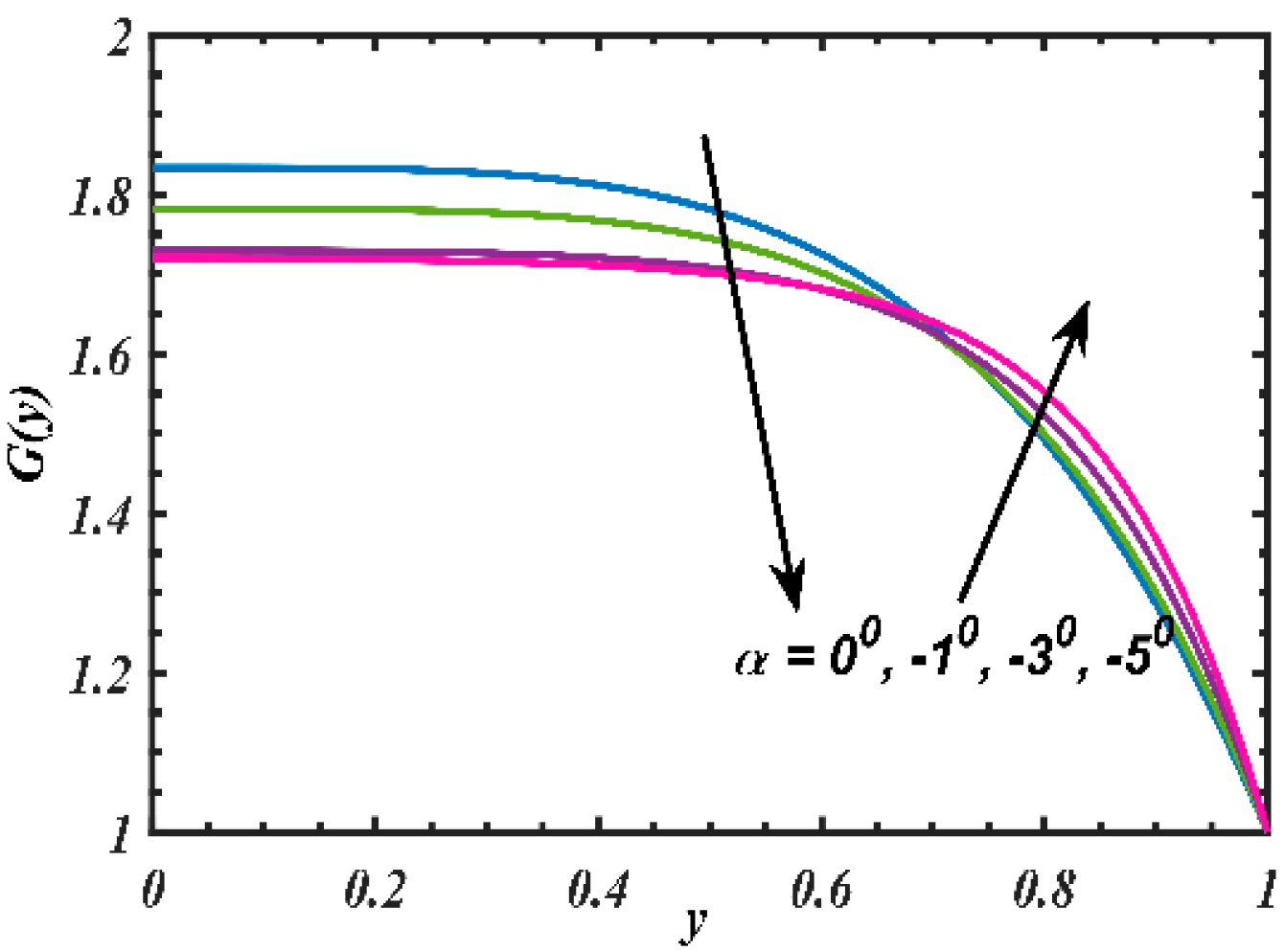
4. Results and Discussion
5. Conclusions
6. Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Sibanda, P.; Motsa, S.; Makukula, Z. A spectral-homotopy analysis method for heat transfer flow of a third-grade fluid between parallel plates. Int. J. Numer. Methods Heat 2012, 22, 4–23. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. BioScience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Ahmed, N.; Abbasi, A.; Khan, U.; Mohyud-Din, S.T. Thermal radiation effects on flow of Jeffery fluid in converging and diverging stretchable channels. Neural Comput. Appl. 2018, 30, 2371–2379. [Google Scholar] [CrossRef]
- Banks, W.; Drazin, P.; Zaturska, M. On perturbations of Jeffery-Hamel flow. J. Fluid Mech. 1988, 186, 559–581. [Google Scholar] [CrossRef]
- Domairry, D.G.; Mohsenzadeh, A.; Famouri, M. The application of homotopy analysis method to solve nonlinear differential equation governing Jeffery–Hamel flow. Commun Nonlinear Sci. 2009, 14, 85–95. [Google Scholar] [CrossRef]
- Esmaili, Q.; Ramiar, A.; Alizadeh, E.; Ganji, D. An approximation of the analytical solution of the Jeffery–Hamel flow by decomposition method. Phys Lett. A 2008, 372, 3434–3439. [Google Scholar] [CrossRef]
- Ganji, Z.; Ganji, D.D.; Esmaeilpour, M. Study on nonlinear Jeffery–Hamel flow by He’s semi-analytical methods and comparison with numerical results. Comput. Math. Appl. 2009, 58, 2107–2116. [Google Scholar] [CrossRef]
- Patel, N.; Meher, R. Analytical investigation of Jeffery-Hemal flow with magnetic field by differential transform method. Int. J. Adv. Appl. Math. Mech. 2018, 6, 1–9. [Google Scholar]
- Dey, P.K.; Zikanov, O. Turbulence and transport of passive scalar in magnetohydrodynamic channel flows with different orientations of magnetic field. Int. J. Heat Fluid Flow 2012, 36, 101–117. [Google Scholar] [CrossRef]
- Guchhait, S.K.; Jana, R. A Study of Some Magnetohydrodynamics Problems with or Without Hall Currents; Vidyasagar University: West Bengal, India, 2018. [Google Scholar]
- Hvasta, M.; Dudt, D.; Fisher, A.; Kolemen, E. Calibrationless rotating Lorentz-force flowmeters for low flow rate applications. Meas. Sci. Technol. 2018, 29, 075303. [Google Scholar] [CrossRef] [Green Version]
- Motsa, S.S.; Sibanda, P.; Awad, F.G.; Shateyi, S. A new spectral-homotopy analysis method for the MHD Jeffery–Hamel problem. Comput. Fluids 2010, 39, 1219–1225. [Google Scholar] [CrossRef]
- Balazadeh, N.; Sheikholeslami, M.; Ganji, D.D.; Li, Z. Semi analytical analysis for transient Eyring-Powell squeezing flow in a stretching channel due to magnetic field using DTM. J. Mol. Liq. 2018, 260, 30–36. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Khan, U.; Din, S.T.M.; Iqbal, M.A.; Wang, W. Differential transform method for unsteady nanofluid flow and heat transfer. Alex. Eng. J. 2018, 57, 1867–1875. [Google Scholar] [CrossRef]
- Ali, J. Application of New Iterative Method and Adomian Decomposition Method to Hamel’s Flow Problem. J. Adv. Civ. Eng. 2018, 4, 10–13. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. The adomian decomposition method for the slip flow and heat transfer of nanofluids over a stretching/shrinking sheet. Rom. Rep. Phys. 2018, 70, 115. [Google Scholar]
- Sobamowo, M.G.; Yinusa, A.A. Transient Combustion Analysis for Iron Micro-particles in a Gaseous Oxidizing Medium Using Adomian Decomposition Method. J. Comput. Eng. Phys. Model. 2018, 1, 1–15. [Google Scholar] [CrossRef]
- Ahmad, I.; Ilyas, H. Homotopy Perturbation Method for the nonlinear MHD Jeffery–Hamel blood flows problem. Appl. Numer. Math. 2019, 141, 124–132. [Google Scholar] [CrossRef]
- Shirkhani, M.; Hoshyar, H.; Rahimipetroudi, I.; Akhavan, H.; Ganji, D. Unsteady time-dependent incompressible Newtonian fluid flow between two parallel plates by homotopy analysis method (HAM), homotopy perturbation method (HPM) and collocation method (CM). Propul. Power Res. 2018, 7, 247–256. [Google Scholar] [CrossRef]
- Ahmad, H. Variational iteration method with an auxiliary parameter for solving differential equations of the fifth order. Nonlinear Sci. Lett. A 2018, 9, 27–35. [Google Scholar]
- Dogan, D.D.; Konuralp, A. Fractional variational iteration method for time-fractional non-linear functional partial differential equation having proportional delays. Therm. Sci. 2018, 14, 33–46. [Google Scholar] [CrossRef]
- Inc, M.; Khan, H.; Baleanu, D.; Khan, A. Modified variational iteration method for straight fins with temperature dependent thermal conductivity. Therm. Sci. 2018, 8, 229–236. [Google Scholar] [CrossRef]
- Wazwaz, A.-M.; Kaur, L. Optical solitons and Peregrine solitons for nonlinear Schrödinger equation by variational iteration method. Optik 2019, 179, 804–809. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Yan, S.; Zhang, X. Approximate solution of a piecewise linear–nonlinear oscillator using the homotopy analysis method. J. Vib. Control 2018, 24, 4551–4562. [Google Scholar] [CrossRef]
- Liu, J.; Wang, B. Solving the backward heat conduction problem by homotopy analysis method. Appl. Numer. Math. 2018, 128, 84–97. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Araghi, M.A.F.; Abbasbandy, S. Finding optimal convergence control parameter in the homotopy analysis method to solve integral equations based on the stochastic arithmetic. Numer. Algorithms 2018, 1, 237–267. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Gupta, Y.; Pop, I. Homotopy analysis method for predicting multiple solutions in the channel flow with stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 183–193. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M. A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD. Appl. Math. Comput. 2018, 316, 381–389. [Google Scholar] [CrossRef]
- Shahid, A.; Zhou, Z.; Bhatti, M.; Tripathi, D. Magnetohydrodynamics Nanofluid Flow Containing Gyrotactic Microorganisms Propagating Over a Stretching Surface by Successive Taylor Series Linearization Method. Microgravity Sci. Technol. 2018, 30, 445–455. [Google Scholar] [CrossRef]
- Shivanian, E.; Alsulami, H.; Alhuthali, M.; Abbasbandy, S. Predictor homotopy analysis method (PHAM) for nano boundary layer flows with nonlinear Navier boundary condition: Existence of four solutions. Filomat 2014, 28, 1687–1697. [Google Scholar] [CrossRef]
- Othman, M.I.; Marin, M. Effect of thermal loading due to laser pulse on thermoelastic porous medium under GN theory. Results Phys. 2017, 7, 3863–3872. [Google Scholar] [CrossRef]
- Moradi, A.; Alsaedi, A.; Hayat, T. Investigation of heat transfer and viscous dissipation effects on the Jeffery-Hamel flow of nanofluids. Therm. Sci. 2015, 19, 563–578. [Google Scholar] [CrossRef]
- Makukula, Z.G.; Sibanda, P.; Motsa, S.S. A Novel Numerical Technique for Two-Dimensional Laminar Flow between Two Moving Porous Walls. Math. Probl. Eng. 2010, 2010, 528956. [Google Scholar] [CrossRef]
- Motsa, S.S.; Shateyi, S.; Marewo, G.T.; Sibanda, P. An improved spectral homotopy analysis method for MHD flow in a semi-porous channel. Numer. Algorithms 2012, 60, 463–481. [Google Scholar] [CrossRef]
- Marin, M. Contributions on uniqueness in thermoelastodynamics on bodies with voids. Cienc. Mat. (Havana) 1998, 16, 101–109. [Google Scholar]
- Hassan, M.; Marin, M.; Ellahi, R.; Alamri, S.Z. Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids. Heat Transf. Res. 2018, 49, 1837–1848. [Google Scholar] [CrossRef]


| H | 1st Order | 2nd Order | 3rd Order | DTM | Shooting |
|---|---|---|---|---|---|
| 0 | −3.539430 | −3.539411 | −3.539415 | −3.539415 | −3.539415 |
| 100 | −3.321491 | −3.321498 | −3.321499 | −3.321499 | −3.321499 |
| 200 | −3.118488 | −3.118486 | −3.118485 | −3.118485 | −3.118485 |
| 300 | −2.929291 | −2.929295 | −2.929295 | −2.929295 | −2.929295 |
| 400 | −2.752923 | −2.752927 | −2.752927 | −2.752927 | −2.752927 |
| 500 | −2.588440 | −2.588448 | −2.588448 | −2.588448 | −2.588448 |
| 600 | −2.434932 | −2.434999 | −2.434997 | −2.434997 | −2.434997 |
| 700 | −2.291726 | −2.291771 | −2.291775 | −2.291775 | −2.291775 |
| 800 | −2.158010 | −2.158041 | −2.158042 | −2.158042 | −2.158042 |
| H | 1st Order | 2nd Order | 3rd Order | DTM | Shooting |
|---|---|---|---|---|---|
| 0 | −2.885879 | −2.885886 | −2.885885 | −2.885885 | −2.885885 |
| 100 | −2.918780 | −2.918780 | −2.918782 | −2.918782 | −2.918782 |
| 200 | −2.961804 | −2.961804 | −2.961804 | −2.961804 | −2.961804 |
| 300 | −3.013646 | −3.013659 | −3.013659 | −3.013659 | −3.013659 |
| 400 | −3.073033 | −3.073031 | −3.073035 | −3.073035 | −3.073035 |
| 500 | −3.138154 | −3.138962 | −3.138960 | −3.138960 | −3.138960 |
| 600 | −3.210500 | −3.210512 | −3.210511 | −3.210511 | −3.210511 |
| 800 | −3.367243 | −3.367331 | −3.367336 | −3.367336 | −3.367336 |
| 1000 | −3.538100 | −3.538122 | −3.538120 | −3.538120 | −3.538120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, A.; Md Basir, M.F.; Ali, U.; Mohd Kasihmuddin, M.S.; Mansor, M.A. Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes 2019, 7, 626. https://doi.org/10.3390/pr7090626
Mahmood A, Md Basir MF, Ali U, Mohd Kasihmuddin MS, Mansor MA. Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes. 2019; 7(9):626. https://doi.org/10.3390/pr7090626
Chicago/Turabian StyleMahmood, Asad, Md Faisal Md Basir, Umair Ali, Mohd Shareduwan Mohd Kasihmuddin, and Mohd. Asyraf Mansor. 2019. "Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method" Processes 7, no. 9: 626. https://doi.org/10.3390/pr7090626







