Analysis of Air–Oil Flow and Heat Transfer inside a Grooved Rotating-Disk System
Abstract
:1. Introduction
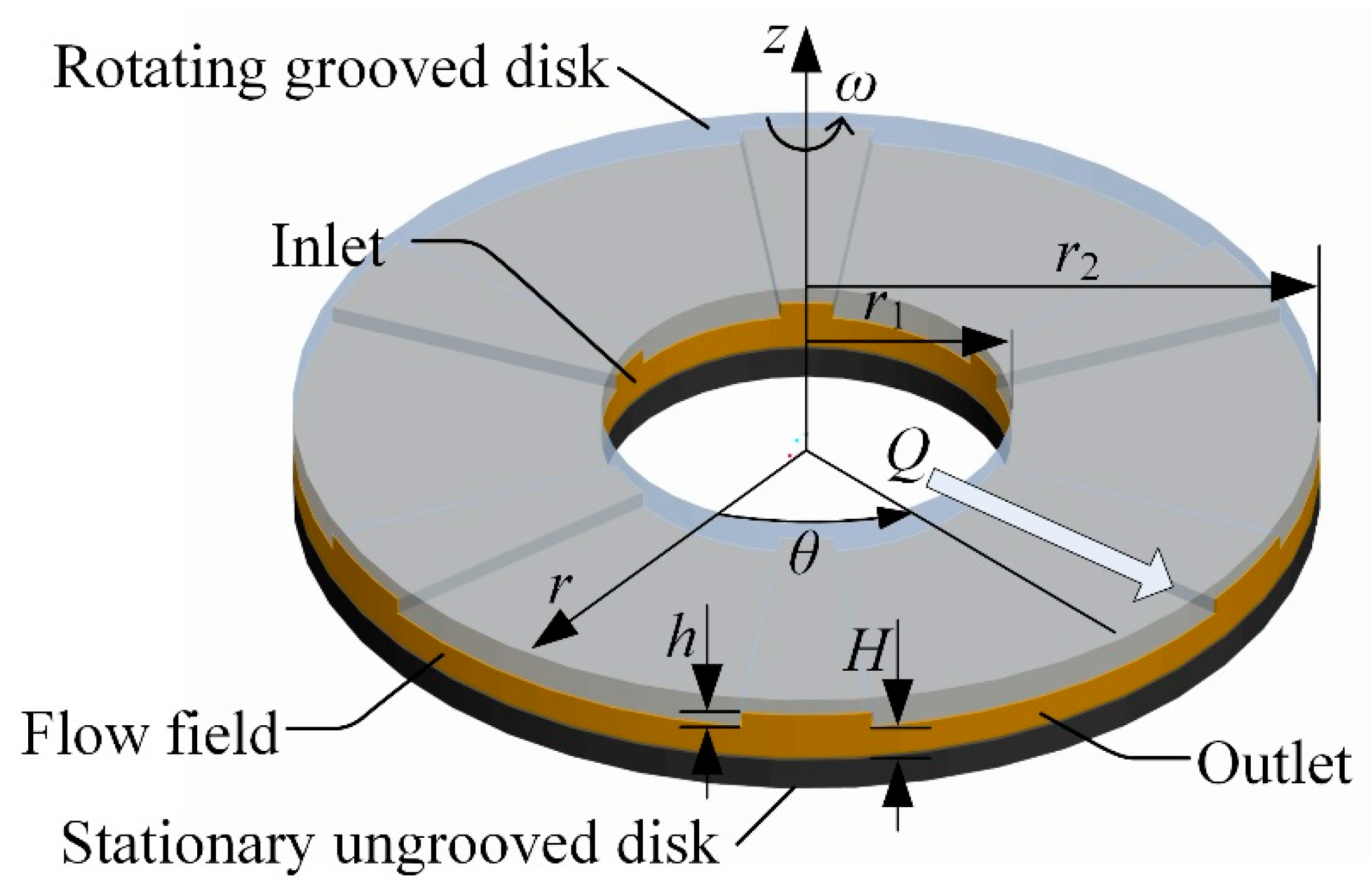
2. Grooved Rotating-Disk System Configuration
3. Grooved Rotating-Disk System Modeling
3.1. Governing Equations
3.2. Computational Model
4. Experimental Apparatus
5. Results and Discussion
5.1. Flow Field Visualization
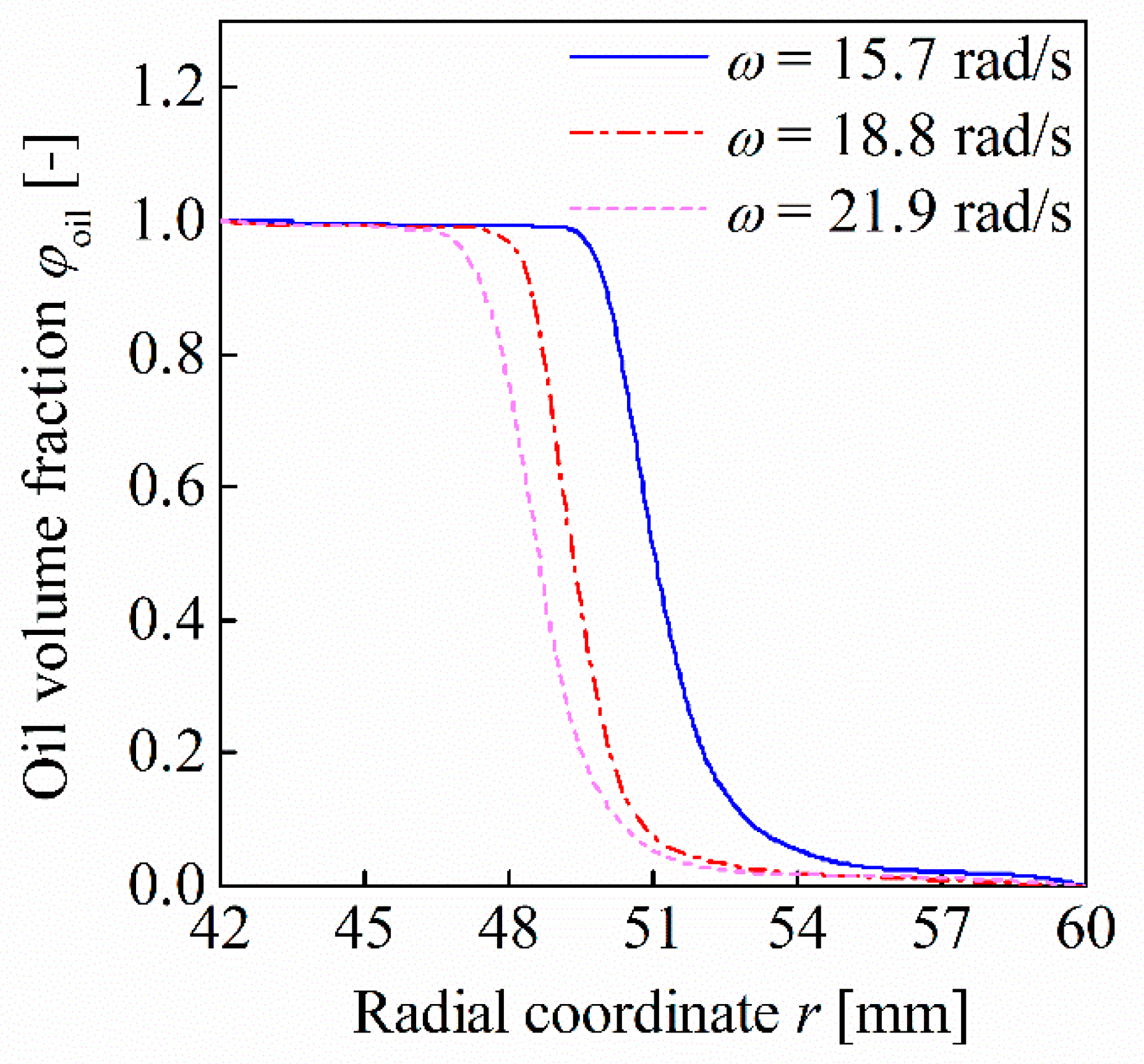
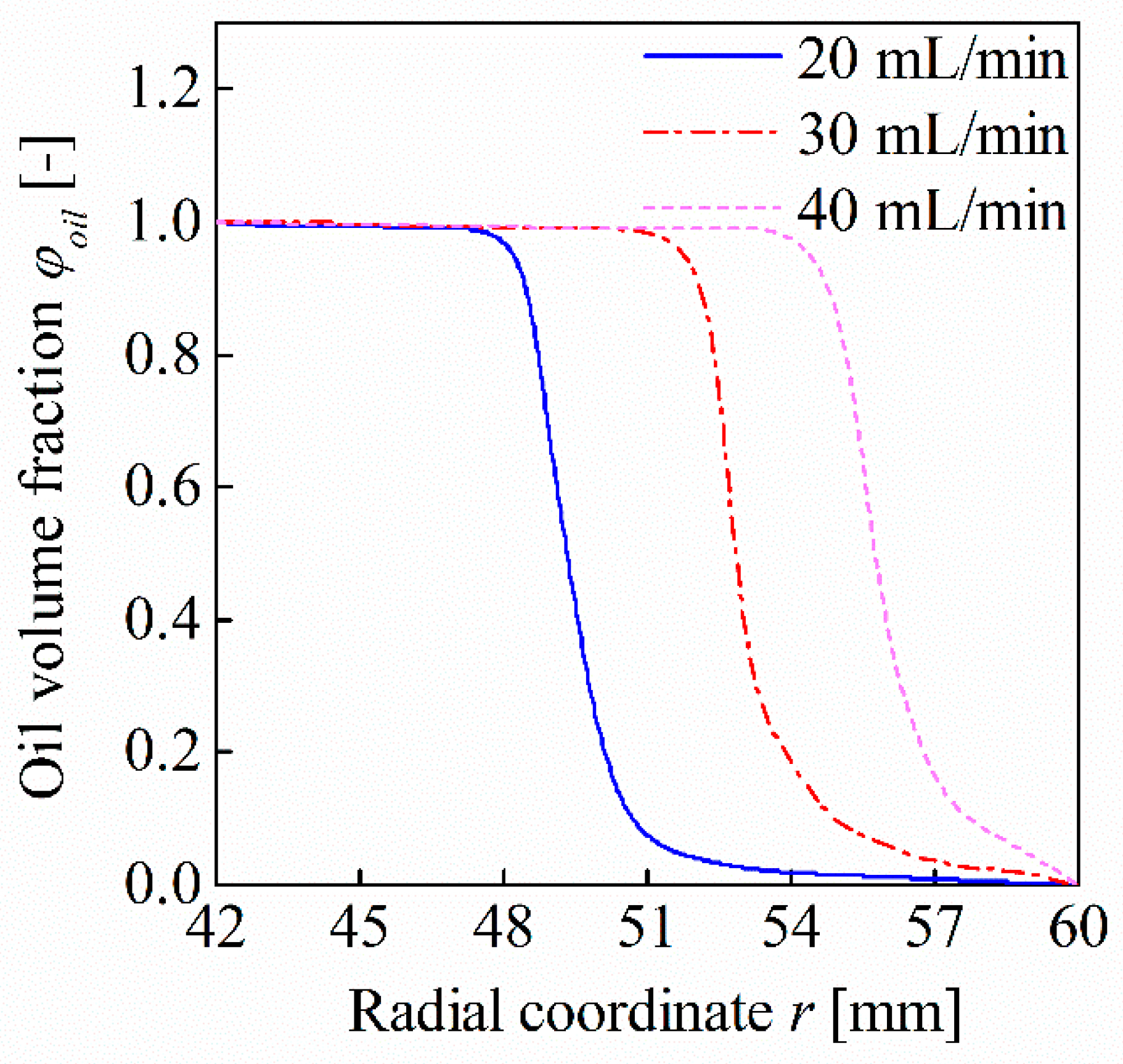
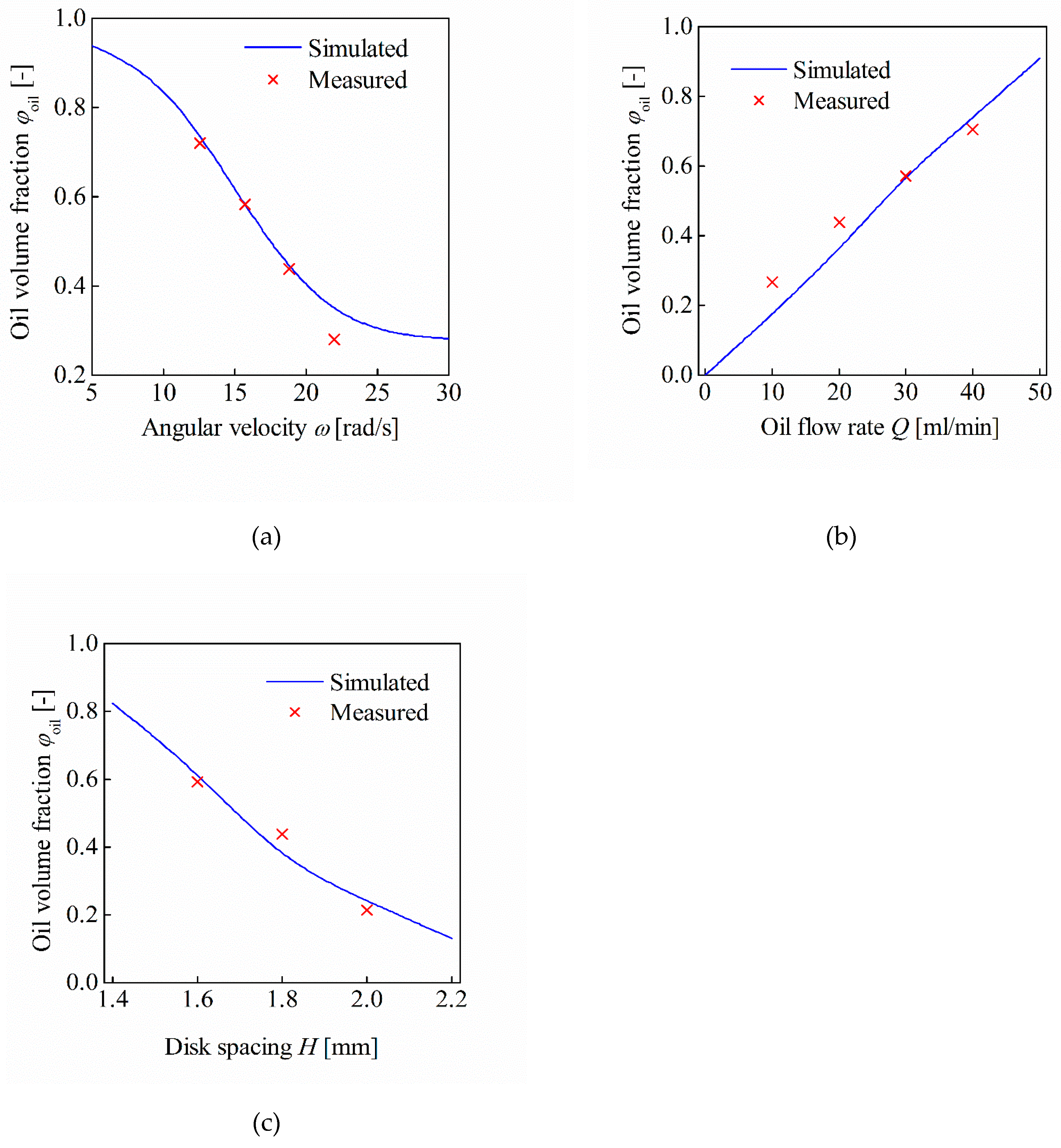
5.2. Parametric Analysis
5.3. Heat Dissipation Capability
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| E | Specific sensible enthalpy, J/kg |
| F | External force, N |
| g | Gravity acceleration, m/s2 |
| h | Depth of radial grooves, m |
| H | Disk spacing, m |
| k | Effective thermal conductivity coefficient of fluid, W/(m·K) |
| ks | Thermal conductivity coefficient of solid structure, W/(m·K) |
| Ng | Groove number |
| Nuav | Average Nusselt number |
| Nul | Local Nusselt number |
| p | Pressure, Pa |
| Q | Oil flow rate, L/min |
| q | Heat flux, W/m2 |
| r | Radial coordinate |
| r1 | Inner radius, m |
| r2 | Outer radius, m |
| T | Temperature of two-phase flow, K |
| TW | Local temperature of stationary disk surface, K |
| TWav | Average temperature of stationary disk surface, K |
| t | Time, s |
| z | Axial coordinate |
| Greek symbols | |
| θ | Azimuthal coordinate |
| μ | Dynamic viscosity, Pa·s |
| ρ | Density, kg/m3 |
| υ | Velocity, m/s |
| φ | Volume fraction |
| ω | Angular velocity, rad/s |
Subscripts
| air | Subscript for the air phase parameterparameter |
| oil | Subscript for the oil phase parameter |
References
- Liu, F.; Wu, W.; Hu, J.; Yuan, S. Design of multi-range hydro-mechanical transmission using modular method. Mech. Syst. Signal Process. 2019, 126, 1–20. [Google Scholar] [CrossRef]
- Cui, J.; Wang, C.; Xie, F.; Xuan, R.; Shen, G. Numerical investigation on transient thermal behavior of multidisk friction pairs in hydro-viscous drive. Appl. Therm. Eng. 2014, 67, 409–422. [Google Scholar] [CrossRef]
- Guha, A.; Sengupta, S. The fluid dynamics of the rotating flow in a Tesla disc turbine. Eur. J. Mech. B/Fluids 2013, 37, 112–123. [Google Scholar] [CrossRef]
- Von Kármán, T. Über laminare und turbulente reibung. J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1921, 1, 233–252. [Google Scholar]
- Batchelor, G.K. Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow. Q. J. Mech. Appl. Math. 1951, 4, 29–41. [Google Scholar] [CrossRef]
- Stewartson, K. On the flow between two rotating coaxial disks. Math. Proc. Camb. Philos. Soc. 1953, 49, 333–341. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Kaladhar, K. Analytical solution for Hall and Ion-slip effects on mixed convection flow of couple stress fluid between parallel disks. Math. Comput. Model. 2013, 57, 2494–2509. [Google Scholar]
- Brady, J.F.; Durlofsky, L. On rotating disk flow. J. Fluid Mech. 1987, 175, 363–394. [Google Scholar] [CrossRef]
- Soong, C.Y.; Wu, C.C.; Liu, T.P.; Liu, T.P. Flow structure between two co-axial disks rotating independently. Exp. Therm. Fluid Sci. 2003, 27, 295–311. [Google Scholar] [CrossRef]
- Schouveiler, L.; Le Gal, P.; Chauve, M.P. Instabilities of the flow between a rotating and a stationary disk. J. Fluid Mech. 2001, 443, 329–350. [Google Scholar] [CrossRef]
- Bai, S.; Peng, X.; Li, Y.; Sheng, S. A hydrodynamic laser surface-textured gas mechanical face seal. Tribol. Lett. 2010, 38, 187–194. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y. An improved analytical model for a lubricated roller bearing including a localized defect with different edge shapes. J. Vib. Control 2018, 24, 3894–3907. [Google Scholar] [CrossRef]
- Fesanghary, M.; Khonsari, M.M. On the modeling and shape optimization of hydrodynamic flexible-pad thrust bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 548–558. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Wang, Q. Discussion on the Reynolds equation for the slipper bearing modeling in axial piston pumps. Tribol. Int. 2018, 118, 140–147. [Google Scholar] [CrossRef]
- Huang, J.H.; Fan, Y.R.; Qiu, M.X.; Fang, W.M. Effects of groove on behavior of flow between hydro-viscous drive plates. J. Cent. South Univ. 2012, 19, 347–356. [Google Scholar] [CrossRef]
- Missimer, J.R.; Johnson, W.S. Flow between a smooth stationary disk and grooved rotating disk. J. Tribol. 1982, 104, 248–254. [Google Scholar] [CrossRef]
- Li, M.; Khonsari, M.M.; McCarthy, D.M.C.; Lundin, J. Parametric analysis for a paper-based wet clutch with groove consideration. Tribol. Int. 2014, 80, 222–233. [Google Scholar] [CrossRef]
- Razzzaque, M.M.; Kato, T. Effects of a groove on the behavior of a squeeze film between a grooved and a plain rotating annular disk. J. Tribol. 1999, 121, 808–815. [Google Scholar] [CrossRef]
- Xie, F.; Wu, D.; Tong, Y.; Zhang, B.; Zhu, J. Effects of structural parameters of oil groove on transmission characteristics of hydro-viscous clutch based on viscosity-temperature property of oil film. Ind. Lubr. Tribol. 2017, 69, 690–700. [Google Scholar] [CrossRef]
- Said, I.A.; Abdel-Aziz, M.H.; El-Taweel, Y.A.; Sedahmed, G.H. Mass and heat transfer behavior of a rotating disc with parallel rectangular grooves. Chem. Eng. Process. Process Intensif. 2016, 105, 110–116. [Google Scholar] [CrossRef]
- Beretta, G.P.; Malfa, E. Flow and heat transfer in cavities between rotor and stator disks. Int. J. Heat Mass Transf. 2003, 46, 2715–2726. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.M.; Chen, B.; Gu, Z.T.; Zhou, C. Flow characteristics of oil film on surface of a rotating disk. J. Propuls. Technol. 2019, 40, 53–60. [Google Scholar]
- Aphale, C.R.; Schultz, W.W.; Ceccio, S.L. The influence of grooves on the fully wetted and aerated flow between open clutch plates. J. Tribol. 2010, 132, 011104. [Google Scholar] [CrossRef]
- Iqbal, S.; Al-Bender, F.; Pluymers, B.; Desmet, W. Model for predicting drag torque in open multi-disks wet clutches. J. Fluids Eng. 2014, 136, 021103. [Google Scholar] [CrossRef]
- Xie, F.; Zheng, X.; Sheng, G.; Sun, Q.; Agarwal, R.K. Numerical investigation of cavitation effect on two-phase oil film flow between a friction pair in hydro-viscous drive. P. I. Mech. Eng. C.-J. Mec. 2018, 232, 4626–4636. [Google Scholar] [CrossRef]
- Hu, J.; Wu, W.; Wu, M.; Yuan, S. Numerical investigation of the air–oil two-phase flow inside an oil-jet lubricated ball bearing. Int. J. Heat Mass Transf. 2014, 68, 85–93. [Google Scholar] [CrossRef]
- Payvar, P. Laminar heat transfer in the oil groove of a wet clutch. Int. J. Heat Mass Transf. 1991, 34, 1791–1798. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M.; Maki, R. Three-dimensional thermohydrodynamic analysis of a wet clutch with consideration of grooved friction surfaces. J. Tribol. 2011, 133, 011703. [Google Scholar] [CrossRef]
- Jen, T.C.; Nemecek, D.J. Thermal analysis of a wet-disk clutch subjected to a constant energy engagement. Int. J. Heat Mass Transf. 2008, 51, 1757–1769. [Google Scholar] [CrossRef]
- Marklund, P.; Mäki, R.; Larsson, R.; Höglund, E.; Khonsari, M.M.; Jang, J. Thermal influence on torque transfer of wet clutches in limited slip differential applications. Tribol. Int. 2007, 40, 876–884. [Google Scholar] [CrossRef]
- Wu, W.; Xiong, Z.; Hu, J.B.; Yuan, S.H. Application of CFD to model oil–air flow in a grooved two-disc system. Int. J. Heat Mass Transf. 2015, 91, 293–301. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Wang, T. Drag Torque Model with Decoupling of Temperature and Radius. J. Comput. Theor. Nanosci. 2016, 13, 1337–1342. [Google Scholar] [CrossRef]
- Wu, W.; Xiao, B.; Hu, J.; Yuan, S.; Hu, C. Experimental investigation on the air-liquid two-phase flow inside a grooved rotating-disk system: Flow pattern maps. Appl. Therm. Eng. 2018, 133, 33–38. [Google Scholar] [CrossRef]
- Neupert, T.; Bartel, D. High-resolution 3D CFD multiphase simulation of the flow and the drag torque of wet clutch discs considering free surfaces. Tribol. Int. 2019, 129, 283–296. [Google Scholar] [CrossRef]
- Pahlovy, S.A.; Mahmud, S.F.; Kubota, M.; Ogawa, M.; Takakura, N. Prediction of Drag Torque in a Disengaged Wet Clutch of Automatic Transmission by Analytical Modeling. Tribol. Online 2016, 11, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Gong, H.; Hu, L.; Yang, H. Coriolis effects on torque transmission of hydro-viscous film in parallel disks with imposed throughflow. Tribol. Int. 2017, 115, 100–107. [Google Scholar] [CrossRef]
- Gong, H.; Xie, H.; Hu, L.; Yang, H. Combined effects of Coriolis force and temperature-viscosity dependency on hydro-viscous transmission of rotating parallel disks. Tribol. Int. 2018, 117, 168–173. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Ganapathy, H.; Shooshtari, A.; Choo, K.; Dessiatoun, S.; Alshehhi, M.; Ohadi, M. Volume of fluid-based numerical modeling of condensation heat transfer and fluid flow characteristics in microchannels. Int. J. Heat Mass Transf. 2013, 65, 62–72. [Google Scholar] [CrossRef]
- Hu, J.; Peng, Z.; Wei, C. Experimental Research on Drag Torque for Single-Plate Wet Clutch. J. Tribol. Trans. ASME 2012, 134, 014502. [Google Scholar]
- Da Riva, E.; Del Col, D. Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel. J. Heat Transf. 2012, 134, 051019. [Google Scholar] [CrossRef]
- Wang, F.J. Principle and Application of CFD Software; Tsinghua University Press: Beijing, China, 2015; pp. 40–44. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Benson, D.J. Volume of fluid interface reconstruction methods for multi-material problems. Appl. Mech. Rev. 2002, 55, 151–165. [Google Scholar] [CrossRef]
- Yuan, Z.X.; Saniei, N.; Yan, X.T. Turbulent heat transfer on the stationary disk in a rotor–stator system. Int. J. Heat Mass Transf. 2003, 46, 2207–2218. [Google Scholar] [CrossRef]










| Speed | 15.7 rad/s | 18.8 rad/s | 21.9 rad/s |
|---|---|---|---|
| Mesh 1 | 0.4841 | 0.3608 | 0.3020 |
| Mesh 2 | 0.4914 | 0.3663 | 0.3062 |
| Mesh 3 | 0.4935 | 0.3721 | 0.3091 |
| Parameter | Value |
|---|---|
| r1 | 42 mm |
| r2 | 60 mm |
| h | 0.4 mm |
| H | 1.6–2.0 mm |
| Ng | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wu, W.; Liu, Y.; Hu, C.; Zhou, J. Analysis of Air–Oil Flow and Heat Transfer inside a Grooved Rotating-Disk System. Processes 2019, 7, 632. https://doi.org/10.3390/pr7090632
Li C, Wu W, Liu Y, Hu C, Zhou J. Analysis of Air–Oil Flow and Heat Transfer inside a Grooved Rotating-Disk System. Processes. 2019; 7(9):632. https://doi.org/10.3390/pr7090632
Chicago/Turabian StyleLi, Chunming, Wei Wu, Yin Liu, Chenhui Hu, and Junjie Zhou. 2019. "Analysis of Air–Oil Flow and Heat Transfer inside a Grooved Rotating-Disk System" Processes 7, no. 9: 632. https://doi.org/10.3390/pr7090632
APA StyleLi, C., Wu, W., Liu, Y., Hu, C., & Zhou, J. (2019). Analysis of Air–Oil Flow and Heat Transfer inside a Grooved Rotating-Disk System. Processes, 7(9), 632. https://doi.org/10.3390/pr7090632




