A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring
Abstract
1. Introduction
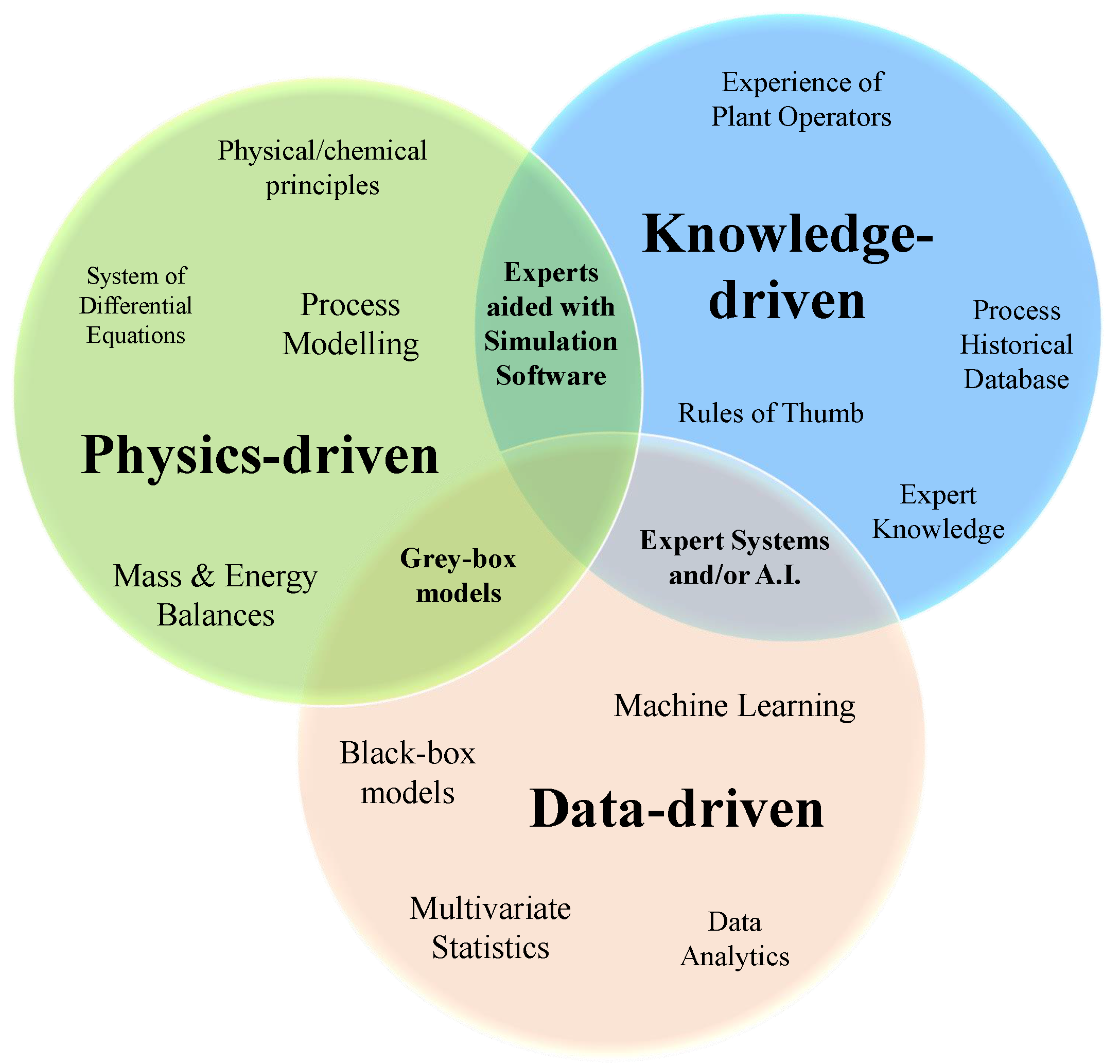
2. Motivation for Using Kernel Methods
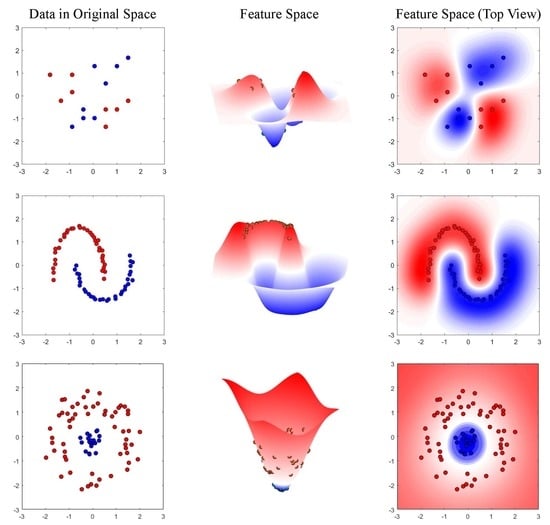
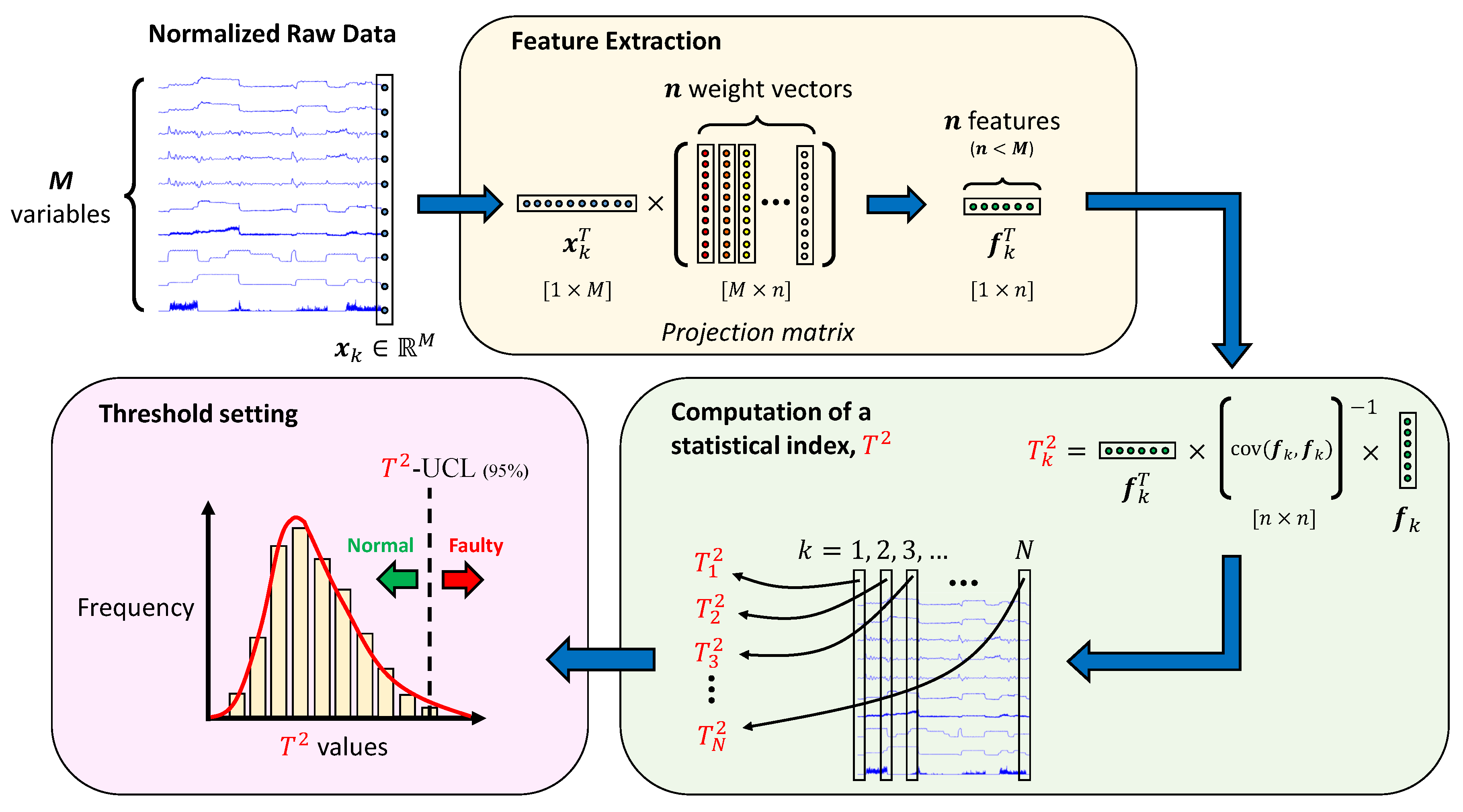
2.1. Feature Extraction Using Kernel Methods
2.2. Kernel Methods in the Machine Learning Context
- Supervised learningClassification: Given data samples labeled as normal and faulty, find a boundary between the two classes; or, given samples from various fault types, find a boundary between the different types.Regression: Given samples of regressors (e.g., process variables) and targets (e.g., key performance indicators), find a function of the former that predicts the latter; or, find a model for predicting the future evolution of process variables whether at normal or faulty conditions.Ensemble methods: Find a strategy to combine results from several models.
- Unsupervised learningDimensionality reduction: Extract low-dimensional features from the original data set that can enable process monitoring or data visualization.Clustering: Find groups of similar samples within the data set, without knowing beforehand whether they are normal or faulty.Density Estimation: Find the probability distribution of the data set.
2.3. Relationship between Kernel Methods and Neural Networks
3. Methodology and Results Summary
3.1. Methodology
3.2. Results Summary
4. Review Findings
4.1. Batch Process Monitoring
4.2. Dynamics, Multi-Scale, and Multi-Mode Monitoring
4.3. Fault Diagnosis in the Kernel Feature Space
4.3.1. Diagnosis by Fault Identification
4.3.2. Diagnosis by Fault Classification
4.3.3. Diagnosis by Causality Analysis
4.4. Handling Non-Gaussian Noise and Outliers
4.5. Improved Sensitivity and Incipient Fault Detection
4.6. Quality-Relevant Monitoring
4.7. Kernel Design and Kernel Parameter Selection
4.7.1. Choice of Kernel Function
4.7.2. Kernel Parameter Selection
4.8. Fast Computation of Kernel Features
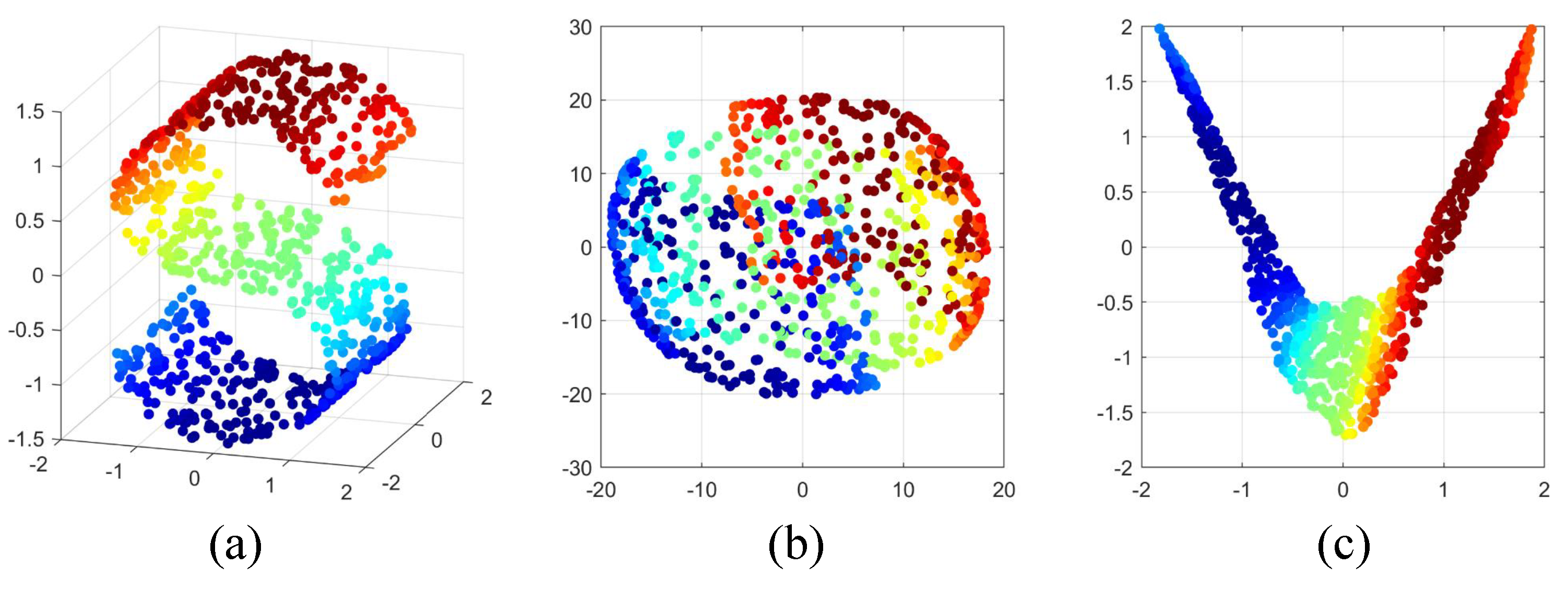
4.9. Manifold Learning and Local Structure Analysis
4.10. Time-Varying Behavior and Adaptive Kernel Computation
4.11. Multi-Block and Distributed Monitoring
4.12. Advanced Methods: Ensembles and Deep Learning
5. A Future Outlook on Kernel-Based Process Monitoring
5.1. Handling Heterogeneous and Multi-Rate Data
5.2. Performing Fault Prognosis
5.3. Developing More Advanced Methods and Improving Kernel Designs
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence | MI | Mutual Information |
| ANN | Artificial Neural Network | MSPM | Multivariate Statistical Process Monitoring |
| CNKI | China National Knowledge Infrastructure | PSE | Process Systems Engineering |
| DTW | Dynamic Time Warping | RKHS | Reproducing Kernel Hilbert Space |
| EWMA | Exponentially Weighted Moving Average | SCADA | Supervisory Control and Data Acquisition |
| FVS | Feature Vector Selection | SDG | Signed Digraph |
| GA | Genetic Algorithm | SFM | Similarity Factor Method |
| GLRT | Generalized Likelihood Ratio Test | SOM | Self-organizing Maps |
| GP | Gaussian Processes | SPA | Statistical Pattern Analysis |
| KDE | Kernel Density Estimation | SVDD | Support Vector Data Description |
| kNN | k-Nearest Neighbors | SVM | Support Vector Machine |
| KPCA | Kernel Principal Components Analysis | UCL | Upper Control Limit |
| AMD | Augmented Mahalanobis distance | ICA | Independent components analysis |
| C-PLS | Concurrent partial least squares | K-means | K-means clustering |
| CCA | Canonical correlation analysis | LLE | Local linear embedding |
| CVA | Canonical variate analysis | LPP | Locality preserving projections |
| DD | Direct decomposition | LS | Least squares |
| DISSIM | Dissimilarity analysis | MVU | Maximum variance unfolding |
| DL | Dictionary learning | NNMF | Non-negative matrix factorization |
| DLV | Dynamic latent variable model | PCA | Principal components analysis |
| ECA | Entropy components analysis | PCR | Principal component regression |
| EDA | Exponential discriminant analysis | PLS | Partial least squares |
| ELM | Extreme learning machine | RPLVR | Robust probability latent variable regression |
| FDA | Fisher discriminant analysis | SDA | Scatter-difference-based discriminant analysis |
| FDFDA | Fault-degradation-oriented FDA | SFA | Slow feature analysis |
| GLPP | Global-local preserving projections | T-PLS | Total partial least squares |
| GMM | Gaussian mixture model | VCA | Variable correlations analysis |
| AEP | Aluminum electrolysis process | HGPWLTP | Hot galvanizing pickling waste liquor |
| AIRLOR | Air quality monitoring network | treatment process | |
| BAFP | Biological anaerobic filter process | HSMP | Hot strip mill process |
| BDP | Butane distillation process | IGT | Industrial gas turbine |
| CAP | Continuous annealing process | IMP | Injection moulding process |
| CFPP | Coal-fired power plant | IPOP | Industrial p-xylene oxidation process |
| CLG | Cyanide leaching of gold | MFF | Multiphase flow facility |
| CPP | Cigarette production process | NE | Numerical example |
| CSEC | Cad System in E. coli | NPP | Nosiheptide production process |
| CSTH | Continuous stirred-tank heater | PCBP | Polyvinyl chloride batch process |
| CSTR | Continuous stirred-tank reactor | PenSim | Penicillin fermentation process |
| DMCP | Dense medium coal preparation | PP | Polymerization process |
| DP | Drying process | PV | Photovoltaic systems |
| DTS | Dissolution tank system | RCP | Real chemical process |
| EFMF | Electro-fused magnesia furnace | SEP | Semiconductor etch process |
| FCCU | Fluid catalytic cracking unit | TEP | Tennessee Eastman plant |
| GCND | Genomic copy number data | TPP | Thermal power plant |
| GHP | Gold hydrometallurgy process | TTP | Three-tank process |
| GMP | Glass melter process | WWTP | Wastewater treatment plant |
| RBF | Gaussian radial basis function kernel | HK | Heat kernel |
| POLY | Polynomial kernel | SIG | Sigmoid kernel |
| COS | Cosine kernel | NSDC | Non-stationary discrete convolution kernel |
| WAV | Wavelet kernel |
References
- Chiang, L.H.; Russell, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer: London, UK, 2005; pp. 1–280. [Google Scholar]
- Reis, M.; Gins, G. Industrial Process Monitoring in the Big Data/Industry 4.0 Era: From Detection, to Diagnosis, to Prognosis. Processes 2017, 5, 35. [Google Scholar] [CrossRef]
- Isermann, R. Model-based fault-detection and diagnosis—Status and applications. Annu. Rev. Control 2005, 29, 71–85. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Incipient Fault Detection, Diagnosis, and Prognosis using Canonical Variate Dissimilarity Analysis. Comput. Aided Chem. Eng. 2019, 46, 1195–1200. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y. Canonical Variate Dissimilarity Analysis for Process Incipient Fault Detection. IEEE Trans. Ind. Inform. 2018, 14, 5308–5315. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Gao, F. Review of recent research on data-based process monitoring. Ind. Eng. Chem. Res. 2013, 52, 3543–3562. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. DROWNING IN DATA: Informatics and modeling challenges in a data-rich networked world. AIChE J. 2009, 55, 2–8. [Google Scholar] [CrossRef]
- Kourti, T. Process analysis and abnormal situation detection: From theory to practice. IEEE Control Syst. Mag. 2002, 22, 10–25. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming. Comput. Chem. Eng. 2019, 125, 434–448. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, S.X.; Huang, B. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Shu, Y.; Ming, L.; Cheng, F.; Zhang, Z.; Zhao, J. Abnormal situation management: Challenges and opportunities in the big data era. Comput. Chem. Eng. 2016, 91, 104–113. [Google Scholar] [CrossRef]
- Chiang, L.; Lu, B.; Castillo, I. Big Data Analytics in Chemical Engineering. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 63–85. [Google Scholar] [CrossRef] [PubMed]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Qin, S.J. Process Data Analytics in the Era of Big Data. AIChE J. 2014, 60, 3092–3100. [Google Scholar] [CrossRef]
- Qin, S.J.; Chiang, L.H. Advances and opportunities in machine learning for process data analytics. Comput. Chem. Eng. 2019, 126, 465–473. [Google Scholar] [CrossRef]
- Patwardhan, R.S.; Hamadah, H.A.; Patel, K.M.; Hafiz, R.H.; Al-Gwaiz, M.M. Applications of Advanced Analytics at Saudi Aramco: A Practitioners’ Perspective. Ind. Eng. Chem. Res. 2019, 58, 11338–11351. [Google Scholar] [CrossRef]
- Ruiz-Cárcel, C.; Cao, Y.; Mba, D.; Lao, L.; Samuel, R.T. Statistical process monitoring of a multiphase flow facility. Control Eng. Pract. 2015, 42, 74–88. [Google Scholar] [CrossRef]
- Ruiz-Cárcel, C.; Lao, L.; Cao, Y.; Mba, D. Canonical variate analysis for performance degradation under faulty conditions. Control Eng. Pract. 2016, 54, 70–80. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification; Springer: London, UK, 2001; p. 785. [Google Scholar] [CrossRef]
- Cover, T.M. Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition. IEEE Trans. Electron. Comput. 1965, EC-14, 326–334. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Max Planck Society. 2019. Available online: https://www.mpg.de/13645470/schoelkopf-koerber-prize (accessed on 30 October 2019).
- Lee, J.M.; Yoo, C.; Choi, S.W.; Vanrolleghem, P.A.; Lee, I.B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Qin, S.J. Survey on data-driven industrial process monitoring and diagnosis. Annu. Rev. Control 2012, 36, 220–234. [Google Scholar] [CrossRef]
- MacGregor, J.; Cinar, A. Monitoring, fault diagnosis, fault-tolerant control and optimization: Data driven methods. Comput. Chem. Eng. 2012, 47, 111–120. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6414–6428. [Google Scholar] [CrossRef]
- Ding, S.X. Data-driven design of monitoring and diagnosis systems for dynamic processes: A review of subspace technique based schemes and some recent results. J. Process Control 2014, 24, 431–449. [Google Scholar] [CrossRef]
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-based techniques focused on modern industry: An overview. IEEE Trans. Ind. Electron. 2015, 62, 657–667. [Google Scholar] [CrossRef]
- Severson, K.; Chaiwatanodom, P.; Braatz, R.D. Perspectives on process monitoring of industrial systems. Annu. Rev. Control 2016, 42, 190–200. [Google Scholar] [CrossRef]
- Tidriri, K.; Chatti, N.; Verron, S.; Tiplica, T. Bridging data-driven and model-based approaches for process fault diagnosis and health monitoring: A review of researches and future challenges. Annu. Rev. Control 2016, 42, 63–81. [Google Scholar] [CrossRef]
- Yin, Z.; Hou, J. Recent advances on SVM based fault diagnosis and process monitoring in complicated industrial processes. Neurocomputing 2016, 174, 643–650. [Google Scholar] [CrossRef]
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Wang, Y.; Si, Y.; Huang, B.; Lou, Z. Survey on the theoretical research and engineering applications of multivariate statistics process monitoring algorithms: 2008–2017. Can. J. Chem. Eng. 2018, 96, 2073–2085. [Google Scholar] [CrossRef]
- Md Nor, N.; Che Hassan, C.R.; Hussain, M.A. A review of data-driven fault detection and diagnosis methods: Applications in chemical process systems. Rev. Chem. Eng. 2018. [Google Scholar] [CrossRef]
- Alauddin, M.; Khan, F.; Imtiaz, S.; Ahmed, S. A Bibliometric Review and Analysis of Data-Driven Fault Detection and Diagnosis Methods for Process Systems. Ind. Eng. Chem. Res. 2018, 57, 10719–10735. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X.; Huang, B. Review and Perspectives of Data-Driven Distributed Monitoring for Industrial Plant-Wide Processes. Ind. Eng. Chem. Res. 2019, 58, 12899–12912. [Google Scholar] [CrossRef]
- Quiñones-Grueiro, M.; Prieto-Moreno, A.; Verde, C.; Llanes-Santiago, O. Data-driven monitoring of multimode continuous processes: A review. Chemom. Intell. Lab. Syst. 2019, 189, 56–71. [Google Scholar] [CrossRef]
- Wang, S.; Aggarwal, C.; Liu, H. Randomized Feature Engineering as a Fast and Accurate Alternative to Kernel Methods. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD’17, Halifax, NS, Canada, 13–17August 2017; pp. 485–494. [Google Scholar] [CrossRef]
- Domingos, P. A few useful things to know about machine learning. Commun. ACM 2012, 55, 78. [Google Scholar] [CrossRef]
- Vert, J.; Tsuda, K.; Schölkopf, B. A primer on kernel methods. Kernel Methods Comput. Biol. 2004, 35–70. [Google Scholar] [CrossRef]
- Cao, D.S.; Liang, Y.Z.; Xu, Q.S.; Hu, Q.N.; Zhang, L.X.; Fu, G.H. Exploring nonlinear relationships in chemical data using kernel-based methods. Chemom. Intell. Lab. Syst. 2011, 107, 106–115. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. Support Vector Machines and Other Kernel-based Learning Methods; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kolesnikov, A.; Zhai, X.; Beyer, L. Revisiting Self-Supervised Visual Representation Learning. arXiv 2019, arXiv:1901.09005. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Dong, D.; McAvoy, T. Nonlinear principal component analysis based on principal curves and neural networks. Comput. Chem. Eng. 1996, 20, 65–78. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Domingos, P. The Master Algorithm; Basic Books: New York City, NY, USA, 2015. [Google Scholar]
- Belkin, M.; Ma, S.; Mandal, S. To understand deep learning we need to understand kernel learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 2, pp. 874–882. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. Proc. IEEE Int. Conf. Comput. Vis. 2015, 2015, 1026–1034. [Google Scholar] [CrossRef]
- Huang, P.S.; Avron, H.; Sainath, T.N.; Sindhwani, V.; Ramabhadran, B. Kernel methods match Deep Neural Networks on TIMIT. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 205–209. [Google Scholar] [CrossRef]
- Skrimpas, G.A.; Sweeney, C.W.; Marhadi, K.S.; Jensen, B.B.; Mijatovic, N.; Holbøll, J. Employment of kernel methods on wind turbine power performance assessment. IEEE Trans. Sustain. Energy 2015, 6, 698–706. [Google Scholar] [CrossRef]
- Song, C.; Liu, K.; Zhang, X. Integration of Data-Level Fusion Model and Kernel Methods for Degradation Modeling and Prognostic Analysis. IEEE Trans. Reliab. 2018, 67, 640–650. [Google Scholar] [CrossRef]
- Eyo, E.N.; Pilario, K.E.S.; Lao, L.; Falcone, G. Development of a Real-Time Objective Gas—Liquid Flow Regime Identifier Using Kernel Methods. IEEE Trans. Cybern. 2019, 1–11. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, G.; Wang, C.; Zeng, W.; Li, J.; Grosse, R. Differentiable compositional kernel learning for Gaussian processes. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; Volume 11, pp. 7676–7696. [Google Scholar]
- Mehrkanoon, S.; Suykens, J.A. Deep hybrid neural-kernel networks using random Fourier features. Neurocomputing 2018, 298, 46–54. [Google Scholar] [CrossRef]
- Mehrkanoon, S. Deep neural-kernel blocks. Neural Netw. 2019, 116, 46–55. [Google Scholar] [CrossRef]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Deep Kernel Learning. Mach. Learn. 2015, 72, 1508–1524. [Google Scholar]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Stochastic variational deep kernel learning. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016; pp. 2594–2602. [Google Scholar]
- Liu, Y.; Yang, C.; Gao, Z.; Yao, Y. Ensemble deep kernel learning with application to quality prediction in industrial polymerization processes. Chemom. Intell. Lab. Syst. 2018, 174, 15–21. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Kan, M.S.; Tan, A.C.C.; Mathew, J. A review on prognostic techniques for non-stationary and non-linear rotating systems. Mech. Syst. Signal Process. 2015, 62, 1–20. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y. Fault detection and diagnosis of non-linear non-Gaussian dynamic processes using kernel dynamic independent component analysis. Inf. Sci. 2014, 259, 369–379. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Mixed kernel canonical variate dissimilarity analysis for incipient fault monitoring in nonlinear dynamic processes. Comput. Chem. Eng. 2019, 123, 143–154. [Google Scholar] [CrossRef]
- Fu, Y.; Kruger, U.; Li, Z.; Xie, L.; Thompson, J.; Rooney, D.; Hahn, J.; Yang, H. Cross-validatory framework for optimal parameter estimation of KPCA and KPLS models. Chemom. Intell. Lab. Syst. 2017, 167, 196–207. [Google Scholar] [CrossRef]
- Vitale, R.; de Noord, O.E.; Ferrer, A. A kernel-based approach for fault diagnosis in batch processes. J. Chemom. 2014, 28, 697–707. [Google Scholar] [CrossRef]
- Chiang, L.H.; Leardi, R.; Pell, R.J.; Seasholtz, M.B. Industrial experiences with multivariate statistical analysis of batch process data. Chemom. Intell. Lab. Syst. 2006, 81, 109–119. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoo, C.K.; Lee, I.B. Fault detection of batch processes using multiway kernel principal component analysis. Comput. Chem. Eng. 2004, 28, 1837–1847. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, S.J. Fault detection of nonlinear processes using multiway kernel independent component analysis. Ind. Eng. Chem. Res. 2007, 46, 7780–7787. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, X.; Deng, X.; Chen, S. Multiway kernel independent component analysis based on feature samples for batch process monitoring. Neurocomputing 2009, 72, 1584–1596. [Google Scholar] [CrossRef]
- Cho, H.W. Nonlinear feature extraction and classification of multivariate data in kernel feature space. Expert Syst. Appl. 2007, 32, 534–542. [Google Scholar] [CrossRef]
- Yu, J. Nonlinear bioprocess monitoring using multiway kernel localized fisher discriminant analysis. Ind. Eng. Chem. Res. 2011, 50, 3390–3402. [Google Scholar] [CrossRef]
- Zhang, Y.; An, J.; Li, Z.; Wang, H. Modeling and monitoring for handling nonlinear dynamic processes. Inf. Sci. 2013, 235, 97–105. [Google Scholar] [CrossRef]
- Tang, X.; Li, Y.; Xie, Z. Phase division and process monitoring for multiphase batch processes with transitions. Chemom. Intell. Lab. Syst. 2015, 145, 72–83. [Google Scholar] [CrossRef]
- Birol, G.; Ündey, C.; Çinar, A. A modular simulation package for fed-batch fermentation: Penicillin production. Comput. Chem. Eng. 2002, 26, 1553–1565. [Google Scholar] [CrossRef]
- Peng, K.; Zhang, K.; Li, G.; Zhou, D. Contribution rate plot for nonlinear quality-related fault diagnosis with application to the hot strip mill process. Control Eng. Pract. 2013, 21, 360–369. [Google Scholar] [CrossRef]
- Li, W.; Zhao, C. Hybrid fault characteristics decomposition based probabilistic distributed fault diagnosis for large-scale industrial processes. Control Eng. Pract. 2019, 84, 377–388. [Google Scholar] [CrossRef]
- Vitale, R.; de Noord, O.E.; Ferrer, A. Pseudo-sample based contribution plots: Innovative tools for fault diagnosis in kernel-based batch process monitoring. Chemom. Intell. Lab. Syst. 2015, 149, 40–52. [Google Scholar] [CrossRef]
- Rashid, M.M.; Yu, J. Nonlinear and non-Gaussian dynamic batch process monitoring using a new multiway kernel independent component analysis and multidimensional mutual information based dissimilarity approach. Ind. Eng. Chem. Res. 2012, 51, 10910–10920. [Google Scholar] [CrossRef]
- Peng, C.; Qiao, J.; Zhang, X.; Lu, R. Phase Partition and Fault Diagnosis of Batch Process Based on KECA Angular Similarity. IEEE Access 2019, 7, 125676–125687. [Google Scholar] [CrossRef]
- Jia, M.; Xu, H.; Liu, X.; Wang, N. The optimization of the kind and parameters of kernel function in KPCA for process monitoring. Comput. Chem. Eng. 2012, 46, 94–104. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, I.B. Nonlinear dynamic process monitoring based on dynamic kernel PCA. Chem. Eng. Sci. 2004, 59, 5897–5908. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, C.; Lee, J.M.; Park, J.H.; Lee, I.B. Fault detection and identification of nonlinear processes based on kernel PCA. Chemom. Intell. Lab. Syst. 2005, 75, 55–67. [Google Scholar] [CrossRef]
- Cho, J.H.; Lee, J.M.; Wook Choi, S.; Lee, D.; Lee, I.B. Fault identification for process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2005, 60, 279–288. [Google Scholar] [CrossRef]
- Yoo, C.K.; Lee, I.B. Nonlinear multivariate filtering and bioprocess monitoring for supervising nonlinear biological processes. Process Biochem. 2006, 41, 1854–1863. [Google Scholar] [CrossRef]
- Lee, D.S.; Lee, M.W.; Woo, S.H.; Kim, Y.J.; Park, J.M. Multivariate online monitoring of a full-scale biological anaerobic filter process using kernel-based algorithms. Ind. Eng. Chem. Res. 2006, 45, 4335–4344. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, W.; Zhao, X.; Shao, H. Nonlinear On-line Process Monitoring and Fault Detection Based on Kernel ICA. In Proceedings of the 2006 International Conference on Information and Automation, Colombo, Sri Lanka, 15–17 December 2006; Volume 1, pp. 222–227. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X. Multivariate Statistical Process Monitoring Using Multi-Scale Kernel Principal Component Analysis. IFAC-PapersOnLine 2006, 6, 108–113. [Google Scholar] [CrossRef]
- Cho, H.W. Identification of contributing variables using kernel-based discriminant modeling and reconstruction. Expert Syst. Appl. 2007, 33, 274–285. [Google Scholar] [CrossRef]
- Sun, R.; Tsung, F.; Qu, L. Evolving kernel principal component analysis for fault diagnosis. Comput. Ind. Eng. 2007, 53, 361–371. [Google Scholar] [CrossRef]
- Choi, S.W.; Morris, J.; Lee, I.B. Nonlinear multiscale modelling for fault detection and identification. Chem. Eng. Sci. 2008, 63, 2252–2266. [Google Scholar] [CrossRef]
- Tian, X.; Deng, X. A fault detection method using multi-scale kernel principal component analysis. In Proceedings of the 27th Chinese Control Conference, Kunming, China, 16–18 July 2008; pp. 25–29. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Zhang, Y.; Zhou, H. Fault detection of nonlinear dynamic processes using dynamic kernel principal component analysis. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 3009–3014. [Google Scholar] [CrossRef]
- Lee, J.M.; Qin, S.J.; Lee, I.B. Fault Detection of Non-Linear Processes Using Kernel Independent Component Analysis. Can. J. Chem. Eng. 2008, 85, 526–536. [Google Scholar] [CrossRef]
- Cui, P.; Li, J.; Wang, G. Improved kernel principal component analysis for fault detection. Expert Syst. Appl. 2008, 34, 1210–1219. [Google Scholar] [CrossRef]
- Cui, J.; Huang, W.; Miao, M.; Sun, B. Kernel scatter-difference-based discriminant analysis for fault diagnosis. In Proceedings of the 2008 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 5–8 August 2008; pp. 771–774. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, S.J. Improved nonlinear fault detection technique and statistical analysis. AIChE J. 2008, 54, 3207–3220. [Google Scholar] [CrossRef]
- Lü, N.; Wang, X. Fault diagnosis based on signed digraph combined with dynamic kernel PLS and SVR. Ind. Eng. Chem. Res. 2008, 47, 9447–9456. [Google Scholar] [CrossRef]
- He, X.B.; Yang, Y.P.; Yang, Y.H. Fault diagnosis based on variable-weighted kernel Fisher discriminant analysis. Chemom. Intell. Lab. Syst. 2008, 93, 27–33. [Google Scholar] [CrossRef]
- Cho, H.W. An orthogonally filtered tree classifier based on nonlinear kernel-based optimal representation of data. Expert Syst. Appl. 2008, 34, 1028–1037. [Google Scholar] [CrossRef]
- Li, J.; Cui, P. Kernel scatter-difference-based discriminant analysis for nonlinear fault diagnosis. Chemom. Intell. Lab. Syst. 2008, 94, 80–86. [Google Scholar] [CrossRef]
- Li, J.; Cui, P. Improved kernel fisher discriminant analysis for fault diagnosis. Expert Syst. Appl. 2009, 36, 1423–1432. [Google Scholar] [CrossRef]
- Zhang, Y. Enhanced statistical analysis of nonlinear processes using KPCA, KICA and SVM. Chem. Eng. Sci. 2009, 64, 801–811. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y. Complex process monitoring using modified partial least squares method of independent component regression. Chemom. Intell. Lab. Syst. 2009, 98, 143–148. [Google Scholar] [CrossRef]
- Shao, J.D.; Rong, G.; Lee, J.M. Learning a data-dependent kernel function for KPCA-based nonlinear process monitoring. Chem. Eng. Res. Des. 2009, 87, 1471–1480. [Google Scholar] [CrossRef]
- Shao, J.D.; Rong, G. Nonlinear process monitoring based on maximum variance unfolding projections. Expert Syst. Appl. 2009, 36, 11332–11340. [Google Scholar] [CrossRef]
- Shao, J.D.; Rong, G.; Lee, J.M. Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis. Chemom. Intell. Lab. Syst. 2009, 96, 75–83. [Google Scholar] [CrossRef]
- Liu, X.; Kruger, U.; Littler, T.; Xie, L.; Wang, S. Moving window kernel PCA for adaptive monitoring of nonlinear processes. Chemom. Intell. Lab. Syst. 2009, 96, 132–143. [Google Scholar] [CrossRef]
- Ge, Z.; Yang, C.; Song, Z. Improved kernel PCA-based monitoring approach for nonlinear processes. Chem. Eng. Sci. 2009, 64, 2245–2255. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, F.; Zhang, Y. Nonlinear process monitoring based on kernel dissimilarity analysis. Control Eng. Pract. 2009, 17, 221–230. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, F.; Wang, F. Nonlinear batch process monitoring using phase-based kernel-independent component analysis-principal component analysis (KICA-PCA). Ind. Eng. Chem. Res. 2009, 48, 9163–9174. [Google Scholar] [CrossRef]
- Jia, M.; Chu, F.; Wang, F.; Wang, W. On-line batch process monitoring using batch dynamic kernel principal component analysis. Chemom. Intell. Lab. Syst. 2010, 101, 110–122. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Hsu, C.C.; Chen, M.C. Adaptive kernel principal component analysis (KPCA) for monitoring small disturbances of nonlinear processes. Ind. Eng. Chem. Res. 2010, 49, 2254–2262. [Google Scholar] [CrossRef]
- Alcala, C.F.; Qin, S.J. Reconstruction-Based Contribution for Process Monitoring with Kernel Principal Component Analysis. Ind. Eng. Chem. Res. 2010, 49, 7849–7857. [Google Scholar] [CrossRef]
- Zhu, Z.B.; Song, Z.H. Fault diagnosis based on imbalance modified kernel Fisher discriminant analysis. Chem. Eng. Res. Des. 2010, 88, 936–951. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, H.; Qin, S.J.; Chai, T. Decentralized Fault Diagnosis of Large-Scale Processes Using Multiblock Kernel Partial Least Squares. IEEE Trans. Ind. Inform. 2010, 6, 3–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Zhou, H. Statistical analysis and adaptive technique for dynamical process monitoring. Chem. Eng. Res. Des. 2010, 88, 1381–1392. [Google Scholar] [CrossRef]
- Xu, J.; Hu, S. Nonlinear process monitoring and fault diagnosis based on KPCA and MKL-SVM. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010; Volume 1, pp. 233–237. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Kernel generalization of PPCA for nonlinear probabilistic monitoring. Ind. Eng. Chem. Res. 2010, 49, 11832–11836. [Google Scholar] [CrossRef]
- Wang, L.; Shi, H. Multivariate statistical process monitoring using an improved independent component analysis. Chem. Eng. Res. Des. 2010, 88, 403–414. [Google Scholar] [CrossRef]
- Sumana, C.; Mani, B.; Venkateswarlu, C.; Gudi, R.D. Improved Fault Diagnosis Using Dynamic Kernel Scatter-Difference-Based Discriminant Analysis. Ind. Eng. Chem. Res. 2010, 49, 8575–8586. [Google Scholar] [CrossRef]
- Sumana, C.; Bhushan, M.; Venkateswarlu, C.; Gudi, R.D. Improved nonlinear process monitoring using KPCA with sample vector selection and combined index. Asia-Pac. J. Chem. Eng. 2011, 6, 460–469. [Google Scholar] [CrossRef]
- Khediri, I.B.; Limam, M.; Weihs, C. Variable window adaptive Kernel Principal Component Analysis for nonlinear nonstationary process monitoring. Comput. Ind. Eng. 2011, 61, 437–446. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS. Chem. Eng. Sci. 2011, 66, 64–72. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Z. On-line batch process monitoring using hierarchical kernel partial least squares. Chem. Eng. Res. Des. 2011, 89, 2078–2084. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Z. Multivariate process monitoring and analysis based on multi-scale KPLS. Chem. Eng. Res. Des. 2011, 89, 2667–2678. [Google Scholar] [CrossRef]
- Zhu, Z.B.; Song, Z.H. A novel fault diagnosis system using pattern classification on kernel FDA subspace. Expert Syst. Appl. 2011, 38, 6895–6905. [Google Scholar] [CrossRef]
- Khediri, I.B.; Weihs, C.; Limam, M. Kernel k-means clustering based local support vector domain description fault detection of multimodal processes. Expert Syst. Appl. 2012, 39, 2166–2171. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Teng, Y. Dynamic processes monitoring using recursive kernel principal component analysis. Chem. Eng. Sci. 2012, 72, 78–86. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, C. Decentralized fault diagnosis using multiblock kernel independent component analysis. Chem. Eng. Res. Des. 2012, 90, 667–676. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Hu, Z. Improved multi-scale kernel principal component analysis and its application for fault detection. Chem. Eng. Res. Des. 2012, 90, 1271–1280. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Hu, Z.; Song, C. Dynamical process monitoring using dynamical hierarchical kernel partial least squares. Chemom. Intell. Lab. Syst. 2012, 118, 150–158. [Google Scholar] [CrossRef]
- Yu, J. A nonlinear kernel Gaussian mixture model based inferential monitoring approach for fault detection and diagnosis of chemical processes. Chem. Eng. Sci. 2012, 68, 506–519. [Google Scholar] [CrossRef]
- Guo, K.; San, Y.; Zhu, Y. Nonlinear process monitoring using wavelet kernel principal component analysis. In Proceedings of the 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China, 19–20 May 2012; pp. 432–438. [Google Scholar] [CrossRef]
- Sumana, C.; Detroja, K.; Gudi, R.D. Evaluation of nonlinear scaling and transformation for nonlinear process fault detection. Int. J. Adv. Eng. Sci. Appl. Math. 2012, 4, 52–66. [Google Scholar] [CrossRef]
- Wang, Y.J.; Jia, M.X.; Mao, Z.Z. Weak fault monitoring method for batch process based on multi-model SDKPCA. Chemom. Intell. Lab. Syst. 2012, 118, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Chang, Y. Reconstruction in integrating fault spaces for fault identification with kernel independent component analysis. Chem. Eng. Res. Des. 2013, 91, 1071–1084. [Google Scholar] [CrossRef]
- Peng, K.; Zhang, K.; Li, G. Quality-related process monitoring based on total kernel PLS model and its industrial application. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, Z.; Jia, M. Feature-points-based multimodel single dynamic kernel principle component analysis (M-SDKPCA) modeling and online monitoring strategy for uneven-length batch processes. Ind. Eng. Chem. Res. 2013, 52, 12059–12071. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Weighted kernel principal component analysis based on probability density estimation and moving window and its application in nonlinear chemical process monitoring. Chemom. Intell. Lab. Syst. 2013, 127, 121–131. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Statistical Monitoring of Chemical Processes Based on Sensitive Kernel Principal Components. Chin. J. Chem. Eng. 2013, 21, 633–643. [Google Scholar] [CrossRef]
- Zhang, Y.; An, J.; Zhang, H. Monitoring of time-varying processes using kernel independent component analysis. Chem. Eng. Sci. 2013, 88, 23–32. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Lu, R. Fault identification of nonlinear processes. Ind. Eng. Chem. Res. 2013, 52, 12072–12081. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Lu, R. Modeling and monitoring of multimode process based on subspace separation. Chem. Eng. Res. Des. 2013, 91, 831–842. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X. Nonlinear process fault pattern recognition using statistics kernel PCA similarity factor. Neurocomputing 2013, 121, 298–308. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X. Sparse kernel locality preserving projection and its application in nonlinear process fault detection. Chin. J. Chem. Eng. 2013, 21, 163–170. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S. Modified kernel principal component analysis based on local structure analysis and its application to nonlinear process fault diagnosis. Chemom. Intell. Lab. Syst. 2013, 127, 195–209. [Google Scholar] [CrossRef]
- Rong, G.; Liu, S.Y.; Shao, J.D. Fault diagnosis by Locality Preserving Discriminant Analysis and its kernel variation. Comput. Chem. Eng. 2013, 49, 105–113. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, H.; Shi, H. Enhanced batch process monitoring using just-in-time-learning based kernel partial least squares. Chemom. Intell. Lab. Syst. 2013, 123, 15–27. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, H.; Shi, H. Robust online monitoring based on spherical-kernel partial least squares for nonlinear processes with contaminated modeling data. Ind. Eng. Chem. Res. 2013, 52, 9155–9164. [Google Scholar] [CrossRef]
- Fan, J.; Qin, S.J.; Wang, Y. Online monitoring of nonlinear multivariate industrial processes using filtering KICA-PCA. Control Eng. Pract. 2014, 22, 205–216. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, N.; Li, S. Fault isolation of nonlinear processes based on fault directions and features. IEEE Trans. Control Syst. Technol. 2014, 22, 1567–1572. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S. Modeling and monitoring of nonlinear multi-mode processes. Control Eng. Pract. 2014, 22, 194–204. [Google Scholar] [CrossRef]
- Cai, L.; Tian, X.; Zhang, N. A kernel time structure independent component analysis method for nonlinear process monitoring. Chin. J. Chem. Eng. 2014, 22, 1243–1253. [Google Scholar] [CrossRef]
- Wang, L.; Shi, H. Improved kernel PLS-based fault detection approach for nonlinear chemical processes. Chin. J. Chem. Eng. 2014, 22, 657–663. [Google Scholar] [CrossRef]
- Elshenawy, L.M.; Mohamed, T.A.M. Fault Detection of Nonlinear Processes Using Fuzzy C-means-based Kernel PCA. In Proceedings of the International Conference on Machine Learning, Electrical and Mechanical Engineering (ICMLEME 2014), Dubai, UAE, 8–9 January 2014; International Institute of Engineers: Dubai, UAE, 2014. [Google Scholar] [CrossRef]
- Mori, J.; Yu, J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach. J. Process Control 2014, 24, 57–71. [Google Scholar] [CrossRef]
- Castillo, I.; Edgar, T.F.; Dunia, R. Nonlinear detection and isolation of multiple faults using residuals modeling. Ind. Eng. Chem. Res. 2014, 53, 5217–5233. [Google Scholar] [CrossRef]
- Peng, K.X.; Zhang, K.; Li, G. Online Contribution Rate Based Fault Diagnosis for Nonlinear Industrial Processes. Acta Autom. Sin. 2014, 40, 423–430. [Google Scholar] [CrossRef]
- Zhao, X.; Xue, Y. Output-relevant fault detection and identification of chemical process based on hybrid kernel T-PLS. Can. J. Chem. Eng. 2014, 92, 1822–1828. [Google Scholar] [CrossRef]
- Godoy, J.L.; Zumoffen, D.A.; Vega, J.R.; Marchetti, J.L. New contributions to non-linear process monitoring through kernel partial least squares. Chemom. Intell. Lab. Syst. 2014, 135, 76–89. [Google Scholar] [CrossRef]
- Kallas, M.; Mourot, G.; Maquin, D.; Ragot, J. Diagnosis of nonlinear systems using kernel principal component analysis. J. Phys. Conf. Ser. 2014, 570. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Comodi, G.; Ferracuti, F.; Fonti, A.; Giantomassi, A.; Longhi, S. Multi-apartment residential microgrid monitoring system based on kernel canonical variate analysis. Neurocomputing 2015, 170, 306–317. [Google Scholar] [CrossRef]
- Li, N.; Yang, Y. Ensemble Kernel Principal Component Analysis for Improved Nonlinear Process Monitoring. Ind. Eng. Chem. Res. 2015, 54, 318–329. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G. Scale-sifting multiscale nonlinear process quality monitoring and fault detection. Can. J. Chem. Eng. 2015, 93, 1416–1425. [Google Scholar] [CrossRef]
- Md Nor, N.; Hussain, M.A.; Hassan, C.R.C. Process Monitoring and Fault Detection in Non-Linear Chemical Process Based On Multi-Scale Kernel Fisher Discriminant Analysis. Comput. Aided Chem. Eng. 2015, 37, 1823–1828. [Google Scholar] [CrossRef]
- Yao, M.; Wang, H. On-line monitoring of batch processes using generalized additive kernel principal component analysis. J. Process Control 2015, 28, 56–72. [Google Scholar] [CrossRef]
- Wang, H.; Yao, M. Fault detection of batch processes based on multivariate functional kernel principal component analysis. Chemom. Intell. Lab. Syst. 2015, 149, 78–89. [Google Scholar] [CrossRef]
- Huang, L.; Cao, Y.; Tian, X.; Deng, X. A Nonlinear Quality-relevant Process Monitoring Method with Kernel Input-output Canonical Variate Analysis. IFAC-PapersOnLine 2015, 48, 611–616. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, W.; Fan, Y.; Zhang, L. Process fault detection using directional kernel partial least squares. Ind. Eng. Chem. Res. 2015, 54, 2509–2518. [Google Scholar] [CrossRef]
- Zhang, N.; Tian, X.; Cai, L.; Deng, X. Process fault detection based on dynamic kernel slow feature analysis. Comput. Electr. Eng. 2015, 41, 9–17. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X.; Cai, L. Nonlinear Process Fault Diagnosis Using Kernel Slow Feature Discriminant Analysis. IFAC-PapersOnLine 2015, 48, 607–612. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, R.; Fan, Y. Fault diagnosis of nonlinear process based on KCPLS reconstruction. Chemom. Intell. Lab. Syst. 2015, 140, 49–60. [Google Scholar] [CrossRef]
- Samuel, R.T.; Cao, Y. Kernel canonical variate analysis for nonlinear dynamic process monitoring. IFAC-PapersOnLine 2015, 28, 605–610. [Google Scholar] [CrossRef]
- Samuel, R.T.; Cao, Y. Improved kernel canonical variate analysis for process monitoring. In Proceedings of the 2015 21st International Conference on Automation and Computing (ICAC), Glasgow, UK, 11–12 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Chakour, C.; Harkat, M.F.; Djeghaba, M. New adaptive kernel principal component analysis for nonlinear dynamic process monitoring. Appl. Math. Inf. Sci. 2015, 9, 1833–1845. [Google Scholar]
- Jiang, Q.; Yan, X. Nonlinear plant-wide process monitoring using MI-spectral clustering and Bayesian inference-based multiblock KPCA. J. Process Control 2015, 32, 38–50. [Google Scholar] [CrossRef]
- Cai, E.; Liu, D.; Liang, L.; Xu, G. Monitoring of chemical industrial processes using integrated complex network theory with PCA. Chemom. Intell. Lab. Syst. 2015, 140, 22–35. [Google Scholar] [CrossRef]
- Luo, L.; Bao, S.; Mao, J.; Tang, D. Nonlinear Process Monitoring Using Data-Dependent Kernel Global-Local Preserving Projections. Ind. Eng. Chem. Res. 2015, 54, 11126–11138. [Google Scholar] [CrossRef]
- Bernal De Lázaro, J.M.; Prieto Moreno, A.; Llanes Santiago, O.; Da Silva Neto, A.J. Optimizing kernel methods to reduce dimensionality in fault diagnosis of industrial systems. Comput. Ind. Eng. 2015, 87, 140–149. [Google Scholar] [CrossRef]
- Bernal-de Lázaro, J.M.; Llanes-Santiago, O.; Prieto-Moreno, A.; Knupp, D.C.; Silva-Neto, A.J. Enhanced dynamic approach to improve the detection of small-magnitude faults. Chem. Eng. Sci. 2016, 146, 166–179. [Google Scholar] [CrossRef]
- Ji, H.; He, X.; Li, G.; Zhou, D. Determining the optimal kernel parameter in KPCA based on sample reconstruction. Chin. Control Conf. 2016, 2016, 6408–6414. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.; Zhu, Q. Multivariate time delay analysis based local KPCA fault prognosis approach for nonlinear processes. Chin. J. Chem. Eng. 2016, 24, 1413–1422. [Google Scholar] [CrossRef]
- Luo, L.; Bao, S.; Mao, J.; Tang, D. Nonlinear process monitoring based on kernel global-local preserving projections. J. Process Control 2016, 38, 11–21. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Y.; Yang, N. Fault diagnosis of multimode processes based on similarities. IEEE Trans. Ind. Electron. 2016, 63, 2606–2614. [Google Scholar] [CrossRef]
- Taouali, O.; Jaffel, I.; Lahdhiri, H.; Harkat, M.F.; Messaoud, H. New fault detection method based on reduced kernel principal component analysis (RKPCA). Int. J. Adv. Manuf. Technol. 2016, 85, 1547–1552. [Google Scholar] [CrossRef]
- Fazai, R.; Taouali, O.; Harkat, M.F.; Bouguila, N. A new fault detection method for nonlinear process monitoring. Int. J. Adv. Manuf. Technol. 2016, 87, 3425–3436. [Google Scholar] [CrossRef]
- Jaffel, I.; Taouali, O.; Harkat, M.F.; Messaoud, H. Moving window KPCA with reduced complexity for nonlinear dynamic process monitoring. ISA Trans. 2016, 64, 184–192. [Google Scholar] [CrossRef]
- Mansouri, M.; Nounou, M.; Nounou, H.; Karim, N. Kernel PCA-based GLRT for nonlinear fault detection of chemical processes. J. Loss Prev. Process Ind. 2016, 40, 334–347. [Google Scholar] [CrossRef]
- Botre, C.; Mansouri, M.; Nounou, M.; Nounou, H.; Karim, M.N. Kernel PLS-based GLRT method for fault detection of chemical processes. J. Loss Prev. Process Ind. 2016, 43, 212–224. [Google Scholar] [CrossRef]
- Samuel, R.T.; Cao, Y. Nonlinear process fault detection and identification using kernel PCA and kernel density estimation. Syst. Sci. Control Eng. 2016, 4, 165–174. [Google Scholar] [CrossRef]
- Ge, Z.; Zhong, S.; Zhang, Y. Semisupervised Kernel Learning for FDA Model and its Application for Fault Classification in Industrial Processes. IEEE Trans. Ind. Inform. 2016, 12, 1403–1411. [Google Scholar] [CrossRef]
- Jia, Q.; Du, W.; Zhang, Y. Semi-supervised kernel partial least squares fault detection and identification approach with application to HGPWLTP. J. Chemom. 2016, 30, 377–385. [Google Scholar] [CrossRef]
- Jia, Q.; Zhang, Y. Quality-related fault detection approach based on dynamic kernel partial least squares. Chem. Eng. Res. Des. 2016, 106, 242–252. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, J.; Yan, X. Performance-driven optimal design of distributed monitoring for large-scale nonlinear processes. Chemom. Intell. Lab. Syst. 2016, 155, 151–159. [Google Scholar] [CrossRef]
- Peng, K.; Zhang, K.; You, B.; Dong, J.; Wang, Z. A quality-based nonlinear fault diagnosis framework focusing on industrial multimode batch processes. IEEE Trans. Ind. Electron. 2016, 63, 2615–2624. [Google Scholar] [CrossRef]
- Xie, L.; Li, Z.; Zeng, J.; Kruger, U. Block adaptive kernel principal component analysis for nonlinear process monitoring. AIChE J. 2016, 62, 4334–4345. [Google Scholar] [CrossRef]
- Wang, G.; Luo, H.; Peng, K. Quality-related fault detection using linear and nonlinear principal component regression. J. Franklin Inst. 2016, 353, 2159–2177. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Related and independent variable fault detection based on KPCA and SVDD. J. Process Control 2016, 39, 88–99. [Google Scholar] [CrossRef]
- Xiao, Y.-W.; Zhang, X.-H. Novel Nonlinear Process Monitoring and Fault Diagnosis Method Based on KPCA–ICA and MSVMs. J. Control Autom. Electr. Syst. 2016, 27, 289–299. [Google Scholar] [CrossRef]
- Feng, J.; Wang, J.; Zhang, H.; Han, Z. Fault diagnosis method of joint fisher discriminant analysis based on the local and global manifold learning and its kernel version. IEEE Trans. Autom. Sci. Eng. 2016, 13, 122–133. [Google Scholar] [CrossRef]
- Sheng, N.; Liu, Q.; Qin, S.J.; Chai, T. Comprehensive Monitoring of Nonlinear Processes Based on Concurrent Kernel Projection to Latent Structures. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1129–1137. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Y.; Du, W. Nonlinear Process Monitoring Using Regression and Reconstruction Method. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1343–1354. [Google Scholar] [CrossRef]
- Jaffel, I.; Taouali, O.; Harkat, M.F.; Messaoud, H. Kernel principal component analysis with reduced complexity for nonlinear dynamic process monitoring. Int. J. Adv. Manuf. Technol. 2017, 88, 3265–3279. [Google Scholar] [CrossRef]
- Lahdhiri, H.; Elaissi, I.; Taouali, O.; Harakat, M.F.; Messaoud, H. Nonlinear process monitoring based on new reduced Rank-KPCA method. Stoch. Environ. Res. Risk Assess. 2017, 32, 1833–1848. [Google Scholar] [CrossRef]
- Lahdhiri, H.; Taouali, O.; Elaissi, I.; Jaffel, I.; Harakat, M.F.; Messaoud, H. A new fault detection index based on Mahalanobis distance and kernel method. Int. J. Adv. Manuf. Technol. 2017, 91, 2799–2809. [Google Scholar] [CrossRef]
- Mansouri, M.; Nounou, M.N.; Nounou, H.N. Multiscale Kernel PLS-Based Exponentially Weighted-GLRT and Its Application to Fault Detection. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 3, 49–58. [Google Scholar] [CrossRef]
- Mansouri, M.; Nounou, M.N.; Nounou, H.N. Improved Statistical Fault Detection Technique and Application to Biological Phenomena Modeled by S-Systems. IEEE Trans. Nanobiosci. 2017, 16, 504–512. [Google Scholar] [CrossRef]
- Sheriff, M.Z.; Karim, M.N.; Nounou, M.N.; Nounou, H.; Mansouri, M. Monitoring of chemical processes using improved multiscale KPCA. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 49–54. [Google Scholar] [CrossRef]
- Cai, L.; Tian, X.; Chen, S. Monitoring nonlinear and non-Gaussian processes using Gaussian mixture model-based weighted kernel independent component analysis. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 122–135. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Qi, Y.; Wang, L.; Gao, X.; Wang, X. Fault detection and diagnosis of chemical process using enhanced KECA. Chemom. Intell. Lab. Syst. 2017, 161, 61–69. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X.; Deng, X. Batch Process Monitoring Based on Multiway Global Preserving Kernel Slow Feature Analysis. IEEE Access 2017, 5, 2696–2710. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X. Batch process monitoring based on batch dynamic Kernel slow feature analysis. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 4772–4777. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, W.; Fan, Y.; Li, X. Comprehensive Correlation Analysis of Industrial Process. IEEE Trans. Ind. Electron. 2017, 64, 9461–9468. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, Y.; Wang, Z.; Feng, L. Fault Detection Based on Modified Kernel Semi-Supervised Locally Linear Embedding. IEEE Access 2017, 6, 479–487. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, X.; Xu, T.; Li, Y. Nearest neighbor difference rule–based kernel principal component analysis for fault detection in semiconductor manufacturing processes. J. Chemom. 2017, 31, 1–12. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S.; Harris, C.J. Deep learning based nonlinear principal component analysis for industrial process fault detection. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1237–1243. [Google Scholar] [CrossRef]
- Deng, X.; Zhong, N.; Wang, L. Nonlinear Multimode Industrial Process Fault Detection Using Modified Kernel Principal Component Analysis. IEEE Access 2017, 5, 23121–23132. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S.; Harris, C.J. Fault discriminant enhanced kernel principal component analysis incorporating prior fault information for monitoring nonlinear processes. Chemom. Intell. Lab. Syst. 2017, 162, 21–34. [Google Scholar] [CrossRef]
- Tan, R.; Samuel, R.T.; Cao, Y. Nonlinear Dynamic Process Monitoring: The Case Study of a Multiphase Flow Facility. Comput. Aided Chem. Eng. 2017, 40, 1495–1500. [Google Scholar] [CrossRef]
- Shang, L.; Liu, J.; Zhang, Y. Efficient recursive kernel canonical variate analysis for monitoring nonlinear time-varying processes. Can. J. Chem. Eng. 2017, 96, 205–214. [Google Scholar] [CrossRef]
- Li, G.; Peng, K.; Yuan, T.; Zhong, M. Kernel dynamic latent variable model for process monitoring with application to hot strip mill process. Chemom. Intell. Lab. Syst. 2017, 171, 218–225. [Google Scholar] [CrossRef]
- Wang, G.; Jiao, J. A Kernel Least Squares Based Approach for Nonlinear Quality-Related Fault Detection. IEEE Trans. Ind. Electron. 2017, 64, 3195–3204. [Google Scholar] [CrossRef]
- Wang, G.; Jiao, J.; Yin, S. A kernel direct decomposition-based monitoring approach for nonlinear quality-related fault detection. IEEE Trans. Ind. Inform. 2017, 13, 1565–1574. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; Zhou, J.; Wu, H. An improved kernel exponential discriminant analysis for fault identification of batch process. In Proceedings of the 2017 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, China, 26–27 May 2017; pp. 16–21. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, N.; Wang, G.; Yin, S. A nonlinear quality-related fault detection approach based on modified kernel partial least squares. ISA Trans. 2017, 66, 275–283. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Quality Relevant and Independent Two Block Monitoring Based on Mutual Information and KPCA. IEEE Trans. Ind. Electron. 2017, 64, 6518–6527. [Google Scholar] [CrossRef]
- Yi, J.; Huang, D.; He, H.; Zhou, W.; Han, Q.; Li, T. A novel framework for fault diagnosis using kernel partial least squares based on an optimal preference matrix. IEEE Trans. Ind. Electron. 2017, 64, 4315–4324. [Google Scholar] [CrossRef]
- Md Nor, N.; Hussain, M.A.; Che Hassan, C.R. Fault diagnosis and classification framework using multi-scale classification based on kernel Fisher discriminant analysis for chemical process system. Appl. Soft Comput. 2017, 61, 959–972. [Google Scholar] [CrossRef]
- Du, W.; Fan, Y.; Zhang, Y.; Zhang, J. Fault diagnosis of non-Gaussian process based on FKICA. J. Frankl. Inst. 2017, 354, 2573–2590. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, C. Stationarity test and Bayesian monitoring strategy for fault detection in nonlinear multimode processes. Chemom. Intell. Lab. Syst. 2017, 168, 45–61. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, J.; Yao, L.; Song, Z.; Hou, B. Similarity based robust probability latent variable regression model and its kernel extension for process monitoring. Chemom. Intell. Lab. Syst. 2017, 161, 88–95. [Google Scholar] [CrossRef]
- Gharahbagheri, H.; Imtiaz, S.A.; Khan, F. Root Cause Diagnosis of Process Fault Using KPCA and Bayesian Network. Ind. Eng. Chem. Res. 2017. [Google Scholar] [CrossRef]
- Gharahbagheri, H.; Imtiaz, S.; Khan, F. Combination of KPCA and causality analysis for root cause diagnosis of industrial process fault. Can. J. Chem. Eng. 2017, 95, 1497–1509. [Google Scholar] [CrossRef]
- Galiaskarov, M.R.; Kurkina, V.V.; Rusinov, L.A. Online diagnostics of time-varying nonlinear chemical processes using moving window kernel principal component analysis and Fisher discriminant analysis. J. Chemom. 2017, e2866. [Google Scholar] [CrossRef]
- Zhu, Q.X.; Meng, Q.Q.; He, Y.L. Novel Multidimensional Feature Pattern Classification Method and Its Application to Fault Diagnosis. Ind. Eng. Chem. Res. 2017, 56, 8906–8916. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Q.; Qin, S.J. Quality-relevant fault detection of nonlinear processes based on kernel concurrent canonical correlation analysis. Proc. Am. Control Conf. 2017, 5404–5409. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, Q.; Qin, S.J.; Chai, T. Dynamic concurrent kernel CCA for strip-thickness relevant fault diagnosis of continuous annealing processes. J. Process Control 2018, 67, 12–22. [Google Scholar] [CrossRef]
- Wang, G.; Jiao, J. Nonlinear Fault Detection Based on An Improved Kernel Approach. IEEE Access 2018, 6, 11017–11023. [Google Scholar] [CrossRef]
- Wang, L. Enhanced fault detection for nonlinear processes using modified kernel partial least squares and the statistical local approach. Can. J. Chem. Eng. 2018, 96, 1116–1126. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Quality-Driven Principal Component Analysis Combined With Kernel Least Squares for Multivariate Statistical Process Monitoring. IEEE Trans. Control Syst. Technol. 2018, 27, 2688–2695. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Relevant and independent multi-block approach for plant-wide process and quality-related monitoring based on KPCA and SVDD. ISA Trans. 2018, 73, 257–267. [Google Scholar] [CrossRef]
- Fezai, R.; Mansouri, M.; Taouali, O.; Harkat, M.F.; Bouguila, N. Online reduced kernel principal component analysis for process monitoring. J. Process Control 2018, 61, 1–11. [Google Scholar] [CrossRef]
- Fezai, R.; Ben Abdellafou, K.; Said, M.; Taouali, O. Online fault detection and isolation of an AIR quality monitoring network based on machine learning and metaheuristic methods. Int. J. Adv. Manuf. Technol. 2018, 99, 2789–2802. [Google Scholar] [CrossRef]
- Mansouri, M.; Baklouti, R.; Harkat, M.F.; Nounou, M.; Nounou, H.; Hamida, A.B. Kernel Generalized Likelihood Ratio Test for Fault Detection of Biological Systems. IEEE Trans. Nanobiosci. 2018, 17, 498–506. [Google Scholar] [CrossRef] [PubMed]
- Jaffel, I.; Taouali, O.; Harkat, M.F.; Messaoud, H. Fault detection and isolation in nonlinear systems with partial Reduced Kernel Principal Component Analysis method. Trans. Inst. Meas. Control 2018, 40, 1289–1296. [Google Scholar] [CrossRef]
- Lahdhiri, H.; Ben Abdellafou, K.; Taouali, O.; Mansouri, M.; Korbaa, O. New online kernel method with the Tabu search algorithm for process monitoring. Trans. Inst. Meas. Control 2018. [Google Scholar] [CrossRef]
- Tan, R.; Cao, Y. Deviation Contribution Plots of Multivariate Statistics. IEEE Trans. Ind. Inform. 2019, 15, 833–841. [Google Scholar] [CrossRef]
- He, F.; Wang, C.; Fan, S.K.S. Nonlinear fault detection of batch processes based on functional kernel locality preserving projections. Chemom. Intell. Lab. Syst. 2018, 183, 79–89. [Google Scholar] [CrossRef]
- Navi, M.; Meskin, N.; Davoodi, M. Sensor fault detection and isolation of an industrial gas turbine using partial adaptive KPCA. J. Process Control 2018, 64, 37–48. [Google Scholar] [CrossRef]
- Chakour, C.; Benyounes, A.; Boudiaf, M. Diagnosis of uncertain nonlinear systems using interval kernel principal components analysis: Application to a weather station. ISA Trans. 2018, 83, 126–141. [Google Scholar] [CrossRef]
- Deng, X.; Wang, L. Modified kernel principal component analysis using double-weighted local outlier factor and its application to nonlinear process monitoring. ISA Trans. 2018, 72, 218–228. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S.; Harris, C.J. Deep Principal Component Analysis Based on Layerwise Feature Extraction and Its Application to Nonlinear Process Monitoring. IEEE Trans. Control Syst. Technol. 2018, 27, 2526–2540. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S.; Harris, C.J. Nonlinear Process Fault Diagnosis Based on Serial Principal Component Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 560–572. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Sun, B.; Wang, L. Improved kernel fisher discriminant analysis for nonlinear process fault pattern recognition. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; pp. 33–37. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X.; Deng, X.; Cao, Y. Batch process fault detection and identification based on discriminant global preserving kernel slow feature analysis. ISA Trans. 2018, 79, 108–126. [Google Scholar] [CrossRef] [PubMed]
- Shang, J.; Chen, M.; Zhang, H. Fault detection based on augmented kernel Mahalanobis distance for nonlinear dynamic processes. Comput. Chem. Eng. 2018, 109, 311–321. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Parallel PCA–KPCA for nonlinear process monitoring. Control Eng. Pract. 2018, 80, 17–25. [Google Scholar] [CrossRef]
- Feng, L.; Di, T.; Zhang, Y. HSIC-based kernel independent component analysis for fault monitoring. Chemom. Intell. Lab. Syst. 2018, 178, 47–55. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, B. Incipient Fault Detection for Complex Industrial Processes with Stationary and Nonstationary Hybrid Characteristics. Ind. Eng. Chem. Res. 2018, 57. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, Y.; Guan, S.; Fu, Y.; Feng, L. Nonlinear process monitoring using kernel nonnegative matrix factorization. Can. J. Chem. Eng. 2018, 96, 554–563. [Google Scholar] [CrossRef]
- Ma, J.; Li, G.; Zhou, D. Fault prognosis technology for non-Gaussian and nonlinear processes based on KICA reconstruction. Can. J. Chem. Eng. 2018, 96, 515–520. [Google Scholar] [CrossRef]
- Lu, Q.; Jiang, B.; Gopaluni, R.B.; Loewen, P.D.; Braatz, R.D. Locality preserving discriminative canonical variate analysis for fault diagnosis. Comput. Chem. Eng. 2018, 117, 309–319. [Google Scholar] [CrossRef]
- Li, W.; Zhao, C.; Gao, F. Linearity Evaluation and Variable Subset Partition Based Hierarchical Process Modeling and Monitoring. IEEE Trans. Ind. Electron. 2018, 65, 2683–2692. [Google Scholar] [CrossRef]
- Chu, F.; Dai, W.; Shen, J.; Ma, X.; Wang, F. Online complex nonlinear industrial process operating optimality assessment using modified robust total kernel partial M-regression. Chin. J. Chem. Eng. 2018, 26, 775–785. [Google Scholar] [CrossRef]
- Zhai, L.; Jia, Q. Simultaneous fault detection and isolation using semi-supervised kernel nonnegative matrix factorization. Can. J. Chem. Eng. 2019, 1–10. [Google Scholar] [CrossRef]
- Fezai, R.; Mansouri, M.; Trabelsi, M.; Hajji, M.; Nounou, H.; Nounou, M. Online reduced kernel GLRT technique for improved fault detection in photovoltaic systems. Energy 2019, 179, 1133–1154. [Google Scholar] [CrossRef]
- Fazai, R.; Mansouri, M.; Abodayeh, K.; Nounou, H.; Nounou, M. Online reduced kernel PLS combined with GLRT for fault detection in chemical systems. Process Saf. Environ. Prot. 2019, 128, 228–243. [Google Scholar] [CrossRef]
- Deng, X.; Deng, J. Incipient Fault Detection for Chemical Processes Using Two-Dimensional Weighted SLKPCA. Ind. Eng. Chem. Res. 2019, 58, 2280–2295. [Google Scholar] [CrossRef]
- Cui, P.; Zhan, C.; Yang, Y. Improved nonlinear process monitoring based on ensemble KPCA with local structure analysis. Chem. Eng. Res. Des. 2019, 142, 355–368. [Google Scholar] [CrossRef]
- Lahdhiri, H.; Said, M.; Abdellafou, K.B.; Taouali, O.; Harkat, M.F. Supervised process monitoring and fault diagnosis based on machine learning methods. Int. J. Adv. Manuf. Technol. 2019, 102, 2321–2337. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Chang, Y.; Gao, F.; He, D. Performance-relevant kernel independent component analysis based operating performance assessment for nonlinear and non-Gaussian industrial processes. Chem. Eng. Sci. 2019, 209, 115167. [Google Scholar] [CrossRef]
- Liu, M.; Li, X.; Lou, C.; Jiang, J. A fault detection method based on CPSO-improved KICA. Entropy 2019, 21, 668. [Google Scholar] [CrossRef]
- Yu, J.; Wang, K.; Ye, L.; Song, Z. Accelerated Kernel Canonical Correlation Analysis with Fault Relevance for Nonlinear Process Fault Isolation. Ind. Eng. Chem. Res. 2019, 58, 18280–18291. [Google Scholar] [CrossRef]
- Guo, L.; Wu, P.; Gao, J.; Lou, S. Sparse Kernel Principal Component Analysis via Sequential Approach for Nonlinear Process Monitoring. IEEE Access 2019, 7, 47550–47563. [Google Scholar] [CrossRef]
- Wu, P.; Guo, L.; Lou, S.; Gao, J. Local and Global Randomized Principal Component Analysis for Nonlinear Process Monitoring. IEEE Access 2019, 7, 25547–25562. [Google Scholar] [CrossRef]
- Harkat, M.F.; Mansouri, M.; Nounou, M.; Nounou, H. Fault detection of uncertain nonlinear process using interval-valued data-driven approach. Chem. Eng. Sci. 2019, 205, 36–45. [Google Scholar] [CrossRef]
- Ma, L.; Dong, J.; Peng, K. A Novel Hierarchical Detection and Isolation Framework for Quality-Related Multiple Faults in Large-Scale Processes. IEEE Trans. Ind. Electron. 2019, 67, 1316–1327. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, X.; Zhang, Y.; Hou, C.; Li, C.; Xin, Z. Nonlinear Process Monitoring Based on Global Preserving Unsupervised Kernel Extreme Learning Machine. IEEE Access 2019, 7, 106053–106064. [Google Scholar] [CrossRef]
- Peng, K.; Ren, Z.; Dong, J.; Ma, L. A New Hierarchical Framework for Detection and Isolation of Multiple Faults in Complex Industrial Processes. IEEE Access 2019, 7, 12006–12015. [Google Scholar] [CrossRef]
- Yan, S.; Huang, J.; Yan, X. Monitoring of quality-relevant and quality-irrelevant blocks with characteristic-similar variables based on self-organizing map and kernel approaches. J. Process Control 2019, 73, 103–112. [Google Scholar] [CrossRef]
- Huang, K.; Wen, H.; Ji, H.; Cen, L.; Chen, X.; Yang, C. Nonlinear process monitoring using kernel dictionary learning with application to aluminum electrolysis process. Control Eng. Pract. 2019, 89, 94–102. [Google Scholar] [CrossRef]
- Zhou, Z.; Du, N.; Xu, J.; Li, Z.; Wang, P.; Zhang, J. Randomized Kernel Principal Component Analysis for Modeling and Monitoring of Nonlinear Industrial Processes with Massive Data. Ind. Eng. Chem. Res. 2019, 58, 10410–10417. [Google Scholar] [CrossRef]
- Deng, J.; Deng, X.; Wang, L.; Zhang, X. Nonlinear Process Monitoring Based on Multi-block Dynamic Kernel Principal Component Analysis. In Proceedings of the 2018 13th World Congress on Intelligent Control and Automation (WCICA), Changsha China, 4–8 July 2018; pp. 1058–1063. [Google Scholar] [CrossRef]
- Wang, G.; Jiao, J.; Yin, S. Efficient Nonlinear Fault Diagnosis Based on Kernel Sample Equivalent Replacement. IEEE Trans. Ind. Inform. 2019, 15, 2682–2690. [Google Scholar] [CrossRef]
- Zhu, W.; Zhen, W.; Jiao, J. Partial Derivate Contribution Plot Based on KPLS-KSER for Nonlinear Process Fault Diagnosis. In Proceedings of the 34th Youth Academic Annual Conference of Chinese Association of Automation, Jinzhou, China, 6–8 June 2019; pp. 735–740. [Google Scholar] [CrossRef]
- Xiao, S. Locality Kernel Canonical Variate Analysis for Fault Detection. J. Phys. Conf. Ser. 2019, 1284, 012003. [Google Scholar] [CrossRef]
- Xiao, S. Kernel Canonical Variate Dissimilarity Analysis for Fault Detection. Chin. Control Conf. 2019, 1284, 6871–6876. [Google Scholar] [CrossRef]
- Shang, L.; Yan, Z.; Qiu, A.; Li, F.; Zhou, X. Efficient recursive kernel principal component analysis for nonlinear time-varying processes monitoring. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3057–3062. [Google Scholar] [CrossRef]
- Geng, Z.; Liu, F.; Han, Y.; Zhu, Q.; He, Y. Fault Diagnosis of Chemical Processes Based on a novel Adaptive Kernel Principal Component Analysis. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu-shi, Japan, 9–12 June 2019; pp. 1495–1500. [Google Scholar]
- Md Nor, N.; Hussain, M.A.; Che Hassan, C.R. Multi-scale kernel Fisher discriminant analysis with adaptive neuro-fuzzy inference system (ANFIS) in fault detection and diagnosis framework for chemical process systems. Neural Comput. Appl. 2019, 9. [Google Scholar] [CrossRef]
- Tan, R.; Cong, T.; Thornhill, N.F.; Ottewill, J.R.; Baranowski, J. Statistical Monitoring of Processes with Multiple Operating Modes. IFAC-PapersOnLine 2019, 52, 635–642. [Google Scholar] [CrossRef]
- Tan, R.; Ottewill, J.R.; Thornhill, N.F. Nonstationary Discrete Convolution Kernel for Multimodal Process Monitoring. IEEE Trans. Neural Netw. Learn. Syst. 2019, 1–12. [Google Scholar] [CrossRef]
- Yao, Y.; Gao, F. A survey on multistage/multiphase statistical modeling methods for batch processes. Annu. Rev. Control 2009, 33, 172–183. [Google Scholar] [CrossRef]
- Rendall, R.; Chiang, L.H.; Reis, M.S. Data-driven methods for batch data analysis—A critical overview and mapping on the complexity scale. Comput. Chem. Eng. 2019, 124, 1–13. [Google Scholar] [CrossRef]
- Larimore, W.E. Canonical variate analysis in identification, filtering, and adaptive control. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; Volume 2, pp. 596–604. [Google Scholar] [CrossRef]
- Wiskott, L.; Sejnowski, T.J. Slow feature analysis: Unsupervised learning of invariances. Neural Comput. 2002, 14, 715–770. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Huang, D.; Zhu, X.; Yang, F.; Braatz, R.D. Canonical variate analysis-based contributions for fault identification. J. Process Control 2015, 26, 17–25. [Google Scholar] [CrossRef]
- Krzanowski, W.J. Between-Groups Comparison of Principal Components. J. Am. Stat. Assoc. 1979, 74, 703–707. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Process monitoring based on independent Component Analysis-Principal Component Analysis (ICA-PCA) and similarity factors. Ind. Eng. Chem. Res. 2007, 46, 2054–2063. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, Y. Fault Detection and Diagnosis of Nonlinear Processes Using Improved Kernel Independent Component Analysis (KICA) and Support Vector Machine (SVM). Ind. Eng. Chem. Res. 2008, 47, 6961–6971. [Google Scholar] [CrossRef]
- Gönen, M.; Alpaydın, E. Multiple Kernel Learning Algorithms. J. Mach. Learn. Res. 2011, 12, 2211–2268. [Google Scholar]
- Yu, J.; Rashid, M.M. A novel dynamic bayesian network-based networked process monitoring approach for fault detection, propagation identification, and root cause diagnosis. AIChE J. 2013, 59, 2348–2365. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2008. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Kano, M.; Nagao, K.; Ohno, H.; Hasebe, S.; Hashimoto, I. Dissimilarity of Process Data for Statistical Process Monitoring. IFAC Proc. Vol. 2000, 33, 231–236. [Google Scholar] [CrossRef]
- Rashid, M.M.; Yu, J. A new dissimilarity method integrating multidimensional mutual information and independent component analysis for non-Gaussian dynamic process monitoring. Chemom. Intell. Lab. Syst. 2012, 115, 44–58. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Statistics pattern analysis: A new process monitoring framework and its application to semiconductor batch processes. AIChE J. 2011, 57, 107–121. [Google Scholar] [CrossRef]
- Genton, M.G. Classes of Kernels for Machine Learning: A Statistics Perspective. J. Mach. Learn. Res. 2001, 2, 299–312. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Pilario, K.E.S. 2019. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/69941-kernel-pca-contour-maps-for-fault-detection (accessed on 25 April 2019).
- Halim, S.; Halim, F. Competitive Programming 3: The New Lower Bound of Progamming Contests; Lulu Press: Morrisville, NC, USA, 2013. [Google Scholar]
- Baudat, G.; Anouar, F. Feature vector selection and projection using kernels. Neurocomputing 2003, 55, 21–38. [Google Scholar] [CrossRef]
- Yang, T.; Li, Y.F.; Mahdavi, M.; Jin, R.; Zhou, Z.H. Nyström Method vs Random Fourier Features: A Theoretical and Empirical Comparison. Adv. NIPS 2012, 485–493. [Google Scholar]
- Saul, L.K.; Roweis, S. Think Globally, Fit Locally: Unsupervised Learning of Low Dimensional Manifolds. J. Mach. Learn. Res. 2003, 4, 119–155. [Google Scholar] [CrossRef][Green Version]
- Van Der Maaten, L.J.P.; Postma, E.O.; Van Den Herik, H.J. Dimensionality Reduction: A Comparative Review. J. Mach. Learn. Res. 2009, 10, 1–41. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality Preserving Projections. In Proceedings of the16th International Conference Neural Information Processing Systems, Whistler, BC, Canada, 9–11 December 2003; pp. 153–160. [Google Scholar]
- Hu, K.; Yuan, J. Multivariate statistical process control based on multiway locality preserving projections. J. Process Control 2008, 18, 797–807. [Google Scholar] [CrossRef]
- Ham, J.; Lee, D.D.; Mika, S.; Schölkopf, B. A kernel view of the dimensionality reduction of manifolds. In Proceedings of the 21st International Machine Learning Conference (ICML ’04), Banff, AB, Canada, 4–8 July 2004; Volume 12, p. 47. [Google Scholar] [CrossRef]
- Hoegaerts, L.; De Lathauwer, L.; Goethals, I.; Suykens, J.A.K.; Vandewalle, J.; De Moor, B. Efficiently updating and tracking the dominant kernel principal components. Neural Netw. 2007, 20, 220–229. [Google Scholar] [CrossRef]
- Hall, P.; Marshall, D.; Martin, R. Adding and subtracting eigenspaces with eigenvalue decomposition and singular value decomposition. Image Vis. Comput. 2002, 20, 1009–1016. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, B. Distributed monitoring for large-scale processes based on multivariate statistical analysis and Bayesian method. J. Process Control 2016, 46, 75–83. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Plant-wide process monitoring based on mutual information-multiblock principal component analysis. ISA Trans. 2014, 53, 1516–1527. [Google Scholar] [CrossRef]
- Melis, G. Dissecting the Winning Solution of the HiggsML Challenge. J. Mach. Learn. Res. Work. Conf. Proc. 2015, 42, 57–67. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2006; ACM Press: New York, NY, USA, 2016; Volume 19, pp. 785–794. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Lucke, M.; Stief, A.; Chioua, M.; Ottewill, J.R.; Thornhill, N.F. Fault detection and identification combining process measurements and statistical alarms. Control Eng. Pract. 2020, 94, 104195. [Google Scholar] [CrossRef]
- Ruiz-Cárcel, C.; Jaramillo, V.H.; Mba, D.; Ottewill, J.R.; Cao, Y. Combination of process and vibration data for improved condition monitoring of industrial systems working under variable operating conditions. Mech. Syst. Signal Process. 2015, 66–67, 699–714. [Google Scholar] [CrossRef]
- Stief, A.; Tan, R.; Cao, Y.; Ottewill, J.R.; Thornhill, N.F.; Baranowski, J. A heterogeneous benchmark dataset for data analytics: Multiphase flow facility case study. J. Process Control 2019, 79, 41–55. [Google Scholar] [CrossRef]
- Vachtsevanos, G.; Lewis, F.L.; Roemer, M.; Hess, A.; Wu, B. Intelligent Fault Diagnosis and Prognosis for Engineering Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ge, Z. Distributed predictive modeling framework for prediction and diagnosis of key performance index in plant-wide processes. J. Process Control 2018, 65, 107–117. [Google Scholar] [CrossRef]






| Year | Reference | Remark |
|---|---|---|
| 2012 | Qin [25] | Discusses the general issues and explains how basic data-driven process monitoring (MSPM) methods work. |
| 2012 | MacGregor and Cinar [26] | Reviews data-driven models not only in process monitoring, but also in optimization and control. |
| 2013 | Ge et al. [6] | Reviews data-driven process monitoring using recent MSPM tools and discusses more recent issues. |
| 2014 | Yin et al. [27] | Reviews data-driven process monitoring but from an application point of view; it also provides a basic monitoring framework. |
| 2014 | Ding et al. [28] | Reviews data-driven process monitoring methods with specific focus on dynamic processes. |
| 2014 | Qin [15] | Gives an overview of process data analytics, in which process monitoring is only one of the applications. |
| 2015 | Yin et al. [29] | Reviews data-driven methods not only in industrial processes, but also in smart grids, energy, and power systems, etc. |
| 2015 | Severson et al. [30] | Gives an overview of process monitoring in a larger context than just data-driven methods, and advocates hybrid methods. |
| 2016 | Tidriri et al. [31] | Compares physics-driven and data-driven process monitoring methods, and reviews recent hybrid approaches. |
| 2016 | Yin and Hou [32] | Reviews process monitoring methods that used support vector machines (SVM) for electro-mechanical systems. |
| 2017 | Lee et al. [9] | Reviews recent progresses and implications of machine learning to the field of PSE. |
| 2017 | Ge et al. [11] | Reviews data-driven methods in the process industries from the point of view of machine learning. |
| 2017 | Ge [33] | Reviews data-driven process monitoring methods with specific focus on dealing with the issues on the plant-wide scale. |
| 2017 | Wang et al. [34] | Reviews MSPM algorithms from 2008 to 2017, including both papers and patents in Web of Science, IEEE Xplore, and the China National Knowledge Infrastructure (CNKI) databases. |
| 2018 | Md Nor et al. [35] | Reviews data-driven process monitoring methods with guidelines for choosing which MSPM and machine learning tools to use. |
| 2018 | Alauddin et al. [36] | Gives a bibliometric review and analysis of the literature on data-driven process monitoring. |
| 2019 | Qin and Chiang [16] | Reviews machine learning and AI in PSE and advocates the integration of data analytics to chemical engineering curricula. |
| 2019 | Jiang et al. [37] | Reviews data-driven process monitoring methods with specific focus on distributed MSPM tools for plant-wide monitoring. |
| 2019 | Quiones-Grueiro et al. [38] | Reviews data-driven process monitoring methods with specific focus on handling the multi-mode issue. |
| This paper | Reviews data-driven process monitoring methods that applied kernel methods for feature extraction. |
| Label | Name of Issue | No. of Papers That Addressed It |
|---|---|---|
| A | Batch process monitoring | 30 |
| B | Dynamics, multi-scale, and multi-mode monitoring | 72 |
| C | Fault diagnosis in the kernel feature space | 100 |
| D | Handling non-Gaussian noise and outliers | 41 |
| E | Improved sensitivity and incipient fault detection | 39 |
| F | Quality-relevant monitoring | 37 |
| G | Kernel design and kernel parameter selection | 30 |
| H | Fast computation of kernel features | 34 |
| I | Manifold learning and local structure analysis | 20 |
| J | Time-varying behavior and adaptive kernel computation | 26 |
| K | Multi-block and distributed monitoring | 15 |
| L | Advanced methods: Ensembles and Deep Learning | 8 |
| Year | Reference | Kernelized | Issues Addressed | Case Studies | Kernel/s Used | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method/s | A | B | C | D | E | F | G | H | I | J | K | L | |||||
| 1 | 2004 | Lee et al. [24] | PCA | First application | NE, WWTP | RBF | |||||||||||
| 2 | 2004 | Lee et al. [71] | PCA | ✓ | PenSim | POLY | |||||||||||
| 3 | 2004 | Choi and Lee [85] | PCA | ✓ | NE, WWTP | RBF | |||||||||||
| 4 | 2005 | Choi et al. [86] | PCA | ✓ | NE, CSTR | RBF | |||||||||||
| 5 | 2005 | Cho et al. [87] | PCA | ✓ | NE, CSTR | RBF | |||||||||||
| 6 | 2006 | Yoo and Lee [88] | PCA | ✓ | ✓ | NE, WWTP | RBF | ||||||||||
| 7 | 2006 | Lee et al. [89] | PCA, PLS | ✓ | BAFP | RBF | |||||||||||
| 8 | 2006 | Zhang et al. [90] | ICA | ✓ | FCCU | - | |||||||||||
| 9 | 2006 | Deng and Tian [91] | PCA | ✓ | ✓ | CSTR | RBF | ||||||||||
| 10 | 2007 | Zhang and Qin [72] | PCA, ICA | ✓ | ✓ | NPP | RBF | ||||||||||
| 11 | 2007 | Cho [74] | FDA | ✓ | ✓ | PCBP, PenSim | POLY | ||||||||||
| 12 | 2007 | Cho [92] | FDA | ✓ | TEP | RBF | |||||||||||
| 13 | 2007 | Sun et al. [93] | PCA | ✓ | ✓ | NE, Rot. Machines | RBF | ||||||||||
| 14 | 2008 | Choi et al. [94] | PCA | ✓ | ✓ | CSTR | RBF | ||||||||||
| 15 | 2008 | Tian and Deng [95] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 16 | 2008 | Wang et al. [96] | PCA | ✓ | ✓ | NPP | RBF | ||||||||||
| 17 | 2008 | Lee et al. [97] | ICA | ✓ | NE, TEP | RBF | |||||||||||
| 18 | 2008 | Cui et al. [98] | FDA | ✓ | NE, TEP | RBF, POLY | |||||||||||
| 19 | 2008 | Cui et al. [99] | SDA | ✓ | TEP | POLY | |||||||||||
| 20 | 2008 | Zhang and Qin [100] | ICA | ✓ | ✓ | TEP, WWTP, PenSim | RBF | ||||||||||
| 21 | 2008 | Lu and Wang [101] | PLS | ✓ | ✓ | ✓ | TEP | - | |||||||||
| 22 | 2008 | He et al. [102] | FDA | ✓ | ✓ | TEP | RBF | ||||||||||
| 23 | 2008 | Cho [103] | FDA | ✓ | TEP | POLY | |||||||||||
| 24 | 2008 | Li and Cui [104] | SDA | ✓ | ✓ | TEP | POLY | ||||||||||
| 25 | 2009 | Li and Cui [105] | FDA | ✓ | ✓ | ✓ | TEP, PenSim | POLY, COS | |||||||||
| 26 | 2009 | Zhang [106] | ICA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 27 | 2009 | Zhang and Zhang [107] | ICA, PLS | ✓ | ✓ | TEP, PenSim | RBF | ||||||||||
| 28 | 2009 | Shao et al. [108] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 29 | 2009 | Shao and Rong [109] | MVU | ✓ | ✓ | TEP | Manifold | ||||||||||
| 30 | 2009 | Shao et al. [110] | LPP | ✓ | ✓ | NE, TEP | Manifold | ||||||||||
| 31 | 2009 | Tian et al. [73] | ICA | ✓ | ✓ | ✓ | PenSim | RBF, POLY | |||||||||
| 32 | 2009 | Liu et al. [111] | PCA | ✓ | ✓ | ✓ | NE, BDP | RBF | |||||||||
| 33 | 2009 | Ge et al. [112] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 34 | 2009 | Zhao et al. [113] | DISSIM | ✓ | NE, TEP | RBF | |||||||||||
| 35 | 2009 | Zhao et al. [114] | ICA | ✓ | ✓ | ✓ | TTP, PenSim | RBF | |||||||||
| 36 | 2010 | Jia et al. [115] | PCA | ✓ | ✓ | NE, PenSim | RBF | ||||||||||
| 37 | 2010 | Cheng et al. [116] | PCA | ✓ | ✓ | ✓ | NE, TEP | RBF | |||||||||
| 38 | 2010 | Alcala and Qin [117] | PCA | ✓ | CSTR | RBF | |||||||||||
| 39 | 2010 | Zhu and Song [118] | FDA | ✓ | TEP | RBF | |||||||||||
| 40 | 2010 | Zhang et al. [119] | PLS | ✓ | ✓ | CAP | RBF | ||||||||||
| 41 | 2010 | Zhang et al. [120] | PCA | ✓ | ✓ | ✓ | NE, PenSim | RBF | |||||||||
| 42 | 2010 | Xu and Hu [121] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 43 | 2010 | Ge and Song [122] | PCA | ✓ | TEP | RBF | |||||||||||
| 44 | 2010 | Wang and Shi [123] | ICA (CCA) | ✓ | WWTP, TEP | RBF | |||||||||||
| 45 | 2010 | Sumana et al. [124] | SDA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 46 | 2011 | Sumana et al. [125] | PCA | ✓ | TEP | RBF | |||||||||||
| 47 | 2011 | Khediri et al. [126] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 48 | 2011 | Zhang and Ma [127] | PCA, PLS | ✓ | CAP, EFMF | RBF | |||||||||||
| 49 | 2011 | Zhang and Hu [128] | PLS | ✓ | ✓ | CAP, PenSim | RBF | ||||||||||
| 50 | 2011 | Zhang and Hu [129] | PLS | ✓ | ✓ | ✓ | NE, PenSim, EFMF | RBF | |||||||||
| 51 | 2011 | Zhu and Song [130] | FDA | ✓ | TEP | RBF | |||||||||||
| 52 | 2011 | Yu [75] | FDA | ✓ | ✓ | ✓ | PenSim | RBF | |||||||||
| 53 | 2012 | Khediri et al. [131] | K-means | ✓ | NE, SEP | RBF | |||||||||||
| 54 | 2012 | Rashid and Yu [82] | ICA | ✓ | ✓ | ✓ | ✓ | PenSim | RBF | ||||||||
| 55 | 2012 | Zhang et al. [132] | PCA | ✓ | ✓ | CAP, PenSim | RBF | ||||||||||
| 56 | 2012 | Zhang and Ma [133] | ICA | ✓ | ✓ | ✓ | CAP | RBF | |||||||||
| 57 | 2012 | Zhang et al. [134] | PCA | ✓ | ✓ | NE, TEP, EFMF | RBF | ||||||||||
| 58 | 2012 | Zhang et al. [135] | PLS | ✓ | ✓ | ✓ | ✓ | PenSim | - | ||||||||
| 59 | 2012 | Yu [136] | GMM | ✓ | ✓ | ✓ | WWTP | RBF | |||||||||
| 60 | 2012 | Guo et al. [137] | PCA | ✓ | ✓ | TEP | WAV | ||||||||||
| 61 | 2012 | Jia et al. [84] | PCA | ✓ | NE, PenSim | RBF, POLY, SIG | |||||||||||
| 62 | 2012 | Sumana et al. [138] | PCA | ✓ | TEP | POLY | |||||||||||
| 63 | 2012 | Wang et al. [139] | PCA | ✓ | ✓ | ✓ | PenSim | POLY | |||||||||
| 64 | 2013 | Liu et al. [140] | ICA | ✓ | ✓ | ✓ | CLG | RBF | |||||||||
| 65 | 2013 | Peng et al. [141] | T-PLS | ✓ | NE, TEP, HSMP | RBF | |||||||||||
| 66 | 2013 | Peng et al. [79] | T-PLS | ✓ | ✓ | HSMP | RBF | ||||||||||
| 67 | 2013 | Wang et al. [142] | PCA | ✓ | ✓ | ✓ | ✓ | PenSim | POLY | ||||||||
| 68 | 2013 | Jiang and Yan [143] | PCA | ✓ | ✓ | NE, CSTR, TEP | RBF | ||||||||||
| 69 | 2013 | Jiang and Yan [144] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 70 | 2013 | Zhang et al. [145] | ICA | ✓ | ✓ | CAP | RBF | ||||||||||
| 71 | 2013 | Zhang et al. [146] | PLS | ✓ | ✓ | NE, EFMF | RBF | ||||||||||
| 72 | 2013 | Zhang et al. [147] | PCA | ✓ | ✓ | PenSim, EFMF | - | ||||||||||
| 73 | 2013 | Zhang et al. [76] | VCA | ✓ | ✓ | EFMF | RBF | ||||||||||
| 74 | 2013 | Deng and Tian [148] | PCA | ✓ | ✓ | ✓ | NE, TEP | RBF | |||||||||
| 75 | 2013 | Deng and Tian [149] | LPP | ✓ | ✓ | CSTR | RBF | ||||||||||
| 76 | 2013 | Deng et al. [150] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 77 | 2013 | Rong et al. [151] | LPP, FDA | ✓ | ✓ | ✓ | TEP, WWTP | RBF | |||||||||
| 78 | 2013 | Hu et al. [152] | PLS | ✓ | ✓ | PP, PenSim | RBF | ||||||||||
| 79 | 2013 | Hu et al. [153] | PLS | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 80 | 2014 | Fan and Wang [66] | ICA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 81 | 2014 | Fan et al. [154] | ICA | ✓ | ✓ | ✓ | ✓ | NE, TEP | RBF | ||||||||
| 82 | 2014 | Zhang et al. [155] | ICA | ✓ | ✓ | EFMF | - | ||||||||||
| 83 | 2014 | Zhang and Li [156] | PCA | ✓ | ✓ | EFMF | RBF | ||||||||||
| 84 | 2014 | Cai et al. [157] | ICA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 85 | 2014 | Wang and Shi [158] | PLS | ✓ | ✓ | TEP | - | ||||||||||
| 86 | 2014 | Elshenawy and Mohamed [159] | PCA | ✓ | TEP | RBF | |||||||||||
| 87 | 2014 | Mori and Yu [160] | PCA, ICA, PLS | ✓ | ✓ | ✓ | PenSim | RBF | |||||||||
| 88 | 2014 | Castillo et al. [161] | PCA | ✓ | Air Heater | RBF | |||||||||||
| 89 | 2014 | Vitale et al. [69] | PCA, PLS, FDA | ✓ | ✓ | NE, PP, DP | RBF, POLY | ||||||||||
| 90 | 2014 | Peng et al. [162] | PCA | ✓ | ✓ | CSTR | RBF | ||||||||||
| 91 | 2014 | Zhao and Xue [163] | T-PLS | ✓ | ✓ | ✓ | TEP | RBF+POLY | |||||||||
| 92 | 2014 | Godoy et al. [164] | PLS | ✓ | ✓ | ✓ | NE | RBF | |||||||||
| 93 | 2014 | Kallas et al. [165] | PCA | ✓ | NE, CSTR | RBF | |||||||||||
| 94 | 2015 | Ciabattoni et al. [166] | CVA | ✓ | Microgrid | RBF | |||||||||||
| 95 | 2015 | Vitale et al. [81] | PCA | ✓ | ✓ | NE, DP, RCP | RBF, POLY | ||||||||||
| 96 | 2015 | Li and Yang [167] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 97 | 2015 | Liu and Zhang [168] | PLS | ✓ | ✓ | NE, PenSim | RBF | ||||||||||
| 98 | 2015 | Md Nor et al. [169] | FDA | ✓ | ✓ | TEP | - | ||||||||||
| 99 | 2015 | Yao and Wang [170] | PCA | ✓ | ✓ | PenSim | RBF | ||||||||||
| 100 | 2015 | Wang and Yao [171] | PCA | ✓ | ✓ | NE, SEP | RBF | ||||||||||
| 101 | 2015 | Huang et al. [172] | CVA | ✓ | ✓ | TEP | RBF | ||||||||||
| 102 | 2015 | Zhang et al. [173] | PLS | ✓ | NE, EFMF | RBF | |||||||||||
| 103 | 2015 | Zhang et al. [174] | SFA | ✓ | NE, TEP | RBF | |||||||||||
| 104 | 2015 | Zhang et al. [175] | SFA, FDA | ✓ | CSTR | RBF | |||||||||||
| 105 | 2015 | Zhang et al. [176] | C-PLS | ✓ | PenSim | - | |||||||||||
| 106 | 2015 | Samuel and Cao [177] | CVA | ✓ | TEP | RBF | |||||||||||
| 107 | 2015 | Samuel and Cao [178] | CVA | ✓ | TEP | RBF | |||||||||||
| 108 | 2015 | Chakour et al. [179] | PCA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 109 | 2015 | Jiang and Yan [180] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 110 | 2015 | Cai et al. [181] | CCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 111 | 2015 | Luo et al. [182] | GLPP | ✓ | ✓ | NE, TEP | RBF, HK | ||||||||||
| 112 | 2015 | Tang et al. [77] | VCA | ✓ | ✓ | ✓ | PenSim | RBF | |||||||||
| 113 | 2015 | Bernal de Lazaro et al. [183] | PCA, FDA | ✓ | ✓ | TEP | RBF | ||||||||||
| 114 | 2016 | Bernal de Lazaro et al. [184] | PCA, ICA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 115 | 2016 | Ji et al. [185] | PCA | ✓ | NE | RBF | |||||||||||
| 116 | 2016 | Xu et al. [186] | PCA | ✓ | ✓ | ✓ | NE, TEP | - | |||||||||
| 117 | 2016 | Luo et al. [187] | GLPP | ✓ | NE, TEP | RBF | |||||||||||
| 118 | 2016 | Zhang et al. [188] | ICA | ✓ | ✓ | TEP | - | ||||||||||
| 119 | 2016 | Taouali et al. [189] | PCA | ✓ | CSTR | RBF | |||||||||||
| 120 | 2016 | Fazai et al. [190] | PCA | ✓ | CSTR, TEP | RBF | |||||||||||
| 121 | 2016 | Jaffel et al. [191] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 122 | 2016 | Mansouri et al. [192] | PCA | ✓ | NE, CSTR | - | |||||||||||
| 123 | 2016 | Botre et al. [193] | PLS | ✓ | CSTR | - | |||||||||||
| 124 | 2016 | Samuel and Cao [194] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 125 | 2016 | Ge et al. [195] | FDA | ✓ | CSTH, TEP | RBF | |||||||||||
| 126 | 2016 | Jia et al. [196] | PLS | ✓ | ✓ | ✓ | NE, HGPWLTP | RBF | |||||||||
| 127 | 2016 | Jia and Zhang [197] | PLS | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 128 | 2016 | Jiang et al. [198] | PCA | ✓ | ✓ | TEP, CSTR | RBF | ||||||||||
| 129 | 2016 | Peng et al. [199] | PLS, Fuzzy C-means | ✓ | ✓ | ✓ | ✓ | HSMP | RBF | ||||||||
| 130 | 2016 | Xie et al. [200] | PCA | ✓ | ✓ | NE, BDP | RBF | ||||||||||
| 131 | 2016 | Wang et al. [201] | PCR | ✓ | NE | RBF | |||||||||||
| 132 | 2016 | Huang and Yan [202] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 133 | 2016 | Xiao and Zhang [203] | PCA, ICA | ✓ | ✓ | TEP | RBF | ||||||||||
| 134 | 2016 | Feng et al. [204] | FDA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 135 | 2016 | Sheng et al. [205] | C-PLS | ✓ | NE, TEP | RBF | |||||||||||
| 136 | 2016 | Zhang et al. [206] | PLS, PCA | ✓ | ✓ | ✓ | CAP | RBF | |||||||||
| 137 | 2017 | Jaffel et al. [207] | PCA | ✓ | ✓ | CSTR, TEP | RBF | ||||||||||
| 138 | 2017 | Lahdhiri et al. [208] | PCA | ✓ | ✓ | NE, CSTR, AIRLOR | RBF | ||||||||||
| 139 | 2017 | Lahdhiri et al. [209] | PCA | ✓ | ✓ | NE, CSTR | RBF | ||||||||||
| 140 | 2017 | Mansouri et al. [210] | PLS | ✓ | ✓ | CSEC, GCND | RBF | ||||||||||
| 141 | 2017 | Mansouri et al. [211] | PCA | ✓ | CSEC | - | |||||||||||
| 142 | 2017 | Sheriff et al. [212] | PCA | ✓ | CSTR | RBF | |||||||||||
| 143 | 2017 | Cai et al. [213] | ICA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 144 | 2017 | Zhang et al. [214] | ECA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 145 | 2017 | Zhang et al. [215] | SFA | ✓ | ✓ | ✓ | NE, PenSim | RBF | |||||||||
| 146 | 2017 | Zhang and Tian [216] | SFA | ✓ | ✓ | PenSim | POLY | ||||||||||
| 147 | 2017 | Zhang et al. [217] | PCA | ✓ | EFMF | - | |||||||||||
| 148 | 2017 | Zhang et al. [218] | PCA, LLE | ✓ | EFMF | - | |||||||||||
| 149 | 2017 | Zhang et al. [219] | PCA | ✓ | NE, SEP | RBF | |||||||||||
| 150 | 2017 | Deng et al. [220] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 151 | 2017 | Deng et al. [221] | PCA | ✓ | ✓ | NE, CSTR | RBF | ||||||||||
| 152 | 2017 | Deng et al. [222] | PCA, FDA | ✓ | ✓ | NE, CSTR | RBF | ||||||||||
| 153 | 2017 | Tan et al. [223] | CVA | ✓ | MFF | - | |||||||||||
| 154 | 2017 | Shang et al. [224] | CVA | ✓ | ✓ | CSTR | RBF | ||||||||||
| 155 | 2017 | Li et al. [225] | DLV | ✓ | HSMP | RBF | |||||||||||
| 156 | 2017 | Wang and Jiao [226] | LS | ✓ | NE, TEP | RBF | |||||||||||
| 157 | 2017 | Wang et al. [227] | DD | ✓ | NE, TEP | RBF | |||||||||||
| 158 | 2017 | Wang et al. [228] | EDA | ✓ | ✓ | PenSim | RBF | ||||||||||
| 159 | 2017 | Jiao et al. [229] | PLS | ✓ | NE, TEP | RBF | |||||||||||
| 160 | 2017 | Huang and Yan [230] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 161 | 2017 | Yi et al. [231] | PLS | ✓ | ✓ | TEP, AEP | - | ||||||||||
| 162 | 2017 | Md Nor et al. [232] | FDA | ✓ | ✓ | TEP | RBF | ||||||||||
| 163 | 2017 | Du et al. [233] | ICA | ✓ | EFMF | - | |||||||||||
| 164 | 2017 | Zhang and Zhao [234] | PCA, Fuzzy C-means | ✓ | ✓ | TEP, MFF | RBF | ||||||||||
| 165 | 2017 | Zhou et al. [235] | RPLVR | ✓ | ✓ | NE, TEP | - | ||||||||||
| 166 | 2017 | Gharahbagheri et al. [236] | PCA | ✓ | DTS, FCCU, TEP | RBF | |||||||||||
| 167 | 2017 | Gharahbagheri et al. [237] | PCA | ✓ | NE, FCCU, TEP | RBF | |||||||||||
| 168 | 2017 | Fu et al. [68] | PCA, PLS | ✓ | NE, GMP, BDP, Mixing | RBF | |||||||||||
| 169 | 2017 | Galiaskarov et al. [238] | FDA | ✓ | ✓ | Pyrolysis gas furnace | POLY | ||||||||||
| 170 | 2017 | Zhu et al. [239] | ICA | ✓ | ✓ | ✓ | TEP | RBF, POLY, SIG | |||||||||
| 171 | 2017 | Zhu et al. [240] | CCA | ✓ | TEP | RBF | |||||||||||
| 172 | 2018 | Liu et al. [241] | CCA | ✓ | ✓ | ✓ | ✓ | CAP | RBF | ||||||||
| 173 | 2018 | Wang and Jiao [242] | PLS | ✓ | NE, TEP | RBF | |||||||||||
| 174 | 2018 | Wang [243] | PLS | ✓ | ✓ | NE, CSTR | RBF | ||||||||||
| 175 | 2018 | Huang and Yan [244] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 176 | 2018 | Huang and Yan [245] | PCA | ✓ | ✓ | ✓ | NE, TEP, IPOP | RBF | |||||||||
| 177 | 2018 | Fezai et al. [246] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 178 | 2018 | Fezai et al. [247] | PCA | ✓ | ✓ | ✓ | ✓ | AIRLOR | RBF | ||||||||
| 179 | 2018 | Mansouri et al. [248] | PCA | ✓ | ✓ | NE, CSEC | RBF | ||||||||||
| 180 | 2018 | Jaffel et al. [249] | PCA | ✓ | ✓ | ✓ | CSTR | RBF | |||||||||
| 181 | 2018 | Lahdhiri et al. [250] | PCA | ✓ | ✓ | ✓ | NE, TEP | RBF | |||||||||
| 182 | 2018 | Tan and Cao [251] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 183 | 2018 | He et al. [252] | LPP | ✓ | ✓ | ✓ | PenSim, HSMP | RBF | |||||||||
| 184 | 2018 | Navi et al. [253] | PCA | ✓ | ✓ | ✓ | IGT | RBF | |||||||||
| 185 | 2018 | Chakour et al. [254] | PCA | ✓ | TEP, Weather station | RBF | |||||||||||
| 186 | 2018 | Deng and Wang [255] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 187 | 2018 | Deng et al. [256] | PCA | ✓ | ✓ | ✓ | NE, TEP | RBF, POLY | |||||||||
| 188 | 2018 | Deng et al. [257] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 189 | 2018 | Deng et al. [258] | FDA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 190 | 2018 | Zhang et al. [259] | SFA | ✓ | ✓ | ✓ | NE, CSTR | RBF | |||||||||
| 191 | 2018 | Shang et al. [260] | AMD | ✓ | NE, TEP | POLY | |||||||||||
| 192 | 2018 | Jiang and Yan [261] | PCA | ✓ | NE, CSTR | - | |||||||||||
| 193 | 2018 | Feng et al. [262] | ICA | ✓ | ✓ | EFMF | RBF | ||||||||||
| 194 | 2018 | Zhao and Huang [263] | PCA, DISSIM | ✓ | TPP, CPP | RBF | |||||||||||
| 195 | 2018 | Zhai et al. [264] | NNMF | ✓ | PenSim | - | |||||||||||
| 196 | 2018 | Ma et al. [265] | ICA | ✓ | ✓ | TEP | RBF | ||||||||||
| 197 | 2018 | Lu et al. [266] | CVA, LPP, FDA | ✓ | ✓ | ✓ | TEP | HK | |||||||||
| 198 | 2018 | Li et al. [267] | PCA | ✓ | ✓ | NE, CPP | - | ||||||||||
| 199 | 2018 | Chu et al. [268] | PLS | ✓ | ✓ | DMCPP | RBF | ||||||||||
| 200 | 2019 | Zhai and Jia [269] | NNMF | ✓ | NE, PenSim | RBF | |||||||||||
| 201 | 2019 | Fezai et al. [270] | PCA | ✓ | ✓ | ✓ | PV | RBF | |||||||||
| 202 | 2019 | Fazai et al. [271] | PLS | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 203 | 2019 | Deng and Deng [272] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 204 | 2019 | Cui et al. [273] | PCA | ✓ | ✓ | NE, TEP | RBF, Manifold | ||||||||||
| 205 | 2019 | Pilario et al. [67] | CVA | ✓ | ✓ | ✓ | ✓ | NE, CSTR | RBF+POLY | ||||||||
| 206 | 2019 | Lahdhiri et al. [274] | PCA | ✓ | ✓ | ✓ | ✓ | AIRLOR | RBF | ||||||||
| 207 | 2019 | Liu et al. [275] | ICA | ✓ | ✓ | ✓ | GHP | RBF | |||||||||
| 208 | 2019 | Liu et al. [276] | ICA | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 209 | 2019 | Yu et al. [277] | CCA | ✓ | ✓ | ✓ | NE, TEP | RBF | |||||||||
| 210 | 2019 | Guo et al. [278] | PCA | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 211 | 2019 | Wu et al. [279] | PCA | ✓ | ✓ | ✓ | NE, TEP | RBF | |||||||||
| 212 | 2019 | Harkat et al. [280] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 213 | 2019 | Ma et al. [281] | CVA, EDA | ✓ | ✓ | ✓ | ✓ | HSMP | - | ||||||||
| 214 | 2019 | Zhang et al. [282] | ELM | ✓ | NE, CSTR | RBF | |||||||||||
| 215 | 2019 | Peng et al. [83] | ECA | ✓ | ✓ | ✓ | NE, PenSim | RBF | |||||||||
| 216 | 2019 | Peng et al. [283] | ICA, EDA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | TEP | - | ||||||
| 217 | 2019 | Yan et al. [284] | PCA, PLS | ✓ | ✓ | NE, TEP | RBF | ||||||||||
| 218 | 2019 | Huang et al. [285] | DL | ✓ | NE, CSTH, AEP | RBF | |||||||||||
| 219 | 2019 | Li and Zhao [80] | FDFDA | ✓ | ✓ | ✓ | NE, IMP, CFPP | RBF | |||||||||
| 220 | 2019 | Zhou et al. [286] | PCA | ✓ | NE, TEP | RBF | |||||||||||
| 221 | 2019 | Deng et al. [287] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 222 | 2019 | Wang et al. [288] | PCA | ✓ | ✓ | ✓ | CSTR, HSMP | RBF | |||||||||
| 223 | 2019 | Zhu et al. [289] | PLS | ✓ | ✓ | ✓ | TEP | RBF | |||||||||
| 224 | 2019 | Xiao [290] | CVA, LPP | ✓ | ✓ | TEP | HK | ||||||||||
| 225 | 2019 | Xiao [291] | CVA | ✓ | ✓ | TEP | RBF | ||||||||||
| 226 | 2019 | Shang et al. [292] | PCA | ✓ | TEP | RBF | |||||||||||
| 227 | 2019 | Geng et al. [293] | PCA | ✓ | ✓ | TEP | RBF | ||||||||||
| 228 | 2019 | Md Nor et al. [294] | FDA | ✓ | ✓ | TEP | - | ||||||||||
| 229 | 2019 | Tan et al. [295] | PCA | ✓ | ✓ | NE, MFF | NSDC | ||||||||||
| 230 | 2019 | Tan et al. [296] | PCA | ✓ | ✓ | NE, MFF | NSDC | ||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilario, K.E.; Shafiee, M.; Cao, Y.; Lao, L.; Yang, S.-H. A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring. Processes 2020, 8, 24. https://doi.org/10.3390/pr8010024
Pilario KE, Shafiee M, Cao Y, Lao L, Yang S-H. A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring. Processes. 2020; 8(1):24. https://doi.org/10.3390/pr8010024
Chicago/Turabian StylePilario, Karl Ezra, Mahmood Shafiee, Yi Cao, Liyun Lao, and Shuang-Hua Yang. 2020. "A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring" Processes 8, no. 1: 24. https://doi.org/10.3390/pr8010024
APA StylePilario, K. E., Shafiee, M., Cao, Y., Lao, L., & Yang, S.-H. (2020). A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring. Processes, 8(1), 24. https://doi.org/10.3390/pr8010024