Static Deformation-Compensation Method Based on Inclination-Sensor Feedback for Large-Scale Manipulators with Hydraulic Actuation
Abstract
:1. Introduction
2. The Structure and the Forward Kinematic Model of the Mobile Concrete Pump Manipulator
2.1. Structure of the Mobile Concrete Pump Manipulator
2.2. Forward Kinematics Model of the Mobile Concrete Pump Manipulator
3. Joint Angle Independent Compensation Method Based on Inclination Sensor Feedback
3.1. Principle of Joint Angle Independent Compensation
- is deflection of the endpoint of the 1st link;
- is length of the 1st link;
- is tangential deformation angle of the 1st link.
3.2. Joint Torque Solution Based on Jacobian Matrix
- is force vector and moment vector acting on the end actuator;
- T is joint torque.
- is torque on the 1st joint produced by the gravity of the 2nd link;
- is torque on the 2nd joint produced by the gravity of the 2nd link.
- is torque on the 1st joint produced by the gravity of the 3rd link;
- is torque on the 2nd joint produced by the gravity of the 3rd link;
- is torque on the 3rd joint produced by the gravity of the 3rd link;
- is torque on the 1st joint;
- is torque on the 2nd joint;
- is torque on the 3rd joint,
3.3. Compensation Angle Solution Based on Cantilever Model Combined Deformation of Compression and Bending
- is Deflection of the corresponding point of the corresponding link;
- is Equivalent density;
- is Equivalent cross-sectional area.
4. Deformation Compensation Verification Based on ANSYS Workbench and MATLAB Co-Simulation
4.1. ANSYS Workbench Parametric Simulation Verification
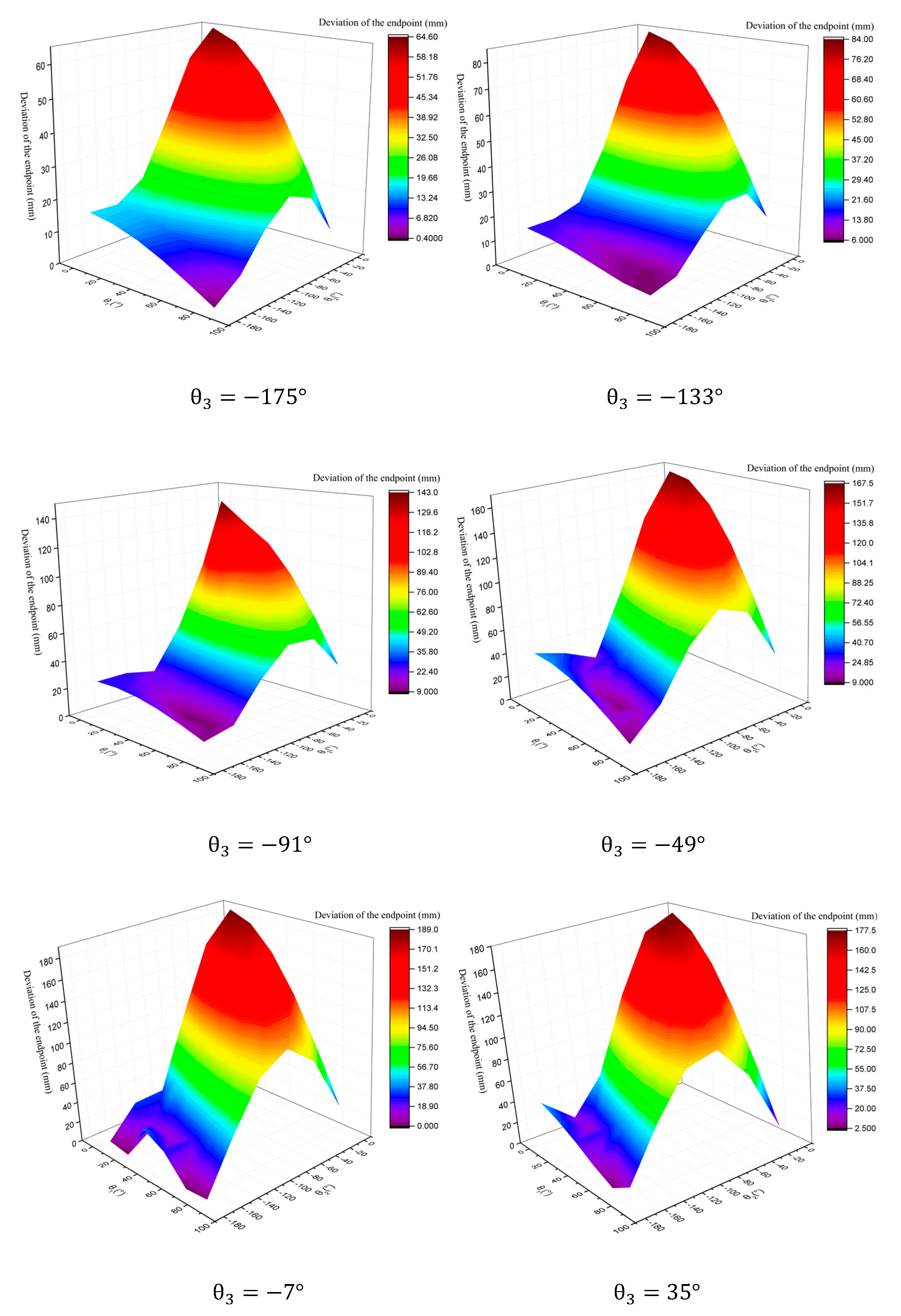
4.1.1. Parametric Simulation of Compensation Angle
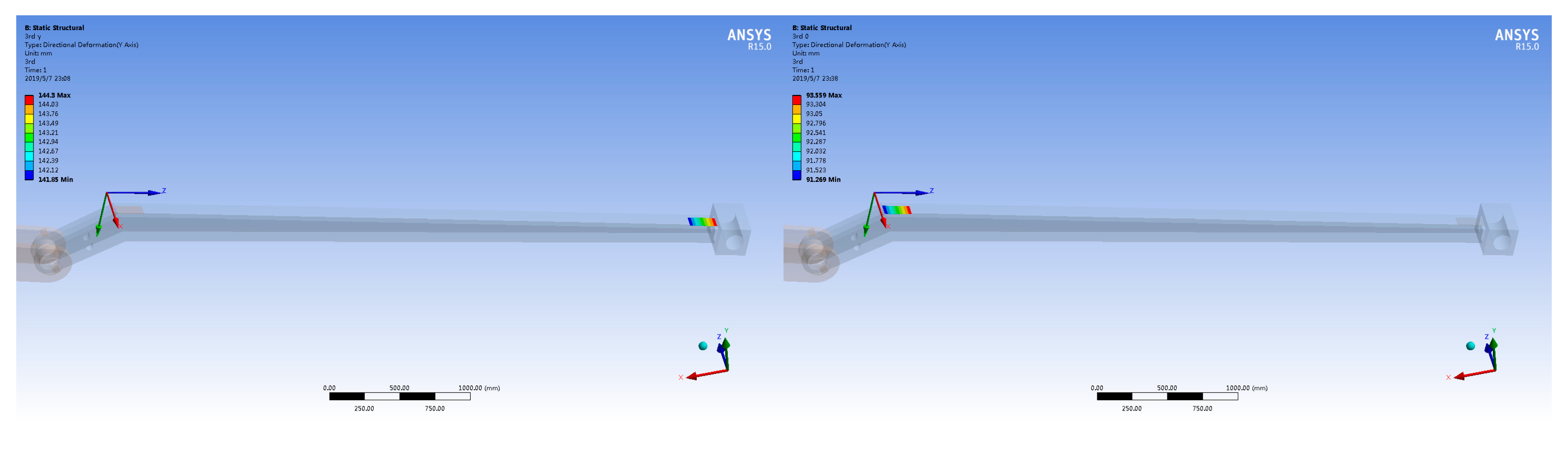
4.1.2. Parametric Simulation to Verify the Reliability of the Compensation Method
4.2. Verification of Deformation Compensation Effect Based on ANSYS Workbench and MATLAB Co-Simulation
4.2.1. Verification of the Static Deformation-Compensation Method’s Validity
4.2.2. Verification of the Static Deformation-Compensation Method’s Universality for Different Loads
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dwivedy, S.K.; Eberhard, P. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2007, 41, 749–777. [Google Scholar] [CrossRef]
- Book, W.J.; Majette, M. Controller design for flexible distributed parameter mechanical arm via combined state-space and frequency domain techniques. Trans. ASME: J. Dyn. Syst. Meas. Contr. 1983, 105, 245–254. [Google Scholar] [CrossRef]
- Azad, A.K.M. Analysis and Design of Control Mechanisms for Flexible Manipulator Systems. Ph.D. Thesis, Department of Automatic Control and Systems Engineering, The University of Sheffield, Sheffield, UK, 1994. [Google Scholar]
- Poerwanto, H. Dynamic Simulation and Control of Flexible Manipulator Systems. Ph.D. Thesis, Department of Automatic Control and Systems Engineering, The University of Sheffield, Sheffield, UK, 1998. [Google Scholar]
- Hartmut, B. Mechydronic for Boom Control on Truck Mounted Concrete Pumps. Tech. Symp. Constr. Equip. Technol. 2003, 1, 12. [Google Scholar]
- Henikl, J.; Kemmetmüller, W.; Meurer, T.; Elsevier, A.K. Infinite-dimensional decentralized damping control of large-scale manipulators with hydraulic actuation. Automatica 2016, 63, 101–115. [Google Scholar] [CrossRef]
- Liu, J.; Dai, L.; Zhao, L.; Cai, J.; Zhang, W. Flexible multi-body dynamics modeling and simulation of concrete pump truck boom. J. Mech. Eng. 2007, 1, 131–135. [Google Scholar] [CrossRef]
- Keating, S.J.; Leland, J.C.; Cai, L. Toward site-specific and self-sufficient robotic fabrication on architectural scales. Sci. Robot. 2017, 2, eaam8986. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, J.; Xu, B.; Ding, R. An Electrohydraulic Load Sensing System based on flow/pressure switched control for mobile machinery. ISA Trans. 2019. [Google Scholar] [CrossRef]
- Bradley, D.A.; Seward, D.W. Developing real-time autonomous excavation-the LUCIE story. In Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995; pp. 3028–3033. [Google Scholar]
- Bradley, D.; Seward, D. The development, control and operation of an autonomous robotic excavator. J. Intell. Robot. Syst. 1998, 21, 73–97. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ha, Q.P.; Rye, D.C.; Durrant-Whyte, H.F. Force/position tracking for electro-hydraulic systems of a robotic excavator. In Proceedings of the 39th IEEE Conference on Decision and control, Sydney, NSW, Australia, 12–15 December 2000; pp. 5224–5229. [Google Scholar]
- Ha, Q.P.; Nguyen, Q.H.; Rye, D.C.; Durrant-Whyte, H.F. Fuzzy sliding-mode controllers with applications. Ieee Trans. Ind. Electron. 2001, 48, 38–46. [Google Scholar] [CrossRef]
- Lee, S.U.; Chang, P.H. Control of a heavy-duty robotic excavator using time delay control with integral sliding surface. Control Eng. Pract. 2002, 10, 697–711. [Google Scholar] [CrossRef]
- Chang, P.H.; Lee, S.J. A straight-line motion tracking control of hydraulic excavator system. Mechatronics 2002, 12, 119–138. [Google Scholar] [CrossRef]
- Budny, E.; Chlosta, M.; Gutkowski, W. Load-independent control of a hydraulic excavator. Autom. Constr. 2003, 12, 245–254. [Google Scholar] [CrossRef]
- Araya, H.; Makoto, K.; Kinugawa, H.; Tatsuo, A. Level luffing control system for crawler cranes. Autom. Constr. 2004, 13, 689–697. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, G.; Li, J. Kinematics analysis and trajectory planning control modeling and simulation of concrete pump truck. Constr. Mach. 2000, 4, 29–32. [Google Scholar]
- Guo, L.; Zhao, M.; Zhang, G.; Huang, Y. Automatic pumping and process simulation of concrete pump truck cloth mechanism. J. Northeast. Univ. (Nat. Sci. Ed.) 2000, 21, 617–619. [Google Scholar]
- Zhipeng, Y. Research on the end Track Control of the Concrete Pump Truck Boom; Wuhan University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Bremer, H. Elastic Multibody Dynamics: A Direct Ritz Approach; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Henikl, J.; Kemmetmüller, W.; Bader, M.; Kugi, A. Modeling, simulation and identification of a mobile concrete pump. Math. Comput. Model. Dyn. Syst. 2015, 21, 180–201. [Google Scholar] [CrossRef]
- Henikl, J.; Kemmetmüller, W.; Kugi, A. Modeling and control of a mobile concrete pump. In Proceedings of the 6th IFAC Symposium of Mechatronic Systems, Hangzhou, China, 10–12 April 2013; pp. 91–98. [Google Scholar]
- Lambeck, S.; Sawodny, O.; Arnold, E. Trajectory tracking control for a new generation of fire rescue turntable ladders. In Proceedings of the 2nd IEEE Conference on Robotics, Automation and Mechatronics, Orlando, FL, USA, 15–19 May 2006; pp. 847–852. [Google Scholar]
- Zimmert, N.; Pertsch, A.; Sawodny, O. 2-DOF control of a fire-rescue turntable ladder. IEEE Trans. Control Syst. Technol. 2012, 20, 438–452. [Google Scholar] [CrossRef]
- Book, W.J. Modeling, design, and control of flexible manipulator arms: A tutorial review. In Proceedings of the IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 500–506. [Google Scholar]
- Rahimi, H.N.; Nazemizadeh, M. Dynamic analysis and intelligent control techniques for flexible manipulators: A review. Adv. Robot. 2013, 28, 63–76. [Google Scholar] [CrossRef]
- Kiang, T.; Spowage, A.; Yoong, C.K. Review of control and sensor system of flexible manipulator. J. Intell. Robot. Syst. 2015, 77, 187–213. [Google Scholar] [CrossRef]
- Theodore, R.J.; Ghosal, A. Comparison of the assumed modes and finite element models for flexible multi-link manipulators. Int. J. Robot. Res. 1995, 14, 91–111. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Chen, L. Partitioned neural network control and fuzzy vibration control for free-floating space flexible manipulator. Eng. Mech. 2012, 37. [Google Scholar] [CrossRef]
- Subudhi, B.; Morris, A.S. Dynamic modelling, simulation and control of a manipulator with flexible links and joints. Rob. Auton. Syst. 2002, 41, 257–270. [Google Scholar] [CrossRef]
- Usoro, P.B.; Nadira, R.; Mahil, S.S. A finite element/lagrangian approach to modeling light weight flexible manipulators. ASME J. Dyn. Syst. Meas. Contr. 1986, 108, 198–205. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method, Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Geradin, M.; Cardona, A. Kinematics and dynamics of rigid and flexible mechanisms using finite elements and quaternion algebra. Comput. Mech. 1988, 4, 115–135. [Google Scholar] [CrossRef]
- Bayo, E. A finite-element approach to control the end point motion of a single link flexible robot. Rob. Syst. 1987, 4, 63–75. [Google Scholar] [CrossRef]
- Jonker, B. A finite element dynamic analysis of flexible spatial mechanisms with flexible links. Comput. Methods Appl. Mech. Eng. 1989, 76, 17–40. [Google Scholar] [CrossRef]
- Jonker, B. A finite element dynamic analysis of flexible manipulators. Int. J. Rob. Res. 1990, 9, 59–74. [Google Scholar] [CrossRef]
- Hastings, G.G.; Book, J.W. Verification of a linear dynamic model for flexible robotic manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Francisco, CA, USA, 7–10 April 1986; pp. 1024–1029. [Google Scholar]
- Kim, J.S.; Uchiyama, M. Vibration mechanism of constrained spatial flexible manipulators. JSME Ser. C 2003, 46, 123–128. [Google Scholar] [CrossRef]
- Feliu, V.; Rattan, K.S.; Brown, H.B. Modeling and control of single-link flexible arms with lumped masses. ASME J.Dyn. Syst. Meas. Contr. 1992, 114, 59–69. [Google Scholar] [CrossRef]
- Khalil, W.; Gautier, M. Modeling of mechanical systems with lumped elasticity. Proc. IEEE Int. Conf. Rob. Autom. 2000, 4, 3964–3969. [Google Scholar]
- Zhu, G.; Ge, S.S.; Lee, T.H. Simulation studies of tip tracking control of a single-link flexible robot based on a lumped model. Robotica 1999, 17, 71–78. [Google Scholar] [CrossRef]
- Raboud, D.W.; Lipsett, A.W.; Faulkner, M.G.; Diep, J. Stability evaluation of very flexible cantilever beams. Int. J.Nonlinear Mech. 2001, 36, 1109–1122. [Google Scholar] [CrossRef]
- Lee, S.J.; Chung, I.S.; Bae, S.Y. Structural design and analysis of CFRP boom for concrete pump truck. Mod. Phys. Lett. B 2019, 33, 787–792. [Google Scholar] [CrossRef]
- Yuan, Q.H.; Lew, J.; Piyabongkarn, D. Motion control of an aerial work platform. In Proceedings of the 2009 American control conference, AACC 2009, Hyatt Regency Riverfront, St. Louis, MO, USA, 10–12 June 2009; pp. 2873–2878. [Google Scholar]
- Xia, J.; Gang, G.; Xin, Z. Research on deformation compensation and trajectory control technology of concrete boom. Constr. Mach. 2016, 5, 70–76. [Google Scholar]
- Xin, Z.; Liang, W.; Jiaqian, W.; Shiyang, H. Research on trajectory control technology of concrete pump truck based on vehicle deformation compensation. J. Mech. Eng. 2015, 13, 492–496. [Google Scholar]
- Wang, X. Research on Trajectory Control Technology of Concerte Pump Arm Frame based on Arm Frame Denaturalization Compensation. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2018. [Google Scholar]
- Pan, D.; Xing, J.; Wang, B. Static Analysis and Dynamic Simulation of Concrete Pump Truck Boom. J. Chongqing Univ. Technol. (Nat. Sci.) 2018, 32, 86–91, 123. [Google Scholar]
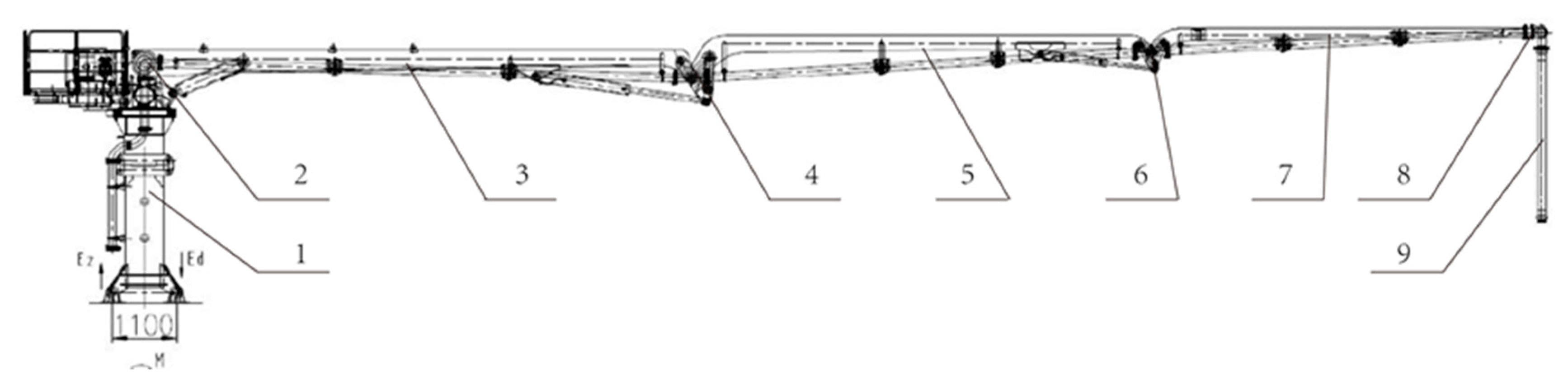
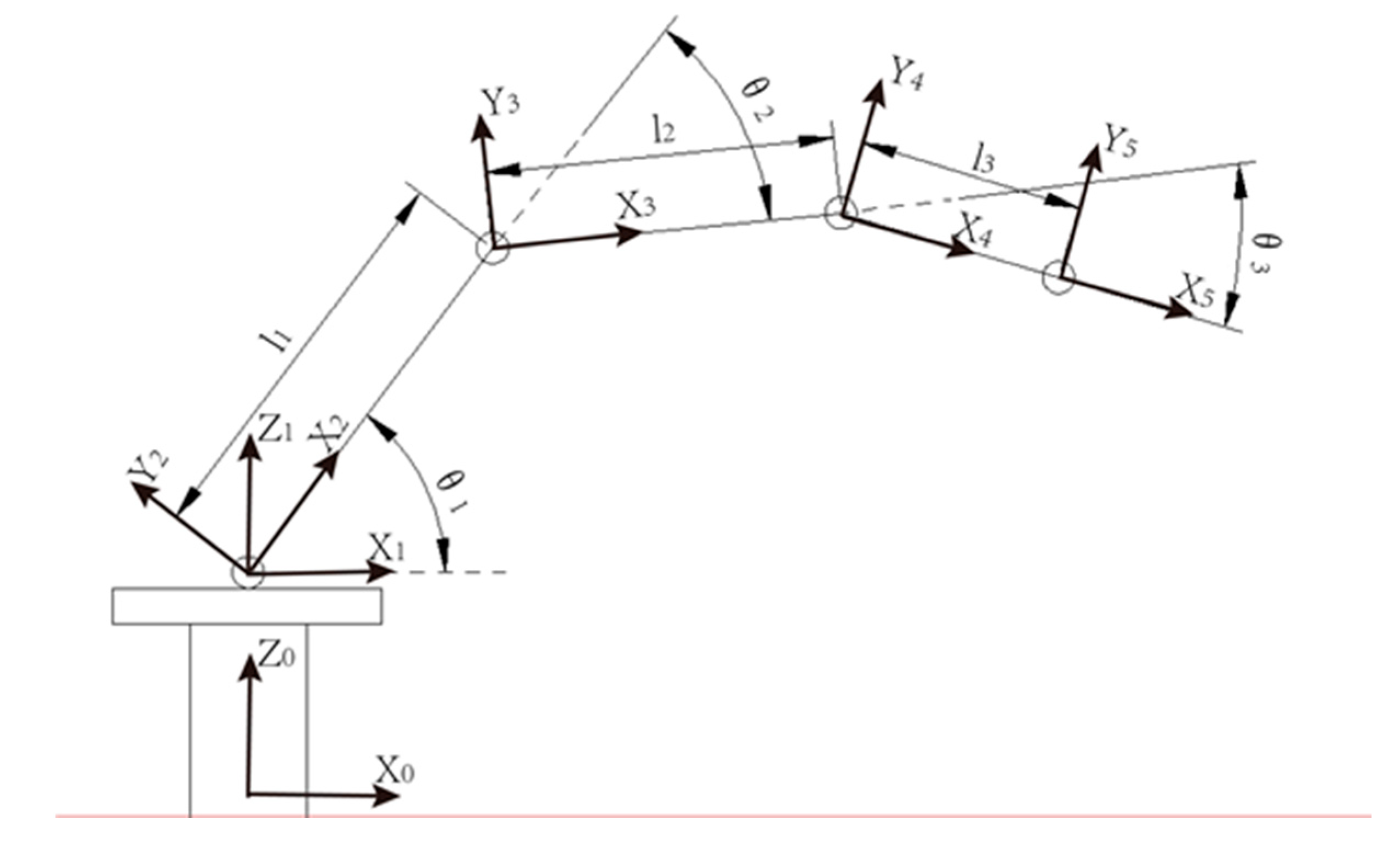
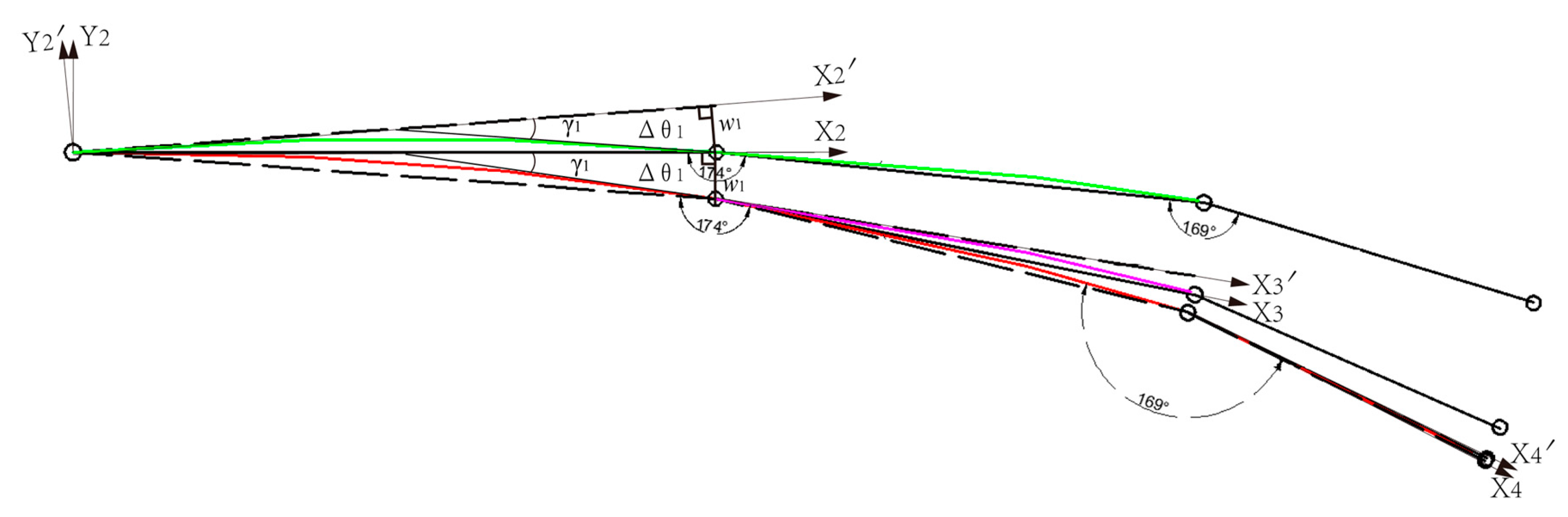
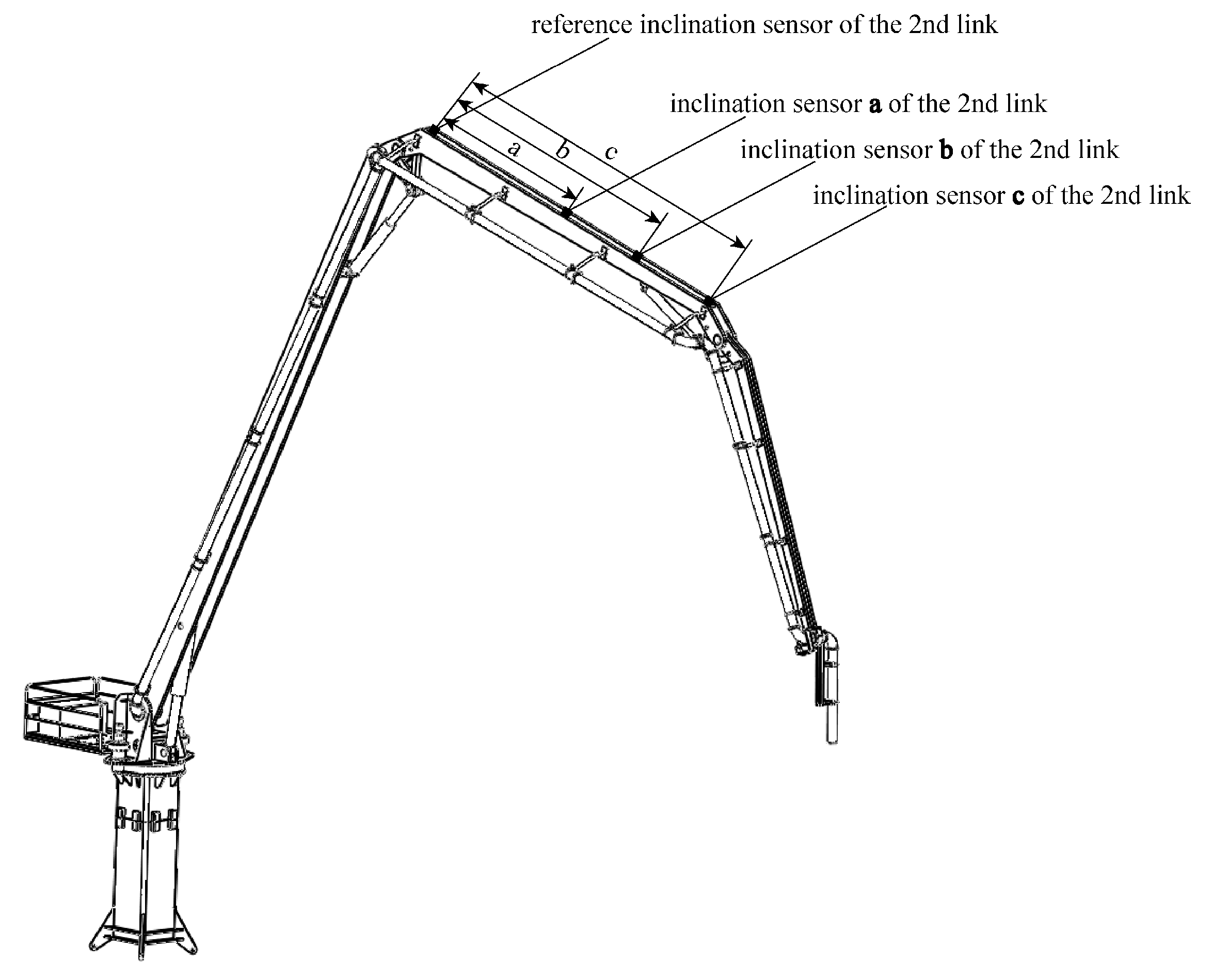


| Serial Number | 1st Link | 2nd Link | 3rd Link |
|---|---|---|---|
| Link length (joint distance) (mm) | 11,204 | 7800 | 4982 |
| Joint angle range (°) | 0°–90° | −180° to 0° | −180° to 40° |
| Endpoint Deviation (mm) | Compensation Angle (°) | Endpoint Target Position (mm) | Endpoint Position before Compensation (mm) | Endpoint Position after Compensation (mm) | Compensation Error (Residual Deviation) (mm) | |
|---|---|---|---|---|---|---|
| (5, −5, 35) | 177.0635 | (0.204, 0.181, 0.042) | (23042, 3834) | (23079.22, 3660.73) | (23055.25, 3784.12) | (13.25, 49.88) |
| (37, −5, 35) | 140.1612 | (0.163, 0.138, 0.022) | (17509, 15462) | (17606.04, 15360.49) | (17539.17, 15432.31) | (30.17, 29.69) |
| (53, −5, 35) | 104.5001 | (0.123, 0.100, 0.010) | (12569, 19689) | (12659.12, 19635.76) | (12596.90, 19673.30) | (27.90, 15.70) |
| (53, −73, −49) | 105.5360 | (0.147, 0.146, 0.015) | (15858, 1629) | (15814.44, 1533.23) | (15829.77, 1596.88) | (28.23, 32.12) |
| (69, −73, −49) | 101.2360 | (0.120, 0.171, 0.027) | (14794, 5937) | (14773.62, 5837.99) | (14777.04, 5901.81) | (16.96, 35.19) |
| (85, −73, −49) | 89.38721 | (0.083, 0.183, 0.037) | (12585, 9785) | (12585.90, 9695.61) | (12578.28, 9753.63) | (6.72, 31.37) |
| Equivalent Density (kg/m3) | Endpoint Deviation (mm) | Compensation Angle (°) | Endpoint Target Position (mm) | Endpoint Position before Compensation (mm) | Endpoint Position after Compensation (mm) | Compensation Error (Residual Deviation) (mm) |
|---|---|---|---|---|---|---|
| 7000 | 177.0635 | (0.204, 0.181, 0.042) | (23042, 3834) | (23079.22, 3660.73) | (23055.25, 3783.82) | (13.25, 50.18) |
| 8272 | 209.2331 | (0.241, 0.214, 0.049) | (23042, 3834) | (23085.98, 3629.25) | (23058.42, 3774.71) | (16.42, 59.29) |
| 11116 | 281.1570 | (0.324, 0.288, 0.066) | (23042, 3834) | (23101.10, 3558.87) | (23063.69, 3754.57) | (21.69, 79.43) |
| 13959 | 353.0808 | (0.407, 0.361, 0.083) | (23042, 3834) | (23116.21, 3488.48) | (23070.30, 3734.47) | (28.30, 99.53) |
| 16803 | 425.0046 | (0.490, 0.435, 0.100) | (23042, 3834) | (23131.33, 3418.10) | (23076.25, 3714.50) | (34.25, 119.50) |
| 19646 | 496.9285 | (0.573, 0.509, 0.117) | (23042, 3834) | (23146.45, 3347.72) | (23082.54, 3694.66) | (40.54, 139.34) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Su, Q.; Zhang, F.; Ma, Y.; Fang, Z.; Xu, B. Static Deformation-Compensation Method Based on Inclination-Sensor Feedback for Large-Scale Manipulators with Hydraulic Actuation. Processes 2020, 8, 81. https://doi.org/10.3390/pr8010081
Qian J, Su Q, Zhang F, Ma Y, Fang Z, Xu B. Static Deformation-Compensation Method Based on Inclination-Sensor Feedback for Large-Scale Manipulators with Hydraulic Actuation. Processes. 2020; 8(1):81. https://doi.org/10.3390/pr8010081
Chicago/Turabian StyleQian, Jianyong, Qi Su, Fu Zhang, Yun Ma, Zifan Fang, and Bing Xu. 2020. "Static Deformation-Compensation Method Based on Inclination-Sensor Feedback for Large-Scale Manipulators with Hydraulic Actuation" Processes 8, no. 1: 81. https://doi.org/10.3390/pr8010081
APA StyleQian, J., Su, Q., Zhang, F., Ma, Y., Fang, Z., & Xu, B. (2020). Static Deformation-Compensation Method Based on Inclination-Sensor Feedback for Large-Scale Manipulators with Hydraulic Actuation. Processes, 8(1), 81. https://doi.org/10.3390/pr8010081




