Numerical Characterization of Cohesive and Non-Cohesive ‘Sediments’ under Different Consolidation States Using 3D DEM Triaxial Experiments
Abstract
:1. Introduction
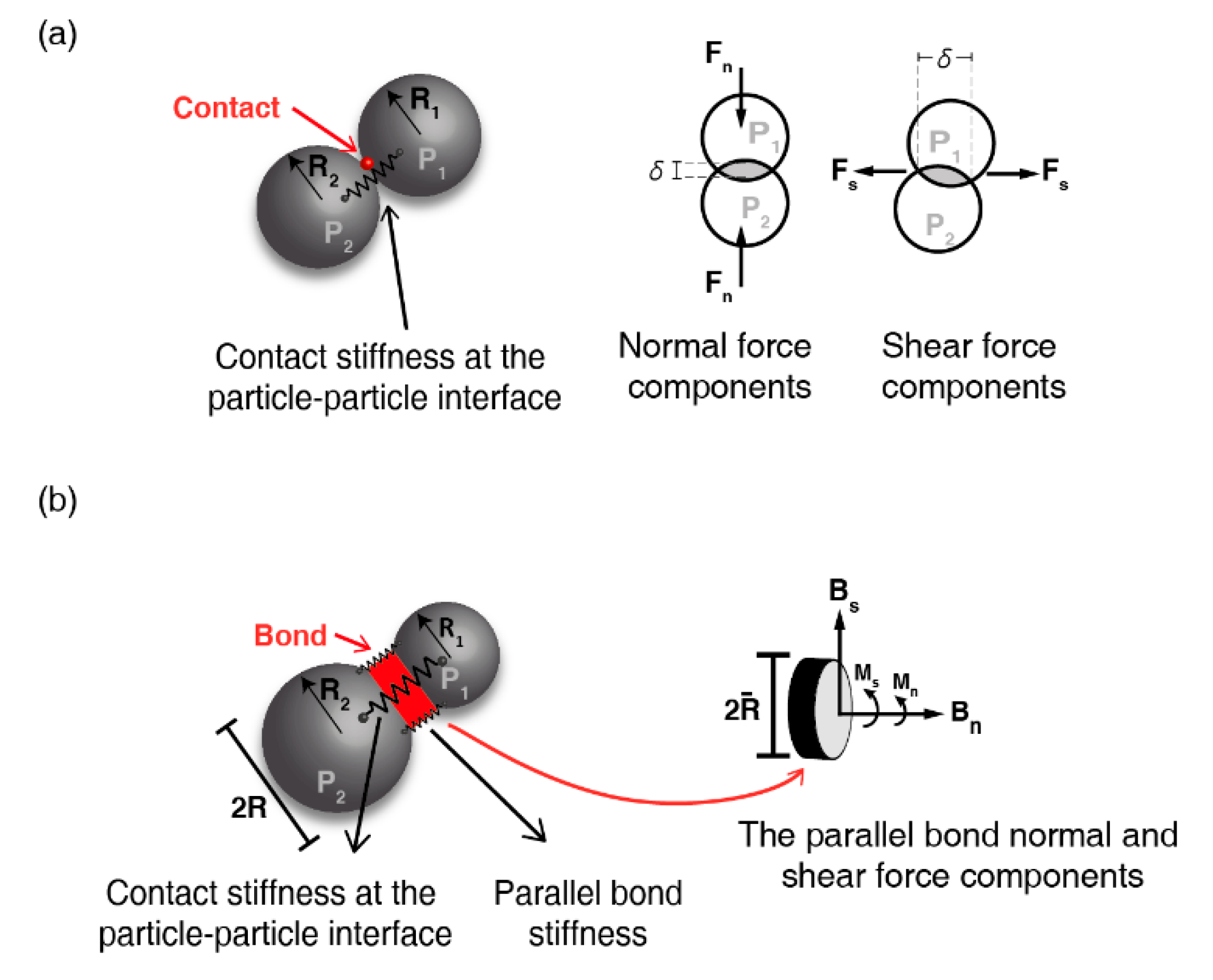
2. The Discrete Element Method—Granular and Bonded Approach
2.1. Granular Approach: The Hertz–Mindlin Contact Model (Cohesionless, Elastoplastic)
2.2. Granular Cohesive Approach: The Linear Parallel-Bond Contact Model (Cohesive, Elastoplastic)
3. Experimental Setup
3.1. Model Geometry
3.2. Particle and Bond Micro-Properties
3.2.1. Hertz–Mindlin Contact Model—Granular ‘Sand-Like’ Materials
3.2.2. Linear Contact Bond Model—Cohesive ‘Clay-Like’ Materials
3.3. Model Run Stages of the Numerical Triaxial Tests
3.4. Model Interpretation and Calculations
4. Results
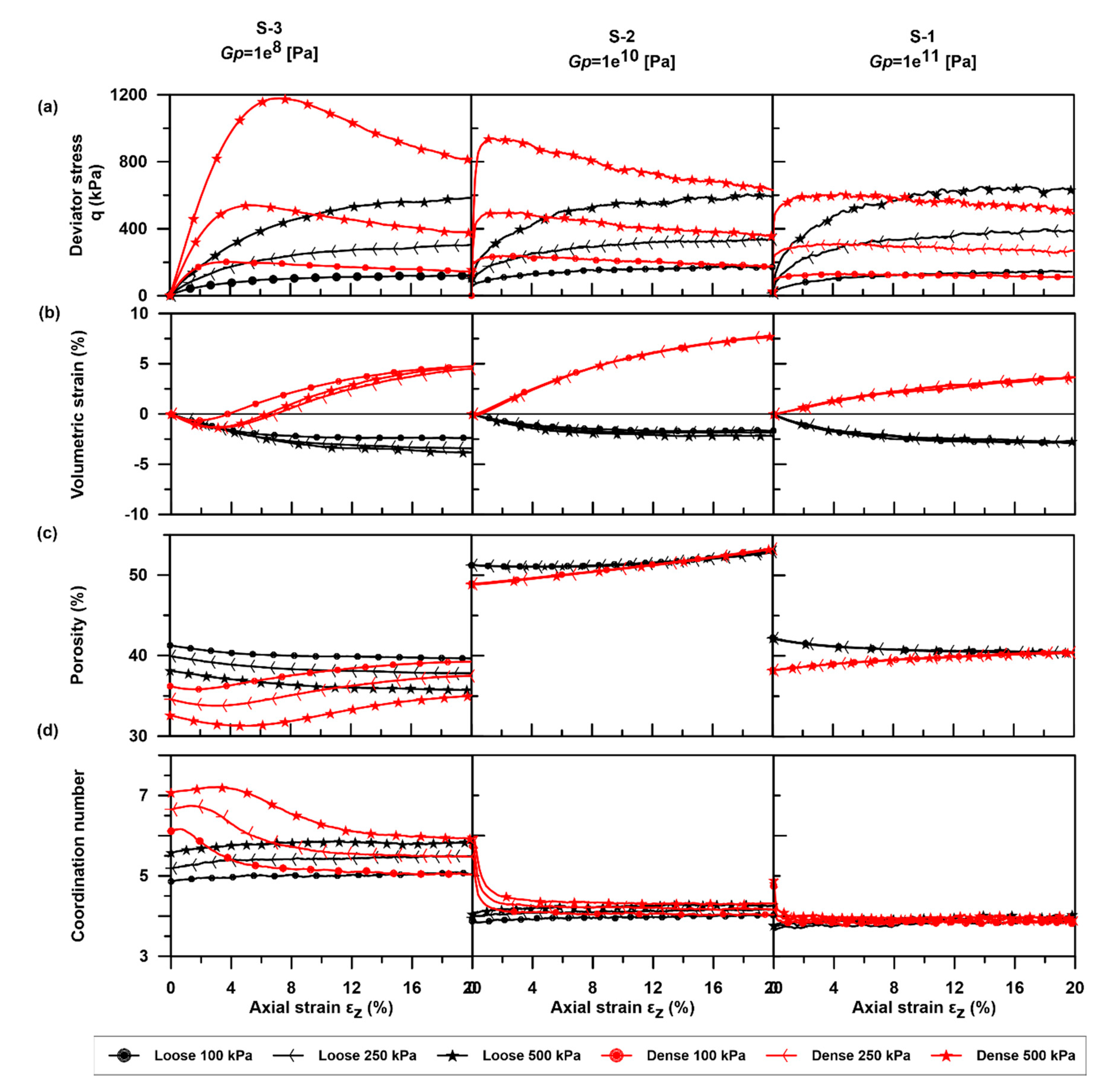
4.1. Stress–Strain Behavior
4.2. Volumetric Strain, Porosity and Coordination Number
4.3. Strain Localization
5. Discussion
5.1. Parametrization of Numerical ‘Sediments’
5.2. Classification of the Granular Assemblage
5.3. Application
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. DEM Force–Displacement Calculation
References
- Ikari, M.J.; Kopf, A.J. Cohesive strength of clay-rich sediment. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Hattab, M.; Hammad, T.; Fleureau, J.M.; Hicher, P.Y. Behaviour of a sensitive marine sediment: Microstructural investigation. Géotechnique 2013, 63, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Guo, P.; Su, X. Shear strength, interparticle locking, and dilatancy of granular materials. Can. Geotech. J. 2007, 44, 579–591. [Google Scholar] [CrossRef]
- van Gent, H.W.; Holland, M.; Urai, J.L.; Loosveld, R. Evolution of fault zones in carbonates with mechanical stratigraphy - Insights from scale models using layered cohesive powder. J. Struct. Geol. 2010, 32, 1375–1391. [Google Scholar] [CrossRef]
- Kinoshita, M.; Tobin, H.; Ashi, J.; Kimura, G.; Lallemant, S.; Screaton, E.J.; Curewitz, D.; Masago, H.; Moe, K.T. Data report: Permeability, compressibility, stress state, and grain size of shallow sediments from Sites C0004, C0006, C0007, and C0008 of the Nankai accretionary complex. Proc. IODP. 2011, 314, 2. [Google Scholar]
- LongJohn, T.; Morgan, J.K.; Dugan, B. Microstructural Evolution of Porosity and Stress During the Formation of Brittle Shear Fractures: A Discrete Element Model Study. J. Geophys. Res. Solid Earth 2018, 123, 2228–2245. [Google Scholar] [CrossRef] [Green Version]
- Kock, I.; Huhn, K. Influence of particle shape on the frictional strength of sediments—A numerical case study. Sediment. Geol. 2007, 196, 217–233. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. BALL–A program to model granular media using the distinct element method. In Technical Note; Advance Technology Group, Dames and Moore: London, UK, 1978; pp. 129–163. [Google Scholar]
- Miyakawa, A.; Yamada, Y.; Matsuoka, T. Effect of increased shear stress along a plate boundary fault on the formation of an out-of-sequence thrust and a break in surface slope within an accretionary wedge, based on numerical simulations. Tectonophysics 2010, 484, 127–138. [Google Scholar] [CrossRef]
- Campbell, C.S.; Cleary, P.W.; Hopkins, M. Large-scale landslide simulations: Global deformation, velocities and basal friction. J. Geophys. Res. 1995, 100, 8267. [Google Scholar] [CrossRef]
- Mair, K.; Abe, S. 3D numerical simulations of fault gouge evolution during shear: Grain size reduction and strain localization. Earth Planet. Sci. Lett. 2008, 274, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A.; Strack, O.D.L. A dicrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wenk, L.; Huhn, K. The influence of an embedded viscoelastic–plastic layer on kinematics and mass transport pattern within accretionary wedges. Tectonophysics 2013, 608, 653–666. [Google Scholar] [CrossRef]
- Morgan, J.K. Numerical simulations of granular shear zones using the distinct element method: 2. Effects of particle size distribution and interparticle friction on mechanical behavior. J. Geophys. Res. Solid Earth 1999, 104, 2721–2732. [Google Scholar] [CrossRef]
- Santamarina, J.; Shin, H. Friction in granular media. Meso-Scale Shear Phys. Earthq. Landslide Mech. 2009, 159–190. [Google Scholar] [CrossRef]
- Rothenburg, L.; Bathurst, R.J. Micromechanical features of granular assemblies with planar elliptical particles. Geotechnique 1992, 42, 79–95. [Google Scholar] [CrossRef]
- Rothenburg, L.; Bathurst, R.J. Influence of particle eccentricity on micromechanical behavior of granular materials. Mech. Mater. 1993, 16, 141–152. [Google Scholar] [CrossRef]
- Thornton, C. Numerical simulations of deviatoric shear deformation of granular media. Géotechnique 2000, 50, 43. [Google Scholar] [CrossRef]
- Guo, Y.; Morgan, J.K. Influence of normal stress and grain shape on granular friction: Results of discrete element simulations. J. Geophys. Res. Solid Earth 2004, 109, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The impact of porosity and crack density on the elasticity, strength and friction of cohesive granular materials: Insights from DEM modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 250–261. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M.R. Smooth convex three-dimensional particle for the discrete-element method. J. Eng. Mech. 2003, 129, 539–547. [Google Scholar] [CrossRef]
- Iwashita, K.; Oda, M. Mechanics of Granular Materials: An Introduction; A.A. Balkema: Rotterdam, The Netherlands, 1999. [Google Scholar]
- Mora, P.; Place, D. Simulation of the frictional stick-slip instability. Pure Appl. Geophys. 1994, 143, 61–87. [Google Scholar] [CrossRef]
- Morgan, J.K.; Boettcher, M.K. Numerical simulations of granular shear zones using the distinct element method 1. Shear zone kinematics and the micromechanics of localization. J. Geophys. Res. 1999, 104, 2703–2719. [Google Scholar] [CrossRef]
- Antonellini, M.A.; Pollard, D.D. Distinct element modeling of deformation bands in sandstone. J. Struct. Geol. 1995, 17, 1165–1182. [Google Scholar] [CrossRef]
- Ask, M.V.S.; Kopf, A. Constraints on the state of in situ effective stress and the mechanical behavior of ODP Leg 186 claystones in the Japan Trench forearc. Isl. Arc 2004, 13, 242–257. [Google Scholar] [CrossRef]
- Mair, K.; Frye, K.M.; Marone, C. Influence of grain characteristics on the friction of granular shear zones. J. Geophys. Res. Solid Earth 2002, 107, ECV 4-1–ECV 4-9. [Google Scholar] [CrossRef]
- Yamamuro, J.A.; Abrantes, A.E.; Lade, P.V. Effect of Strain Rate on the Stress-Strain Behavior of Sand. J. Geotech. Geoenviron. Eng. 2011, 137, 1169–1178. [Google Scholar] [CrossRef]
- Abe, S.; van Gent, H.; Urai, J.L. DEM simulation of normal faults in cohesive materials. Tectonophysics 2011, 512, 12–21. [Google Scholar] [CrossRef]
- Anantanasakul, P.; Yamamuro, J.A.; Lade, P.V. Three-dimensional drained behavior of normally consolidated anisotropic kaolin clay. Soils Found. 2012, 52, 146–159. [Google Scholar] [CrossRef] [Green Version]
- Itasca Consulting Group Inc. PFC—Particle Flow Code, Ver. 5.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2014. [Google Scholar]
- Sadek, M.A.; Chen, Y.; Liu, J. Simulating shear behavior of a sandy soil under different soil conditions. J. Terramech. 2011, 48, 451–458. [Google Scholar] [CrossRef]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Huhn, K.; Kock, I.; Kopf, A.J. Comparative numerical and analogue shear box experiments and their implications for the mechanics along the failure plane of landslides. Nor. Geol. Tidsskr. 2006, 86, 209–220. [Google Scholar]
- Pichel, L.M.; Finch, E.; Gawthorpe, R.L. The Impact of Pre-Salt Rift Topography on Salt Tectonics: A Discrete-Element Modeling Approach. Tectonics 2019, 38, 1466–1488. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.J.; Zhu, D. Hertz Theory: Contact of Spherical Surfaces. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.-W., Eds.; Springer: Boston, MA, USA, 2013; ISBN 978-0-387-92896-8. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact under Varying Oblique Forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar]
- Yimsiri, S.; Soga, K. Effects of soil fabric on behaviors of granular soils: Microscopic modeling. Comput. Geotech. 2011, 38, 861–874. [Google Scholar] [CrossRef]
- Manchanda, R.; Olson, J.E.; Sharma, M.M. Mechanical, failure and flow properties of sands: Micro-mechanical models. 46th US Rock Mech. Geomech. Symp. 2012 2012, 3, 1555–1569. [Google Scholar]
- Yamamoto, T.; Nye, T.; Kuru, M. Porosity, permeability, shear strength: Crosswell tomography below an iron foundry. Geophysics 1994, 59, 1530–1541. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Gylland, A.S.; Rueslåtten, H.; Jostad, H.P.; Nordal, S. Microstructural observations of shear zones in sensitive clay. Eng. Geol. 2013, 163, 75–88. [Google Scholar] [CrossRef]
- Saltzer, S.D.; Pollard, D.D. Distinct element modeling of structures formed in sedimentary overburden by extensional reactivation of basement normal faults. Tectonics 1992, 11, 165–174. [Google Scholar] [CrossRef]
- Mair, K.; Abe, S. Breaking Up: Comminution Mechanisms in Sheared Simulated Fault Gouge. Pure Appl. Geophys. 2011, 168, 2277–2288. [Google Scholar] [CrossRef] [Green Version]
- Cheung, G.; O’Sullivan, C. Effective simulation of flexible lateral boundaries in two- and three-dimensional DEM simulations. Particuology 2008, 6, 483–500. [Google Scholar] [CrossRef]
- Morrow, C.A.; Moore, D.E.; Lockner, D.A. Frictional strength of wet and dry montmorillonite. J. Geophys. Res. Solid Earth 2017, 122, 3392–3409. [Google Scholar] [CrossRef]
- Rathbun, A.P.; Marone, C. Effect of strain localization on frictional behavior of sheared granular materials. J. Geophys. Res. 2010, 115, 1–16. [Google Scholar] [CrossRef]
- Kock, I.; Huhn, K. Numerical investigation of localization and micromechanics in a stratified soil specimen. J. Struct. Geol. 2007, 29, 1679–1694. [Google Scholar] [CrossRef]
- Nandanwar, M.; Chen, Y. Modeling and measurements of triaxial tests for a sandy loam soil. Can. Biosyst. Eng. 2017, 59, 2.1–2.8. [Google Scholar] [CrossRef] [Green Version]
- Turcotte, D.; Schubert, G. Geodynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cheung, L.Y.G.; O’Sullivan, C.; Coop, M.R. Discrete element method simulations of analogue reservoir sandstones. Int. J. Rock Mech. Min. Sci. 2013, 63, 93–103. [Google Scholar] [CrossRef]
- Huhn, K.; Strozyk, F.; Kock, I. Quantifying the key role of slope material peak strength–using discrete element simulations. In Proceedings of the Submarine Mass Movements and their Consequences; Springer: Cham, Switzerland, 2016; pp. 537–545. [Google Scholar]
- Feng, K.; Montoya, B.M.; Evans, T.M. Discrete element method simulations of bio-cemented sands. Comput. Geotech. 2017, 85, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Marri, A.; Wanatowski, D.; Yu, H.S. Drained behaviour of cemented sand in high pressure triaxial compression tests. Geomech. Geoeng. 2012, 7, 159–174. [Google Scholar] [CrossRef]
- Wanatowski, D.; Chu, J. Drained behaviour of Changi sand in triaxial and plane-strain compression. Geomech. Geoeng. 2008, 3, 85–96. [Google Scholar] [CrossRef]
- De Bono, J.P.; McDowell, G.R. DEM of triaxial tests on crushable sand. Granul. Matter 2014, 16, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Zhang, L.; Zhu, H.; Zhang, Q. Effect of Model Scale and Particle Size Distribution on PFC3D Simulation Results. Rock Mech. Rock Eng. 2014, 47, 2139–2156. [Google Scholar] [CrossRef]
- Schöpfer, M.P.J.; Childs, C.; Manzocchi, T. Three-dimensional failure envelopes and the brittle-ductile transition. J. Geophys. Res. Solid Earth 2013, 118, 1378–1392. [Google Scholar] [CrossRef]
- Craig, R.F. Craig’s Soil Mechanics; CRC Press: New-York, USA, 2004. [Google Scholar]
- Lommen, S.; Schott, D.; Lodewijks, G. DEM speedup: Stiffness effects on behavior of bulk material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Eisenstadt, G.; Sims, D. Evaluating sand and clay models: Do rheological differences matter? J. Struct. Geol. 2005, 27, 1399–1412. [Google Scholar] [CrossRef]
- Schellart, W.P. Shear test results for cohesion and friction coefficients for different granular materials: Scaling implications for their usage in analogue modelling. Tectonophysics 2000, 324, 1–16. [Google Scholar] [CrossRef]
- Park, L.K.; Suneel, M.; Chul, I.J. Shear strength of jumunjin sand according to relative density. Mar. Georesources Geotechnol. 2008, 26, 101–110. [Google Scholar] [CrossRef]
- Salgado, R.; Bandini, P.; Karim, A. Shear strength and stiffness of silty sand. J. Geotech. Geoenviron. Eng. 2000, 126, 451–462. [Google Scholar] [CrossRef]
- Saffer, D.M.; Marone, C. Comparison of smectite- and illite-rich gouge frictional properties: Application to the updip limit of the seismogenic zone along subduction megathrusts. Earth Planet. Sci. Lett. 2003, 215, 219–235. [Google Scholar] [CrossRef]
- Jocković, S.; Vukićević, M. Bounding surface model for overconsolidated clays with new state parameter formulation of hardening rule. Comput. Geotech. 2017, 83, 16–29. [Google Scholar] [CrossRef]
- Hicher, P.Y.; Wahyudi, H.; Tessier, D. Microstructural analysis of inherent and induced anisotropy in clay. Mech. Cohesive-Frict. Mater. 2000, 5, 341–371. [Google Scholar] [CrossRef]
- Hattab, M.; Fleureau, J.M. Experimental study of kaolin particle orientation mechanism. Geotechnique 2010, 60, 323–331. [Google Scholar] [CrossRef]
- Djéran-Maigre, I.; Tessier, D.; Grunberger, D.; Velde, B.; Vasseur, G. Evolution of microstructures and of macroscopic properties of some clays during experimental compaction. Mar. Pet. Geol. 1998, 15, 109–128. [Google Scholar] [CrossRef]
- Hattab, M.; Hammad, T.; Fleureau, J.M. Internal friction angle variation in a kaolin/montmorillonite clay mix and microstructural identification. Geotechnique 2015, 65, 1–11. [Google Scholar] [CrossRef]
- Bennett, R.H.; Bryant, W.R.; Keller, G.H. Clay Fabric of Selected Submarine Sediments: Fundamental Properties and Models. Sepm J. Sediment. Res. 1981, 51, 217–232. [Google Scholar]
- Locat, J.; Lee, H.; Kayen, R.; Israel, K.; Savoie, M.C.; Boulanger, É. Shear strength development with burial in Eel River margin slope sediments. Mar. Georesources Geotechnol. 2002, 20, 111–135. [Google Scholar] [CrossRef]
- Davis, W.R. The role of bioturbation in sediment resuspension and its interaction with physical shearing. J. Exp. Mar. Biol. Ecol. 1993, 171, 187–200. [Google Scholar] [CrossRef]
- Perret, D.; Locat, J.; Leroueil, S. Strength development with burial in fine-grained sediments from the Seguenay Fhord, Quebec. Can. Geotech. J. 1995, 32, 247–262. [Google Scholar] [CrossRef]
- Ikari, M.J.; Kopf, A.J. The role of cohesion and overconsolidation in submarine slope failure. Mar. Geol. 2015, 369, 153–161. [Google Scholar] [CrossRef]





| Parameters | Unit of Measure | Symbol | Value |
|---|---|---|---|
| Fixed Properties | |||
| Sample dimensions: width; height; length | (m) | 220; 220; 220 | |
| Total number of particles in a sample | 21,172 | ||
| Radius (particles) | (m) | Rp | 3.7; 3.9; 4.6; 5.5 |
| Particle density | (kg/m3) | ρp | 2650 |
| Damping coefficient | damp | 0.7 | |
| Particle friction coefficient (during triaxial test) | µtest | 0.5 | |
| Particle friction coefficient (initial) | µsetup | 0.1 (dense) 0.5 (loose) | |
| Wall properties | |||
| Wall friction coefficient | µ(wall) | 0.0 | |
| Wall normal stiffness | (Pa) | 1e12 | |
| Hertz–Mindlin micro-properties (‘sand’) | |||
| Poisson’s ratio | dimensionless | ν | 0.25 |
| Shear modulus (small; medium; large) | (Pa) | 1e11; 1e10; 1e8 | |
| Parallel-bond micro-properties (‘clay’) | |||
| Parallel-bond contact normal and shear stiffness | (Pa) | 1e10 | |
| Bond radius multiplier | λ | 1 | |
| Bond friction coefficient | 0.54 | ||
| Bond stiffness | (Pa) | 1e5 | |
| Bond cohesive strength (small; medium; large) | (Pa) | 210e3; 110e3; 55e3 | |
| Bond tensile strength (small; medium; large) | (Pa) | 110e3; 55e3; 25e3 | |
| Experiment | Mean Normal Stress (kPa) | Peak Shear Strength (τmax) (kPa) | Macro-Friction Coefficient (µM) | Bulk Cohesion C (kPa) | Experiment | Mean Normal Stress σ3 (kPa) | Peak Shear Strength (τmax) (kPa) | Macro-Friction Coefficient (µM) | Bulk Cohesion (kPa) |
|---|---|---|---|---|---|---|---|---|---|
| ‘Sand’ | |||||||||
| LS-3 ( = 1e8 Pa) | 153 | 53.3 | 0.35 | (3.1) | DS-3 ( = 1e8 Pa) | 241 | 141.9 | 0.64 | (33.3) |
| 382 | 132.4 | 624 | 374.0 | ||||||
| 754 | 254.5 | 1280 | 780.0 | ||||||
| LS-2 ( = 1e10 Pa) | 191 | 91.2 | 0.37 | (26.1) | DS-2 ( = 1e10 Pa) | 224 | 124.1 | 0.52 | (21.2) |
| 425 | 175.2 | 504 | 254.1 | ||||||
| 808 | 308.7 | 976 | 475.9 | ||||||
| LS-1 ( = 1e11 Pa) | 190 | 90.6 | 0.47 | (23.3) | DS-1 ( = 1e11 Pa) | 166 | 66.6 | 0.40 | (4.1) |
| 513 | 263.4 | 407 | 157.2 | ||||||
| 903 | 403.7 | 808 | 308.2 | ||||||
| ‘Clay’ | |||||||||
| LC-3 (PBcoh = 55e3 Pa) | 287 | 187.6 | 0.38 | 92.6 | DC-3 (PBcoh = 55e3 Pa) | 531 | 431.7 | 0.53 | 199 |
| 528 | 278.4 | 801 | 551.8 | ||||||
| 911 | 411.4 | 1291 | 791.5 | ||||||
| LC-2 (PBcoh = 110e3 Pa) | 226 | 126.2 | 0.44 | 52.8 | DC-2 (PBcoh = 110e3 Pa) | 390 | 290.4 | 0.55 | 112 |
| 537 | 287.2 | 679 | 429.9 | ||||||
| 906 | 406.4 | 1174 | 674.4 | ||||||
| LC-1 (PBcoh = 210e3 Pa) | 223 | 123.0 | 0.43 | 32 | DC-1 (PBcoh = 210e3 Pa) | 315 | 215.5 | 0.50 | 81 |
| 452 | 202.8 | 597 | 347.5 | ||||||
| 884 | 384.8 | 1050 | 550.7 | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elyashiv, H.; Bookman, R.; Siemann, L.; ten Brink, U.; Huhn, K. Numerical Characterization of Cohesive and Non-Cohesive ‘Sediments’ under Different Consolidation States Using 3D DEM Triaxial Experiments. Processes 2020, 8, 1252. https://doi.org/10.3390/pr8101252
Elyashiv H, Bookman R, Siemann L, ten Brink U, Huhn K. Numerical Characterization of Cohesive and Non-Cohesive ‘Sediments’ under Different Consolidation States Using 3D DEM Triaxial Experiments. Processes. 2020; 8(10):1252. https://doi.org/10.3390/pr8101252
Chicago/Turabian StyleElyashiv, Hadar, Revital Bookman, Lennart Siemann, Uri ten Brink, and Katrin Huhn. 2020. "Numerical Characterization of Cohesive and Non-Cohesive ‘Sediments’ under Different Consolidation States Using 3D DEM Triaxial Experiments" Processes 8, no. 10: 1252. https://doi.org/10.3390/pr8101252
APA StyleElyashiv, H., Bookman, R., Siemann, L., ten Brink, U., & Huhn, K. (2020). Numerical Characterization of Cohesive and Non-Cohesive ‘Sediments’ under Different Consolidation States Using 3D DEM Triaxial Experiments. Processes, 8(10), 1252. https://doi.org/10.3390/pr8101252




