Abstract
In group key management, the implementation of encryption often fails because multicast communication does not provide reliable linkage. In this paper, a new group key management scheme is proposed for multicast communication in fog computing networks. In the proposed scheme, any legal fog user belonging to a fog node will be able to decrypt a ciphertext encrypted by a secret shared key. The shared secret key is divided into key segments. In the rekeying operation process, each key segment is split into two factors with its shared production mechanism. The key updates are required to belong to the fog provider or the group management device. Fog users will have independent key segments unchanged. Then, the cost, the message of rekeying, and the dependence on credible channels will be decreased. This method can resist collusion attacks and ensure backward security and forward security, even if the number of users leaving is larger than the threshold value. Our scheme is also suitable for untrusted affiliate networks.
1. Introduction
Multicast communication technology is important for different network applications [1,2], especially for wireless networks. It is effective in transferring data from one source to many different destinations. Multicast communication technology has been used in network video, online e-sports, and real-time online conferences, which gets to be susceptible to different security assaults, e.g., refusal of service, eavesdropping, and attacks to capture the physical nodes [3]. At a given time, the message of a source can be sent to many destinations using multicast communication technology. Therefore, the security of multi-directional communication will be a challenging issue [4,5,6], and security schemes are needed for security, authentication, integrity, and non-repudiation of multicast communication [7].
Multicast communication technology is applied to untrusted networks, and tolerances forwarding network [8], such as deep space network, in which the time latency is very long and unreliable links generate rekeying errors [9]. Some solutions have also been proposed to combine multicast communication with other emerging effective technology, such as fog computing technology, which is deployed at the edge of the network near to the users [10]. There have also been many proposals to ensure data security and safety for multicast communication technology in fog computing [11,12]. In [13,14], the authors discuss the fog computing model for security and privacy issues, the advantages and applications of fog computing, like the smart grid, smart traffic lights in a vehicular network, and software-defined networks. In [15], the author uses visual cryptography and zero watermarking to develop a biometric security mechanism in fog computing. The paper [16] proposes identity authentication schemes based on fog computing, checking data integrity, data encryption to meet security, resolution, and availability of face recognition. To authenticate users, a secure key management scheme is proposed for fog computing services in [17]. In [18], the authors discussed problems related to fog computing, such as applications, challenges, and technologies, through surveying with different fog computing models. In [19], the authors have proposed an effective method in fog computing with an anti-duplication privacy protection technique to manage ownership. In [20], to ensure secure communication between a group of fog nodes and clouds, the authors have designed a key exchange scheme as an attribute-based encryption scheme. In [21], the authors propose an anonymous summary scheme, in which fog nodes are responsible for synthesizing data from the terminal nodes, and then transfer the aggregate data to the public cloud server. In [22], the author presents a summary of the research contributions and outlines future research directions to solve various security and privacy challenges in the fog computing field.
In multicast communication security, there are many proposed technologies. Group key management (GKM) is one of the important technologies [23,24,25]. It is a platform for security and efficiency, to support access, authentication, key agreement, etc. Therefore, to design schemes of GKM for multicast communication needs to be reviewed in detail for efficiency and security. Especially, the joining or leaving operation of members in the network, and the network resource costs for rekeying operations, must be ensured for forward and backward security [24,26]. GKM schemes have been proposed and applied and can classify into two categories following the member’s role. First is the key agreement protocol, such as the group key agreement [27,28], the communication-efficient group key agreement [29,30], the tree-based group key agreement [28], and the Diffie-Hellman-Logical Key Hierarchy (DH-LKH) [31,32]. Before communication, a shared key needs to be agreed upon by all group members. Part of the key material needs to be contributed to calculate the shared keys. The key management works the same on all members. The updated members have the rekeying tasks, and the computing costs are related to the scale of the networks, as given the autonomic group key management in deep space DTN (AGKM) in [33], and the autonomous shared key management scheme for space networks (AKMSN) [34]. There is no need to have a key management center as a powerful entity for key agreement protocol. The security channel does not need to be configured and some failed members can be accepted during the negotiation process. However, the Key Agreement Protocol has some inherent shortcomings, such as the scale of the network involves costs for rekeying operations. The implementation of public cryptographic arithmetic and the main time for exchanging materials between members is very high, so it consumes a lot of network resources. However, when the current wireless network is sensitive with the delay time or is limited with the resources, key agreement protocol is not suitable. Second is the key distribute protocol. The key management center plays a key role, such as having a strong entity. They undertake the task of creating, distributing, updating, and revoking. In the key distribute protocol, the shared keys will be sent for each legitimate member before joining the network to establish a secure channel. Two members can contact each other successfully, when they had a shared key, such as pairs key management [35], a key management scheme of random pre-distribution [36,37,38], and logical key hierarchy (LKH++) [39]. The network resource cost and time latency will be lower in these protocols, compared to those in the key agreement protocol.
In multicast communication, most GKM proposals are based on the ciphertext of the encryption key model, which can only be decoded successfully with a decryption key (Dk). In the rekeying operation, all members need to participate, which leads to the problem of 1-affect-n that considers whether the member updates. This affects the rest of the group as long as one member changes. The cause is that only one traffic encryption key (TEK) or group key is applied in group communication. To enforce security, after a single membership change, TEK needs to be updated for all members of the group. TEK is used to evaluate a 1-effect-n phenomenon. Otherwise, the group application suffers from the 1-affect-n phenomenon and consequent performance deterioration. Some other proposals are proposed in [40,41,42,43,44] to reduce the rekeying scale. In general, group key management has an important target to improve efficiency that decreases delay time, resource overheads, and scale in rekeying operations.
In [35], the authors propose a GKM scheme based on the multi-decryption key one-encryption key model. The multi-decryption keys have independent properties with each other corresponding to one encryption key. In the rekeying operation, the legitimacy of the decryption key that pertains to non-updated members is not destroyed by the updated decryption key. It can be said that this model is suitable for multicast communication. Consequently, the multi-decryption key protocol of one encryption key is promising to be widely applied in [42,43,44,45], in bilinear pairings [46], and threshold cryptography [47]. However, the schemes have some shortcomings, where the rekeying operation is still related to the network scale, and members who join or leave the network must participate in the rekeying operation, which is the ineffective cause in the collusion attack. Through collecting key segments with more than one threshold value, an attacker can negotiate the shared key.
In group key management, the implementation of encryption often fails because multicast networks do not provide reliable linkage. In this paper, we try to a group key management scheme for multicast communication fog computing networks, named GKMSFC. The main contributions are as follows:
- Any legal fog user who belongs to a fog node will be able to decrypt a ciphertext encrypted by a secret shared key.
- The shared secret key is divided into key segments, In the rekeying operation process, each key segment is split into two factors with his shared production mechanism, key updates are required to belong to the fog provider or the group management device.
- For the security aspect, because a different random value is chosen by the source in every process of decrypting, it is not possible to damage the decryption key, and the proposed scheme can ensure the backward and forward security and can against the collusion attacks.
The following sections of this paper are organized as follows. In Section 2, we illustrate the basic fog network structure and security requirements; In Section 3, we present and describe the knowledge of bilinear pairing and threshold cryptography. In Section 4, a group key management diagram is proposed, which includes the details of the use of main keys and a secret shared key. In Section 5, bases on security properties, such as the repairs, forward / backward security, and collusion attack, we analyze the security of the proposed model. In Section 6, we compare the performance of other group key management schemes with the proposed scheme; and finally, the conclusion of the article is given in Section 7.
2. Fog Computing Environment
2.1. Fog Network
Fog computing is defined as a computing server device at the edge of the network and includes devices close to the end-user. It plays as an intermediary layer between user devices and the cloud, in other words, it is the extended part of the cloud towards user devices. Fog nodes exist in fog computing networks, which can be considered as a “mini-cloud” located at the edge of the network and implemented through a variety of edge devices [48,49]. A fog computing-based network model is portrayed in Figure 1, which is represented by a hierarchy including cloud layer, fog layer, and end-user layer. The system entities are explained below:
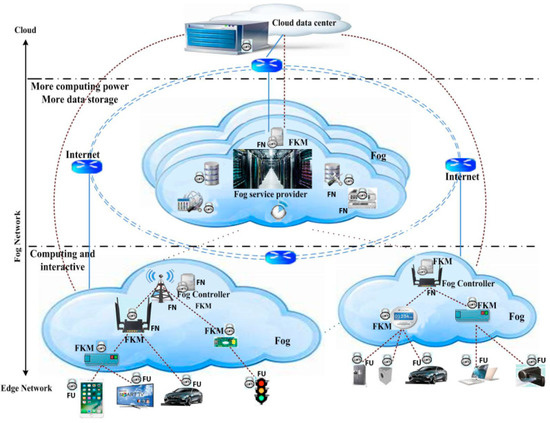
Figure 1.
Network model of fog structure.
- Cloud: Store, control, handle all data centers, and online services. It receives all data from Fog nodes, analyzes, and processes data according to the requirements of some applications.
- Fog Node (FN): Is an important active component for processing, calculating, and storing secret keys. It includes devices between the cloud and end-users, such as the base stations, servers, gateways, routers, switches, and access points. Each fog node serves the end-users in its communication range. We assume that the entities are reliable and well protected.
- Fog User (FU): Are the types of terminals that use services provided by the cloud or the providers of fog services. These types of devices are structured as heterogeneous (such as vehicle networks, smartphones, IoT devices, etc.). They connect short communication with the Fog node, in which the devices can be equipped with sensors and the ability to communicate to perceive environmental phenomena and send data through channels of communication to the fog node.
- Fog Key Management Center (FKM): Computes and creates secret keys, session keys, and private keys for users. In the fog network system, it is completely trusted by all members. The results and discussions may be presented separately, or in one combined section, and may optionally be divided into headed subsections.
2.2. Security Requirements
To ensure secure access, each fog service has a service key and each user or a group is sharing the same service key for access and is served by the fog devices. New challenges will arise, such as efficiency, performance, and scalability, if a group of dynamic users is sharing the same service key. Then, in group communication, only legitimate users can access the service and should follow the following rules:
- Backward security: When a new member joins the fog node to use the services, the GKM must ensure that a new member cannot decrypt the data before it joins the fog node. Then the GKM system is secure.
- Forward security: When a member loses the privilege of accessing the fog to use the service, it will not decrypt any group keys and any future group messages. Then the GKM system is secure.
- Collusion attacks: A secure GKM system will not be compromised, when some members cooperate to use the old keying documents to regain the group key.
2.3. Fog Security Devices Role
In each fog point, the FN is a member. It also acts as a representation of its Fog Users (FUs) cluster in its parent fog. When the FN receives the parent’s fog notification, it announces the message to the FU in its cluster. All FNs use the same shared key (Sk), and the FN’s task is to publish the received notifications. In this configuration, a single membership change in any fog cluster will result in a new Sk distribution to all fog users in all fog zones, as a common Sk is used. When one of the security fogs becomes the driving force for the member’s change, it is better to isolate the cluster from the other fog clusters, and divide it into segments to limit the effects of re-tracking of dynamic fog, and thus to reduce the 1-affects-n phenomenon. In our plan, we propose that in such situations the dynamic FN would decide to use an Sk independent of its fog cluster and Let (s, tk) be the threshold in the cryptographic protocol, where s is the key segments divided from the secret shared key (Sk), tk is a number of key thresholds, and each user collects a key section. Fog Users (FUs) can re-store shared keys if they own more key segments than the threshold tk. The rekeying operation only includes the resources of the encryption key, and the decoding of end-user FU does not change when a member of the group joins or leaves. The decryption key of the group members is not affected by the joining users’ rekeying operation. In this action, only the decryption key (Dk) is updated by FKM. Do not lose the legitimacy of the Dk when the member leaves without affecting the remaining members, it means that the FKM updates still own the decryption key without changing.
3. Key Establishment
3.1. Bilinear Pairings
Let () and () respectively denote a cyclical addition and multiplication group of large prime order . A generator is denoted by , which belongs to the cyclic group G with order . A bilinear map is given by , and a generator of is . There are three properties in a bilinear map [50,51].
- Bilinearity. For , we have and , where ;
- Computability. For , there continually exists an efficient algorithm to calculate the value of ;
- Nondegeneracy. If , then we have .
Based on the Bilinear Pairings, we will propose a security scheme, and define a probabilistic polynomial-time algorithm by the bilinear map instance generator. For the Bilinear Decision Diffie-Hellman Problem, we need to calculate the value by giving , where , decide .
3.2. Threshold Cryptography
Let (s, tk) be the threshold cryptographic protocol, where s is the key segment which is divided from the secret shared key, tk is the number of key thresholds. Each user collects a key section. Users can re-store the shared keys if they own more key segments than the threshold tk [52].
Each legal has a unique identity (),. In all identities form the FKM selects k random value in . From a tk-degree polynomial equation, we have,
Constructing an equation of tk − 1 degree polynomial,
In a key distribution (KD) is the shared key, FKM computes,
With a set, via a secure channel, receives the value as key segments . In a key recovery phase, FU is able to decrypt the encrypted ciphertext by using the shared key, because it collects tk key segments.
The polynomial equation is shown according to the Lagrange’s interpolation formula as follows,
where .
The formula that can be used to calculate shared keys is
To concise, we assign a parameter with
When is showed as
3.3. Shared Secret Product
In substance, the threshold (s, tk) based secret product shared mechanism comes from the multiplication of two factors, where the two factors are illustrated by two formulas: with a degree polynomial and random parameter sets , and with a degree polynomial and random parameter sets . Based on this secret product shared mechanism, FU can compute a product correctly, but it is unable to calculate to get any information on the two factors [53].
Constructing a degree polynomial as follows
are divided into s segments corresponding to the two formulas and , and each member receives a key segments . Then is a segment of production .
The formula is shown
and
4. Group Key Management Scheme in Fog Computing Network
In this section, we will give out the proposed scheme, named GKMSFC, which is a new group key management scheme for multicast communication fog computing networks), there are FKM is Fog Key Management Center, The whole scheme is divided into four stages, including initialization stage, encryption stage, decryption stage and rekeying stage. is the algorithm of the symmetric encryption key, is the algorithm of a symmetric decryption key, the hash function and N is the number of members.
4.1. Initialization Stage
Random numbers are selected and kept secretly by FKM from , to construct formulas and with δ—1-degree polynomial, is a formula with ε—1-degree polynomial. With the shared secret product mechanism, and are given as follows
Polynomial formula with the degree is
The FKM selects numbers and constructing several sets as follows
Then calculating , where are selected by FKM as the main encryption key. The FKM selects two numbers and computes
After the first step is finished, a Fog user () has some decryption keys and an encryption key , which are expressed as
In the , an encipherer of a session key is decrypted by the main encryption key , has the decryption key for its decoder.
4.2. Encryption Stage
A source wants to send a plaintext to some destinations, main encryption key creates session key to encrypt the into a ciphertext Cipt through the following steps:
- A random number q is selected by the source to calculates ;
- Session key with and handles encryption are calculated by the source;
- The source calculatesand ;
- Finally, the ciphertext is sent to the destinations by the source.
4.3. Decryption Stage
An end-user uses the decryption key to decrypt a Cipt to obtain a plaintext . The steps are given as follows:
- An end-user calculates with and , where
- decrypts the ciphertext with ;
- The will accept a valid plaintext (Mas’) in case I’= I, else it will be rejected.
4.4. Rekeying Stage
The rekeying operation only includes the resources of the encryption key, the decoding of the end-user. FU does not change when a member of the group joins or leaves.
- JoinWe assume a new user joins as , this activity will take place as follows:
- (1)
- FKM selects id random numbers for , having a new set ;
- (2)
- FKM selects , replaces with , so with degree polynomial
FKM calculates with
The decryption key of the group members is not affected by the joining users’ rekeying operation. However, in this action, only the Dk is updated by FKM.
- LeaveWe assume a new user leaves as , this activity will take place as follows:
- (1)
- The FKM deletes from ;
- (2)
- FKM selects , replaces with , so with degree polynomial
FKM calculates with
Do not lose the legitimacy of the Dk, when the member leaves without affecting the remaining members, it means that the FKM updates still own the decryption key without changing.
5. Security Analysis
In this section, we demonstrate the process of decrypting a ciphertext by a legitimate member through the process of modifying. Through the security section, we demonstrate that the calculation of the probability of an attacker cracking is equal to the BDDH problem, and the probability of this attack is insignificant for the attacker to crack. Our scheme guarantees the security of Collusion attacks, Backward secrecy, and Forward secrecy.
5.1. Adjusting
The primary key encrypts a session key if any member with a valid Dk can decrypt a ciphertext to obtain the right plaintext Mas. uses Fog service legally with . The process of successfully decrypting Mas with the decryption key is as follows
5.2. Security
If the security of the program can be deduced into a complex and difficult issue, our project still satisfies the safety of the system. In the Probability Polynomial Time (PPT), we prove that it is a non-negligible probability for attacker cracks the BDDH problem (Bilinear Decision Diffie-Hellman Problem). We primarily center the security of main Ek within the equation , because security depends on but the security of depends on the main Ek. We deduce security for the BDDH problem by building an emulator as given in Algorithm 1:
| Algorithm 1 Steps for Building the Emulator |
Input: set , and is a random number
polynomial with degree, polynomial with degree, with degrees, then send to the attacker a set ; 5.2. The attacker selects and sends two same size keys to emulator; 5.3. The emulator chooses randomly, and sends that is ciphertext; 5.4. The attacker analyzes to receive and sends it to the emulator. If y′ = y, Then output . Else, output . If , Then is an valid ciphertext with . If Then is an invalid ciphertext with |
Therefore, if c is an invalid ciphertext the attacker will not be able to retrieve any information. The probability of success or failure when prediction y is equal, it can show as,
Judgment probability of emulator program when value is,
The attacker obtains a valid ciphertext, when , with the probability of , is organized according to the formula,
Therefore, the judgment probability of the emulator program is valid
In short, the advantage of cracking BDDH problems is
Thus, from (30) GKMSFC and the BDDH problem have an equal probability of cracking key, this probability is negligible for the probability polynomial-time attacker.
5.3. Collusion Attack
Collusion attacks will threaten shared secret keys, if the number of secret key’s segments held by the attacker is greater than tk. Therefore, some GKM schemes based on cryptographic thresholds are not able to avoid this type of attack [45,46]. Because when a member leaves, the main encryption key remains unchanged. Then these members can collude with each other or malicious people can invade and compromise encryption keys with members leaving by taking the main Ek material with tk segments. Then it will calculate on Ek and can successfully calculate Ek as
Thus, to prevent a collusion attack, every time a member joins or leaves the network, the of the main key must be updated, because the encryption Sk can be successfully cracked by an attacker if it does not know the main key and q′. For our GKMSFC, even if the attacker collects more keys than the number of the threshold, it cannot recover the main key. At the installation step with with degree , , the main key is divided into some key segments. The source takes the id of the key segment of and nKD key segments of . The destination receives KD segments of . The destination is not able to calculate before the decrypting step, because it does not have enough key segments even when is a known number. At the decrypting step, the source sends a ciphertext on where q is a random number, with BDDH cracking probability. is negligible for a destination to retrieve . Therefore, it is impossible to restore the main key with the segments of the compromised members. The attacker can compromise and get more key segments than the number of , when the number of members leaves is . The other attackers get on and , on and , on in all encrypting operations. If the source chooses random q, then respond and , an attacker can calculate the encryption key Ek as follows
Therefore, to defend the session key Sk and the main key , conditions are required on and . on does not match the updated key segments . So, any malicious person can steal and more key segments than the number of the upper threshold, but it is not able to recover .
5.4. Forward/Backward Security
These are some important targets of security in GKM. Before and after the key update is at risk of being cracked by many members. The model in [45,46] cannot resist the collusion attack. In scheme [45,46], if the number of joining or leaving members is more than tk, it will be unable to guaranteed security. We propose a GKMSFC scheme with better performance because this scheme controls the random number q depended on the main key . Enemies cannot attack, even if they capture the main key , because they do not have a random session key q. Moreover, the FKM updates to update , the main key is unable to be recovered before updating by a new joining member, but only recover the main key with by a new joining member, therefore it can ensure backward security. For the case when a member leaves, , can be updated by the FKM with updated the main key after the update is difficult to calculate with , and before the updating, it can only restore the .
6. Analysis Performance of KMGSFC
In this section, we analyze our model performance by comparison with other models through parameters, such as computation overhead, message overhead, rekeying efficiency, network load, scalability, 1-affect-n problem, and time latency.
6.1. Computation Overhead
The calculation of the bilinear pair in the GKMSFC scheme is considered with the most complex activities, which includes scalar multiplication in , , pairing calculations, and exponential modules.
- id for scalar multiplication , nKD scalar multiplication for in , scalar multiplication for are all done by FKM. Then we can calculate the total cost of computation, id + 2nKD + 2, for scalar multiplication in .
- For the encrypting phase, we can calculate the total cost of computation as id + nKD + 1, for scalar multiplication in and exponential modules. The source performs scalar multiplication for , id scalar multiplication for , nKD scalar multiplication for , and exponential module for .
- For the decoding phase, we can calculate the total cost of calculation as the scalar multiplication id + KD in G, KD + 1 in (Equation (25)), because id scalar multiplication is deployed for KD with scalar multiplication in with KD in , and multiplication in is done in the numerator of Formula (25).
6.2. Message Overhead
Suppose N1 is the size of the group , , the size ofis N2, and the size of is N3. Then in the encryption phase,, and the network scale affects the message cost .
6.3. Rekeying Efficiency
In our key management model, the cost of messages and network connections are zero, because a member leaves or joins, the other members still retain the decryption key. Only FKM updates the encryption key by recalculating and . In , FKM performs scalar multiplication for a joining , or scalar multiplication for a leaving . However, in the scheme [45,46], the rekeying protocol ought to be redeployed to send a new Dk to the members and in the scheme the rekeying protocol ought to be redeployed to send a new key service to the members.
If the polynomial in the scheme [45,46] has a degree the decoder has id key segments and enciphers with KD key segments. In , key management center performs scalar multiplication for a joining and the key segments are updated for members with n + 1 messages cost, or scalar multiplication for a leaving and the key segments are updated for members with the cost given by n–1 messages.
In Table 1, we provide a performance comparison of some GKM schemes with our scheme. These schemes are effective as they can be executed by cryptographic hash functions and symmetric encryption schemes. We offer accurate analytical formulas rather than numerical data, using a set of system parameters that can be used to evaluate complexity and efficiency without network simulation. In each comparison, we introduce a bulletin to guarantee that an asynchronous member can calculate the updated group key regardless of how many rekey processing procedures are missed. The communication overhead is the number of transmitted tokens, the computation overhead is the number of performed activities for a member and the storage overhead is the number of stored keys for a member during the rekey and recovery processes.

Table 1.
Comparison of group key management (GKM) different schemes.
Table 1 shows that Scheme [55] requires a message sent from the Fog Security Gateway to the end-users to request rekeying operation when a member joins or leaves, but our proposal outperformed the performance in this operation without any messages from the fog device. Furthermore, our proposal can prevent collusion attacks, ensure forward/backward security. However, Scheme [55] and Scheme [54] only protect forward/backward security. Although GKMSFC and Scheme [45,46] have the same computational cost, GKMSFC has less network load and message costs. Computation cost in AKMSN is more than the computation cost of Scheme [45,46] and GKMSFC, during the update of the rekeying re-establishment.
6.4. Scalability
In our proposal, the joining or leaving action is easy, without the involvement operation of other members [45,46]. Although the program needs support from FKM as well as Scheme [45,46] with the support of key management center, our proposal has better scalability than Scheme [45,46], because of the operation of the Scheme [45,46]’s rekeying process requires all members to join members who are joining. In the GKMSFC, the decryption key will not change for the remaining members, so the rekeying time will be less.
6.5. 1-affect-n Problem
We run the simulation using the Python Network library and obtain the average results over many iterations per simulation scenarios. We study 1 affects n phenomenon of each simulation protocol and the amount of decryption and re-encryption operations required for communication, by comparing KMGSFC with three existing approaches using single SK: independent SK per smog, centralized scheme, and scheme in [55].
In Figure 2, the features of the proposed scheme reduce to zero with the impact of the 1-affect-n phenomenon and improve the performance of GKM. In addition, the proposed scheme also maintains the quality of service (QoS) of group applications, especially for some high-security group applications, such as military communications where the group communication has to be interrupted during key updating. In conclusion, the 1-affect-n phenomenon in GKMSFC can be minimized to zero.
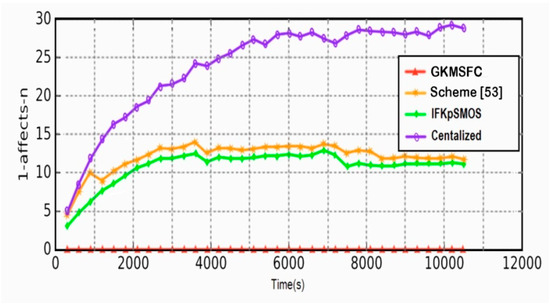
Figure 2.
Compare 1-affect-n phenomenon.
6.6. Time Latency
In key management, computing and communication of two activities will increase the latency: hardware performances when objects joining the network, and the complexity of key management algorithm. This paper focuses on communication latency, especially the latency in deep space networks. Because the calculation latency is significantly less than the spread latency, this latency will be determined by the channel’s physical properties when the link is reliable and the radio waves speed is fixed. Then more distance leads to more latency, and spread latency can be significantly increased in case there is unreliability to the channel. It can be sent multiple times to meet the task’s requirements with the same message. In this manner, the procedure of our proposition is based on the distribution of fog devices, and its advantages are the computing abilities near the end-user, to increase the link reliability. Moreover, our key management program reduces the dependence of reliable links, because the redundant members are eliminated, and in rekeying the key updating of legitimacy, members can be ignored. Attempting to gather as many key segments as possible with all the members, reducing the retransmission as many times as possible, the ability to not send the key material in unreliable links can reduce the latency in GKM. Without a reliable link, the legitimacy of the member’s Dk and the secret shared key can also be updated and revoked by the proposed FKM.
This scheme is tested to check the effectiveness in the probability of connection of the link from 0.1 to 1, and the threshold of threshold cryptography value is 10 with 100 members participating. The time latency of Scheme [45,46] and GKMSFC are almost similar in different connectivity probability links. As shown in Figure 3, with the x-axis showing the probability of the connection link, the y-axis shows the success rekeying rate.
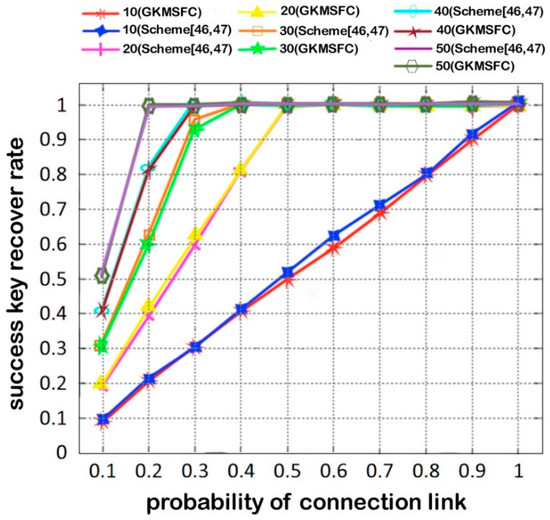
Figure 3.
Compare the time latency of the group key management scheme for multicast communication fog computing networks (GKMSFC) and Scheme [45,46].
In the GKMSFC Scheme, FKM has the task of rekeying without interactions between members, so it has a better performance than that of the Scheme [45,46]. However, in scheme [46,47], the success rekeying rate decreases with the decreasing probability of connection. In rekeying operation, GKMSFC has less time latency than Scheme [45,46], as shown in Figure 3.
The transmission time latency of GKMSFC and Scheme [45,46] is compared in Figure 4, with 2 selected random members, respectively source and destination. The distance between the two members are 10 hops, and each hop has a latency of 1ms. The relay member gets to be an updated member with a probability of 0.5 because during the transition member data can update the key. It can be seen that GKMSFC has less time latency than Scheme [45,46] because when there is a change of members, the old members are not involved in the rekeying process, as shown in Figure 5.
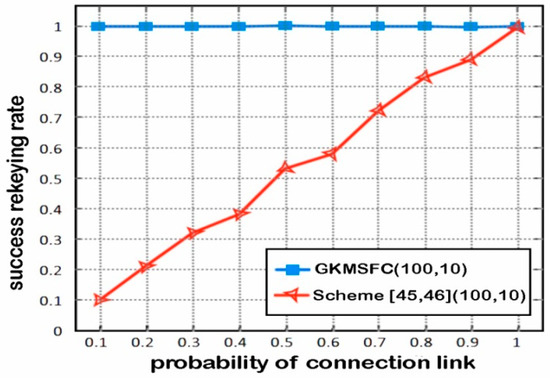
Figure 4.
Rekeying success rate under different connectivity probability.
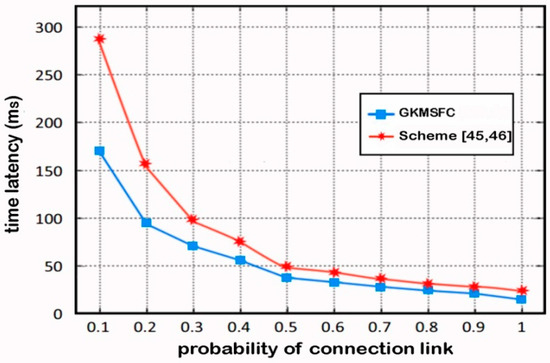
Figure 5.
Compare time latency between GKMSFC and Scheme [45,46].
7. Conclusions
Based on the common secret product of the cryptography threshold and the bilinear pairs, we have proposed GKMSFC based scheme, which is a profile of a key management diagram that has better performance. The independence of the key is met by the decryption keys, with the advantage of an encryption key that corresponds to multi-decryption keys, including two components, fog computing and the end-users, respectively. In the rekeying operation, the key segments are divided into two elements, one is kept secret by FMK, where it can update the main key by its method. The other one is known by members which is unchanged, to help to improve the rekeying efficiency for time latency. The failure to update the decryption key of all remaining members would improve the cost of messaging and calculation. For the security aspect, because a different random value is chosen by the source in every process of decrypting, it is not possible to damage the decryption key, even an attacker has several key segments that exceed the threshold. GKMSFC can ensure the backward and forward security and can against the collusion attacks.
Author Contributions
Methodology, M.T.D.; software, M.T.D.; formal analysis, H.X.; resources, H.X.; data curation, M.T.D.; writing—original draft preparation, M.T.D.; writing—review and editing, M.T.D. and H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation Project of China with No. 61971032, 61931001, the Fundamental Research Funds for the Central Universities with No. FRF-BD-20-11A.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biradar, R.C.; Manvi, S.S. Review of multicast routing mechanisms in mobile ad hoc networks. J. Netw. Comput. Appl. 2012, 35, 221–239. [Google Scholar] [CrossRef]
- Dinesh, C.; Rajneesh, K. QoS Enabled Cross-Layer Multicast Routing over Mobile Ad Hoc Networks. Procedia Comput. Sci. 2018, 125, 215–227. [Google Scholar]
- Park, M.H.; Park, Y.H.; Jeong, H.Y.; Seo, S.W. Key Management for Multiple Multicast Groups in Wireless Networks. IEEE Trans. Mob. Comput. 2012, 12, 1712–1723. [Google Scholar] [CrossRef]
- Omar, C. Secure Group Communication in Wireless Sensor Networks: A Survey. J. Netw. Comput. Appl. 2013, 61, 115–132. [Google Scholar]
- Hui, H.; Zhou, C.; Xu, S.; Lin, F. A Novel Secure Data Transmission Scheme in Industrial Internet of Things. China Commun. 2020, 17, 73–88. [Google Scholar] [CrossRef]
- Gong, C.; Lin, F.; Gong, X.; Lu, Y. Intelligent Cooperative Edge Computing in the Internet of Things. IEEE Internet Things J. 2020, 7, 9372–9382. [Google Scholar] [CrossRef]
- Judge, P.; Ammar, M. Security issues and solutions in multicast content distribution: A survey. IEEE Netw. Mag. Glob. Internetworking 2003, 17, 30–36. [Google Scholar] [CrossRef]
- Saadawi, T. A delay-tolerant networking architecture for airborne networking. Def. Tech. Inf. Cent. 2010, 1–31. [Google Scholar]
- Mukherjee, J.; Ramamurthy, B. Communication technologies and architectures for space network and interplanetary Internet. IEEE Commun. Surv. Tutor. 2013, 15, 881–897. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, X.; Wang, J.; Chen, H.H. Security in space networks. IEEE Commun. Mag. 2015, 53, 82–88. [Google Scholar] [CrossRef]
- Kadhim, A.J.; Seno, S.A.H. Energy-efficient multicast routing protocol based on SDN and fog computing for vehicular networks. Ad Hoc Netw. 2019, 84, 68–81. [Google Scholar] [CrossRef]
- Yi, S.; Qin, Z.; Li, Q. Security and Privacy Issues of Fog Computing: A Survey. In International Conference on Wireless Algorithms, Systems, and Applications; Springer: Cham, Switzerland, 2015; pp. 685–695. [Google Scholar]
- Stojmenovic, I.; Wen, S. The Fog Computing Paradigm: Scenarios and Security Issues. In Proceedings of the Federated Conference on Computer Science and Information Systems, Warsaw, Poland, 7–10 September 2014; pp. 1–8. [Google Scholar]
- Zhang, P.Y.; Zhou, M.C.; Fortino, G. Security and trust issues in Fog computing: A survey. Future Gener. Comput. Syst. 2018, 88, 16–27. [Google Scholar] [CrossRef]
- Wadood, A.; Ali, Z.A.; Ghouzali, S.; Alfawaz, B.; Muhammad, G.; Hossain, M.S. Biometric security through visual encryption for fog edge computing. IEEE Access 2017, 5, 5531–5538. [Google Scholar]
- Hu, P.; Ning, H.; Qiu, T.; Song, H.; Wang, Y.; Yao, X. Security and privacy preservation scheme of face identification and resolution framework using fog computing in the internet of things. IEEE Internet Things J. 2017, 4, 1143–1155. [Google Scholar] [CrossRef]
- Wazid, M.; Das, A.K.; Kumar, N.; Vasilakos, A.V. Design of secure key management and user authentication scheme for fog computing services. Future Gener. Comput. Syst. 2019, 91, 475–492. [Google Scholar] [CrossRef]
- Hu, P.; Dhelim, S.; Ning, H.; Qiu, T. Survey on fog computing: Architecture, key technologies, applications and open issues. J. Netw. Comput. Appl. 2017, 98, 27–42. [Google Scholar] [CrossRef]
- Kooa, D.; Hura, J. Privacy-preserving deduplication of encrypted data with dynamic ownership management in fog computing. Future Gener. Comput. Syst. 2018, 78, 739–752. [Google Scholar] [CrossRef]
- Alrawais, A.; Alhothaily, A.; Hu, C.; Xing, X.; Cheng, X. An attribute-based encryption scheme to secure fog communications. IEEE Access 2017, 5, 9131–9138. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Domingo-Ferrer, J. Anonymous and secure aggregation scheme in fog-based public cloud computing. Future Gener. Comput. Syst. 2018, 78, 712–719. [Google Scholar] [CrossRef]
- Mukherjee, M.; Matam, R.; Shu, L.; Maglaras, L.; Ferrag, M.A.; Choudhury, N. Security and privacy in fog computing: Challenges. IEEE Access 2017, 5, 19293–19304. [Google Scholar] [CrossRef]
- Yacine, C.; Hamida, S. Group key management protocols: A novel taxonomy. Int. J. Inf. Technol. 2005, 2, 105–118. [Google Scholar]
- Sandro, R.; David, H. A survey of key management for secure group communication. ACM Comput. Surv. 2003, 35, 309–329. [Google Scholar]
- Manivannan, D.; Neelamegam, P. WSN: Key issues in key management schemes—A review. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 3188–3200. [Google Scholar]
- Xu, Q.; Tan, C.; Fan, Z.; Zhu, W.; Xiao, Y.; Cheng, F. Open AccessArticle Secure Data Access Control for Fog Computing Based on Multi-Authority Attribute-Based Signcryption with Computation Outsourcing and Attribute Revocation. Sensors 2018, 18, 1609. [Google Scholar] [CrossRef]
- Chen, C.W.; Wang, S.J.; Tsai, Y.R. Fast-Refreshing Tree-Based Group Key Agreement for Mobile Ad Hoc Networks. In Proceedings of the Seventh Asia Joint Conference on Information Security, Tokyo, Japan, 9–10 August 2012. [Google Scholar]
- Kim, Y.; Perrig, A.; Tsudik, G. Tree-based group key agreement. ACM Trans. Inf. Syst. Secur. 2004, 7, 60–96. [Google Scholar] [CrossRef]
- Ermiş, O.; Bahtiyar, Ş.; Anarım, E.; Çağlayan, M.U. A secure and efficient group key agreement approach for mobile ad hoc networks. Ad Hoc Netw. 2017, 67, 24–39. [Google Scholar] [CrossRef]
- Steer, D.; Strawczynski, L.L.; Diffie, W.; Weiner, M.A. Secure Audio Teleconference System. In CRYPTO’88; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Burmester, M.; Desmedt, Y. A Secure and Efficient Conference Key Distribution System. In EUROCRYPT’94; Springer: Berlin/Heidelberg, Germany, 1994; Volume 950, pp. 275–286. [Google Scholar]
- Steiner, M.; Tsudik, G.; Waidner, M. Diffle–Hellman Key Distribution Extended to Group Communication. In Proceedings of the 3rd ACM Conference on Computer and Communication Security, New Delhi, India, 14–16 March 1996; pp. 31–37. [Google Scholar]
- Zhou, J.; Song, M.; Song, J.; Zhou, X.W.; Sun, L. Autonomic group key management in deep space DTN. Wirel. Pers. Commun. 2014, 77, 269–287. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, X.W. Autonomous shared key management scheme for space networks. Wirel. Pers. Commun. 2013, 72, 2425–2443. [Google Scholar] [CrossRef]
- Haohua, C.; Lintian, Q.; Klara, N.; Hua, W.; Ritesh, J. A secure multicast protocol with copyright protection. ACM SIGCOMM Comput. Commun. Rev. 2002, 32, 42–60. [Google Scholar]
- Kishore, R.; Radha, S.; Ramasamy, P. A secure key predistribution scheme for WSN using elliptic curve cryptography. ETRI J. 2011, 33, 791–801. [Google Scholar]
- Haowen, C.; Perrig, A.; Song, D. Random key predistribution schemes for sensor networks. In Proceedings of the 2003 Symposium on Security and Privacy, Berkeley, CA, USA, 11–14 May 2003; pp. 197–213. [Google Scholar]
- Chung, K.W.; Mohamed, G.; Simon, S.; Fellow, L. Secure group communications using key graphs. IEEE ACM Trans. Netw. 2000, 8, 16–29. [Google Scholar] [CrossRef]
- Yao, W.; Han, S.; Li, X. LKH++ based group key management scheme for wireless sensor network. Wirel. Pers. Commun. 2015, 83, 3057–3073. [Google Scholar] [CrossRef]
- Klaoudatou, E.; Konstantinou, E.; Kambourakis, G.; Gritzalis, S. A survey on cluster-based group key agreement protocols for WSNs. IEEE Commun. Surv. Tutor. 2011, 13, 429–442. [Google Scholar] [CrossRef]
- Li, H.; Zhou, C.; Xu, H.; Lv, X.; Han, Z. Joint Optimization Strategy of Computation Offloading and Resource Allocation in Multi-access Edge Computing Environment. IEEE Trans. Veh. Technol. 2020. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. SIAM J. Comput. 2003, 32, 586–615. [Google Scholar] [CrossRef]
- Desmedt, Y.; Frankel, Y. Threshold cryptosystems, advances in cryptology. In CRYPTO’89 Proceedings; Springer: Berlin/Heidelberg, Germany, 1990; Volume 435, pp. 101–109, 307–315. [Google Scholar]
- Chiou, G.H.; Chen, W.T. Secure broadcast using secure lock. IEEE Trans. Softw. Eng. 1989, 15, 929–934. [Google Scholar] [CrossRef]
- Liao, J.P.; Hui, X.L.; Qing, Q.P.; Yi, L.; Yu, M.W. A public-key encryption scheme with one-encryption and multi-decryption. Chin. J. Comput. 2012, 35, 1059–1067. [Google Scholar]
- Kurosawa, K. Multi-Recipient Public-Key Encryption with Shortened Ciphertext. In Proceedings of the 5th International Workshop on Practice and Theory in Public-Key Cryptosystem, Paris, France, 12–14 February 2002; pp. 48–63. [Google Scholar]
- Wu, L.; Wang, J.; Choo, K.K.; Li, Y.; He, D. An efficient provably-secure identity-based authentication scheme using bilinear pairings for Ad hoc network. J. Inf. Secur. Appl. 2017, 37, 112–121. [Google Scholar] [CrossRef]
- Marín-Tordera, E.; Masip-Bruin, X.; García-Almiñana, J.; Jukan, A.; Ren, G.J.; Zhu, J. Do we all really know what a fog node is? Current trends towards an open definition. Comput. Commun. 2017, 109, 117–130. [Google Scholar] [CrossRef]
- Tordera, E.M.; Masip-Bruin, X.; Garcia-Alminana, J.; Jukan, A.; Ren, G.J.; Zhu, J.; Farré, J. What Is a Fog Node? A Tutorial on Current Concepts towards a Common Definition. Available online: https://arxiv.org/abs/1611.09193 (accessed on 28 November 2016).
- Teven, D.G.; Kenneth, G.P.; Nigel, P.S. Pairings for cryptographers. Discret. Appl. Math. 2008, 156, 3113–3121. [Google Scholar]
- Joux, A. A one round protocol for tripartite Diffie-Hellman. Lect. Notes Comput. Sci. 2000, 1838, 385–393. [Google Scholar]
- Desmedt, Y. Threshold cryptography. Eur. Trans. Telecommun. 1994, 5, 449–458. [Google Scholar] [CrossRef]
- Desmedt, Y. Some recent research aspects of threshold cryptography. Lect. Notes Comput. Sci. 1998, 1396, 158–173. [Google Scholar]
- Li, Z.; Liu, Y.; Liu, D.; Li, C.; Cui, W.; Hu, G. A Key Management Scheme Based on Hypergraph for Fog Computing. China Commun. 2018, 15, 158–170. [Google Scholar] [CrossRef]
- Challal, Y.; Fatima, Z.B.; Omar, N. Scalable Key Management for Elastic Security Domains in Fog Networks. In Proceedings of the IEEE 27th International Conference on Enabling Technologies: Infrastructure for Collaborative Enterprises, Paris, France, 27–29 June 2018; pp. 187–192. [Google Scholar]
- Han, S.; Tian, B.; Zhang, Y.; Hu, J. An Efficient Self-Healing Key Distribution Scheme with Constant-Size Personal Keys for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar]
- Lin, J.C.; Huang, K.H.; Lai, F.; Lee, H.C. Secure and efficient group key management with shared key derivation. Comput. Stand. Interfaces 2009, 31, 192–208. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, M.; Bacchus, A.; Lin, X. Towards collusion-attack-resilient group key management using one-way function tree. Comput. Netw. 2016, 104, 16–26. [Google Scholar] [CrossRef]
- Kim, J.; Susilo, W.; Au, M.H.; Seberry, J. Adaptively secure identity-based broadcast encryption with a constant-sized ciphertext. IEEE Trans. Inf. Forensics Secur. 2015, 10, 679–693. [Google Scholar]
- Harn, L.; Lin, C. Authenticated group key transfer protocol based on secret sharing. IEEE Trans. Comput. 2010, 59, 842–846. [Google Scholar] [CrossRef]
- Tang, S.; Xu, L.; Liu, N.; Huang, X.; Ding, J.; Yang, Z. Provably secure group key management approach based upon hyper-sphere. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3253–3263. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).