The Brooks and Corey Capillary Pressure Model Revisited from Pore Network Simulations of Capillarity-Controlled Invasion Percolation Process
Abstract
:1. Introduction
2. Model Description
- (1)
- Initially, all the pores and throats are completely filled with water. Neglecting pressure difference due to liquid head, the liquid pressure in the network and the liquid reservoir are set to zero for simplicity, without affecting the final capillary–pressure relationship. The air pressure necessary for any of the interior throats to be displaced with air is computed. We use Equation (5) to find the pressure difference between air and water necessary for a meniscus to penetrate the throat:where (Pa) is the capillary pressure, (Pa) is the gas pressure and (Pa) denotes the liquid pressure. Thus, the capillary pressure is equal to the gas pressure.
- (2)
- For the menisci that have been formed in the previous step, the capillary threshold is calculated by Equation (4). The meniscus throats with the smallest capillary thresholds are detected.
- (3)
- The air pressure is increased to the smallest capillary threshold calculated in step 2 (called entry pressure Pe) to invade accessible throats with that threshold and create meniscus throats.
- (4)
- Once a meniscus pore is invaded, it forms the active capillary thresholds at neighbor throats, which still contain liquid. When a meniscus throat is invaded, it forms a new active meniscus pore. Hence, the newly formed menisci (meniscus throats/pores) are identified, along with calculating their capillary threshold pressures.
- (5)
- The network saturation is calculated by integrating all residual liquid volume in the network and dividing it by the total void space volume. The smallest capillary threshold pressure is then assigned to the gas pressure. This is one data point in the capillary pressure–saturation curve.
- (6)
- Due to the random radius distribution of throats/pores, the initially backbone liquid cluster may be divided into several liquid clusters (may be isolated from the bottom reservoir). We account for the number of liquid clusters by a variant of the Hoshen–Kopelman algorithm [31]. The invasion percolation happens simultaneously in each cluster, which is still connected to the liquid reservoir according to step 3. If the invading pressure is greater than the capillary threshold of any of them, they are also invaded.
- (7)
- This algorithm is repeated from steps 2 to 6 until the clusters get isolated from the liquid reservoir, which is connected to the network bottom. This means all the pores at the bottom layer are unfilled of water. The remaining liquid in the network is considered as the irreducible saturation.
3. Results and Discussion
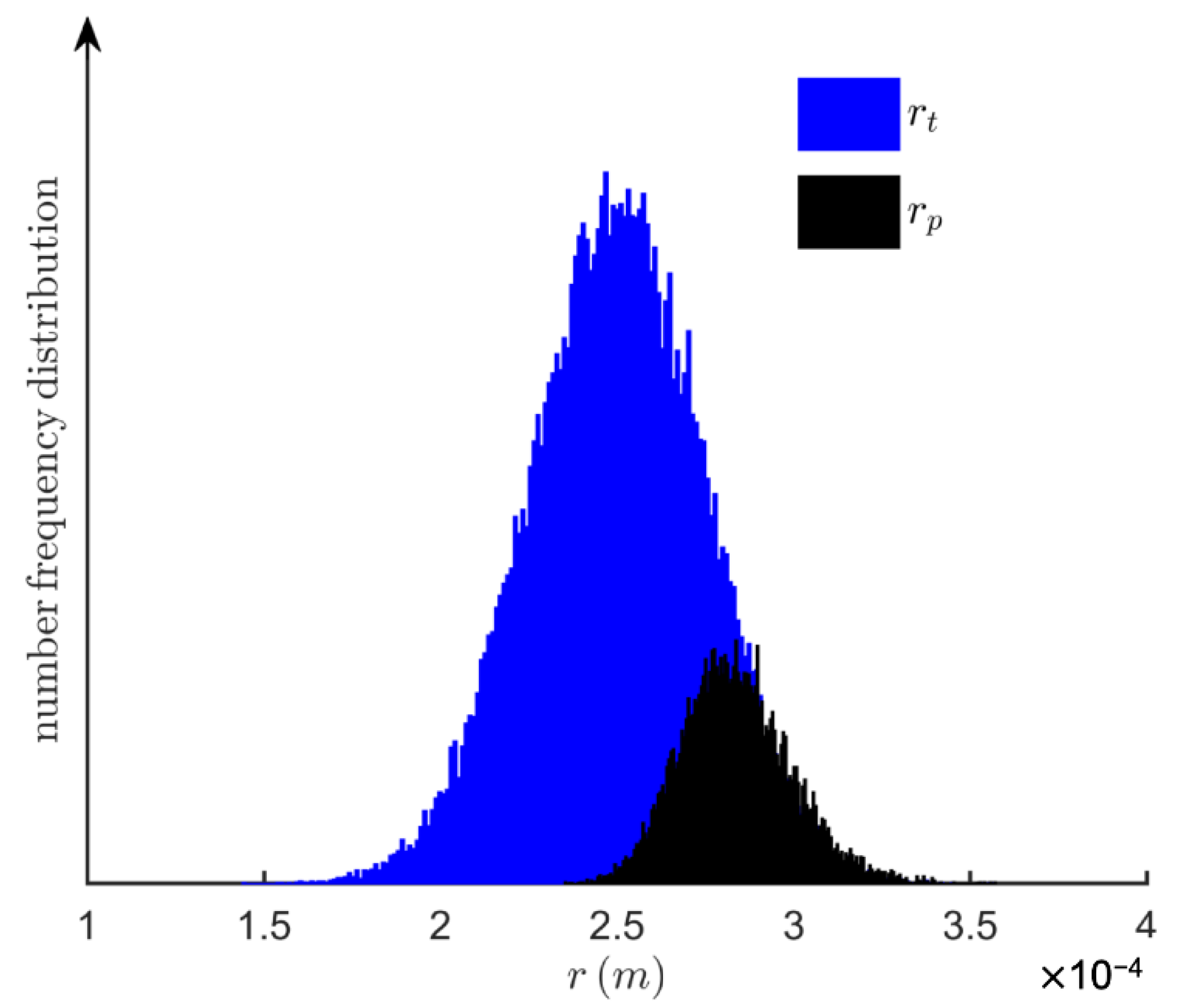
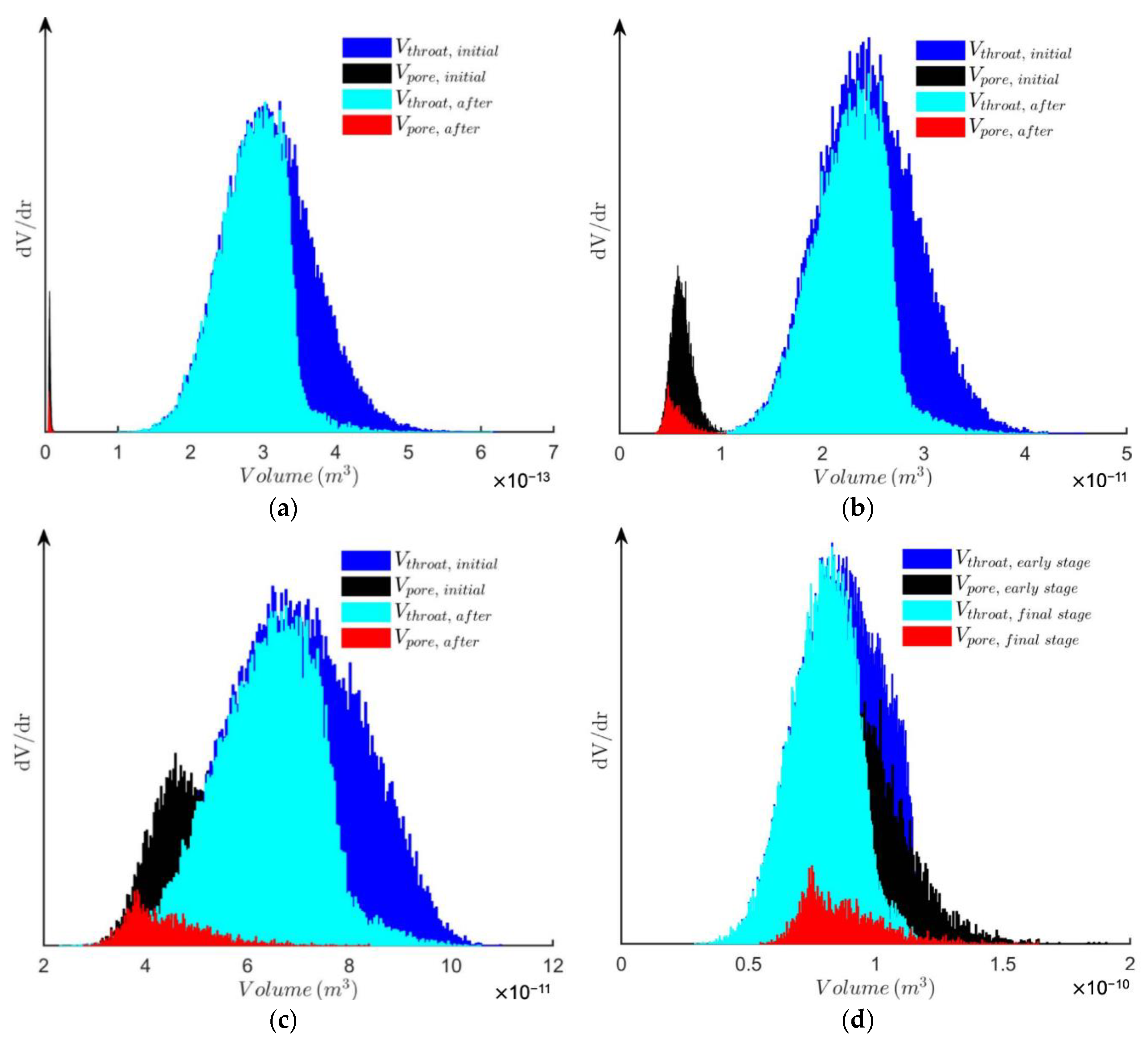
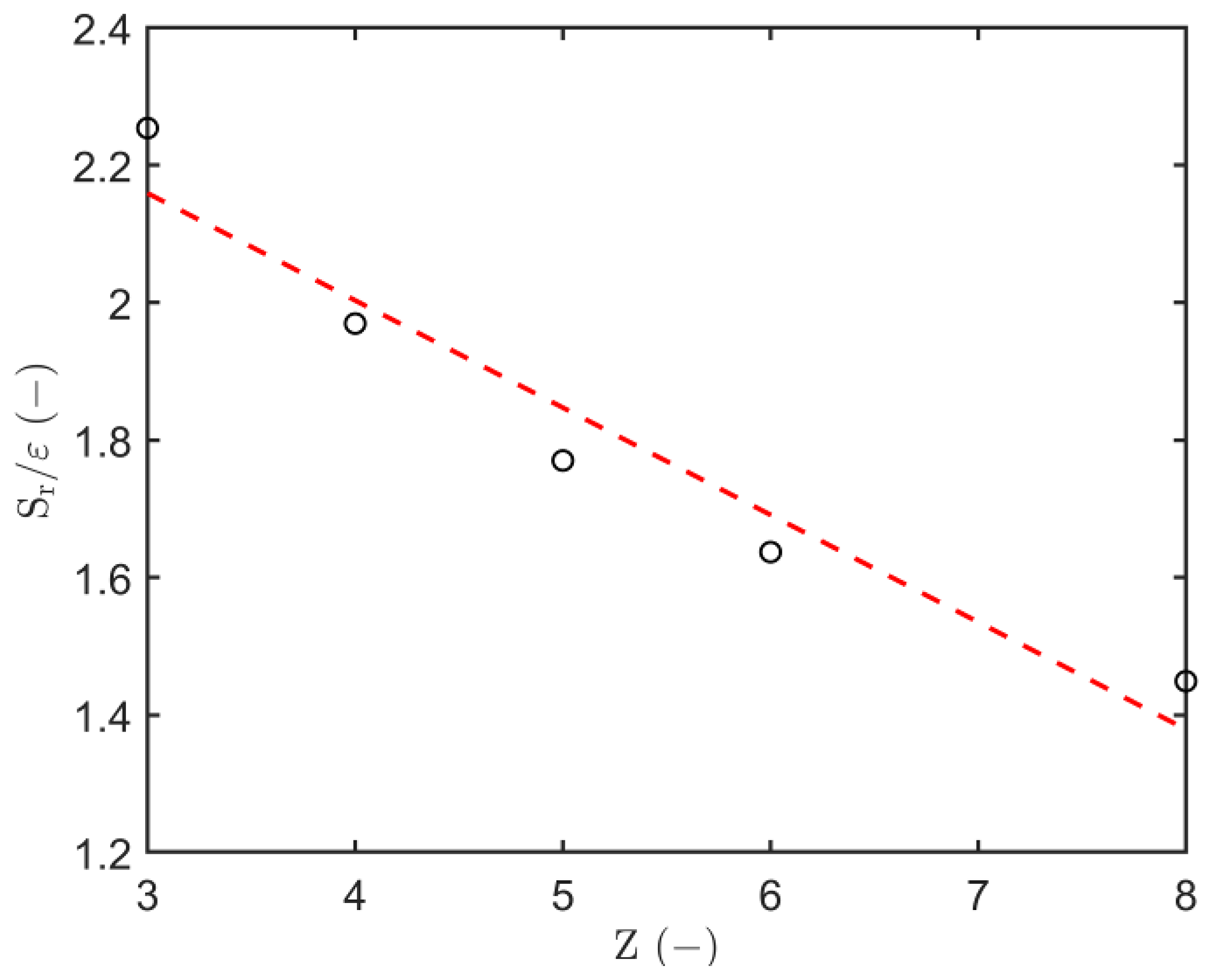
3.1. Wetting Phase Residual Saturation ()
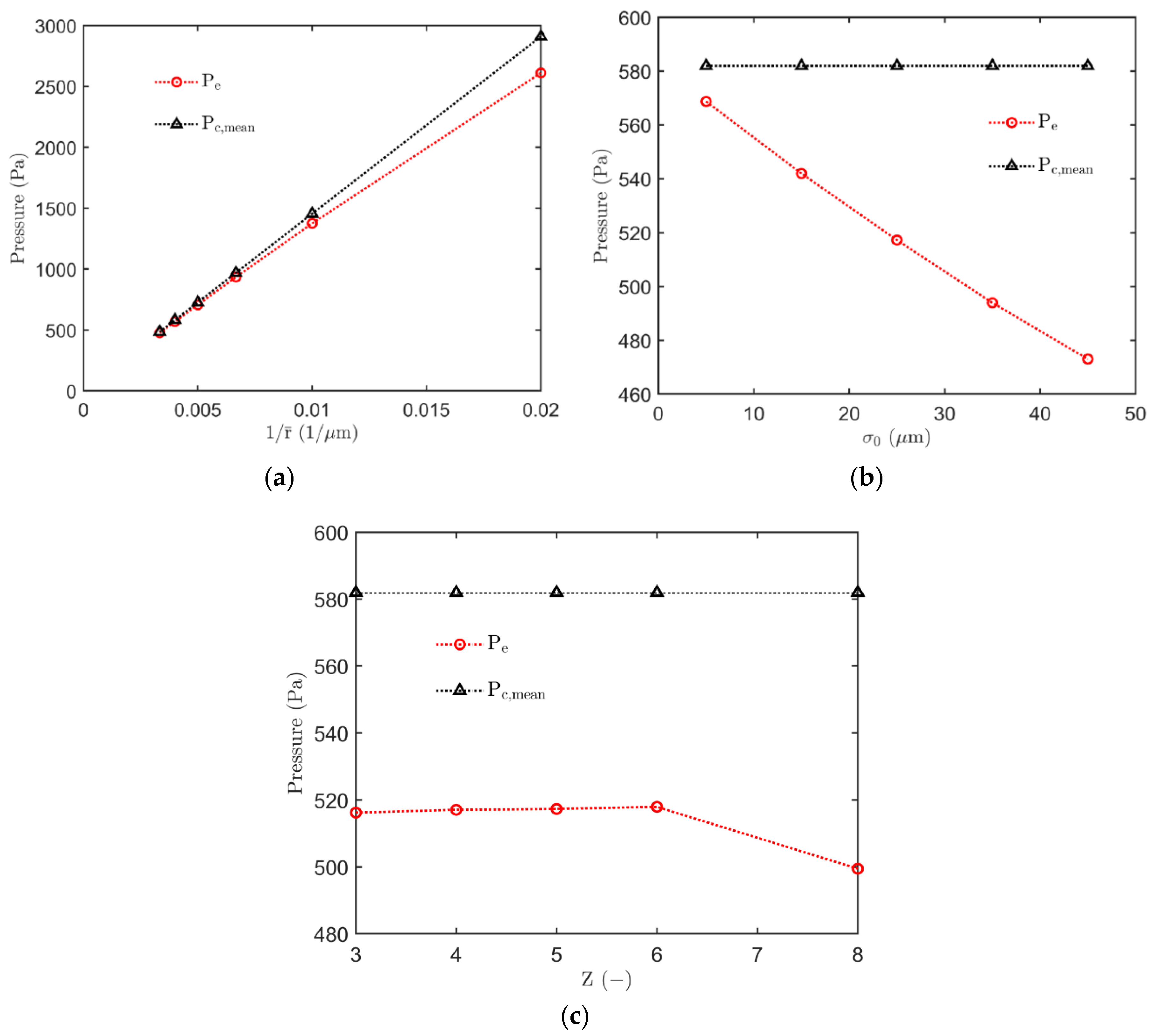
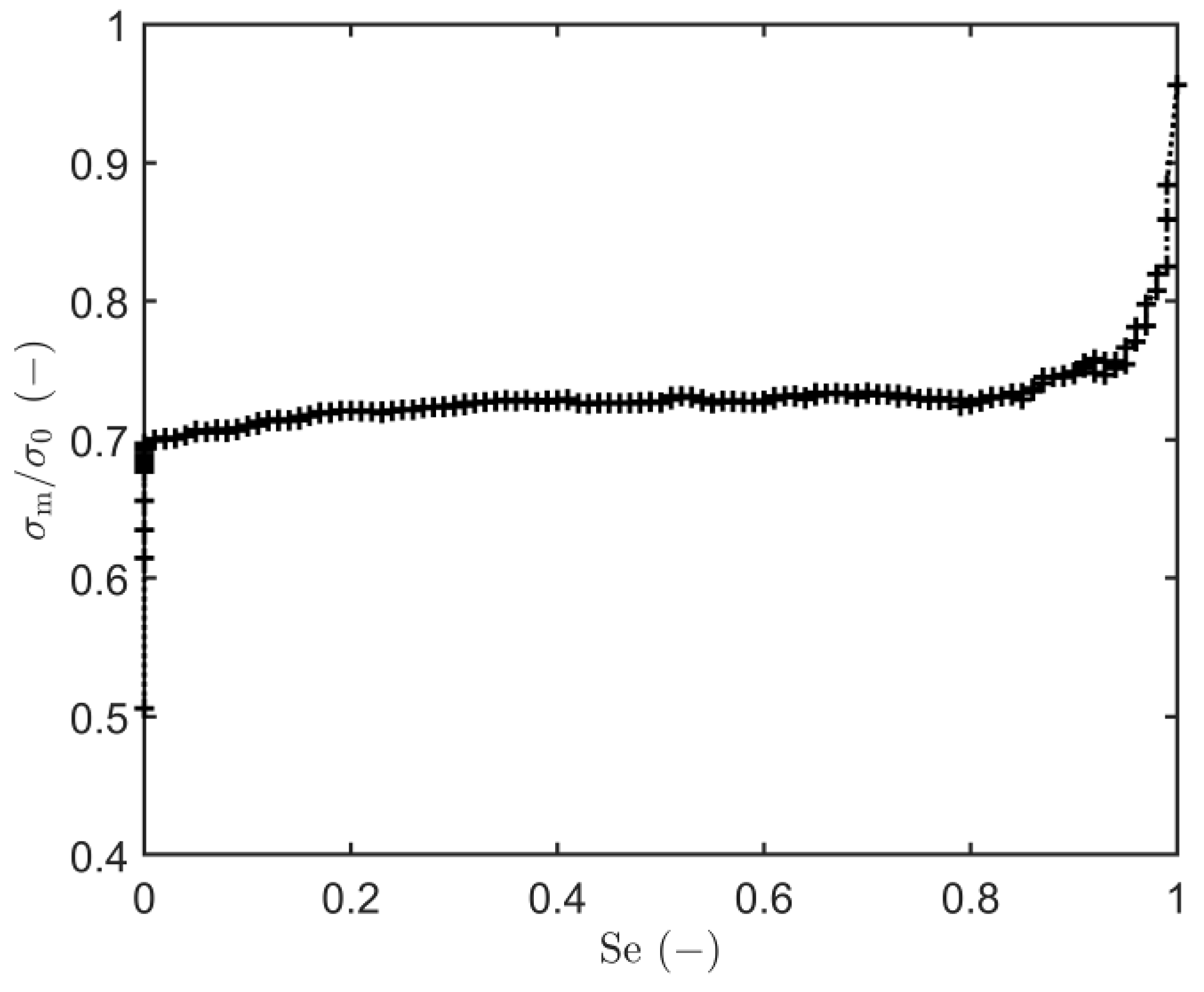
3.2. The Entry Pressure (Pe)
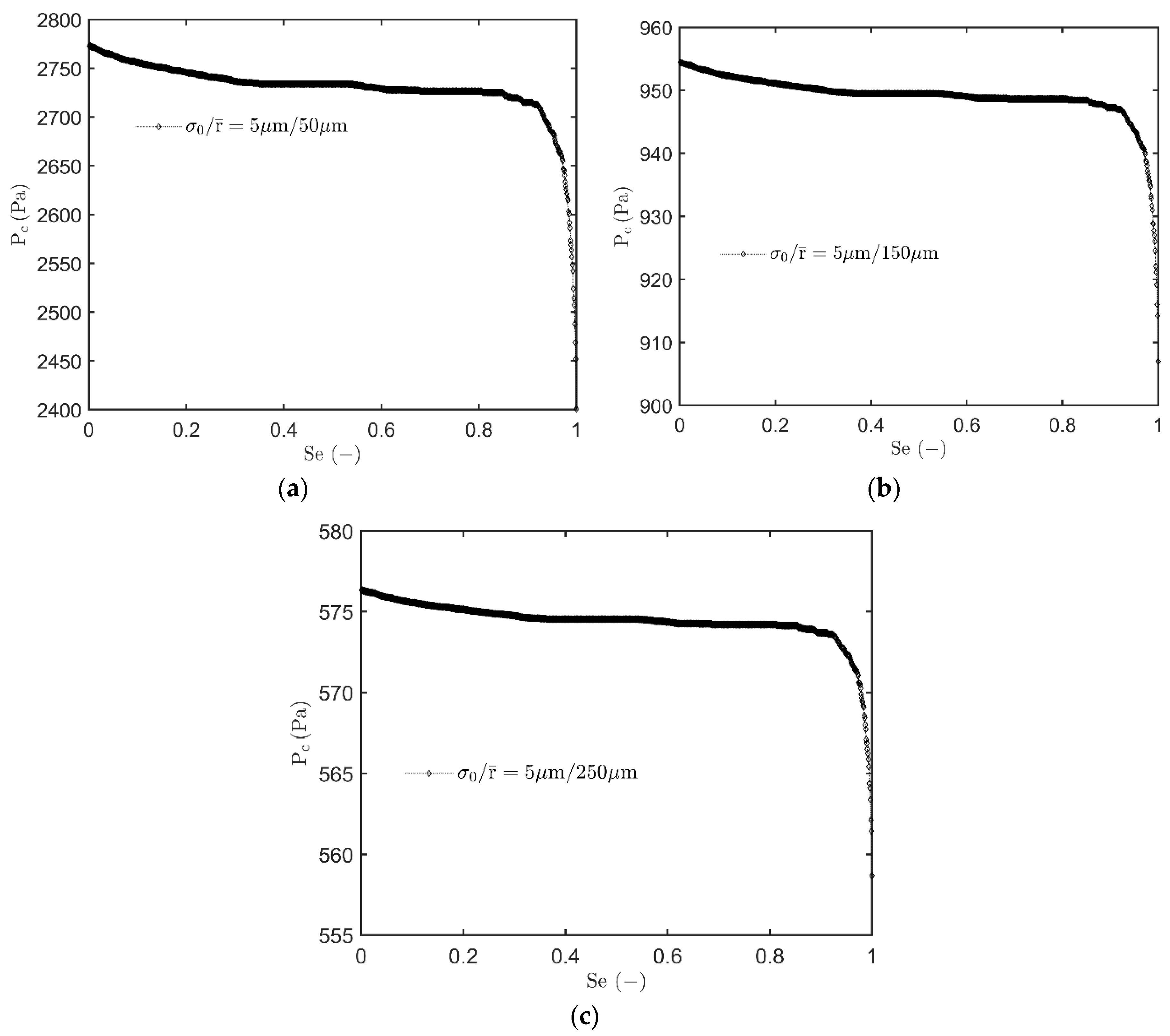
3.3. Evaluating Capillary Pressure-Effective Saturation
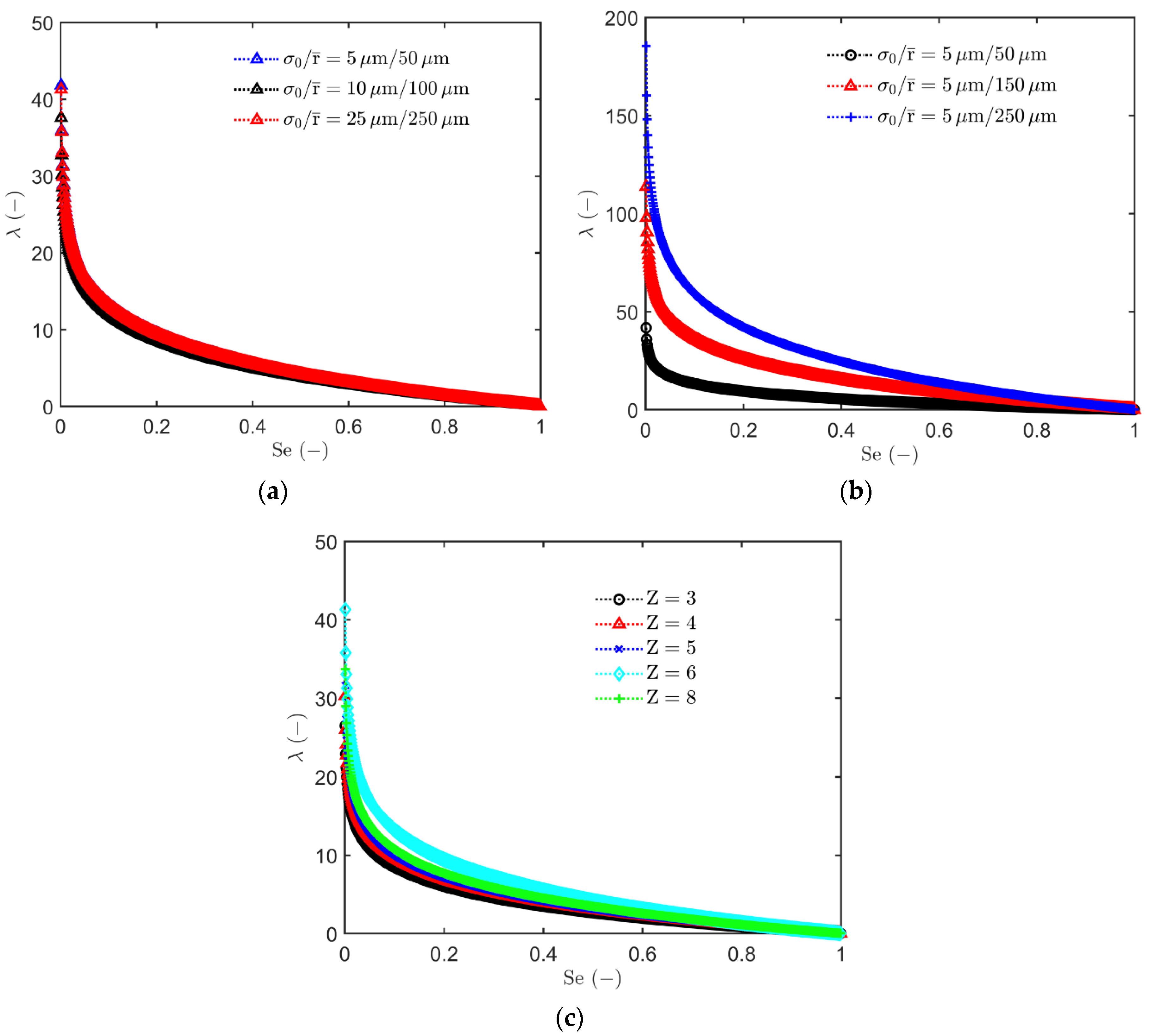
3.4. Evaluating the Pore Size Distribution Index (λ) Based on the Capillary Pressure-Effective Saturation
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| L | length, m |
| mean throat length, m | |
| Pc | capillary pressure, Pa |
| Pc,mean | mean capillary pressure, Pa |
| Pe | entry pressure, Pa |
| Pg | gas pressure, Pa |
| Pl | liquid pressure, Pa |
| r | radius, m |
| mean radius, m | |
| S | saturation |
| Se | effective saturation |
| Sr | irreducible saturation |
| V | volume, m3 |
| Z | connectivity |
| Greek symbols | |
| ε | network porosity |
| equilibrium contact angle, ° | |
| 0 | standard distribution, m |
| m | standard distribution of meniscus, m |
| surface tension, N/m | |
| λ | size distribution index |
| Subscripts/superscripts | |
| t | throat |
| p | pore |
| Abbreviations | |
| IP | invasion percolation |
| PNMs | pore network models |
| PSD | pore size distribution |
| TSD | throat size distribution |
References
- Wilkinson, D.; Willemsen, J.F. Invasion percolation: A new form of percolation theory. J. Phys. A Math. Gen. 1983, 16, 3365–3376. [Google Scholar] [CrossRef]
- Chandler, R.; Koplik, J.; Lerman, K.; Willemsen, J.F. Capillary displacement and percolation in porous media. J. Fluid Mech. 1982, 119, 249–267. [Google Scholar] [CrossRef]
- Mason, G.; Mellor, D.W. Simulation of Drainage and Imbibition in a Random Packing of Equal Spheres. J. Coll. Interf. Sci. 1995, 176, 214–225. [Google Scholar] [CrossRef]
- Prat, M. Percolation model of drying under isothermal conditions in porous media. Int. J. Multiph. Flow 1993, 19, 691–704. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irr. Drain. Div. 1966, 92, 61–88. [Google Scholar]
- Conner, W.C., Jr.; Blanco, C.; Coyne, K.; Neil, J.; Pajares, J. Analysis of the morphology of high surface area solids: Studies of agglomeration and the determination of shape. J. Catal. 1987, 106, 202–209. [Google Scholar] [CrossRef]
- Conner, W.; Lane, A.; Ng, K.; Goldblatt, M. Measurement of the morphology of high surface area solids: Porosimetry of agglomerated particles. J. Catal. 1983, 83, 336–345. [Google Scholar] [CrossRef]
- Portsmouth, R.; Gladden, L. Determination of pore connectivity by mercury porosimetry. Chem. Eng. Sci. 1991, 46, 3023–3036. [Google Scholar] [CrossRef]
- Conner, W.; Lane, A.M. Measurement of the morphology of high surface area solids: Effect of network structure on the simulation of porosimetry. J. Catal. 1984, 89, 217–225. [Google Scholar] [CrossRef]
- Tsakiroglou, C.D.; Payatakes, A.C. Effects of pore-size correlations on mercury porosimetry curves. J. Coll. Interf. Sci. 1991, 146, 479–494. [Google Scholar] [CrossRef]
- Knackstedt, M.A.; Sheppard, A.; Sahimi, M. Pore network modelling of two-phase flow in porous rock: The effect of correlated heterogeneity. Adv. Water Resour. 2001, 24, 257–277. [Google Scholar] [CrossRef]
- White, N.F.; Duke, H.R.; Sunada, D.K.; Corey, A.T. Physics of desaturation in porous materials. J. Irr. Drain. Div. 1996, 96, 165–191. [Google Scholar]
- Rabbani, H.S.; Joekar-Niasar, V.; Shokri, N. Effects of intermediate wettability on entry capillary pressure in angular pores. J. Colloid Interface Sci. 2016, 473, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Ferrari, A.; Lunati, I. Direct numerical simulations of interface dynamics to link capillary pressure and total surface energy. Adv. Water Resour. 2013, 57, 19–31. [Google Scholar] [CrossRef]
- Kewen, L. Theoretical development of the Brooks-Corey capillary pressure model from fractal modeling of porous media. In Proceedings of the SPE/DOE Fourteenth Symposium on Improved Oil Recovery, Tulsa, OK, USA, 17–21 April 2004. [Google Scholar] [CrossRef]
- Moseley, W.A.; Dhir, V.K. Capillary pressure-saturation relations in porous media including the effect of wettability. J. Hydrol. 1996, 178, 33–53. [Google Scholar] [CrossRef]
- Kjosavik, A.; Ringen, J.; Skjaeveland, S. Relative Permeability Correlation for Mixed-Wet Reservoirs. SPE J. 2002, 7, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Papatzacos, P.; Skjæveland, S.M. Relative permeability from capillary pressure. In Proceedings of the SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar] [CrossRef]
- Oren, P.-E.; Bakke, S.; Arntzen, O. Extending Predictive Capabilities to Network Models. SPE J. 1998, 3, 324–336. [Google Scholar] [CrossRef]
- Lerdahl, T.R.; Oren, P.-E.; Bakke, S. A Predictive Network Model for Three-Phase Flow in Porous Media. SPE Impr. Oil Recov. Symp. 2000, 13–26. [Google Scholar] [CrossRef]
- Blunt, M.J.; Jackson, M.D.; Piri, M.; Valvatne, P.H. Detailed physics, predictive capabilities and macroscopic consequences for pore-network models of multiphase flow. Adv. Water Resour. 2002, 25, 1069–1089. [Google Scholar] [CrossRef]
- Joekar-Niasar, V.; Hassanizadeh, S.M.; Leijnse, A. Insights into the Relationships Among Capillary Pressure, Saturation, Interfacial Area and Relative Permeability Using Pore-Network Modeling. Transp. Por. Med. 2007, 74, 201–219. [Google Scholar] [CrossRef] [Green Version]
- Moghaddam, A.A.; Kharaghani, A.; Tsotsas, E.; Prat, M. A pore network study of evaporation from the surface of a drying non-hygroscopic porous medium. AIChE J. 2017, 64, 1435–1447. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Kharaghani, A.; Tsotsas, E.; Prat, M. Kinematics in a slowly drying porous medium: Reconciliation of pore network simulations and continuum modeling. Phys. Fluids 2017, 29, 022102. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Kharaghani, A.; Tsotsas, E. Transport parameters of macroscopic continuum model determined from discrete pore network simulations of drying porous media: Throat-node vs. throat-pore configurations. Chem. Eng. Sci. 2020, 223, 115723. [Google Scholar] [CrossRef]
- Ahmad, F.; Talbi, M.; Prat, M.; Tsotsas, E.; Kharaghani, A. Non-local equilibrium continuum modeling of partially saturated drying porous media: Comparison with pore network simulations. Chem. Eng. Sci. 2020, 228, 115957. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Prat, M.; Tsotsas, E.; Kharaghani, A. Evaporation in Capillary Porous Media at the Perfect Piston-Like Invasion Limit: Evidence of Nonlocal Equilibrium Effects. Water Resour. Res. 2017, 53, 10433–10449. [Google Scholar] [CrossRef] [Green Version]
- Metzger, T.; Irawan, A.; Tsotsas, E. Influence of pore structure on drying kinetics: A pore network study. AIChE J. 2007, 53, 3029–3041. [Google Scholar] [CrossRef]
- Cieplak, M.; Robbins, M.O. Influence of contact angle on quasistatic fluid invasion of porous media. Phys. Rev. B 1990, 41, 11508–11521. [Google Scholar] [CrossRef]
- Metzger, T.; Irawan, A.; Tsotsas, E. Remarks on the paper “Extension of Hoshen–Kopelman algorithm to non-lattice environments” by A. Al-Futaisi and T.W. Patzek, Physica A 321 (2003) 665–678. Phys. A Stat. Mech. Its Appl. 2006, 363, 558–560. [Google Scholar] [CrossRef]
- Fengpeng, L.; Li, Z.; Zhang, W.; Dong, H.; Kong, F.; Jiang, Z. Investigation of Pore Characteristics and Irreducible Water Saturation of Tight Reservoir Using Experimental and Theoretical Methods. Energy Fuels 2018, 32, 3368–3379. [Google Scholar] [CrossRef]
- Sok, R.M.; Knackstedt, M.A.; Sheppard, A.P.; Pinczewski, W.; Lindquist, W.; Venkatarangan, A.; Paterson, L. Direct and Stochastic Generation of Network Models from Tomographic Images; Effect of Topology on Residual Saturations. Transp. Por. Media 2002, 46, 345–371. [Google Scholar] [CrossRef]
- Ojha, S.P.; Misra, S.; Tinni, A.; Sondergeld, C.H.; Rai, C. Estimation of Pore-Network Characteristics and Irreducible Saturations in Wolfcamp and Eagle Ford Shales Using Low-Pressure-Nitrogen-Adsorption/Desorption-Isotherm Measurements. SPE Reserv. Eval. Eng. 2018, 21, 373–391. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Informa UK Limited: London, UK, 2018. [Google Scholar]
- Hunt, A. Pressure Saturation Curves and the Critical Volume Fraction for Percolation. In Percolation Theory for Flow in Porous Media; Springer: Berlin/Heidelberg, Germany, 2005; pp. 121–143. [Google Scholar]
- Ferreira, F.C.; Booth, R.; Oliveira, R.; Bize-Forest, N.; Boyd, A.; Souza, A.; Carneiro, G.; Mesquita, P. Modelling Irreducible Water Saturation in Heterogeneous Rocks from Pore-Size Distribution. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 7–10 November 2016. [Google Scholar] [CrossRef]
- Prat, M. Recent advances in pore-scale models for drying of porous media. Chem. Eng. J. 2002, 86, 153–164. [Google Scholar] [CrossRef]
- Hilpert, M.; Miller, C.T. Pore-morphology-based simulation of drainage in totally wetting porous media. Adv. Water Resour. 2001, 24, 243–255. [Google Scholar] [CrossRef]
- Sweijen, T.; Aslannejad, H.; Hassanizadeh, S.M. Capillary pressure–saturation relationships for porous granular materials: Pore morphology method vs. pore unit assembly method. Adv. Water Resour. 2017, 107, 22–31. [Google Scholar] [CrossRef]
- Srikiatden, J.; Roberts, J.S. Moisture Transfer in Solid Food Materials: A Review of Mechanisms, Models, and Measurements. Int. J. Food Prop. 2007, 10, 739–777. [Google Scholar] [CrossRef]
- Yiotis, A.G.; Salin, D.; Tajer, E.S.; Yortsos, Y.C. Drying in porous media with gravity-stabilized fronts: Experimental results. Phys. Rev. E 2012, 86, 026310. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Kharaghani, A.; Metzger, T.; Tsotsas, E. Pore Network Drying Model for Particle Aggregates: Assessment by X-Ray Microtomography. Dry. Technol. 2012, 30, 1800–1809. [Google Scholar] [CrossRef]
- Prat, M. On the influence of pore shape, contact angle and film flows on drying of capillary porous media. Int. J. Heat Mass Transf. 2007, 50, 1455–1468. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Kharaghani, A.; Adloo, H.; Tsotsas, E. The Brooks and Corey Capillary Pressure Model Revisited from Pore Network Simulations of Capillarity-Controlled Invasion Percolation Process. Processes 2020, 8, 1318. https://doi.org/10.3390/pr8101318
Lu X, Kharaghani A, Adloo H, Tsotsas E. The Brooks and Corey Capillary Pressure Model Revisited from Pore Network Simulations of Capillarity-Controlled Invasion Percolation Process. Processes. 2020; 8(10):1318. https://doi.org/10.3390/pr8101318
Chicago/Turabian StyleLu, Xiang, Abdolreza Kharaghani, Hadi Adloo, and Evangelos Tsotsas. 2020. "The Brooks and Corey Capillary Pressure Model Revisited from Pore Network Simulations of Capillarity-Controlled Invasion Percolation Process" Processes 8, no. 10: 1318. https://doi.org/10.3390/pr8101318
APA StyleLu, X., Kharaghani, A., Adloo, H., & Tsotsas, E. (2020). The Brooks and Corey Capillary Pressure Model Revisited from Pore Network Simulations of Capillarity-Controlled Invasion Percolation Process. Processes, 8(10), 1318. https://doi.org/10.3390/pr8101318







