Revisiting the Role of Mass and Heat Transfer in Gas–Solid Catalytic Reactions
Abstract
:1. Introduction
2. Mass and Heat Transfer in a Single Catalytic Particle
2.1. Diffusion with Reaction in a Single Catalytic Particle: Mass and Heat Balance Equations
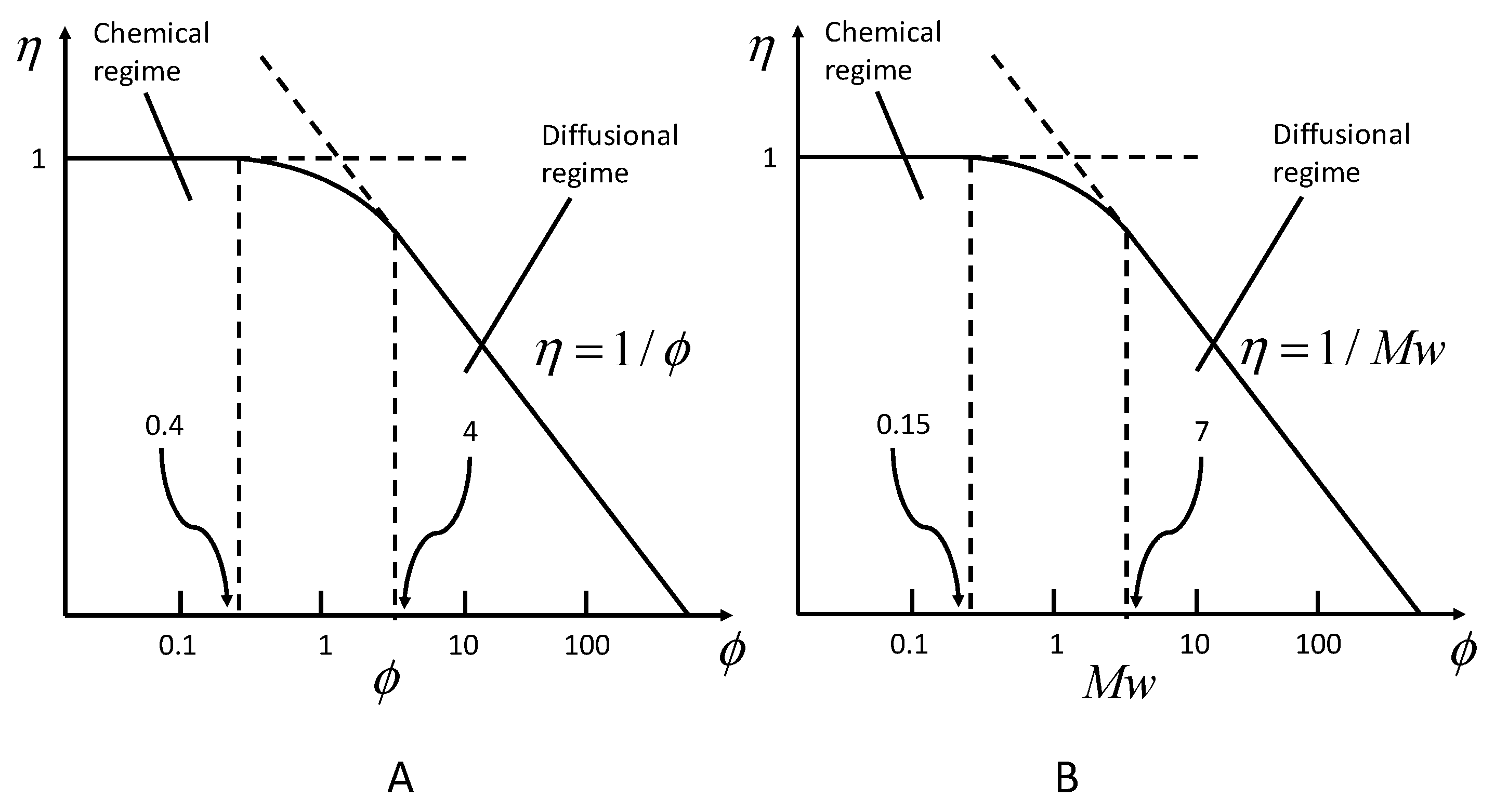
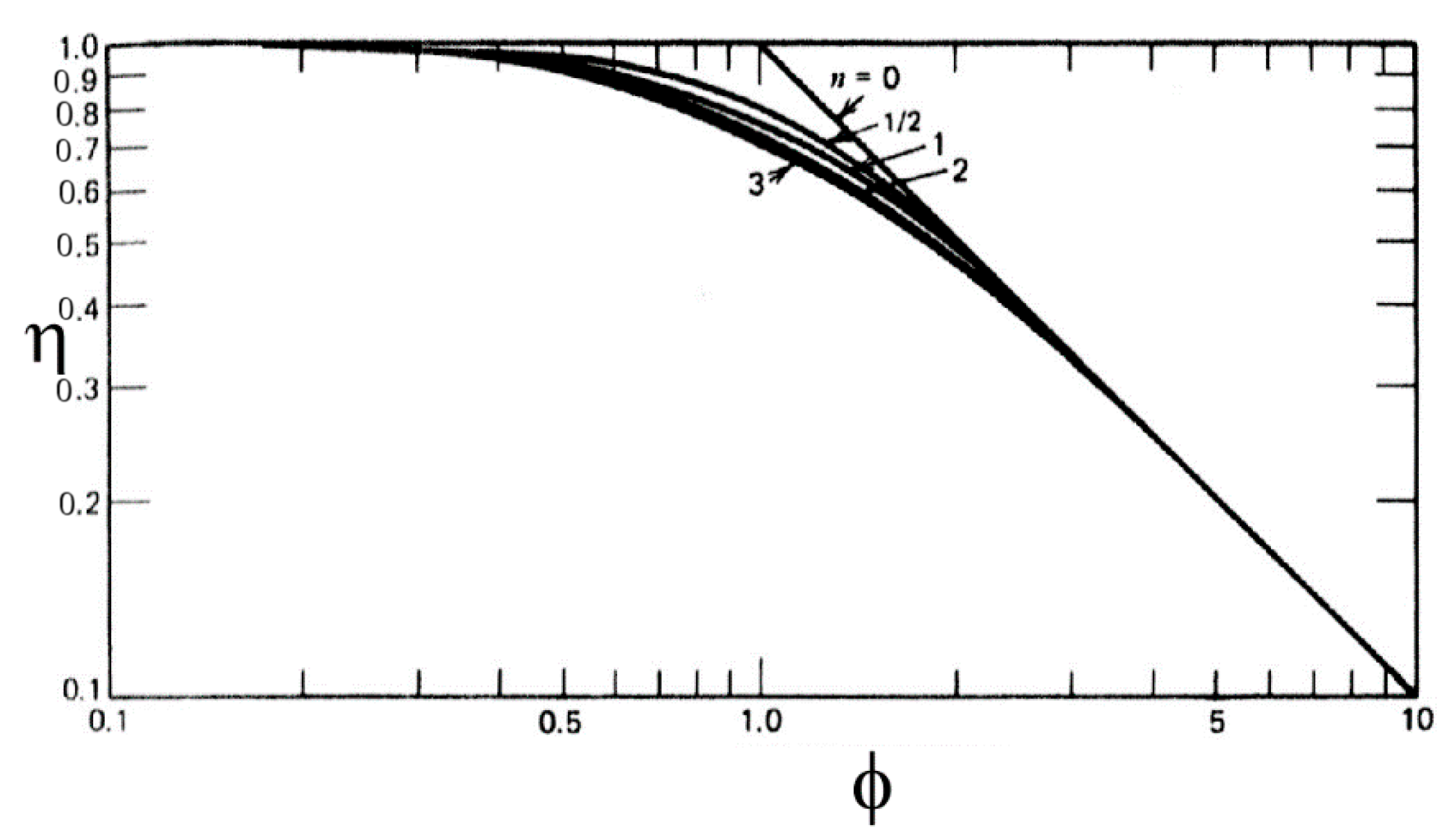
2.2. Definition and Evolution of the Effectiveness Factor
- (a)
- a heat generation parameter:
- (b)
- the reaction rate exponential parameter:
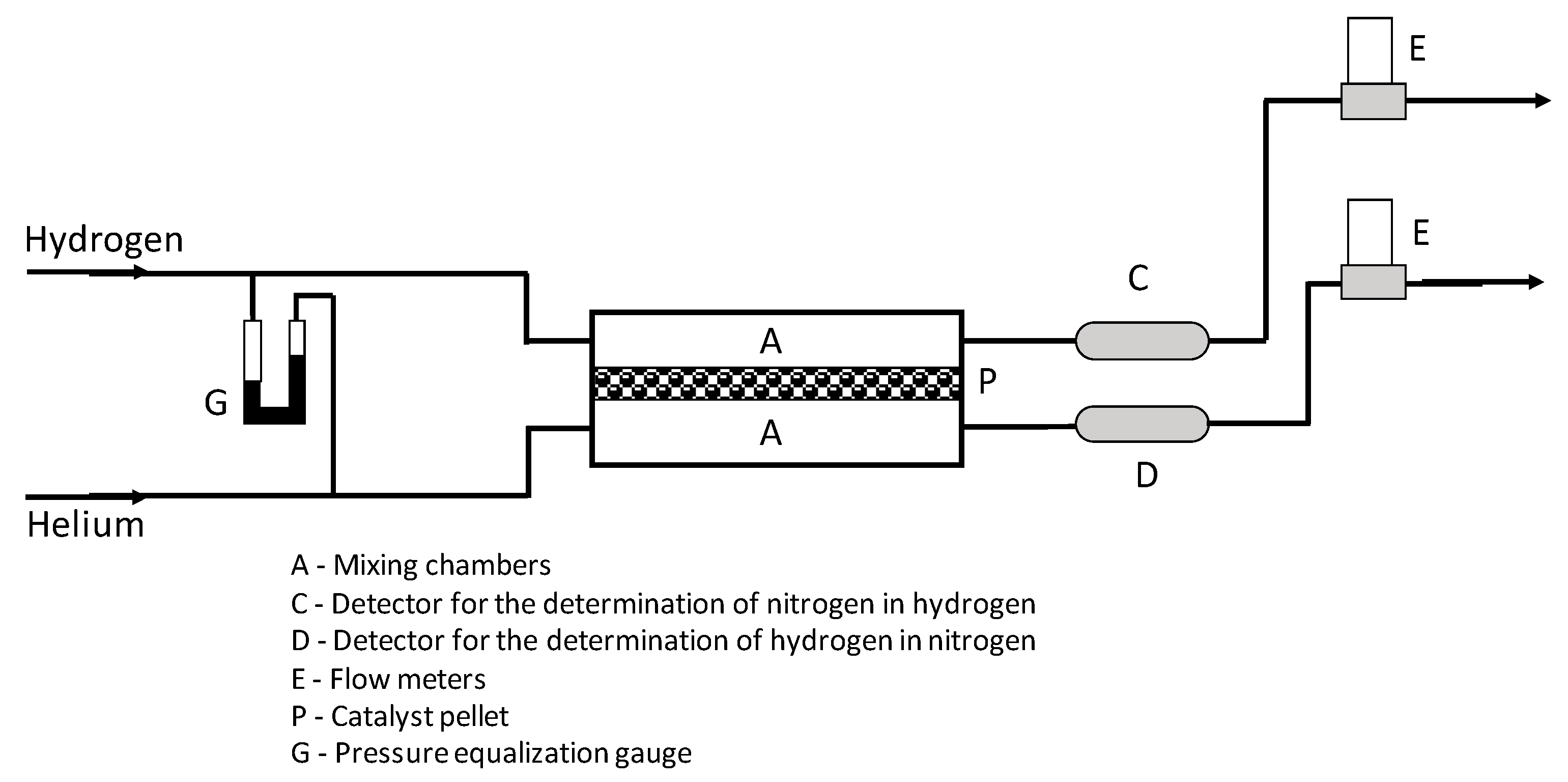
2.3. Determination of the Effective Diffusional Coefficient Deff and the Effective Thermal Conductivity keff
2.4. External Gradients
2.5. Diffusion and Selectivity

2.6. Effectiveness Factor for a Complex Reaction Network
2.7. An Example of Calculation of Effectiveness Factor Complex Reactions
- -
- Catalytic particle is spherical with uniform reactivity, density, and thermal conductivity.
- -
- The heat of reactions does not change with the temperature.
- -
- The external diffusion resistance is negligible, and therefore the surface concentration is equal to the one of the bulk.
- -
- The effective diffusivity has been assumed equal for all the involved chemical species.
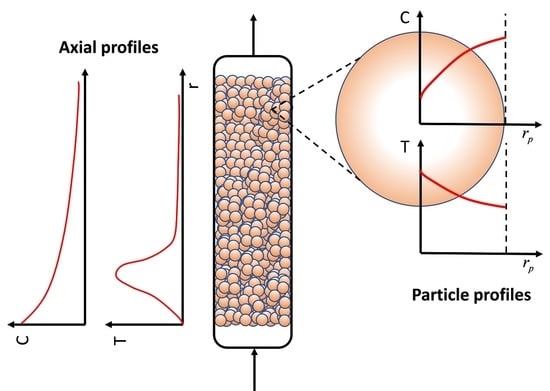
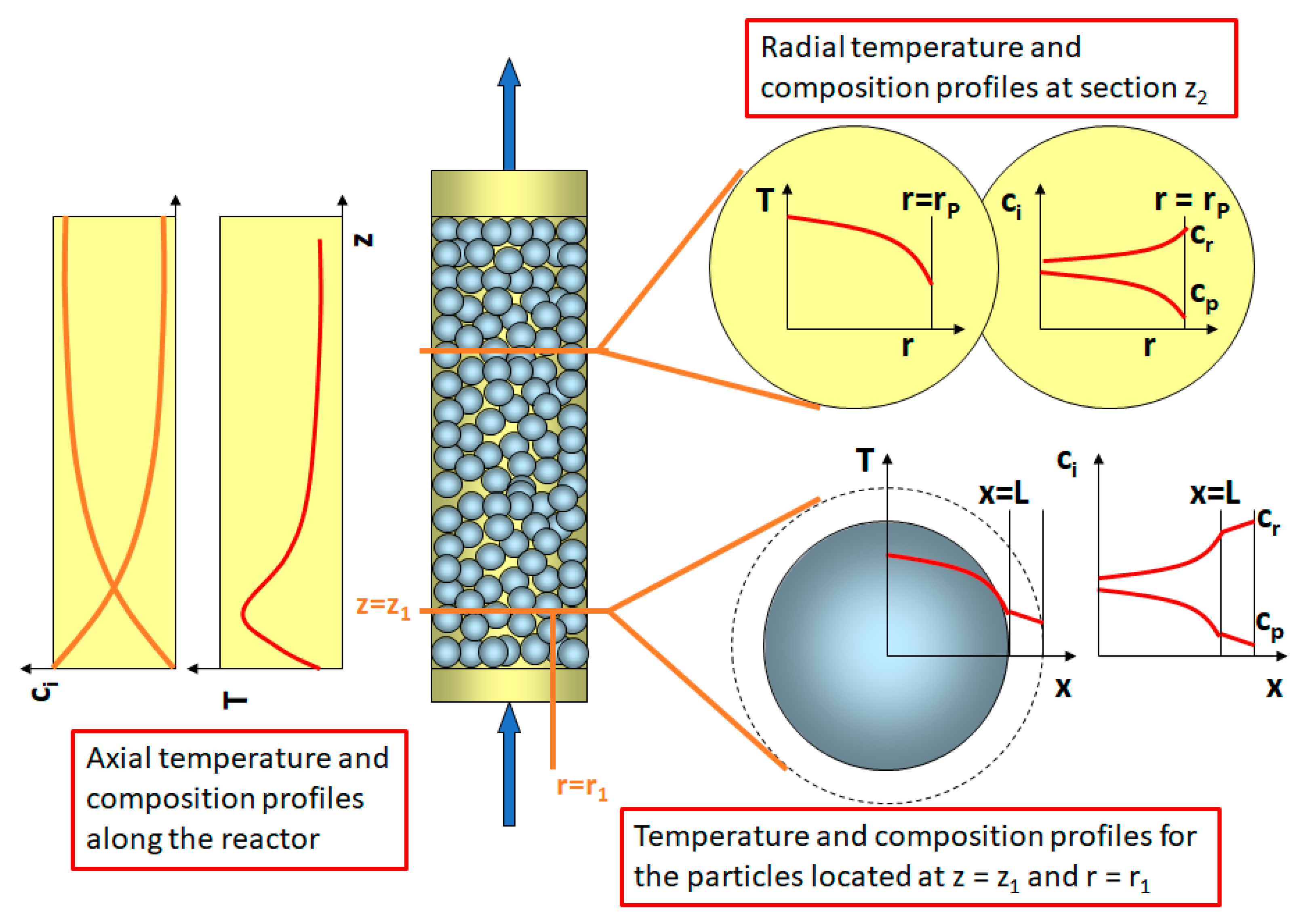
3. Mass and Heat Transfer in Packed Bed Reactors: Long Range Gradients
3.1. Conservation Equations for Fixed-Bed Reactors: Mass and Energy Balances
3.2. External Transport Resistance and Particle Gradients
- -
- kg—gas-solid mass transfer coefficient (film);
- -
- L—characteristic length of particle (radius for spherical pellets);
- -
- ciS—surface concentration of component i;
- -
- ciP—particle internal concentration of component i;
- -
- Dei—effective diffusivity of component i into the particle;
- -
- x—particle radial coordinate;
- -
- ηj—effectiveness factor for reaction j;
- -
- vr,j—intrinsic rate of reaction j.
- -
- h—film heat transfer coefficient;
- -
- TS—temperature at the surface of the pellet;
- -
- TP—temperature inside the pellet;
- -
- Keff—effective thermal conductivity of the catalytic particle.
- -
- εP—catalytic particle void fraction;
- -
- ρP—catalytic particle density;
- -
- CPP—catalytic particle specific heat.
3.3. Conservation Equations in Dimensionless Form and Possible Simplification
- -
- dP—particle diameter;
- -
- R—fixed-bed reactor radius;
- -
- Z—fixed-bed reactor length;
- -
- cB(in)i—reactor inlet concentration;
- -
- TB(in)—reactor inlet temperature.
3.4. Examples of Applications
3.4.1. Isothermal Conditions
3.4.2. Adiabatic Conditions
- -
- G—mass velocity;
- -
- cross section of the reactor tube;
- -
- FA, F0A component molar flow rate;
- -
- —reaction rate for reaction j based on catalyst mass.
4. Non-Isothermic and Non-Adiabatic Conditions
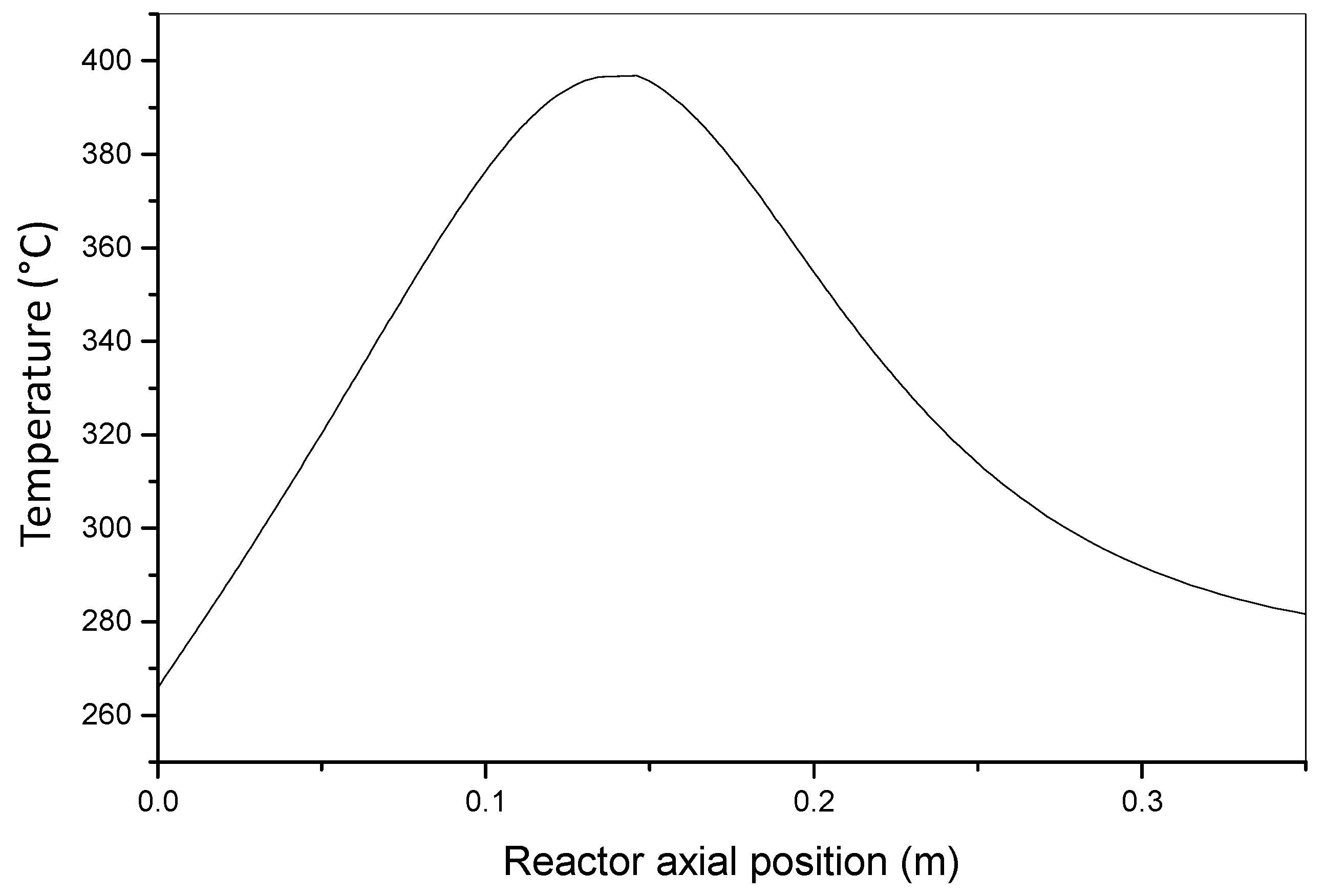
4.1. Conversion of o-Xylene to Phthalic Anhydride

- No axial and radial dispersion;
- No radial temperature and concentration gradients in the reactor body;
- Plug flow behavior of the reactor;
- No limitation related to internal diffusion in catalytic particles.
- -
- Q—volumetric overall flow rate;
- -
- A—cross section of the reactor tube;
- -
- Dr—reactor diameter;
- -
- Fi—component molar flow rate;
- -
- yi—mole fraction of component i;
- -
- mI—mass of inert per unit mass of catalyst (dilution ratio);
- -
- —reaction rate for reaction j based on catalyst mass.
- -
- G—mass velocity;
- -
- MF—average molecular weight of mixture.
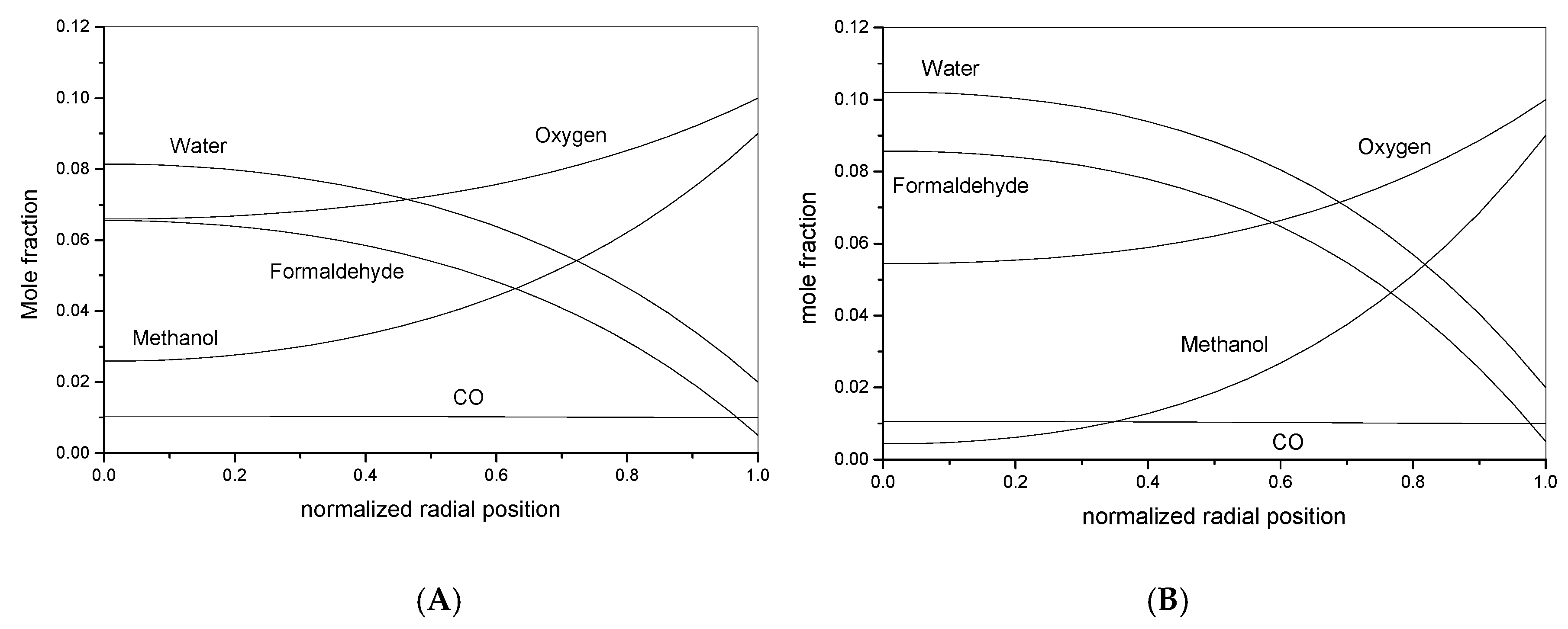
4.2. Conversion of Methanol to Formaldehyde
- Negligible dispersion in axial and radial directions;
- Absence of concentration and temperature profiles along the reactor radius;
- Plug flow reactor behavior.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Glossary
| List of Symbols | |
| am | Specific surface area |
| A | Reactor cross section |
| bw | Water adsorption equilibrium constant |
| c | Generic concentration |
| ci | Concentration of component i |
| ci° | Initial i concentration |
| cb | Generic concentration of a component in the bulk |
| ciB | Concentration of i in the bulk |
| ciP | Concentration of i inside a catalytic particle |
| cS | Generic concentration at the catalytic surface |
| ciS | Concentration of i at the surface |
| Cp | Average gas specific heat |
| CpP | Particle specific heat |
| Δc | Concentration gradient |
| Δcmin | Minimum concentration gradient |
| D | Reactor diameter |
| dp | Particle diameter |
| D | Generic molecular diffusivity |
| Di | Molecular diffusivity of component i |
| Di,j | Mutual binary diffusion coefficient |
| D12 | Mutual binary diffusion coefficient |
| Dim | Diffusion coefficient of i in a mixture m |
| Deff | Effective molecular diffusivity |
| (Di)eff | Effective molecular diffusivity of component i |
| Dbe | Bulk diffusion coefficient |
| Dke | Knudsen diffusion coefficient |
| Dei | Effective diffusivity inside particle |
| Dai | Axial diffusivity of component i |
| Dri | Radial diffusivity of component i |
| Fi | Molar flow rate of component i |
| F | Overall molar flow rate |
| G | Mass velocity |
| h | Film heat transfer coefficient |
| hw | Wall heat transfer coefficient |
| ΔH | Generic reaction enthalpy |
| ΔHj | Enthalpy of reaction j |
| Ji | Molar flux of component i |
| JD, JH | Terms for mass and heat transfer analogy |
| k, ki | Generic kinetic constant |
| kB | Boltzmann’s constant |
| kT | Generic thermal conductivity of the fluid |
| kf | Thermal conductivity of the bulk |
| keff | Effective thermal conductivity |
| kSol | Thermal conductivity of the solid |
| Ka | Axial thermal conductivity |
| Kr | Radial thermal conductivity |
| Ke | Particle thermal conductivity |
| kS | Kinetic constant |
| kc | Film mass transfer coefficients (concentration gradient) |
| kg | Film mass transfer coefficients (pressure gradient) |
| km | Mass transfer coefficient |
| L | Characteristic length |
| Le | Lewis’s number |
| m | Radial aspect ratio |
| mI | Inert dilution ratio |
| M, Mi | Molecular weight |
| MF | Average molecular weight of the mixture |
| Mw | Weisz modulus |
| NC | Number of components |
| Nre | Number of reactions |
| Nr | Molar flux |
| Ni, NA | Molar flux |
| N | Number of nodes |
| n | Reaction order |
| P | Total pressure |
| Pm | Methanol partial pressure |
| Pf | Formaldehyde partial pressure |
| Pw | Water partial pressure |
| PO2 | Oxygen partial pressure |
| Pma | Axial Peclet’s number for mass |
| Pmr | Radial Peclet’s number for mass |
| Pha | Axial Peclet’s number for heat |
| Phr | Radial Peclet’s number for heat |
| Pr | Prandtl’s number |
| Q | Rate of heat transfer |
| Qv | Overall volumetric flow rate |
| q | Heat flux |
| r | Reactor radial coordinate |
| rP | Particle spherical radius |
| R | Gas constant |
| Rr | Reactor radius |
| Rni | Reaction rate at node i |
| Rj | Reaction rate (fluid volume) |
| Reaction rate (catalyst mass) | |
| rcj | Intrinsic reaction rate |
| Re | Reynold’s number |
| Sv | Specific surface area |
| Sh | Sherwood’s number |
| Sc | Schmidt’s number |
| S | Selectivity |
| Sg | Specific surface area |
| T | Generic temperature |
| TS | Temperature at particle surface |
| TP | Temperature inside the particle |
| Tb | Bulk temperature |
| Tc | Cooling fluid temperature |
| ΔTmax | Maximum temperature difference |
| t | Time |
| u | Velocity |
| uz | Velocity in z direction |
| U | Overall heat transfer coefficient |
| vr | Reaction rate |
| vr,i | Reaction rate, reaction i-th |
| vr,jG | Reaction rate (pellet volume) |
| Vci | Critical volume of component i |
| x | Particle radial coordinate |
| Xi | Fractional conversion |
| yi | Gas phase mole fraction component i |
| z | Axial reactor coordinate |
| Z | Reactor length |
| Greek Letters | |
| αA | Constant in Equation (89) |
| αB | Constant in Equation (89) |
| αE | Reaction rate exponential parameter |
| αJ | Constant in Equation (38) |
| αH | Constant in Equation (40) |
| β | Prater’s number |
| βJ | Constant in Equation (38) |
| βH | Constant in Equation (40) |
| γdr | Dimensionless concentration |
| γij | Stoichiometric coefficient |
| δ | Thickness of boundary layer |
| εdr | Dimensionless radius |
| εB | Bed void fraction |
| εBs | Bed void fraction of the solid |
| εJ | Constant in Equation (38) |
| εH | Constant in Equation (40) |
| εij | Interaction parameter |
| εp | Particle void fraction |
| η, ηj | Effectiveness factor |
| µ | Viscosity |
| θ | Porosity of the solid |
| ρ | Average gas density |
| ρp | Particle density |
| ρd | Intermolecular distance |
| σij | Kinetic diameter |
| τ | Tortuosity factor |
| ϕ | Thiele modulus |
| ϕLJ | Lennard–Jones potential |
| ydr | Dimensionless reaction rate |
| ΩD | Collision integral |
| Nabla operator | |
References
- Santacesaria, E.; Tesser, R. The Chemical Reactor from Laboratory to Industrial Plant; Springer: Berlin, Germany, 2018. [Google Scholar]
- Froment, G.F. The kinetics of complex catalytic reactions. Chem. Eng. Sci. 1987, 42, 1073–1087. [Google Scholar] [CrossRef]
- Smith, J.M. Chemical Engineering Kinetics; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice-Hall International: Upper Saddle River, NJ, USA, 1986. [Google Scholar]
- Horak, J.; Pasek, J. Design of Industrial Chemical Reactors from Laboratory Data; Hayden Publishing: London, UK, 1978. [Google Scholar]
- Satterfield, C.N.; Sherwood, T.K. The Role of Diffusion in Catalysis; Addison-Wesley Publishing: Boston, MA, USA, 1963. [Google Scholar]
- Levenspiel, O. The Chemical Reactor Omnibook; OSU Book Store: Corvallis, OR, USA, 1984. [Google Scholar]
- Satterfield, C.N. Heterogeneous Catalysis in Practice; Addison-Wesley Publishing: Boston, MA, USA, 1972. [Google Scholar]
- Holland, C.D.; Anthony, R.G. Fundamentals of Chemical Reaction Engineering; Prentice-Hall: London, UK, 1979. [Google Scholar]
- Westerterp, K.R.; van Swaaij, W.P.M.; Beenackers, A.A.C.M. Chemical Reactor Design and Operation; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Davis, M.E.; Davis, R.J. Fundamentals of Chemical Reaction Engineering; Dover Publications, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Vogel, G.H. Process Development Wiely—VCH; John Wiley & Sons: Weinheim, Germany, 2005. [Google Scholar]
- Winterbottom, J.M.; King, M.B. Reactor Design for Chemical Engineers; Stanley Thornes Ltd.: Cheltenham Glos, UK, 1999. [Google Scholar]
- Wheeler, A. Reaction rates and selectivity in catalyst pores. In Advances in Catalysis; Academic Press: Cambridge, MA, USA, 1951; Volume 3. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Fenomeni di Trasporto; Casa Editrice Ambrosiana: Milan, Italy, 1970. [Google Scholar]
- Missen, R.W.; Mims, C.A.; Saville, B.A. Chemical Reaction Engineering and Kinetics; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Carberry, J.J. Physico chemical aspects of mass and heat transfer in heterogeneous catalysis. In Catalysis; Springer: Berlin/Heidelberg, Germany, 1987; pp. 131–171. [Google Scholar]
- Thiele, E.W. Relation between catalytic activity and size of particle. In Industrial and Engineering Chemistry; ACS Publications: Washington, DC, USA, 1939; Volume 31, pp. 916–920. [Google Scholar]
- Weisz, P.B.; Prater, C.D. Interpretation of measurements in experimental catalysis. In Advances in Catalysis; Academic Press: New York, NY, USA, 1954; Volume 6, pp. 143–196. [Google Scholar] [CrossRef]
- Santacesaria, E. Catalysis and transport phenomena in heterogeneous gas-solid and gas-liquid-solid systems. In Catalysis Today; Elsevier Science: Amsterdam, The Netherlands, 1997; Volume 34, pp. 411–420. [Google Scholar]
- Froment, G.F.; Bishoff, K.B. Chemical Reaction Analysis and Design; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Woodside, W.W.; Messner, J.H. Thermal conductivity of porous media. J. Appl. Phys. 1961, 32, 1688. [Google Scholar] [CrossRef]
- Hindmarsh, A.C. LSODE and LSODI, two initial value ordinary differential equation solvers. ACM Signum 1980, 15, 10–11. [Google Scholar] [CrossRef]
- Palm, W.J. Introduction to MATLAB for Engineers; Mc Graw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Tesser, R.; Santacesaria, E. Catalytic oxidation of methanol to formaldehyde: An example of kinetics with transport phenomena in a packed -bed reactor. Catal. Today 2003, 77, 325–333. [Google Scholar] [CrossRef]
- Mars, J.; Krevelen, D.W. Oxidations carried out by means of vanadium oxide catalysts. Chem. Eng. Sci. 1954, 3, 41. [Google Scholar] [CrossRef]
- Santacesaria, E.; Morbidelli, M.; Carrà, S. Kinetics of the catalytic oxidation of methanol to formaldehyde. Chem. Eng. Sci. 1981, 36, 909–918. [Google Scholar] [CrossRef]
- Dente, M.; Collina, A.; Pasquon, I. Verifica di un reattore tubolare per l’ossidazione del metanolo a formaldeide. La Chimica Industria 1966, 48, 581–588. [Google Scholar]
- Riggs, J.B. Introduction to Numerical Methods for Chemical Engineers; Texas Tech University Press: Lubbock, TX, USA, 1988. [Google Scholar]
- Carrà, S.; Forzatti, P. Engineering aspects of selective hydrocarbons oxidation. Catal. Rev. Sci. Eng. 1977, 15, 1–52. [Google Scholar] [CrossRef]
- Carberry, J.J. Chemical and Catalitic Reaction Engineering; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Lee, H.H. Heterogeneous Reactors Design; Butterwoth Publisher: Oxford, UK, 1984. [Google Scholar]
- Froment, G.F. Fixed bed catalytic reactors—Current design status. Ind. Eng. Chem. 1967, 59, 18–27. [Google Scholar] [CrossRef]










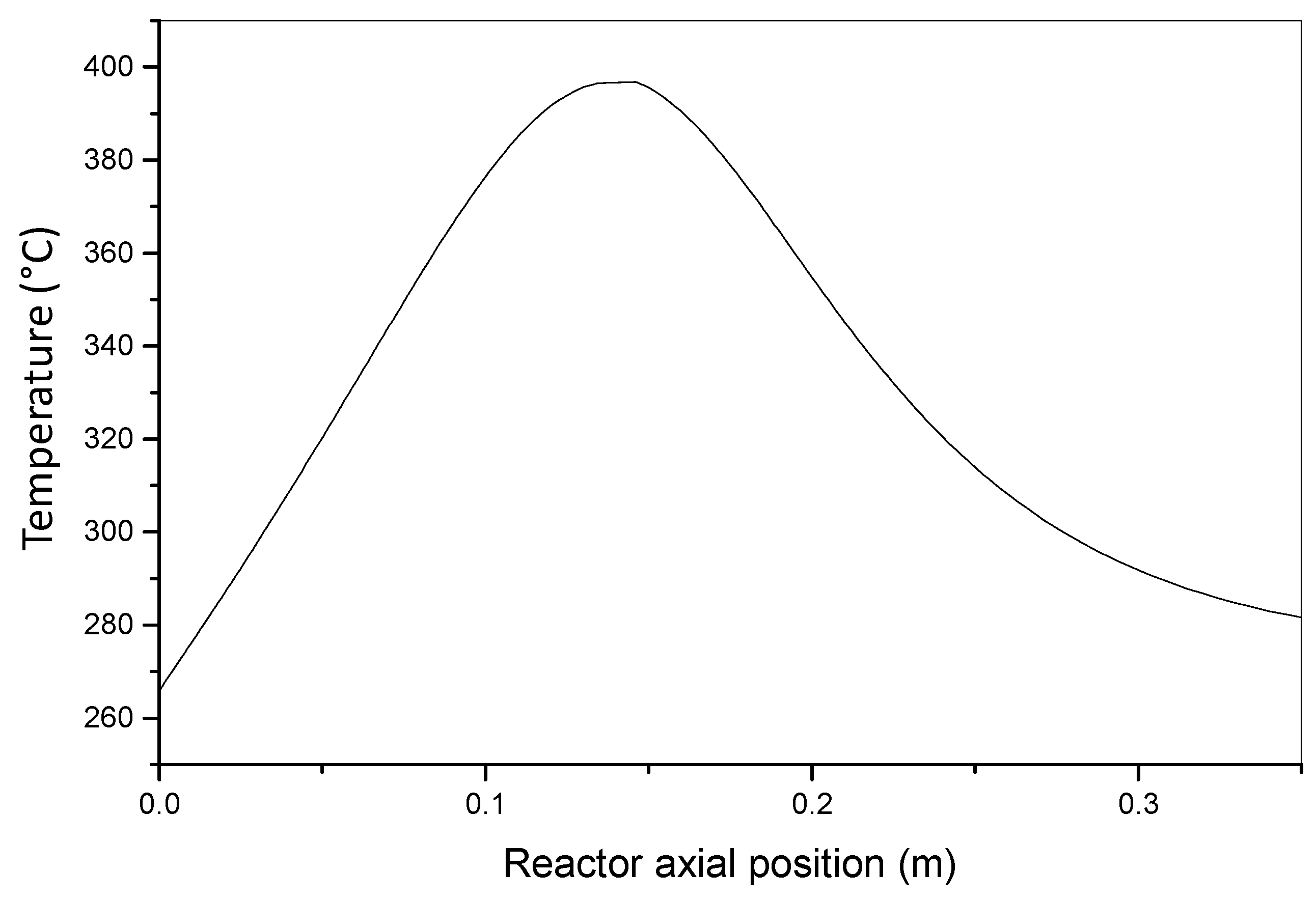

| Ke = 2.72 × 10−4 | KJ/(s m K) | effective thermal conductivity |
| De = 1.07 × 10−5 exp(-672/T) | m2/s | effective diffusivity |
| ρP = 1180 | Kg/m3 | particle density |
| Cp = 2.5 | KJ/(mole K) | particle specific heat |
| P = 1.68 | atm | total pressure |
| TS = 539 | K | surface temperature |
| dP = 3.5 × 10−3 | m | particle diameter |
| Bulk gas composition | mol% | |
| CH3OH | 9.0 | |
| O2 | 10.0 | |
| CH2O | 0.5 | |
| H2O | 2.0 | |
| CO | 1.0 | |
| N2 | 77.5 | |
| k1 = 5.37 × 102 exp(-7055/T) |
| k2 = 6.42 × 10−5 exp(-1293/T) |
| a1 = 5.68 × 102 exp(-1126/T) |
| a2 = 8.37 × 10−5 exp(7124/T) |
| b1 = 6.45 × 10−9 exp(12,195/T) |
| b2 = 2.84 × 10−3 exp(4803/T) |
| ΔH1 = 37,480 cal/mole |
| ΔH2 = 56,520 cal/mole |
| Reactor Conditions | Aspect Ratio Criteria | Left-Hand Side of Equations (71) and (72) |
|---|---|---|
| Isothermal | ||
| Adiabatic | ||
| Non-isothermal and non-adiabatic | ||
| r1 = k1 POX PO (Kmol/Kg-cat h) | ln k1= −27,000/RT + 19.837 |
| r2 = k2 PPA PO (Kmol/Kg-cat h) | ln k2= −31,000/RT + 20.860 |
| r3 = k3 POX PO (Kmol/Kg-cat h) | ln k3= −28,600/RT + 18.970 |
| ΔH1 = −307 Kcal/mol | |
| ΔH2 = −783 Kcal/mol | |
| ΔH3= −1090 Kcal/mol | |
| U = 82.7 Kcal/ m2 h °C | overall heat transfer coefficient |
| D = 0.025 m | reactor diameter |
| Z = 3 m | reactor length |
| dP = 0.003 m | particle diameter |
| CP = 0.25 Kcal/Kg °C | average specific heat |
| ρB =1300 Kg/m3 | bulk density of the bed |
| Feed composition: | yOX = 0.0093 |
| yO = 0.208 | |
| Feed molar flow rate | F = 0.779 moles/h |
| Inert dilution of the catalyst | mI =0.5 for the first quarter |
| Inlet temperature | T0 = 370 °C |
| Inlet temperature | 539 K |
| Total pressure | 1.68 atm |
| Bulk density of the bed | 0.88 Kg/m3 |
| Overall heat transfer coefficient U | 0.171 KJ/(m2 s K) |
| Heating medium temperature | 544 K |
| Reactor diameter | 2.54 x 10−2 m |
| Particles diameter | 3.5 x 10−3 m |
| Reactor length | 0.35 m |
| Gas inlet composition | mol % |
| CH3OH | 9 |
| O2 | 10 |
| CH2O | 0.5 |
| H2O | 2 |
| CO | 1 |
| N2 | 77.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tesser, R.; Santacesaria, E. Revisiting the Role of Mass and Heat Transfer in Gas–Solid Catalytic Reactions. Processes 2020, 8, 1599. https://doi.org/10.3390/pr8121599
Tesser R, Santacesaria E. Revisiting the Role of Mass and Heat Transfer in Gas–Solid Catalytic Reactions. Processes. 2020; 8(12):1599. https://doi.org/10.3390/pr8121599
Chicago/Turabian StyleTesser, Riccardo, and Elio Santacesaria. 2020. "Revisiting the Role of Mass and Heat Transfer in Gas–Solid Catalytic Reactions" Processes 8, no. 12: 1599. https://doi.org/10.3390/pr8121599
APA StyleTesser, R., & Santacesaria, E. (2020). Revisiting the Role of Mass and Heat Transfer in Gas–Solid Catalytic Reactions. Processes, 8(12), 1599. https://doi.org/10.3390/pr8121599