The Dependence of Effective Distribution Coefficient on Growth Rate and Mass Transfer Coefficient for P-Xylene in Solid-Layer Melt Crystallization
Abstract
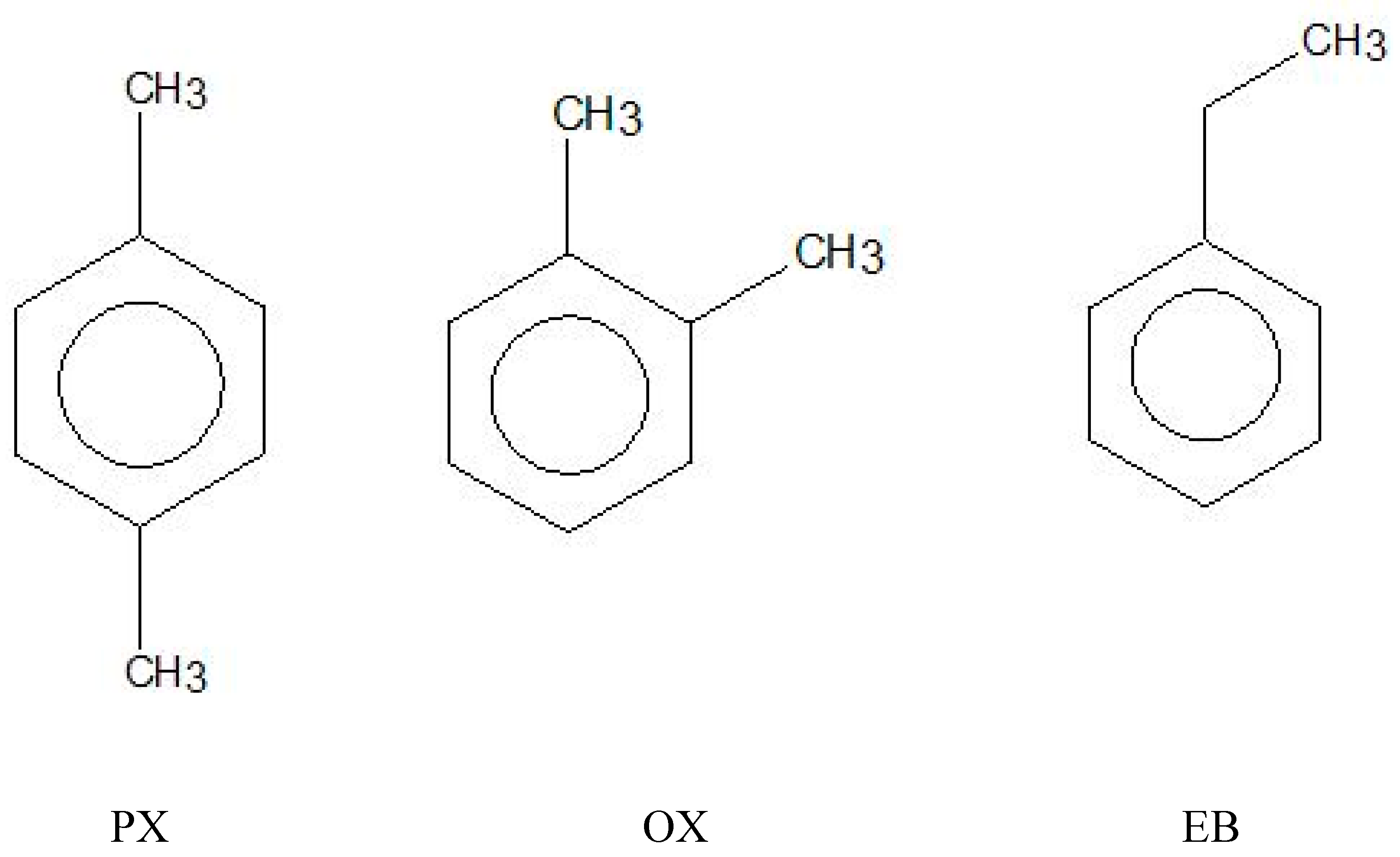
1. Introduction
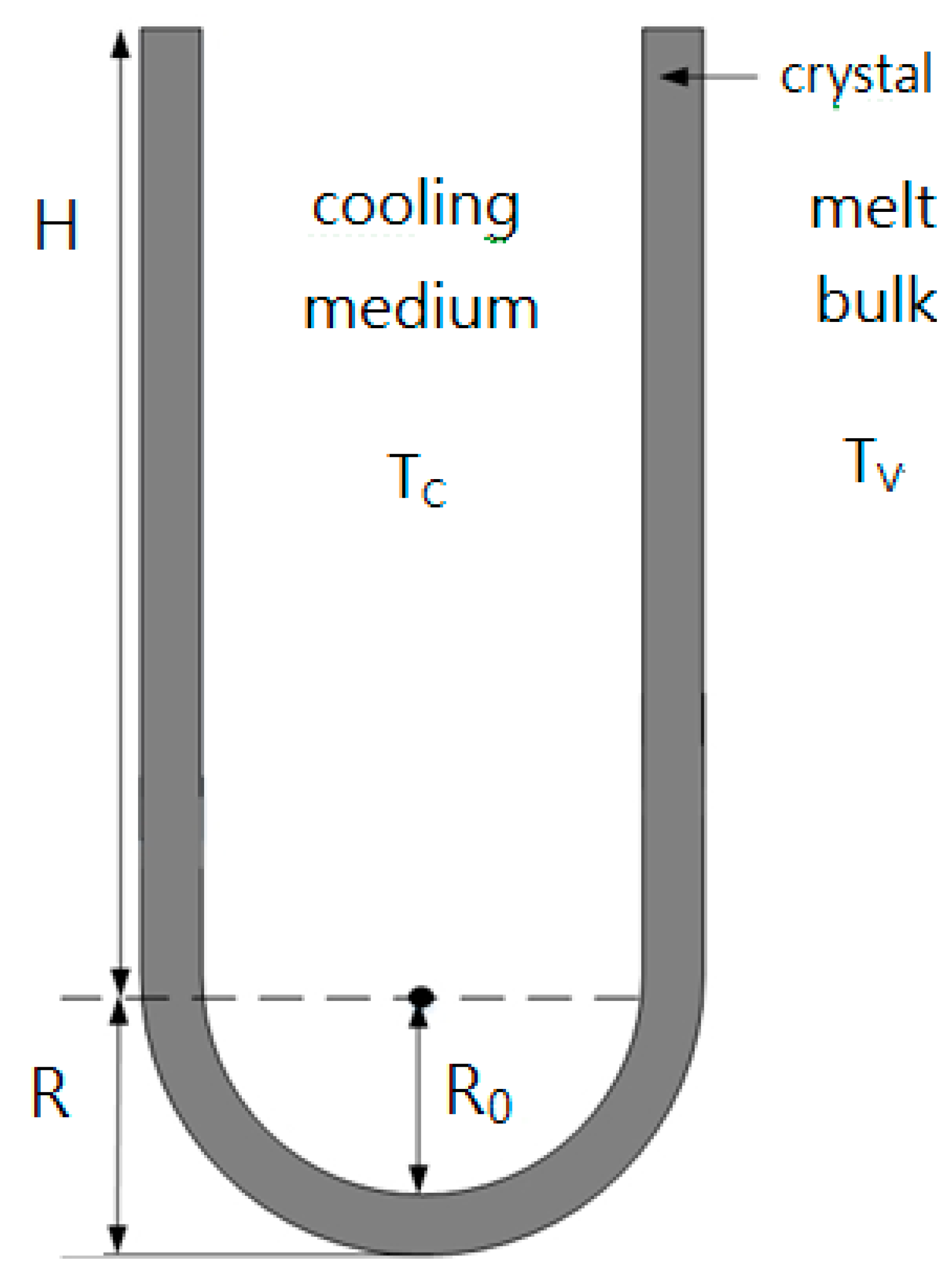
2. Theory
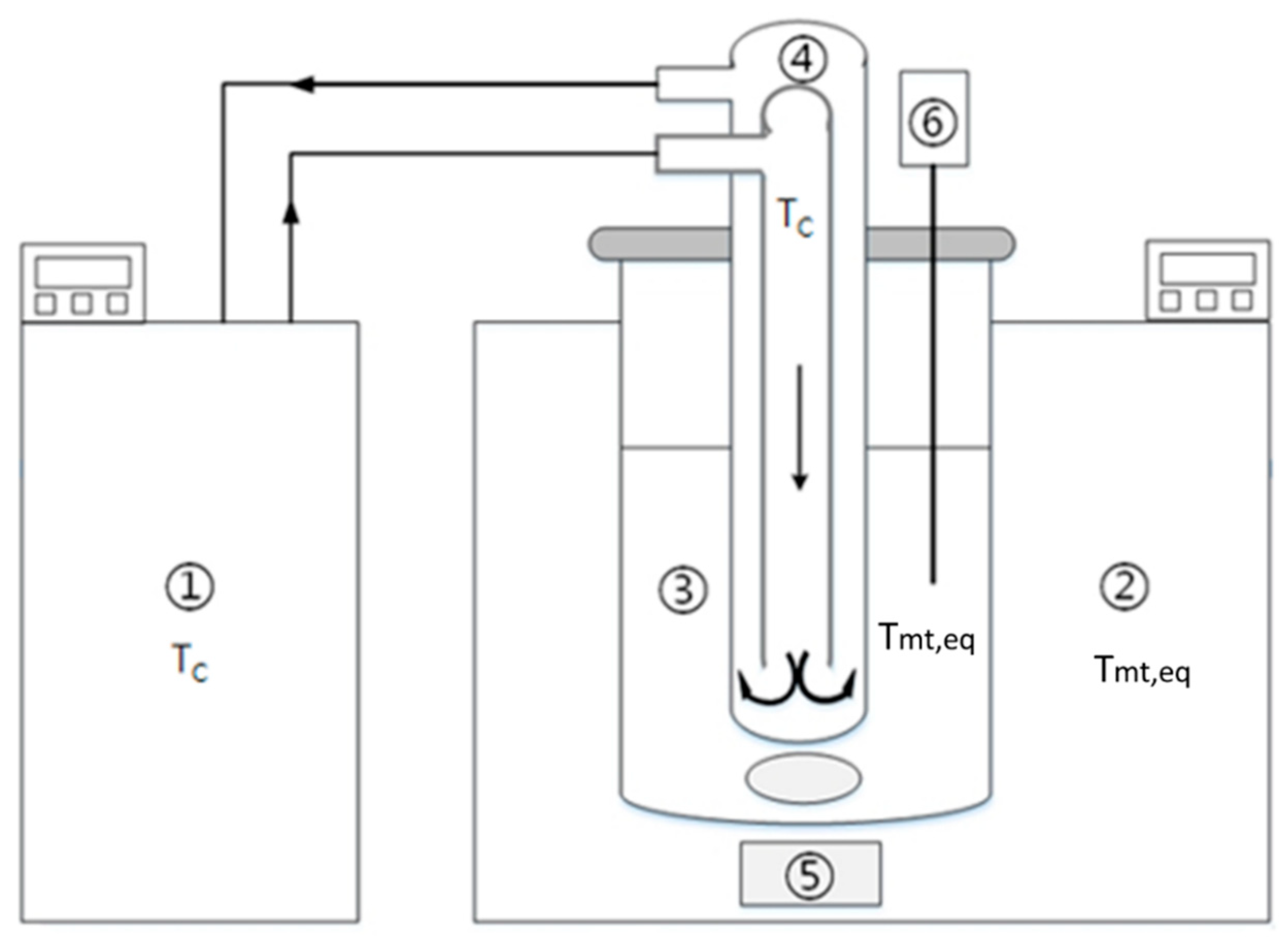
3. Experimental
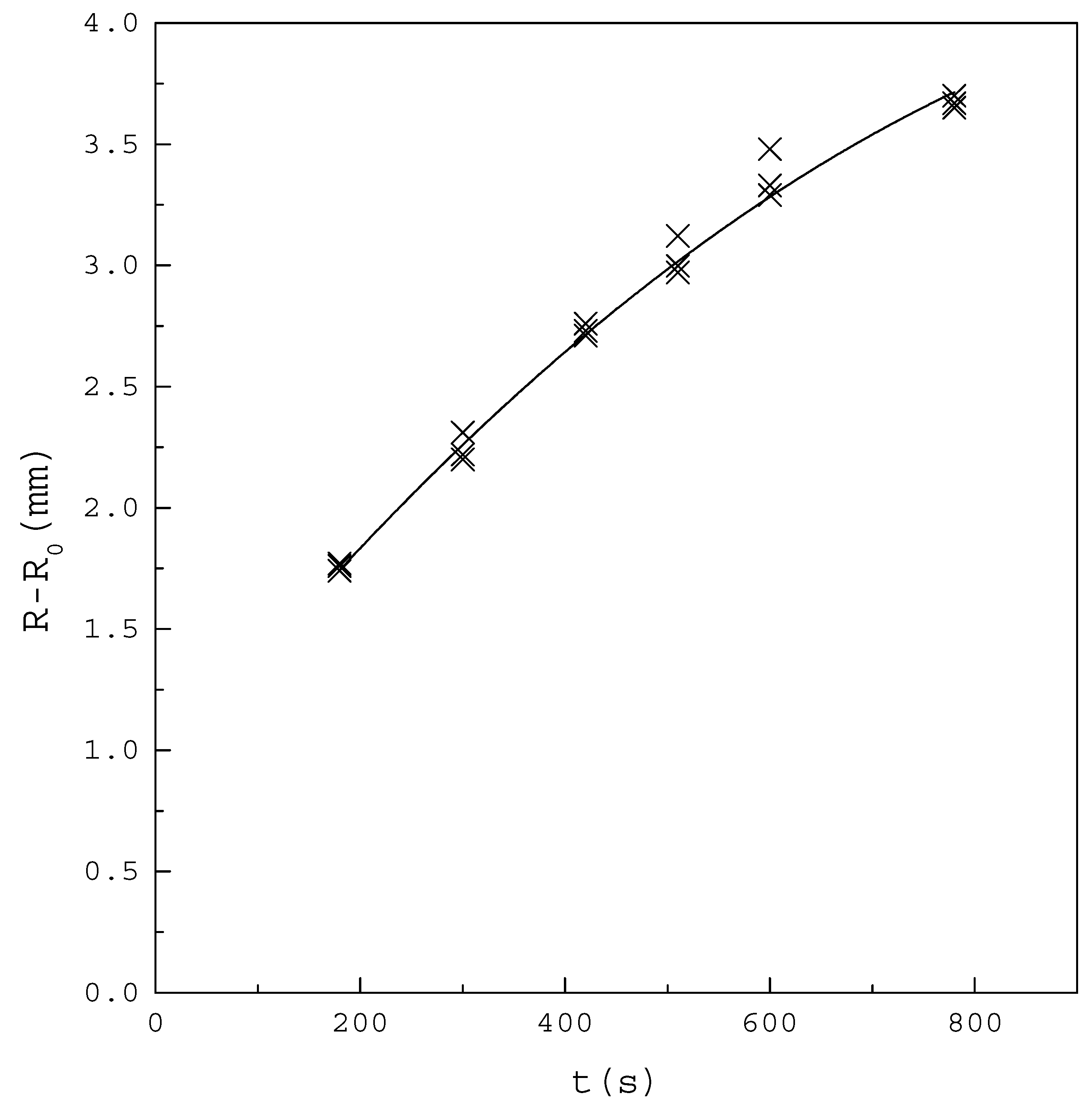
4. Results and Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Notation
| impurity mole fraction in crystal layer | |
| impurity mole fraction at the crystal-melt interface | |
| impurity mole fraction at the position in the boundary layer | |
| impurity mole fraction in melt | |
| mole fraction of the crystallized substance in melt | |
| diffusivity | |
| growth rate | |
| height of the crystal layer on the cooling finger | |
| heat of melting | |
| mass transfer coefficient | |
| effective distribution coefficient | |
| mass of total crystal layer | |
| outer radius of the cooling finger | |
| outer radius of the crystal layer on the cooling finger | |
| ideal gas constant | |
| cooling temperature of the cooling medium | |
| melting temperature | |
| equilibrium temperature of the melt | |
| temperature gradient between melt and cooling medium | |
| time | |
| total growth time | |
| distance perpendicular to the crystal-melt interface |
Greek Letters
| crystal density | |
| thickness of the boundary layer |
References
- Mullin, J.W. Crystallization; Butterworth-Heinemann: Oxford, UK, 1993. [Google Scholar]
- Arkenbout, G.J. Melt Crystallization Technology; Technomic Publishing Company Inc.: Lancaster, PA, USA, 1995. [Google Scholar]
- Ulrich, J.; Glade, H. Melt Crystallization: Fundamentals, Equipment and Applications; Shaker Aachen: Düren, Germany, 2003. [Google Scholar]
- Jiang, X.; Li, M.; He, G.; Wang, J. Research process and model development of crystal layer growth and impurity distribution in layer melt crystallization: A review. Ind. Eng. Chem. Res. 2014, 53, 13211–13227. [Google Scholar] [CrossRef]
- Wang, T.; Lu, H.; Wang, J.; Xiao, Y.; Zhou, Y.; Bao, Y.; Hao, H. Recent progress of continuous crystallization. J. Ind. Eng. Chem. 2017, 54, 14–29. [Google Scholar] [CrossRef]
- Chianese, A.; Santilli, N. Modelling of the solid layer growth from melt crystallization-the integral formulation approach. Chem. Eng. Sci. 1998, 53, 107–111. [Google Scholar] [CrossRef]
- Parisi, M.; Chianese, A. The crystal layer growth from a well-mixed melt. Chem. Eng. Sci. 2001, 56, 4245–4256. [Google Scholar] [CrossRef]
- Kim, K.J.; Ulrich, J. Impurity distribution in a solid-liquid interface during static layer crystallization. J. Colloid Interface Sci. 2002, 252, 161–168. [Google Scholar] [CrossRef]
- Jiang, X.; Hou, B.; He, G.; Wang, J. Falling film melt crystallization (I): Model development, experimental validation of crystal layer growth and impurity distribution process. Chem. Eng. Sci. 2012, 84, 120–133. [Google Scholar] [CrossRef]
- Zhou, L.; Su, M.; Benyahia, B.; Singh, A.; Barton, P.I.; Trout, B.; Myerson, A.S.; Braatz, R.D. Mathematical modeling and design of layer crystallization in a concentric annulus with and without recirculation. AIChE J. 2013, 59, 1308–1321. [Google Scholar] [CrossRef]
- Beierling, T.; Osiander, J.; Sadowski, G. Melt crystallization of isomeric long-chain aldehydes from hydroformylation. Sep. Purif. Technol. 2013, 118, 13–24. [Google Scholar] [CrossRef]
- Beierling, T.; Gorny, R.; Sadowski, G. Modeling growth rates in static layer melt crystallization. Cryst. Growth Des. 2013, 13, 5229–5240. [Google Scholar] [CrossRef]
- Beierling, T.; Micovic, J.; Lutze, P.; Sadowski, G. Using complex layer melt crystallization models for the optimization of hybrid distillation/melt crystallization processes. Chem. Eng. Process. 2014, 85, 10–23. [Google Scholar] [CrossRef]
- Yazdanpanah, N.; Myerson, A.; Trout, B. Mathematical modeling of layer crystallization on a cold column with recirculation. Ind. Eng. Chem. Res. 2016, 55, 5019–5029. [Google Scholar] [CrossRef]
- Fukui, K.; Fujikawa, T.; Satone, H.; Yamamoto, T.; Maeda, K. Application of solute distribution theory to melt crystallization of fatty acids. Chem. Eng. Sci. 2016, 143, 114–121. [Google Scholar] [CrossRef]
- Ioannou, I.S.; Kontos, S.S.; Koutsoukos, P.G.; Paraskeva, C.A. Mathematical modeling and experimental coupling of solution layer crystallization on a vertically cold surface. Sep. Purif. Technol. 2018, 197, 8–17. [Google Scholar] [CrossRef]
- Patience, D.B.; Rawlings, J.B.; Mohameed, H.A. Crystallization of p-xylene in scraped-surface crystallizers. AIChE J. 2001, 47, 2441–2451. [Google Scholar] [CrossRef]
- Mohameed, H.A.; Jdayil, B.A.; Takrouri, K. Separation of para-xylene from xylene mixture via crystallization. Chem. Eng. Process. 2007, 46, 25–36. [Google Scholar] [CrossRef]
- Shiau, L.D.; Wen, C.C.; Lin, B.S. Separation and purification of p-xylene from the mixture of m-xylene and p-xylene by distillative freezing. Ind. Eng. Chem. Res. 2005, 44, 2258–2265. [Google Scholar] [CrossRef]
- Shiau, L.D.; Wen, C.C.; Lin, B.S. Application of distillative freezing in the separation of o-xylene and p-xylene. AIChE J. 2006, 52, 1962–1967. [Google Scholar] [CrossRef]
- Shiau, L.D.; Wen, C.C.; Lin, B.S. Separation of p-xylene from the multicomponent xylene system by stripping crystallization. AIChE J. 2008, 54, 337–342. [Google Scholar] [CrossRef]
- Shiau, L.D.; Liu, K.F. Investigations into the effects of the cooling rate on stripping crystallization. Ind. Eng. Chem. Res. 2013, 52, 1716–1722. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 6th ed.; McGraw-Hill: Singapore, 2001. [Google Scholar]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; John Willey & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Burton, J.A.; Prim, R.C.; Slichter, W.P. The distribution of solute in crystals grown from the melt. Part I. Theoretical. J. Chem. Phys. 1953, 21, 1987–1991. [Google Scholar] [CrossRef]
- Burton, J.A.; Kolb, E.D.; Slichter, W.P.; Struthers, J.D. Distribution of solute in crystals grown from the melt. Part II. Experimental. J. Chem. Phys. 1953, 21, 1991–1996. [Google Scholar] [CrossRef]
- Wellinghoff, G.; Wintermantel, K. Schmelzkristallisation-theoretische Voraussetzungen und technische Grenzen. Chem. Ing. Tech. 1991, 63, 881–891. [Google Scholar] [CrossRef]
- Guardani, R.; Neiro, S.M.S.; Bulau, H.; Ulrich, J. Experimental comparison and simulation of static and dynamic solid layer melt crystallization. Chem. Eng. Sci. 2001, 56, 2371–2379. [Google Scholar] [CrossRef]
- De Goede, R.; van Rosmalen, G.M. Modelling of crystal growth kinetics: A simple but illustrative approach. J. Cryst. Growth 1990, 104, 392–398. [Google Scholar] [CrossRef]
- De Goede, R.; van Rosmalen, G.M. Crystal growth phenomenon of paraxylene crystals. J. Cryst. Growth 1990, 104, 399–410. [Google Scholar] [CrossRef]

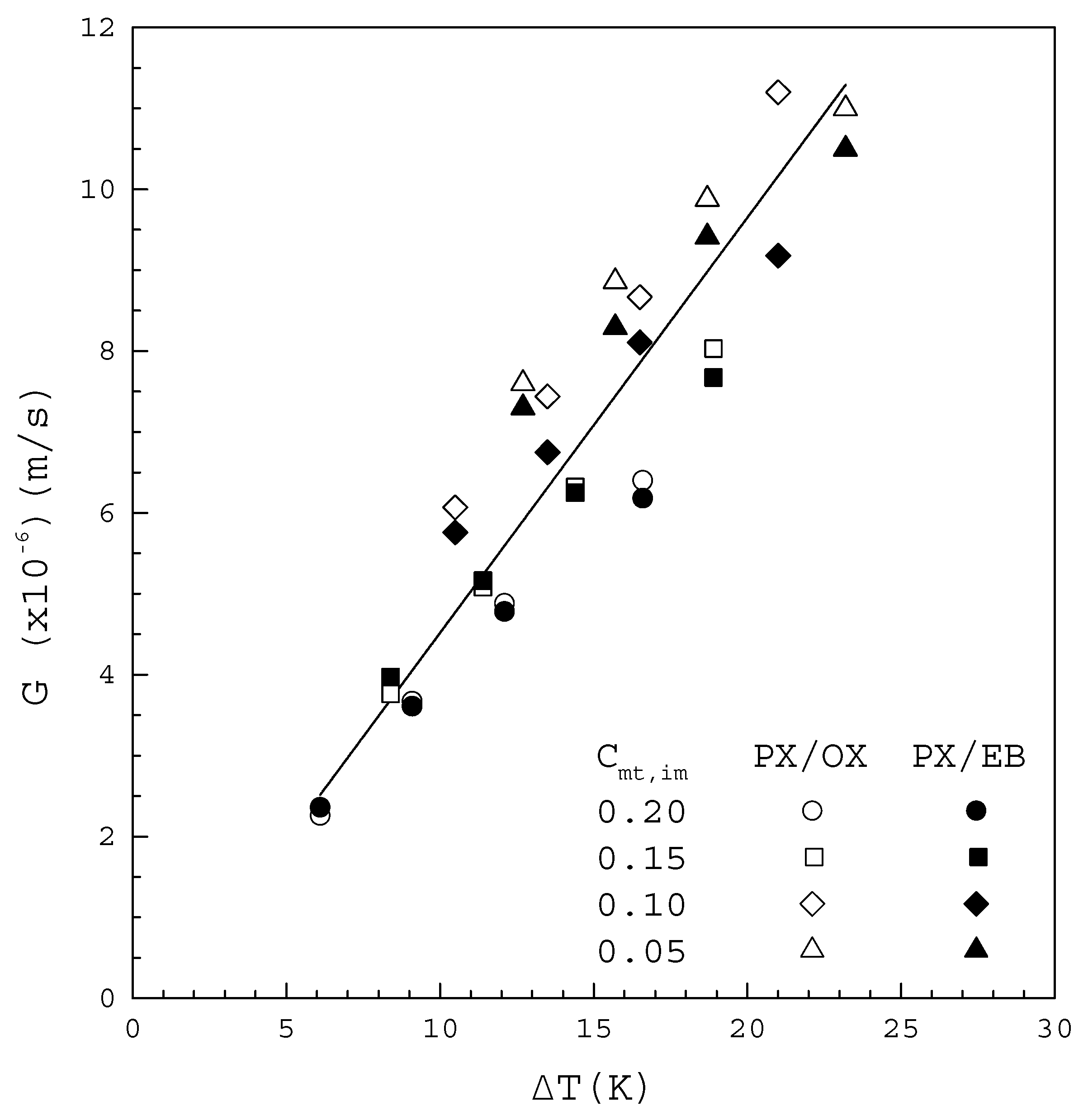
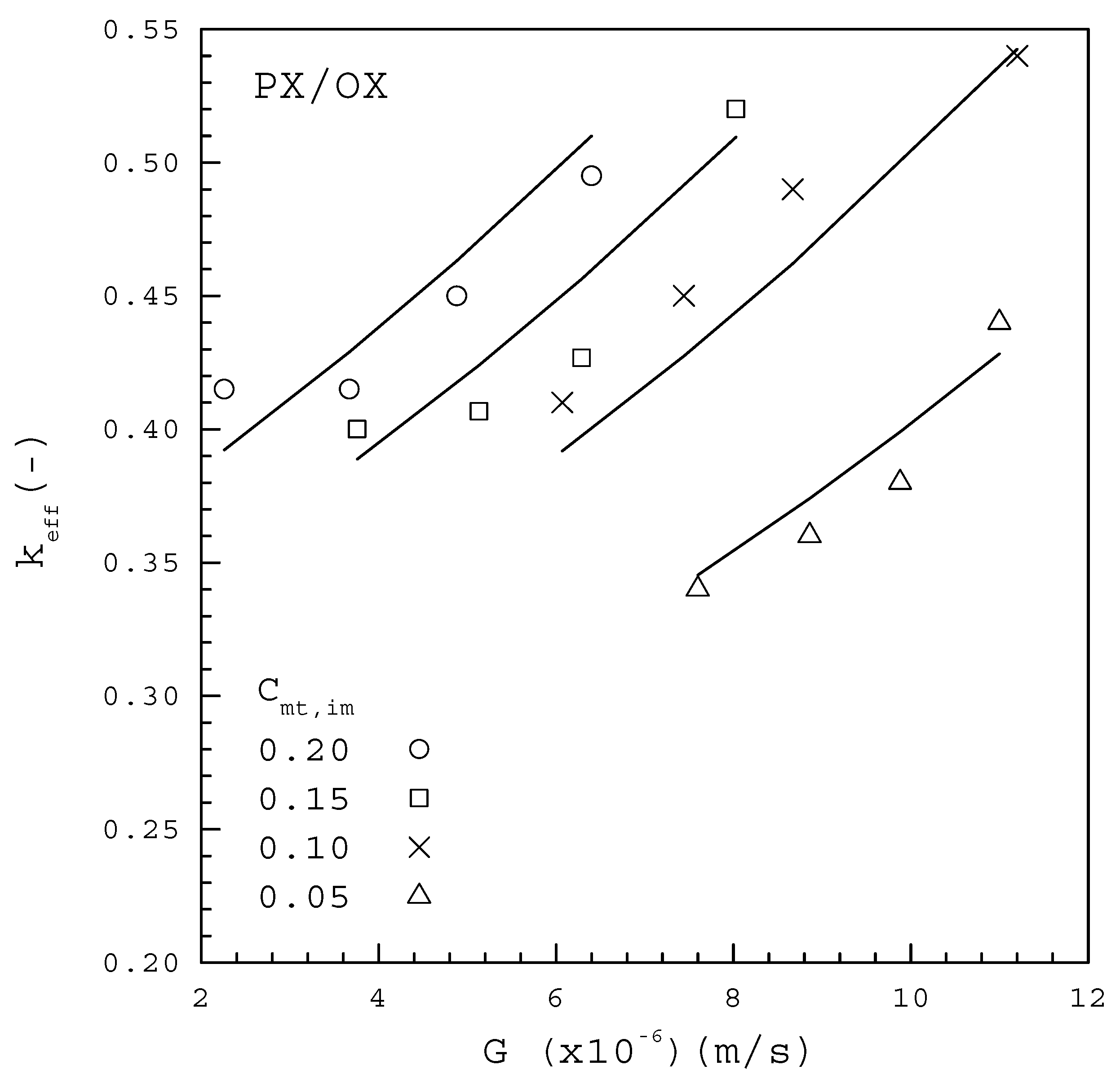
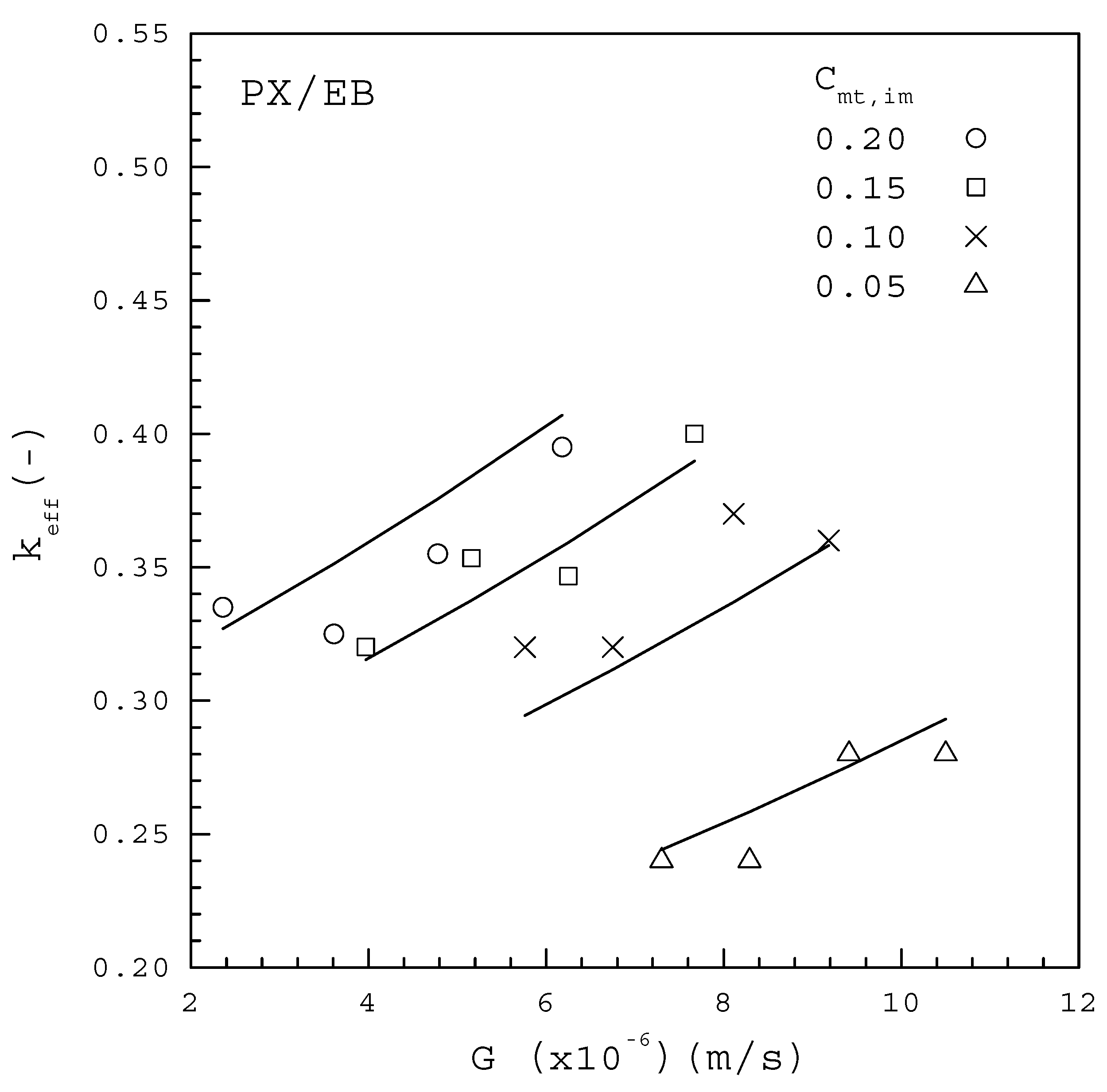

(-) | (K) | (K) | (K) | (m/s) | (-) | (-) |
|---|---|---|---|---|---|---|
| 0.05 | 284.4 | 271.7 | 12.7 | 7.60 | 0.017 | 0.0704 |
| 268.7 | 15.7 | 8.86 | 0.018 | 0.0741 | ||
| 265.7 | 18.7 | 9.88 | 0.019 | 0.0770 | ||
| 261.2 | 23.2 | 11.00 | 0.022 | 0.0782 | ||
| 0.10 | 282.2 | 271.7 | 10.5 | 6.07 | 0.041 | 0.128 |
| 268.7 | 13.5 | 7.44 | 0.045 | 0.133 | ||
| 265.7 | 16.5 | 8.67 | 0.049 | 0.137 | ||
| 261.2 | 21.0 | 11.20 | 0.055 | 0.147 | ||
| 0.15 | 280.1 | 271.7 | 8.4 | 3.76 | 0.060 | 0.174 |
| 268.7 | 11.4 | 5.13 | 0.061 | 0.184 | ||
| 265.7 | 14.4 | 6.29 | 0.064 | 0.192 | ||
| 261.2 | 18.9 | 8.03 | 0.078 | 0.198 | ||
| 0.20 | 277.8 | 271.7 | 6.1 | 2.26 | 0.083 | 0.218 |
| 268.7 | 9.1 | 3.67 | 0.083 | 0.231 | ||
| 265.7 | 12.1 | 4.88 | 0.090 | 0.240 | ||
| 261.2 | 16.6 | 6.40 | 0.099 | 0.251 |
(-) | (K) | (K) | (K) | (m/s) | (-) | (-) |
|---|---|---|---|---|---|---|
| 0.05 | 284.4 | 271.7 | 12.7 | 7.30 | 0.012 | 0.0697 |
| 268.7 | 15.7 | 8.29 | 0.012 | 0.0731 | ||
| 265.7 | 18.7 | 9.41 | 0.014 | 0.0757 | ||
| 261.2 | 23.2 | 10.50 | 0.014 | 0.0797 | ||
| 0.10 | 282.2 | 271.7 | 10.5 | 5.76 | 0.032 | 0.127 |
| 268.7 | 13.5 | 6.75 | 0.032 | 0.132 | ||
| 265.7 | 16.5 | 8.11 | 0.037 | 0.137 | ||
| 261.2 | 21.0 | 9.18 | 0.036 | 0.144 | ||
| 0.15 | 280.1 | 271.7 | 8.4 | 3.97 | 0.048 | 0.176 |
| 268.7 | 11.4 | 5.16 | 0.053 | 0.183 | ||
| 265.7 | 14.4 | 6.25 | 0.052 | 0.192 | ||
| 261.2 | 18.9 | 7.67 | 0.060 | 0.200 | ||
| 0.20 | 277.8 | 271.7 | 6.1 | 2.36 | 0.067 | 0.219 |
| 268.7 | 9.1 | 3.61 | 0.065 | 0.231 | ||
| 265.7 | 12.1 | 4.78 | 0.071 | 0.241 | ||
| 261.2 | 16.6 | 6.18 | 0.079 | 0.251 |
| Number of Data Points (n) | Number of Parameters (k) | Computed F Value * | Critical F Value | ||
|---|---|---|---|---|---|
| Equation (15) | 16 | 3 | 0.895 | 55.4 | 6.70 |
| Equation (16) | 16 | 3 | 0.890 | 52.6 | 6.70 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiau, L.-D. The Dependence of Effective Distribution Coefficient on Growth Rate and Mass Transfer Coefficient for P-Xylene in Solid-Layer Melt Crystallization. Processes 2020, 8, 175. https://doi.org/10.3390/pr8020175
Shiau L-D. The Dependence of Effective Distribution Coefficient on Growth Rate and Mass Transfer Coefficient for P-Xylene in Solid-Layer Melt Crystallization. Processes. 2020; 8(2):175. https://doi.org/10.3390/pr8020175
Chicago/Turabian StyleShiau, Lie-Ding. 2020. "The Dependence of Effective Distribution Coefficient on Growth Rate and Mass Transfer Coefficient for P-Xylene in Solid-Layer Melt Crystallization" Processes 8, no. 2: 175. https://doi.org/10.3390/pr8020175
APA StyleShiau, L.-D. (2020). The Dependence of Effective Distribution Coefficient on Growth Rate and Mass Transfer Coefficient for P-Xylene in Solid-Layer Melt Crystallization. Processes, 8(2), 175. https://doi.org/10.3390/pr8020175





