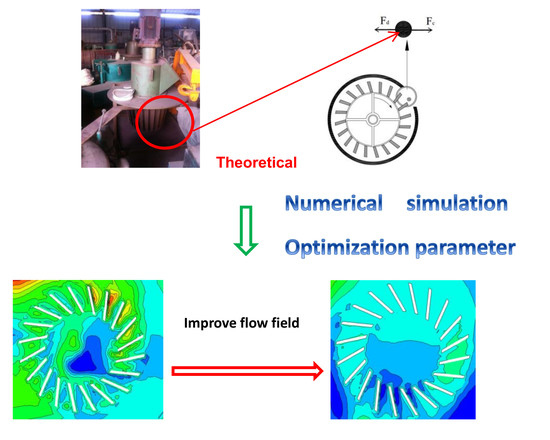
1. Introduction
Currently, ultrafine powders are widely used in various fields, and the powder separation technique has gradually occupied an important position in industry. The main production equipment for ultrafine powders is the turbo air classifier. The classification performance of the classifier directly affects the efficiency of powder production. Therefore, many researchers [
1,
2,
3,
4,
5,
6,
7] have conducted extensive studies on the theoretical analysis, flow field simulation, structural optimization, and other aspects of pneumatic grading equipment, and have made progress by obtaining many valuable results and providing the basis for the optimization of classifiers, performance enhancements, and fine separations. The main factors affecting the classification sharpness index and performance during the classification process are the rotor cage speed and the air inlet velocity inside the classifier [
6,
7,
8]. According to the principle of classification, a material is subjected to inertial centrifugal force and air drag force at the same time during the classification process. Some researchers analyzed the effect of the rotor cage rotary speed on the classification sharpness index, using the Fluent software, and obtained a reasonable parameter combination for classification. Gao, Yu, and Liu [
9,
10] found that increasing the rotor cage rotary speed resulted in a finer product, but the higher speed caused the flow field to become uneven, and increased the classification sharpness index. Through the study of the classifier airflow velocity, Diao et al. [
11] found that increasing the air inlet velocity could improve the classification efficiency. However, the inertial centrifugal forces of small- and large-sized materials are different. The distribution of small-diameter materials in the flow field is relatively uniform, but large-particle-sized materials are easily moved to the outside of the flow field. This leads to a high concentration outside the flow field and reduces the classification performance.
Based on above researches, in order to further study the classification performance, many scholars have found that it is meaningful to conduct in-depth research on the evaluation index of classification performance. Some scholars [
12,
13,
14] pointed out that the Whiten’s efficiency curve equation needs to be revised. Hence, the parameters in the Whiten’s equation were correlated with the operating conditions of the air classifier as well as the material characteristics. The fish-hook phenomenon was demonstrated in a circulating-air classifier. Based on the experimental data, a process model was developed to predict the bypass fraction within the classifier [
15]. Xing et al. [
16] measured and analyzed the vortex swirling between rotor blades, using the particle image velocimetry (PIV) technique. They found changes in the regulation of the classification efficiency and cut-size, and optimized the operating parameters to achieve the minimum cut-size. However, in the actual classification process, the agglomeration and inclusion of fine particles in the coarse particles would cause a decrease of the classification sharpness index. Some researchers [
17] demonstrated secondary airflow and found that when the ratio of the secondary airflow to the main airflow was maintained at 0.168, the classification was optimum. Based on the narrow particle size distribution experimental system, the best rotor cage speed difference between two turbo air classifiers was found, and the results showed that with a decreasing rotation speed difference, the productivity of the narrow-level product decreased and the uniformity increased. Nevertheless, many evaluation indexes of classification performance can accurately judge the grading performance, but it is very troublesome in actual production. Therefore, it is especially important to propose an efficient and simple evaluation index [
18,
19,
20,
21,
22].
Due to limitations, such as the processing cost and other factors, it is difficult for enterprises and research institutes to produce a variety of grading wheels for structural parameters. Therefore, in the production process, one or more optimal processes are obtained through manual adjustment and matching of various process parameters. In the above studies, scholars mainly studied the effect of a single factor (rotation speed, airflow velocity, etc.) on the classification performance; however, research on the influence of various factors on the classification performance is rare. Consequently, this study applied the combination of process parameters as variables in numerical simulations and material experiments to obtain the optimum process parameters of the KFF (‘KFF’ is a code for a vertical turbo air classifier type) series turbine air classifier. Thus, in the production process, using the different manually controlled process parameters, one or more optimal process parameters can be obtained. In addition, a new evaluation index, the relative classification sharpness index, is proposed. The test results showed that it is the same as other classification performance evaluation indicators. It can be used to determine whether the classification status is good, simple, and easy, and has a certain guiding effect on industrial production.
2. Details of the Calculation Methodology
2.1. Description of the Equipment
The equipment for the experiment comprised of a KFF series turbo air classifier, high-pressure induced-draft fan, cyclone collector, pulse bag-filter, and electrical control system. The sketch of the KFF series turbo air classifier is shown in
Figure 1a. The schematic diagrams of the vertical turbo air classifier with corresponding geometric parameters are shown in
Figure 1b,c. The air supply system consisted of induced-draft fans. The induced-draft fan is “pumping” at the end of the turbo air classifier, providing the transport power for the particles. Firstly, the material is sent to the main classifier by the feeding system, and effective classification of the material is achieved by adjusting the rotor cage speed and matching it with a reasonable secondary air inlet velocity. Under the action of centrifugal force, the coarse powder is collected along the wall of the cylinder and the fine powder continues to be classified by the airflow into the next grading machine so that a reasonably super-fine material is collected when it enters the cyclone separator or dust removal system.
2.2. Particle Cutting Size Calculations
The force diagram at the edge of the classifier rotor cage after the material particles enter the classifier is shown in
Figure 2. According to the theoretical method in the literature [
15,
16], we know that the particle is mainly influenced by the centrifugal and drag forces when it is delivered at the inlet edge of the rotor cage. In this experiment, the radial velocity of the airflow moving around the rotor cage is denoted as
Vr, and the rotational speed of the rotor cage generating the centrifugal force is
n. It was assumed that the tangential and radial velocities in the circumferential and vertical directions are uniform and that the particles are spherical. The mathematical definitions of the forces are given in Equations (1)–(3):
It was assumed that there is no slip between the particle and the air tangential velocity. When the centrifugal and fluid drag forces reach equilibrium on the particle at the outer periphery of the rotor cage, and if the radial velocity of the particle is zero, the size of the particle is called the cut size (
d50). The
d50 can be expressed as follows from Equations (1)–(3):
By testing the classifier inlet air volume, the corresponding airflow radial velocity can be calculated:
Using the known rotor cage speed, the tangential velocity of the particles at the outer edge of the grading wheel can be calculated:
The following equation can be derived from Equations (4)–(6):
where:
: Particle diameter (μm);
: Radial velocity of airflow at the outer cylindrical periphery ();
: Tangential velocity of airflow at the outer cylindrical periphery of the rotor cage ();
: Particle radial velocity ();
: Density of airflow ();
: Particle density ();
: Radius of rotor cage (mm);
: Blade height (mm);
: Mass of particle ();
: Rotor cage speed (rpm);
: Total volumetric flow rate of air ();
: Drag coefficient;
: Reynolds number; and
: Cut size of classification (μm).
2.3. Mathematical Model
2.3.1. Continuous Phase Governing Equations
The three-dimensional steady simulation was performed using ANSYS-FLUENT 15.0. For the case of incompressible flow, the mass and momentum equations are as follows:
Where
,
,
,
P, and
represent the fluid velocity, position, time, constant fluid density, static pressure, and gas viscosity, respectively.
is the Reynolds stress term. Choosing a suitable turbulence model in the case is of paramount importance. Furthermore, the RNG k-e model has been proven to be an appropriate model to describe the turbulence of turbo air classifier flow [
21]. The turbulent kinetic energy and turbulent dissipation rate are expressed as follows:
where
and
represent the components of the turbulent kinetic energy caused by the average velocity gradient and buoyancy.
is the effect of compressible turbulent pulsation expansion on the total dissipation rate. The values of the constant are
= 0.7692,
= 1,
= 1.44,
= 1.92,
= 0.09.
The turbulent viscosity coefficient can be calculated as:
where
.
2.3.2. Discrete Phase Governing Equations
The choice of a multiphase flow model is mainly determined by the particle volume loading rate, , and mass loading rate, , which are demonstrated in the following two parts:
(1) Volume loading rate is the ratio of the particle volume to gas volume per unit time in a space. It can be expressed as follows:
where:
,—Particle volume and gas volume passing through the effective section at per unit time; and
,—Particle density and air density.
Using the particle volume loading rate, the dimensionless distance between particles and particles in the particle phase can be calculated:
where:
L—The distance between particle and particle; and
—Particle diameter.
(2) Mass loading rate is the ratio of particle mass to gas mass across an effective section in a certain space per unit time. It is expressed as follows:
In this study, the airflow and material are fed into the classifier by a circular section inlet. Thus, the gas volume passing through the effective section per unit time can be calculated:
where
V0 is the air inlet velocity, which was set in the range from 6 to 12 m/s in this study.
is the radius of the section at the inlet. The feeding speed is 240 kg/h. Combined with Equations (13)–(15), the range of the volume loading rate can be calculated from 2.624 × 10
−6 to 4.34 × 10
−6. Meanwhile, the range of the mass loading rate can be calculated from 0.0257 to 0.0342. These values are very small. However, the dimensionless distance between particles and particles ranged from 32.09 to 37.9. According to the calculated results, the value of the particle volume loading rate and mass loading rate is very small, and the value of the dimensionless distance between particles and particles is very large. Therefore, the particle phase is considered to be highly sparse, which satisfies the DPM calculation conditions. Furthermore, it can also be considered that the coupling between the particles and the gas phase is unidirectional. Namely, only the influence of gas on the particles is taken into account, rather than the influence of particles on the gas.
Through the DPM of FLUENT, the trajectory of a discrete phase particle can be calculated in a Lagrangian reference frame by integrating the force balance on the particle. This force balance equation can be written in Cartesian coordinates:
where
is the drag force per unit particle mass,
is the fluid phase velocity,
is the particle velocity,
is the kinematic viscosity of fluids,
is the fluid density,
is the particle density,
is the particle diameter,
is the relative Reynolds number (particle Reynolds number) (the define of Particle Reynolds number can be calculated by Equation (19))
is the drag coefficient, and
is an additional acceleration (force/unit particle mass) term.
2.4. Boundary Conditions and Parameter Setting
The model was designed to be imported into the ANSYS-Fluent software for numerical calculations. There is one entrance and two exits in the model. A ‘‘velocity inlet” boundary condition was used at the air-inlet, the air velocity was assumed to be uniformly distributed at the air inlet section, and its direction is normal to the air-inlet boundary. The boundary condition at the turbo air classifier was prescribed as a fully developed pipe flow and treated as ‘‘outflow”. A no-slip boundary condition was used on the wall boundary and the near wall treatment was a standard wall function. The SIMPLEC algorithm was adopted for the pressure–velocity coupling, and the QUICK difference scheme were used for the convection and diffusion. The convection terms of the discrete equations were all in the default format. An insufficient relaxation factor empirical selection was used. In total, 2000 steps were iterated to set the solution accuracy at 1e–03.
3. Simulation Results and Analysis
According to Equation (7), the two main factors affecting the particle size grading are the tangential velocity, VT, and radial velocity, Vr, of the gas flow, when the other parameters, such as the radius and height of the runner, are quantitative. The tangential velocity of the airflow is directly related to the rotor cage speed, and the radial velocity of the airflow is related to the total volumetric flow rate of air. Increasing the rotor cage speed can result in particles with finer particle sizes, but this can cause an uneven distribution of the flow field, affect the classification sharpness index, and reduce the classification performance. When the air volume of the system is changed, if the airflow rate is too low, the feeding force of the raw materials becomes too low, resulting in grading failure; if the main airflow is too high, the compulsive action of the grading wheel may be invalidated, and the coarse particles are rejected. The airflow is transmitted into the fine powder, and when the classifier cuts the particle size, the classification effectiveness worsens. Therefore, changing the rotor cage speed or the air inlet velocity of the system alone cannot help obtain the optimum process parameters. Only by simultaneously controlling the air inlet velocity of the system and the corresponding rotor cage speed to perform particle grading can one or more sets of optimal process parameter combinations be obtained
Numerical simulation experiments were performed using multiple groups of variables by setting different simulation parameters to achieve quantitative changes in VT and Vr, and the particle velocity map of the impeller surface was used as a reference to judge the better process parameter. Owing to the actual process parameters, the limited range of the rotation speed of the rotor wheel was 500–3000 rpm and the range of air volume was 2700–5500 m3/h. Calculated according to Equation (7) and the actual working condition limit, four groups of the rotor cage speed were set: 1800, 2000, 2200, and 2400 rpm. The air inlet velocity was set in four groups: 6, 8, 10, and 12 m/s. The above four groups of rotor cage speed and air inlet velocity were combined to perform an orthogonal numerical simulation test.
3.1. The Tangential Velocity Distribution in the Classifier.
There are two important grading functional zones in the classifier: One of them is the flow region between the blades (I: blade zone, it called the separation functional zone), another is an annular region surrounding the inlet boundary of the rotor cage (II: annular zone, it called the decentralized separation functional zone) [
18]. The rotation of the rotor cage causes turbulence in the annular zone, and the turbulence in the annular zone has some influence on the classification effect, which causes a decrease in the classification efficiency and classification sharpness index. In addition, if the tangential velocity in the blade zone is much larger than the tangential velocity in the annular zone, the fine particles can also move to the annular zone under strong centrifugal force, and finally settle along the side wall to become coarse powder, which causes a decrease in the classification efficiency and classification sharpness index. Therefore, it is necessary to study the tangential velocity distribution of zone I and zone II.
Figure 3 shows the tangential velocity details of the rotor cage section. The grading wheel surface (select a section at half the height of the rotor cage, Y = 260 mm) tangential velocity contour diagrams for 16 groups and tangential velocity contrast under different radial distances from the axis are shown in
Figure 3.
According to the above analysis, the more uniform tangential velocity distribution of the airflow in the annular zone (II) and blade zone (I), the more stable the flow field. Based on
Figure 3a, under the condition that the air inlet velocity remains unchanged at 6 m/s, a comparison of the tangential speed profiles of the blade zone and annular zone under different process parameters indicates that the tendency of the tangential distribution at rotor cage speeds of 1600 and 2200 rpm is more stable than that at rotor cage speeds of 1800 and 2000 rpm. Based on
Figure 3b, under the condition that the air inlet velocity remains unchanged at 8 m/s, a comparison of the tangential speed profiles of the blade zone and annular zone under different process parameters indicates that the tendency of the tangential distribution at he rotor cage speeds of 1800 rpm is more stable than that at rotor cage speeds of 1600, 2000, and 2200 rpm. Nevertheless, the tendency of the tangential change gradient amplitude at rotor cage speeds of 2200 rpm is slower than that at rotor cage speeds of 1600 and 2000 rpm. Based on
Figure 3c, under the condition that the air inlet velocity remains unchanged at 10 m/s, it can be clearly seen that the tendency of the tangential distribution at rotor cage speeds of 1800 and 2000 rpm is more stable than that at rotor cage speeds of 1600 and 2200 rpm. Based on
Figure 3d, under the condition that the air inlet velocity remains unchanged at 12 m/s, it can be clearly seen that the tendency of the tangential distribution at rotor cage speeds of 2000 and 2200 rpm is more stable than that at rotor cage speeds of 1600 and 1800 rpm.
From the above discussion, the conclusion can be reached that eight groups of process parameters (Vin-n,6-1600,6-2200,8-1800,8-2200,10-1800,10-2000,12-2000,12-2200) may be better than others.
3.2. The Radial Velocity Distribution in the Classifier
In the process of grading, the blade zone (I) is an important grading functional zone, and its main function is to transport fine powder and separate the coarse and fine powder. Furthermore, after the airflow enters the rotor cage, on the one hand, it is driven by the rotation of the rotating blades, and on the other hand, it moves inward along the blade under the action of the central negative pressure. Finally, inertial anti-vortex will be formed between the blades. The material is transported by radial airflow in zone I. As the radial airflow in the passage between adjacent blades is affected by the inertial anti-vortex, it leads to uniformity of the radial velocity distribution. The fine powder that has entered the cage will leave the cage under the influence of the anti-vortex. Finally, the cutting particle size is dispersed, which decreases the classification sharpness index. In addition, if the radial velocity distribution is not uniform in the blade zone, the coarse particles are also collected by the airflow into fine powder, which affects the classification sharpness index. Therefore, the radial velocity distribution of the airflow in blade zone (I) must be studied.
Figure 4 shows the radial velocity details of the rotor cage section. The grading wheel surface (select a section at half the height of the rotor cage, Y = 260 mm) radial velocity contour diagrams for 16 groups and radial velocity contrast under different radial distances from the axis are shown in
Figure 4.
In the classification process, the vane flow velocity near the “surface of the advance blade” (the surface that is in the blade facing in the direction of rotation) is larger than the “surface of the back blade” (the surface that in the blade is back to the direction of rotation). Therefore, it can be observed whether the positive vortex and the anti-vortex exist between the blades to judge whether the flow field between the rotor cage blades is uniform. As is shown in
Figure 4a–d, the size of the vortex and the velocity gradient between the blades can be easily and intuitively found, as eight groups of process parameters (
Vin-n,6-1600,6-2200,8-1800,8-2200,10-1800,10-2000,12-2000,12-2200) may be better than others. The conclusion is the same as the results of the tangential velocity.
3.3. Discrete-Phase Simulated Results and Analysis
In the particle classification process, the movement process of particles is intuitively described and is revealed by the particle trajectory, which can also explain the particle separation mechanism. Consequently, the discrete phase model was established to simulate the particle trajectory, and the particle motions for eight groups of process parameters were contrasted.
3.3.1. Simulated Results and Analysis of Single Particle
Iron ore powder particle (12 μm) was chosen as the material, and steady flow simulation was set up. According to the continuous phase simulation, eight groups of process parameters were better than others. Therefore, these eight groups of process parameters were selected for discrete phase simulation. The particle tracks cloud diagrams for the eight groups are as follows:
As is shown in
Figure 5, comparing the particle tracks under the process parameters for the eight groups in the numerical simulations, as seen from the
Figure 5a–h, it can be found that the number of particle tracks(a), (c), (f), (h) are more than (b–e), (g). Therefore, it can be simply inferred that four process parameters can be estimated as better than the others for producing the particle size of 12 μm, rotor speed of 1600 rpm with the air inlet velocity at 6 m/s, rotor speed of 1800 rpm with the air inlet velocity at 8 m/s, rotor speed of 2000 rpm with the air inlet velocity at 10 m/s, and rotor speed of 2200 rpm with the air inlet velocity at 12 m/s.
3.3.2. Simulated Results and Analysis of Multi-Particle
The authors used the ANASYS-fluent discrete phase model for numerical simulation, and investigation of gas flow behaviors in the turbo air classifier. In order to obtain the simulated Tromp curve at different process parameters, the authors set up 13 different particle sizes for each set of process parameters. In order for better comparison with the electronic test report, the specific particle size parameters were set as follows:
Iron ore fines: 1, 2, 4, 5.13, 6.21, 7.51, 8, 10, 11, 12.66, 16.62, 19.5, and 23.6 μm
Barite powder: 4, 5.13, 6.21, 7.51, 8, 11, 12.66, 13.31, 16.62, 19.5, 23.6, 28.56, 32, and 41.8 μm
The number of particles escaped and trapped was calculated by the numerical simulation, and the upper limit of the particle calculation step was 20,000. Finally, the tromp curve was drawn the light of the percentage of escape particles in the total number of particles. The pictures are shown in
Figure 6a,b. The purpose of this study was to research the combination of two process parameter variables. Therefore, according to the result of the numerical simulation, the cut size under the combination of the rotor speed and air flow rate can be roughly estimated. The results are shown in
Figure 6c,d. The effect of the rotor speed and air inlet velocity on the cut size can be found.
Figure 6a,b shows the schematic diagram of the numerical simulated Tromp curve by different process parameters. It is not easy to obtain the classification sharpness
K (
K =
d75/
d25) under different process parameters through observation of the tromp curve. However, it can be roughly judged by the cut size by different process parameters. According to Equation (7), it can be easily inferred that with the air inlet velocity increase, the cut size will increase, or with the rotor speed increase, the cut size will decrease. However, when the air inlet velocity and the rotor speed increase simultaneously, we cannot conclude whether the cut size is increased or decreased. From
Figure 6, it can be easily found that the effect of the rotor speed on the cut size is more than the air inlet velocity. In addition, in order to select which combination-type process parameter is better than others, the optimum process parameter was verified using a material grading experiment.
4. Classification Experiment and Discussion
The raw materials for this experiment were iron ore fines and barite, with material densities of 7.83 and 4.3 g/cm3, respectively (the densities of materials were detected by an HX-TD-type true density tester). According to the numerical simulation results, four process parameters (1#rotation speed of 1600 rpm and an air inlet speed of 6 m/s; 2# rotation speed of 1800 rpm and an air inlet speed of 8 m/s; 3# rotation speed of 2000 rpm and an air inlet speed of 10 m/s; 4# rotation speed of 2200 rpm and an air inlet speed of 12 m/s) were better than others.
4.1. Particle Size Distribution and the Classification Efficiency
Therefore, the iron ore fines and barite raw materials were divided into two groups and subjected to grading tests under four kinds of process parameters. The grading of the particle size distribution maps are as follows:
According to the powder particle size distribution diagrams in
Figure 7a,b, it can be found that the particle size distributions of the product by four process parameters are evidently different.
Firstly, iron ore powder with a particle size distribution ranges from 9 to 13 μm is mainly produced. It can be found that the second group of process parameters has the highest existence of the particle size distribution ranges from 8 to 12 μm. In addition, the highest existence of the barite particle size distribution ranges from 11 to 16 μm, and the best process parameters are in the second group. The case studies of the particle classification efficiency are shown in
Figure 7c,d. These curves depict the same changing tendency of the distorted S-shape. As the particle size decreases, the classification efficiency of the particles first decreases and then increases. This phenomenon is commonly referred to as the hook effect. With the increase of the rotor cage speed and air inlet velocity, the fish-hook effect is found to be enhanced. Generally, the hook effect will decrease corresponding to the increase of the air inlet velocity. However, with the rotor cage speed increases, the particle cut size decreases, the d
50 also decreases correspondingly. The consequence is that the Tromp curve will move to the left, causing the agglomeration to advance. At last, the fish-hook effect will increase. Therefore, considering these two factors of the air inlet velocity and rotor cage speed, it can be found that the hook effect is increasing. On the other hand, the bypass value (δ) is an important index to evaluate the performance of classification. As is shown in
Figure 7c,d, the bypass value (δ
2< δ
1< δ
3< δ
4) of the second process parameters is the smallest. It can be considered that the performance of the second process parameters’ classification is better than the others.
4.2. Coarse Powder Yield and Newton Efficiency
For most airflow grading equipment, the powder is classified according to a certain cutting particle size. The large particle portion after classification is referred to as coarse products, and the small particle portion is referred to as fine products. Commonly, Newton’s classification efficiency is a main classification performance index. It comprehensively examines the degree of separation of coarse and fine powder particles. The expression is:
where
is the coarse powder yield,
is the fine powder yield,
is the mass percentage of coarse particle in raw material,
A and
B are the mass of the collected coarse fraction and collected fine fraction,
F is the mass of the raw material,
and
are the mass percentage of coarse particles (
dp >
d50) in the collected coarse fraction.
Figure 8a,b, shows the effects of four process parameters on the iron ore coarse powder yield (
) and Newton efficiency (
). It can be found that with the rotor cage speed and air inlet velocity increase, the collection efficiency of the coarse particle gradually decreases. The reason is that the increase in the amount of air entering the main air causes the air drag to rise and more and more coarse particles are taken away; therefore, the value of
decreases. In addition, as the rotation speed of the runner and the air intake speed increase, Newton’s classification efficiency increases initially, but as the rotation speed and air intake speed of the runner continue to increase, Newton’s classification efficiency decreases. It means that an excessive rotor cage speed and air inlet velocity is not good for classification. Finally, according to the results of Newton’s classification efficiency, it can be considered that the performance of the second process parameters’ classification is better than the others.
4.3. Classification Sharpness Index (K)
There are roughly three kinds of indicators for evaluating the grading effectiveness [
19,
20,
21,
22]. The representative index is the classification sharpness index. The index proposed by Germany’s Leschonski is
K =
d75/
d25. Currently, in an effective grading apparatus for a commercial field, if the sharpness index is close to 1, the performance of the grading apparatus is considered perfect. In an actual industry experiment, if the value of the K is in the range from 1.4 to 2.0, the performance of the grading apparatus is considered good; if the value of the K is in the range from 1.0 to 1.4, the performance of the grading apparatus is considered excellent. According to the classification experiment results, the effects of four process parameters on the classification sharpness index are shown in
Figure 9. It can be easily found that the classification sharpness index (
K) value of the second process parameters is closest to 1. Therefore, the performance of the second process parameters’ classification is better than others.
4.4. Relative Classification Sharpness Index
The author proposes a relative classification sharpness index as the examination index for this experiment. As shown in
Figure 10a,b, the curves f, a, and b represent the raw material particle size distribution, the classified fine powder particle size distribution, and the classified coarse powder particle size distribution, respectively.
d10coarse indicates a particle size of 10% for the cumulative content in the coarse powder after classification,
d90fine indicates a particle size of 90% for the cumulative content in the fine powder after classification, and d’ indicates the distribution frequency of the fine powder in the coarse powder and the coarse powder in the fine powder is equivalent. The expression for the relative grading sharpness index is:
The value of the relative classification sharpness index, δ, is the index for testing this experiment. A larger δ indicates a better grading effectiveness and a smaller δ indicates a poorer grading effectiveness. Judging from the numerical simulation results, the authors chose four sets of process parameters for the actual experiment, with the powder particle size distribution as the inspection index, to investigate the effectiveness of the four sets of process parameters on the relative classification sharpness index of the powder.
The test instrument selected was the LS-C (IIA) laser particle size analyzer (error ≤ 3%).
Based on the data in
Table 1, a graph of δ changing with the process parameters was plotted, as shown in
Figure 11. As the rotation speed of the runner and the air intake speed increase, the relative classification sharpness index increases initially, but as the rotation speed and air intake speed of the runner continue to increase, the relative classification sharpness index decreases. According to the results of the relative classification sharpness index, it can be found that the performance of the second process parameters’ classification is better than the others.
5. Conclusions
This study was based on the kinetics of single particles. The trajectory of the particles was quantitatively analyzed under different rotation speeds and intake air volumes. The following conclusions were obtained:
- (1)
The grading experiment results for iron ore fines and barite powder materials indicate that the better process parameter combination for the production of 12-μm particles using the KFF series turbo air classifier is a 1800 rpm rotor speed and 8 m/s air inlet velocity.
- (2)
For the same process parameters, when the same grain size of 12-μm barite and iron ore fines are produced, the relative classification sharpness index is different, indicating that the grading effectiveness for the smaller density particles is higher.
- (3)
Numerical simulation experiments showed that the air inlet velocity has an effect on the grading effectiveness rather than the rotor cage speed.
- (4)
The proposed new evaluation index, the relative classification sharpness index, could accurately evaluate the classification performance.
Author Contributions
The author S.Z. provided help in the preliminary investigation of this article. M.L. provided resources such as experimental equipment. Y.Z. (Yang Zhou) conducted in-depth research on the evaluation index of classification performance, then proposed the concept of the relative classification sharpness index, which could be applied in the classification performance tests of actual production. Y.Z. (Yun Zeng) was in charge of the entire research experiment, statistics all the data and sorted it out. Finally wrote and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This project was supported financially by the National Key R&D project (2016YFC0303703), the National Natural Science Foundation of China (No. 51674040 and No. 51904181), and the National Natural Science Foundation of Hubei province (No. 2016CFC740). The authors would like to thank all the members of the project team for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, W.; Liu, J.; Yu, Y. Design of a rotor cage with non-radial arc blades for turbo air classifiers. Powder Technol. 2016, 292, 46–53. [Google Scholar] [CrossRef]
- Xiong, D.; Li, S.; Huang, P. Effect of feeding type on classification performance of superfine classifier. CIESC J. 2012, 63, 3818–3825. [Google Scholar]
- Huang, Q.; Liu, J.; Yu, Y. Turbo air classifier guide vane improvement and inner flow field numerical simulation. Powder Technol. 2012, 226, 10–15. [Google Scholar] [CrossRef]
- Shapiro, M.; Galperin, V. Air classification of solid particles: Are view. Chem. Eng. Process. 2005, 44, 279–285. [Google Scholar] [CrossRef]
- Morimoto, H.; Shakouchi, T. Classification of ultrafine powder by a new pneumatic type classifier. Powder Technol. 2003, 131, 71–79. [Google Scholar] [CrossRef]
- Liu, R.; Liu, J.; Yu, Y. Effects of axial inclined guide vanes on a turbo air classifier. Powder Technol. 2015, 280, 1–9. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Yang, X.; Yuan, Y.; Wang, Q.; Liu, J. Effects of fine particle outlet on performance and flow field of a centrifugal air classifier. Chem. Eng. Res. Des. 2017, 117, 139–148. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Liu, J.; Yang, X. CFD simulation and optimization of the flow field in horizontal turbo air classifiers. Adv. Powder Technol. 2017, 28, 1474–1485. [Google Scholar] [CrossRef]
- Gao, L.; Yu, Y.; Liu, J. Effect of rotor cage rotary speed on classification accuracy in turbo air classifier. CIESC J. 2012, 63, 1056–1062. [Google Scholar]
- Gao, L.; Yu, Y.; Liu, J. Study on the cut size of a turbo air classifier. Powder Technol. 2013, 237, 520–528. [Google Scholar] [CrossRef]
- Xiong, D.; Li, S.; Huang, P. Numerical Simulation of Distribution Characteristics of Particle Concentration in Inlet Tube of Superfine Classifier. Chin. J. Process. Eng. 2011, 11, 729–735. [Google Scholar]
- Okay, A.; Nurettin, A.T.; Hakan, B.; Ozgun, D. Multi component modelling of an air classifier. Miner. Eng. 2016, 93, 50–56. [Google Scholar]
- Okay, A.; Hakan, B. Selection and mathematical modelling of high efficiency air classifiers. Powder Technol. 2014, 264, 1–8. [Google Scholar]
- Benzer, H.; Ergun, L.; Lynch, A.J.; Oner, M.; Gunlu, M.; Celik, I.B.; Aydogan, N.A. Modelling cement grinding circuits. Miner. Eng. 2001, 14, 1469–1482. [Google Scholar] [CrossRef]
- Eswaraiah, C.; Angadi, S.I.; Mishra, B.K. Mechanism of particle separation and analysis of fish-hook phenomenon in a circulating air classifier. Powder Technol. 2012, 218, 57–63. [Google Scholar] [CrossRef]
- Xing, W.; Wang, Y.; Zhang, Y.; Yoshiyuki, Y.; Saga, M.; Lu, J.; Zhang, H.; Jin, Y. Experimental study on velocity field between two adjacent blades and gas–solid separation of a turbo air classifier. Powder Technol. 2015, 286, 240–245. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, C.H.; Chen, H.Y.; Zhang, M.; Fu, Y.; Wang, X. Effects of secondary air on the classification performances of LNJ-36A air classifier. Chem. Ind. Eng. Prog. 2015, 34, 3859–3863. [Google Scholar]
- Liu, J.; Xia, J.; He, T. Air flow field characteristics analyzing and classification process of the turbo classifier. J. Chin. Ceram. Soc. 2003, 31, 485–489. [Google Scholar]
- Tao, Z.; Zheng, S. Powder Engineering and Equipment; Chemical Industry Press: Beijing, China, 2010. [Google Scholar]
- Zhang, S.; Chen, Y.; Li, S. Effects of process parameters on particle size distribution and productivity of narrow level product in turbo air classifier. Chem. Ind. Eng. Prog. 2015, 33, 1113–1117+1155. [Google Scholar]
- Napier-Munn, T.J. Mineral Comminution Circuits; Julius Kruttschnitt Mineral Research Centre: Queensland city, Australia, 1996. [Google Scholar]
- Tirado, J.M.; Kumar, S.; Vandewinckel, J. Ladder Shelf System. U.S. Patent 10,167,669, 1 January 2002. [Google Scholar]
Figure 1.
Diagram of the experiment equipment (a) and the 3D view of the geometry (b) and dimensions (c) of the turbo air classifier.
Figure 1.
Diagram of the experiment equipment (a) and the 3D view of the geometry (b) and dimensions (c) of the turbo air classifier.
Figure 2.
Particle-influencing forces at the inlet of the rotor cage.
Figure 2.
Particle-influencing forces at the inlet of the rotor cage.
Figure 3.
Contours of the tangential velocity distribution and air tangential velocity contrast under different radial distances from the axis at different process parameters (305–345 mm is the area between the rotor blades, 345–365 mm is the annular zone). (a) Air inlet velocity 6 m/s and 4 different rotor cgae speed. (b) Air inlet velocity 8 m/s and 4 different rotor cgae speed. (c) Air inlet velocity 10 m/s and 4 different rotor cgae speed. (d) Air inlet velocity 12 m/s and 4 different rotor cgae speed.
Figure 3.
Contours of the tangential velocity distribution and air tangential velocity contrast under different radial distances from the axis at different process parameters (305–345 mm is the area between the rotor blades, 345–365 mm is the annular zone). (a) Air inlet velocity 6 m/s and 4 different rotor cgae speed. (b) Air inlet velocity 8 m/s and 4 different rotor cgae speed. (c) Air inlet velocity 10 m/s and 4 different rotor cgae speed. (d) Air inlet velocity 12 m/s and 4 different rotor cgae speed.
Figure 4.
Contours of the air radial velocity distribution between rotor blades and radial velocity contrast under different radial distances from the axis at different process parameters (−345–305mm, 305–345mm is the area between the rotor blades, −305–305 mm is the central region).(a) Air inlet velocity 6 m/s and 4 different rotor cgae speed. (b) Air inlet velocity 8 m/s and 4 different rotor cgae speed. (c) Air inlet velocity 10 m/s and 4 different rotor cgae speed. (d) Air inlet velocity 12 m/s and 4 different rotor cgae speed.
Figure 4.
Contours of the air radial velocity distribution between rotor blades and radial velocity contrast under different radial distances from the axis at different process parameters (−345–305mm, 305–345mm is the area between the rotor blades, −305–305 mm is the central region).(a) Air inlet velocity 6 m/s and 4 different rotor cgae speed. (b) Air inlet velocity 8 m/s and 4 different rotor cgae speed. (c) Air inlet velocity 10 m/s and 4 different rotor cgae speed. (d) Air inlet velocity 12 m/s and 4 different rotor cgae speed.
Figure 5.
Particle tracks for 8 groups of different rotor speeds and air inlet velocity. (a) Rotor speed 1600 rpm, air inlet velocity 6 m/s. (b) Rotor speed 2200 rpm, air inlet velocity 6 m/s. (c) Rotor speed 1800 rpm, air inlet velocity 8 m/s. (d)Rotor speed 2200 rpm, air inlet velocity 8 m/s. (e) Rotor speed 1800 rpm, air inlet velocity 10 m/s. (f) Rotor speed 2000 rpm, air inlet velocity 10 m/s. (g) Rotor speed 2000 rpm, air inlet velocity 12 m/s. (h) Rotor speed 2200 rpm, air inlet velocity 12 m/s.
Figure 5.
Particle tracks for 8 groups of different rotor speeds and air inlet velocity. (a) Rotor speed 1600 rpm, air inlet velocity 6 m/s. (b) Rotor speed 2200 rpm, air inlet velocity 6 m/s. (c) Rotor speed 1800 rpm, air inlet velocity 8 m/s. (d)Rotor speed 2200 rpm, air inlet velocity 8 m/s. (e) Rotor speed 1800 rpm, air inlet velocity 10 m/s. (f) Rotor speed 2000 rpm, air inlet velocity 10 m/s. (g) Rotor speed 2000 rpm, air inlet velocity 12 m/s. (h) Rotor speed 2200 rpm, air inlet velocity 12 m/s.
Figure 6.
The numerical partial classification efficiency curves and cut size of four different process parameters. (a) Iron ore powder numerical Tromp curves (b) Barite powder numerical Tromp curves (c) Iron ore powder numerical cut size (d) Barite powder numerical cut size
Figure 6.
The numerical partial classification efficiency curves and cut size of four different process parameters. (a) Iron ore powder numerical Tromp curves (b) Barite powder numerical Tromp curves (c) Iron ore powder numerical cut size (d) Barite powder numerical cut size
Figure 7.
The particle size distribution and the classification efficiency of two different materials. (a) Iron ore powder experiments distribution curves (b) Barite powder experiments distribution curves (c) Iron ore powder experiments Tromp curves (d) Barite powder experiments Tromp curves.
Figure 7.
The particle size distribution and the classification efficiency of two different materials. (a) Iron ore powder experiments distribution curves (b) Barite powder experiments distribution curves (c) Iron ore powder experiments Tromp curves (d) Barite powder experiments Tromp curves.
Figure 8.
Effects of four process parameters on two different materials of the coarse powder yield (Yc) and Newton efficiency (). (a) Iron ore powder (b) Barite powder.
Figure 8.
Effects of four process parameters on two different materials of the coarse powder yield (Yc) and Newton efficiency (). (a) Iron ore powder (b) Barite powder.
Figure 9.
Effects of four process parameters on the classification sharpness index (K).
Figure 9.
Effects of four process parameters on the classification sharpness index (K).
Figure 10.
Coarse- and fine-grade product size distribution curve. (a) d10coarse < d90fine. (b) d10coarse > d90fine.
Figure 10.
Coarse- and fine-grade product size distribution curve. (a) d10coarse < d90fine. (b) d10coarse > d90fine.
Figure 11.
Comparison of relative classification accuracies for different process parameters.
Figure 11.
Comparison of relative classification accuracies for different process parameters.
Table 1.
Relative classification accuracies under different process parameters.
Table 1.
Relative classification accuracies under different process parameters.
| Material Name | Number | Wheel Speed Rpm | Air inlet Velocity m/s | Particle Size/μm | δ |
|---|
| d10coarse | d90fine | d′ |
|---|
| Steel Powder | 1# | 1600 | 6 | 8.66 | 7.08 | 7.58 | 0.208 |
| 2# | 1800 | 8 | 8.78 | 6.36 | 7.25 | 0.334 |
| 3# | 2000 | 10 | 9.61 | 10.23 | 9.98 | −0.621 |
| 4# | 2200 | 12 | 9.43 | 10.49 | 9.92 | −0.106 |
| Barite Powder | 1# | 1600 | 6 | 14.62 | 13.36 | 13.87 | 0.091 |
| 2# | 1800 | 8 | 14.95 | 11.01 | 12.36 | 0.318 |
| 3# | 2000 | 10 | 15.73 | 16.66 | 15.95 | −0.583 |
| 4# | 2200 | 12 | 16.28 | 17.69 | 16.89 | −0.083 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).