Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling
Abstract
:1. Introduction
2. Experimental Procedure and Numerical Simulation
2.1. Experiment Using Off-line Rolling Simulator
2.2. Numerical Simulation
3. Results
3.1. Measured Temperature of a Workpiece with Area
3.2. Temperature Distribution of Workpiece by Numerical Simulation
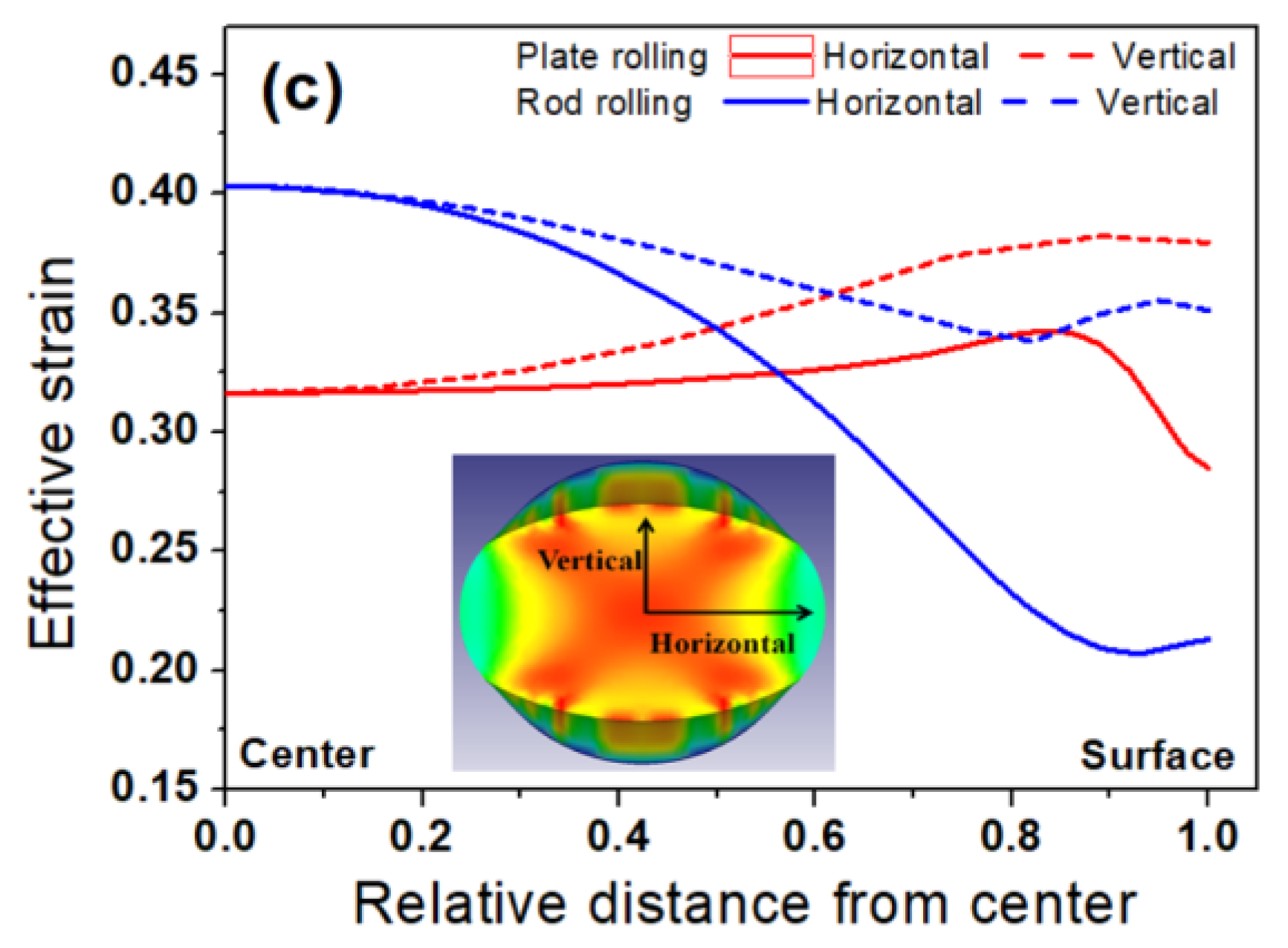
4. Discussion
4.1. Effect of Conduction Heat Transfer in the Workpiece-roll Interface
4.2. Effect of Heat Generation due to Plastic Deformation
5. Conclusions
Funding
Conflicts of Interest
References
- Kwon, H.C.; Lee, H.W.; Kim, H.Y.; Im, Y.T.; Park, H.D.; Lee, D.L. Surface wrinkle defect of carbon steel in the hot bar rolling process. J. Mater. Process. Technol. 2009, 209, 4476–4483. [Google Scholar] [CrossRef]
- Lee, H.W.; Kwon, H.C.; Im, Y.T.; Hodgson, P.D.; Zahiri, S.H. Local austenite grain size distribution in hot bar rolling of AISI 4135 steel. ISIJ Int. 2005, 45, 706–712. [Google Scholar] [CrossRef] [Green Version]
- Laasraoui, A.; Jonas, J.J. Prediction of temperature distribution, flow stress and microstructure during the multipass hot rolling of steel plate and strip. ISIJ Int. 1991, 31, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Nioi, M.; Pinna, C.; Celotto, S.; Swart, E.; Farrugia, D.; Husain, Z.; Ghadbeigi, H. Finite element modelling of surface defect evolution during hot rolling of Silicon steel. J. Mater. Process. Technol. 2019, 268, 181–191. [Google Scholar] [CrossRef]
- Li, Y.; Cao, J.; Qiu, L.; Kong, N.; He, A.; Zhou, Y. Effect of strip edge temperature drop of electrical steel on profile and flatness during hot rolling process. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pesin, A.; Pustovoytov, D. Research of edge defect formation in plate rolling by finite element method. J. Mater. Process. Technol. 2015, 220, 96–106. [Google Scholar] [CrossRef]
- Devadas, C.; Samarasekera, I.V.; Hawbolt, E.B. The thermal and metallurgical state of steel strip during hot rolling: Part 1. Characterization of heat transfer. Metall. Trans. A 1991, 22A, 307–319. [Google Scholar] [CrossRef]
- Chen, W.C.; Samarasekera, I.V.; Hawbolt, E.B. Fundamental phenomena governing heat transfer during rolling. Metall. Trans. A 1993, 24A, 1307–1320. [Google Scholar] [CrossRef]
- Chen, B.K.; Thomson, P.F.; Choi, S.K. Temperature distribution in the roll-gap during hot flat rolling. J. Mater. Process. Technol. 1992, 30, 115–130. [Google Scholar] [CrossRef]
- Serajzadeh, S.; Taheri, A.K.; Nejati, M.; Izadi, J.; Fattahi, M. An investigation on strain inhomogeneity in hot strip rolling process. J. Mater. Process. Technol. 2002, 128, 88–99. [Google Scholar] [CrossRef]
- Karagiozis, A.N.; Lenard, J.G. Temperature distribution in a slab during hot rolling. J. Eng. Mater. Technol. 1988, 110, 17–21. [Google Scholar] [CrossRef]
- Hlady, C.O.; Brimacombe, J.K.; Samarasekera, I.V.; Hawbolt, E.B. Heat transfer in the hot rolling of metals. Metall. Mater. Trans. B 1995, 26B, 1019–1027. [Google Scholar] [CrossRef]
- Shirizly, A.; Lenard, J.G. The effect of scaling and emulsion delivery on heat transfer during the hot rolling of steel strips. J. Mater. Process. Technol. 2000, 101, 250–259. [Google Scholar] [CrossRef]
- Komori, K.; Kato, K. Analysis of temperature distribution in caliber rolling of a bar. JSME Int. J. 1989, 32, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Said, A.; Lenard, J.G.; Ragab, A.R.; Abo Elkhier, M. The temperature, roll force and roll torque during hot bar rolling. J. Mater. Process. Technol. 1999, 88, 147–153. [Google Scholar] [CrossRef]
- Yuan, S.Y.; Zhang, L.W.; Liao, S.L.; Jiang, G.D.; Yu, Y.S.; Qi, M. Simulation of deformation and temperature in multi-pass continuous rolling by three-dimensional FEM. J. Mater. Process. Technol. 2009, 209, 2760–2766. [Google Scholar] [CrossRef]
- Xue, J.; Liu, M. A new control volume-based 2D method for calculating the temperature distribution of rod during multi-pass hot rolling. ISIJ Int. 2013, 53, 1836–1840. [Google Scholar] [CrossRef] [Green Version]
- Serajzadeh, S.; Mirbagheri, H.; Taheri, A.K. Modelling the temperature distribution and microstructural changes during hot rod rolling of a low carbon steel. J. Mater. Process. Technol. 2002, 125, 89–96. [Google Scholar] [CrossRef]
- Serajzadeh, S. Prediction of microstructural changes during hot rod rolling. Int. J. Mach. Tools Manuf. 2003, 43, 1487–1495. [Google Scholar] [CrossRef]
- Choi, S.; Lee, Y. An approach to predict the depth of the decarburized ferrite layer of spring steel based on measured temperature history of material during cooling. ISIJ Int. 2014, 54, 1682–1689. [Google Scholar] [CrossRef] [Green Version]
- Hwang, J.K. Effects of process conditions, material properties, and initial shape of flaw on the deformation behavior of surface flaw during wire drawing. ISIJ Int. 2019, 59, 2052–2061. [Google Scholar] [CrossRef]
- Kim, H.Y.; Kwon, H.C.; Lee, H.W.; Im, Y.T.; Byon, S.M.; Park, H.D. Processing map approach for surface defect prediction in the hot bar rolling. J. Mater. Process. Technol. 2008, 205, 70–80. [Google Scholar] [CrossRef]
- Hwang, J.K. The temperature distribution and underlying cooling mechanism of steel wire rod in the Stelmor type cooling process. Appl. Therm. Eng. 2018, 142, 311–320. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, H.J.; Hwnag, S.M. Analytic model for the prediction of mean effective strain in rod rolling process. J. Mater. Process. Technol. 2001, 114, 129–138. [Google Scholar] [CrossRef]
- Kwon, H.C.; Lee, Y.; Kim, S.Y.; Woo, J.S.; Im, Y.T. Numerical prediction of austenite grain size in round-oval-round bar rolling. ISIJ Int. 2003, 43, 676–683. [Google Scholar] [CrossRef] [Green Version]
- Awais, M.; Lee, H.W.; Im, Y.T.; Kwon, H.C.; Byon, S.M.; Park, H.D. Plastic work approach for surface defect prediction in the hot bar rolling process. J. Mater. Process. Technol. 2008, 201, 73–78. [Google Scholar] [CrossRef]
- Bontcheva, N.; Petzov, G. Total simulation model of the thermo-mechanical process in shape rolling of steel rods. Comput. Mater. Sci. 2005, 34, 377–388. [Google Scholar] [CrossRef]
- Son, I.H.; Lee, J.D.; Choi, S.; Lee, D.L.; Im, Y.T. Deformation behavior of the surface defects of low carbon steel in wire rod rolling. J. Mater. Process. Technol. 2008, 201, 91–96. [Google Scholar] [CrossRef]
- Ochiai, I.; Ohba, H.; Hida, Y.; Nagumo, M. Effect of precipitation behavior of AlN on abnormal growth of ferrite grains in low-carbon steel wires. Tetsu-to-Hagane 1984, 70, 2001–2008. [Google Scholar] [CrossRef] [Green Version]
- Na, D.H.; Lee, Y. A study to predict the creation of surface defects on material and suppress them in caliber rolling process. Int. J. Precis. Eng. Manuf. 2013, 14, 1727–1734. [Google Scholar] [CrossRef]
- Nalawade, R.S.; Puranik, A.J.; Balachandran, G.; Mahadik, K.N.; Balasubramanian, V. Simulation of hot rolling deformation at intermediate passed and its industrial validity. Int. J. Mech. Sci. 2013, 77, 8–16. [Google Scholar] [CrossRef]
- Kim, S.Y.; Im, Y.T. Three-dimensional finite element analysis of non-isothermal shape rolling. J. Mater. Process. Technol. 2002, 127, 57–63. [Google Scholar] [CrossRef]
- Bagheripoor, M.; Bisadi, H. Effects of rolling parameters on temperature distribution in the hot rolling of alumimum strips. Appl. Therm. Eng. 2011, 31, 1556–1565. [Google Scholar] [CrossRef]
- Zhou, S.X. An integrated model for hot rolling of steel strips. J. Mater. Process. Technol. 2003, 134, 338–351. [Google Scholar] [CrossRef]
- Li, Y.H.; Sellars, C.M. Comparative investigations of interfacial heat transfer behaviour during hot forging and rolling of steel with oxide scale formation. J. Mater. Process. Technol. 1998, 80, 282–286. [Google Scholar] [CrossRef]
- Wu, J.; Liang, X.; Tang, A.; Pan, F. Interfacial heat transfer under mixed lubrication condition for metal rolling: A theoretical calculation study. Appl. Therm. Eng. 2016, 106, 1002–1009. [Google Scholar] [CrossRef]
- Malinowski, Z.; Lenard, J.G.; Davies, M.E. A study of the heat-transfer coefficient as a function of temperature and pressure. J. Mater. Process. Technol. 1994, 41, 125–142. [Google Scholar] [CrossRef]
- Curtze, S.; Kuokkala, V.T. Dependence of tensile deformation behavior of TWIP steels on stacking fault energy, temperature and strain rate. Acta Mater. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Ding, J.; Zhao, Z.; Jiao, Z.; Wang, J. Central infiltrated performance of deformation in ultra-heavy plate rolling with large deformation resistance gradient. Appl. Therm. Eng. 2016, 98, 29–38. [Google Scholar] [CrossRef]











| Parameters | Value | |
|---|---|---|
| Workpiece | Material | AISI 1020 |
| Initial temperature of workpiece | 1150 °C | |
| Rolling mill | Rolling speed | 10 RPM |
| Roll diameter | 400 mm | |
| Temperature of roll | 21 °C | |
| Process conditions | Reduction ratio of height of plate | 25.5% |
| RA per pass of rod | 20.2% | |
| Surrounding temperature | 21 °C |
| Contact Conduction (kWm−2K−1) | Convection (Wm−2K−1) | Ratio of Mechanical Work to Heat | Rolling Type | Reference |
|---|---|---|---|---|
| 5 | 10 | - | Shape rolling | [30] |
| 10 | 10 | - | Shape rolling | [31] |
| 24 | 2.33 | 0.9 | Round-oval | [2] |
| 72 | 2.33 | 0.9 | Square-diamond | [2] |
| 4.8 | 30 | - | Shape rolling | [32] |
| 40 | 10 | - | Flat rolling | [33] |
| 45–85 | - | 0.85–0.95 | Flat rolling | [10] |
| 54–71 | - | - | Flat rolling | [34] |
| 7.6–17.6 | - | - | Flat rolling | [35] |
| 20–45 | Flat rolling | [36] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, J.-K. Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling. Processes 2020, 8, 327. https://doi.org/10.3390/pr8030327
Hwang J-K. Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling. Processes. 2020; 8(3):327. https://doi.org/10.3390/pr8030327
Chicago/Turabian StyleHwang, Joong-Ki. 2020. "Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling" Processes 8, no. 3: 327. https://doi.org/10.3390/pr8030327
APA StyleHwang, J.-K. (2020). Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling. Processes, 8(3), 327. https://doi.org/10.3390/pr8030327





