Robust Mixed H₂/H_∞ State Feedback Controller Development for Uncertain Automobile Suspensions with Input Delay

Abstract

In order to achieve better dynamics performances of a class of automobile active suspensions with the model uncertainties and input delays, this paper proposes a generalized robust linear H₂/H_∞ state feedback control approach. First, the mathematical model of a half-automobile active suspension is established. In this model, the H_∞ norm of body acceleration is determined as the performance index of the designed controller, and the hard constraints of suspension dynamic deflection, tire dynamic load and actuator saturation are selected as the generalized H₂ performance output index of the designed controller to satisfy the suspension safety requirements. Second, a generalized H₂/H_∞ guaranteed cost state-feedback controller is developed in terms of Lyapunov stability theory. In addition, the Cone Complementarity Linearization (CCL) algorithm is employed to convert the generalized H₂/H_∞ output-feedback control problem into a finite convex optimization problem (COP) in a linear matrix inequality framework. Finally, a numerical simulation case of this half-automobile active suspension is presented to illustrate the effectiveness of the proposed controller in frequency-domain and time-domain.

1. Introduction

With the application and implement of automobile suspension design, it is necessary to attain a well balance between the handling stability and ride quality, which are usually contradictive with each other [1,2,3]. To mention that, how to cooperate with these two conflicting performance indicators has been a research hotspot currently [4,5,6]. Over the past decades, to address the issue of active suspension control, many researchers have proposed a lot of control methods such as linear optimal control [7], fuzzy neutral network control [8], adaptive robust control [9], robust control and nonlinear control [10], etc.

In a real engineering application, a class of active suspension system (ASS) should keep the desirable dynamics performance in case of sustaining the model uncertainty caused by the body mass, and the actuator input delay that is unavoidable in the control system, see [11] in detail. On one side, if the model parameter uncertainties are not taken into account in the process of controller design, then it will deteriorate suspension performances to some extent, which not only affects the ride comfort, but also endangers the driving safety. Therefore, it is very necessary to take the parametric uncertainties of the control plant into account, and then to develop a robust control method with higher accuracy. On the other side, as demonstrated in [12], for the controller design of a vehicle active suspension, there inevitably exists input delay that may generated from the controller calculations, the signal acquiring of sensor, along with the actuator operation. Once occurring the input delay in a closed-loop system, it means that the working stats of the control system at one time will not only be determined by the current system states, but also be affected by the system condition at the previous time. Although the input delay is very important in the control scheme design and development, it is usually ignored by a lot of researchers, like [7,8,9,10,11,12]. However, it is needed to know that even a small input delay may result in the decrease of control efficiency and the instability of control system [13,14].

In recent years, the robust H_∞ and H₂ control theory and technique have received extensive attentions. This is because the H_∞ control approach can easily handle the hard constraint problem of ASS in time domain, and the safety constraints condition can be restrained within a finite range, thus the vehicle body vibrations can be maximally inhibited in the presence of uneven road surface; moreover, H₂ control can effectively handle the convergence rate of the closed-loop control system. For instances, literature [15,16] designed a mixed H₂/H_∞ controller by using linear matrix inequality (LMI) method, and conducted a comparative study for the ASS with H_∞ controller by itself. Note that the effects of the parameter perturbations in vehicle active suspensions on the designed controller are not considered. Literature [17,18] also designed a class of mixed H₂/H_∞ controllers for ASS, but the model uncertainty issue is not considered. In literature [19], the authors have developed a full-state feedback controller with considering the input delay for a seat suspension system, and this controller achieved better control effects in a certain delay range. These studies inspired our study along this direction.

Synthesizing the above discussions, this paper presents a robust generalized H₂/H_∞ full state feedback controller for the ASS. Compared with the related studies in [12,13,14,15,16,17,18,19,20,21], the key contribution points lie in the two aspects:

(1) a comprehensive dynamics model of ASS is established with incorporating the input delay and parametric uncertainties, and the H_∞ norm of the body vertical acceleration is taken as the controller output performance index, meanwhile, the hard constraints of suspension dynamic deflections, tire dynamic loads and the actuator saturations are taken as the generalized H₂ performance index for the desirable controller.

(2) a generalized robust H₂/H_∞ state feedback control law is designed and this controller design issue is converted into a COP in the LMI framework, which simplifies the controller solution.

Finally, a numerical example of half-vehicle suspension is presented to validate the effectiveness of our proposed mixed H₂/H_∞ full state feedback controller.

We organize the rest of this work as follows. Section 2 gives the system model and problem formulation. The proposed controller is discussed in Section 3 in detail. Section 4 summarizes the simulation investigations to reveal the designed controller’s effectiveness. In Section 5, we will display the conclusions.

2. System Model and Problem Formulation

2.1. Automobile Active Suspension with Input Time Delay

Figure 1 shows a half-automobile dynamics model that is extensively employed in literatures such as [14,20]. According to the second law of Newton, the dynamics equations can be constructed as

$${\mathit{M}}_s\ddot{\mathit{q}}\left(t\right)=\mathit{G}{\mathit{K}}_s\left(z_u\left(t\right)-z_s\left(t\right)\right)+\mathit{G}{\mathit{C}}_s\left({\dot{z}}_u\left(t\right)-{\dot{z}}_s\left(t\right)\right)+\mathit{G}\mathit{u}\left(t-\tau \right)$$

(1)

$${\mathit{M}}_u{\ddot{z}}_u\left(t\right)={\mathit{K}}_s\left(z_s\left(t\right)-z_u\left(t\right)\right)-\mathit{u}\left(t-\tau \right)+{\mathit{C}}_s\left({\dot{z}}_s\left(t\right)-{\dot{z}}_u\left(t\right)\right)+K_u\left(z_r\left(t\right)-z_u\left(t\right)\right)$$

(2)

where $\mathit{q}(t)={[z_c(t),\varphi (t)]}^{\mathrm{T}}$, $z_s(t)={[z_{sf}(t),z_{sr}(t)]}^{\mathrm{T}}$ and $z_u(t)={[z_{uf}(t),z_{ur}(t)]}^{\mathrm{T}}$; $z_r(t)={[z_{rf}(t),z_{rr}(t)]}^{\mathrm{T}}$ is the input vector of road surface, $\mathit{u}={[u_f(t-\tau ),u_r(t-\tau )]}^{\mathrm{T}}$ is the input vector of actuator control force for this ASS. In Equations (1) and (2), the coefficient matrices of ${\mathit{M}}_s$, ${\mathit{M}}_u$, ${\mathit{C}}_s$, ${\mathit{K}}_s$, ${\mathit{K}}_u$ and $\mathit{G}$ are respectively given as

$${\mathit{M}}_s=\left[\begin{array}{cc}{m}_s& 0\\ 0& I_y\end{array}\right],{\mathit{M}}_u=\left[\begin{array}{cc}{m}_{uf}& 0\\ 0& m_{ur}\end{array}\right],{\mathit{C}}_s=\left[\begin{array}{cc}{c}_f& 0\\ 0& c_r\end{array}\right],{\mathit{K}}_s=\left[\begin{array}{cc}{k}_f& 0\\ 0& k_r\end{array}\right],{\mathit{K}}_u=\left[\begin{array}{cc}{k}_{tf}& 0\\ 0& k_{tr}\end{array}\right],\mathit{G}=\left[\begin{array}{cc}1& 1\\ -a& b\end{array}\right].$$

To ensure that ASS has a better dynamics characteristic and meets this automobile suspension safety performance’s requirements, the control objectives can be summarized as [22]:

(1) Ride comfort

To obtain better the performances of vehicle dynamics, the designed controller should guarantee the minimization of ${\ddot{z}}_c$ and $\ddot{\varphi }$.

(2) Running safety

① The dynamic displacements should be less than its allowable maximum value of $z_{\max }$, which are expressed by

$$\Delta {\mathbf{y}}_i=\left|z_{si}\left(t\right)-z_{ui}\left(t\right)\right|\le \Delta {\mathbf{y}}_i{}_{\max },i=f,r$$

(3)

② The tire’s dynamic load must be restrained within the corresponding static load, i.e., $F_{\mathrm{radio}}^i=k_{ti}\left(z_{ui}-z_{ri}\right)/F_{ti}<1$, wherein $k_{ti}(z_{ui}-z_{ri})$ is the dynamic loads at the front and rear tire, $F_{ti}$ is expressed by

$$\{\begin{array}{c}{F}_{tf}=\left(b{m}_{s}g+\left(a+b\right)m_{uf}g\right){\left(a+b\right)}^{-1}\\ F_{tr}=\left(a{m}_{s}g+\left(a+b\right)m_{ur}g\right){\left(a+b\right)}^{-1}\end{array}$$

(4)

③ The control forces should not exceed its maximum value of $u_{\max }$, which is given by

$$\left|u_i\right|\le u_{\max },i=f,r$$

(5)

To achieve the above control goals, define $z_1$ as the dynamics output vector, and $z_2$ as the normalized constraint output vector, for this automobile ASS, which are expressed by

$$z_1\left(t\right)=\left[\begin{array}{c}{\ddot{z}}_c\left(t\right)\\ \ddot{\varphi }\left(t\right)\end{array}\right],z_2=\left[\begin{array}{c}{z}_s-z_u\\ {\mathit{F}}_k\left(z_u-z_r\right)\\ \mathit{u}\end{array}\right]\in R^6$$

where ${\mathit{F}}_k=\mathrm{diag}\left(\frac{k_{tf}}{F_{tf}},\frac{k_{tr}}{F_{tr}}\right)$.

Considering input time delay τ, the system can be obtained.

$$\begin{array}{l}\dot{\mathit{x}}(t)=\mathit{A}\mathit{x}(t)+{\mathit{B}}_1\mathit{w}(t)+{\mathit{B}}_2\mathit{u}(t-\tau )\hfill \\ z_1(t)={\mathit{C}}_1\mathit{x}(t)+{\mathit{D}}_1\mathit{u}(t-\tau )\hfill \\ z_2(t)={\mathit{C}}_2\mathit{x}(t)+{\mathit{D}}_2\mathit{u}(t-\tau )\hfill \\ \mathit{x}\left(t\right)=\phi \left(t\right),\forall t\in \left[-\tau ,0\right]\hfill \end{array}\}$$

(6)

where $\mathit{x}\left(t\right)={\left[\begin{array}{cccc}{\left(z_s\left(t\right)-z_u\left(t\right)\right)}^{\mathrm{T}}& {\dot{z}}_s^{\mathrm{T}}\left(t\right)& {\left(z_u\left(t\right)-z_r\left(t\right)\right)}^{\mathrm{T}}& {\dot{z}}_u^{\mathrm{T}}\left(t\right)\end{array}\right]}^{\mathrm{T}}$ is the state vector, $\mathit{u}\left(t\right)={\left[\begin{array}{cc}{u}_f\left(t\right)& u_r\left(t\right)\end{array}\right]}^{\mathrm{T}}$ is the control force vector, $\mathit{w}(t)={[{\dot{z}}_{rf}(t),{\dot{z}}_{rr}(t)]}^{\mathrm{T}}$ is the input disturbance vector, $\phi \left(t\right)$ is the continuous differentiable initial condition function. $\mathit{A}$, ${\mathit{B}}_1$, ${\mathit{B}}_2$, ${\mathit{C}}_1$, ${\mathit{D}}_1$, ${\mathit{C}}_2$ and ${\mathit{D}}_2$ are the corresponding coefficient matrices with appropriate dimension, which are given as follows:

$$\mathit{A}=\left[\begin{array}{cc}{\mathit{A}}_1& {\mathit{A}}_2\end{array}\right],{\mathit{A}}_2=\left[\begin{array}{ll}{\mathbf{0}}_2\hfill & -{\mathit{I}}_2\hfill \\ {\mathbf{0}}_2\hfill & {\mathit{G}}^{\mathrm{T}}{\mathit{M}}_s^{-1}\mathit{G}{\mathit{C}}_s\hfill \\ {\mathbf{0}}_2\hfill & {\mathit{I}}_2\hfill \\ -{\mathit{M}}_u^{-1}{\mathit{K}}_u\hfill & -{\mathit{M}}_u^{-1}{\mathit{C}}_s\hfill \end{array}\right],{\mathit{A}}_1=\left[\begin{array}{ll}{\mathbf{0}}_2\hfill & {\mathit{I}}_2\hfill \\ -{\mathit{G}}^{\mathrm{T}}{\mathit{M}}_s^{-1}\mathit{G}{\mathit{K}}_s\hfill & -{\mathit{G}}^{\mathrm{T}}{\mathit{M}}_s^{-1}\mathit{G}{\mathit{C}}_s\hfill \\ {\mathbf{0}}_2\hfill & {\mathbf{0}}_2\hfill \\ {\mathit{M}}_u^{-1}{\mathit{K}}_s\hfill & {\mathit{M}}_u^{-1}{\mathit{C}}_s\hfill \end{array}\right],{\mathit{B}}_1=\left[\begin{array}{c}{\mathbf{0}}_2\\ {\mathbf{0}}_2\\ -{\mathit{I}}_2\\ {\mathbf{0}}_2\end{array}\right]$$

$${\mathit{B}}_2=\left[\begin{array}{c}{\mathbf{0}}_2\\ {\mathit{G}}^{\mathrm{T}}{\mathit{M}}_s^{-1}\mathit{G}\\ {\mathbf{0}}_2\\ {\mathit{M}}_u^{-1}\end{array}\right],{\mathit{C}}_1=\left[\begin{array}{c}-{\mathit{M}}_s^{-1}\mathit{G}{\mathit{K}}_s\\ -{\mathit{M}}_s^{-1}\mathit{G}{\mathit{C}}_s\\ 0\\ {\mathit{M}}_s^{-1}\mathit{G}{\mathit{C}}_s\end{array}\right],{\mathit{C}}_2=\left[\begin{array}{cccc}{\mathit{I}}_2& {\mathbf{0}}_2& {\mathbf{0}}_2& {\mathbf{0}}_2\\ {\mathbf{0}}_2& {\mathbf{0}}_2& {\mathit{F}}_k& {\mathbf{0}}_2\\ {\mathbf{0}}_2& {\mathbf{0}}_2& {\mathbf{0}}_2& {\mathbf{0}}_2\end{array}\right],{\mathit{D}}_1=\left[{\mathit{M}}_s^{-1}\right],{\mathit{D}}_2=\left[\begin{array}{c}{\mathbf{0}}_2\\ {\mathbf{0}}_2\\ {\mathit{I}}_2\end{array}\right].$$

where in A, B₁, B₂, C, D and E are the coefficient matrices with appropriate dimension, respectively, and they are dependent with the model parametric uncertainties, which will be illustrated in the subsequent section, and all the detailed matrices are given in Appendix A.

2.2. Active Suspension Model with Time Delay and Parameter Uncertainties

Based on Equation (6), the following closed-loop systems against parameter uncertainties and time delay can be obtained as

$$\begin{array}{l}\dot{\mathit{x}}(t)=\left(\mathit{A}+\Delta \mathit{A}\right)\mathit{x}(t)+{\mathit{B}}_1\mathit{w}(t)+\left({\mathit{B}}_2+\Delta {\mathit{B}}_2\right)\mathit{u}(t-\tau )\hfill \\ z_1(t)={\mathit{C}}_1\mathit{x}(t)+{\mathit{D}}_1\mathit{u}(t-\tau )\hfill \\ z_2(t)={\mathit{C}}_2\mathit{x}(t)+{\mathit{D}}_2\mathit{u}(t-\tau )\hfill \\ \mathit{x}\left(t\right)=\phi \left(t\right),\forall t\in \left[-\tau ,0\right]\hfill \end{array}\}$$

(7)

where $\Delta \mathit{A}$, $\Delta {\mathit{B}}_2$ represent the quantized uncertainty of m_s, and it can be expressed in a norm-bounded form as

$$\left[\begin{array}{cc}\Delta \mathit{A}& \Delta {\mathit{B}}_2\end{array}\right]=\mathit{H}\mathit{F}\left(t\right)\left[\begin{array}{cc}{\mathit{E}}_1& {\mathit{E}}_2\end{array}\right]$$

(8)

where in $\mathit{H}$, ${\mathit{E}}_1$ and ${\mathit{E}}_2$ are the corresponding coefficient matrices with appropriate dimension, and $\mathit{F}\left(t\right)$ is the unknown time-varying matrix function, which are mathematically constrained by

$${\mathit{F}}^{\mathrm{T}}\left(t\right)\mathit{F}\left(t\right)\le \mathit{I},t\ge 0$$

(9)

According to the performance requirements of ASS, the designed state-feedback control law is designed as

$$\mathit{u}(t)=\mathit{K}\mathit{x}(t)$$

(10)

where $\mathit{K}\in {\mathit{R}}^2$ is the determined controller gain matrix.

Substituting Equation (10) into Equation (7) yields

$$\begin{array}{l}\dot{\mathit{x}}(t)=\left(\mathit{A}+\Delta \mathit{A}\right)\mathit{x}(t)+{\mathit{B}}_1\mathit{w}(t)+\left({\mathit{B}}_2+\Delta {\mathit{B}}_2\right)\mathit{K}\mathit{x}(t-\tau )\hfill \\ z_1(t)={\mathit{C}}_1\mathit{x}(t)+{\mathit{D}}_1\mathit{K}\mathit{x}(t-\tau )\hfill \\ z_2(t)={\mathit{C}}_2\mathit{x}(t)+{\mathit{D}}_2\mathit{K}\mathit{x}(t-\tau )\hfill \\ \mathit{x}\left(t\right)=\phi \left(t\right),\forall t\in \left[-\tau ,0\right]\hfill \end{array}\}$$

(11)

Herein, by referring to [4,5,6], we summarize the robust state feedback controller (RSFC) design in Equation (11) as follows:

(a)

The system in Equation (11) is asymptotically stable.

(b)

Given $\forall w(t)\in L_2\left[0,+\infty \right)$, the H_∞ norm of the transfer function $T_{z_{1}w}$ from $w(t)$ to $z_1(t)$ should be satisfied with Equation (12) under the zero initial conditions.

$${\Vert T_{z_{1}w}\Vert }_{\infty }=\underset{w\in L^2}{\sup }\frac{{\Vert z_1(t)\Vert }_2}{{\Vert w(t)\Vert }_2}<{\gamma }_{\infty }$$

(12)

where ${\gamma }_{\infty }$ is a minimized positive value and ${\Vert z_1(t)\Vert }_2=\sqrt{{\displaystyle {\int }_0^{\infty }{z}_1^T(t)z_1(t)dt}}$.

(c)

Given $\forall w(t)\in L_2\left[0,+\infty \right)$ and the positive constant ${\gamma }_2$, under zero initial conditions, the generalized H₂ norm of the transfer function $T_{z_{2}w}$ from $w(t)$ to $z_2(t)$ should be satisfied as follows:

$${\Vert T_{z_{2}w}\Vert }_{{\mathrm{GH}}_2}=\underset{w\in L^2}{\sup }\frac{{\Vert z_2(t)\Vert }_{\infty }}{{\Vert w(t)\Vert }_2}<{\gamma }_2$$

(13)

where ${\Vert w(t)\Vert }_2=\sqrt{{\displaystyle {\int }_0^{\infty }{w}^2(t)dt}}$, ${\Vert z_2(t)\Vert }_{\infty }=\underset{1\le j\le 6}{\max }\left|z_{2_j}(t)\right|$, $z_{2_j}(t)$ indicates the deterministic constraint index in the vector $z_2(t)$.

3. Robust Controller Design with Input Delay and Parameter Uncertainties

Lemma 1.

[23]: Assume that $\mathit{a}(·)\in {\mathit{R}}^{{\mathit{n}}_{\mathit{a}}}$, $\mathit{b}(·)\in {\mathit{R}}^{{\mathit{n}}_{\mathit{b}}}$ and $\mathit{N}\in {\mathit{R}}^{{\mathit{n}}_{\mathit{a}}\times {\mathit{n}}_{\mathit{b}}}$ are defined on the interval $\mathsf{\Omega }$, then there exists an arbitrary matrix $\mathit{X}\in {\mathit{R}}^{{\mathit{n}}_{\mathit{a}}\times {\mathit{n}}_{\mathit{b}}}$, $\mathit{Y}\in {\mathit{R}}^{{\mathit{n}}_{\mathit{a}}\times {\mathit{n}}_{\mathit{b}}}$ and $\mathit{Z}\in {\mathit{R}}^{{\mathit{n}}_{\mathit{a}}\times {\mathit{n}}_{\mathit{b}}}$ satisfying

$$-2{\displaystyle \underset{\mathsf{\Omega }}{\int }{\mathit{a}}^{\mathrm{T}}\left(\alpha \right)}\mathit{N}\mathit{b}\left(\alpha \right)\mathit{d}\alpha \le {{\displaystyle \underset{\mathsf{\Omega }}{\int }\left[\begin{array}{c}\mathit{a}\left(\alpha \right)\\ \mathit{b}\left(\alpha \right)\end{array}\right]}}^{\mathrm{T}}\left[\begin{array}{cc}\mathit{X}& \mathit{Y}-\mathit{N}\\ {\mathit{Y}}^{\mathit{T}}-{\mathit{N}}^{\mathit{T}}& \mathit{Z}\end{array}\right]\left[\begin{array}{c}\mathit{a}\left(\alpha \right)\\ \mathit{b}\left(\alpha \right)\end{array}\right]\mathit{d}\alpha$$

(14)

where

$$\left[\begin{array}{cc}\mathit{X}& \mathit{Y}\\ {\mathit{Y}}^{\mathrm{T}}& \mathit{Z}\end{array}\right]>0$$

Lemma 2.

[22]: Given matrices $\mathit{Y}$, $\mathit{C}$, $\mathit{D}$ satisfies $\mathit{Y}+\mathit{C}\mathit{F}\left(t\right)\mathit{D}+{\mathit{D}}^{\mathrm{T}}{\mathit{F}}^{\mathrm{T}}\left(t\right){\mathit{C}}^{\mathrm{T}}<0$ for all $\mathit{F}\left(t\right)$ satisfying ${\mathit{F}}^{\mathrm{T}}\left(t\right)\mathit{F}\left(t\right)\le I$, if and only if there exists some $\epsilon >0$ such that

$$\mathit{Y}+\epsilon \mathit{C}{\mathit{C}}^{\mathrm{T}}+{\epsilon }^{-1}{\mathit{D}}^{\mathrm{T}}\mathit{D}<0$$

(15)

Theorem 1.

The system in Equation (11) for the automobile active suspension model has the asymptotical stability property satisfying Equations (12) and (13) for all non-zero $\forall w(t)\in L_2[0,+\infty )$, ${\gamma }_{\infty }>0$, ${\gamma }_2>0$, and $0\le \tau \le \overline{\tau }$. If and only if there exists positive definite matrices $\mathit{L}>0$, $\mathit{R}>0$, $\mathit{W}>0$, $\epsilon >0$, $\mathit{M}$, $\mathit{V}$ and $\mathit{N}$ such that the inequalities are satisfied

$$\left[\begin{array}{ccc}\mathbf{\Gamma }& {\mathbf{\Theta }}_2^{\mathrm{T}}& \epsilon {\mathbf{\Theta }}_1\\ \ast & -\epsilon \mathit{I}& 0\\ \ast & \ast & -\epsilon \mathit{I}\end{array}\right]<0$$

(16)

$$\left[\begin{array}{cc}\mathit{M}& \mathit{N}\\ \ast & \mathit{L}{\mathit{R}}^{-1}\mathit{L}\end{array}\right]>0$$

(17)

$$\left[\begin{array}{cc}\mathit{L}& \mathit{L}{\mathit{C}}_2^T\\ \ast & {\gamma }_2^2/{\gamma }_{\infty }^2\end{array}\right]>0$$

(18)

where $\mathbf{\Gamma }$, ${\mathbf{\Theta }}_1$, ${\mathbf{\Theta }}_2$ is expressed as

$$\mathbf{\Gamma }=\left[\begin{array}{ccccc}{\mathsf{\Psi }}_6& {\mathit{B}}_2\mathit{V}-\mathit{N}& {\mathit{B}}_1& \overline{\tau }\mathit{L}{\mathit{A}}^{\mathrm{T}}& \mathit{L}{\mathit{C}}_1^{\mathrm{T}}\\ \ast & -\mathit{W}& 0& \overline{\tau }{\mathit{V}}^{\mathrm{T}}{B}_2^{\mathrm{T}}& {\mathit{V}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}& \overline{\tau }{\mathit{B}}_1^{\mathrm{T}}& 0\\ \ast & \ast & \ast & -\overline{\tau }\mathit{R}& 0\\ \ast & \ast & \ast & \ast & -\mathit{I}\end{array}\right],$$

$${\mathbf{\Theta }}_1={\left[\begin{array}{ccccc}{\mathit{H}}^{\mathrm{T}}& 0& 0& \overline{\tau }{\mathit{H}}^{\mathrm{T}}& 0\end{array}\right]}^{\mathrm{T}},$$

$${\mathbf{\Theta }}_2=\left[\begin{array}{ccccc}{\mathit{E}}_1\mathit{L}& {\mathit{E}}_2\mathit{V}& 0& 0& 0\end{array}\right].$$

where

$${\mathsf{\Psi }}_6=\mathrm{sym}\left(\mathit{A}\mathit{L}+\mathit{N}\right)+\overline{\tau }\mathit{M}+\mathit{W}$$

Proof. 

For the closed-loop system in Equation (11), one can design the Lyapunov-Krasovskii as

$$V\left(t\right)=V_1+V_2+V_3$$

(19)

where $V_1={\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}\mathit{x}\left(t\right)$, $V_2={\displaystyle {\int }_{-\tau }^0{\displaystyle {\int }_{t+\beta }^t{\dot{\mathit{x}}}^{\mathrm{T}}\left(t\right)}}\mathit{Z}\mathit{x}\left(t\right)d\alpha d\beta$, $V_3={\displaystyle {\int }_{t-\tau }^0{\displaystyle {\int }_{t+\beta }^t{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{Q}}}\mathit{x}\left(t\right)d\alpha d\beta$. It is noted that $\mathit{P}>0$, $\mathit{Z}>0$ and $\mathit{Q}>0$ are the undetermined matrices.

In order to acquire the designed controller, two steps are provided to prove Theorem 1.

Step 1. Validate the asymptotical stability of the closed-loop system in Equation (11) with guaranteeing the H_∞ performance index of system in Equation (11) and satisfying $\Vert T_{Z1W}\Vert \le {\gamma }_{\infty }$.

The time derivative of V₁ in Equation (19) is

$${\dot{V}}_1={\dot{\mathit{x}}}^{\mathrm{T}}\left(t\right)\mathit{P}\mathit{x}\left(t\right)+{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}\dot{\mathit{x}}\left(t\right)$$

(20)

According to Leibniz–Newton formula, we have

$$\mathit{x}\left(t-\tau \right)=\mathit{x}\left(t\right)-{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\theta \right)}d\theta .$$

(21)

Substituting Equation (20) into Equation (11) of parameter certainties leads to

$$\dot{\mathit{x}}(t)=\left(\mathit{A}+{\mathit{B}}_2\mathit{K}\right)\mathit{x}\left(t\right)-{\mathit{B}}_2\mathit{K}{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\theta \right)}d\theta +{\mathit{B}}_{1}w\left(t\right).$$

(22)

Substituting Equation (22) to Equation (20), we have

$$\begin{array}{l}{\dot{\mathit{V}}}_1={\dot{\mathit{x}}}^{\mathrm{T}}\left(t\right)\mathit{P}\mathit{x}\left(t\right)+{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}\dot{\mathit{x}}\left(t\right)\\ ={\mathit{x}}^{\mathrm{T}}\left(t\right)\left[\mathrm{sym}\left(\mathit{P}\mathit{A}+\mathit{P}{\mathit{B}}_2\mathit{K}\right)\right]\mathit{x}\left(t\right)-2{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{B}}_2\mathit{K}\\ {\displaystyle {\int }_{t-\tau }^t\dot{x}\left(\theta \right)}d\theta +{\mathit{w}}^{\mathrm{T}}\left(t\right){\mathit{B}}_1^{\mathrm{T}}\mathit{P}x\left(t\right)+{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{B}}_1\mathit{w}\left(t\right).\end{array}$$

(23)

Define $\mathit{a}(·)=\mathit{x}\left(t\right)$, $\mathit{b}(·)=\dot{\mathit{x}}\left(\theta \right)$, $\mathit{N}=\mathit{P}{\mathit{B}}_2\mathit{K}$, according to Lemma 1, we have

$$\begin{array}{l}-2{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{N}{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\alpha \right)}d\alpha \le {{\displaystyle {\int }_{t-\tau }^t\left[\begin{array}{c}\mathit{x}\left(t\right)\\ \dot{\mathit{x}}\left(\alpha \right)\end{array}\right]}}^{\mathrm{T}}\left[\begin{array}{cc}\mathit{X}& \mathit{Y}-\mathit{N}\\ \ast & \mathit{Z}\end{array}\right]\left[\begin{array}{c}\mathit{x}\left(t\right)\\ \dot{\mathit{x}}\left(\alpha \right)\end{array}\right]d\alpha \\ ={\dot{\mathit{x}}}^{\mathrm{T}}\left(\alpha \right)\mathit{Z}\mathit{x}\left(\alpha \right)]d\alpha +{\displaystyle {\int }_{t-\tau }^t\left[{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{X}\mathit{x}\left(t\right)+2{\mathit{x}}^{\mathrm{T}}\left(t\right)\left(\mathit{Y}-\mathit{N}\right)\right]\dot{\mathit{x}}\left(\alpha \right)}\\ =\tau {\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{X}\mathit{x}\left(t\right)+2{\mathit{x}}^{\mathrm{T}}\left(t\right)\left(\mathit{Y}-\mathit{N}\right){\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\alpha \right)d}\alpha \\ +{\displaystyle {\int }_{t-\tau }^t{\dot{\mathit{x}}}^{\mathrm{T}}\left(\alpha \right)}\mathit{Z}\mathit{x}\left(\alpha \right)d\alpha \le \overline{\tau }{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{X}\mathit{x}\left(t\right)+2{\mathit{x}}^{\mathrm{T}}\left(t\right)\left(\mathit{Y}-\mathit{P}{\mathit{B}}_2\mathit{K}\right)\\ \left[\mathit{x}\left(t\right)-\mathit{x}\left(t-\tau \right)\right]+{\displaystyle {\int }_{t-\tau }^t{\dot{\mathit{x}}}^{\mathrm{T}}\left(\alpha \right)}\mathit{Z}\mathit{x}\left(\alpha \right)d\alpha \end{array}$$

(24)

where

$$\left[\begin{array}{cc}\mathit{X}& \mathit{Y}\\ {\mathit{Y}}^{\mathrm{T}}& \mathit{Z}\end{array}\right]>0$$

(25)

Substituting Equation (24) to Equation (23), we have

$$\begin{array}{c}{\dot{V}}_1\le {\mathit{x}}^{\mathrm{T}}\left(t\right)\left[\mathrm{sym}\left(\mathit{P}\mathit{A}+\mathit{Y}\right)+\overline{\tau }\mathit{X}\right]\mathit{x}\left(t\right)+2{\mathit{x}}^{\mathrm{T}}\left(t\right)\left(\mathit{P}{\mathit{B}}_2\mathit{K}-\mathit{Y}\right)\mathit{x}\left(t-\tau \right)\\ +{\mathit{w}}^{\mathrm{T}}{\mathit{B}}_1^{\mathrm{T}}\mathit{P}\mathit{x}\left(t\right)+{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{B}}_1\mathit{w}\left(t\right)+{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\alpha \right)}\mathit{Z}\dot{\mathit{x}}\left(\alpha \right)d\alpha \end{array}$$

(26)

The derivative of V₂ is

$$\begin{array}{l}{\dot{V}}_2=\tau {\dot{\mathit{x}}}^{\mathrm{T}}\left(t\right)\mathit{Z}\mathit{x}\left(t\right)-{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}}\left(\alpha \right)\mathit{Z}\mathit{x}\left(\alpha \right)d\alpha \le \overline{\tau }{\left[\mathit{A}\mathit{x}\left(t\right)+{\mathit{B}}_1\mathit{w}\left(t\right)+{\mathit{B}}_2\mathit{K}\mathit{x}\left(t-\tau \right)\right]}^{\mathrm{T}}\\ \mathit{Z}\left[\mathit{A}\mathit{x}\left(t\right)+{\mathit{B}}_1\mathit{w}\left(t\right)+{\mathit{B}}_2\mathit{K}\mathit{x}\left(t-\tau \right)\right]-{\displaystyle {\int }_{t-\tau }^t\dot{\mathit{x}}\left(\alpha \right)\mathit{Z}}\dot{\mathit{x}}\left(\alpha \right)d\alpha \end{array}$$

(27)

The derivative of V₃ is

$${\dot{V}}_3={\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{Q}\mathit{x}\left(t\right)-{\mathit{x}}^{\mathrm{T}}\left(t-\tau \right)\mathit{Q}\mathit{x}\left(t-\tau \right)$$

(28)

Substituting Equations (26), (27) and (28) into Equation (19), we obtain

$$\begin{array}{l}\dot{V}={\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3\le {\mathit{x}}^{\mathrm{T}}\left(t\right)\left[\mathrm{sym}\left(\mathit{P}\mathit{A}+\mathit{Y}\right)+\overline{\tau }\mathit{X}\right]{\mathit{x}}^{\mathrm{T}}\left(t\right)+2{\mathit{x}}^{\mathrm{T}}\left(t\right)\left(\mathit{P}{\mathit{B}}_2\mathit{K}-\mathit{Y}\right)\mathit{x}\left(t-\tau \right)\\ +\overline{\tau }{\left[\mathit{A}\mathit{x}\left(t\right)+{\mathit{B}}_1\mathit{w}\left(t\right)+{\mathit{B}}_2\mathit{K}\mathit{x}\left(t-\tau \right)\right]}^{\mathrm{T}}\mathit{Z}\left[\mathit{A}\mathit{x}\left(t\right)+{\mathit{B}}_1\mathit{w}\left(t\right)+{\mathit{B}}_2\mathit{K}\mathit{x}\left(t-\tau \right)\right]\\ +{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{Q}\mathit{x}\left(t\right)-{\mathit{x}}^{\mathrm{T}}\left(t-\tau \right)\mathit{Q}\mathit{x}\left(t-\tau \right)+{\mathit{w}}^{\mathrm{T}}\left(t\right){\mathit{B}}_1^{\mathrm{T}}\mathit{P}\mathit{x}\left(t\right)+{\mathit{x}}^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{B}}_1\mathit{w}\left(t\right).\end{array}$$

(29)

Assume $\phi \left(t\right)=0$, $\forall t\in \left[\begin{array}{cc}-\tau ,& 0\end{array}\right]$, then $V(t)|{}_{t=0}=0$. Consider the following index

$$J_{z_{1}w}={\displaystyle {\int }_0^{\infty }\left[z^{\mathrm{T}}\left(t\right)z\left(t\right)-{\gamma }_{\infty }^2{\mathit{w}}^{\mathrm{T}}\left(t\right)\mathit{w}\left(t\right)\right]}dt$$

(30)

Then, for non-zero $\forall w(t)\in L_2\left[0,+\infty \right)$, we have

$$\begin{array}{l}{J}_{z_{1}w}\le {\displaystyle {\int }_0^{\infty }\left[z^{\mathrm{T}}\left(t\right)z\left(t\right)-{\gamma }_{\infty }^2{\mathit{w}}^{\mathrm{T}}\left(t\right)\mathit{w}\left(t\right)\right]}dt+{V\left(t\right)|}_{t=\infty }-{V\left(t\right)|}_{t=0}\\ ={\displaystyle {\int }_0^{\infty }\left[z^{\mathrm{T}}\left(t\right)z\left(t\right)-{\gamma }_{\infty }^2{\mathit{w}}^{\mathrm{T}}\left(t\right)\mathit{w}\left(t\right)+\dot{V}\left(t\right)\right]}dt\\ ={\displaystyle {\int }_0^{\infty }{\eta }^{\mathrm{T}}}\left(t\right)\mathbf{\Pi }\eta \left(t\right)dt,\end{array}$$

(31)

where

$$\eta \left(t\right)={\left[\begin{array}{ccc}\mathit{x}\left(t\right)& \mathit{x}\left(t-\tau \right)& \mathit{w}\left(t\right)\end{array}\right]}^{\mathrm{T}},$$

$$\mathbf{\Pi }=\left[\begin{array}{ccc}\mathsf{\Phi }& {\mathsf{\Psi }}_1& \overline{\tau }{\mathit{A}}^{\mathrm{T}}\mathit{Z}{\mathit{B}}_1+\mathit{P}{\mathit{B}}_1\\ \ast & {\mathsf{\Psi }}_2& \overline{\tau }{\mathit{K}}^{\mathrm{T}}{\mathit{B}}_2^{\mathrm{T}}\mathit{Z}{\mathit{B}}_1\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}+\overline{\tau }{\mathit{B}}_1^{\mathrm{T}}\mathit{Z}{\mathit{B}}_1\end{array}\right],$$

$${\mathsf{\Psi }}_1=\mathit{P}{\mathit{B}}_2\mathit{K}-\mathit{Y}+\overline{\tau }{\mathit{A}}^{\mathrm{T}}\mathit{Z}{\mathit{B}}_2\mathit{K}+{\mathit{C}}_1^{\mathrm{T}}{\mathit{D}}_{12}\mathit{K},$$

$${\mathsf{\Psi }}_2=-\mathit{Q}+\overline{\tau }{\mathit{K}}^{\mathrm{T}}{\mathit{B}}_2^{\mathrm{T}}\mathit{Z}{\mathit{B}}_2\mathit{K}+{\mathit{K}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}{\mathit{D}}_{12}\mathit{K},$$

$$\mathsf{\Phi }=\mathrm{sym}\left(\mathit{P}\mathit{A}+\mathit{Y}\right)+\overline{\tau }\mathit{X}+\mathit{Q}+\overline{\tau }{\mathit{A}}^{\mathrm{T}}\mathit{Z}\mathit{A}+{\mathit{C}}_1^{\mathrm{T}}{\mathit{C}}_1.$$

when assuming $w(t)=0$, if $\mathbf{\Pi }<0$, then $\dot{V}\left(t\right)<0$ and (11) is asymptotically stable. Moreover, for w(t) $\in L_2\left[0,\infty \right)$, $\mathbf{\Pi }<0$ we can get $J_{z_{1}w}<0$ and ${\Vert z_1\left(t\right)\Vert }_2^2<{\gamma }_{\infty }^2{\Vert w\left(t\right)\Vert }_2^2$, in zero initial conditions, it can guarantees that the system in Equation (11) has a given attenuation level ${\gamma }_{\infty }$.

By using Schur complement, the inequality $\mathbf{\Pi }<0$ is transformed into

$$\left[\begin{array}{ccccc}{\mathsf{\Psi }}_3& \mathit{P}{\mathit{B}}_2\mathit{K}-\mathit{Y}& \mathit{P}{\mathit{B}}_1& \overline{\tau }{\mathit{A}}^{\mathrm{T}}\mathit{Z}& {\mathit{C}}_1^{\mathrm{T}}\\ \ast & -\mathit{Q}& 0& \overline{\tau }\mathit{K}{\mathit{B}}_2^{\mathrm{T}}\mathit{Z}& {\mathit{K}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}& \overline{\tau }{\mathit{B}}_1^{\mathrm{T}}\mathit{Z}& 0\\ \ast & \ast & \ast & -\overline{\tau }\mathit{Z}& 0\\ \ast & \ast & \ast & \ast & -\mathit{I}\end{array}\right]<0$$

(32)

where ${\mathsf{\Psi }}_3=\mathrm{sym}\left(\mathit{P}\mathit{A}+\mathit{Y}\right)+\overline{\tau }\mathit{X}+\mathit{Q}$.

Define $\mathit{L}={\mathit{P}}^{-1},$ pre-and post-multiplying Equation (32) by $\mathrm{diag}{\left(\begin{array}{ccccc}\mathit{L}& \mathit{L}& \mathit{I}& {\mathit{Z}}^{-1}& \mathit{I}\end{array}\right)}^{\mathrm{T}}$ and its transpose, we obtain

$$\left[\begin{array}{ccccc}{\mathsf{\Psi }}_4& {\mathit{B}}_2\mathit{K}\mathit{L}-\mathit{L}\mathit{Y}\mathit{L}& {\mathit{B}}_1& \overline{\tau }\mathit{L}{\mathit{A}}^{\mathrm{T}}& \mathit{L}{\mathit{C}}_1^{\mathrm{T}}\\ \ast & -\mathit{L}\mathit{Q}\mathit{L}& 0& \overline{\tau }\mathit{L}{\mathit{K}}^{\mathrm{T}}{\mathit{B}}_2^{\mathrm{T}}& \mathit{L}{\mathit{K}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}& \overline{\tau }{\mathit{B}}_1^{\mathrm{T}}& 0\\ \ast & \ast & \ast & -\overline{\tau }{\mathit{Z}}^{-1}& 0\\ \ast & \ast & \ast & \ast & -\mathit{I}\end{array}\right]<0$$

(33)

where ${\mathsf{\Psi }}_4=\mathrm{sym}\left(\mathit{A}\mathit{L}+\mathit{L}\mathit{Y}\mathit{L}\right)+\overline{\tau }\mathit{L}\mathit{X}\mathit{L}+\mathit{L}\mathit{Q}\mathit{L}$.

After substituting $\mathit{V}=\mathit{K}\mathit{L},$ $\mathit{M}=\mathit{L}\mathit{X}\mathit{L},$ $\mathit{N}=\mathit{L}\mathit{Y}\mathit{L},$ $\mathit{W}=\mathit{L}\mathit{Q}\mathit{L},$ $\mathit{R}={\mathit{Z}}^{-1}$, we further obtain

$$\left[\begin{array}{ccccc}{\mathsf{\Psi }}_5& {\mathit{B}}_2\mathit{V}-\mathit{N}& {\mathit{B}}_1& \overline{\tau }\mathit{L}{\mathit{A}}^{\mathrm{T}}& \mathit{L}{\mathit{C}}_1^{\mathrm{T}}\\ \ast & -\mathit{W}& 0& \overline{\tau }{\mathit{V}}^{\mathrm{T}}{\mathit{B}}_2^{\mathrm{T}}& {\mathit{V}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}& \overline{\tau }{\mathit{B}}_1^{\mathrm{T}}& 0\\ \ast & \ast & \ast & -\overline{\tau }\mathit{R}& 0\\ \ast & \ast & \ast & \ast & -\mathit{I}\end{array}\right]<0$$

(34)

$${\mathsf{\Psi }}_5=\mathrm{sym}\left(\mathit{A}\mathit{L}+\mathit{N}\right)+\overline{\tau }\mathit{M}+\mathit{W}$$

Considering the parameter uncertainties, replacing A by $\mathit{A}+\Delta \mathit{A}$ and B by ${\mathit{B}}_2+\Delta {\mathit{B}}_2$ in Equation (34), we can get

$$\mathbf{\Gamma }+\mathrm{sym}\left[{\mathbf{\Theta }}_{1}F\left(t\right){\mathbf{\Theta }}_2\right]<0$$

where

$$\mathbf{\Gamma }=\left[\begin{array}{ccccc}{\mathsf{\Psi }}_6& {\mathit{B}}_2\mathit{V}-\mathit{N}& {\mathit{B}}_1& \overline{\tau }\mathit{L}{\mathit{A}}^{\mathrm{T}}& \mathit{L}{\mathit{C}}_1^{\mathrm{T}}\\ \ast & -\mathit{W}& 0& \overline{\tau }{\mathit{V}}^{\mathrm{T}}{\mathit{B}}_2^{\mathrm{T}}& {\mathit{V}}^{\mathrm{T}}{\mathit{D}}_{12}^{\mathrm{T}}\\ \ast & \ast & -{\gamma }_{\infty }^2\mathit{I}& \overline{\tau }{\mathit{B}}_1^{\mathrm{T}}& 0\\ \ast & \ast & \ast & -\overline{\tau }\mathit{R}& 0\\ \ast & \ast & \ast & \ast & -\mathit{I}\end{array}\right],$$

(35)

$${\mathsf{\Psi }}_6=\mathrm{sym}\left(\mathit{A}\mathit{L}+\mathit{N}\right)+\overline{\tau }\mathit{M}+\mathit{W}$$

$${\mathbf{\Theta }}_1={\left[\begin{array}{ccccc}{\mathit{H}}^{\mathrm{T}}& 0& 0& \overline{\tau }{\mathit{H}}^{\mathrm{T}}& 0\end{array}\right]}^{\mathrm{T}},$$

$${\mathbf{\Theta }}_2=\left[\begin{array}{ccccc}{\mathit{E}}_1\mathit{L}& {\mathit{E}}_2\mathit{V}& 0& 0& 0\end{array}\right].$$

By using Lemma 2 in the above equation, there exist a scalar $\tilde{\epsilon }>0$ such that

$$\mathbf{\Gamma }+\tilde{\epsilon }{\mathbf{\Theta }}_1{\mathbf{\Theta }}_1^{\mathrm{T}}+{\tilde{\epsilon }}^{-1}{\mathbf{\Theta }}_2^{\mathrm{T}}{\mathbf{\Theta }}_2<0$$

(36)

By applying Schur complement, the inequalities of Equation (36) is equivalent to

$$\left[\begin{array}{ccc}\mathbf{\Gamma }& {\mathbf{\Theta }}_2^{\mathrm{T}}& {\tilde{\epsilon }}_1^{-1}{\mathbf{\Theta }}_1\\ \ast & -{\tilde{\epsilon }}^{-1}\mathit{I}& 0\\ \ast & \ast & -{\tilde{\epsilon }}_1^{-1}\mathit{I}\end{array}\right]<0$$

(37)

Substitute $\epsilon ={\tilde{\epsilon }}^{-1}$ into Equation (37), we obtain Equation (16).

Pre- and post-multiplying the inequality in Equation (25) by $\mathrm{diag}\left(\begin{array}{cc}\mathit{L}& {\mathit{L}}^{\mathrm{T}}\end{array}\right)$ and its transpose, we can obtain

$$\left[\begin{array}{cc}\mathit{L}\mathit{X}\mathit{L}& \mathit{L}\mathit{Y}\mathit{L}\\ \ast & \mathit{L}\mathit{Z}\mathit{L}\end{array}\right]\ge 0$$

(38)

Substitute $\mathit{M}=\mathit{L}\mathit{X}\mathit{L},$ $\mathit{N}=\mathit{L}\mathit{Y}\mathit{L}$ and $\mathit{R}={\mathit{Z}}^{-1}$ into the above equation, we obtain Equation (17).

Step 2. Guarantee that generalized H₂ performance index of Equation (11) satisfies with ${\Vert z_2(t)\Vert }_{\infty }<{\gamma }_2{\Vert w(t)\Vert }_2$.

According to Equation (30) and $\Pi <0$, we have

$$z_1^{\mathrm{T}}\left(t\right)z_1\left(t\right)-{\gamma }_{\infty }^2{\mathit{w}}^{\mathrm{T}}\left(t\right)\mathit{w}\left(t\right)+\dot{V}\left(t\right)<0$$

(39)

Due to $z_1^{\mathrm{T}}\left(t\right)z_1\left(t\right)\ge 0$, we have

$$\dot{V}\left(t\right)<{\gamma }_{\infty }^2{w}^{\mathrm{T}}\left(t\right)w\left(t\right)$$

(40)

Integrating Equation (40) gives

$$V\left(t\right)<{\gamma }_{\infty }^2{\displaystyle \int {}_0^t}{w}^{\mathrm{T}}\left(t\right)w\left(t\right)$$

(41)

Synthesizing the above discussions, we can derive that the last two terms of Equation (19) are positive definite, so we can further get

$${\mathit{x}}_g^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{x}}_g\left(t\right)<{\gamma }_{\infty }^2{\displaystyle {\int }_0^t{w}^{\mathrm{T}}\left(s\right)}w\left(s\right)ds$$

(42)

Multiplying the inequality in Equation (42) by $\frac{{\gamma }_2^2}{{\gamma }_{\infty }^2}$, we have

$$\frac{{\gamma }_2^2}{{\gamma }_{\infty }^2}{\mathit{x}}_g^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{x}}_g\left(t\right)<{\gamma }_2^2{\displaystyle {\int }_0^t{w}^{\mathrm{T}}\left(s\right)}w\left(s\right)ds$$

(43)

So that, only if the inequality holds with $t\in \left[0,\infty \right)$ and ${\Vert z_2\left(t\right)\Vert }_{\infty }^2\ge z_2^{\mathrm{T}}\left(\mathrm{t}\right)z_2\left(t\right)$

$${\Vert z_2\left(t\right)\Vert }_{\infty }^2<\frac{{\gamma }_2^2}{{\gamma }_{\infty }^2}{\mathit{x}}_g^{\mathrm{T}}\left(t\right)\mathit{P}{\mathit{x}}_g\left(t\right)$$

(44)

Consequently, we further get

$$z_2^{\mathrm{T}}\left(t\right)z_2\left(t\right)={\mathit{x}}^{\mathrm{T}}\left(t\right){\mathit{C}}_2^{\mathrm{T}}{\mathit{C}}_2\mathit{x}\left(t\right)<{\mathit{x}}^{\mathrm{T}}\left(t\right)\frac{{\gamma }_2^2}{{\gamma }_{\infty }^2}\mathit{P}\mathit{x}\left(t\right)<{\gamma }_2^2{\displaystyle {\int }_0^t{\mathit{w}}^{\mathrm{T}}\left(t\right)}\mathit{w}\left(t\right)$$

(45)

If Equation (45) holds, it is only needed to be ensured that Equation (46) comes into existence.

$${\mathit{C}}_2^{\mathrm{T}}{\mathit{C}}_2<\frac{{\gamma }_2^2}{{\gamma }_{\infty }^2}\mathit{P}$$

(46)

By Schur complement, we obtain

$$\left[\begin{array}{cc}\mathit{P}& {\mathit{C}}_2^{\mathrm{T}}\\ \ast & {\gamma }_2^2/{\gamma }_{\infty }^2\end{array}\right]>0$$

(47)

Multiplying the inequality in Equation (47) by $\mathrm{diag}\left\{{\mathit{P}}^{-1},{\mathit{I}}_2\right\}$ and then using the congruent transformation in matrix, we get (18). The proof is completed. □

The nonlinear term LR⁻¹L in Equation (17) lead to the inability to use the LMI algorithm to solve the controller gain K. We need to transform inequalities into cone complementary linearization iterative problem of LMI algorithm.

For the nonlinear term LR⁻¹L in Equation (17), there is a new variable S such that

$$\left[\begin{array}{cc}\mathit{M}& \mathit{N}\\ \ast & \mathit{S}\end{array}\right]>0$$

(48)

$$\mathit{L}{\mathit{R}}^{-1}\mathit{L}-\mathit{S}\ge 0$$

(49)

According to Equation (49), we have

$${\mathit{L}}^{-1}\mathit{R}{\mathit{L}}^{-1}-{\mathit{S}}^{-1}\le 0$$

(50)

By applying Schur complement, the condition of Equation (50) is equal to

$$\left[\begin{array}{cc}{\mathit{S}}^{-1}& {\mathit{L}}^{-1}\\ {\mathit{L}}^{-1}& {\mathit{R}}^{-1}\end{array}\right]>0$$

(51)

By introducing new variables $\mathit{T}={\mathit{S}}^{-1},$ $\mathit{J}={\mathit{L}}^{-1},$ $\mathit{G}={\mathit{R}}^{-1}$, we obtain

$$\left[\begin{array}{cc}\mathit{T}& \mathit{J}\\ \mathit{J}& \mathit{G}\end{array}\right]>0$$

(52)

Now, in terms of a CCL problem description, it is suggested that the orignal non-convex feasibility problem of Theorem 1 can be trasnformed into the following non-linear minimization problem with LMI conditions:

$$\begin{array}{c}\min \mathrm{tr}\left(\mathit{S}\mathit{T}+\mathit{L}\mathit{J}+\mathit{R}\mathit{G}\right)\\ \mathrm{subject}\mathrm{to}\left(10\right),\left(12\right)\end{array},$$

$$\{\begin{array}{l}\left[\begin{array}{cc}\mathit{M}& \mathit{N}\\ \ast & \mathit{S}\end{array}\right]>0,\left[\begin{array}{cc}\mathit{T}& \mathit{J}\\ \mathit{J}& \mathit{G}\end{array}\right]>0\hfill \\ \left[\begin{array}{cc}\mathit{S}& \mathit{I}\\ \mathit{I}& \mathit{T}\end{array}\right]>0,\left[\begin{array}{cc}\mathit{L}& \mathit{I}\\ \mathit{I}& \mathit{J}\end{array}\right]>0,\left[\begin{array}{cc}\mathit{R}& \mathit{I}\\ \mathit{I}& \mathit{G}\end{array}\right]>0.\hfill \end{array}$$

(53)

The specific steps for solving the above problem in Equation (53) are described as follows:

Step-1, Given initial value $\overline{\tau },$${\gamma }_2$ and ${\gamma }_{\infty }$.

Step-2, Find out a feasible set (${\mathit{S}}_0,$${\mathit{T}}_0,$${\mathit{J}}_0,$${\mathit{G}}_0,$${\mathit{L}}_0,$${\mathit{R}}_0,$${\mathit{W}}_0,$${\mathit{N}}_0,$${\mathit{M}}_0,$${\mathit{V}}_0$) with satisfying Equations (16), (18) and (53). If there is no solution, then exit. If there exist solutions, verify whether the condition in Equation (17) holds. Find the feasible set that meets the above requirements, if condition (17) is established, the iteration is completed. If it is not established, it enters Step-3 and sets k = 1.

Step-3, Solve the following LMI problem for the variables ($\mathit{S},$$\mathit{T},$$\mathit{J},$$\mathit{G},$$\mathit{L},$$\mathit{R},$$\mathit{W},$$\mathit{N},$$\mathit{M},$$\mathit{V}$)

$$\min \mathrm{tr}\left({\mathit{S}}_k\mathit{T}+{\mathit{T}}_k\mathit{S}+{\mathit{L}}_k\mathit{J}+{\mathit{J}}_k\mathit{L}+{\mathit{R}}_k\mathit{G}+{\mathit{G}}_k\mathit{R}\right)$$

Subject to Equations (16), (18) and (53). Set ${\mathit{J}}_{k+1}=\mathit{J},$ ${\mathit{G}}_{k+1}=\mathit{G},$ ${\mathit{L}}_{k+1}=\mathit{L},$ ${\mathit{R}}_{k+1}=\mathit{R},$ ${\mathit{S}}_{k+1}=\mathit{S}$ and ${\mathit{T}}_{k+1}=\mathit{T}$.

Step-4, Substitute the result obtained in Step-3 into Equation (17), we need to verify whether the inequality holds. If it is true, the iteration ends. If it is not true, and the number of iterations is within 100 times, perform Step-3 again and continue the iteration.

Step-5, Repeat Step-2~Step-4 by decreasing ${\gamma }_{\infty }$ appropriately and iterate again.

4. Simulation Investigation and Discussion

In this section, a numerical example is uesd to verify the proposed robust controller’s effectiveness under bump and random road disturbances, respectively.

Table 1. The parameters of half-vehicle ASS.

ms	Iy	muf	mur
500 kg	1222 kg·m2	36 kg	36 kg
a	b	kr	kf
1.5 m	2.5 m	26,000 N−1	16,000 N·m−1
ktr	ktf	cf	cr
16,000 N·m−1	160,000 N·m−1	980N·s·m−1	980 N·s·m−1

give the used parameters of the simulation.

It is assumed that z_fmax = z_rmax = 0.1 m, F_max = 1500 N, m_s has a perturbation of ± 10% and the matrix H, E₁, E₂ for the uncertain in Equation (4).

$$\mathit{H}={\left[00\frac{1}{10m_s}\frac{1}{10m_s}0000\right]}^{\mathrm{T}}{\mathit{E}}_2=\left[\begin{array}{cc}1& 1\end{array}\right],{\mathit{E}}_1=\left[\begin{array}{llllllll}-k_f\hfill & -k_r\hfill & -c_f\hfill & -c_r\hfill & 0\hfill & 0\hfill & c_f\hfill & c_r\hfill \end{array}\right].$$

In the condition of the given time delay τ(t) = 20ms and the generalized H₂ performance index of 26.4537, the H_∞ performance index is elected as 28.2843. Based on Theorem 1, the input delay of the proposed robust controller can be calculated by the cone complement linearization algorithm. The control gain matrix K is obtained as

$$\mathit{K}={10}^4\times [\begin{array}{llll}0.1385\hfill & 0.3031\hfill & -0.1015\hfill & 0.0146\hfill \\ 0.0363\hfill & -0.1378\hfill & 0.0039\hfill & -0.0684\hfill \end{array}\begin{array}{llll}-0.4037\hfill & 0.9008\hfill & -0.0782\hfill & 0.0240\hfill \\ 0.1712\hfill & -1.2296\hfill & -0.0093\hfill & -0.0907\hfill \end{array}]$$

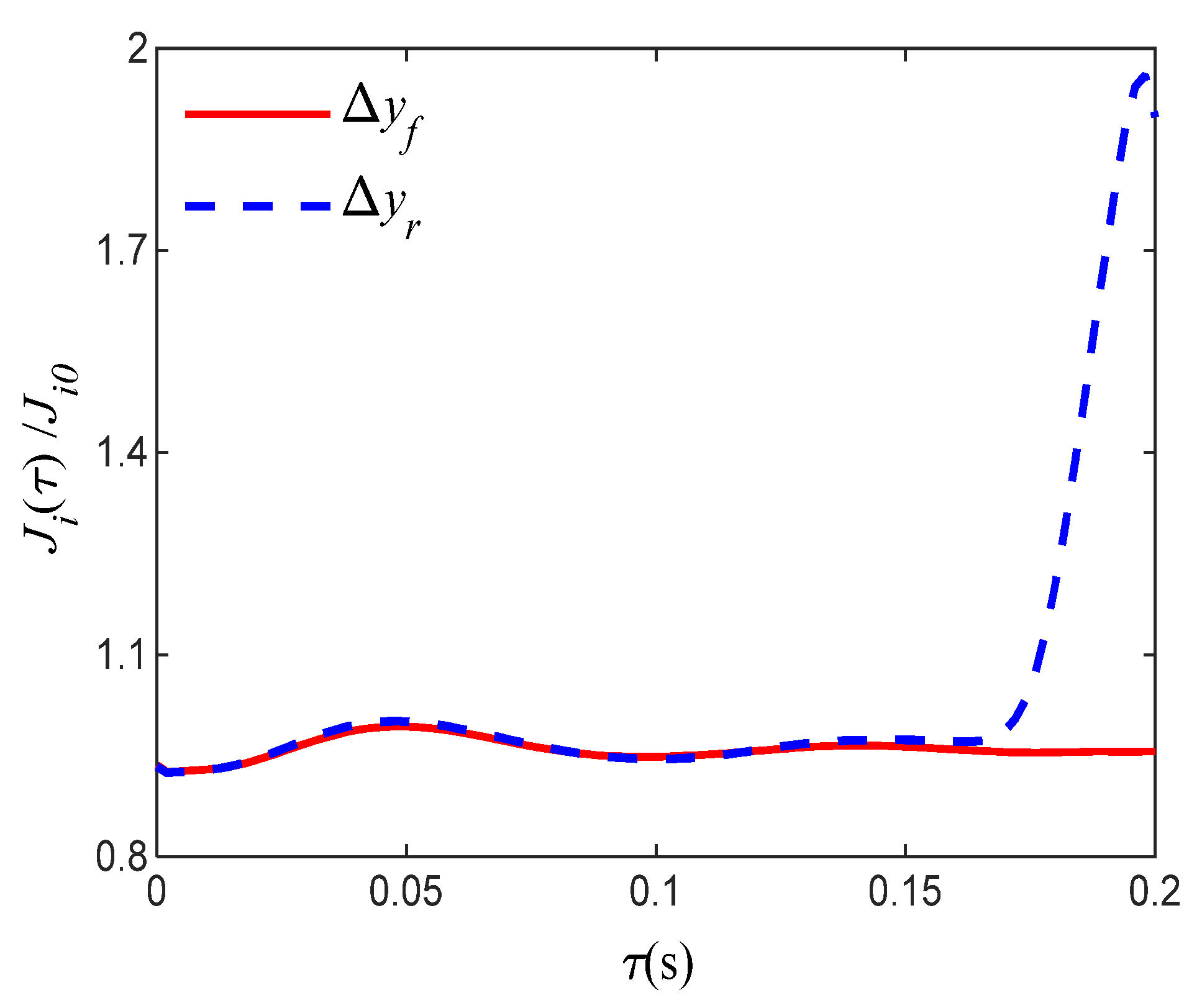
4.1. Simulation Results in Frequency Domain

Based on ISO 2361 criteria, in vertical vibration, the human bodies are sensitive to about 4–8 Hz, in pitch vibration directions, the human bodies are sensitive to about 1–2 Hz.

Figure 2 shows the response comparisons of ${\ddot{z}}_c$ and $\ddot{\phi }$ in the frequency domain in case of m_s = 454.5 kg, m_s = 500 kg and m_s = 555.5 kg, respectively. It is obvious that, compared to the passive control (PC), RSFC can attain a better control performance on the whole, especially in the frequency ranges of 4–8 Hz for the vertical direction, and 1–2 Hz for the pitch direction, respectively. In addition, even for the propsoed RSFC, we can see that the parameter uncertianty of body mass m_s hardly impose any effects on the output performances, which means the desinged RSFC can be tolerant with the variatons of body mass uncertainty.

4.2. Bump Road Response in Time Domain

The bump road is also utilized to conduct the simulations under bump road surface, which is described in literature [21] and is mathematically given by

$$z_{rf}=\{\begin{array}{cc}\frac{h_b}{2}(1-\cos (5\pi t)),& 1\le t\le 0.4\hfill \\ 0,& otherwise\hfill \end{array}$$

(54)

where h_b, and v represent the height of the bump, and the vehicle forward speed, respectively, and the time input delay is expressed by (a + b)/v, where their corresponding values is given as h_b = 0.1 m and v = 45 (km/h).

Figure 3 and Figure 4 show the bump responses results of ${\ddot{z}}_c$, $\ddot{\phi }$, $\Delta y_f$, $\Delta y_r$, $F_{\mathrm{radio}}^f$, $F_{\mathrm{radio}}^r$, $u_f$ and $u_r$ for the passsive controlled system (u(t) = 0) and ASS with the proposed RSFC when there exists time delay as $\tau =0\mathrm{s}$, $\tau =0.02\mathrm{s}$ and $\tau =0.12\mathrm{s}$, respectively. The simulation results from Figure 3a,b show that when the input delay $\tau$ are 0 and 0.02 s, compared with PC, ${\ddot{z}}_c$ and $\ddot{\phi }$ with RSFC can be remarkably reduced, and then reach into asymptotic stability within a shorter time. However, when the input delay $\tau$ is increased to 0.12 s, the amplitude of ${\ddot{z}}_c$ and $\ddot{\phi }$ is very high, and the dynamic stability cannot be achieved in the simulation time 3 s. The ASS’s index of $\Delta y_f$ and $\Delta y_r$ with RSFC have the smaller positive peaks, they are all less than the value of $\Delta y_f$ and $\Delta y_r$ in PC system; $F_{\mathrm{radio}}^f$ and $F_{\mathrm{radio}}^r$ are always less than 1, implying that the dynamic load is less than its static load and ensuring the firm uninterrupted contact from the wheels to the road. Additionally, it can be seen from Figure 4 that $u_f$ and $u_r$ are always less than u_max, satisfying the actuator input saturation requirement.

4.3. Random Road Response in Time Domain

In order to further verify the control effectiveness of the designed RSFC, a random road surface mimicked by the Gaussian white noise is used to conduct the simulation, which is expressed by [24]

$${\dot{z}}_r\left(t\right)-2\pi f_0{z}_r\left(t\right)+2\pi n_0\sqrt{G_{0}u}\omega (t)$$

(55)

wherein n₀ represent the reference spatial frequency, f₀ represent the lower cut-off frequency for different road profiles, ω(t) represent zero mean the white Gaussian noise signal, G_q(n₀) represent the road roughness coefficient. Herein, the parameter values of road surface are chosen as n₀ = 0.1 (1/m), G_q(n₀) = 64 × 10⁻⁶ (m³) and v = 45 (km/h), which corresponds to B-class road surface.

The root mean square (RMS) is employed to further analyze the robustness of the RSFC to different input delays and the influence of ASS’s control performance. The RMS expression of the variable x(t) is defined [23]:

$${\mathrm{RMS}}_x=\sqrt{(1/T){\displaystyle {\int }_0^{\mathrm{T}}{x}^{\mathrm{T}}(t)x(t)dt}}$$

(56)

For different input time delay in the closed-loop system, the controller’s effectiveness in dealing with the time delay problem is studied by calculating the following RMS ratios as

$$\frac{J_i\left(\tau \right)}{J_{io}}$$

(57)

Among Equation (57), $J_1$, $J_2$, $J_3$, $J_4$, $J_5$ and $J_6$ mean the RMS values of the proposed RSFC system, and $J_{io}$ means the RMS value of the PC system.

As shown in Figure 5, Figure 6 and Figure 7, the RMS ratios of ${\ddot{z}}_c$, $\ddot{\phi }$, $\Delta y_f$, $\Delta y_r$, $F_{\mathrm{radio}}^f$ and $F_{\mathrm{radio}}^r$ are all less than 1 when $\tau <0.12\mathrm{s}$, which denotes that the designed controller’s performance is much better than the passive suspension. With the increase of time delay, the RMS ratio, especially ${\ddot{z}}_c$, $\ddot{\phi }$, $\Delta y_f$ and $\Delta y_r$, increases dramatically, which reflects the sharp deterioration of ASS performance under the input time delay of about 0.12 s or more, and the controlled ASS tends to be unstable.

The results reveal that the proposed design method is conservative. Additionally, it can be seen from Figure 8 that $u_f$ and $u_r$ are always less than u_max with satisfying the actuator input saturation requirement.

5. Conclusions

(1)

A half-vehicle active suspension model considering the parameter uncertainties, input delay, as well as the external road surface disturbances is established. the H_∞ norm of vehicle body acceleration is selected as the performance index of the controller output. The hard constraints of suspension dynamic deflections, tire dynamic loads and actuator saturations are taken as the generalized H₂ performance output index of the designed controller. A robust controller based on cone complementary linearization algorithm is proposed.

(2)

The simulation experiments under different road excitations show that the generalized H₂/H_∞ controller in this paper can tolerate the performance loss and fluctuation caused by the parameters uncertainty and the control input delay. It can not only enhance the ride comfort of vehicles, but also meet the hard constraints of ASS in time domain and frequency domain, respectively.

(3)

In the next stage work, the author will consider the effects of time-varying input delay on the control stability and discuss how to design a stable and reliable active fault-tolerant controller when the actuators occur faults or failures.