Research on State Recognition and Failure Prediction of Axial Piston Pump Based on Performance Degradation Data
Abstract
:1. Introduction
2. Theoretical Background
2.1. Selection of Degenerative Characteristics of Piston Pump
- Establishment of variational problems.The analytical signals of each component function (t) are obtained by Hilbert transform and the corresponding unilateral spectrum is calculated:where, the meaning of * is convolution operation. By parsing the signals in each component, center frequencyis is mixed and estimated. Adjust the spectrum of each component to its respective baseband:Estimating the frequency range of each component signal, the variational problem when constrained is as follows:where, , .
- Analytical processing.Introducing the Lagrange multipliers (t) and the penalty factor to transform the constrained variational problem into an unconstrained variational problem. Where (t) can keep the constraints rigorous, can ensure the reconstruction accuracy of the signals when the signals contained Gaussian noise. The extended Lagrangian expression is as follows:Solving it by the alternating directions method of multipliers, alternately update , and to find the critical point in the extended Lagrangian expression that is neither a maximum nor a minimum. The task consists of the following steps:
- Initialize , and n = 1.
- Update , , according to Equations (5) and (6).
- Update , according to .
- Repeat steps b and c, for the given discrimination precision e > 0, If stop iteration and get IMFs.
2.2. Binary Gaussian Process Classification
2.3. Gaussian Process Regression
3. Performance Degradation Test of Axial Piston Pump
4. Test Data Processing Of Vibration Signals
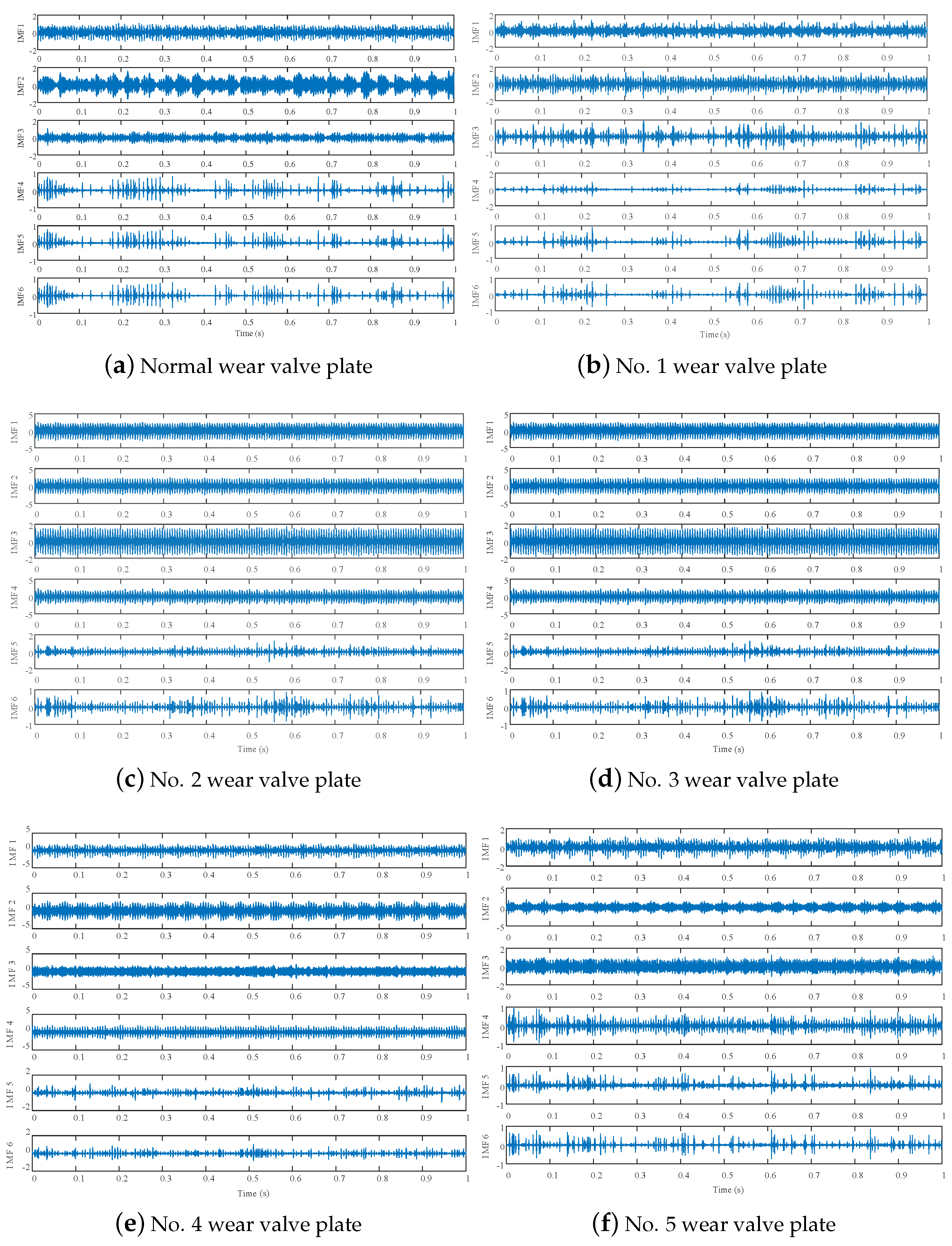
4.1. VMD-Based Test Data Processing
4.2. Feature Extraction Method Based on MPE
4.3. Axial Piston Pump State Identification Based on Multi-Class Gaussian Process Classification
- In the training phase of the binary Gaussian process classification, the eigenvector data of the normal valve plate is marked as , the others are marked as . The first two-class classifier can be obtained by the Gaussian processes for binary classification used in Section 2.2.
- The value of K is defined from 2 to 6 in turning. The training data of class K is indicated as and the other five training data are marked as K-class members of . Then, we get the training model of classifiers with different wear degrees, and finally six two-class classifiers are obtained.
- The probability of the test data belonging to the class K can be obtained by the above-mentioned six two-class classifiers respectively, and then a probability vector is obtained. Finally, can be classified as category (K) by maximum probability, which can be found from .
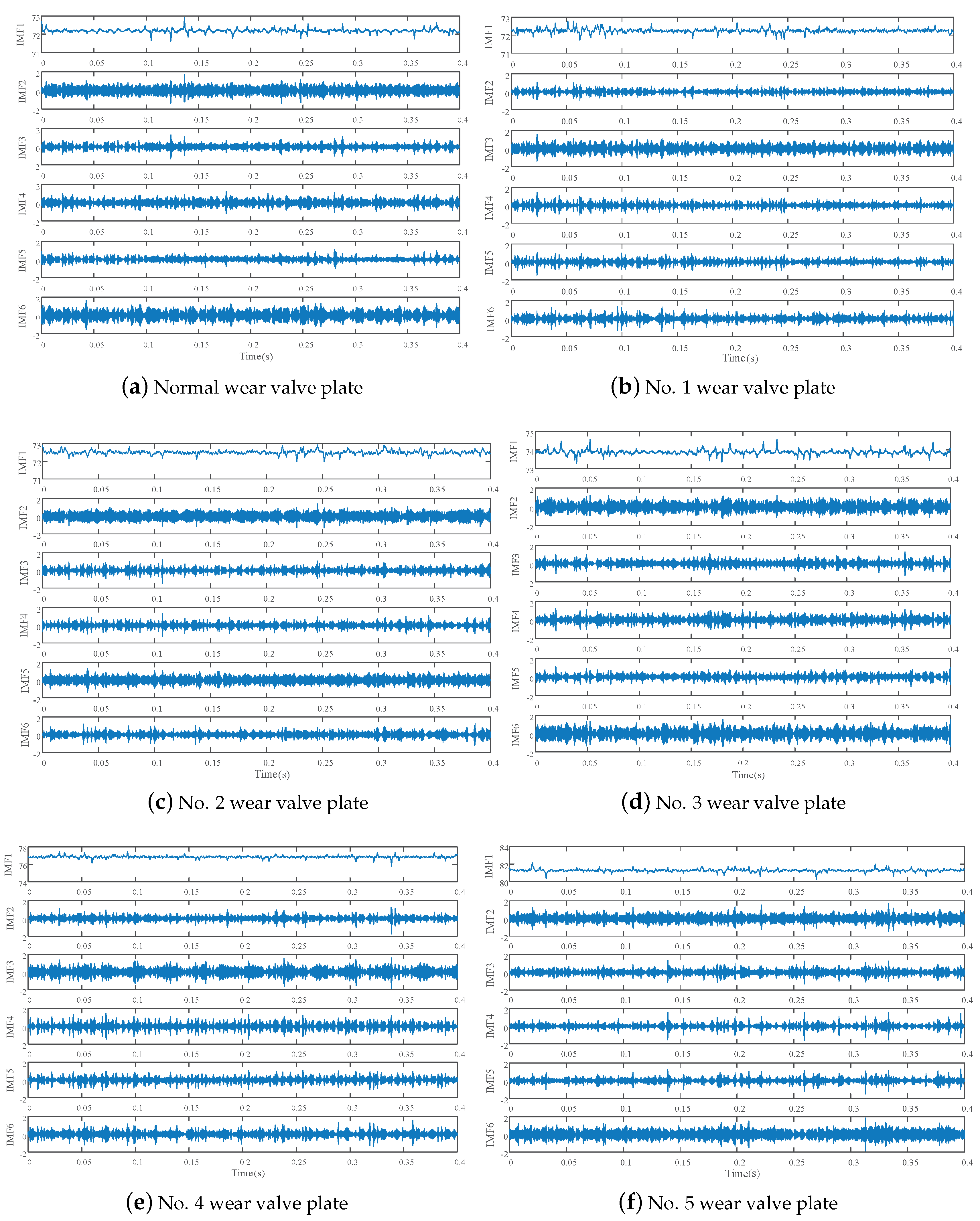
5. Test Data Processing of Flow Signals
Failure Prediction of Axial Piston Pump
6. Conclusions
- The combination of VMD, MPE, and ReliefF has obvious advantages in feature extraction. Moreover, the complexity and time of the operation are decreased by reducing the dimension of the feature. At the same time, the discrimination of the feature vectors in different degraded states is very high, and there is almost no overlap of data values.
- The multi-class Gaussian process classification model is used to realize the state recognition, which has high accuracy and enriches the research on the vibration signals processing and analysis of axial piston pump. In the same test conditions, compared with the BP neural network and the SVM method, the multi-class Gaussian process classification provides a better recognition effect and shorter decision time.
- The mathematical model of the relationship between the flow and the wear of the valve plate is established by using the GPR, and compared with the actual curve to determine its superiority. Therefore, the failure prediction by GPR provides a new idea for the research on the relationship between the wear and failure of axial piston pump.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stefan, G.; Hubertus, M. Simulation of the Lubricating Film between Contoured Piston and Cylinder. Int. J. Fluid Power 2010, 11, 15–24. [Google Scholar]
- Olems, L. Investigation of the Temperature Behavior of the Piston Cylinder Assembly in Axial Piston Pumps. Int. J. Fluid Power 2000, 1, 27–39. [Google Scholar] [CrossRef]
- Li, H.R.; Wang, Y.K.; Ma, J.Q.; Ye, P. Fault pattern recognition of hydraulic pumps based on MMSE and ABCSVM. J. Vib. Shock 2016, 35, 152–158. [Google Scholar]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Zamanian, A.H.; Ohadi, A. Gear fault diagnosis based on Gaussian correlation of vibrations signals and wavelet coefficients. Appl. Soft Comput. J. 2011, 11, 4807–4819. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.S.; Chen, Q. Fault diagnosis of rolling bearings based on multifractal detrended fluctuation analysis and Mahalanobis distance criterion. Mech. Syst. Signal Process. 2013, 38, 515–533. [Google Scholar] [CrossRef]
- Wang, Y.K.; Li, H.R.; Huang, Z.J. Transform Relative Spectrum Entropy and It Application in Degradation State Identification of Hydraulic Pump. Acta Armamentarii 2016, 37, 979–987. [Google Scholar]
- Li, N.; Zhou, R.; HU, Q.H.; Liu, X.H. Mechanical fault diagnosis based on redundant second generation wavelet packet transform, neighborhood rough set and support vector machine. Mech. Syst. Signal Process. 2012, 28, 608–621. [Google Scholar] [CrossRef]
- Zeng, Q.H.; Qiu, J.; Liu, G.J.; Tan, X.D. Research on equipment degradation state recognition and fault prognostics method based on KPCA-Hidden Semi-Markov Model. Chin. J. Sci. Instrum. 2009, 30, 1341–1346. [Google Scholar]
- Gao, Y.J.; Kong, X.D. Wavelet Packets Analysis Based Method for Hydraulic Pump Condition Monitoring. J. Mech. Eng. 2009, 45, 80–88. [Google Scholar] [CrossRef]
- Sun, J.; Li, H.R.; Tian, Z.K. A degradation feature extraction method for hydraulic pumps based on fusion of sensitive components. Chin. J. Sci. Instrum. 2016, 37, 1290–1298. [Google Scholar]
- Wang, S.P.; Wan, Z.K.; Yang, G.Q. Study on Fault Diagnosis of Data Fussion in Hydraulic Pump. China Mech. Eng. 2005, 5, 47–51. [Google Scholar]
- Wu, C.Q.; Jiang, W.L. Multi-source and multi-feature fused fault diagnosis on piston pumps based on evidence theory. Chin. J. Constr. Mach. 2011, 9, 98–102. [Google Scholar]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized svm. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Lu, C.; Wang, S.; Maids, V. Fault severity recognition of aviation piston pump based on feature extraction of eemd paving and optimized support vector regression model. Aerosp. Sci. Technol. 2017, 67, 105–117. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Bi, F.; Bi, X.; Shao, K. Fault diagnosis of diesel engine based on adaptive wavelet packets and eemd-fractal dimension. Mech. Syst. Signal Process. 2013, 41, 581–597. [Google Scholar] [CrossRef]
- Zhao, S.F.; Liang, L.; Xu, G.H.; Wang, J.; Zhang, W.M. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mech. Syst. Signal Process. 2013, 40, 154–177. [Google Scholar] [CrossRef]
- Ji, N.; Ma, L.; Dong, H.; Zhang, X. EEG Signals Feature Extraction Based on DWT and EMD Combined with Approximate Entropy. Brain Sci. 2019, 9, 201. [Google Scholar] [CrossRef] [Green Version]
- Widodo, A.; Shim, M.C.; Caesarendra, W.; Yang, B.S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Tan, J.; Fu, W.; Wang, K.; Xue, X.; Hu, W.; Shan, Y. Fault Diagnosis for Rolling Bearing Based on Semi-Supervised Clustering and Support Vector Data Description with Adaptive Parameter Optimization and Improved Decision Strategy. Appl. Sci. 2019, 9, 1676. [Google Scholar] [CrossRef] [Green Version]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Rolo, A. A method for the correlation dimension estimation for on-line condition monitoring of large rotating machinery. Mech. Syst. Signal Process. 2005, 19, 939–954. [Google Scholar] [CrossRef]
- Richman, J.S.; Randall, M.J. Physiological time-series analysis, using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Si, L.; Wang, Z.; Liu, X.; Tan, C. A sensing identification method for shearer cutting state based on modified multi-scale fuzzy entropy and support vector machine. Engineering Applications of Artificial Intelligence. Eng. Appl. Artif. Intell. 2019, 78, 86–101. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2019, 29, 474–484. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of eeg recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Bect, P.; Simeu-Abazi, Z.; Maisonneuve, P.L. Diagnostic and decision support systems by identification of abnormal events: Application to helicopters. Aerosp. Sci. Technol. 2015, 46, 339–350. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, W. An experimental comparison of gene selection by lasso and dantzig selector for cancer classification. Comput. Biol. Med. 2011, 41, 1033–1040. [Google Scholar] [CrossRef]
- Jaffel, I.; Taouali, O.; Harkat, M.F.; Messaoud, H. Kernel principal component analysis with reduced complexity for nonlinear dynamic process monitoring. Int. J. Adv. Manuf. Technol. 2016, 88, 9–12. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, M.; Zhao, S.; Hu, S.; Shi, Z.; Cao, Y. ReliefF-Based EEG Sensor Selection Methods for Emotion Recognition. Sensors 2016, 16, 1558. [Google Scholar] [CrossRef]
- Jiang, W.L.; Wang, Y.R.; Wang, Z.W.; Zhu, Y. Fault Feature Dimension Reduction Method Combined ReliefF Algorithm with Correlation Calculation and Its Application. Chin. Hydraul. Pneum. 2015, 12, 18–24. [Google Scholar]
- Bevilacqua, M.; Braglia, M.; Montanari, R. The classification and regression tree approach to pump failure rate analysis. Reliab. Eng. Syst. Saf. 2003, 79, 59–67. [Google Scholar] [CrossRef]
- Turksoy, K.; Roy, A.; Cinar, A. Real-time model-based fault detection of continuous glucose sensor measurements. IEEE Trans. Biomed. Eng. 2016, 64, 1437–1445. [Google Scholar] [CrossRef] [PubMed]
- Saravanan, N.; Ramachandran, K.I. Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN). Expert Syst. Appl. 2010, 37, 4168–4181. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y.; Tang, H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, S. Multitask multiclass support vector machines: Model and experiments. Pattern Recognit. 2013, 46, 914–924. [Google Scholar] [CrossRef]
- Riihimki, J.; Jylnki, P.; Vehtari, A. Nested expectation propagation for Gaussian process classification. J. Mach. Learn. Res. 2013, 14, 75–109. [Google Scholar]
- Wei, Z.; Wang, Y.; He, S.; Sao, J. A novel intelligent method for bearing fault diagnosis based on affinity propagation clustering and adaptive feature selection. Knowl. Based Syst. 2017, 116, 1–12. [Google Scholar] [CrossRef]
- Park, C.; Huang, J.Z.; Ding, Y. Domain decomposition approach for fast Gaussian process regression of large spatial data sets. J. Mach. Learn. Res. 2011, 12, 1697–1728. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.K.; Li, H.R.; Ye, P. Fault Identification of Hydraulic Pump Based on Multi-scale Permutation Entropy. China Mech. Eng. 2015, 26, 518–523. [Google Scholar]
- Kuss, M.; Rasmussen, C.E.; Herbrich, R. Assessing Approximate Inference for Binary Gaussian Process Classification. J. Mach. Learn. Res. 2005, 6, 1679–1704. [Google Scholar]
- Sun, B.; Yao, H.; Liu, T. Short-term wind speed forecasting based on Gaussian process regression model. Proc. Chin. Soc. Electr. Eng. 2012, 32, 104–109. [Google Scholar]
- He, Z.H.; Liu, G.B.; Zhao, X.J.; Wang, M.H. Overview of Gaussian process regression. Control Decis. 2013, 28, 1121–1129. [Google Scholar]
- Wu, M.; Feng, Z.; Huang, G.Y.; Mou, Z.Q. Early fault diagnosis of check valve based on variational mode decomposition and Wigner-Ville. China Meas. Test 2019, 45, 116–122. [Google Scholar]
- Decarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292–307. [Google Scholar] [CrossRef]
- Zheng, J.D.; Cheng, J.S.; Yang, Y. Multi-scale Permutation Entropy and Its Application to Rolling Bearings Fault Diagnosis. China Mech. Eng. 2013, 24, 2641–2646. [Google Scholar]
- Wei, S.X.; Sun, Z.H. A Multi-Classification Method Based on Gaussian Processes. Appl. Mech. Mater. 2012, 6, 1333–1337. [Google Scholar] [CrossRef]
- Wong, W.K.; Yuen, C.W.M.; Fan, D.D. Stitching defect detection and classification using wavelet transform and BP neural network. Expert Syst. Appl. 2009, 36, 3845–3856. [Google Scholar] [CrossRef]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Xie, J.H.; Liu, J.; Shang, J. Analysis and Calculation of Leakage of Swash-plate Axial Piston Pump. Fluid Mach. 2016, 44, 55–58+70. [Google Scholar]










| Wear Distribution Plate | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 |
|---|---|---|---|---|---|
| Maximum wear (m) | 2 | 7 | 12 | 18 | 22 |
| Average wear (m) | 0.67 | 2.33 | 4 | 6 | 7.3 |
| K | Center Frequency | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 289 | 1484 | – | – | – | – | – |
| 3 | 288 | 1061 | 2194 | – | – | – | – |
| 4 | 195 | 341 | 1451 | 2261 | – | – | – |
| 5 | 195 | 341 | 1068 | 1843 | 2608 | – | – |
| 6 | 195 | 341 | 1039 | 1573 | 2208 | 2880 | – |
| 7 | 184 | 339 | 858 | 1421 | 2177 | 2880 | 2883 |
| Status of Valve Plate | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
|---|---|---|---|---|---|---|
| Normal | 3.9203 | 3.8484 | 4.1237 | 3.9698 | 4.0062 | 4.0229 |
| No. 1 | 2.0680 | 2.1577 | 2.2345 | 2.1181 | 3.4882 | 3.5078 |
| No. 2 | 2.0651 | 3.1914 | 1.5823 | 2.9004 | 2.4964 | 2.3559 |
| No. 3 | 3.6037 | 1.6157 | 2.3695 | 2.6594 | 1.5350 | 1.5569 |
| No. 4 | 1.8410 | 2.7826 | 1.6882 | 1.9628 | 2.3981 | 2.5837 |
| No. 5 | 3.1968 | 3.0251 | 3.0395 | 3.6564 | 1.6581 | 3.1946 |
| Number of Samples | Number of Test Samples | Identify the Number | Recognition Accuracy | |
|---|---|---|---|---|
| Normal | 20 | 30 | 29 | 0.967 |
| No. 1 | 20 | 30 | 29 | 0.967 |
| No. 2 | 20 | 30 | 30 | 1 |
| No. 3 | 20 | 30 | 30 | 1 |
| No. 4 | 20 | 30 | 30 | 1 |
| No. 5 | 20 | 30 | 30 | 1 |
| Classification Method | Correct Identifications | Recognition Accuracy (%) | Decision Time (s) |
|---|---|---|---|
| back propagation (BP) neural network | 167 | 92.8 | 3.135 |
| support vector machine (SVM) | 171 | 95.0 | 1.903 |
| Multi-class Gaussian process classification | 178 | 98.9 | 1.257 |
| Reference | Feature Extraction Method | Feature Reduction Method | Classification Technique | Recognition Rate (%) |
|---|---|---|---|---|
| [6] | empirical mode decomposition (EMD), wavelet transform (WT), multifractal detrended fluctuation analysis (MF-DFA) | – | Mahalanobis distance criterion | 94.4–100 |
| [7] | Smooth Processing, Transform Relative Spectrum Entropy | – | weighted grey correlation | 88.8 |
| [8] | redundant second-generation wavelet packet transform (RSGWPT) | neighborhood rough set (NRS) | SVM | 93.9 |
| [9] | wavelet correlation feature scale entropy (WCFSE) | Kernel Principal component analysis (KPCA) | hidden Semi–Markov model(HSMM) | 90 |
| [12] | WT, time domain, frequency domain, time-frequency domain | principal component analysis (PCA) | BP neural network | 89.4–94.4 |
| [14] | ensemble empirical mode decomposition (EEMD), Permutation entropy | – | SVM | 93.4–98.3 |
| [15] | EEMD, correlation coefficient method, time domain, frequency domain, time-frequency domain | PCA | support vector regression (SVR) | 97.8–100 |
| Present work | VMD, Kurtosis and MPE | ReliefF | multi-class Gaussian process classification | 98.9 |
| Valve Plate | Normal | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 |
|---|---|---|---|---|---|---|
| Average flow (L/h) | 72.1869 | 72.2447 | 72.5100 | 73.8853 | 76.8569 | 81.2677 |
| Evaluation Index | SSE | RMSE | |
|---|---|---|---|
| Gaussian regression | 0.1114 | 0.1362 | 0.9991 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Zhao, Z.; Huo, S.; Jin, Z.; Zhao, J.; Gao, D. Research on State Recognition and Failure Prediction of Axial Piston Pump Based on Performance Degradation Data. Processes 2020, 8, 609. https://doi.org/10.3390/pr8050609
Guo R, Zhao Z, Huo S, Jin Z, Zhao J, Gao D. Research on State Recognition and Failure Prediction of Axial Piston Pump Based on Performance Degradation Data. Processes. 2020; 8(5):609. https://doi.org/10.3390/pr8050609
Chicago/Turabian StyleGuo, Rui, Zhiqian Zhao, Saiyu Huo, Zhijie Jin, Jingyi Zhao, and Dianrong Gao. 2020. "Research on State Recognition and Failure Prediction of Axial Piston Pump Based on Performance Degradation Data" Processes 8, no. 5: 609. https://doi.org/10.3390/pr8050609
APA StyleGuo, R., Zhao, Z., Huo, S., Jin, Z., Zhao, J., & Gao, D. (2020). Research on State Recognition and Failure Prediction of Axial Piston Pump Based on Performance Degradation Data. Processes, 8(5), 609. https://doi.org/10.3390/pr8050609






