Mechanism, Thermodynamics and Kinetics of Rutile Leaching Process by Sulfuric Acid Reactions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation Methods
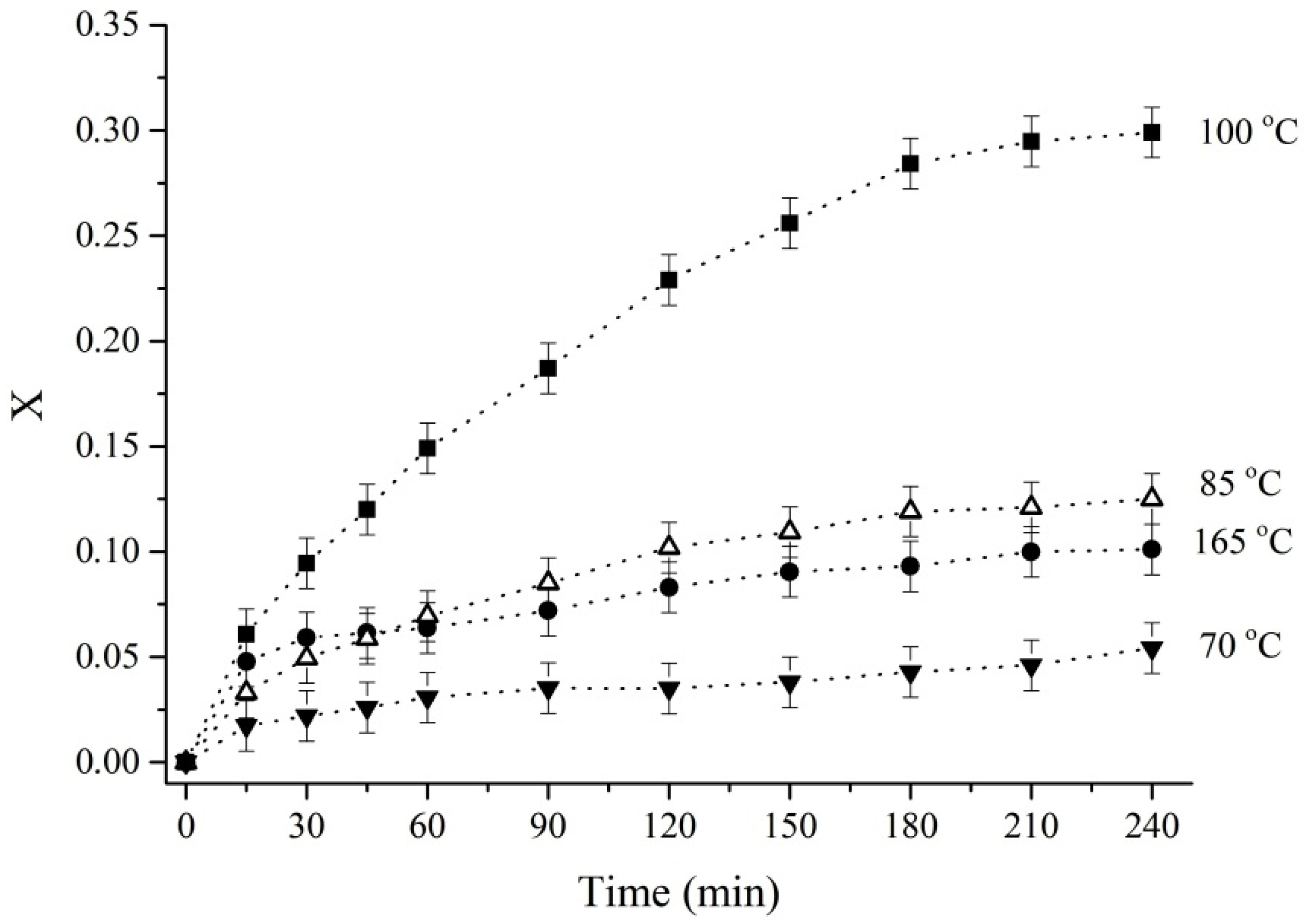
2.2. Experimental Methods and Procedures
3. Results and Discussion
3.1. Model Selection for Thermodynamic Modeling
3.2. Leaching of Titanium from Rutile with Sulfuric Acid
3.3. Sulfate-Fluoride Leaching of Titanium from Rutile
- (a)
- For 100% acid:TiO2 + 5H2SO4 + 2NaF = Ti(SO4)2 + Na2SO4 + 2(H2SO4·H2O) + 2HF↑TiO2 + 5H2SO4 + NaF = Ti(SO4)2 + NaHSO4 + 2(H2SO4·H2O) + HF↑TiO2 + 3H2SO4 + 2NaF = TiOSO4 + Na2SO4 + H2SO4·H2O + 2HF↑TiO2 + 3H2SO4 + NaF = TiOSO4 + NaHSO4 + H2SO4·H2O + HF↑
- (b)
- For 85% acid:TiO2 + 8(H2SO4·H2O) + 2NaF = Ti(SO4)2 + Na2SO4 + 5(H2SO4·2H2O) + 2HF↑TiO2 + 8(H2SO4·H2O) + NaF = Ti(SO4)2 + NaHSO4 + 5(H2SO4·2H2O) + HF↑TiO2 + 5(H2SO4·H2O) + 2NaF = TiOSO4 + Na2SO4 + 3(H2SO4·2H2O) + 2HF↑TiO2 + 5(H2SO4·H2O) + NaF = TiOSO4 + NaHSO4 + 3(H2SO4·2H2O) + HF↑
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Filimonov, A. Mirovoy rynok v tsifrakh [World market in numbers]. Chem. J. 2005, 10–11, 56. [Google Scholar]
- Haverkamp, R.G.; Kruger, D.; Rajashekar, R. The digestion of New Zealand ilmenite by hydrochloric acid. Hydrometallurgy 2016, 163, 198–203. [Google Scholar] [CrossRef]
- Hosseini, E.; Rashchi, F.; Ataie, A. Ti leaching from activated ilmenite–Fe mixture at different milling energy levels. Int. J. Miner. Metall. Mater. 2018, 25, 1263–1274. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, J.; Li, H. Influence of phase and microstructure on the rate of hydrochloric acid leaching in pretreated Panzhihua ilmenite. Particuology 2014, 14, 83–90. [Google Scholar] [CrossRef]
- Chen, Y.; Williams, J.S.; Campbell, S.J.; Wang, G.M. Increased dissolution of ilmenite induced by high-energy ball milling. Mater. Sci. Eng. A 1999, 271, 485–490. [Google Scholar] [CrossRef]
- Yarkadaş, G.; Toplan, H.; Yildiz, K. Effect of mechanical activation and iron powder addition on acidic leaching of effect of mechanical activation and iron powder addition on acidic leaching of pseudorutile. Saü. Fen Bilim. Derg. 2009, 13, 18–21. [Google Scholar]
- Amer, A.M. Alkaline pressure leaching of mechanically activated Rosetta ilmenite concentrate. Hydrometallurgy 2002, 67, 125–133. [Google Scholar] [CrossRef]
- Li, C.; Liang, B.; Guo, L.H.; Wu, Z.B. Effect of mechanical activation on the dissolution of Panzhihua ilmenite. Miner. Eng. 2006, 19, 1430–1438. [Google Scholar] [CrossRef]
- Sasikumar, C.; Rao, D.S.; Srikanth, S.; Mukhopadhyay, N.K.; Mehrotra, S.P. Dissolution studies of mechanically activated Manavalakurichi ilmenite with HCl and H2SO4. Hydrometallurgy 2007, 88, 154–169. [Google Scholar] [CrossRef]
- Sasikumar, C.; Rao, D.S.; Srikanth, S.; Ravikumar, B.; Mukhopadhyay, N.K.; Mehrotra, S.P. Effect of mechanical activation on the kinetics of sulfuric acid leaching of beach sand ilmenite from Orissa, India. Hydrometallurgy 2004, 75, 189–204. [Google Scholar] [CrossRef]
- Kalashnykov, Y.V.; Nikolenko, N.V.; Kachalova, A.S.; Dubenko, A.V.; Abramova, A.M. Effect of mechanical activation of malyshevsky ilmenite on its phase composition and leaching rate. Vopr. Khimii I Khimicheskoi Tekhnologii 2015, 5, 63–71. [Google Scholar]
- Urakaev, F.K. Influence of the conditions of mechanical activation of the mixture of ilmenite and carbon on the pigment preparation. Int. J. Miner. Process. 2011, 101, 37–41. [Google Scholar] [CrossRef]
- Li, C.; Liang, B.; Chen, S.P. Combined milling-dissolution of Panzhihua ilmenite in sulfuric acid. Hydrometallurgy 2006, 82, 93–99. [Google Scholar] [CrossRef]
- Hiraki, T.; Maruyama, Y.; Suzuki, Y.; Itoh, S.; Nagasaka, T. Up-grading of natural ilmenite ore by combining oxidation and acid leaching. Int. J. Miner. Metall. Mater. 2018, 25, 729–736. [Google Scholar] [CrossRef]
- Jabłoński, M.; Tylutka, S. The influence of initial concentration of sulfuric acid on the degree of leaching of the main elements of ilmenite raw materials. J. Anal. Calorim. 2016, 124, 355–361. [Google Scholar] [CrossRef]
- Goroschenko, Y.G.; Belyakova, E.P.; Kozachek, N.N.; Dvernyakova, A.A.; Lykov, E.P.; Parakhnevich, L.A.; Shirokova, G.A. Tehnicheskaya Dvuokis Titana i ee Poluchenie iz Izmenennogo Ilmenita Sernokislotnyim Metodom [Technical Titanium Dioxide and Its Preparation from Altered Ilmenite by the Sulfuric Acid Method]; Kyiv: Naukova Dumka, Ukraine, 1968. [Google Scholar]
- Liang, B.; Li, C.; Zhang, C.; Zhang, Y. Leaching kinetics of Panzhihua ilmenite in sulfuric acid. Hydrometallurgy 2005, 76, 173–179. [Google Scholar] [CrossRef]
- Han, K.N.; Rubcumintara, T.; Fuerstenau, M.C. Leaching behavior of ilmenite with sulfuric acid. Metall. Trans. B 1987, 18, 325–330. [Google Scholar] [CrossRef]
- Lasheen, T.A. Sulfate digestion process for high purity TiO2 from Titania slag. Front. Chem. Eng. China 2009, 3, 155–160. [Google Scholar] [CrossRef]
- Jia, L.; Liang, B.; Lü, L.; Yuan, S.; Zheng, L.; Wang, X.; Li, C. Beneficiation of titania by sulfuric acid pressure leaching of Panzhihua ilmenite. Hydrometallurgy 2014, 150, 92–98. [Google Scholar] [CrossRef]
- Rahman, T.P. Optimization H2SO4 concentration on the leaching process of extracting titanium from zircon. In Handbook on the Emerging Trends in Scientific Research; PAK Publishing Group: Kuala Lumpur, Malaysia, 2014; pp. 791–794. [Google Scholar]
- Razavi, R.; Hosseini, S.M.A.; Ranjbar, M. Production of nanosized synthetic rutile from ilmenite concentrate by sonochemical HCl and H2SO4 leaching. Iran. J. Chem. Chem. Eng. 2014, 33, 29–36. [Google Scholar]
- Xiong, X.; Wang, Z.; Wu, F.; Li, X.; Guo, H. Preparation of TiO2 from ilmenite using sulfuric acid decomposition of the titania residue combined with separation of Fe3+ with EDTA during hydrolysis. Adv. Powder Technol. 2013, 24, 60–67. [Google Scholar] [CrossRef]
- Baba, A.A.; Swaroopa, S.; Ghosh, M.K.; Adekola, F.A. Mineralogical characterization and leaching behavior of Nigerian ilmenite ore. Trans. Nonferrous Metals Soc. China 2013, 23, 2743–2750. [Google Scholar] [CrossRef]
- Young, T.F.; Blatz, L.A. The Variation of the properties of electrolytic solutions with degrees of dissociation. Chem. Rev. 1949, 44, 93–115. [Google Scholar] [CrossRef] [PubMed]
- Wahyuningsih, S.; Ramelan, A.H.; Munifa, R.M.I.; Saputri, L.N.M.Z.; Chasanah, U. Synthesis of TiO2 nanorods from titania and titanyl sulfate produced from ilmenite dissolution by hydrothermal method. J. Phys. Conf. Ser. 2016, 776, 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Yue, H.; Yuan, S.; Liu, C.; Tang, S.; Liang, B. Effects of mechanical activation on the digestion of ilmenite in dilute H2SO4. Chin. J. Chem. Eng. 2019, 27, 575–586. [Google Scholar] [CrossRef]
- Welham, N.J.; Llewellyn, D.J. Mechanical enhancement of the dissolution of ilmenite. Miner. Eng. 1998, 11, 827–841. [Google Scholar] [CrossRef]
- Nikolenko, N.V.; Dubenko, A.V.; Suschinskii, A.D.; Kalashnikov, Y.V. Decomposition of altered ilmenite by sulphuric acid. Vopr. Khimii I Khimicheskoi Tekhnologii 2016, 2, 55–62. [Google Scholar]
- Karelin, V.A.; Kameneva, O.V. Ftoridnyj metod pererabotki rutilovogo koncentrata [Fluoride method for processing rutile concentrate]. Bull. Tomsk Polytech. Univ. 2006, 309, 94–99. [Google Scholar]
- Karelin, V.A.; Karelin, A.I. Ftoridnaya Tehnologiya Pererabotki Kontsentratov Redkih Metallov [Fluoride Technology of the Processing Rare Metal Concentrates]; NTL: Tomsk, Russia, 2004; ISBN 5895031277. [Google Scholar]
- Laptash, N.M.; Maslennikova, I.G. Fluoride processing of titanium-containing minerals. Adv. Mater. Phys. Chem. 2012, 2, 21–24. [Google Scholar] [CrossRef] [Green Version]
- Dubenko, A.V.; Nikolenko, N.V.; Vashkevich, E.Y.; Tolstopyat, A.T. Fluoride Anions Desorption from Titanium Oxyhydroxide Surface. In Proceedings of the XVI Polish-Ukrainian Symposium on Theoretical and Experimental Studies of Interfacial Phenomena and their Technological Applications, Lublin, Poland, 28–31 August 2018; p. 31. [Google Scholar]
- Opalovsky, A.A.; Labkov, E.U.; Torosyan, S.S.; Dzhambek, A.A. DTA study of the reactions of non-metal fluorides with inorganic compounds. J. Anal. 1979, 15, 67–77. [Google Scholar] [CrossRef]
- Biswas, R.K.; Mondal, M.G.K. A study on the dissolution of ilmenite sand. Hydrometallurgy 1987, 17, 385–390. [Google Scholar] [CrossRef]
- Hansen, D.A.; Traut, D.E. The kinetics of leaching rock ilmenite with hydrofluoric acid. JOM 1989, 41, 34–36. [Google Scholar] [CrossRef]
- Gordienko, P.S.; Dostovalov, V.A.; Pashnina, E.V. Hydrofluoride method of complex processing of titanium-containing raw materials. Solid State Phenom. 2017, 265, 542–547. [Google Scholar] [CrossRef]
- Maslennikova, I.G. Influence of the amount of ammonium hydrogen difluoride on the degree of fluorination of mineral raw materials. Russ. J. Appl. Chem. 2009, 82, 1333–1337. [Google Scholar] [CrossRef]
- Gordienko, P.; Scheka, S.; Bakeeva, N.; Pashnina, E. Gidroftoridnyiy metod pererabotki ilmenitovyih kontsentratov [Hydrofluoride method for processing ilmenite concentrates]. Min. Inf. Anal. Bull. Sci. Tech. J. 2010, 4, 278–288. [Google Scholar]
- D’yachenko, A.N. Ftoroammonijnyj metod polucheniya dioksida titana [Fluoroammonium method for producing titanium dioxide]. Bull. Tomsk Polytech. Univ. 2004, 309, 99–102. [Google Scholar]
- Adhyapak, S.V.; Wani, B.N.; Rao, U.R.K.; Kulshreshtha, S.K. Reactions of ammonium hydrogen fluoride with oxides of iron in solid state. Synth. React. Inorg. Met. Chem. 1992, 22, 337–348. [Google Scholar] [CrossRef]
- Laptash, N.M.; Maslennikova, I.G.; Kaidalova, T.A. Ammonium oxofluorotitanates. J. Fluor. Chem. 1999, 99, 133–137. [Google Scholar] [CrossRef]
- Nikolenko, N.V.; Samchilev, I.S.; Kalashnikova, A.N.; Ananchenko, B.A. Thermodynamic and kinetic analyses of the decomposition of iron molybdate with soda ash solutions. Russ. J. Appl. Chem. 2015, 88, 208–215. [Google Scholar] [CrossRef]
- Nikolenko, N.V.; Kosynyuk, A.O.; Kalashnikov, Y.V.; Cheremis, E.A. The calculation of the thermodynamic equilibrium in Fe3+/MoO42-/H+(OH-)/H2O system and determination of reasonable conditions for iron molybdate deposition. Russ. J. Appl. Chem. 2012, 85, 1814–1819. [Google Scholar] [CrossRef]
- Nikolenko, N.V.; Samchileev, I.S.; Kachalova, A.S.; Kostynyk, A.O. The thermodynamic analysis of sintering process of molybdenum-containing and iron-containing raw material with soda ash. Vopr. Khimii I Khimicheskoi Tekhnologii 2015, 104, 19–25. [Google Scholar]
- Nikolenko, N.V.; Kalashnikova, A.N.; Samchileev, I.S.; Kalashnikov, Y.V.; Kachalova, A.S. The model of the “contracting core” in the study of heterogeneous chemical processes in the L-S system. Vopr. Khimii I Khimicheskoi Tekhnologii 2015, 2, 103–119. [Google Scholar]
- Ravdel, A.A.; Ponomareva, A.M. Kratkij Spravochnik Fiziko-Himicheskih Velichin [A Quick Reference to Physico-Chemical Quantities]; Specialnaya Literatura: St. Petersburg, Russia, 1998; Volume 238. [Google Scholar]
- Malina, K.M. Spravochnik Sernokislotchika [Sulfur Acid Guide], 2nd ed.; Khimiya: Moscow, Russia, 1971; Volume 744. [Google Scholar]
- Electronic Database Ivtanthermo. Moscow State University. Available online: http://www.chem.msu.ru/cgi-bin/tkv.pl?show=welcome.html (accessed on 1 April 2020).
- Temkin, M.I.; Shvarcman, L.A. Vspomogatel’naya tablica dlya raschyotov po himicheskoj termodinamike [Auxiliary table for calculations in chemical thermodynamics]. Uspekhi Him. 1948, 17, 259–262. [Google Scholar]
- Belokoskov, I.V. Issledovanie sul’fatov titana v sisteme TiO2-SO3-H2O metodom rastvorimosti v intervale temperatur 100–300 °C [The study of titanium sulfates in the TiO2-SO3-H2O system by the solubility method in the temperature range 100–300 °C]. Zhurnal Neorg. Him. 1962, 7, 1443–1452. [Google Scholar]
- Nikolenko, N.V.; Dubenko, A.V.; Vashkevich, E.Y.; Dmitrikova, L.V. Temperature optimum of the process of the dissolution of altered ilmenite in sulfuric acid. Vopr. Khimii I Khimicheskoi Tekhnologii 2018, 3, 70–78. [Google Scholar]
- Solovov, V.; Kovalenko, V.; Nikolenko, N.V.; Kotok, V.; Vlasova, E. Influence of temperature on the characteristics of Ni(II), Ti(IV) layered double hydroxides synthesised by different methods. East.-Eur. J. Enterp. Technol. 2017, 1, 16–22. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Nicol, M.J. Kinetics of the dissolution of ilmenite in sulfuric acid solutions under reducing conditions. Hydrometallurgy 2010, 103, 196–204. [Google Scholar] [CrossRef] [Green Version]
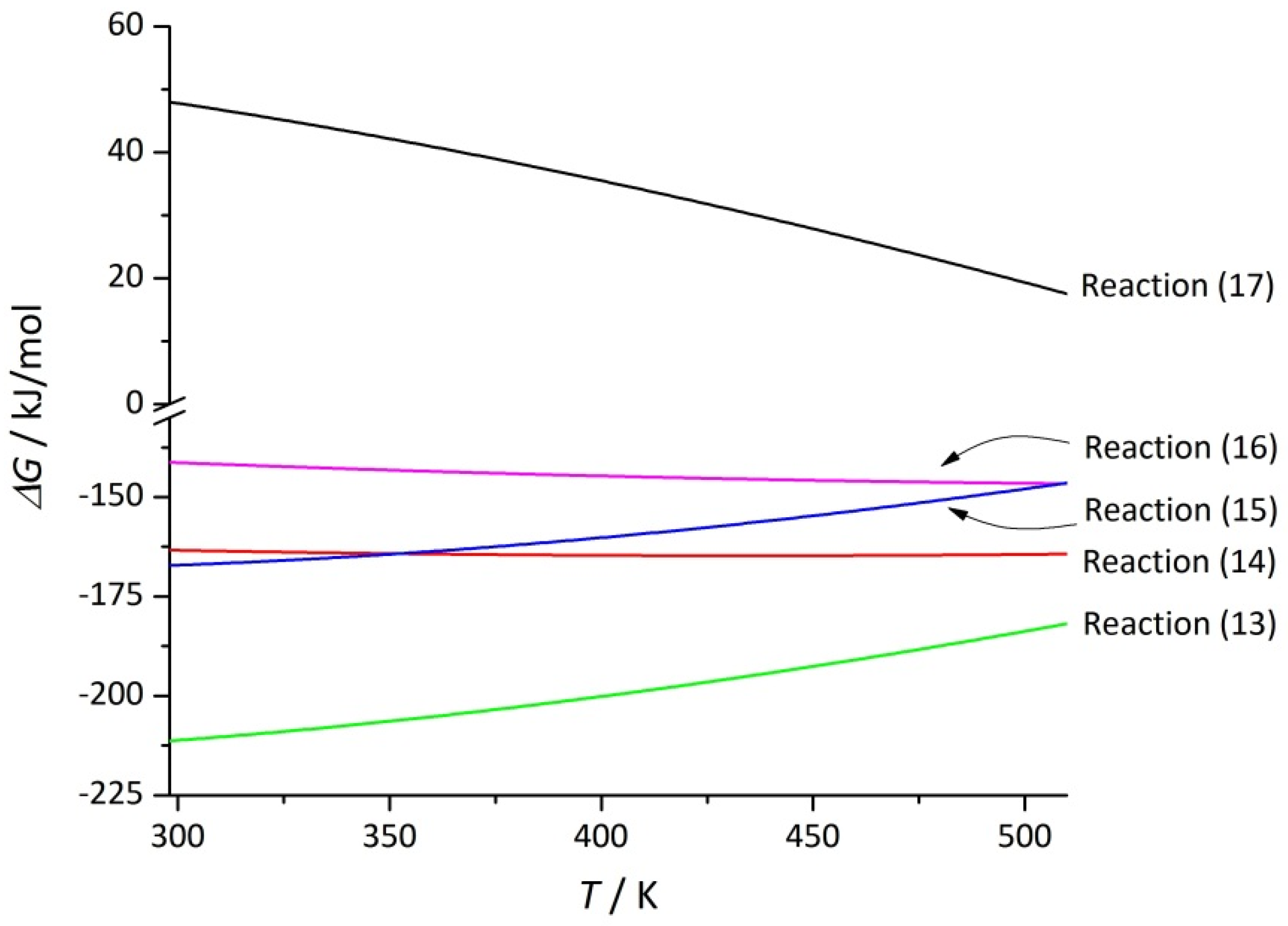

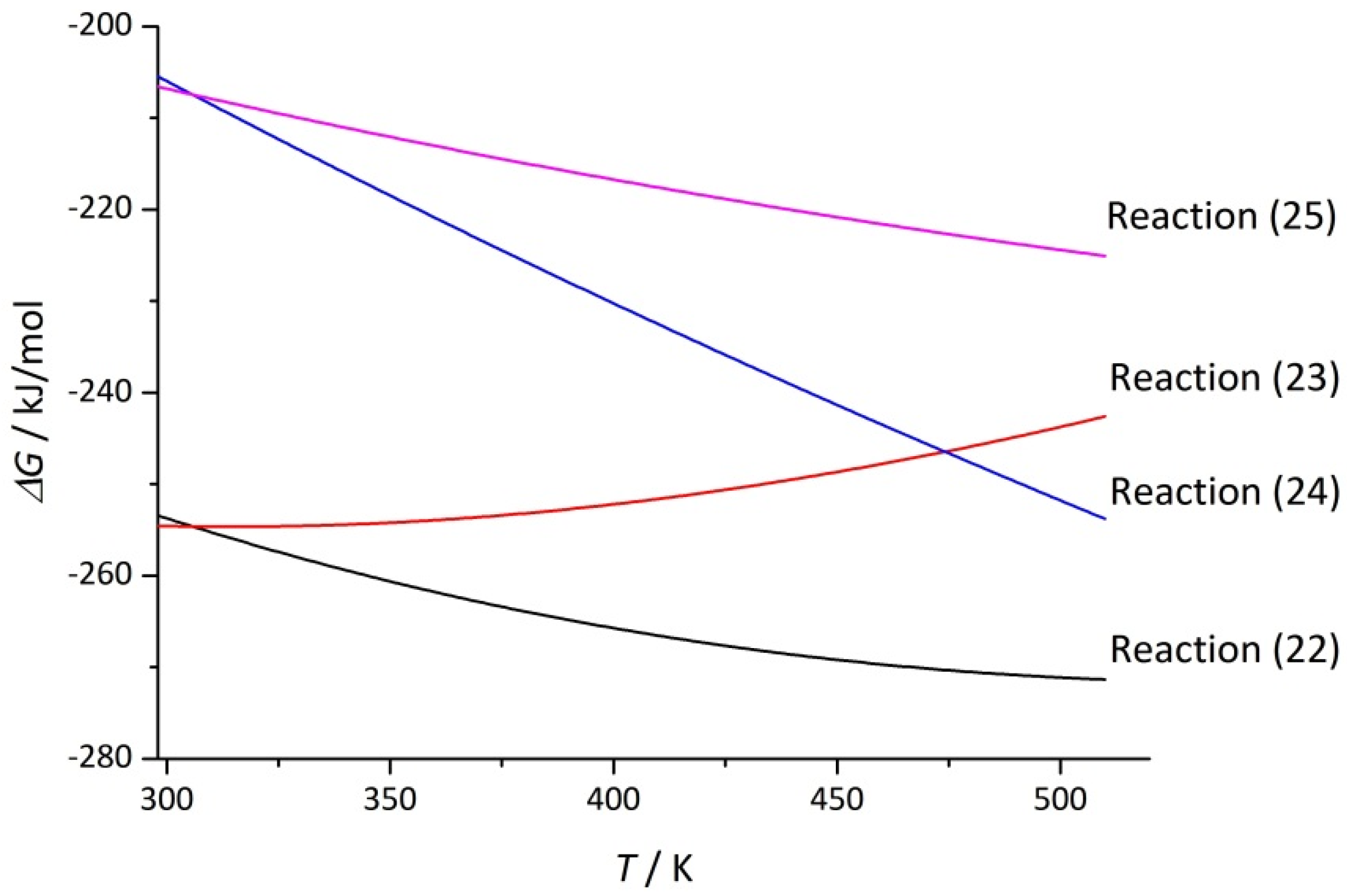
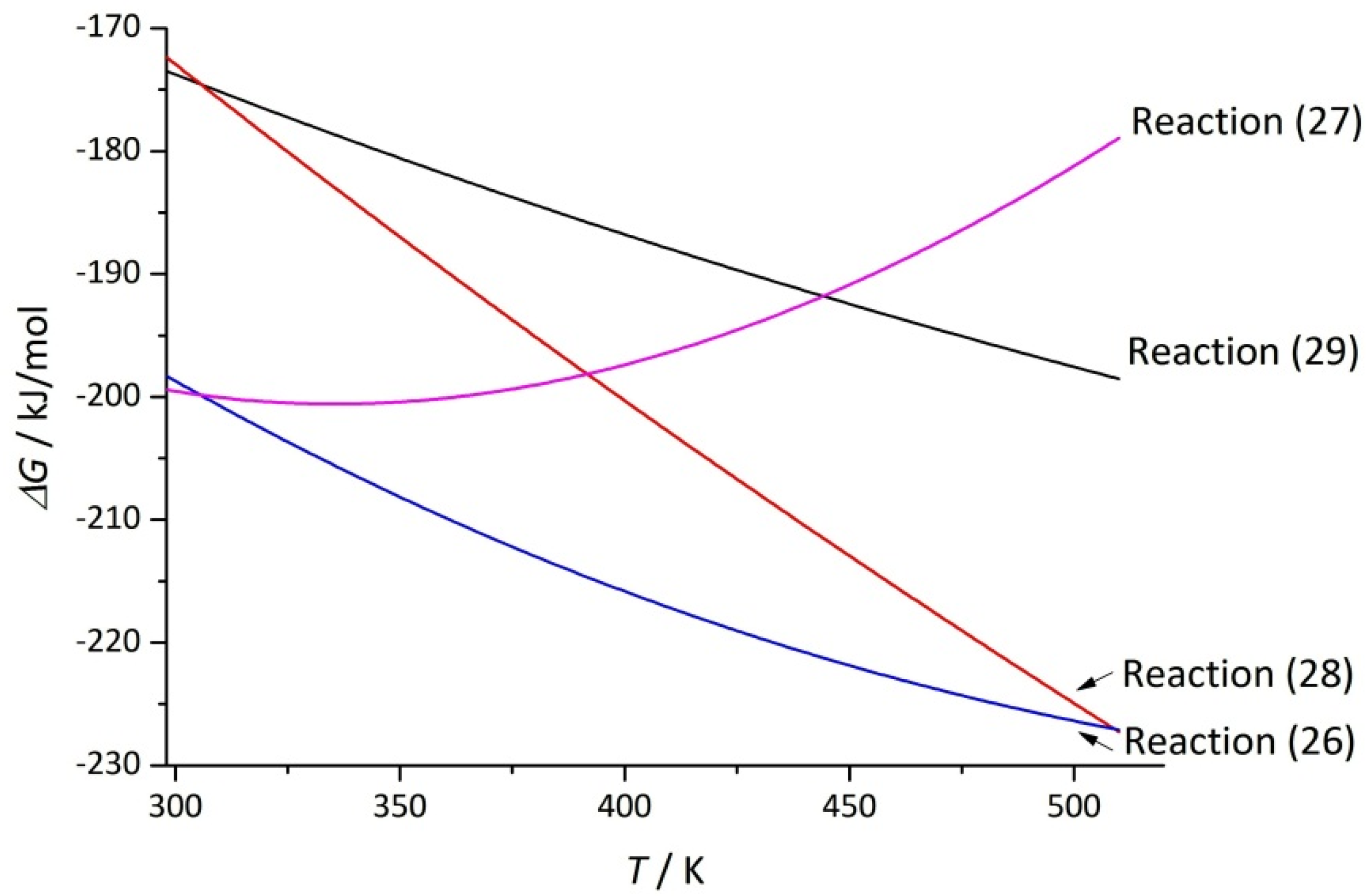
| Reaction | Δa | Δb·103 | Δc·10−5 | |||
|---|---|---|---|---|---|---|
| TiO2 + 4H2SO4 = Ti(SO4)2 + 2(H2SO4 H2O) | −235.2 | −79.9 | −211.3 | −226.7 | −58 | 56.9 |
| TiO2 + 6(H2SO4·H2O) = Ti(SO4)2 + 4(H2SO4·2H2O) | −178.8 | −38.7 | −167.2 | −226.7 | −58 | 56.9 |
| TiO2 + 2H2SO4 = TiOSO4 + H2SO4·H2O | −157.3 | 20.4 | −163.4 | −69.8 | −30 | 33.4 |
| TiO2 + 3(H2SO4·H2O) = TiOSO4 + 2(H2SO4·2H2O) | −129.1 | 41.0 | −141.3 | −69.8 | −30 | 33.4 |
| Ti(SO4)2 + H2SO4·H2O = TiOSO4 + 2H2SO4 | 77.9 | 100.3 | 48.0 | 156.9 | 28 | −23.5 |
| Reaction | Δa | Δb·103 | Δc·10−5 | |||
|---|---|---|---|---|---|---|
| TiO2 + 5H2SO4 + 2NaF = Ti(SO4)2 + Na2SO4 + 2HF↑ + 2(H2SO4·H2O) | −206.4 | 157.8 | −253.4 | −334.5 | 43 | 85.3 |
| TiO2 + 5H2SO4 + NaF = Ti(SO4)2 + NaHSO4 + HF↑ + 2(H2SO4·H2O) | −251.2 | 11.2 | −254.6 | −317.9 | 55 | 82.8 |
| TiO2 + 3H2SO4 + 2NaF = TiOSO4 + Na2SO4 + 2HF↑ + H2SO4·H2O | −128.5 | 258.1 | −205.4 | −177.6 | 71 | 61.8 |
| TiO2 + 3H2SO4 + NaF = TiOSO4 + NaHSO4 + HF↑ + H2SO4·H2O | −173.4 | 111.5 | −206.6 | −161.0 | 84 | 59.4 |
| TiO2 + 8(H2SO4·H2O) + 2NaF = Ti(SO4)2 +Na2SO4 + 2HF↑ + 5(H2SO4·2H2O) | −135.9 | 209.3 | −198.3 | −334.5 | 43 | 85.3 |
| TiO2 + 8(H2SO4·H2O) + NaF = Ti(SO4)2 + NaHSO4 + HF↑ + 5(H2SO4·2H2O) | –180.7 | 62.7 | –199.4 | –631.7 | 55 | 82.8 |
| TiO2 + 5(H2SO4·H2O) + 2NaF = TiOSO4 + Na2SO4 + 2HF↑ + 3(H2SO4·2H2O) | –86.2 | 289.0 | –172.4 | –177.6 | 71 | 61.8 |
| TiO2 + 5(H2SO4·H2O) + NaF = TiOSO4 + NaHSO4 + HF↑ + 3(H2SO4·2H2O) | –131.1 | 142.4 | –173.5 | –161.0 | 84 | 59.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubenko, A.V.; Nikolenko, M.V.; Aksenenko, E.V.; Kostyniuk, A.; Likozar, B. Mechanism, Thermodynamics and Kinetics of Rutile Leaching Process by Sulfuric Acid Reactions. Processes 2020, 8, 640. https://doi.org/10.3390/pr8060640
Dubenko AV, Nikolenko MV, Aksenenko EV, Kostyniuk A, Likozar B. Mechanism, Thermodynamics and Kinetics of Rutile Leaching Process by Sulfuric Acid Reactions. Processes. 2020; 8(6):640. https://doi.org/10.3390/pr8060640
Chicago/Turabian StyleDubenko, Anastasiia V., Mykola V. Nikolenko, Eugene V. Aksenenko, Andrii Kostyniuk, and Blaž Likozar. 2020. "Mechanism, Thermodynamics and Kinetics of Rutile Leaching Process by Sulfuric Acid Reactions" Processes 8, no. 6: 640. https://doi.org/10.3390/pr8060640
APA StyleDubenko, A. V., Nikolenko, M. V., Aksenenko, E. V., Kostyniuk, A., & Likozar, B. (2020). Mechanism, Thermodynamics and Kinetics of Rutile Leaching Process by Sulfuric Acid Reactions. Processes, 8(6), 640. https://doi.org/10.3390/pr8060640










