A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline
Abstract
:1. Introduction
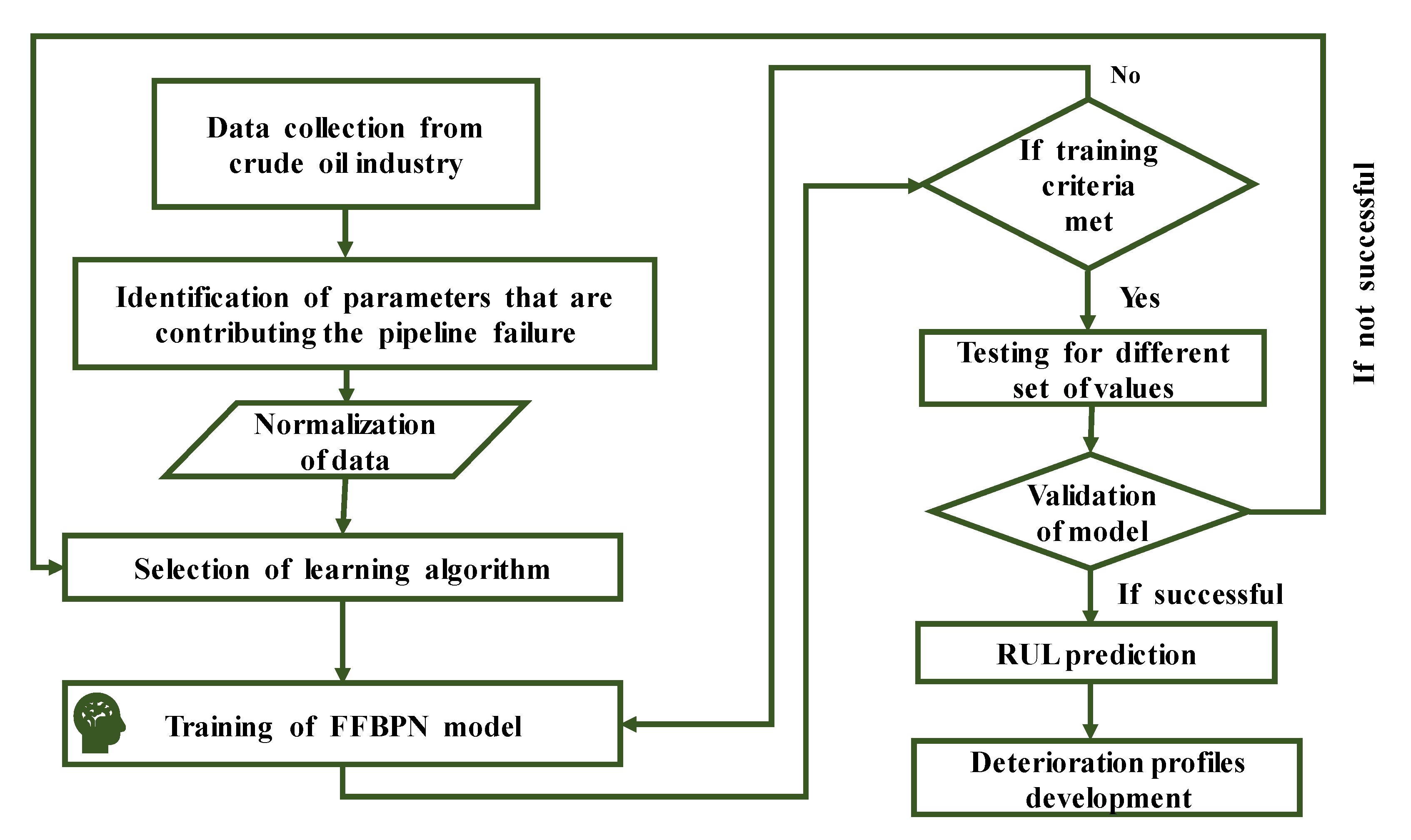
2. Proposed Feed Forward Back Propagation Network (FFBPN) Approach
2.1. Data Collection
2.2. Impact of Critical Factors on Pipeline Condition
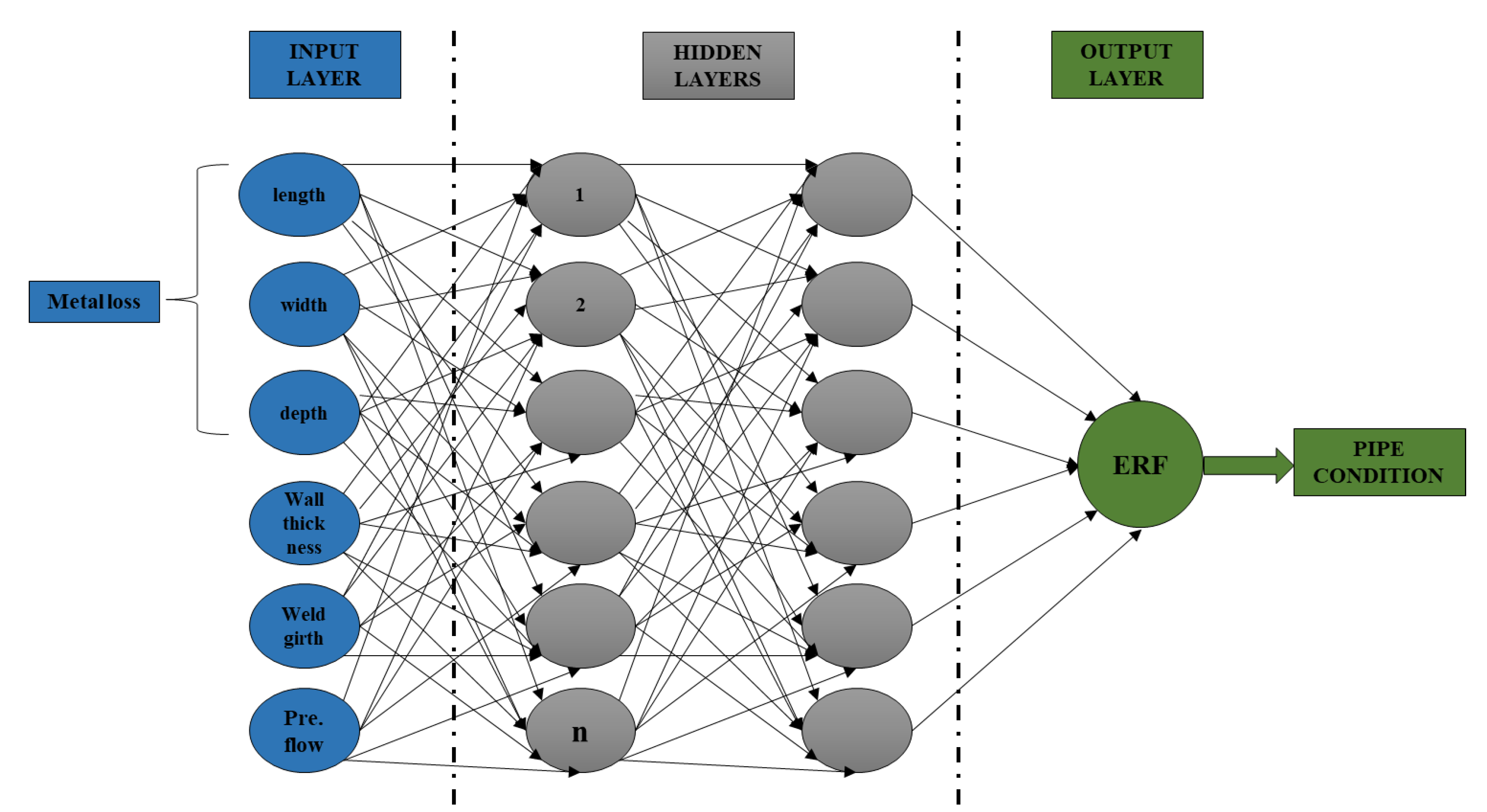
2.3. Parameters Considered for the Model Development
2.4. Data Normalization
2.5. FFBPN Model Development
3. Results and Discussions
3.1. FFBPN Model Training
3.2. FFBPN Model Testing
3.3. Metal Loss Growth Rate Calculation Results
3.4. Remaining Useful Life Calculation Results
3.5. Sensitivity Analysis
4. Conclusions
- The prediction model to assess the condition of the crude oil pipeline was developed using the Back Propagation Neural Network technique focused on specific factors such as metal loss anomalies (across length, width and depth), wall thickness, weld girth and pressure flow.
- The results of FFBPN model found to be satisfactory based on an R2 value of 0.9998. The predicted output accuracy was found to be highly dependent on the number of neurons.
- The model was tested with a new data set and the results were found to be good, with the R2 value of 0.99.
- The FFBPN model was validated using a new sample data and the results were found to be accurate with Root Mean Square Error (RMSE) and Mean Absolute Percentage Error (MAPE) values of 0.02514 and 0.02526, respectively.
- The deterioration curves were generated to know the effect of each factor selected on the pipeline condition; it was found that pressure has a major negative effect on pipeline condition and weld girth has a minor negative effect on pipeline condition.
- The proposed FFBPN was validated with other published models for its robustness and it was found that FFBPN performed better than the previous approaches based on R2 and RMSE.
- In terms of maintenance scheduling, the proposed approach will be beneficial. The developed model can be applied to real-time data to help pipeline operators take the necessary actions to prevent product losses in the oil and gas pipeline industries.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kennedy, J.L. Oil and Gas Pipeline Fundamentals; Pennwell Books: Tulsa, OK, USA, 1993. [Google Scholar]
- El-Abbasy, M.S.; Senouci, A.; Zayed, T.; Mosleh, F. A condition assessment model for oil and gas pipelines using integrated simulation and analytic network process. Struct. Infrastruct. Eng. 2015, 11, 263–281. [Google Scholar] [CrossRef]
- Shabarchin, O.; Tesfamariam, S. Internal corrosion hazard assessment of oil & gas pipelines using Bayesian belief network model. J. Loss Prev. Process Ind. 2016, 40, 479–495. [Google Scholar]
- Dey, P.K.; Ogunlana, S.O.; Naksuksakul, S. Risk-based maintenance model for offshore oil and gas pipelines: A case study. J. Qual. Maint. Eng. 2004, 10, 169–183. [Google Scholar] [CrossRef]
- Jinhai, L.; Huaguang, Z.; Jian, F.; Heng, Y. A new fault detection and diagnosis method for oil pipeline based on rough set and neural network. In Proceedings of the International Symposium on Neural Networks, Nanjing, China, 3–7 June 2007; pp. 561–569. [Google Scholar]
- Peng, X.-Y.; Zhang, P.; Chen, L.-Q. Long-distance oil/gas pipeline failure rate prediction based on fuzzy neural network model. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Angeles, CA, USA, 31 March–2 April 2009; pp. 651–655. [Google Scholar]
- Tabesh, M.; Soltani, J.; Farmani, R.; Savic, D. Assessing pipe failure rate and mechanical reliability of water distribution networks using data-driven modeling. J. Hydroinform. 2009, 11, 1–17. [Google Scholar] [CrossRef]
- Bersani, C.; Citro, L.; Gagliardi, R.V.; Sacile, R.; Tomasoni, A.M. Accident Occurrance Evaluation in the Pipeline Transport of Dangerous Goods. Chem. Eng. Trans. 2010, 249–254. [Google Scholar] [CrossRef]
- Noor, N.; Yahaya, N.; Ozman, N.; Othman, S. The forecasting residual life of corroding pipeline based on semi-probabilistic method. J. Civ. Eng. Sci. Technol. 2010, 1, 1–6. [Google Scholar]
- Dawotola, A.W.; Van Gelder, P.; Vrijling, J. Decision analysis framework for risk management of crude oil pipeline system. Adv. Decis. Sci. 2011, 2011, 456824. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, M.A.; Ebadi, M.; Shokrollahi, A.; Majidi, S.M.J. Evolving artificial neural network and imperialist competitive algorithm for prediction oil flow rate of the reservoir. Appl. Soft Comput. 2013, 13, 1085–1098. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Senouci, A.; Zayed, T.; Mirahadi, F.; Parvizsedghy, L. Artificial neural network models for predicting condition of offshore oil and gas pipelines. Autom. Constr. 2014, 45, 50–65. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Ayegba, P.; Abdulkadir, M.; Hernandez-Perez, V.; Lowndes, I.; Azzopardi, B.J. Applications of artificial neural network (ANN) method for performance prediction of the effect of a vertical 90 bend on an air–silicone oil flow. J. Taiwan Inst. Chem. Eng. 2017, 74, 59–64. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Ahmad, S.; Hashmi, H.N. Performance assessment of artificial neural networks and support vector regression models for stream flow predictions. Environ. Monit. Assess. 2018, 190, 704. [Google Scholar]
- Zabihi, R.; Mowla, D.; Karami, H.R. Artificial intelligence approach to predict drag reduction in crude oil pipelines. J. Pet. Sci. Eng. 2019, 178, 586–593. [Google Scholar] [CrossRef]
- Tan, Z.X.; Thambiratnam, D.P.; Chan, T.H.; Gordan, M.; Abdul Razak, H. Damage detection in steel-concrete composite bridge using vibration characteristics and artificial neural network. Struct. Infrastruct. Eng. 2019, 1–15. [Google Scholar] [CrossRef]
- Aguilar, V.; Sandoval, C.; Adam, J.M.; Garzón-Roca, J.; Valdebenito, G. Prediction of the shear strength of reinforced masonry walls using a large experimental database and artificial neural networks. Struct. Infrastruct. Eng. 2016, 12, 1661–1674. [Google Scholar] [CrossRef]
- Basha, S.N.; Rao, P.S. A Simulated Model for Assesing the Line Condition of Onshore Pipelines. In Proceedings of the MATEC Web of Conferences, Perak, Malaysia, 18–19 September 2018. [Google Scholar]
- Moayedi, H.; Aghel, B.; Vaferi, B.; Foong, L.K.; Bui, D.T. The feasibility of Levenberg–Marquardt algorithm combined with imperialist competitive computational method predicting drag reduction in crude oil pipelines. J. Pet. Sci. Eng. 2020, 185, 106634. [Google Scholar] [CrossRef]
- Taqvi, S.A.; Tufa, L.D.; Zabiri, H.; Maulud, A.S.; Uddin, F. Fault detection in distillation column using NARX neural network. Neural Comput. Appl. 2018, 1–17. [Google Scholar] [CrossRef]
- Sarbayev, M.; Yang, M.; Wang, H. Risk assessment of process systems by mapping fault tree into artificial neural network. J. Loss Prev. Process Ind. 2019, 60, 203–212. [Google Scholar] [CrossRef]
- Senouci, A.; Elabbasy, M.; Elwakil, E.; Abdrabou, B.; Zayed, T. A model for predicting failure of oil pipelines. Struct. Infrastruct. Eng. 2014, 10, 375–387. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Senouci, A.; Zayed, T.; Mirahadi, F.; Parvizsedghy, L. Condition prediction models for oil and gas pipelines using regression analysis. J. Constr. Eng. Manag. 2014, 140, 04014013. [Google Scholar] [CrossRef]
- Senouci, A.; El-Abbasy, M.S.; Zayed, T. Fuzzy-based model for predicting failure of oil pipelines. J. Infrastruct. Syst. 2014, 20, 04014018. [Google Scholar] [CrossRef]









| Parameter | Unit |
|---|---|
| Max. Allowable Operating Pressure (MAOP) | 97 (bar) |
| Product type | Waxy crude oil |
| Diameter | 32 (inches) |
| Material | API 5L X 65/X 70 |
| Length | 1135.88 (km) |
| Nominal wall thickness | 11.71 (mm)/18.91 (mm) |
| Design Factor | 0.72 |
| Assessment pressure | 80 (bar) |
| Design pressure | 100 (bar) |
| Inspection years | 2009 and 2015 |
| No. of Neurons | Training | Validation | Testing | Overall R2 | |||
|---|---|---|---|---|---|---|---|
| MSE | R2 | MSE | R2 | MSE | R2 | ||
| 6 | 11.2354 | 0.9513 | 21.6136 | 0.9571 | 16.0711 | 0.7641 | 0.9372 |
| 7 | 10.0785 | 0.9609 | 60.7338 | 0.8935 | 19.8944 | 0.9463 | 0.9547 |
| 8 | 1.3699 | 0.9931 | 11.6083 | 0.7578 | 25.8974 | 0.8624 | 0.9645 |
| 9 | 3.5939 | 0.9880 | 20.6453 | 0.9796 | 24.8692 | 0.1707 | 0.9604 |
| 10 | 19.5869 | 0.9252 | 10.8580 | 0.3483 | 14.4814 | 0.8686 | 0.9045 |
| 11 | 4.9530 | 0.9768 | 10.9544 | 0.8166 | 30.9652 | 0.8871 | 0.9430 |
| 12 | 3.7410 | 0.9824 | 10.6335 | 0.8287 | 71.8311 | 0.6975 | 0.9215 |
| 13 | 2.3421 | 0.9780 | 0.0464 | 0.9787 | 56.0370 | 0.9144 | 0.9376 |
| 14 | 2.4702 | 0.9867 | 10.3475 | 0.9409 | 7.3257 | 0.9091 | 0.9749 |
| 15 | 0.9471 | 0.9945 | 20.8847 | 0.9022 | 13.8276 | 0.9275 | 0.9665 |
| 16 | 0.0894 | 0.9973 | 0.1046 | 0.9970 | 0.0783 | 0.9977 | 0.9998 |
| 17 | 1.6581 | 0.9908 | 10.9430 | 0.9465 | 26.9734 | 0.8224 | 0.9622 |
| 18 | 1.7737 | 0.9887 | 9.9706 | 0.9658 | 66.2021 | 0.6006 | 0.9276 |
| 19 | 2.0126 | 0.9876 | 16.7679 | 0.9224 | 13.1037 | 0.9619 | 0.9677 |
| 20 | 2.3673 | 0.9848 | 35.6957 | 0.8710 | 20.8974 | 0.9494 | 0.9509 |
| Range | Metal Loss Depth Level | Depth Recorded in 2009 Inspection (%wt) | Depth Recorded in 2015 Inspection (%wt) | Max. Growth Rate (mm/yr) |
|---|---|---|---|---|
| Optimistic | 0%wt ≤ D < 10%wt | 0 | 9 | 0.27 |
| Average | 10%wt ≤ D < 20%wt | 0 | 19 | 0.58 |
| Pessimistic | 30%wt ≤ D < 40%wt | 0 | 30 | 0.91 |
| Optimistic | Average | Pessimistic | |
|---|---|---|---|
| Rate | 0.27 | 0.58 | 0.91 |
| Predicted RUL | 26 years | 14 years | 10 years |
| Individual Factor | Relative Percentage (%) |
|---|---|
| Length | 10.72638761 |
| Width | 8.534201257 |
| Depth | 2.856189363 |
| Wall thickness | 37.2331322 |
| Pressure | 40.5805349 |
| Weld Girth | 0.069554677 |
| Total | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaik, N.B.; Pedapati, S.R.; Taqvi, S.A.A.; Othman, A.R.; Dzubir, F.A.A. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes 2020, 8, 661. https://doi.org/10.3390/pr8060661
Shaik NB, Pedapati SR, Taqvi SAA, Othman AR, Dzubir FAA. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes. 2020; 8(6):661. https://doi.org/10.3390/pr8060661
Chicago/Turabian StyleShaik, Nagoor Basha, Srinivasa Rao Pedapati, Syed Ali Ammar Taqvi, A. R. Othman, and Faizul Azly Abd Dzubir. 2020. "A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline" Processes 8, no. 6: 661. https://doi.org/10.3390/pr8060661
APA StyleShaik, N. B., Pedapati, S. R., Taqvi, S. A. A., Othman, A. R., & Dzubir, F. A. A. (2020). A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes, 8(6), 661. https://doi.org/10.3390/pr8060661







