Application of Combined Developments in Processes and Models to the Determination of Hot Metal Temperature in BOF Steelmaking
Abstract
:1. Introduction
2. Materials and Methods
2.1. Proposed Workflow
2.2. Process-Model Understanding
2.3. Process and Model Alternatives
- Direct measurement with thermocouples
- Indirect measurement with IR thermometer
- Prediction with stochastic models
- Prediction with machine learning models
2.4. Process Development
2.4.1. Direct Measurement
- On the torpedoes, directly before starting pouring
- On the hot metal ladle, before completing the hot metal transfer
- Several automated measuring stations and additional labor would be required to measure on torpedoes, since several hot metal transfer points exist at each steel mill. If the measurement is to be made on hot metal ladles, at least two measuring stations would be necessary.
- Direct measurement implies delaying the execution of the BOF load model until the last possible moment. This requires that not only the preparation of the hot metal, but also the preparation of the associated scrap load be postponed. This has a very negative impact on the productivity of the steel mill.
- Despite the fact that thermocouples are accurate, the obtained temperature is not representative of the real conditions in which the hot metal will finally be loaded into the converter. To remedy this, several processes occurring after the thermocouple measurement would require additional modelling, e.g., the holding time in the torpedo, hot metal pouring from the torpedo to the ladle, the holding time in the ladle and the skimming of the hot metal ladle.
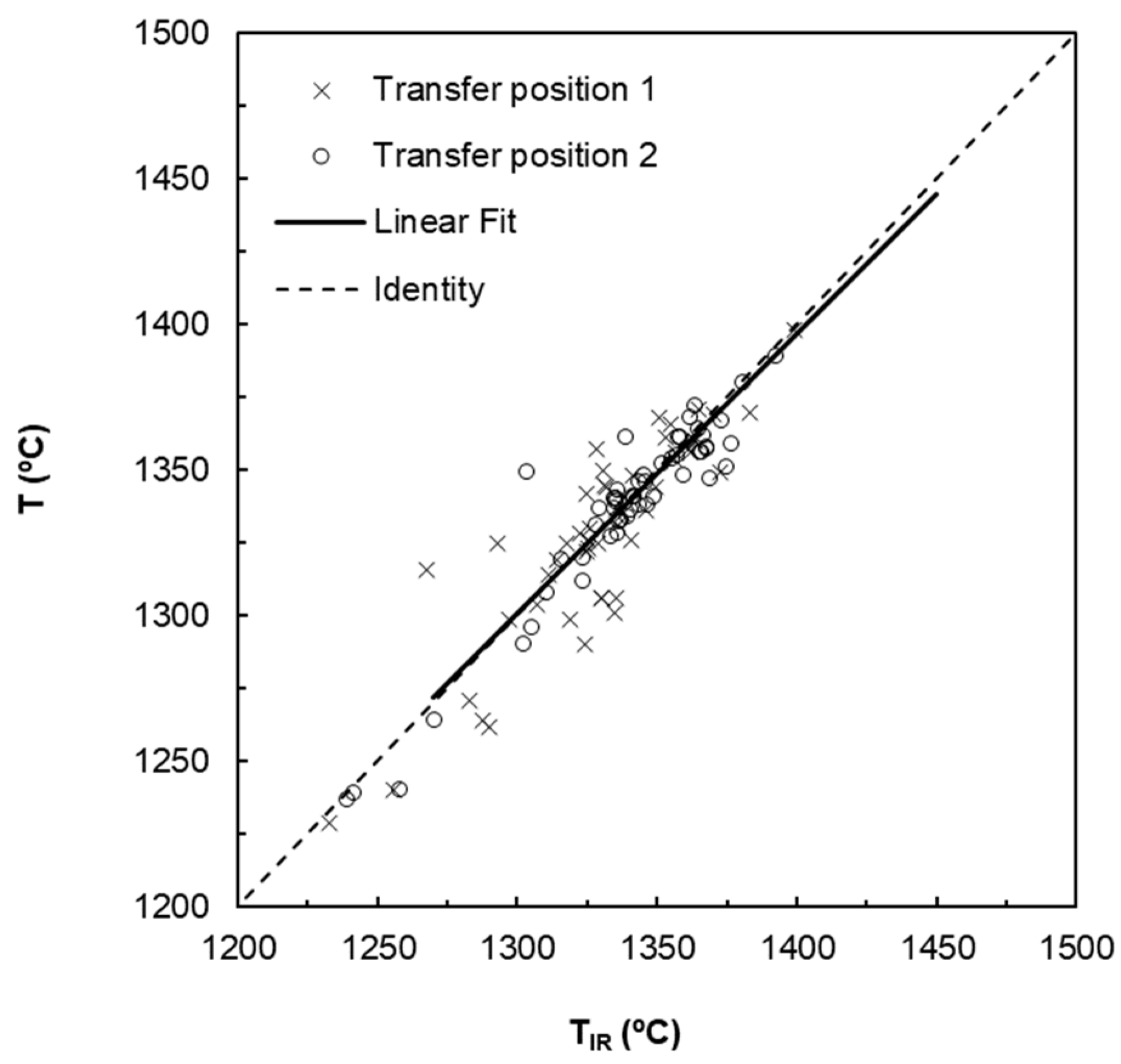
2.4.2. Indirect Measurement
2.5. Model Development
2.5.1. Stochastic Modelling
2.5.2. Machine Learning
3. Results
4. Discussion
- Multidisciplinary work team. Throughout this research, colleagues from different sectors have worked together: academic, R&D, process engineers and sensor suppliers.
- Long-term sustainability of achievements. Adaptive and unattended predictive models were developed. Moreover, the sequential development of these models has allowed their validation over extended periods of time.
- Analysis of different process-model alternatives. Different options for improving temperature determination were assessed. Solutions were obtained from the combined use of sensors and models subject to the requirements of the process.
- Analyses of variable importance and of data quality. The BOF thermal model made it possible to identify which variables had the greatest impact in the carbon footprint. Careful data processing was a prerequisite for developing the predictive models.
- Oriented to knowledge construction. The interest of the BOF thermal model extends beyond the present research. Likewise, the application of MMARSL models can be extended to other steel mill subprocesses.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Worldsteel Steel Statistical Yearbook 2019. Available online: http://www.worldsteel.org/steel-by-topic/statistics/steel-statistical-yearbook.html (accessed on 23 April 2020).
- ArcelorMittal Climate Action Report. Available online: https://annualreview2018.arcelormittal.com/~/ media/Files/A/Arcelormittal-AR-2018/AM_ClimateActionReport_2018.pdf (accessed on 7 December 2019).
- McLean, A. The science and technology of steelmaking—Measurements, models, and manufacturing. Metall. Mater. Trans. B 2006, 37, 319–332. [Google Scholar] [CrossRef]
- Mazumdar, D.; Evans, J.W. Elements of mathematical modeling. In Modeling of Steelmaking Processes; CRC Press: Boca Raton, FL, USA, 2009; pp. 139–173. ISBN 1-4398-8302-5. [Google Scholar]
- Valentini, R.; Colla, V.; Vannucci, M. Neural predictor of the end point in a converter. Rev. Metal. 2004, 40, 416–419. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, B.; Xiong, X. Basic oxygen furnace steelmaking end-point prediction based on computer vision and general regression neural network. Optik 2014, 125, 5241–5248. [Google Scholar] [CrossRef]
- Iwamura, T. Breakthrough Control Technologies in the Japanese Steel Industry. SICE J. Control Meas. Syst. Integr. 2008, 1, 352–361. [Google Scholar] [CrossRef]
- Wang, G.; Tang, L. A column generation for locomotive scheduling problem in molten iron transportation. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 2227–2233. [Google Scholar]
- Goldwaser, A.; Schutt, A. Optimal torpedo scheduling. J. Artif. Intell. Res. 2018, 63, 955–986. [Google Scholar] [CrossRef]
- Du, T.; Cai, J.; Li, Y.; Wang, J. Analysis of Hot Metal Temperature Drop and Energy-Saving Mode on Techno-Interface of BF-BOF Route. Iron Steel China 2008, 12, 83–86. [Google Scholar]
- Wu, M.; Zhang, Y.; Yang, S.; Xiang, S.; Liu, T.; Sun, G. Analysis of hot metal temperature drop in torpedo car. Iron Steel China 2002, 37, 12–15. [Google Scholar]
- Liu, S.; Yu, J.; Yan, Z.; Liu, T. Factors and control methods of the heat loss of torpedo-ladle. J. Mater. Metall. 2010, 9, 159–163. [Google Scholar]
- Díaz, J.; Fernandez, F.; Gonzalez, A. Prediction of hot metal temperature in a BOF converter using an ANN. In Proceedings of the IRCSEEME, Mieres, Spain, 25–27 July 2018; pp. 27–28. [Google Scholar]
- Díaz, J.; Fernández, F.J.; Suárez, I. Hot Metal Temperature Prediction at Basic-Lined Oxygen Furnace (BOF) Converter Using IR Thermometry and Forecasting Techniques. Energies 2019, 12, 3235. [Google Scholar] [CrossRef] [Green Version]
- Díaz, J.; Fernández, F.J.; Prieto, M.M. Hot Metal Temperature Forecasting at Steel Plant Using Multivariate Adaptive Regression Splines. Metals 2020, 10, 41. [Google Scholar] [CrossRef] [Green Version]
- Díaz, J.; Fernández, F.J. Synergies in Combined Development of Processes and Models: The Cases of BOF Steelmaking and Building Energy Management. Processes. (manuscript in preparation).
- Díaz, J.; Fernández, F.J. The impact of hot metal temperature on CO2 emissions from basic oxygen converter. Environ. Sci. Pollut. Res. 2020, 27, 33–42. [Google Scholar] [CrossRef]
- Miller, T.W.; Jimenez, J.; Sharan, A.; Goldstein, D.A. Oxygen Steelmaking Processes. In The Making, Shaping, and Treating of Steel; AISE Steel Foundation: Pittsburgh, PA, USA, 1998; pp. 475–524. ISBN 978-0-930767-03-7. [Google Scholar]
- Ghosh, A.; Chatterjee, A. Ironmaking and Steelmaking: Theory and Practice; Eastern economy edition; 3 print; PHI Learning: New Delhi, India, 2010; ISBN 978-81-203-3289-8. [Google Scholar]
- Ares, R.; Balante, W.; Donayo, R.; Gómez, A.; Perez, J. Getting more steel from less hot metal at Ternium Siderar steel plant. Rev. Métallurgie–Int. J. Metall. 2010, 107, 303–308. [Google Scholar] [CrossRef]
- Wirth, R.; Hipp, J. CRISP-DM: Towards a standard process model for data mining. In Proceedings of the 4th International Conference on the Practical Applications of Knowledge Discovery and Data Mining, Crowne Plaza Midland Hotel, Manchester, UK, 11–13 April 2000; Springer-Verlag: London, UK, 2000; pp. 29–39. [Google Scholar]
- Mariscal, G.; Marbán, Ó.; Fernández, C. A survey of data mining and knowledge discovery process models and methodologies. Knowl. Eng. Rev. 2010, 25, 137–166. [Google Scholar] [CrossRef]
- Barati, M. Energy intensity and greenhouse gases footprint of metallurgical processes: A continuous steelmaking case study. Energy 2010, 35, 3731–3737. [Google Scholar] [CrossRef]
- Sun, W.; Cai, J.; Ye, Z. Advances in energy conservation of China steel industry. Sci. World J. 2013, 2013, 247035. [Google Scholar] [CrossRef] [PubMed]
- Grip, C.-E.; Larsson, M.; Harvey, S.; Nilsson, L. Process integration. Tests and application of different tools on an integrated steelmaking site. Appl. Therm. Eng. 2013, 53, 366–372. [Google Scholar] [CrossRef]
- Kadrolkar, A.; Dogan, N. Model development for refining rates in oxygen steelmaking: Impact and slag-metal bulk zones. Metals 2019, 9, 309. [Google Scholar] [CrossRef] [Green Version]
- Penz, F.M.; Schenk, J.; Ammer, R.; Klösch, G.; Pastucha, K. Evaluation of the Influences of Scrap Melting and Dissolution during Dynamic Linz–Donawitz (LD) Converter Modelling. Processes 2019, 7, 186. [Google Scholar] [CrossRef] [Green Version]
- Díaz, J. Predicción de la Temperatura del Arrabio en la Acería y Evaluación de su Impacto en las Emisiones de CO2 Mediante el Desarrollo Conjunto de Procesos y Modelos (Hot Metal Temperature Forecasting at Steel Plant and Evaluation of Carbon Emissions by Combined Development in Process and Models). Ph.D. Thesis, Universidad de Oviedo, Oviedo, Asturias, Spain, 2020. [Google Scholar]
- Kudrin, V.A. Steelmaking; Mir Publishers: Moscow, Russia, 1985; ISBN 978-5-03-000859-2. [Google Scholar]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov/ (accessed on 12 June 2020).
- Kelley, K.K. Contributions to the Data on Theoretical Metallurgy; US Government Printing Office: Washington, DC, USA, 1962. [Google Scholar]
- ENSIDESA. Curso de Formación Metalúrgica Para Jefes de Sección; ENSIDESA: Oviedo, Spain, 1985. [Google Scholar]
- Ryman, C.; Larsson, M. Reduction of CO2 emissions from integrated steelmaking by optimised scrap strategies: Application of process integration models on the BF–BOF system. ISIJ Int. 2006, 46, 1752–1758. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.V. Control of oxygen steelmaking. In Control and Analysis in Iron and Steelmaking; Butterworths monographs in materials; Butterworths: London, Boston, 1983; pp. 147–176. ISBN 978-0-408-10713-6. [Google Scholar]
- Kozlov, V.; Malyshkin, B.Y. Accuracy of measurement of liquid metal temperature using immersion thermocouples. Metallurgist 1969, 13, 354–356. [Google Scholar] [CrossRef]
- He, F.; He, D.; Xu, A.; Wang, H.; Tian, N. Hybrid model of molten steel temperature prediction based on ladle heat status and artificial neural network. J. Iron Steel Res. Int. 2014, 21, 181–190. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 481–514. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. The forecaster’s toolbox. In Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018; pp. 47–81. ISBN 0-9875071-1-7. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. ARIMA models. In Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018; pp. 221–274. ISBN 0-9875071-1-7. [Google Scholar]
- ARIMA Model Including Exogenous Covariates. Available online: https://es.mathworks.com/help/econ/ arima-model-including-exogenous-regressors.html (accessed on 18 April 2020).
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Friedman, J.H.; Roosen, C.B. An introduction to multivariate adaptive regression splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef]
- Nieto, P.J.G.; Suárez, V.M.G.; Antón, J.C.Á.; Bayón, R.M.; Blanco, J.Á.S.; Fernández, A.M.D. A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach. Materials 2015, 8, 3562–3583. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, A.; Iqbal, A. Prediction of mechanical property of steel strips using multivariate adaptive regression splines. J. Appl. Stat. 2009, 36, 1–9. [Google Scholar] [CrossRef]
- Yu, W.H.; Yao, C.G.; Yi, X.D. A Predictive Model of Hot Rolling Flow Stress by Multivariate Adaptive Regression Spline. In Materials Science Forum; Trans Tech Publications: Stafa-Zurich, Switzerland, 2017; Volume 898, pp. 1148–1155. [Google Scholar]
- Smith, P.L. Curve Fitting and Modeling with Splines Using Statistical Variable Selection Techniques; NASA: Washington, DC, USA, 1982. [Google Scholar]
- Jekabsons, G. ARESLab Adaptive Regression Splines toolbox for Matlab/Octave ver. 1.13.0 2016. Available online: http://www.cs.rtu.lv/jekabsons/Files/ARESLab.pdf (accessed on 19 April 2020).
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Predicting the Electrical Energy Consumption of Electric Arc Furnaces Using Statistical Modeling. Metals 2019, 9, 959. [Google Scholar] [CrossRef] [Green Version]
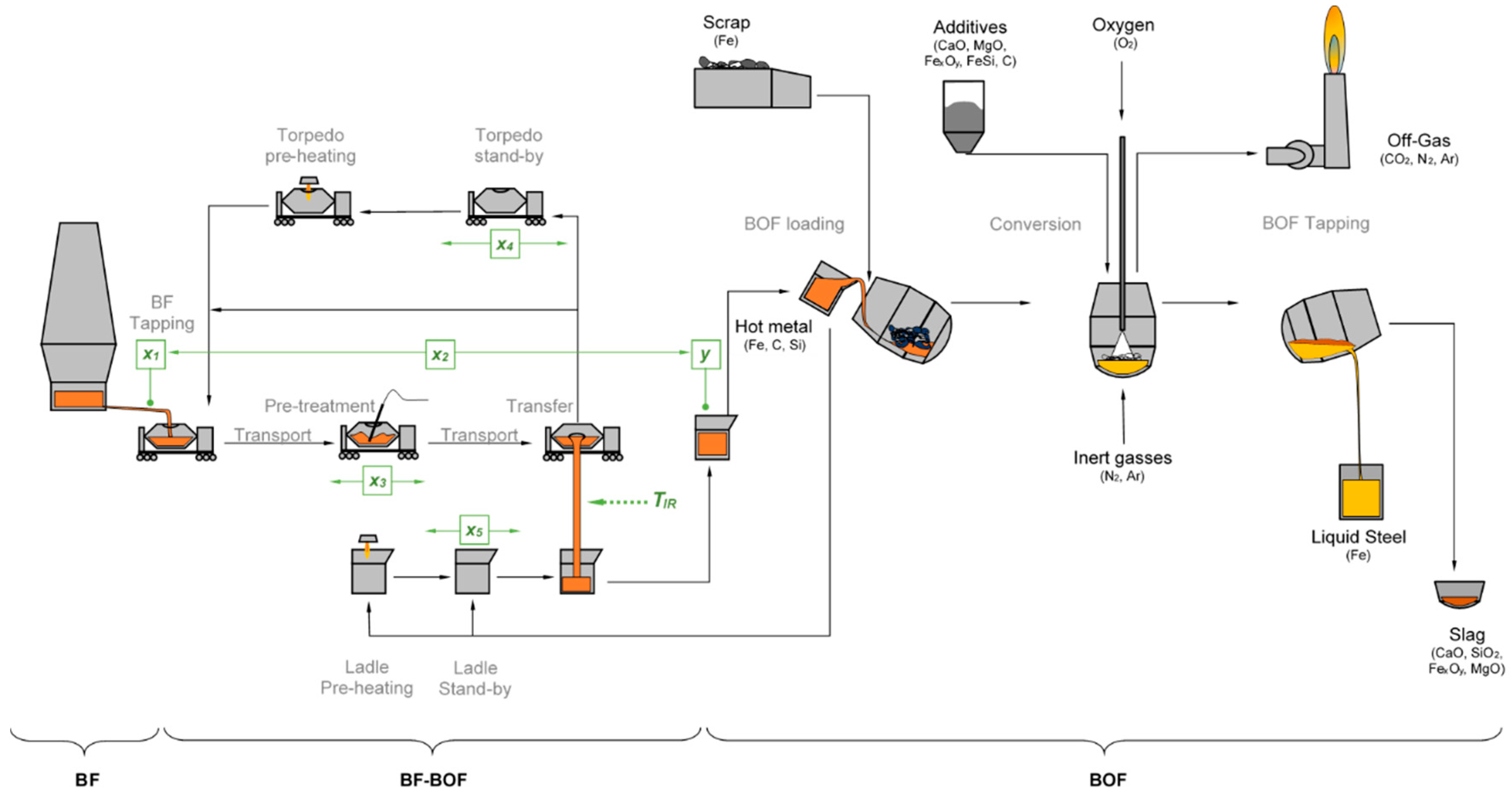



| Description | Symbol | Min | Max | Unit |
|---|---|---|---|---|
| Initial temperature | x1 | 1400 | 1540 | °C |
| Total holding time | x2 | 2 | 20 | h |
| Pretreatment duration | x3 | 0 | 40 | min |
| Empty torpedo duration | x4 | 1 | 16 | h |
| Empty ladle duration | x5 | 0 | 8 | h |
| Final temperature | y | 1200 | 1420 | °C |
| Model | Expression | |
|---|---|---|
| Standard Value | SV | |
| Naïve Forecasting | NF | |
| Moving Average Smoothing | MAS | |
| Auto-Regressive Moving Average with Integration | ARIMA | |
| ARIMA with eXogenous predictors | ARIMAX | |
| Moving ARIMA | MARIMA | |
| Moving ARIMAX | MARIMAX | |
| Model | Expression | |
|---|---|---|
| Multivariate Adaptive Regression Splines | MARS | |
| Moving MARS | MMARS | |
| Moving MARS with Lagged observations | MMARSL | |
| Method | Number of Variables, N | Number of Observations, w | Earliest Result in Advance (min) | |
|---|---|---|---|---|
| Min. | Opt. | |||
| SV | 0 | 0 | 0 | inf. |
| NF | 1 | 1 | 1 | 10 |
| Initial | 1 | 50 | 50 | 10 |
| MAS | 1 | 1 | 5 | 10 |
| MARIMA | 1 | 100 | 1000 | 10 |
| MARIMAX5 | 6 | 300 | 1000 | 10 |
| MMARS | 5 | 20 | 2000 | 30 |
| MMARSL4 | 9 | 200 | 2000 | 10 |
| IR | 1 | 1 | 1 | -10 |
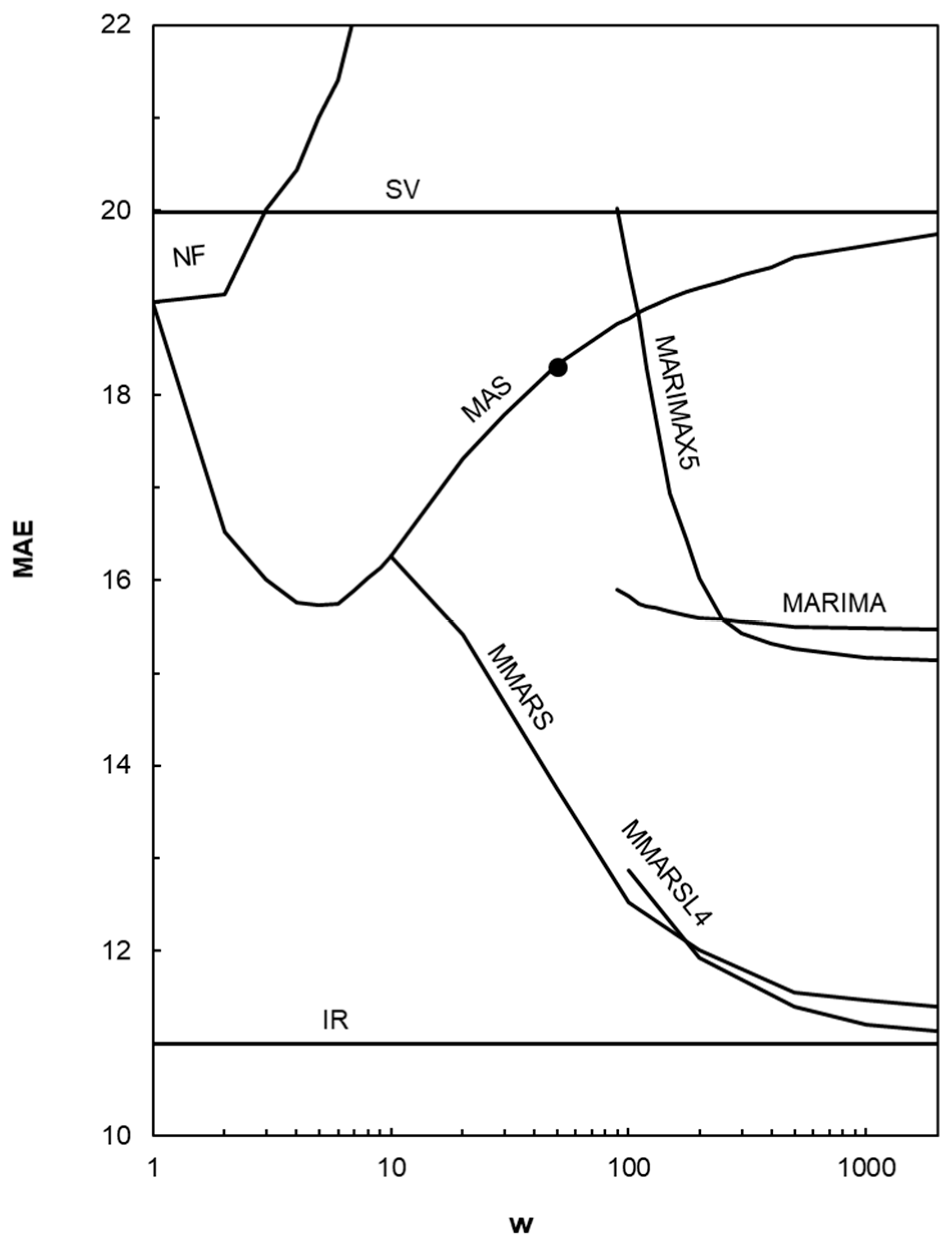
| Method | MAE (°C) | St. dev. of Error (°C) | Carbon Footprint Reduction (kgCO2/t) | Running Time (s) | Applicability (%) | Order i |
|---|---|---|---|---|---|---|
| SV | 20.0 | 25.2 | −0.9 | <0.1 | 100 | 8 |
| NF | 19.3 | 24.3 | −0.5 | <0.1 | 99 | 7 |
| Initial | 18.3 | 22.9 | 0.0 | <0.1 | 99 | - |
| MAS | 15.9 | 20.2 | 1.2 | <0.1 | 99 | 6 |
| MARIMA | 15.4 | 19.3 | 1.5 | 0.7 | 95 | 5 |
| MARIMAX5 | 15.1 | 19.0 | 1.6 | 1.4 | 93 | 4 |
| MMARS | 11.4 | 14.5 | 3.5 | 2.9 | 97 | 3 |
| MMARSL4 | 11.1 | 14.1 | 3.6 | 3.5 | 87 | 2 |
| IR | 11 | 12.9 | 3.7 | <0.1 | 40 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, J.; Fernández, F.J. Application of Combined Developments in Processes and Models to the Determination of Hot Metal Temperature in BOF Steelmaking. Processes 2020, 8, 732. https://doi.org/10.3390/pr8060732
Díaz J, Fernández FJ. Application of Combined Developments in Processes and Models to the Determination of Hot Metal Temperature in BOF Steelmaking. Processes. 2020; 8(6):732. https://doi.org/10.3390/pr8060732
Chicago/Turabian StyleDíaz, José, and Francisco Javier Fernández. 2020. "Application of Combined Developments in Processes and Models to the Determination of Hot Metal Temperature in BOF Steelmaking" Processes 8, no. 6: 732. https://doi.org/10.3390/pr8060732
APA StyleDíaz, J., & Fernández, F. J. (2020). Application of Combined Developments in Processes and Models to the Determination of Hot Metal Temperature in BOF Steelmaking. Processes, 8(6), 732. https://doi.org/10.3390/pr8060732






