Dynamic Characteristics and Wall Effects of Bubble Bursting in Gas-Liquid-Solid Three-Phase Particle Flow
Abstract
1. Introduction
2. Developing the Numerical Model
2.1. Flow Field Governing Equations
2.2. Particle Motion Equations
2.3. Bubble Radial Differential Equations
2.4. Numerical Simulation Algorithm
2.5. Numerical Model and Boundary Condition
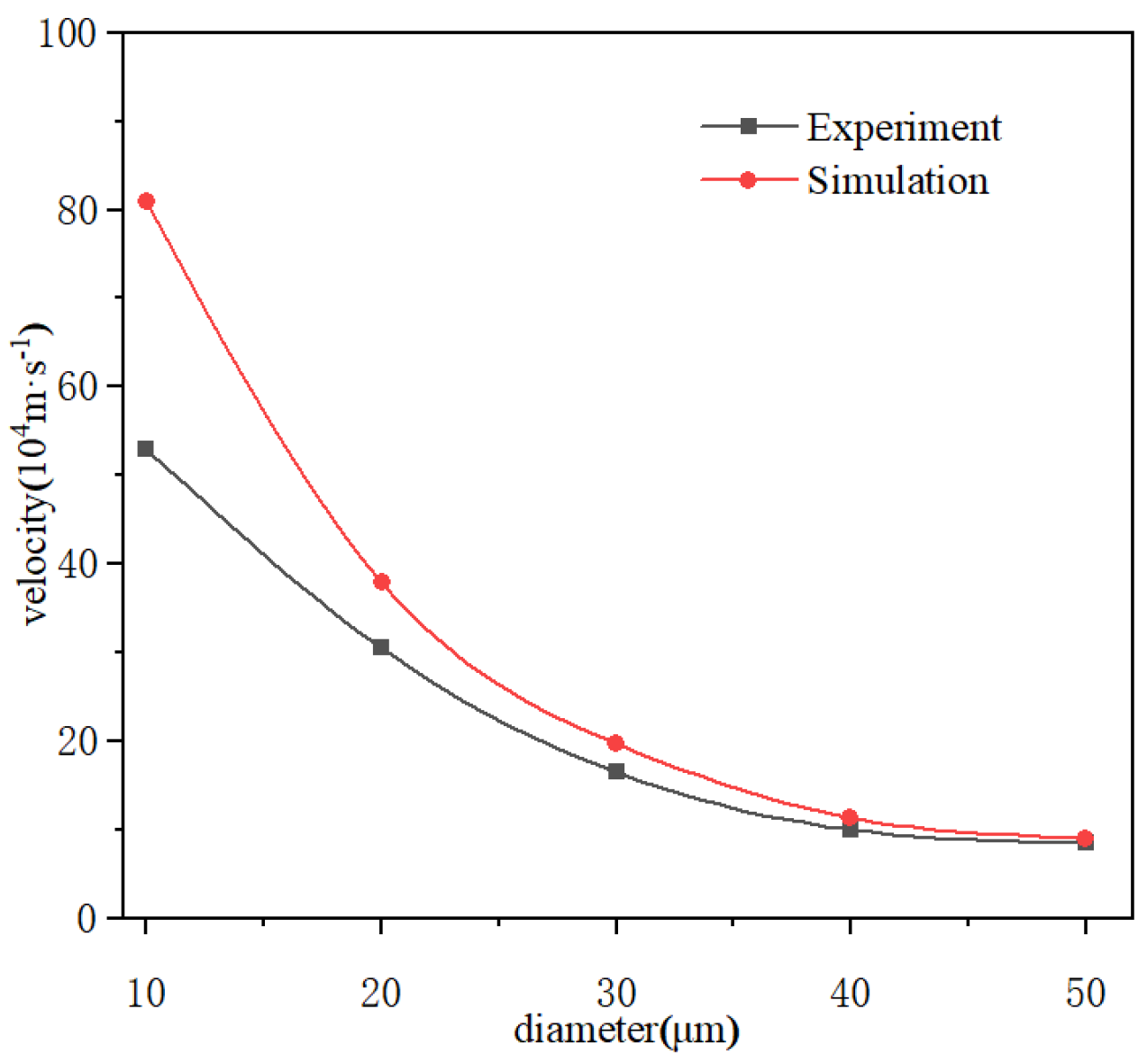
2.6. Model Validation
3. Numerical Results and Discussions
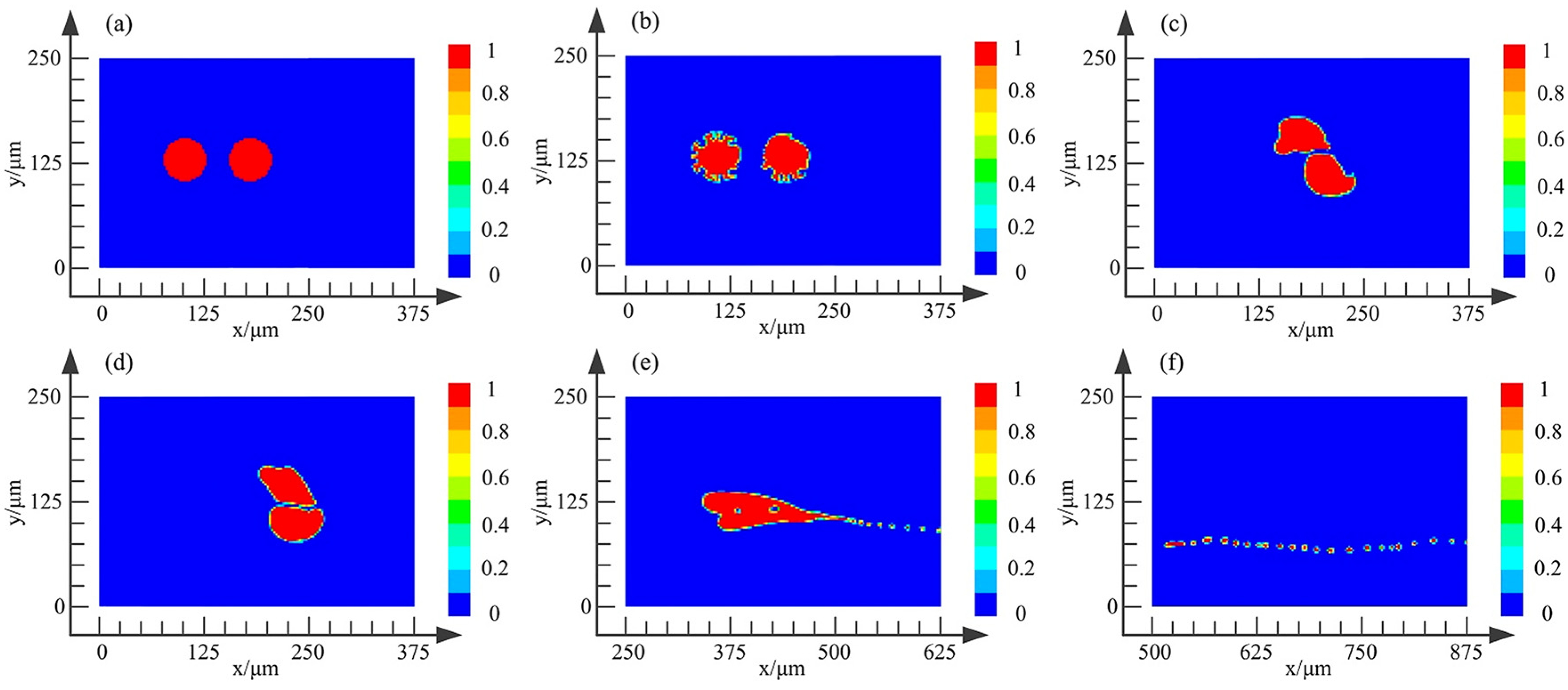
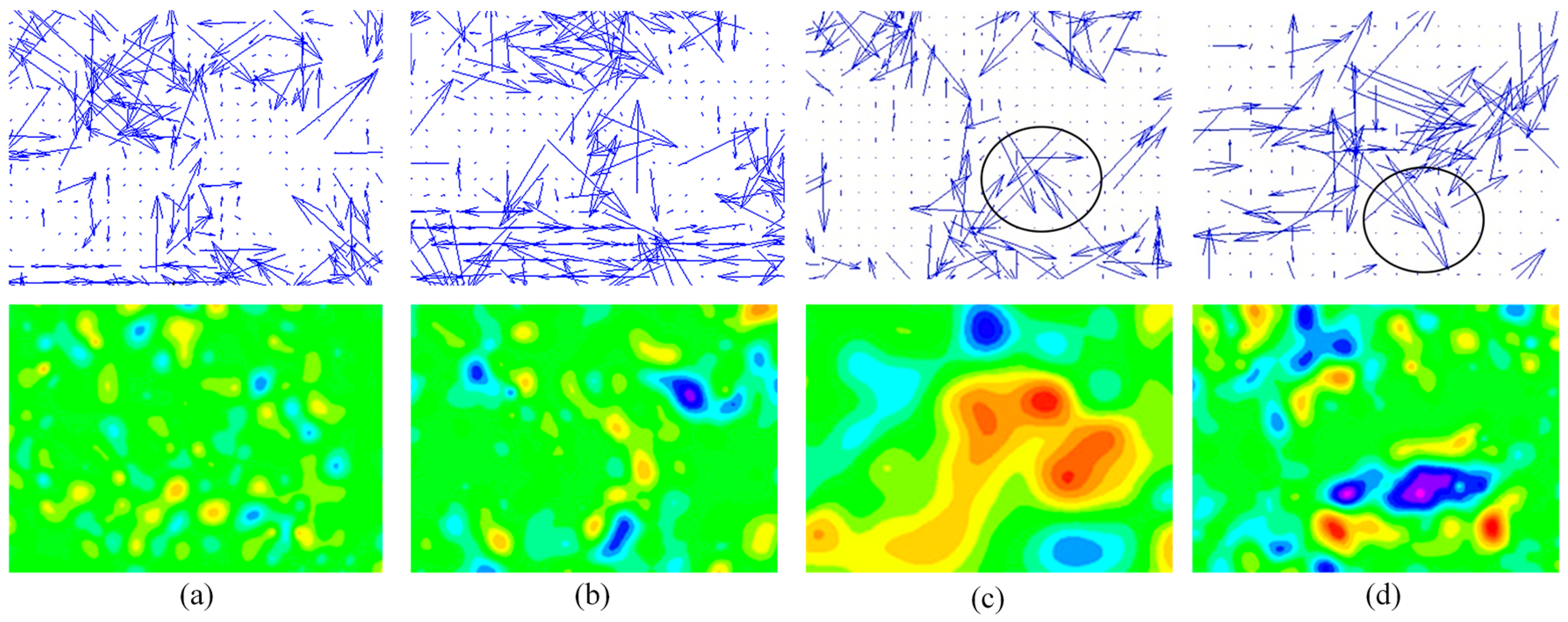
3.1. Bubble Burst Near the Wall
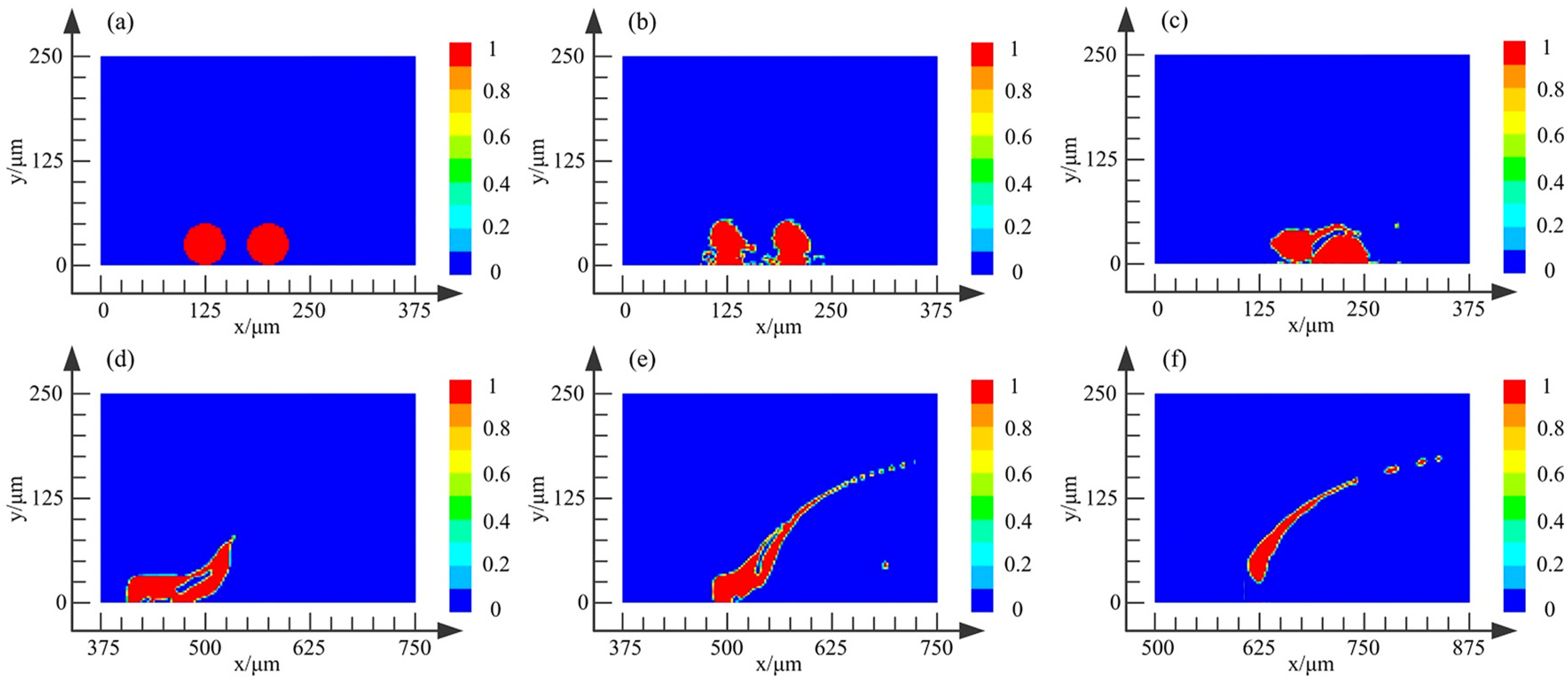
3.2. Bubble Burst on the Wall
4. Observation Experiment and Results Discussion
4.1. Experimental Setup
4.2. Developing the Numerical Model
5. Conclusions
- Since the pressure difference between the inside and outside of the bubble tail is the largest, the bubble mainly begins to burst from the bubble tail.
- The dynamic characteristics of the bubble bursting on the wall are mainly consistent with that near the wall. But due to the action range of the high-speed jet being less than 10% of the bubble diameter, as the distance between the bubble and wall increases, the jet intensity decreases exponentially. In addition, compared with the bubble burst near the wall, the time of bubble burst on the wall is shorter, making the wall impact effect more obvious. Since the sphere of influence of micro-jet is very small, the bubble bursts as much as possible on the wall.
- Through the analysis of bubble bursting on the wall with different flow rates, it is found that the bubble burst is the fastest and most sufficient when the flow rate is 50 m/s, and the impact effect on the wall is the most obvious. When the flow rate is 60 m/s, due to the fluid rate being too fast, the micro-nano bubbles on the wall will escape from the wall and move along the velocity direction without bursting.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Velocity (m s−1) | |
| Fluid pressure (Pa) | |
| Gravitational acceleration (m s−2) | |
| Time (s) | |
| Total volume of the phase | |
| Total volume of a grid cell | |
| Normal direction of real line | |
| Positive direction of x-axis | |
| Positive direction of y-axis | |
| Intercept | |
| Area of fluid region | |
| Area of shaded region | |
| Temperature (K) | |
| The number of Prandtl | |
| The highest pressure (Pa) | |
| Pressure of cavitating water jet (Pa) | |
| Initial pressure of bubble | |
| Gas content | |
| Bubble radius (m) | |
| Initial radius of bubble (m) | |
| Continuous jet impact pressure (Pa) | |
| Initial gas temperature (K) | |
| Turbulent kinetic energy (J) | |
| Fluid velocity (m s−1) | |
| Turbulent kinetic energy caused by average velocity gradient (J) | |
| Modulus of the time-averaged strain tensor | |
| Coefficient | |
| Coefficient | |
| Time-averaged strain tensor | |
| Net force on the particle (N) | |
| Particle mass (kg) | |
| Particle velocity (m s−1) | |
| Gravity (N) | |
| Buoyancy force (N) | |
| Stokesley of flow field (N) | |
| Drag force on particle (N) | |
| Pressure gradient force on particle (N) | |
| Saffman lift force on a particle (N) | |
| Particle diameter (m) | |
| Drag force coefficient | |
| Relative velocity between bubble and particle (m s−1) | |
| Fluid velocity (m s−1) | |
| Particle velocity (m s−1) | |
| Bubble radius (m) | |
| The first order derivatives of versus time | |
| The second order derivatives of versus time | |
| Saturated vapor pressure (Pa) | |
| Hydrostatic pressure (Pa) | |
| Bubble velocity (m s−1) | |
| Greek symbols | |
| ρ | Averaged fluid density (kg m−3) |
| Hydrodynamic viscosity (N s m−2) | |
| Proportion of the space occupied by the fluid in the grid | |
| Volume fraction of water-phase | |
| Volume fraction of gas-phase | |
| Fluid density (kg m−3) | |
| Gas density (kg m−3) | |
| Adiabatic index | |
| Dissipation rate | |
| The Prandtl number of | |
| The Prandtl number of | |
| Eddy viscosity | |
| Turbulent viscosity | |
| Intermediate variable | |
| Particle density (kg m−3) | |
| Empirical coefficient | |
| Surface tension (N) | |
References
- Qian, W.W.; Li, W.F.; Shi, Z.H. Characteristics of surface waves on the granular sheet of dense granular jet impingement. Acta Phys. Sin. 2016, 65, 225–231. [Google Scholar] [CrossRef]
- Ramirez-Argaez, M.A.; Dutta, A.; Amaro-Villeda, A.; Gonzalez-Rivera, C.; Conejo, A.N. A novel multiphase methodology simulating three phase flows in a steel ladle. Processes 2019, 7, 175. [Google Scholar] [CrossRef]
- Zeng, X.; Ji, S.M.; Tan, D.P.; Jin, M.S.; Wen, D.H.; Zhang, L. Softness consolidation abrasives material removal characteristic oriented to laser hardening surface. Int. J. Adv. Manuf. Technol. 2013, 69, 2323–2332. [Google Scholar] [CrossRef]
- Nakhaei, M.; Lu, B.N.; Tian, Y.J.; Wang, W.; Dam-Johansen, K.; Wu, H. CFD modeling of gas-solid cyclone separators at ambient and elevated temperatures. Processes 2020, 8, 228. [Google Scholar] [CrossRef]
- Li, C.; Ji, S.M.; Tan, D.P. Softness abrasive flow method oriented to tiny scale mold structural surface. Int. J. Adv. Manuf. Technol. 2012, 61, 975–987. [Google Scholar] [CrossRef]
- Tan, D.P.; Ji, S.M.; Fu, Y.Z. An improved soft abrasive flow finishing method based on fluid collision theory. Int. J. Adv. Manuf. Technol. 2016, 85, 1261–1274. [Google Scholar] [CrossRef]
- Mottyll, S.; Skoda, R. Numerical 3D flow simulation of ultrasonic horns with attached cavitation structures and assessment of flow aggressiveness and cavitation erosion sensitive wall zones. Ultrason. Sonochem. 2016, 31, 570–589. [Google Scholar] [CrossRef]
- Bremond, N.; Arora, M.; Dammer, S.; Lohse, D. Interaction of cavitation bubbles on a wall. Phys. Fluids 2006, 18, 1–10. [Google Scholar] [CrossRef]
- Chahine, G.L.; Kapahi, A.; Choi, J.K.; Hsiao, C.T. Modeling of surface cleaning by cavitation bubble dynamics and collapse. Ultrason. Sonochem. 2016, 29, 528–549. [Google Scholar] [CrossRef]
- Alex, N.; Darsh, W. Air bubble bursting phenomenon at the air-water interface monitored by the piezoelectric-acoustic method. Adv. Colloid Interface Sci. 2019, 272, 101998. [Google Scholar] [CrossRef]
- Tan, D.P.; Chen, S.T.; Bao, G.J.; Zhang, L.B. An embedded lightweight GUI component library and the ergonomics optimization method for industry process monitoring. Front. Inform. Technol. Elect. Eng. 2018, 19, 604–625. [Google Scholar] [CrossRef]
- Li, Y.B.; Tan, D.P.; Wen, D.H.; Ji, S.M.; Cai, D.H. Parameters optimization of a novel 5-DOF gasbag polishing machine tool. Chin. J. Mech. Eng. 2013, 26, 680–688. [Google Scholar] [CrossRef]
- Brujan, E.A.; Ikeda, T.; Matsumoto, Y. Shock wave emission from a cloud of bubbles. Soft Matter. 2012, 8, 5777–5783. [Google Scholar] [CrossRef]
- Vignoli, L.L.; de Barros, A.L.F. Modeling the dynamics of single-bubble sonoluminescence. Eur. J. Phys. 2013, 34, 679–688. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.S. Numerical simulation of micro bubble collapse near solid wall in fluent environment. Tribology 2008, 28, 311–315. [Google Scholar]
- Aniszewski, W.; Menard, T.; Marek, M. Volume of Fluid (VOF) type advection methods in two-phase flow: A comparative study. Comput. Fluids 2014, 97, 52–73. [Google Scholar] [CrossRef]
- Ge, J.Q.; Tan, D.P.; Ji, S.M. A gas-liquid-solid three-phase abrasive flow processing method based on bubble collapsing. Int. J. Adv. Manuf. Technol. 2018, 95, 1069–1085. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.W.; Zhang, P.; Li, J.L.; Chen, G.H. Interaction between gas-liquid mass transfer and bubble behaviours. R. Soc. Open Sci. 2019, 6, 190136. [Google Scholar] [CrossRef]
- Li, L.; Qi, H.; Yin, Z.C. Investigation on the multiphase sink vortex Ekman pumping effects by a CFD-DEM coupling method. Powder Technol. 2020, 360, 462–480. [Google Scholar] [CrossRef]
- Li, L.; Lu, J.; Fang, H.; Yin, Z.; Wang, T.; Wang, R.; Fan, X.; Zhao, L.; Tan, D.; Wan, Y. Lattice Boltzmann method for fluid-thermal systems: Status, hotspots, trends and outlook. IEEE Access 2020, 8, 27649–27675. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, L.; Zhu, Y.L.; Zheng, S.; Yin, Z.C.; Li, D.F. Critical penetration condition and Ekman suction-extraction mechanism of a sink vortex. J. Zhejiang Univ. Sci. A 2019, 20, 61–72. [Google Scholar] [CrossRef]
- Lindken, R.; Merzkirch, W. A novel PIV technique for measurements in multiphase flows and its application to two-phase bubbly flows. Exp. Fluids 2002, 33, 814–825. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, L.; Zhu, Y.L.; Zheng, S.; Ruan, H.J.; Jiang, X.Y. An embedded cloud database service method for distributed industry monitoring. IEEE Trans. Ind. Inform. 2018, 14, 2881–2893. [Google Scholar] [CrossRef]
- Zhang, L.B.; Lv, H.P.; Tan, D.P.; Xu, F.; Chen, J.L.; Bao, G.J.; Cai, S.B. An adaptive quantum genetic algorithm for task sequence planning of complex assembly systems. Electron. Lett. 2018, 54, 870–871. [Google Scholar] [CrossRef]
- Goharzadeh, A.; Molki, A. Measurement of fluid velocity development behind a circular cylinder using particle image velocimetry (PIV). Eur. J. Phys. 2015, 36, 015001. [Google Scholar] [CrossRef]
- Jiang, Q.S.; Tan, D.P.; Li, Y.B.; Ji, S.M.; Cai, C.P.; Zheng, Q.M. Object detection and classification of metal polishing shaft surface defects based on convolutional neural network deep learning. Appl. Sci. 2020, 10, 87. [Google Scholar] [CrossRef]
- Qiu, L.; Zeng, X.; Ji, S.M.; Tan, D.P.; Ge, M.; Qiu, W.B. Research on abrasive belt based machining technology for milling shaped aero-engine blades. Teh. Vjesn. 2019, 26, 1353–1362. [Google Scholar] [CrossRef]
- Wu, R.Z.; Shu, D.; Sun, B.D.; Wang, J.; Lu, Y.L. Observation and theoretic analysis of gas-bubble formation and growth in water-model. Trans. Nonferr. Met. Soc. 2005, 15, 1130–1137. [Google Scholar]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas-liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Tan, D.P.; Zhang, L.B. A WP-based nonlinear vibration sensing method for invisible liquid steel slag detection. Sens. Actuat. B-Chem. 2014, 202, 1257–1269. [Google Scholar] [CrossRef]
- Lopez, J.; Hernandez, J.; Gomez, P.; Faura, F. An improved PLIC-VOF method for tracking thin fluid structures in incompressible two-phase flows. J. Comput. Phys. 2005, 208, 51–74. [Google Scholar] [CrossRef]
- Qi, H.; Qin, S.K.; Cheng, Z.C.; Zou, Y.L.; Wen, D.H.; Cai, D.H. Performance evaluation on the ultrasonic vibration-assisted abrasive finishing of the cutting edge using Discrete Element Method. Powder Technol. in Press.
- Cifani, P.; Michalek, W.R.; Priems, G.J.M.; Kuerten, J.G.M.; van der Geld, C.W.M.; Geurts, B.J. A comparison between the surface compression method and an interface reconstruction method for the VOF approach. Comput. Fluids 2016, 136, 421–435. [Google Scholar] [CrossRef]
- Dai, D.Z.; Tong, A.Y. An analytical interface reconstruction algorithm in the PLIC-VOF method for 2D polygonal unstructured meshes. Int. J. Numer. Methods Fluids 2018, 88, 265–276. [Google Scholar] [CrossRef]
- Hoque, M.M.; Mitra, S.; Evans, G.M.; Pareek, V.; Joshi, J.B. Effect of bubble on the pressure spectra of oscillating grid turbulent flow at low Taylor-Reynolds number. Chem. Eng. Sci. 2018, 190, 28–39. [Google Scholar] [CrossRef]
- Tan, D.P.; Ni, Y.S.; Zhang, L.B. Two-phase sink vortex suction mechanism and penetration dynamic characteristics in ladle teeming process. J. Iron Steel Res. Int. 2017, 24, 669–677. [Google Scholar] [CrossRef]
- Ye, L.Z.; Zhu, X.J. Analysis of the effect of impact of near-wall acoustic bubble collapse micro-jet on Al 1060. Ultrason Sonochem. 2016, 36, 507–516. [Google Scholar] [CrossRef]
- Li, J.; Ji, S.M.; Tan, D.P. Improved soft abrasive flow finishing method based on turbulent kinetic energy enhancing. Chin. J. Mech. Eng. 2017, 30, 301–309. [Google Scholar] [CrossRef]
- Li, X.N.; Liu, M.Y.; Ma, Y.L.; Dong, T.T.; Yao, D. Experiments and meso-scale modeling of phase holdups and bubble behavior in gas-liquid-solid mini-fluidized beds. Chem. Eng. Sci. 2018, 192, 725–738. [Google Scholar] [CrossRef]
- Chen, J.L.; Xu, F.; Tan, D.P.; Shen, Z.; Zhang, L.B.; Ai, Q.L. A control method for agricultural greenhouses heating based on computational fluid dynamics and energy prediction model. Appl. Energy 2015, 141, 106–118. [Google Scholar] [CrossRef]
- Tan, D.P.; Yang, T.; Zhao, J.; Ji, S.M. Free sink vortex Ekman suction-extraction evolution mechanism. ACTA Phys. Sin. 2016, 65, 054701. [Google Scholar] [CrossRef]
- Gruber, M.C.; Radl, S.; Khinast, J.G. Effect of bubble-particle interaction models on flow predictions in three-phase bubble columns. Chem. Eng. Sci. 2016, 146, 226–243. [Google Scholar] [CrossRef]
- Ji, S.M.; Xiao, F.Q.; Tan, D.P. Analytical method for softness abrasive flow field based on discrete phase model. Sci. China-Technol. Sci. 2010, 53, 2867–2877. [Google Scholar] [CrossRef]
- Man, V.H.; Li, M.S.; Derreumaux, P.; Nguyen, P.H. Rayleigh-Plesset equation of the bubble stable cavitation in water: A nonequilibrium all-atom molecular dynamics simulation study. J. Chem. Phys. 2018, 148, 194505. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, S.; Tan, D.; Cao, H. Cavitation based soft abrasive flow processing method. Int. J. Adv. Manuf. Technol. 2019. in Press. [Google Scholar] [CrossRef]
- Shi, H.T.; Bai, X.T. Model-based uneven loading condition monitoring of full ceramic ball bearings in starved lubrication. Mech. Syst. Signal Process. 2020, 139, 106583. [Google Scholar] [CrossRef]
- Lu, J.; Huang, J.T.; Xu, X.Q. Bubble collapse in solid-liquid two-phase fluid. Acta Mech. Sin. 1995, 8, 4–22. [Google Scholar]
- Yamada, K.; Emori, H.; Nakazawa, K. Time-evolution of bubble formation in a viscous liquid. Earth Planets Space 2008, 60, 661–679. [Google Scholar] [CrossRef]
- Hu, X.X.; Xu, F.; Tan, D.P. Synchronous sampling-based direct current estimation method for self-sensing active magnetic bearings. Sensors 2020, 20, 3497. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Wen, D.H.; Lu, J.F.; Yang, J.; Hong, T.; Qi, H. Surface quality improvement by using a novel driving system design in single-side planetary abrasive lapping. J. Manuf. Process. in Press.
- Tan, D.P.; Li, L.; Yin, Z.C.; Li, D.F.; Zhu, Y.L.; Zheng, S. Ekman boundary layer mass transfer mechanism of free sink vortex. Int. J. Heat Mass Transfer. 2019, 150, 119250. [Google Scholar] [CrossRef]
- Shi, H.T.; Guo, L.; Tan, S.; Bai, X.T. Rolling bearing initial fault detection using long short-term memory recurrent network. IEEE Access 2019, 7, 171559–171569. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, Z.M.; Tan, D.P.; Huang, Y. An Improved abrasive flow processing method for complex geometric surfaces of titanium alloy artificial joints. Appl. Sci. 2018, 28, 1037. [Google Scholar] [CrossRef]
- Hokmabad, B.V.; Ghaemi, S. Effect of flow and particle-plastron collision on the longevity of superhydrophobicity. Sci. Rep. 2017, 7, 41448. [Google Scholar] [CrossRef] [PubMed]
- Paulsen, O.; Rorvik, S.; Muggerud, A.M.F.; Juel, M. Bubble distribution in fused quartz crucibles studied by micro X-Ray computational tomography. Comparing 2D and 3D analysis. J. Cryst. Growth 2019, 520, 96–104. [Google Scholar] [CrossRef]
- Tan, D.P.; Li, P.Y.; Ji, Y.X.; Wen, D.H.; Li, C. SA-ANN-based slag carry-over detection method and the embedded WME platform. IEEE Trans. Ind. Electron. 2013, 60, 4702–4713. [Google Scholar] [CrossRef]
- Ji, S.M.; Ge, J.Q.; Tan, D.P. Wall contact effects of particle-wall collision process in two-phase particle fluid. J. Zhejiang Univ.-Sci. A 2017, 18, 958–973. [Google Scholar] [CrossRef]
- Tan, K.L.; Yeo, S.H. Velocity estimation of micro-particles driven by cavitation bubble collapses through controlled erosion experiments. Int. J. Multiph. Flow 2020, 127, UNSP 103271. [Google Scholar] [CrossRef]
- Wang, J.; Tan, D.; Cao, B.; Fan, J.; Deep, S. An independent path-based process recommendation algorithm for improving biomedical process modeling. Electron. Lett. 2020, 56, 531–533. [Google Scholar] [CrossRef]
- He, J.; Chu, J.; Wu, S.F.; Peng, J. Mitigation of soil liquefaction using microbially induced desaturation. J. Zhejiang Univ.-Sci. A 2016, 17, 577–588. [Google Scholar] [CrossRef]
- Lv, L.; Zhang, Y.X.; Zhang, Y.N. Experimental investigations of the particle motions induced by a laser-generated cavitation bubble. Ultrason. Sonochem. 2019, 56, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.R.; Zhu, C.Y.; Fu, T.T.; Ma, Y.G. Systematic study on the coalescence and breakup behaviors of multiple parallel bubbles rising in power-law fluid. Ind. Eng. Chem. Res. 2014, 53, 4850–4860. [Google Scholar] [CrossRef]
- Wang, J.X.; Cao, B.; Zheng, X.; Tan, D.P.; Fan, J. Detecting difference between process models using edge network. IEEE Access 2019, 360, 142916–142925. [Google Scholar] [CrossRef]
- Bourne, N.K.; Field, J.E. Shock-induced collapse and luminescence by cavities. Philos. Trans. R. Soc. A 1999, 3357, 295–311. [Google Scholar] [CrossRef][Green Version]
- Hattori, S.; Hirose, T.; Sugiyama, K. Prediction method for cavitation erosion based on measurement of bubble collapse impact loads. Wear 2010, 269, 507–514. [Google Scholar] [CrossRef]
- Ni, B.Y.; Li, S. Jet splitting after bubble breakup at the free surface. Acta Phys. Sin. 2013, 62, 124704. [Google Scholar] [CrossRef]
- Wu, M.G.; Lu, C.D.; Tan, D.P.; Hong, T.; Chen, G.H.; Wen, D.H. Effects of metal buffer layer for amorphous carbon film of 304 stainless steel bipolar plate. Thin Solid Films 2016, 616, 507–514. [Google Scholar] [CrossRef]
- Tan, D.P.; Zhang, L.B.; Ai, Q.L. An embedded self-adapting network service framework for networked manufacturing system. J. Intell. Manuf. 2019, 30, 539–556. [Google Scholar] [CrossRef]
- Jin, T.; Xu, B.; Tang, K.; Hong, J.P. Bubble counter based on photoelectric technique for leakage detection of cryogenic valves. J. Zhejiang Univ.-Sci. A 2008, 9, 88–92. [Google Scholar] [CrossRef]
- Oguchi, K.; Enoki, M.; Hirata, N. Numerical Simulation for Cavitation Bubble Near Free Surface and Rigid Boundary. Mater. Trans. 2015, 56, 534–538. [Google Scholar] [CrossRef]
- Chakraborty, I.; Biswas, G.; Ghoshdastidar, P.S. A coupled level-set and volume-of-fluid method for the buoyant rise of gas bubbles in liquids. Int. J. Heat Mass Transf. 2013, 58, 240–259. [Google Scholar] [CrossRef]
- Cerqueira, R.F.L.; Paladino, E.E.; Ynumaru, B.K.; Maliska, C.R. Image processing techniques for the measurement of two-phase bubbly pipe flows using particle image and tracking velocimetry (PIV/PTV). Chem. Eng. Sci. 2018, 189, 1–23. [Google Scholar] [CrossRef]
- Wang, Y.X.; Ni, P.C.; Wen, D.H.; Tan, D.P. Dynamic performance optimization of circular sawing machine gearbox. Appl. Sci. 2019, 9, 4458. [Google Scholar] [CrossRef]
- Ji, S.M.; Ge, J.Q.; Tan, D.P.; Zeng, X. Three-phase abrasive flow polishing and distribution characteristics of bubble collapse. Opt. Precis. Sci. 2018, 26, 388–398. [Google Scholar] [CrossRef]
- Zeng, X.; Ji, S.M.; Jin, M.S.; Tan, D.P.; Ge, J.Q. Research on dynamic characteristic of softness consolidation abrasives in machining process. Int. J. Adv. Manuf. Technol. 2016, 82, 1115–1125. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.S.; Tan, D.P.; Yuan, Z.M. Gas compensation-based abrasive flow processing method for complex titanium alloy surfaces. Int. J. Adv. Manuf. Technol. 2017, 92, 3385–3397. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Effect of Froude number on bubble clustering in a hydraulic jump. J. Hydraul. Res. 2010, 48, 504–508. [Google Scholar] [CrossRef]
- Li, H.N.; Wang, J.P.; Wu, C.J.; Zhao, Y.J. Damage behaviors of unidirectional CFRP in orthogonal cutting: A comparison between single- and multiple-pass strategies. Compos. Part B-Eng. 2020, 185, 107774. [Google Scholar] [CrossRef]
- Bahmanpouri, F. Experimental Study of Air Entrainment in Hydraulic Jump on Pebbled Rough Bed. Ph.D. Thesis, Department of Civil, Architectural and Environmental Engineering, The University of Napoli Federico II, Napoli, Italy, 2019. [Google Scholar]

















| Name | Symbol | Equation |
|---|---|---|
| The highest pressure | ||
| Pressure of cavitating water jet | ||
| Gas temperature |
| Name | Symbol | Equation |
|---|---|---|
| Turbulent kinetic energy | ||
| Coefficient | ||
| Intermediate variable | ||
| Time-averaged strain tensor |
| Forces and Torques | Symbol | Equation |
|---|---|---|
| Gravity | ||
| Buoyancy | ||
| Stokesley | ||
| Drag force | ||
| Pressure gradient force | ||
| Saffman force |
| Item | Attribute |
|---|---|
| Inlet | Velocity inlet |
| Outlet | Free inlet |
| Zone | Air, water, silicon carbide |
| Wall | No-slip wall |
| Inlet diameter (mm) | 2.3 |
| Outlet diameter (mm) | 1 |
| Inlet velocity (m·s−1) | 30–60 |
| Reference pressure (Pa) | 101,000 |
| Parameter | Value |
|---|---|
| Water density (kg·m−3) | 998.2 |
| Water viscosity (Pa·s) | 0.001003 |
| Air density (kg·m−3) | 1.225 |
| Bubble diameter (μm) | 50 |
| Particle density (kg·m−3) | 3170 |
| Particle diameter (μm) | 10 |
| Particle mass fraction (%) | 5 |
| Hydraulic diameter (mm) | 2 |
| Surface tension coefficient | 0.023 |
| Gravity acceleration (kg·m−3) | −9.81 |
| Turbulent intensity (%) | 5 |
| Temperature (°C) | 40 |
| Reynolds number | 14,000 |
| Bubble Diameter (μm) | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| Simulation velocity (104 m·s−2) | 81 | 38.1 | 19.8 | 11.4 | 9 |
| Experiment velocity (104 m·s−2) | 53 | 30.5 | 16.5 | 10 | 8.5 |
| Error | 0.346 | 0.199 | 0.167 | 0.123 | 0.056 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, T.; Li, L.; Yin, Z.; Wang, R.; Fan, X.; Tan, D. Dynamic Characteristics and Wall Effects of Bubble Bursting in Gas-Liquid-Solid Three-Phase Particle Flow. Processes 2020, 8, 760. https://doi.org/10.3390/pr8070760
Lu J, Wang T, Li L, Yin Z, Wang R, Fan X, Tan D. Dynamic Characteristics and Wall Effects of Bubble Bursting in Gas-Liquid-Solid Three-Phase Particle Flow. Processes. 2020; 8(7):760. https://doi.org/10.3390/pr8070760
Chicago/Turabian StyleLu, Jianfei, Tong Wang, Lin Li, Zichao Yin, Ronghui Wang, Xinghua Fan, and Dapeng Tan. 2020. "Dynamic Characteristics and Wall Effects of Bubble Bursting in Gas-Liquid-Solid Three-Phase Particle Flow" Processes 8, no. 7: 760. https://doi.org/10.3390/pr8070760
APA StyleLu, J., Wang, T., Li, L., Yin, Z., Wang, R., Fan, X., & Tan, D. (2020). Dynamic Characteristics and Wall Effects of Bubble Bursting in Gas-Liquid-Solid Three-Phase Particle Flow. Processes, 8(7), 760. https://doi.org/10.3390/pr8070760






