Mathematical Model Describing HIV Infection with Time-Delayed CD4 T-Cell Activation
Abstract
:1. Introduction
2. Model without CD4 T-Cell Activation Time
2.1. Model Formulation
2.2. Stability Analysis
2.2.1. Virus-Free Equilibrium
2.2.2. Endemic Equilibrium
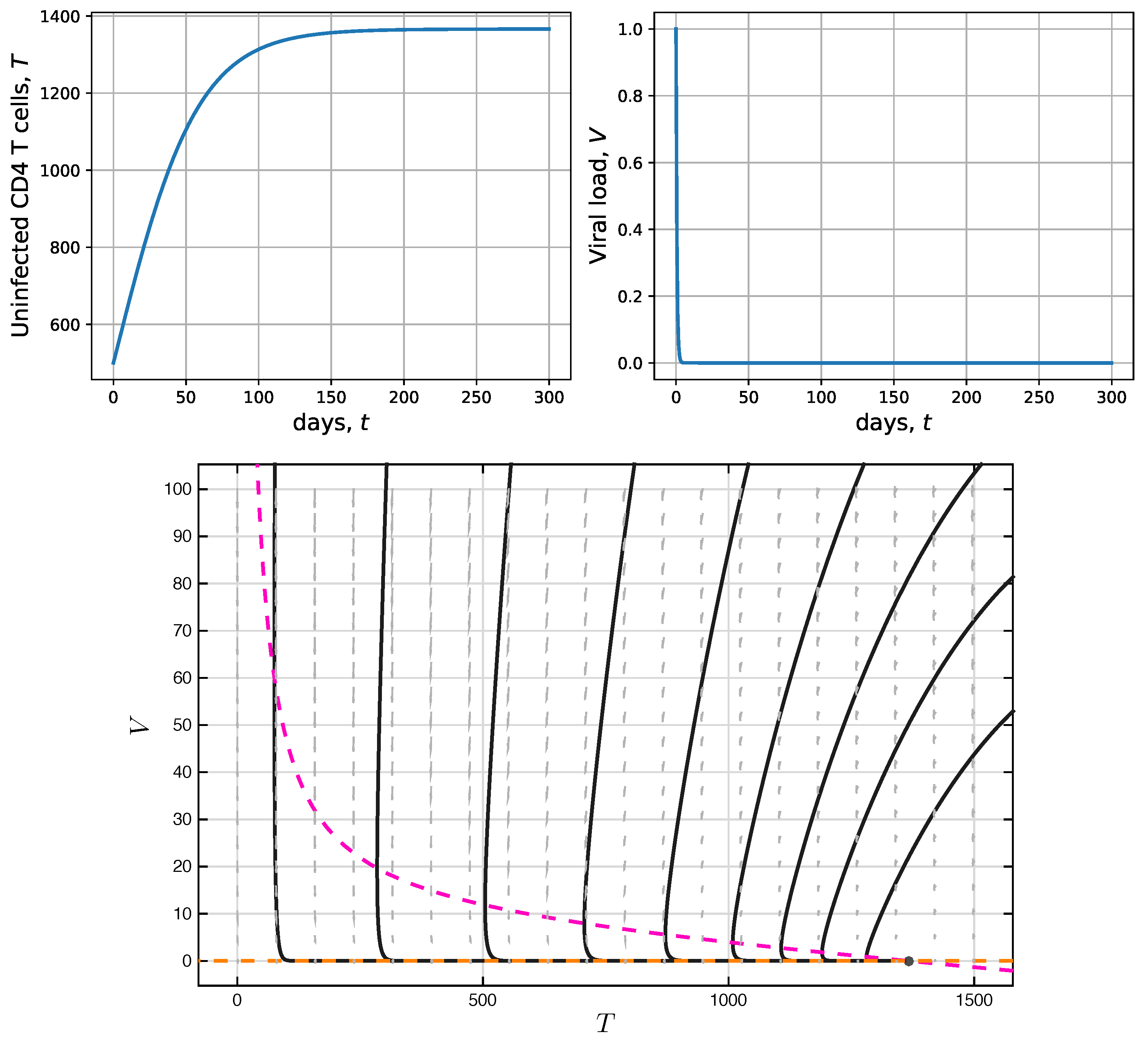
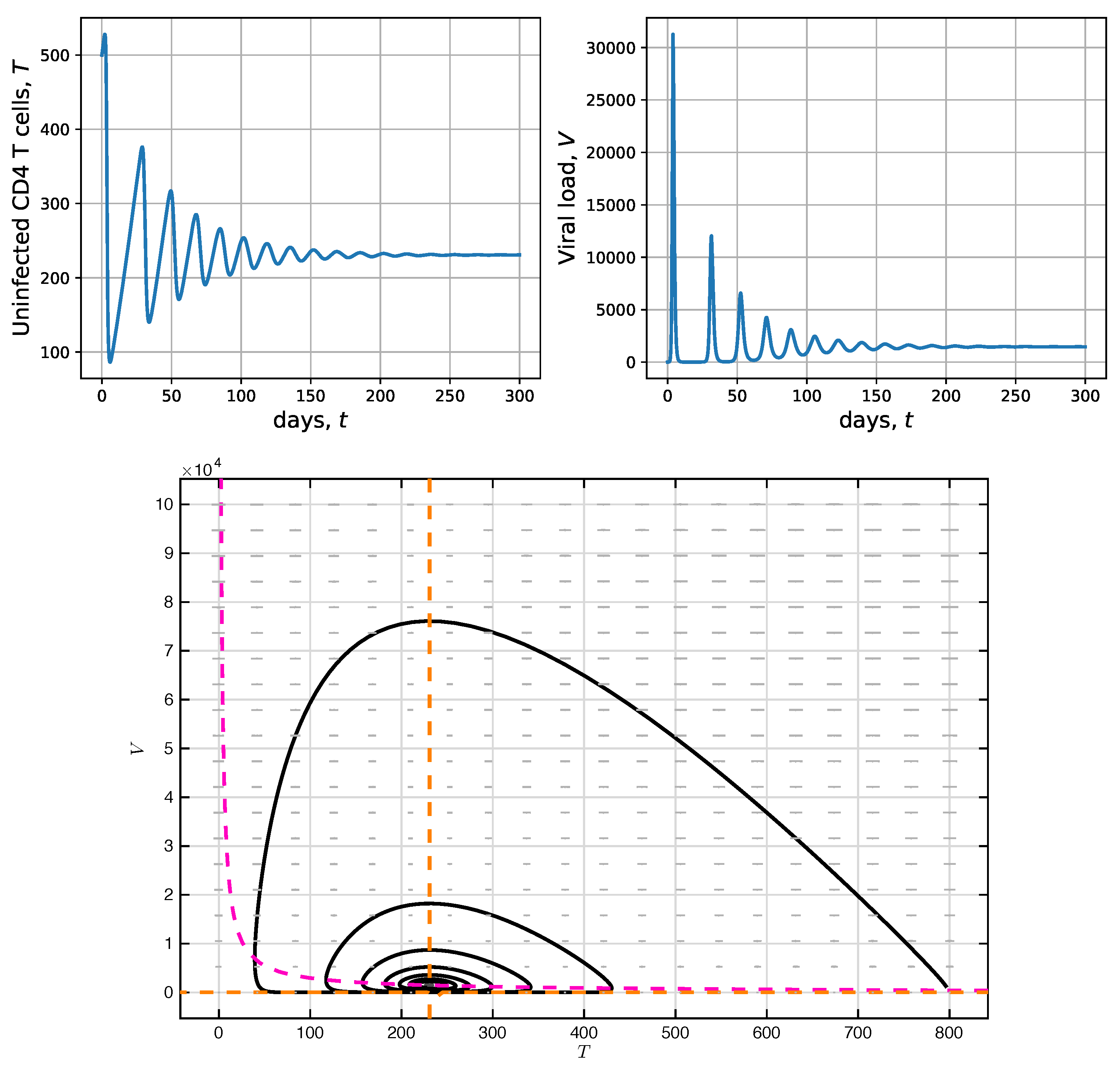
2.3. Simulation without CD4 T-Cell Activation Time
3. Model with CD4 T-Cell Activation Time
3.1. Model Formulation
3.2. Stability Analysis with CD4 T-Cell Activation Time
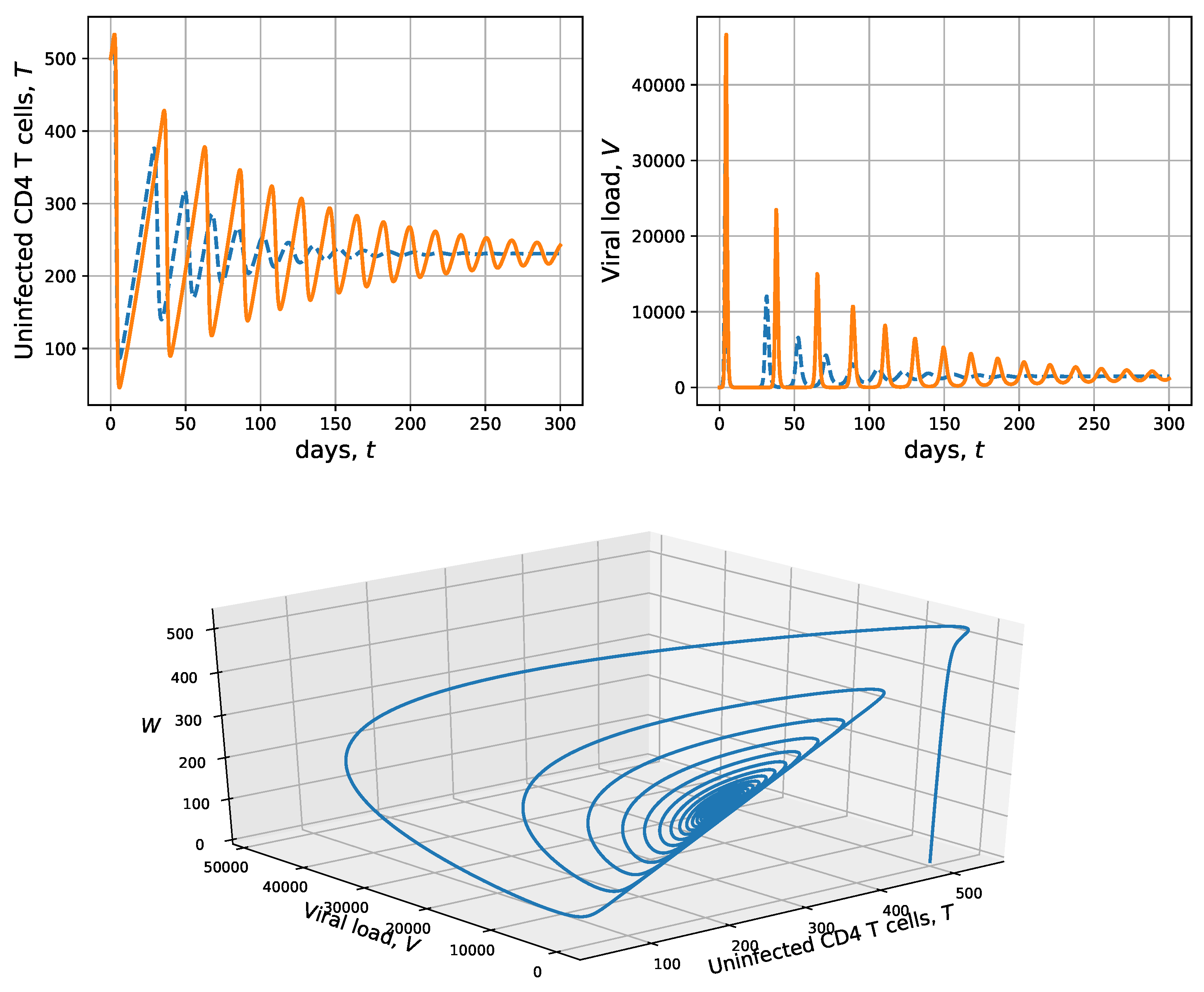
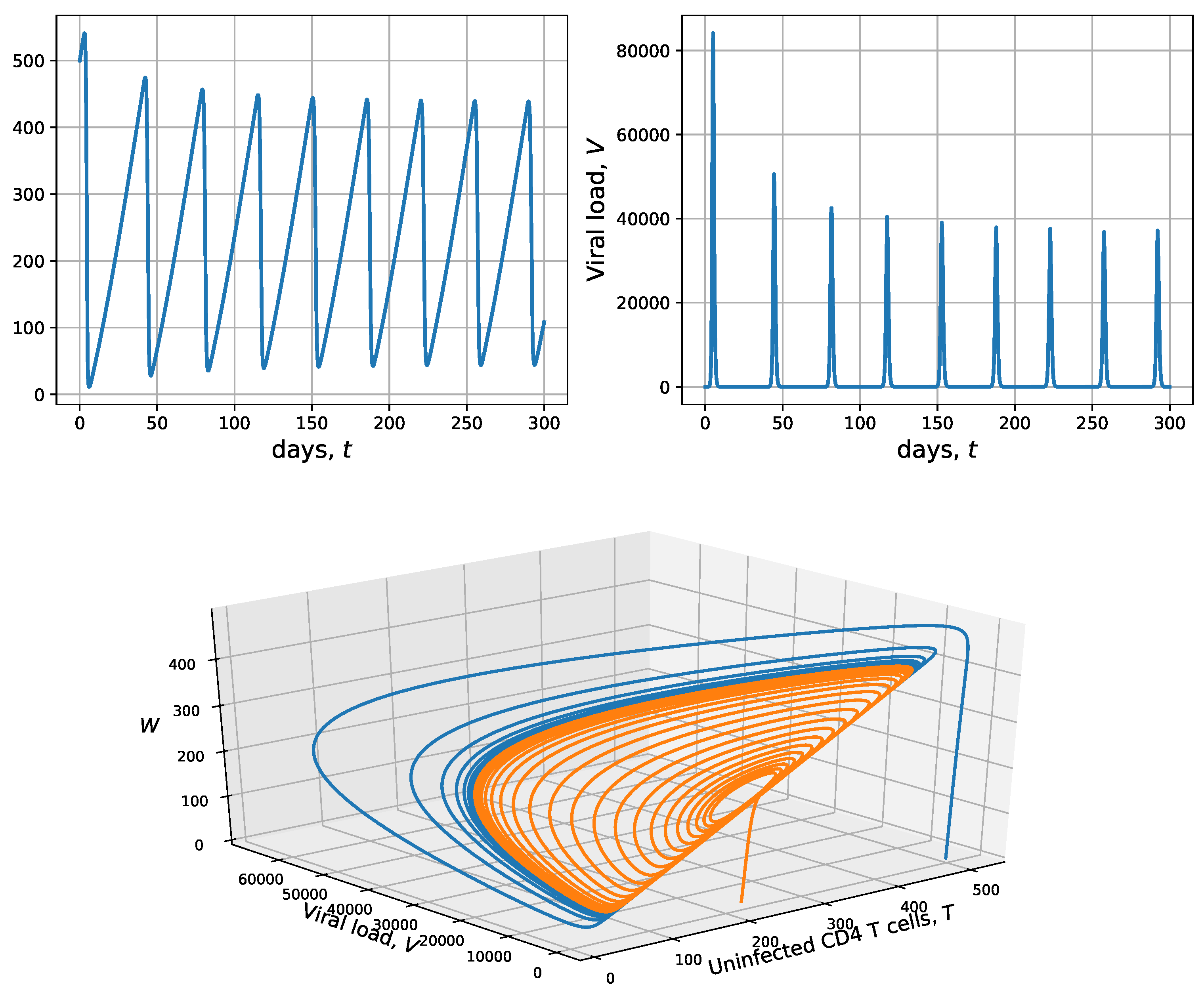
3.3. Simulation with CD4 T-Cell Activation Time
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HIV | Human immunodeficiency virus |
| AIDS | Acquired immune deficiency syndrome |
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
References
- Caballero-Hoyos, R.; Villaseñor-Sierra, A. Conocimientos sobre VIH/SIDA en adolescentes urbanos: Consenso cultural de dudas e incertidumbres. Salud PúBlica MéXico 2003, 45, s109–s114. [Google Scholar] [CrossRef] [Green Version]
- Pan American Health Organization. HIV and AIDS in the Americas: An Epidemic with Many Faces; PAHO: Washington, DC, USA, 2001.
- Ramírez, Z.; Díaz, F.J.; Jaimes, F.A.; Rugeles, M.T. Origen no infeccioso del sida: ¿mito o realidad? Infectio 2007, 11, 190–200. [Google Scholar]
- Castro-Espin, M. Reunión de alto nivel de ONU para poner fin al VIH-sida, junio, 2016. Rev. Sexol. Soc. 2016, 22, 113–115. [Google Scholar]
- Joint United Nations Programme on HIV/AIDS (UNAIDS). North American, Western and Central Europe: AIDS Epidemic Update Regional Summary; UNAIDS: Geneva, Switzerland, 2018; pp. 1–16. [Google Scholar]
- OPS. ¿Qué es el sida? In Ed. Organización Panamericana de la Salud; OPS: Washington, DC, USA, 2005. [Google Scholar]
- Alcamí, J. Avances en la inmunopatología de la infección por el VIH. Enfermedades Infecc. Microbiol. ClíNica 2004, 22, 486–496. [Google Scholar]
- Alshorman, A.; Wang, X.; Joseph Meyer, M.; Rong, L. Analysis of HIV models with two time delays. J. Biol. Dyn. 2017, 11 (Suppl. 1), 40–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bairagi, N.; Adak, D. Global analysis of HIV-1 dynamics with Hill type infection rate and intracellular delay. Appl. Math. Model. 2014, 38, 5047–5066. [Google Scholar] [CrossRef]
- Guo, T.; Qiu, Z.; Rong, L. Analysis of an HIV model with immune responses and cell-to-cell transmission. Bull. Malays. Math. Sci. Soc. 2020, 43, 581–607. [Google Scholar] [CrossRef]
- Joshi, H.R. Optimal control of an HIV immunology model. Optim. Control. Appl. Methods 2002, 23, 199–213. [Google Scholar] [CrossRef] [Green Version]
- Jiang, D.; Liu, Q.; Shi, N.; Hayat, T.; Alsaedi, A.; Xia, P. Dynamics of a stochastic HIV-1 infection model with logistic growth. Phys. Stat. Mech. Its Appl. 2017, 469, 706–717. [Google Scholar] [CrossRef]
- Kirschner, D.; Webb, G.F. A model for treatment strategy in the chemotherapy of AIDS. Bull. Math. Biol. 1996, 58, 367–390. [Google Scholar] [CrossRef]
- Kirschner, D.E.; Webb, G.F. Immunotherapy of HIV-1 infection. J. Biol. Syst. 1998, 6, 71–83. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.F. Dynamics of two time delays differential equation model to HIV latent infection. Phys. Stat. Mech. Its Appl. 2019, 514, 384–395. [Google Scholar] [CrossRef]
- Maziane, M.; Hattaf, K.; Yousfi, N. Spatiotemporal Dynamics of an HIV Infection Model with Delay in Immune Response Activation. Int. J. Differ. Equ. 2018. [Google Scholar] [CrossRef] [Green Version]
- Orellana, J.M. Optimal drug scheduling for HIV therapy efficiency improvement. Biomed. Signal Process. Control 2011, 6, 379–386. [Google Scholar] [CrossRef]
- Pawelek, K.A.; Liu, S.; Pahlevani, F.; Rong, L. A model of HIV-1 infection with two time delays: Mathematical analysis and comparison with patient data. Math. Biosci. 2012, 235, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Perelson, A.S.; Kirschner, D.E.; De Boer, R. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef] [Green Version]
- Perelson, A.S.; Nelson, P.W. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 1999, 41, 3–44. [Google Scholar] [CrossRef]
- Perez-Ibarra, J.L.; Toro-Zapata, H.D. Modeling the cytotoxic immune response effects on human immunodeficiency virus. VisióN ElectróNica Algo MáS Que Estado SóLido 2014, 8, 54–62. [Google Scholar]
- Srivastava, P.K.; Chandra, P. Modeling the dynamics of HIV and CD4+ T cells during primary infection. Nonlinear Anal. Real World Appl. 2010, 11, 612–618. [Google Scholar] [CrossRef]
- Toro-Zapata, H.D.; Roa-Vásquez, E.; Mesa-Mazo, M.J. Modelo estocástico para la infección con VIH de las células T CD4+ del sistema inmune. Rev. MatemáTica TeoríA Apl. 2017, 24, 287–313. [Google Scholar] [CrossRef] [Green Version]
- Toro, H.D.; Caicedo, A.G.; Bichara, D.; Lee, S. Role of Active and Inactive Cytotoxic Immune Response in Human Immunodeficiency Virus Dynamics. Osong Public Health Res. Perspect. 2014, 5, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trujillo, C.A.; Toro, H.D. Simulation Model for AIDS Dynamics and Optimal Control Through antiretroviral Treatment. In Analysis, Modelling, Optimization, and Numerical Techniques; Tost, G.O., Vasilieva, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 121. [Google Scholar]
- Wang, J.; Guo, M.; Liu, X.; Zhao, Z. Threshold dynamics of HIV-1 virus model with cell-to-cell transmission, cell-mediated immune responses and distributed delay. Appl. Math. Comput. 2016, 291, 149–161. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T.; Liu, J. Viral dynamics of an HIV stochastic model with cell-to-cell infection, CTL immune response and distributed delays. Math. Biosci. Eng. 2019, 16, 7126–7154. [Google Scholar] [CrossRef] [PubMed]
- Cassels, S.; Clark, S.J.; Morris, M. Mathematical models for HIV transmission dynamics: Tools for social and behavioral science research. J. Acquir. Immune Defic. Syndr. 2008, 47 (Suppl. 1), S34. [Google Scholar] [CrossRef] [Green Version]
- Desai, K.; Boily, M.C.; Garnett, G.P.; Mâsse, B.R.; Moses, S.; Bailey, R.C. The role of sexually transmitted infections in male circumcision effectiveness against HIV—Insights from clinical trial simulation. Emerg. Themes Epidemiol. 2006, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Johnson, L.F.; Dorrington, R.E. Modelling the demographic impact of HIV/AIDS in South Africa and the likely impact of interventions. Demogr. Res. 2006, 14, 541–574. [Google Scholar] [CrossRef] [Green Version]
- Toro-Zapata, H.D.; Mesa-Mazo, M.J.; Prieto-Medellín, D.A. Modelo de simulación para la transmisión del VIH y estrategias de control basadas en diagnóstico. Rev. Salud PúBlica 2014, 16, 126–138. [Google Scholar]
- Toro-Zapata, H.D.; Rodríguez-Osorio, A.J.; Prieto-Medellín, D.A. Modelo para el acceso efectivo al tratamiento antirretroviral en relación con el fracaso terapéutico de la infección por VIH. Revista EIA 2019, 16, 115–130. [Google Scholar] [CrossRef] [Green Version]
- Trujillo-Salazar, C.A.; Toro-Zapata, H.D. Análisis teórico de la transmisión y el control del VIH/SIDA en un centro de reclusión. Mat. Ser. Conf. Semin. Trab. Mat. 2014, 19, 17–26. [Google Scholar] [CrossRef]
- Deschamps, M.M.; Noel, F.; Bonhomme, J.; Dévieux, J.G.; Saint-Jean, G.; Zhu, Y.; Malow, R.M. Prevention of mother-to-child transmission of HIV in Haiti. Rev. Panam. Salud PúBlica 2009, 25, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Gómez, M. Comparación de tres estrategias de tamizaje para la prevención de la infección perinatal por VIH en Colombia: Análisis de decisiones. Rev. Panam. Salud PúBlica 2008, 24, 256–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toro-Zapata, H.D.; Trujillo-Salazar, C.A.; Prieto-Medellín, D.A. Evaluación teórica de estrategias óptimas y sub-óptimas de terapia antirretroviral para el control de la infección por VIH. Revista de Salud Pública 2018, 20, 117–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toro-Zapata, H.D.; Calderón-Gutiérez, J.L.; Molina-Díaz, O.E. Modelo para la transmisión del VIH en una población con diferenciación de sexos y usos de medidas preventivas. Rev. MatemáTica: TeoríA Apl. 2018, 25, 293–318. [Google Scholar] [CrossRef] [Green Version]
- Toro-Zapata, H.D.; Trujillo-Salazar, C.A. Modelo para el control óptimo del VIH con tasa de infección dependiente de la densidad del virus. Rev. MatemáTica: TeoríA Apl. 2018, 25, 261–294. [Google Scholar] [CrossRef] [Green Version]
- Maartens, G.; Celum, C.; Lewin, S.R. HIV infection: Epidemiology, pathogenesis, treatment, and prevention. Lancet 2014, 384, 258–271. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-differential equation model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S.; Spiteri, R.J. Optimal HIV treatment by maximising immune response. J. Math. Biol. 2004, 48, 545–562. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, M.; Chattopadhyay, J. Ratio-dependent predator–prey model: Effect of environmental fluctuation and stability. Nonlinearity 2005, 18, 913. [Google Scholar] [CrossRef]
- Birkhoff, G.; Rota, G. Ordinary Differential Equations, 4th ed.; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Tabares, P.C.; Ferreira, J.D.; Rao, V. Weak Allee effect in a predator-prey system involving distributed delays. Comput. Appl. Math. 2011, 30, 675–699. [Google Scholar] [CrossRef] [Green Version]
- Farkas, M. Periodic Motions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994; Volume 104. [Google Scholar]
- Ferreira, J.D.; Trujillo-Salazar, C.A.; Carmona-Tabares, P.C. Weak Allee effect in a predator–prey model involving memory with a hump. Nonlinear Anal. Real World Appl. 2013, 14, 536–548. [Google Scholar] [CrossRef]
- Wörz-Busekros, A. Global stability in ecological systems with continuous time delay. SIAM J. Appl. Math. 1978, 35, 123–134. [Google Scholar] [CrossRef]
- Kot, M. Elements of Mathematical Ecology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Hurwitz, A. Über einen Satz des Herrn Kakeya. Tohoku Math. J. First Ser. 1913, 4, 89–93. [Google Scholar]
- Farkas, M.; Stépán, G. On perturbation of the kernel in infinite delay systems. Zamm J. Appl. Math. Mech. FüR Angew. Math. Und Mech. 1992, 72, 153–156. [Google Scholar] [CrossRef]
| State Variables | Initial Conditions | Reference | |
|---|---|---|---|
| T | Uninfected CD4 T-cell concentration | 500 mm | [13,19] |
| V | Infectious viral load | 1 mm | [13,19] |
| Parameters | Value | Reference | |
| Constant CD4 T-cell production | 10 mmd | [17,22,41] | |
| Uninfected CD4 T-cell proliferation rate | 0.03 d | [19,40] | |
| Uninfected CD4 T-cell natural death rate | 0.01d | [17,22,41] | |
| Infected CD4 T-cell death rate | 0.26 d | [17,40] | |
| Effective contact rate between CD4 T-cells and virus | and mmd | [13,17,19,40] | |
| N | Number of viral particles produced per infected cell | 1000 | [41] |
| c | Viral elimination rate | 2.4 d | [17,19] |
| k | CD4 T-cell carrying capacity | 1500 mm | [19,40] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toro-Zapata, H.D.; Trujillo-Salazar, C.A.; Carranza-Mayorga, E.M. Mathematical Model Describing HIV Infection with Time-Delayed CD4 T-Cell Activation. Processes 2020, 8, 782. https://doi.org/10.3390/pr8070782
Toro-Zapata HD, Trujillo-Salazar CA, Carranza-Mayorga EM. Mathematical Model Describing HIV Infection with Time-Delayed CD4 T-Cell Activation. Processes. 2020; 8(7):782. https://doi.org/10.3390/pr8070782
Chicago/Turabian StyleToro-Zapata, Hernán Darío, Carlos Andrés Trujillo-Salazar, and Edwin Mauricio Carranza-Mayorga. 2020. "Mathematical Model Describing HIV Infection with Time-Delayed CD4 T-Cell Activation" Processes 8, no. 7: 782. https://doi.org/10.3390/pr8070782
APA StyleToro-Zapata, H. D., Trujillo-Salazar, C. A., & Carranza-Mayorga, E. M. (2020). Mathematical Model Describing HIV Infection with Time-Delayed CD4 T-Cell Activation. Processes, 8(7), 782. https://doi.org/10.3390/pr8070782





