Prediction of Particle-Collection Efficiency for Vacuum-Blowing Cleaning System Based on Operational Conditions
Abstract
:1. Introduction
2. Numerical Models
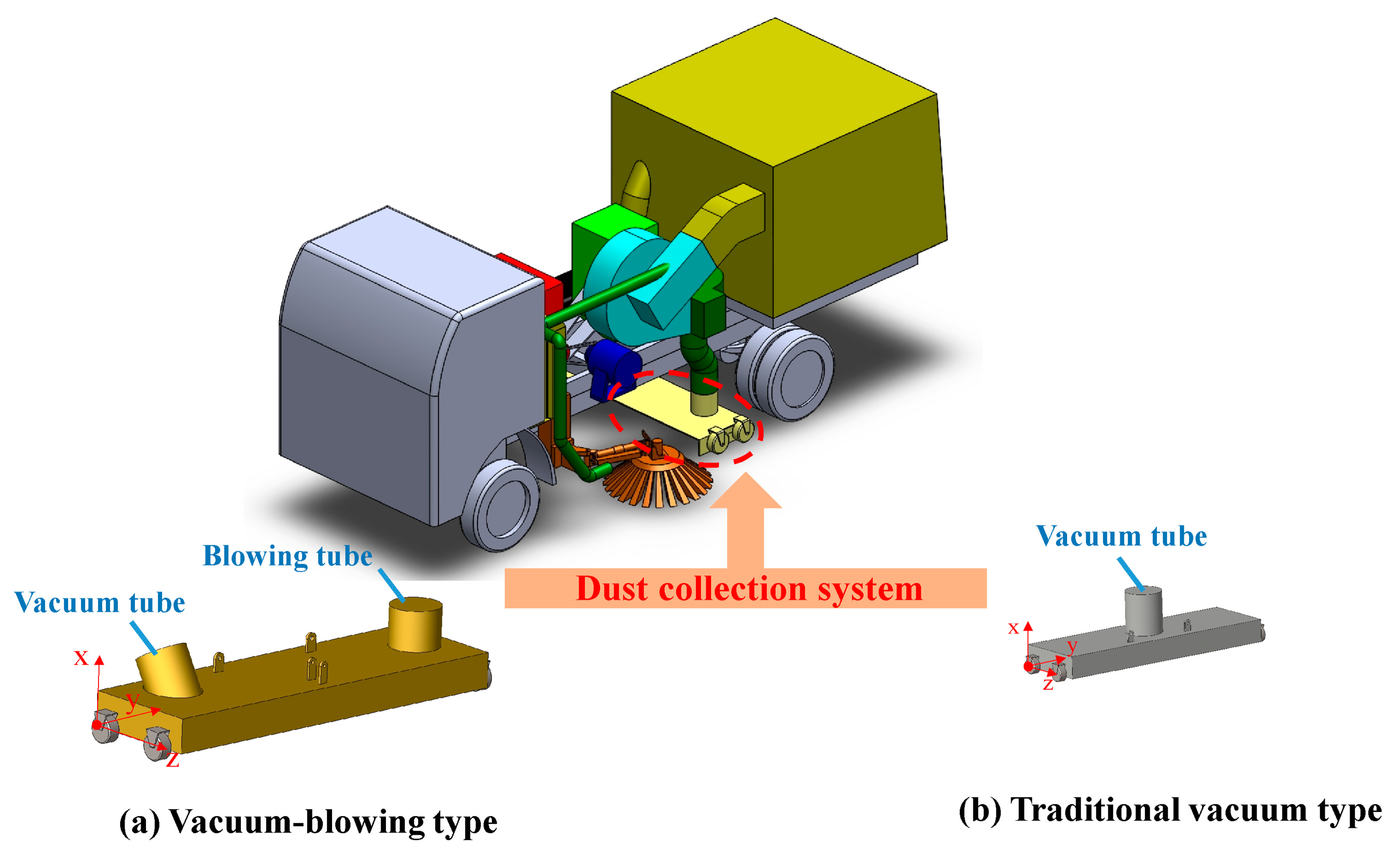
2.1. CFD Model Construction
2.2. Mathematical Model
2.3. Boundary Conditions and Solution Controls
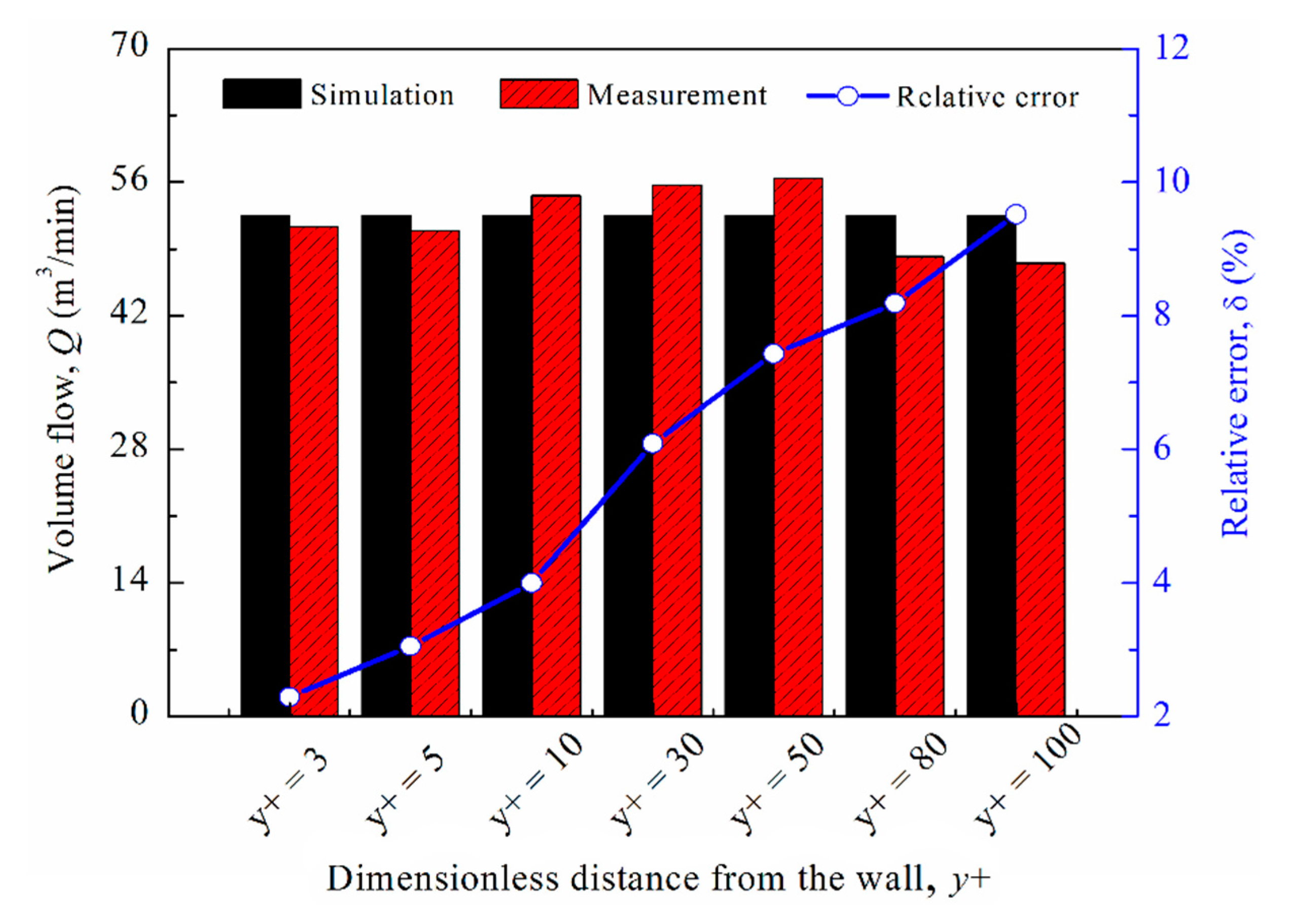
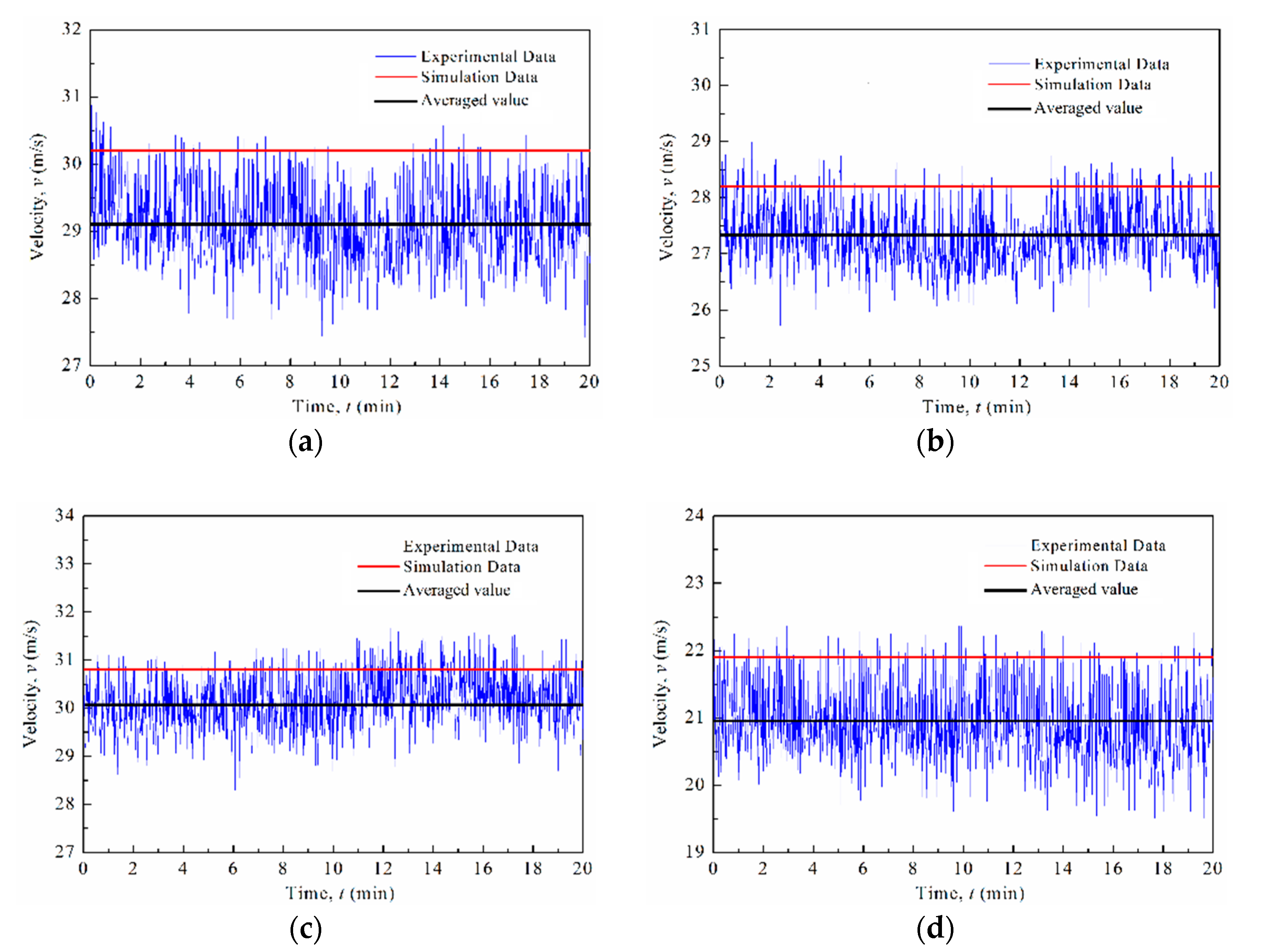
2.4. Grid Generation
3. Results and Discussion
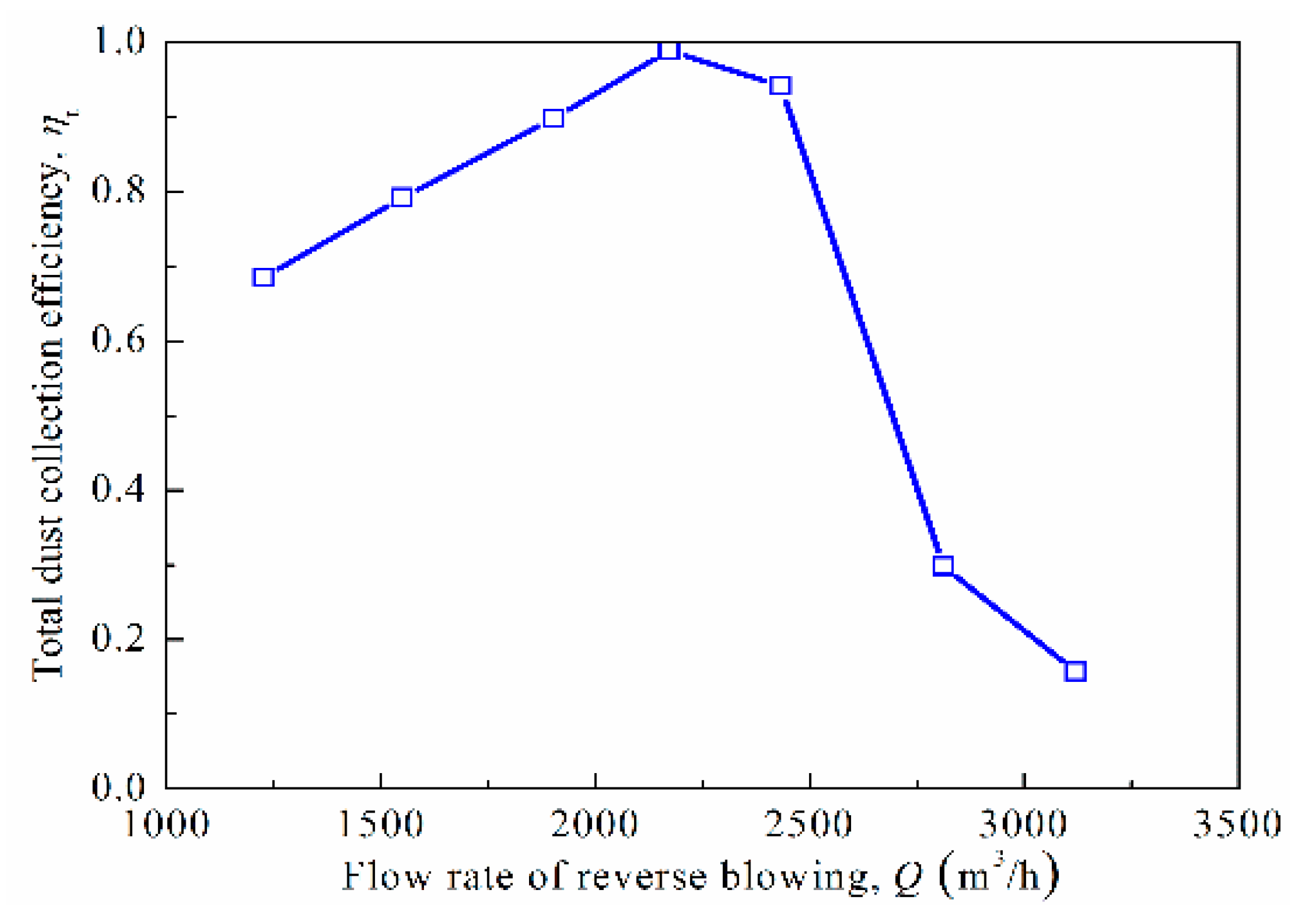
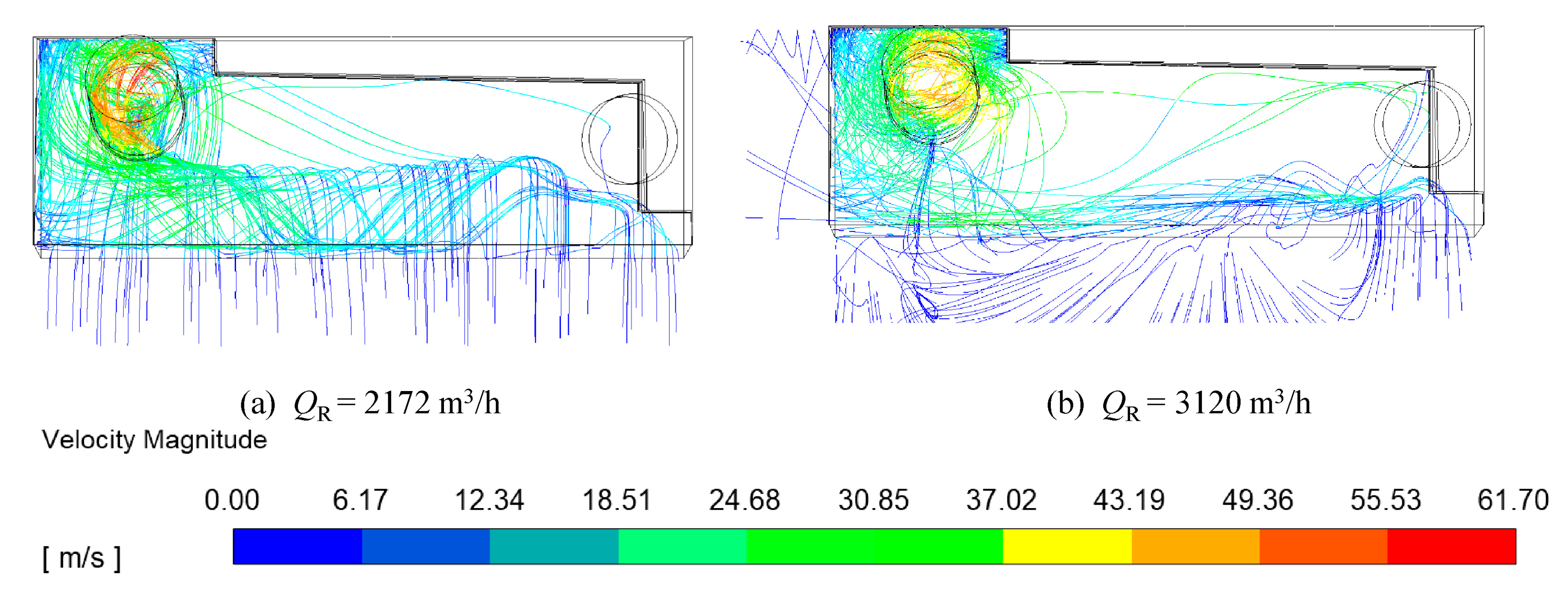
3.1. Influence of Reverse-Blowing Flow Rate on the Separation Efficiency
3.2. Influence of Pressure Drop on the Separation Efficiency
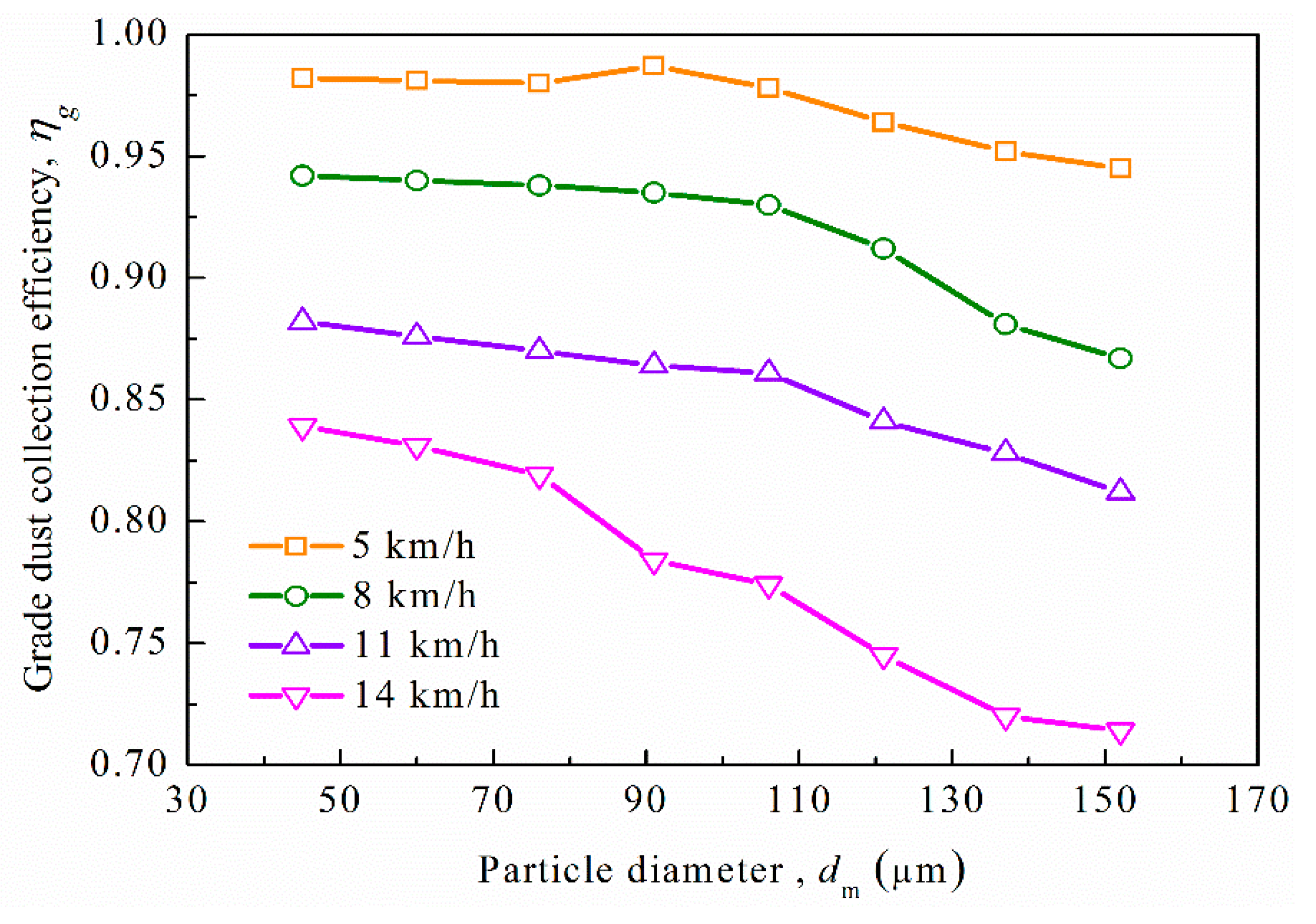
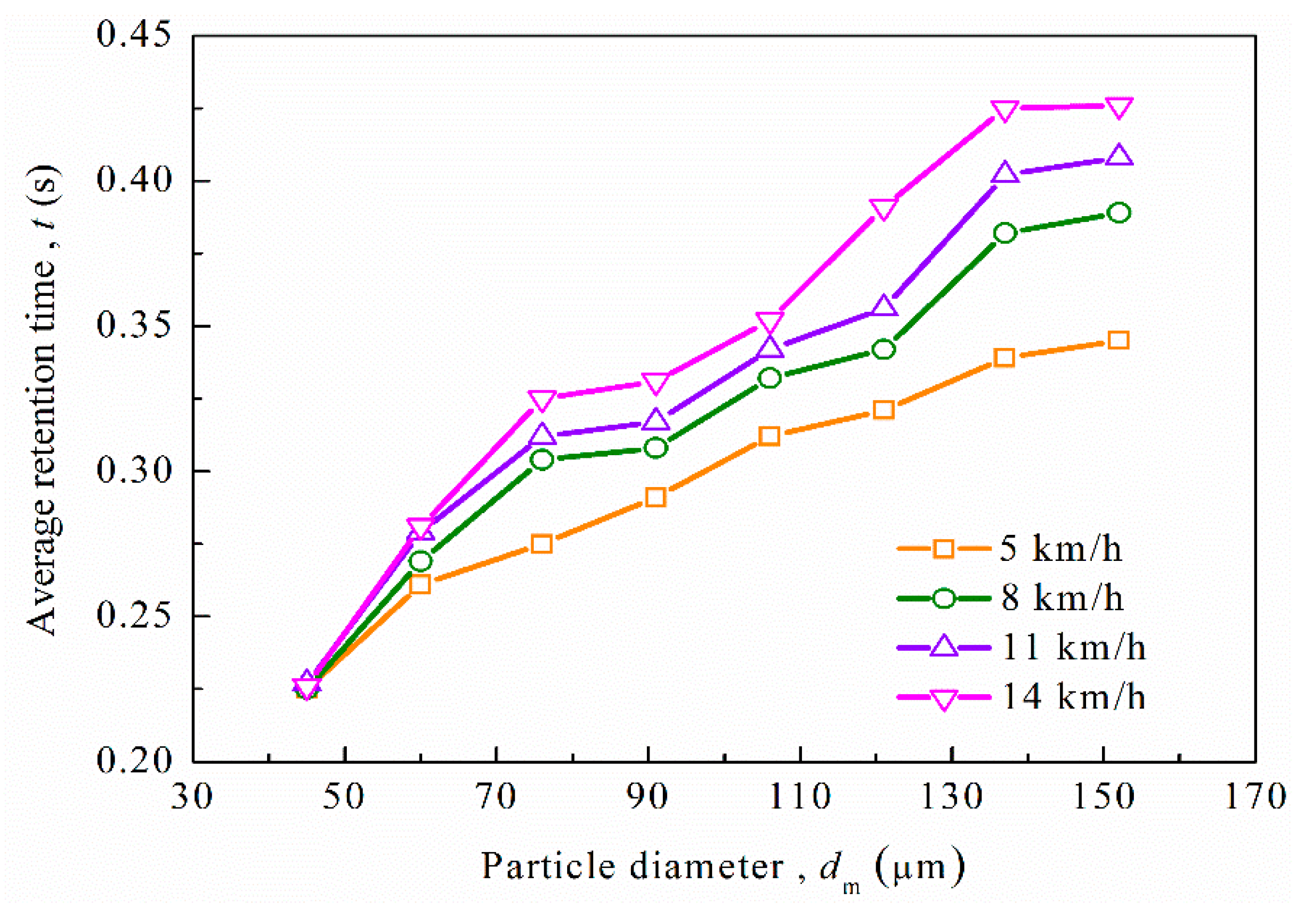
3.3. Influence of Traveling Speed on the Separation Efficiency
4. Uniform Design and Statistical Analysis
Experiment Design and Multiple Regression Model Building
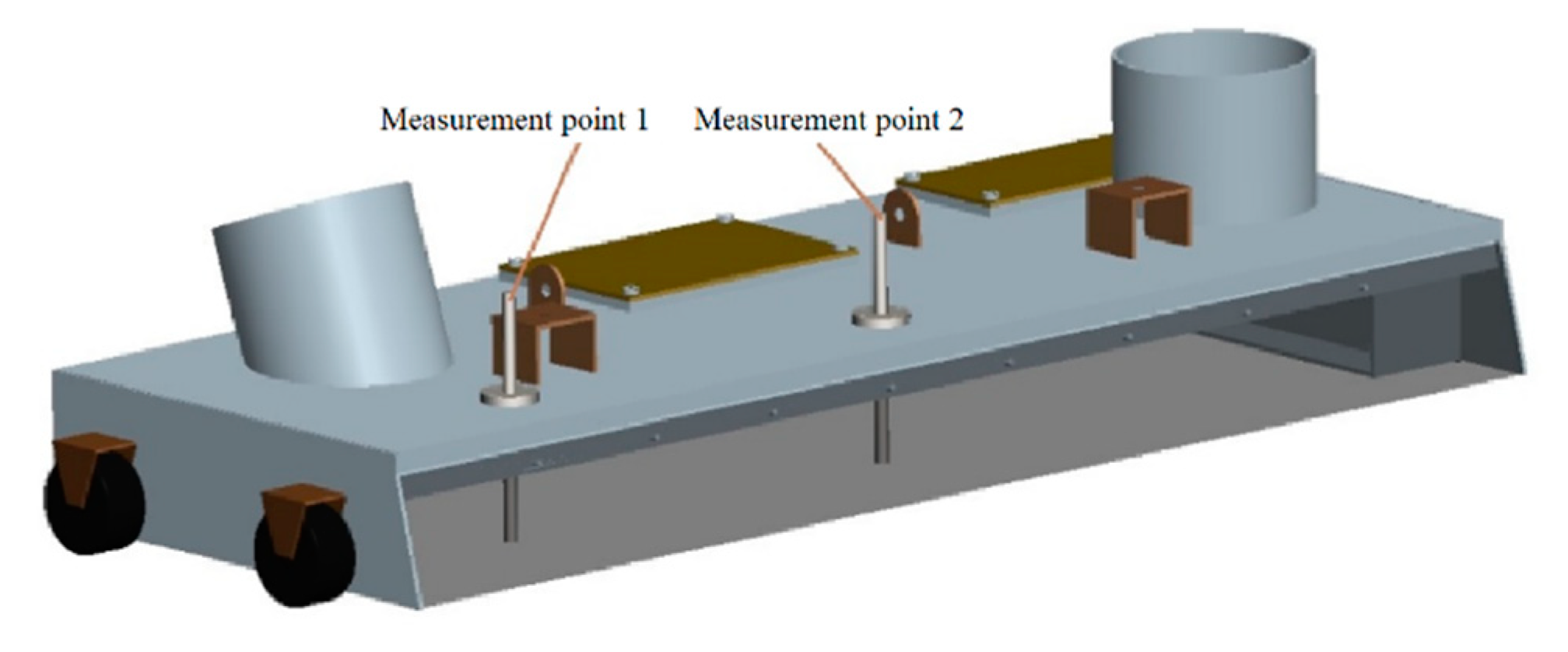
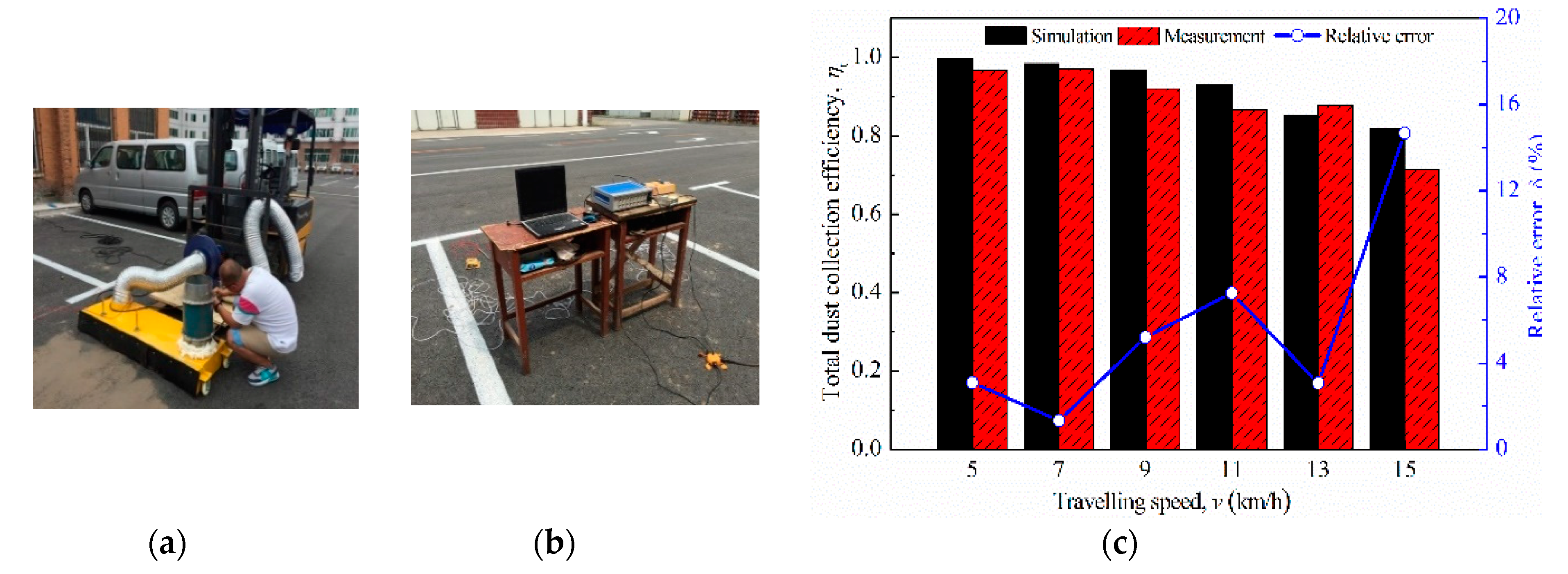
5. Verification and Site Test for Total Dust-Collection Efficiency
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| B | width, mm |
| H | thickness, mm |
| D1 | suction inlet diameter, mm |
| D2 | reverse- jet diameter, mm |
| y+ | wall distance |
| TKE prandtl number | 1, constant |
| TDR prandtl number | 1.3, constant |
| Energy prandtl number | 0.85, constant |
| Wall prandtl number | 0.85, constant |
| Cmu | 0.89, constant |
| C1ε | 1.46, constant |
| C2ε | 1.89, constant |
| qm | total flow rate, kg·s−1 |
| dm | particle mean diameter, μm |
| n | spread parameter, |
| xi | influence factor |
| yi | predicted response value, % |
| b0 | constant term |
| bii | quadratic term coefficient |
| bij | interaction term coefficient |
| t | average retention time, s |
| QR | reverse blowing flow rate, m3/h |
| Greek Letters | |
| α | front damper angle, ° |
| β | suction inlet inclination angle, ° |
| δ | ground clearance, mm |
| δε | 1.4, constant |
| ρg | gas density, kg·m−3 |
| ρp | particle density, kg·m−3 |
| ρd | particle density, kg·m−3 |
| enormal | normal restitution coefficient |
| etangential | tangential restitution coefficient |
| ηt | total dust-collection efficiency, % |
| ηg | grade dust-collection efficiency, % |
References
- Wang, J.S.; Huang, J.J.; Li, J. Characterization of the pollutant build-up processes and concentration/mass load in road deposited sediments over a long dry period. Sci. Total Environ. 2020, 718, 12. [Google Scholar] [CrossRef] [PubMed]
- Amato, F.; Pandolfi, M.; Viana, M.; Querol, X.; Alastuey, A.; Moreno, T. Spatial and chemical patterns of PM10 in road dust deposited in urban environment. Atmos. Environ. 2009, 43, 1650–1659. [Google Scholar] [CrossRef]
- Gao, J.H.; Woodward, A.; Vardoulakis, S.; Kovats, S.; Wilkinson, P.; Li, L.P.; Xu, L.; Li, J.; Yang, J.; Li, J.; et al. Haze, public health and mitigation measures in China: A review of the current evidence for further policy response. Sci. Total Environ. 2017, 578, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.; Latif, M.T.; Soo, C.I.; Faisal, A.H.; Roslina, A.M.; Andrea, Y.L.B.; Hassan, T. Short communication: Diagnosis of lung cancer increases during the annual southeast Asian haze periods. Lung Cancer 2017, 113, 1–3. [Google Scholar] [CrossRef]
- Yun, Y.; Gao, R.; Yue, H.F.; Guo, L.; Li, G.K.; Sang, N. Sulfate Aerosols Promote Lung Cancer Metastasis by Epigenetically Regulating the Epithelial-to-Mesenchymal Transition (EMT). Environ. Sci. Technol. 2017, 51, 11401–11411. [Google Scholar] [CrossRef]
- Chen, Z.J.; Wu, X.Y.; Xu, G.P.; Wang, A.Q. Experimental Study on Suction Mouth of Vacuum Sweeper. J. Tongji Univ. 2001, 29, 1483–1485. [Google Scholar]
- Daichin; Lee, S.J. Experimental analysis of flow fields inside intake heads of a vacuum cleaner. J. Mech. Sci. Technol. 2005, 19, 894–904. [Google Scholar] [CrossRef]
- Bofu, W.; Jinlai, M.; Jie, C. Study of the Particle Separation Performance of a Dust-settling Hopper. Chem. Prod. Process Mod. 2011, 6, 27. [Google Scholar] [CrossRef]
- Avsar, E.; Hanedar, A.; Toroz, I.; Alp, K.; Kaynak, B. Investigation of PM10 Concentrations and Noise Levels of the Road Sweepers Operating in Istanbul-Turkey: A Case Study. Fresenius Environ. Bull. 2010, 19, 2033–2039. [Google Scholar]
- Zeng, G.-y.; Li, X.-f.; Xiao, T.-y.; Xu, Y. Simulation for the design of dust suction system of highway sweeper. J. Syst. Simul. 2004, 16, 2770–2773. [Google Scholar]
- Xu, Y.; Li, X.-f.; Xiao, T.-y.; Zeng, G.-y. Research on applications of computational dynamic fluid in the simulation analysis of highway mechanical sweeper. J. Syst. Simul. 2004, 16, 270–273. [Google Scholar]
- Aoki, P.M.; Honicky, R.J.; Mainwaring, A.; Myers, C.; Paulos, E.; Subramanian, S.; Woodruff, A. A Vehicle for Research: Using Street Sweepers to Explore the Landscape of Environmental Community Action; 27th Annual CHI Conference on Human Factors in Computing Systems; ACM Press: New York, NY, USA, 2009; pp. 375–384. [Google Scholar]
- Wu, B.; Men, I.; Chen, I. Improving the design of a pickup head for particle removal using computational fluid dynamics. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2011, 225, 939–948. [Google Scholar] [CrossRef]
- Wu, B.F.; Men, J.L.; Chen, J. Numerical study on particle removal performance of pickup head for a street vacuum sweeper. Powder Technol. 2010, 200, 16–24. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Liu, F.; Wu, Q.; Zhang, M.; Guo, Y. Structure design and flow field simulation analysis of a dust collector based on tornado principle. Harbin Gongye Daxue Xuebao/J. Harbin Inst. Technol. 2020, 52, 106–114. [Google Scholar] [CrossRef]
- Xi, Y.; Cheng, K.; Li, G.-X.; Cheng, L. Effect of Front Baffle Inclination Angle and Pressure Drop on Absorption Performance of a Pickup Mouth. J. Donghua Univ., Engl. Ed. 2016, 33, 8–12. [Google Scholar]
- Xi, Y.; Cheng, K.; Lou, X.-t.; Cheng, L.; Dong, C. Numerical Simulation of Gas-Solid Two-Phase Flow in Reverse Blowing Pickup Mouth. J. Donghua Univ., Engl. Ed. 2015, 32, 530–535. [Google Scholar]
- He, Y.; Deen, N.G.; van Sint Annaland, M.; Kuipers, J.A.M. Gas-Solid Turbulent Flow in a Circulating Fluidized Bed Riser: Experimental and Numerical Study of Monodisperse Particle Systems. Ind. Eng. Chem. Res. 2009, 48, 8091–8097. [Google Scholar] [CrossRef]
- Guo, Y.; Stevanovic, S.; Verma, P.; Jafari, M.; Jabbour, N.; Brown, R.; Cravigan, L.; Alroe, J.; Osuagwu, C.G.; Brown, R.; et al. An experimental study of the role of biodiesel on the performance of diesel particulate filters. Fuel 2019, 247, 67–76. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Li, A.; Ahmadi, G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow. Aerosol Sci. Technol. 1992, 16, 209–226. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Yang, C.Z.; Baker, C.; Chen, M.; Zou, X.; Dai, W.L. Effects of expanding zone parameters of vacuum dust suction mouth on flow simulation results. J. Cent. South Univ. 2014, 21, 2547–2552. [Google Scholar] [CrossRef]
- Ludwig, W.; Pluszka, P. Euler-Lagrange model of particles circulation in a spout-fluid bed apparatus for dry coating. Powder Technol. 2018, 328, 375–388. [Google Scholar] [CrossRef]
- Ludwig, W.; Pluszka, P. The analysis of the influence of the normal restitution coefficient model on calculated particles velocities by means of Eulerian-Lagrangian approach. Powder Technol. 2019, 344, 140–151. [Google Scholar] [CrossRef]
- Chuah, T.G.; Gimbun, J.; Choong, T.S.Y. A CFD study of the effect of cone dimensions on sampling aerocyclones performance and hydrodynamics. Powder Technol. 2006, 162, 126–132. [Google Scholar] [CrossRef]
- Othman, S.R.; Yahaya, N.; Noor, N.M.; Sing, L.K.; Zardasti, L.; Rashid, A.S.A. Modeling of External Metal Loss for Corroded Buried Pipeline. J. Press. Vessel Technol.-Trans. ASME 2017, 139, 12. [Google Scholar] [CrossRef] [Green Version]
- Ping, H.L.; Xu, G.H.; Wu, S.F. System optimization of cyclohexane dehydrogenation under multiphase reaction conditions using the uniform design method. Int. J. Hydrog. Energy 2015, 40, 15923–15932. [Google Scholar] [CrossRef]
- Xu, Q.S.; Xu, Y.D.; Li, L.; Fang, K.T. Uniform experimental design in chemometrics. J. Chemometr. 2018, 32, 10. [Google Scholar] [CrossRef]
- Chen, W.Y.; Yang, J.; Chen, Z.Y.; Luo, F.Y.; Wu, C.L.; Peng, Z.S. Predicting photosynthetic rate of sunflowers using back propagation neural network based on uniform design. Afr. J. Agric. Res. 2011, 6, 5817–5821. [Google Scholar] [CrossRef]
- Fang, F.; Zang, G.L.; Sun, M.; Yu, H.Q. Optimizing multi-variables of microbial fuel cell for electricity generation with an integrated modeling and experimental approach. Appl. Energy 2013, 110, 98–103. [Google Scholar] [CrossRef]
- Zhou, X.P.; Huang, X.C.; Liu, P.F.; Li, T.F. A probabilistic method to analyze collapse failure of shallow rectangular tunnels. Tunn. Undergr. Space Technol. 2018, 82, 9–19. [Google Scholar] [CrossRef]
- Zhu, G.R.; Tan, W.; Yu, Y.; Liu, L.Y. Experimental and Numerical Study of the Solid Concentration Distribution in a Horizontal Screw Decanter Centrifuge. Ind. Eng. Chem. Res. 2013, 52, 17249–17256. [Google Scholar] [CrossRef]
- Bunyawanichakul, P.; Kirkpatrick, M.P.; Sargison, J.E.; Walker, G.J. Numerical and experimental studies of the flow field in a cyclone dryer. J. Fluids Eng.-Trans. ASME 2006, 128, 1240–1250. [Google Scholar] [CrossRef]
- Luan, Y.G.; Sun, H.O. Experimental and Numerical Study on the Resistance Performance of an Axial Flow Cyclone Separator. Math. Probl. Eng. 2015, 1–9. [Google Scholar] [CrossRef] [Green Version]


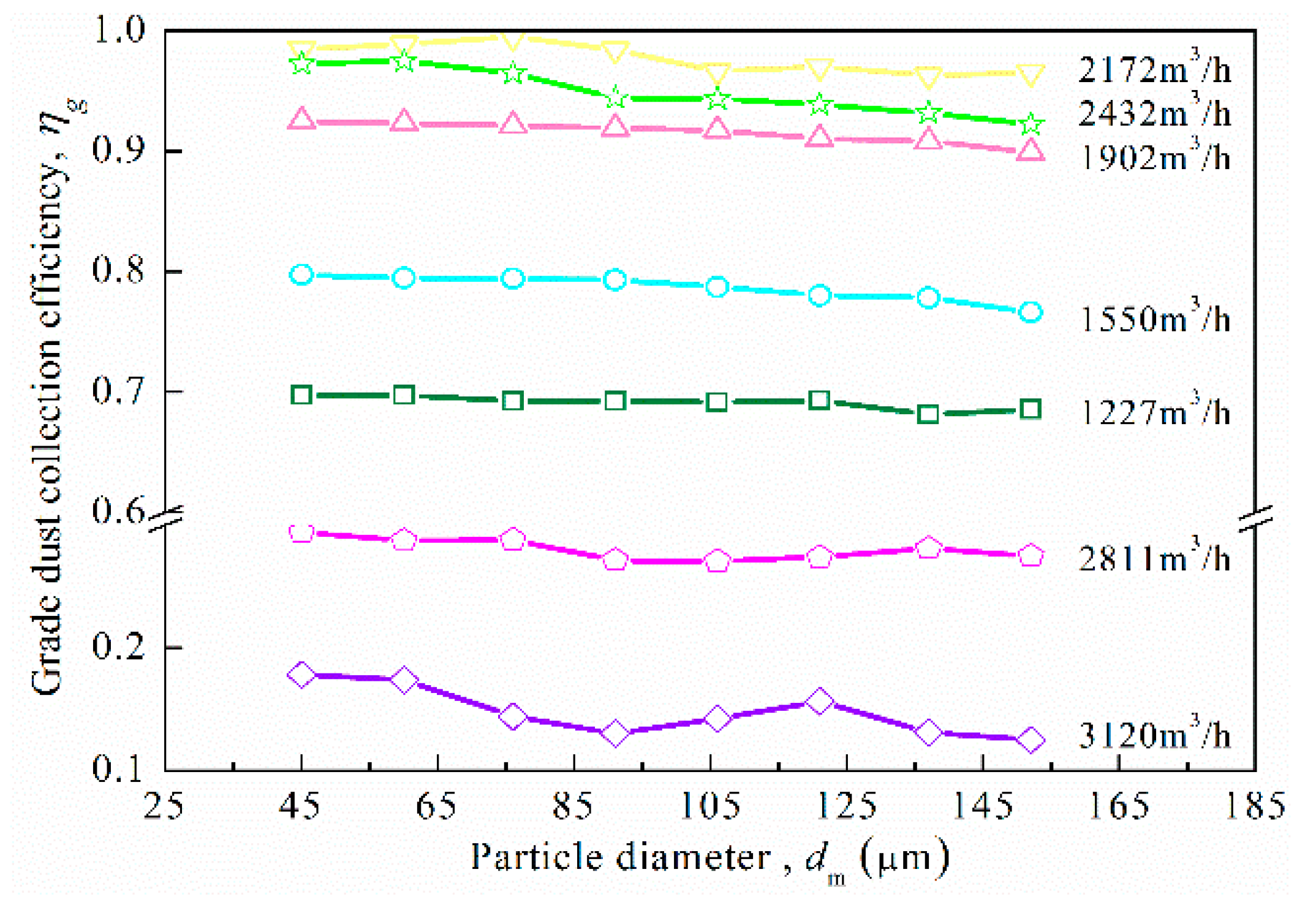
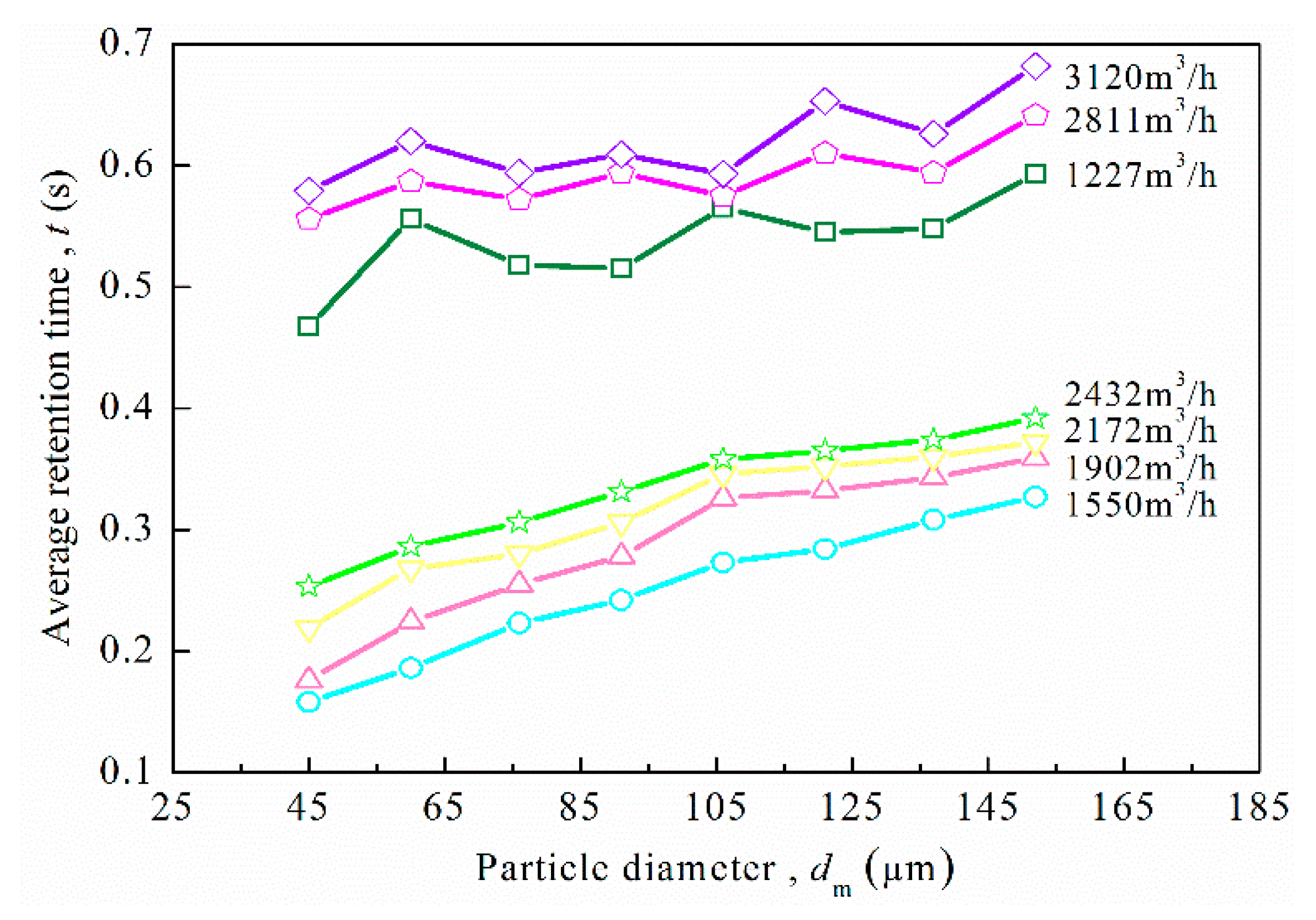

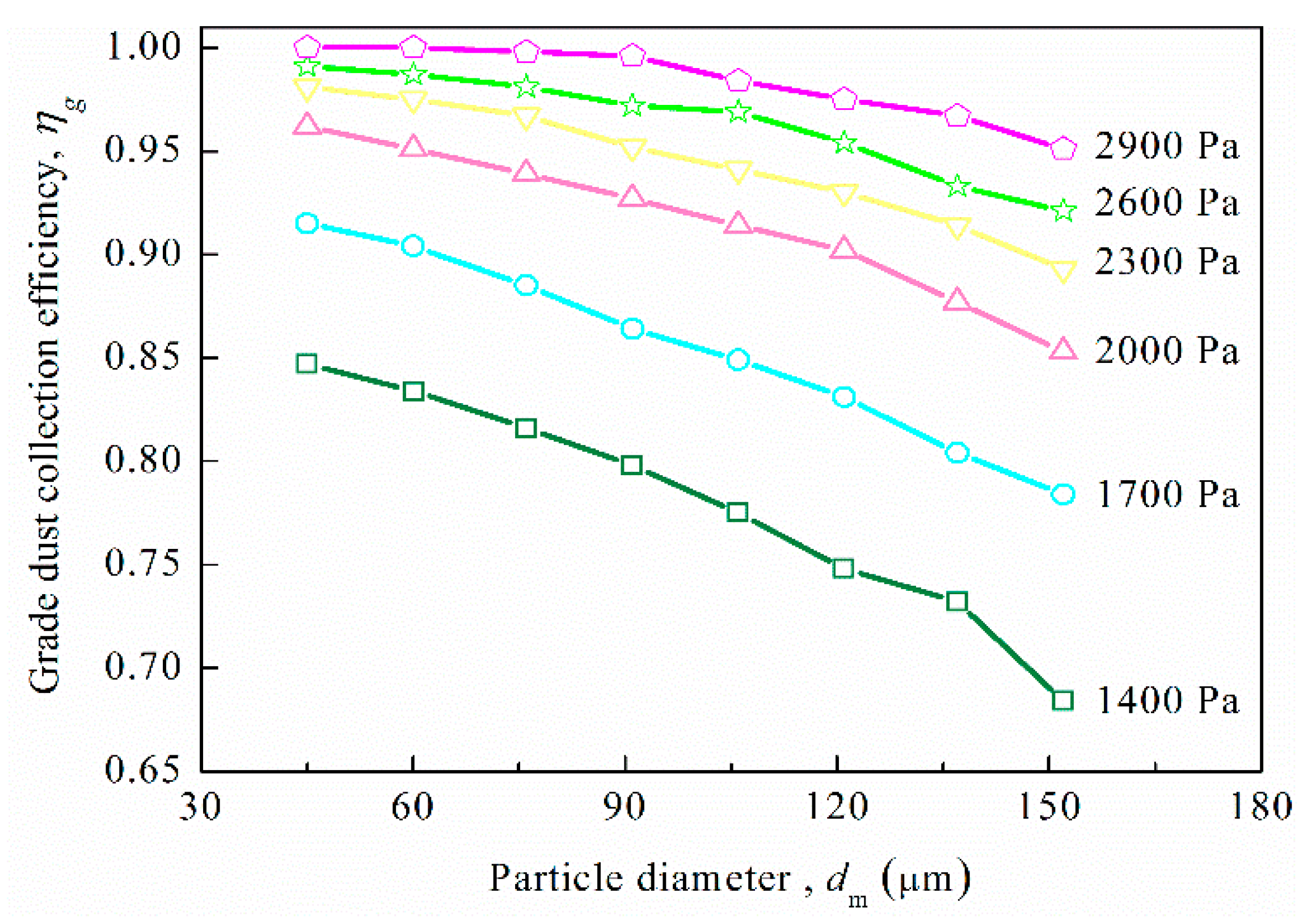
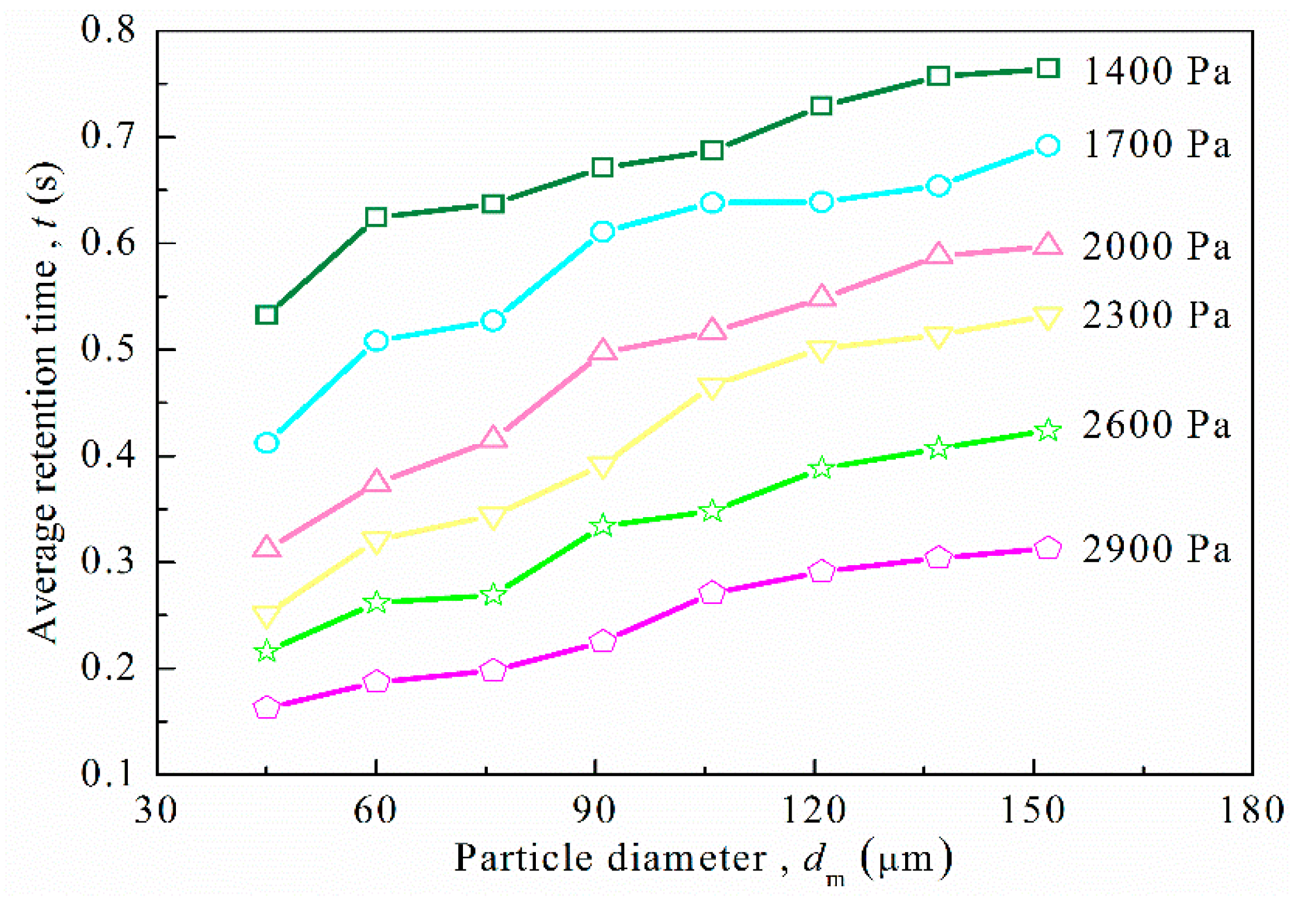


| Parameter | Value |
|---|---|
| length, L (mm) | 1400 |
| width, B (mm) | 540 |
| thickness, H (mm) | 150 |
| front damper angle, α (°) | 105 |
| suction inlet inclination angle, β (°) | 110 |
| suction inlet diameter, D1(mm) | 200 |
| reverse-jet diameter, D2 (mm) | 200 |
| ground clearance, δ (mm) | 10 |
| length of the expansion areas, lea (mm) | 180 |
| height of the expansion areas, hea (mm) | 150 |
| slant angle of the expansion areas, θea(°) | 55 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Near-Wall treatment | Scalable wall function | particle model | Rosin–Rammler |
| TKE prandtl number | 1 | total flow rate, qm (kg·s−1) | 0.5 |
| TDR prandtl number | 1.3 | gas density, ρg (kg·m−3) | 1.225 |
| Energy prandtl number | 0.85 | particle density, ρp (kg·m−3) | 2500 |
| Wall prandtl number | 0.85 | distribution density, ρd (kg·m−2) | 0.15 |
| coefficient, Cmu | 0.89 | particle mean diameter, dm (μm) | 81 |
| coefficient, C1ε | 1.46 | spread parameter, n | 5.95 |
| constant, C2ε | 1.89 | normal restitution coefficient, e normal | 0.95 |
| constant, δε | 1.4 | tangential restitution coefficient, e tangential | 0.85 |
| NO. | x1 Reverse Blowing Flow Rate (m3/h) | x2 Traveling Speed (km/h) | x3 Pressure Drop (Pa) | y Particle-Separation Efficiency (%) |
|---|---|---|---|---|
| 1 | 2570 | 8 | 1900 | 66.03 |
| 2 | 2570 | 14 | 2900 | 80.79 |
| 3 | 3120 | 14 | 1900 | 3.23 |
| 4 | 3120 | 5 | 2900 | 59.23 |
| 5 | 2073 | 8 | 2400 | 94.34 |
| 6 | 1550 | 11 | 2900 | 94.73 |
| 7 | 2073 | 5 | 1400 | 96.74 |
| 8 | 3120 | 8 | 1400 | 2.41 |
| 9 | 1550 | 5 | 2400 | 99.13 |
| 10 | 2570 | 11 | 2400 | 78.78 |
| 11 | 2073 | 11 | 1900 | 83.24 |
| 12 | 1550 | 14 | 1400 | 70.32 |
| Source of Variance | Degree of Freedom | Quadratic Sum of Deviation | Variance | F-Value |
|---|---|---|---|---|
| Regression | 9 | 12,274.63 | 1363.85 | 269.01 |
| Partial regression | 2 | 10.14 | 5.07 | |
| Total | 11 | 12,284.77 |
| 2.8036 | 0.8914 | 2.5053 | 0.9289 | 3.1875 | 0.3596 | 1.4883 | 5.3905 | 2.9637 |
| x1 | x12 | x1x2 | x1x3 | |
|---|---|---|---|---|
| Regression coefficient | 0.17992545 | −0.00004963 | −0.00099563 | 0.00000919 |
| Standardized result | 3.2743 | −4.2421 | −0.3046 | 0.5277 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Y.; Dai, Y.; Zhang, X.; Zhang, X. Prediction of Particle-Collection Efficiency for Vacuum-Blowing Cleaning System Based on Operational Conditions. Processes 2020, 8, 809. https://doi.org/10.3390/pr8070809
Xi Y, Dai Y, Zhang X, Zhang X. Prediction of Particle-Collection Efficiency for Vacuum-Blowing Cleaning System Based on Operational Conditions. Processes. 2020; 8(7):809. https://doi.org/10.3390/pr8070809
Chicago/Turabian StyleXi, Yuan, Yan Dai, Xi–long Zhang, and Xing Zhang. 2020. "Prediction of Particle-Collection Efficiency for Vacuum-Blowing Cleaning System Based on Operational Conditions" Processes 8, no. 7: 809. https://doi.org/10.3390/pr8070809
APA StyleXi, Y., Dai, Y., Zhang, X., & Zhang, X. (2020). Prediction of Particle-Collection Efficiency for Vacuum-Blowing Cleaning System Based on Operational Conditions. Processes, 8(7), 809. https://doi.org/10.3390/pr8070809





