2.1. Compounds vs. Solutions
The most critical aspect when evaluating the equilibrium state of a system is to consider all the phases that may potentially form. The phase selection prior to a calculation needs to be performed with great care. The omission of phases may impact drastically the identified equilibrium state. Two types of phases can form in a system: i.e., stoichiometric compounds and solutions.
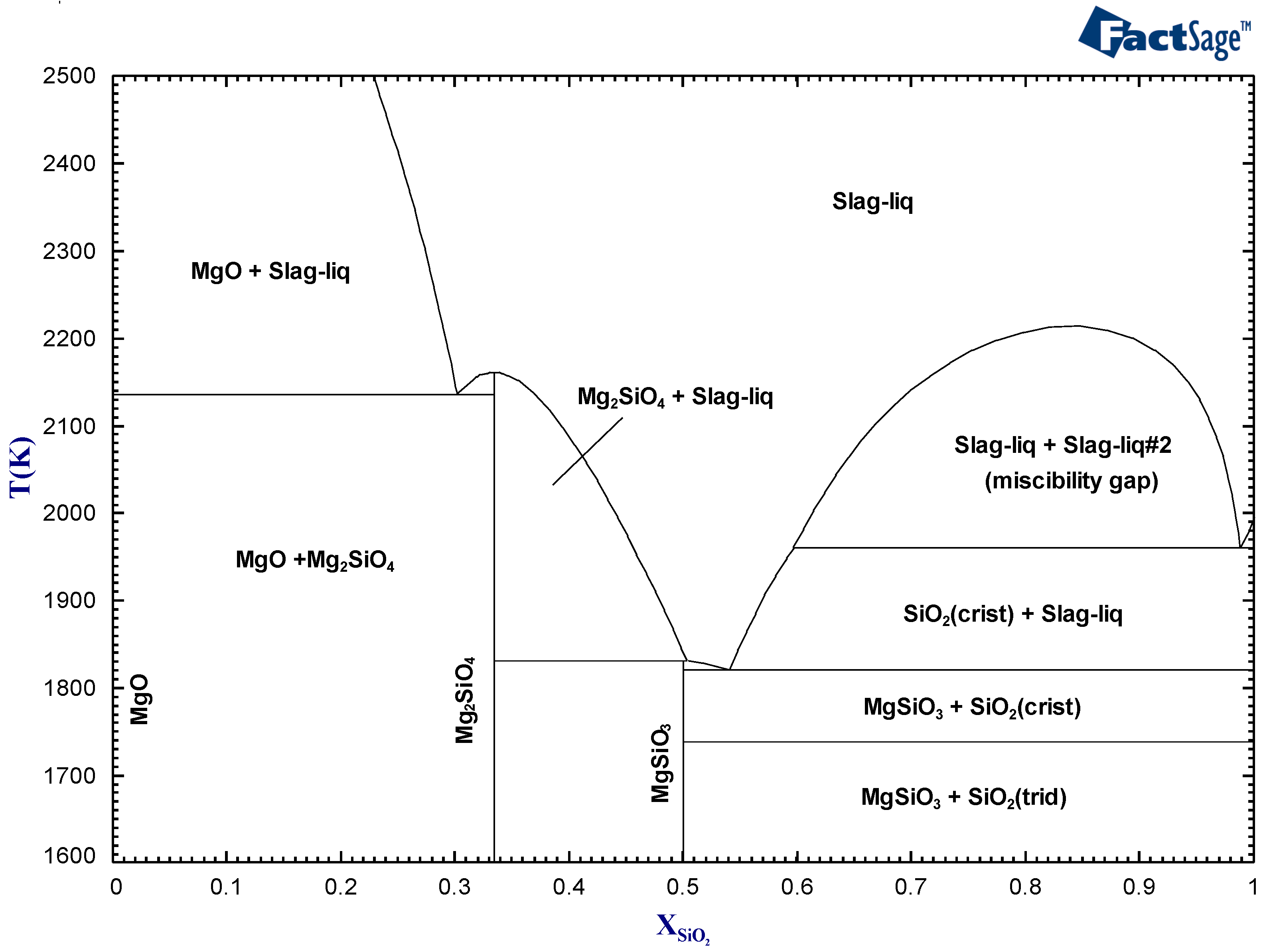
A stoichiometric compound is a phase that can, to a good approximation, be represented by having a single chemical composition. It appears as a vertical line on conventional phase diagrams (ex.: Mg
SiO
and MgSiO
in
Figure 1). These phases are typically forming in multicomponent systems that have a large and negative enthalpy of mixing. The strong heterogeneous chemical interactions stabilize these compounds.
The Gibbs energy function of a stoichiometric phase, i.e.,
, is defined as follows:
Equation (
1) is built using three fundamental thermodynamic properties: the specific standard enthalpy of formation (
), the specific isobaric heat capacity (
) and the specific standard entropy (
). It is to be noted here that the absolute enthalpy of a system is not accessible in classical thermodynamics as nuclear and weak forces are not described. To overcome this limitation, we use reference states to express this quantity. Historically, the thermodynamic community has set the enthalpy of pure elements in their stable state at standard temperature and pressure conditions (298.15 K and 10
Pa) to be equal to zero [
5]. The specific standard entropy is evaluated by integrating the isobaric heat capacity from 0K to the reference temperature:
Equation (
2) requires the measurement of the low temperature behavior of the isobaric heat capacity. For many stable and most metastable compounds, experimental heat capacity data are not available, especially in the low temperature range. Traditionally, the CALPHAD community used to estimate unknown
(and heat capacities) using the Neumann–Kopp rule [
6]. This rule simply assumes a linear behavior of the estimated thermodynamic property versus composition. For disordered solid solutions and molten phases, the Kopp–Neumann rule has been proven to be a good approximation in many cases. However, for stoichiometric compounds, it has severe limitations, mainly related to the difference in the electronic structure between the compound and its constituent elements (in their stable solid structures). To overcome this lack of experimental data, it is nowadays possible to use atomistic simulations based on Density Functional Theory (DFT) using the Kohn–Sham approximation [
7,
8]. Ground-state DFT simulations of solid phases have shown a very good accuracy in predicting the enthalpy of formation, elastic properties, and phonon spectrum within reasonably low calculation times, especially for inorganic materials [
9]. The quasi-harmonic approximation is typically coupled with DFT simulations to evaluate the
evolution of a given solid phase as a function of temperature [
10]. Examples of our DFT simulations based on a thermodynamically self-consistent method [
11,
12] used to determine the
function of compounds are illustrated in
Figure 2 for the AlNi
Ti phase (a Heusler compound with an
structure—Fm
m) and for the Al
Zr intermetallic (D0
structure—I4/mmm), respectively. In this figure, the heat capacities of these two compounds have been predicted from DFT simulations and compared with available experimental data. The introduction of both phonon (vibrational) and electronic contributions into the description of the isobaric heat capacity leads to an accurate prediction of each
(and therefore of the entropy as well when integrated from 0 K) as shown in this figure.
In contrast, a solution is a phase that is thermodynamically stable over a range of composition. It is formed by mixing different components that have a specific Gibbs free energy
. For solids, it implies the definition of sub-lattices occupied by specific components. The presence of vacancies and interstitial as well as substitutional defects can be considered using models such as the Compound Energy Formalism (CEF) [
15]. For liquid solutions, there is no long-range chemical ordering which leads to a loss of periodic symmetry. Strong chemical interactions between the components of a solution may lead to short-range chemical ordering which can be described with thermodynamic approaches like the Modified Quasichemical Model (MQM) [
16]. The slag phase in
Figure 1 is an example of a solution. The general expression used to describe the specific Gibbs free energy of a solution is formulated as follows:
with
In Equation (
3), two contributions need to be defined: (1) the mechanical mixing term
which accounts for the individual energetic contribution of each component of the solution (
) weighted by their mole fractions (
), and (2) the Gibbs energy of mixing
, which is directly linked to the strength of the chemical interactions in the system. Different approaches exist in the literature to express
. For solid solutions, the cluster variation method and the cluster site approximations may be used to describe
of solid solutions that show order–disorder transitions. For liquid solutions, the quasichemical formalism is suited to describe short-range ordering in the liquid phase by allowing coordination numbers to change with composition.
A list of a few technologically important compounds that form in metallic alloys is presented in
Table 1. A similar list of some solutions that must be considered when performing metallurgical process simulations is shown in
Table 2.
2.2. Calphad Approach and Thermodynamic Databases
Nowadays, the CALPHAD (CALculation of PHAse Diagrams) methodology is widely used to develop thermodynamic databases for diverse systems. It was originally introduced by Kaufman and Bernstein in the 1960s [
17] and first applied to metallic systems. The main aim is to be able to predict phase equilibria in multicomponent systems, using the model parameters obtained for the lower-order (mainly binary and ternary) subsystems along with interpolation methods [
18], thus avoiding tedious and costly experiments. As a first step, the Gibbs free energies of the pure (unary) components (for instance, NaCl, MgCl
, CaCl
and MnCl
in the case of the NaCl-MgCl
-CaCl
-MnCl
quaternary system) need to be defined, based on the available thermodynamic properties (standard enthalpy at 298.15 K, standard entropy at 298.15 K, and heat capacity as a function of temperature). Then, for every binary subsystem of the multicomponent system of interest, all available experimental data (i.e., phase diagram, enthalpy of mixing of the liquid, activities derived from
emf measurements, enthalpy of formation at 298.15 K of an intermediate compound, etc.) are collected from the literature and critically evaluated in order to obtain a set of model parameters for all phases involved. In this way, the data are rendered self-consistent and discrepancies among them are identified.
For instance, let us consider the NaCl-MnCl
binary system, which was modelled previously [
19]. The liquid phase was modelled using the Modified Quasichemical Model for short-range ordering [
16], and an expression of its Gibbs free energy as a function of temperature and composition was obtained. The calculated phase diagram, enthalpy of mixing of the liquid at 1083.15 K, and activity of NaCl (relative to liquid standard state) in the liquid at 885.15 K and 1085.15 K are shown along with the available measurements in
Figure 3,
Figure 4, and
Figure 5, respectively. As can be seen in
Figure 3, there are five stoichiometric compounds (Na
MnCl
, Na
MnCl
, Na
Mn
Cl
, Na
Mn
Cl
, and NaMn
Cl
). The enthalpies of formation from solid NaCl and MnCl
of Na
MnCl
, Na
MnCl
, Na
Mn
Cl
, and metastable Na
Mn
Cl
(ilmenite structure) at 298.15 K have been measured by solution calorimetry. In addition, the Gibbs free energy changes for various reactions of formation of the five intermediate compounds have been measured over specific temperature ranges using an
emf technique. All these data are reproduced by the model within the experimental error limits [
19]. A similar approach needs to be used for all remaining subsystems of the multicomponent system of interest (i.e., NaCl-MgCl
, NaCl-CaCl
, MgCl
-CaCl
, MgCl
-MnCl
and CaCl
-MnCl
for NaCl-MgCl
-CaCl
-MnCl
). If only phase diagram data are available for a given binary subsystem, some assumptions may have to be made. For instance, for MgCl
-MnCl
, a solid solution was reported over the entire composition range [
20]. Thus, in principle, there is an infinite number of sets of excess Gibbs free energy expressions for the solid solution and the liquid phase permitting one to reproduce the experimental phase diagram. However, owing to the very similar cationic radii of Mg
and Mn
[
21], the MgCl
-MnCl
liquid can be assumed to be close to ideality, thus permitting one to model the solid solution unambiguously. Calorimetric measurements at 1083.15 K exhibiting a maximum enthalpy of mixing of about 350 J/mol confirm the validity of this assumption [
20]. For a given binary subsystem, if there are only liquidus data and if negligible solid solubility is observed, then only the chemical potentials of the two components in the liquid phase along the liquidus are defined. In that case, in the absence of enthalpy of mixing data, only enthalpic parameters without any excess non-ideal entropic parameters ought to be introduced in the optimized excess Gibbs free energy of the liquid phase. Finally, if phase diagram data are lacking, estimations might be made from a chemically similar binary system for which such data are available. Although the corresponding results might not be quantitatively accurate, a reasonable trend should be observed.
The third and final step in developing a database for the multicomponent liquid solution is to choose a suitable interpolation method for every ternary subsystem of the multicomponent system of interest, whereby the thermodynamic properties of any ternary subsystem can be estimated from the optimized model parameters of the corresponding binary subsystems. If experimental ternary data are available, then empirical ternary interaction parameters describing the mutual interaction between all three components may be included in the liquid model. All model parameters are stored in a thermodynamic database, and the models can then be used along with a Gibbs free energy minimization software to make predictions in the multicomponent system. For molten salts, the Kohler-like (symmetric) and Kohler–Toop-like (asymmetric) interpolation methods are commonly used [
29]. For instance, the NaCl-MgCl
-CaCl
-MnCl
subsystem comprises the monovalent alkali cation Na
and the divalent cations Mg
, Ca
and Mn
. Therefore, the MgCl
-CaCl
-MnCl
subsystem was designated as symmetric, whereas the three remaining ternary subsystems were asymmetric with NaCl as the asymmetric component [
19]. For salt systems, when ternary model parameters are required, both their number and amplitude are often not large. For the NaCl-MgCl
-CaCl
-MnCl
subsystem, to our knowledge, no ternary data are available in the literature. However, quaternary data were reported [
19]. As an example, the calculated section at a constant mass ratio MgCl
/CaCl
/MnCl
= 1/1/1 is compared with the available measurements in
Figure 6. The various solid solutions were modelled with the Compound Energy Formalism [
15]. The calculations in
Figure 6 were made using only the optimized model parameters for the six binary subsystems; they show that the Modified Quasichemical Model is well suited to perform reliable calculations in multicomponent salt systems. The thermodynamic models for the NaCl-MgCl
-CaCl
-MnCl
system and for several other chloride, fluoride, and chloro-fluoride systems are available in the FTsalt database of FactSage [
4].
2.3. Stable State vs. Metastable State
A point of fundamental importance when simulating thermodynamic aspects of a real-life pyrometallurgical process is to distinguish between stable and metastable phases. It is common that a thermodynamically stable phase cannot form because of kinetic constraints. The manufacturing of alloys usually involves the generation of a liquid phase followed by its rapid solidification. At this point, the material is thermodynamically unstable and requires energy to reach a desired pseudo-stable state. Heat treatments are subsequently performed to enhance solid diffusion and to promote phase transitions. As an example, carbon saturation in iron is typically defined in metallurgy by establishing a metastable equilibrium with cementite (Fe
C). Graphite, which can lower the Gibbs free energy of the system, is not easily formed.
Figure 7a shows the Fe-C phase diagram calculated using graphite (blue line) and cementite (red line), respectively, as the C-saturating phases. At a temperature of 1200 K, the carbon solubility in Fe-FCC is lower when graphite is considered as it is slightly more thermodynamically stable than cementite.
It is possible to account for the metastability of a given phase by considering it as dormant in an equilibrium calculation. In this calculation mode, the dormant phase is not part of the phase assemblage, but its activity (also called affinity) is evaluated [
3].
Figure 7b illustrates graphically how to calculate the activity of a dormant phase—in this case, graphite. The red line in this figure defines the Gibbs free energy hyperplane of the metastable equilibrium state (with
the chemical potential of species i), while the blue line defines the Gibbs free energy of the dormant phase (in this case graphite). The calculation of a phase activity ultimately allows the evaluation of the thermodynamic driving force (
) for the formation of this dormant phase, which is expressed as follows:
Equation (
5) shows that the closer the activity of the dormant phase is to unity, the smaller is the thermodynamic driving force for its formation. In our example (i.e.,
Figure 7b), dormant graphite has an activity of 1.06 at 1200 K at cementite saturation, which represents a small thermodynamic driving force for its formation. A phase with an activity that is lower than one is not stable.
2.4. Isobaric-Isothermal NPT Ensemble Phase Equilibria
At the atomic scale, the available internal energy
U of a given chemical system is quantified by a potential contribution (
) and a kinetic contribution (
). The potential internal energy arises from the chemical interactions (i.e., electromagnetic forces) between the species that constitute the system while the kinetic internal energy is a direct consequence of the atomic vibration induced by temperature. The first law of thermodynamics defines how this state property changes as a function of the imposed conditions. For a reversible process performed on a closed system, this can be expressed as follows:
The entropy
S and volume
V are rarely controlled parameters in real-life applications. Pyro-metallurgical reactors are most of the time controlled by constraining their temperature
T, their pressure
P, and their mass balances that are expressed using a vector
n. In this case, the Gibbs free energy
G is the adequate thermodynamic function to be analyzed:
The basis of computational thermochemistry is therefore to define the Gibbs free energy of the system .
2.5. Thermodynamic Constraints Used in Process Simulations
One misconception about computational thermochemistry is that it cannot represent a dynamic system that has not reached its equilibrium state. At any time t, classical thermodynamics will correctly define the state of the system if adequate constraints are used to perform the equilibrium calculations. These constraints can be deformations , stresses , chemical potentials , molar ratios , etc. The challenge is then to identify which constraints need to be applied to evaluate the equilibrium state at time t.
In pyro-metallurgical applications, chemical potentials
(not mass balances) are often required to constrain the phase assemblage evolution of a system. The corrosion of refractories by a molten alloy is a perfect example. In this case, there is always enough mass of the reactive/corrosive element(s) to promote the surface reaction. The growth of the corrosion product layer will be limited by diffusion (
Figure 8).
For completely solid systems that are initially not at equilibrium, it is also possible to identify elements that diffuse substantially faster than others. Diffusion of carbon and hydrogen in austenitic stainless steels via interstitial site displacements is one example. In this case, we assume that the molar ratios of the non-diffusing elements (i.e., Fe, Cr, Ni) are constant. This type of constrained calculations is called para-equilibrium and is of prime importance in the thermodynamic study of metallic materials. It is to be noted that it is also possible to constrain the chemistry of a given phase to match for example experimental evidence.
Finally, with the advent of new thermodynamic models of solid solutions that explicitly account for the effect of atomic inter-distances in the description of the enthalpy, we can now impose volumetric constraints to solidified alloys to predict their initial state. The stored internal potential energy released upon heat treatments and the resulting phase transitions can be evaluated with this approach.