A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations
Abstract
:1. Introduction
- Regarding that, a projected literature review on a number of highlighted research studies are demonstrated (Section 4).
- A new perspective of FJSSP is outlined and tackled through a case study (Section 5).
- A proposed two stages approach is designed considering improved steps to enhance the neighborhoods shaking search (Section 6).
- Finally, the results and conclusion are present in Section 7, followed by the future discussion.
2. JSSP Evolution
3. Heuristics
3.1. Heuristics
3.2. Common Components of Heuristic Based Algorithms
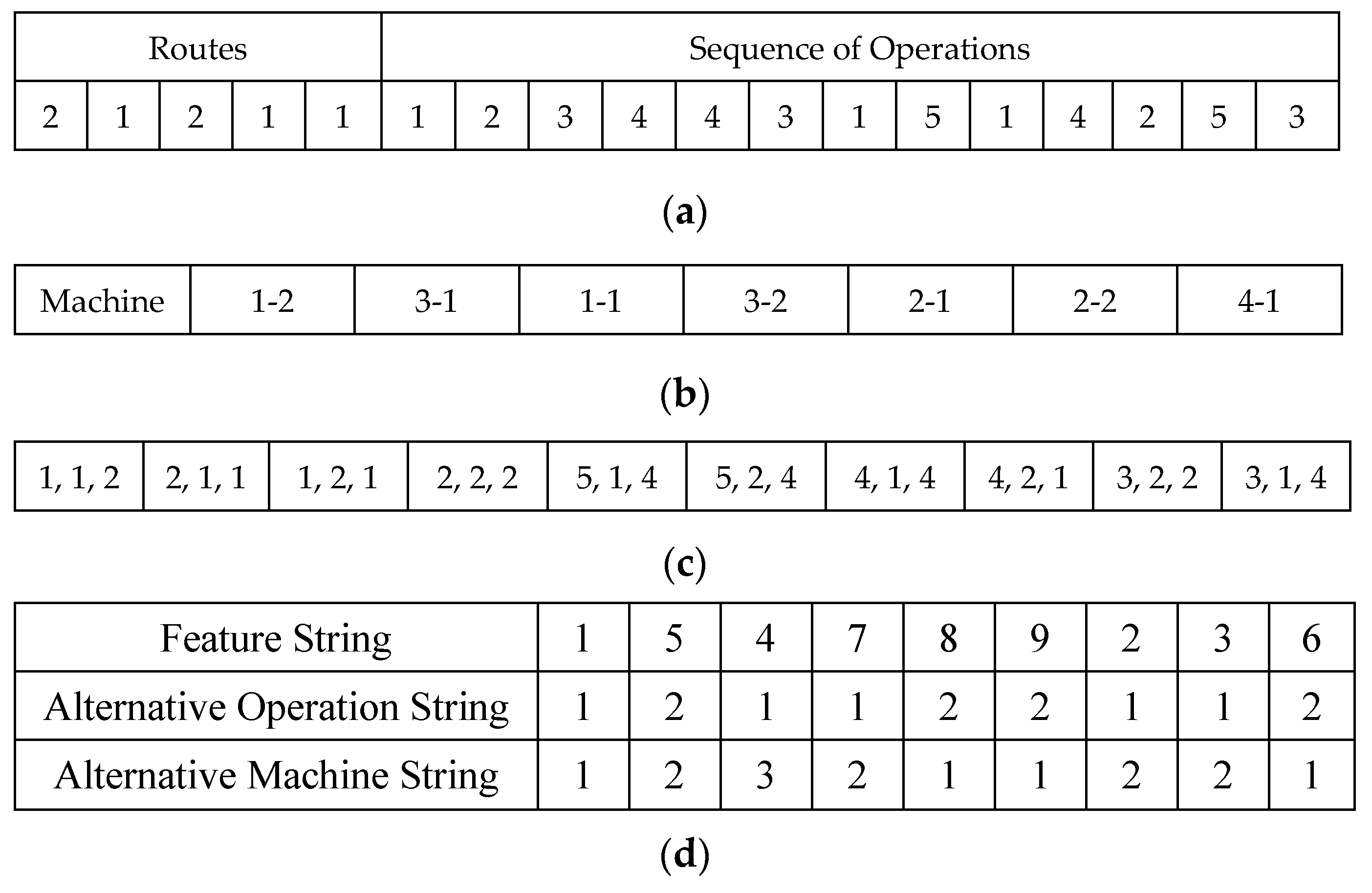
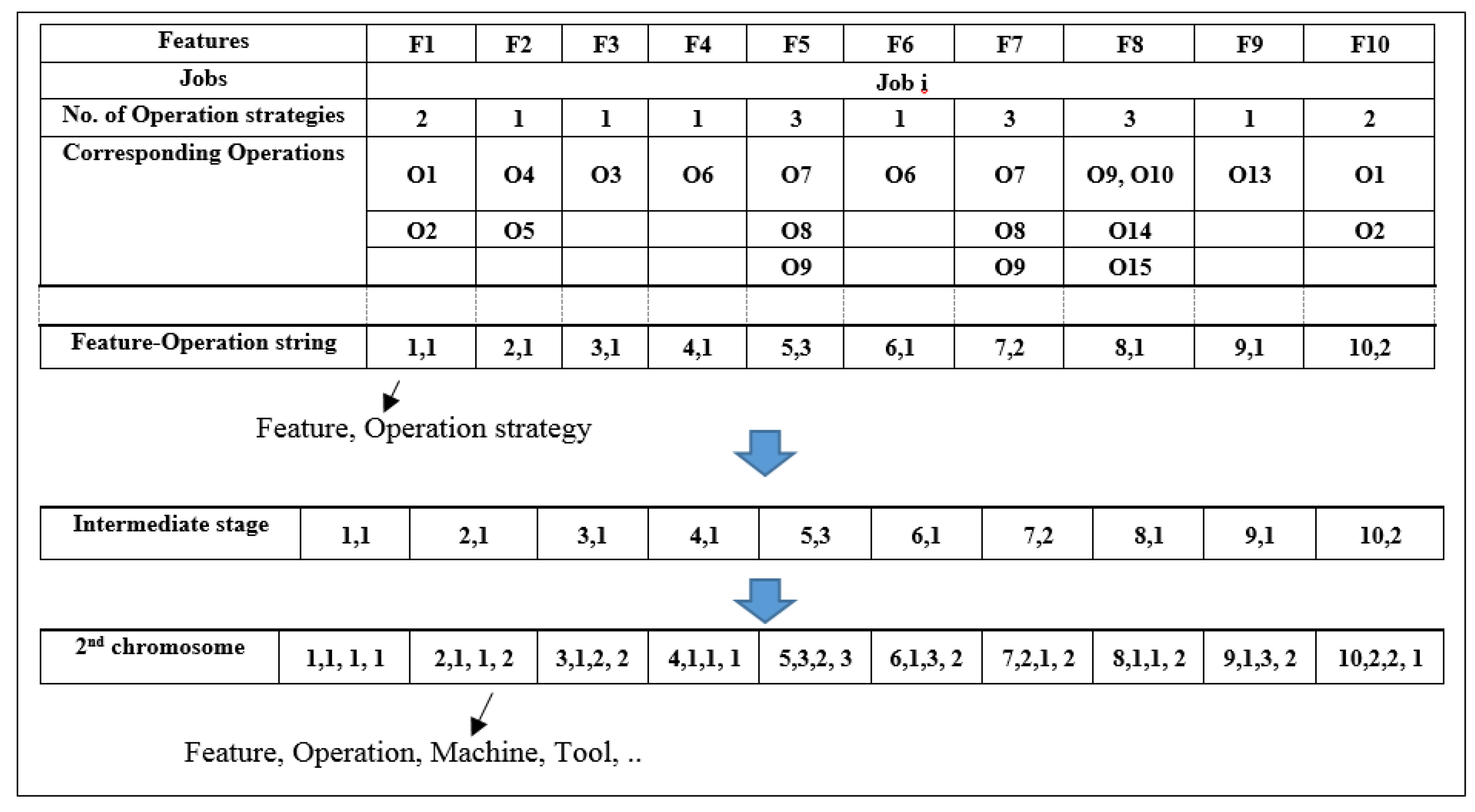
3.2.1. Problem Encoding and Decoding
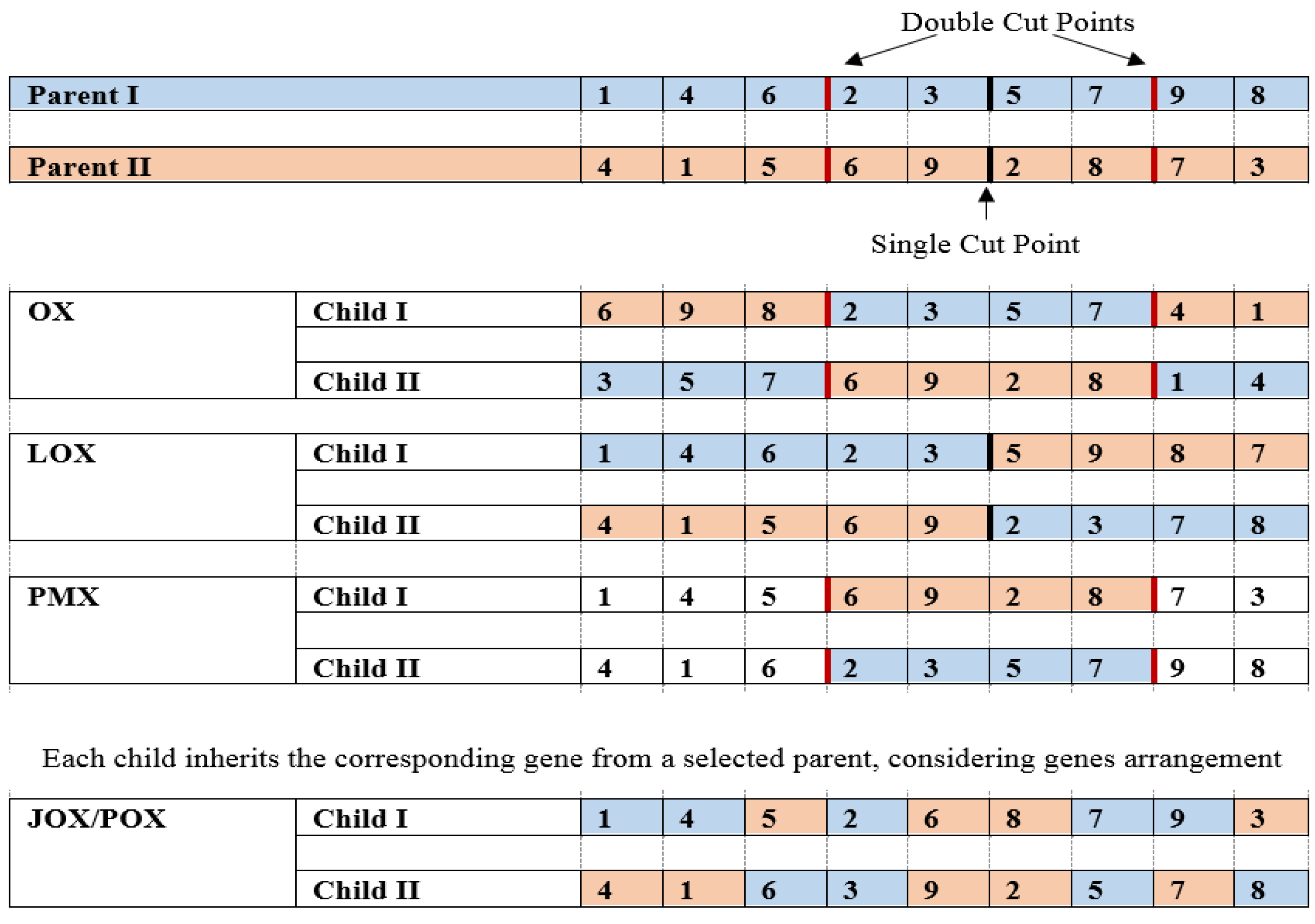
3.2.2. Mating Procedures
- a.
- Crossover Procedure
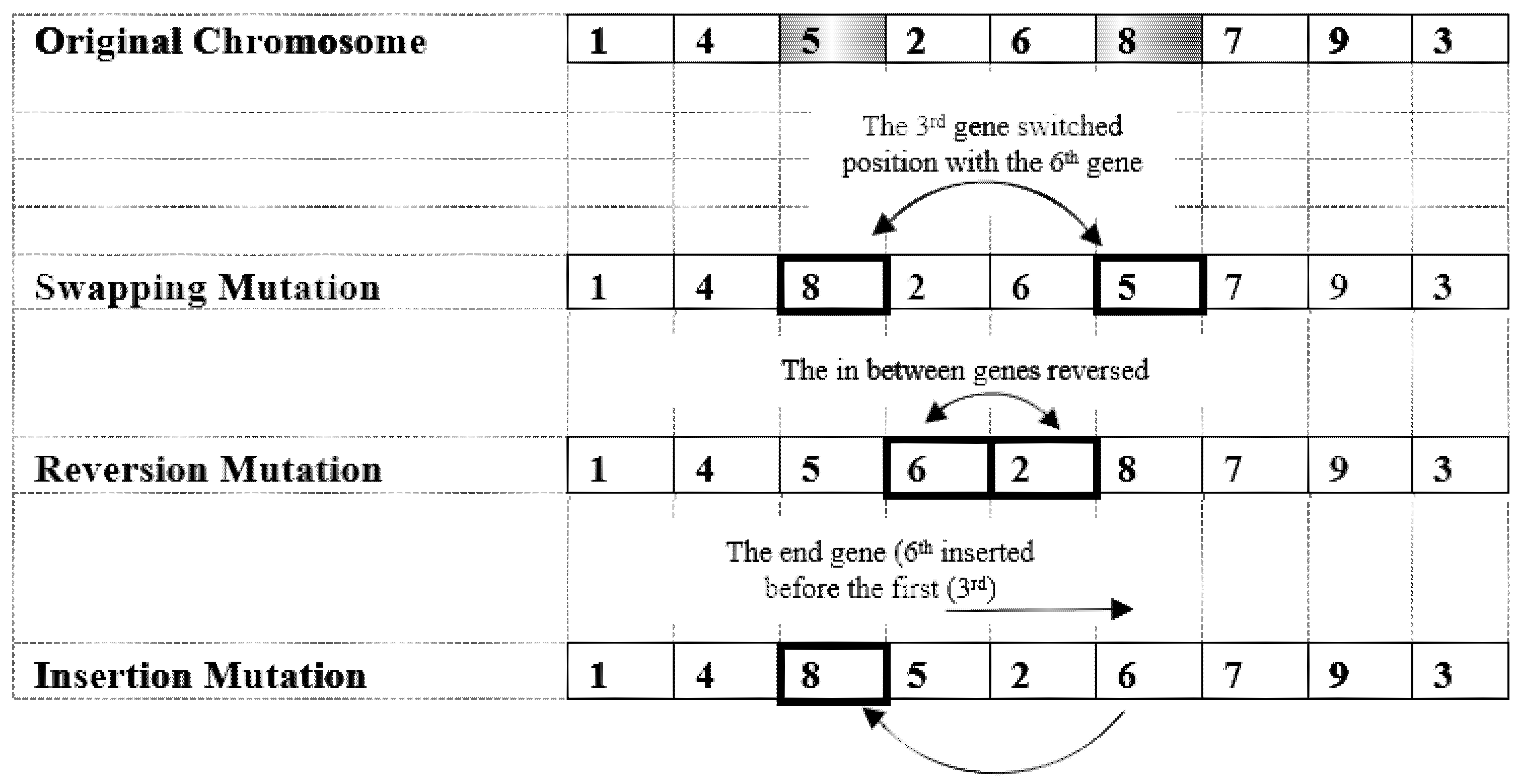
- b.
- Mutation Procedure
- c.
- Selection Procedure
- d.
- Objective Function
4. Literature Review
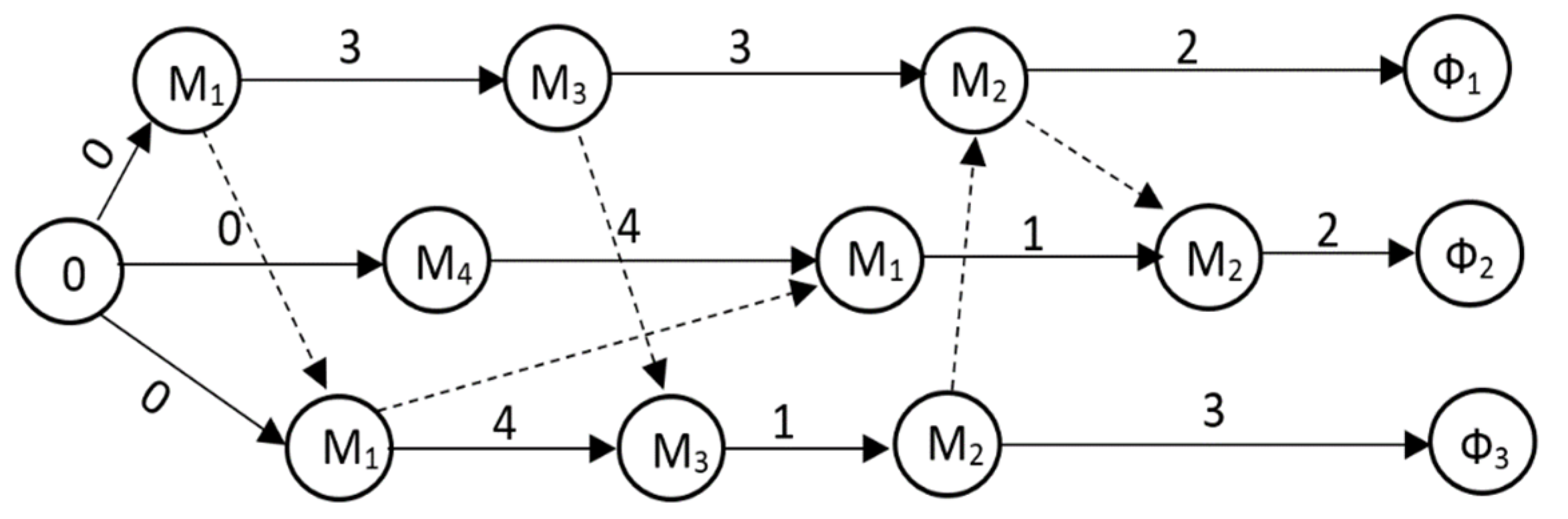
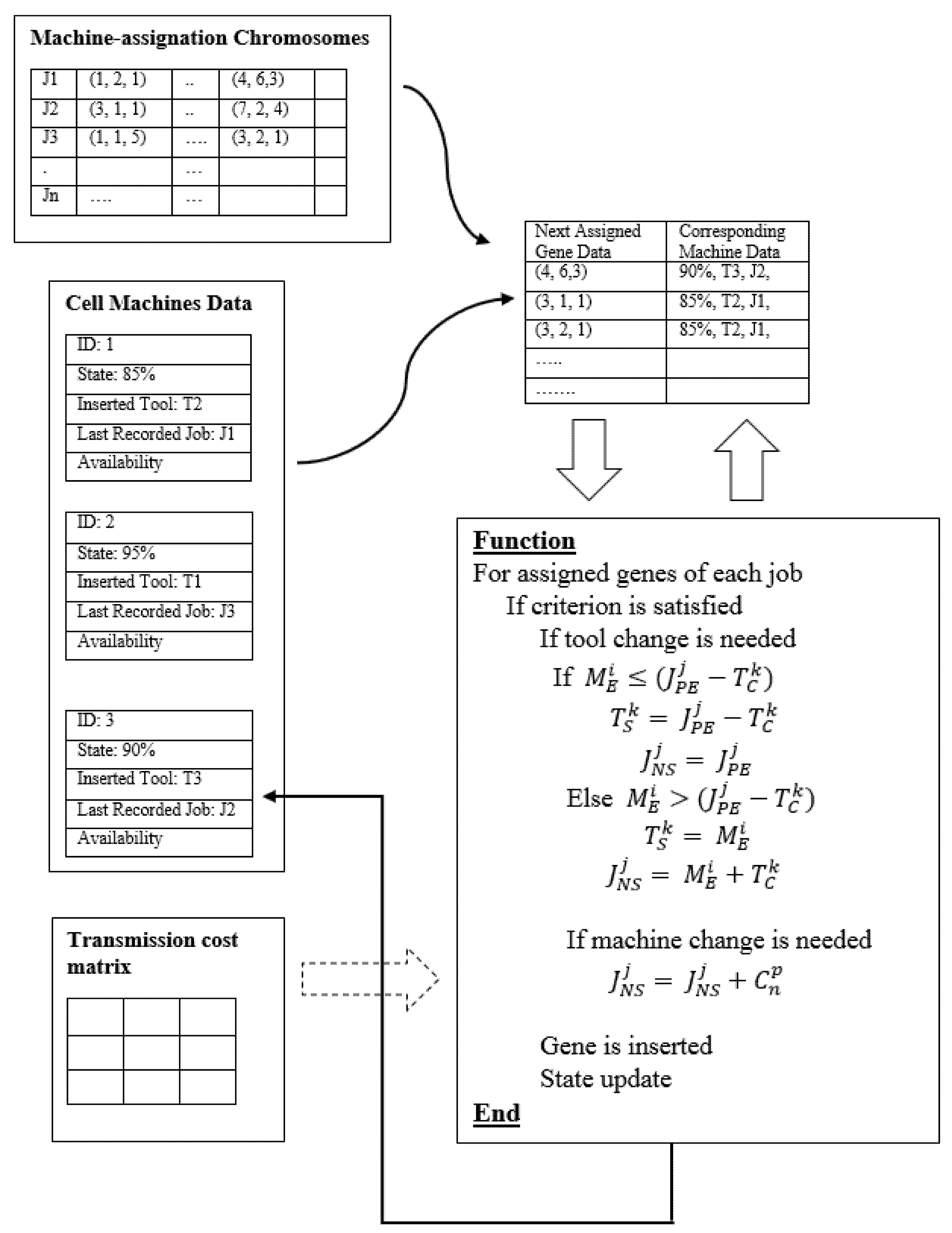
5. Case Study Formulation
- (1)
- Each work-piece has its job that is independent from others.
- (2)
- Each machine within the cell can process a single job per time, and each machining concurrent time slot can only has a job once.
- (3)
- No job pre-emption present.
- (4)
- A machine availability is governed by its efficiency.
- (5)
- An operation may be performed by multiple machines.
- (6)
- Processing a job along machines takes into count the transmission time, no immediate processing.
- (7)
- Tool insertion setup time is considered.
- (8)
- Supporting flexibility, alternative strategies for machining present in more than a level: feature level, process level and machine level.
- (9)
- Precedence constraints are considered during feature-operation level or operation machine level.
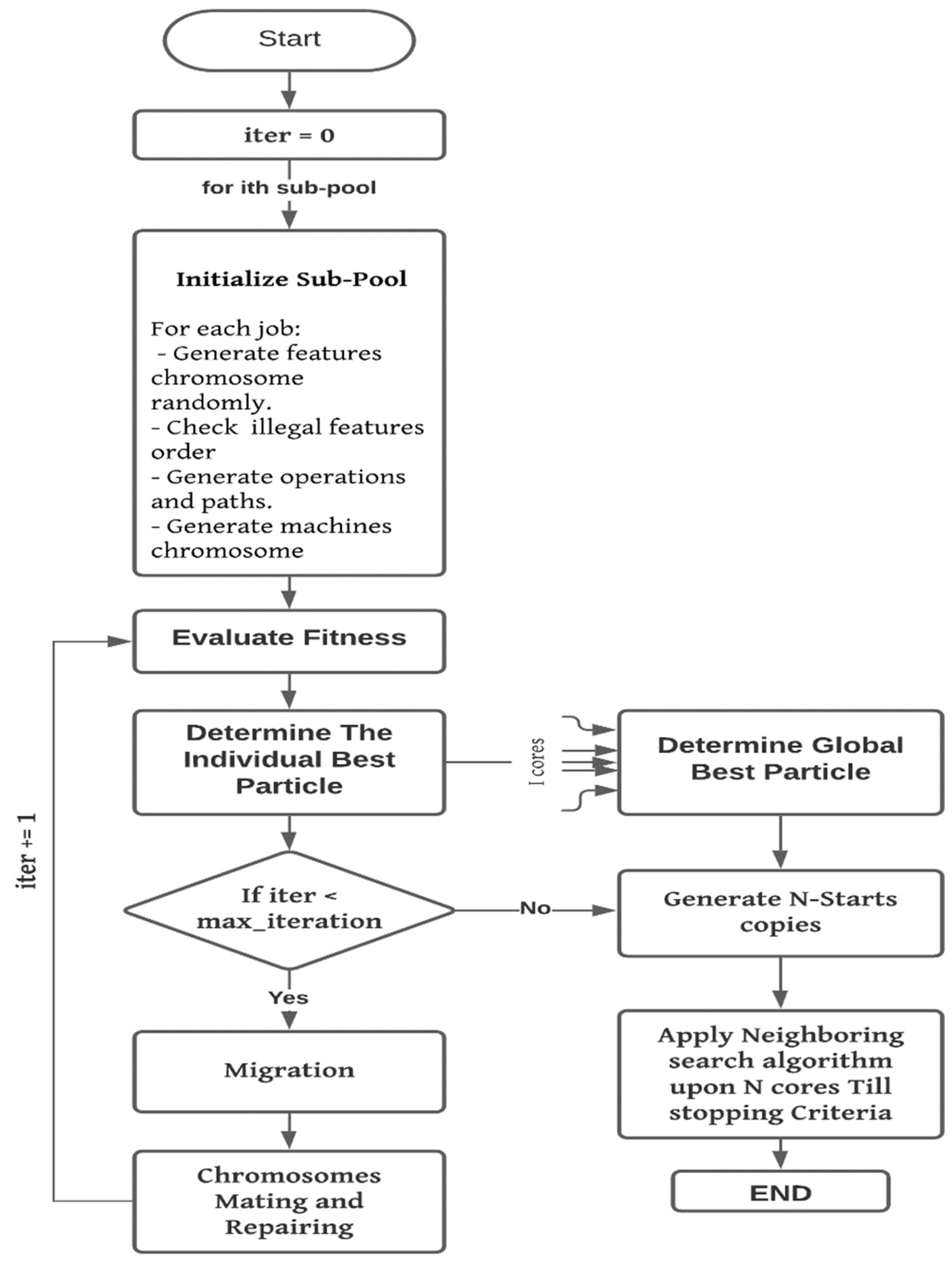
6. The Proposed Algorithm
6.1. Coding Steps
6.2. Path Creation Phase
6.3. Mating Phase
6.3.1. Crossover
6.3.2. Mutation Procedure
6.3.3. Precedence Repairing Mechanism
6.4. Objective Function
6.5. Neighborhood Searching Algorithm
6.5.1. Modified SA
6.5.2. Modified TS
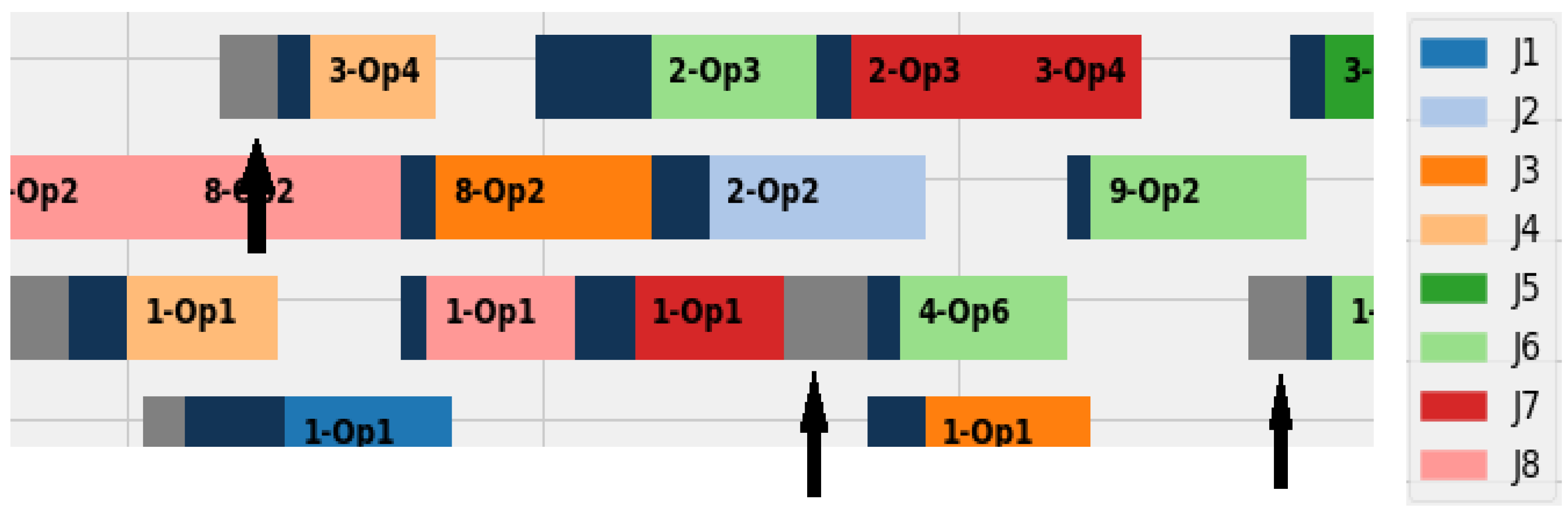
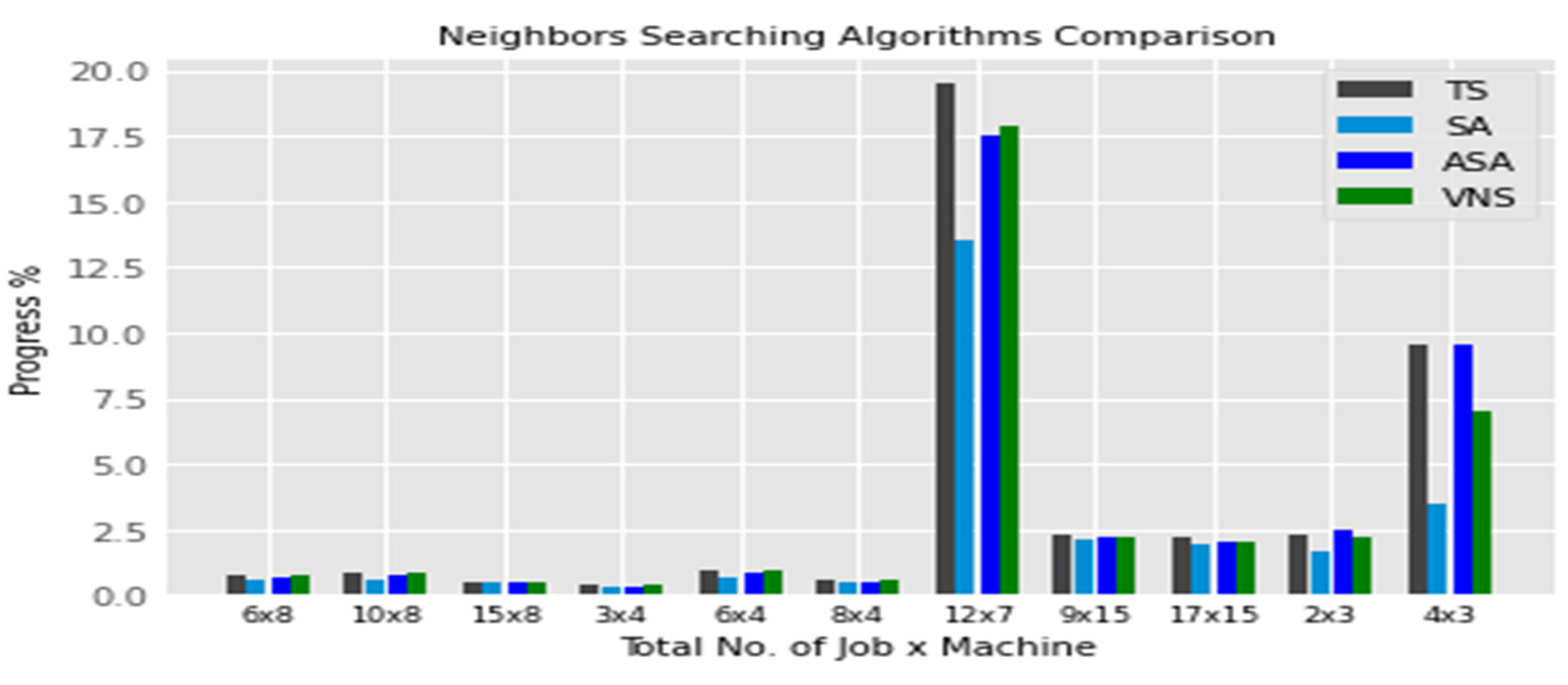
7. Results and Discussions
- Minimum transmission cost.
- Workload to maintenance balance based.
- Minimum make-span.
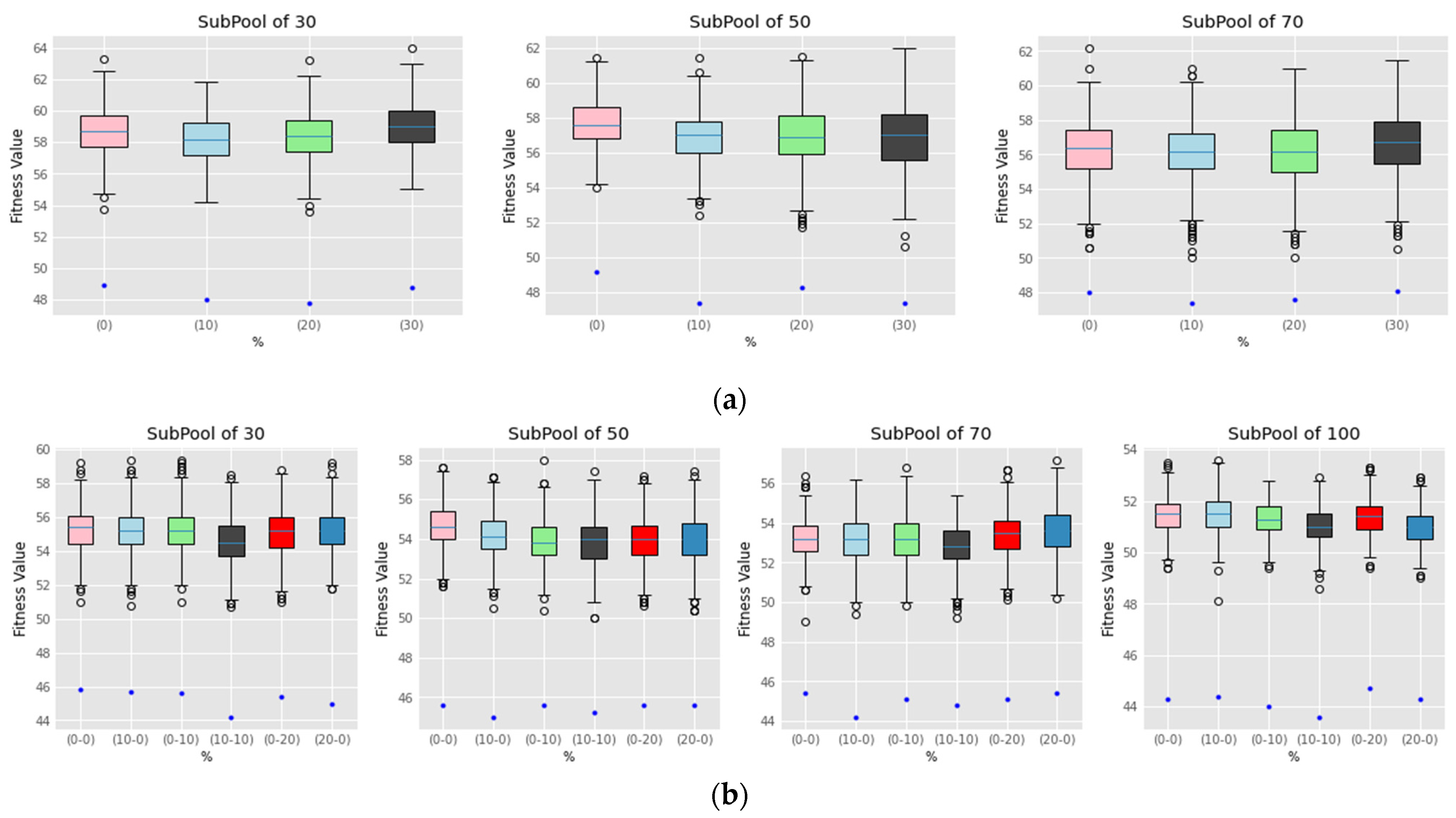
7.1. Experiments Set
7.2. Experiments Set 2
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pereira, A.C.; Romero, F. A review of the meanings and the implications of the Industry 4.0 concept. Procedia Manuf. 2017, 13, 1206–1214. [Google Scholar] [CrossRef]
- Dalenogarea, L.S.; Beniteza, G.B.; Ayalab, N.F.; Franka, A.G. The expected contribution of Industry 4.0 technologies for industrial performance. Int. J. Prod. Econ. 2018, 204, 383–394. [Google Scholar] [CrossRef]
- Gronau, N. Determining the appropriate degree of autonomy in cyber-physical production systems. CIRP J. Manuf. Sci. Technol. 2019, 26, 70–80. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y.; Wang, B.; Yao, S.; Liu, Z. Review on cyber-physical systems. IEEE/CAA J. Autom. Sin. 2017, 4, 27–40. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Wang, L.; Nee, A. Digital Twins and Cyber–Physical Systems toward Smart Manufacturing and Industry 4.0: Correlation and Comparison. Engineering 2019, 5, 653–661. [Google Scholar] [CrossRef]
- Vachalek, J.; Bartalsky, L.; Rovny, O.; Sismisova, D.; Morhac, M.; Loksik, M. The digital twin of an industrial production line within the industry 4.0 concept. In Proceedings of the 2017 21st International Conference on Process Control (PC), Strbske Pleso, Slovakia, 6–9 June 2017; pp. 258–262. [Google Scholar] [CrossRef]
- Koulamas, C.; Kalogeras, A. Cyber-Physical Systems and Digital Twins in the Industrial Internet of Things Cyber-Physical Systems. Computer 2018, 51, 95–98. [Google Scholar] [CrossRef]
- de Sousa Jabbour, A.B.L.; Jabbour, C.J.C.; Foropon, C.; Godinho Filho, M. When titans meet—Can industry 4.0 revolutionise the environmentally-sustainable manufacturing wave? The role of critical success factors. Technol. Forecast. Soc. Chang. 2018, 132, 18–25. [Google Scholar] [CrossRef]
- Tolio, T.; Copani, G.; Terkaj, W. Key esearch priorities for factories of the future: The Italian flagship initiative. In Factories of the Future: The Italian Flagship Initiative; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–494. [Google Scholar]
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent Manufacturing in the Context of Industry 4.0: A Review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Fisher, O.; Watson, N.; Porcu, L.; Bacon, D.; Rigley, M.; Gomes, R.L. Cloud manufacturing as a sustainable process manufacturing route. J. Manuf. Syst. 2018, 47, 53–68. [Google Scholar] [CrossRef]
- Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ausaf, M.F.; Li, X.; Gao, L. Optimization algorithms for integrated process planning and scheduling problem—A survey. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 5287–5292. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Shao, X. An active learning genetic algorithm for integrated process planning and scheduling. Expert Syst. Appl. 2012, 39, 6683–6691. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Wen, X. Application of an efficient modified particle swarm optimization algorithm for process planning. Int. J. Adv. Manuf. Technol. 2013, 67, 1355–1369. [Google Scholar] [CrossRef]
- Barzanji, R.; Naderi, B.; Begen, M.A. Decomposition algorithms for the integrated process planning and scheduling problem. Omega 2020, 93, 102025. [Google Scholar] [CrossRef]
- Guo, Y.; Li, W.; Mileham, A.; Owen, G. Applications of particle swarm optimisation in integrated process planning and scheduling. Robot. Comput. Manuf. 2009, 25, 280–288. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, P. A Cyber-physical System Architecture in Shop Floor for Intelligent Manufacturing. Procedia Cirp 2016, 56, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Gyulai, D.; Bergmann, J.; Gallina, V.; Gaal, A. Towards a connected factory: Shop-floor data analytics in cyber-physical environments. Procedia Cirp 2019, 86, 37–42. [Google Scholar] [CrossRef]
- Zhang, M.; Tao, F.; Nee, A. Digital Twin Enhanced Dynamic Job-Shop Scheduling. J. Manuf. Syst. 2021, 58, 146–156. [Google Scholar] [CrossRef]
- Coelho, P.; Pinto, A.; Moniz, S.; Silva, C. Thirty Years of Flexible Job-Shop Scheduling: A Bibliometric Study. Procedia Comput. Sci. 2021, 180, 787–796. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Shukla, A.K.; Nath, R.; Akinyelu, A.A.; Agushaka, J.O.; Chiroma, H.; Muhuri, P.K. Metaheuristics: A comprehensive overview and classification along with bibliometric analysis. Artif. Intell. Rev. 2021, 54, 4237–4316. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Harifi, S.; Mohammadzadeh, J.; Khalilian, M.; Ebrahimnejad, S. Giza Pyramids Construction: An ancient-inspired metaheuristic algorithm for optimization. Evol. Intell. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Stegherr, H.; Heider, M.; Hähner, J. Classifying Metaheuristics: Towards a unified multi-level classification system. Nat. Comput. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Mohan, J.; Lanka, K.; Rao, A.N. A Review of Dynamic Job Shop Scheduling Techniques. Procedia Manuf. 2019, 30, 34–39. [Google Scholar] [CrossRef]
- Johar, F.M.; Azmin, F.A.; Suaidi, M.K.; Shibghatullah, A.; Ahmad, B.H.; Salleh, S.N.; Aziz, M.Z.A.A.; Shukor, M.M. A review of Genetic Algorithms and Parallel Genetic Algorithms on Graphics Processing Unit (GPU). In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering; Institute of Electrical and Electronics Engineers (IEEE), Penang, Malaysia, 29 November–1 December 2013; Volume 8, pp. 264–269. [Google Scholar]
- Somani, A.; Singh, D.P. Parallel Genetic Algorithm for solving Job-Shop Scheduling Problem Using Topological sort. In Proceedings of the 2014 International Conference on Advances in Engineering Technology Research (ICAETR-2014), Singapore, Singapore, 29–30 March 2014; pp. 1–8. [Google Scholar]
- Lin, G.; Yao, X.; Macleod, I.; Kang, L.; Chen, Y. Parallel genetic algorithm on PVM. Wuhan Univ. J. Nat. Sci. 1996, 1, 605–610. [Google Scholar] [CrossRef]
- Luo, J.; El Baz, D.; Xue, R.; Hu, J. Solving the dynamic energy aware job shop scheduling problem with the heterogeneous parallel genetic algorithm. Futur. Gener. Comput. Syst. 2020, 108, 119–134. [Google Scholar] [CrossRef]
- Coelho, P.; Silva, C. Parallel Metaheuristics for Shop Scheduling: Enabling Industry 4.0. Procedia Comput. Sci. 2021, 180, 778–786. [Google Scholar] [CrossRef]
- Cheng, J.R.; Gen, M. Accelerating genetic algorithms with GPU computing: A selective overview. Comput. Ind. Eng. 2019, 128, 514–525. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Liu, T.-K.; Chen, Y.-P.; Chou, J.-H. Solving Distributed and Flexible Job-Shop Scheduling Problems for a Real-World Fastener Manufacturer. IEEE Access 2014, 2, 1598–1606. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yin, H.L.; Wang, J. Genetic algorithm with new encoding scheme for job shop scheduling. Int. J. Adv. Manuf. Technol. 2009, 44, 977–984. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Li, D.; Murlidhar, B.R.; Armaghani, D.J.; Kassim, K.A.; Komoo, I. The effects of ABC, ICA, and PSO optimization techniques on prediction of ripping production. Eng. Comput. 2019, 36, 1355–1370. [Google Scholar] [CrossRef]
- Alharkan, I.; Saleh, M.; Ghaleb, M.A.; Kaid, H.; Farhan, A.; Almarfadi, A. Tabu search and particle swarm optimization algorithms for two identical parallel machines scheduling problem with a single server. J. King Saud Univ.-Eng. Sci. 2020, 32, 330–338. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, L.; Hu, B.; Lin, C. An Adaptive Scheduling Algorithm for Dynamic Jobs for Dealing with the Flexible Job Shop Scheduling Problem. Bus. Inf. Syst. Eng. 2019, 61, 299–309. [Google Scholar] [CrossRef] [Green Version]
- García-León, A.A.; Dauzère-Pérès, S.; Mati, Y. An efficient Pareto approach for solving the multi-objective flexible job-shop scheduling problem with regular criteria. Comput. Oper. Res. 2019, 108, 187–200. [Google Scholar] [CrossRef]
- Zheng, F.; Sui, Y. Bi-objective Optimization of Multiple-route Job Shop Scheduling with Route Cost. IFAC-Pap. 2019, 52, 881–886. [Google Scholar] [CrossRef]
- Defersha, F.M.; Rooyani, D. An efficient two-stage genetic algorithm for a flexible job-shop scheduling problem with sequence dependent attached/detached setup, machine release date and lag-time. Comput. Ind. Eng. 2020, 147, 106605. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Choi, I.-C.; Kim, S.-I.; Kim, H.-S. A genetic algorithm with a mixed region search for the asymmetric traveling salesman problem. Comput. Oper. Res. 2003, 30, 773–786. [Google Scholar] [CrossRef]
- Zalzala, A.M.S.; Fleming, P.J. Genetic Algorithms in Engineering Systems; Institution of Electrical Engineers: London, UK, 1997. [Google Scholar]
- Bierwirth, C. A generalized permutation approach to job shop scheduling with genetic algorithms. Oper. Res. Spectr. 1995, 17, 87–92. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Pan, Q.; Wan, L.; Chao, K.-M. An Effective Hybrid Genetic Algorithm and Variable Neighborhood Search for Integrated Process Planning and Scheduling in a Packaging Machine Workshop. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1933–1945. [Google Scholar] [CrossRef]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. [Google Scholar] [CrossRef] [Green Version]
- Nedjah, N.; de Macedo Mourelle, L. Real-World Multi-Objective System Engineering; Nova Publishers: Hauppauge, NY, USA, 2005. [Google Scholar]
- Ding, W.; Yurcik, W.J.; Yin, X. Outsourcing internet security: Economic analysis of incentives for managed security service providers. In International Workshop on Internet and Network Economics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 947–958. [Google Scholar]
- Ahmadi, E.; Zandieh, M.; Farrokh, M.; Emami, S.M. A multi objective optimization approach for flexible job shop scheduling problem under random machine breakdown by evolutionary algorithms. Comput. Oper. Res. 2016, 73, 56–66. [Google Scholar] [CrossRef]
- Singh, M.R.; Mahapatra, S. A quantum behaved particle swarm optimization for flexible job shop scheduling. Comput. Ind. Eng. 2016, 93, 36–44. [Google Scholar] [CrossRef]
- Li, X.; Peng, Z.; Du, B.; Guo, J.; Xu, W.; Zhuang, K. Hybrid artificial bee colony algorithm with a rescheduling strategy for solving flexible job shop scheduling problems. Comput. Ind. Eng. 2017, 113, 10–26. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Trentesaux, D.; Ammari, A.C.; Niar, S. Two stage particle swarm optimization to solve the flexible job shop predictive scheduling problem considering possible machine breakdowns. Comput. Ind. Eng. 2017, 112, 595–606. [Google Scholar] [CrossRef]
- Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng. 2020, 149, 106863. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y. A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 2018, 172, 3249–3264. [Google Scholar] [CrossRef]
- Che, A.; Wu, X.; Peng, J.; Yan, P. Energy-efficient bi-objective single-machine scheduling with power-down mechanism. Comput. Oper. Res. 2017, 85, 172–183. [Google Scholar] [CrossRef]
- Mokhtari, H.; Hasani, A. An energy-efficient multi-objective optimization for flexible job-shop scheduling problem. Comput. Chem. Eng. 2017, 104, 339–352. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.B.; Xu, Y.C.; Li, W.D. Energy-aware Integrated Process Planning and Scheduling for Job Shops. In Sustainable Manufacturing and Remanufacturing Management; Springer: Berlin/Heidelberg, Germany, 2019; pp. 13–36. [Google Scholar]
- Li, X.; Li, W.; He, F. A multi-granularity NC program optimization approach for energy efficient machining. Adv. Eng. Softw. 2018, 115, 75–86. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Shao, X.; Ren, Y. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot. Comput. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Mahmoodjanloo, M.; Tavakkoli-Moghaddam, R.; Baboli, A.; Bozorgi-Amiri, A. Flexible job shop scheduling problem with reconfigurable machine tools: An improved differential evolution algorithm. Appl. Soft Comput. 2020, 94, 106416. [Google Scholar] [CrossRef]
- Ambrogio, G.; Guido, R.; Palaia, D.; Filice, L. Job shop scheduling model for a sustainable manufacturing. Procedia Manuf. 2020, 42, 538–541. [Google Scholar] [CrossRef]
- Deng, G.; Su, Q.; Zhang, Z.; Liu, H.; Zhang, S.; Jiang, T. A population-based iterated greedy algorithm for no-wait job shop scheduling with total flow time criterion. Eng. Appl. Artif. Intell. 2020, 88, 103369. [Google Scholar] [CrossRef]
- Jing, Z.; Hua, J.; Yi, Z. Multi-objective Integrated Optimization Problem of Preventive Maintenance Planning and Flexible Job-Shop Scheduling. In Proceedings of the 23rd International Conference on Industrial Engineering and Engineering Management 2016; 2017; pp. 137–141. Available online: https://link.springer.com/chapter/10.2991/978-94-6239-255-7_25 (accessed on 20 September 2021). [CrossRef] [Green Version]
- Lin, C.-S.; Li, P.-Y.; Wei, J.-M.; Wu, M.-C. Integration of process planning and scheduling for distributed flexible job shops. Comput. Oper. Res. 2020, 124, 105053. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, R.; Peng, T.; Tao, L.; Jia, S. A method for minimizing the energy consumption of machining system: Integration of process planning and scheduling. J. Clean. Prod. 2016, 137, 1647–1662. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, M.; Chen, F. Single-machine-based joint optimization of predictive maintenance planning and production scheduling. Robot. Comput. Manuf. 2018, 51, 238–247. [Google Scholar] [CrossRef]
- Yavari, M.; Isvandi, S. Integrated decision making for parts ordering and scheduling of jobs on two-stage assembly problem in three level supply chain. J. Manuf. Syst. 2018, 46, 137–151. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.-J.; Zheng, L.-Y. Multi-Agent Based Hyper-Heuristics for Multi-Objective Flexible Job Shop Scheduling: A Case Study in an Aero-Engine Blade Manufacturing Plant. IEEE Access 2019, 7, 21147–21176. [Google Scholar] [CrossRef]
- Lu, P.-H.; Wu, M.-C.; Tan, H.; Peng, Y.-H.; Chen, C.-F. A genetic algorithm embedded with a concise chromosome representation for distributed and flexible job-shop scheduling problems. J. Intell. Manuf. 2018, 29, 19–34. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Li, C. The flexible job-shop scheduling problem considering deterioration effect and energy consumption simultaneously. Comput. Ind. Eng. 2019, 135, 1004–1024. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X. Flexible job-shop scheduling problem with job precedence constraints and interval grey processing time. Comput. Ind. Eng. 2020, 149, 106781. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, M.; Wang, Z.Y.; Zhu, Q.B. Robust scheduling based on extreme learning machine for bi-objective flexible job-shop problems with machine breakdowns. Expert Syst. Appl. 2020, 158, 113545. [Google Scholar] [CrossRef]
- Rabiee, M.; Zandieh, M.; Ramezani, P. Bi-objective partial flexible job shop scheduling problem: NSGA-II, NRGA, MOGA and PAES approaches. Int. J. Prod. Res. 2012, 50, 7327–7342. [Google Scholar] [CrossRef]
- Vela, C.R.; Afsar, S.; Palacios, J.J.; González-Rodríguez, I.; Puente, J. Evolutionary tabu search for flexible due-date satisfaction in fuzzy job shop scheduling. Comput. Oper. Res. 2020, 119, 104931. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, Y.; Sun, J.; Zhang, W. An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints. Swarm Evol. Comput. 2020, 54, 100664. [Google Scholar] [CrossRef]
- Samarghandi, H. Solving the no-wait job shop scheduling problem with due date constraints: A problem transformation approach. Comput. Ind. Eng. 2019, 136, 635–662. [Google Scholar] [CrossRef]
- Tang, H.; Chen, R.; Li, Y.; Peng, Z.; Guo, S.; Du, Y. Flexible job-shop scheduling with tolerated time interval and limited starting time interval based on hybrid discrete PSO-SA: An application from a casting workshop. Appl. Soft Comput. 2019, 78, 176–194. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Gholami, O. Mixed graph model and algorithms for parallel-machine job-shop scheduling problems. Int. J. Prod. Res. 2014, 55, 1–16. [Google Scholar] [CrossRef]
- Fanjul-Peyro, L. Models and an exact method for the Unrelated Parallel Machine scheduling problem with setups and resources. Expert Syst. Appl. X 2020, 5, 100022. [Google Scholar] [CrossRef]
- Pacini, E.; Mateos, C.; Garino, C.G. Dynamic Scheduling based on Particle Swarm Optimization for Cloud-based Scientific Experiments. CLEI Electron. J. 2014, 17, 1. [Google Scholar] [CrossRef]
- Awad, M.A.; Abd-Elaziz, H.M. An Efficient Modified Genetic Algorithm For Integrated Process Planning-Job Scheduling. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), Cairo, Egypt, 26–27 May 2021; pp. 319–323. [Google Scholar]
- Baykasoğlu, A.; Madenoğlu, F.S.; Hamzadayı, A. Greedy randomized adaptive search for dynamic flexible job-shop scheduling. J. Manuf. Syst. 2020, 56, 425–451. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part I. Informas J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef] [Green Version]
- Rego, C.; Alidaee, B. Metaheuristic Optimization via Memory and Evolution Tabu Search and Scatter Search; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Chen, J.C.; Chen, Y.-Y.; Chen, T.-L.; Lin, J.Z. Comparison of simulated annealing and tabu-search algorithms in advanced planning and scheduling systems for TFT-LCD colour filter fabs. Int. J. Comput. Integr. Manuf. 2016, 30, 516–534. [Google Scholar] [CrossRef]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by Localization and Multiobjective Evolutionary Optimization for Flexible Job-Shop Scheduling Problems. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Kacem, I.; Hammadi, S.; Borne, P. Pareto-optimality approach for flexible job-shop scheduling problems: Hybridization of evolutionary algorithms and fuzzy logic. Math. Comput. Simul. 2002, 60, 245–276. [Google Scholar] [CrossRef]
- Chan, F.T.; Kumar, V.; Tiwari, M.K. Optimizing the Performance of an Integrated Process Planning and Scheduling Problem: An AIS-FLC based Approach. In Proceedings of the 2006 IEEE Conference on Cybernetics and Intelligent Systems, Bangkok, Thailand, 7–9 June 2006; Volume 59, pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Gen, M.; Sun, L. Scheduling jobs and maintenances in flexible job shop with a hybrid genetic algorithm. J. Intell. Manuf. 2006, 17, 493–507. [Google Scholar] [CrossRef]
- Teekeng, W.; Thammano, A. Modified Genetic Algorithm for Flexible Job-Shop Scheduling Problems. Procedia Comput. Sci. 2012, 12, 122–128. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Shao, X.; Li, P.; Gao, L. An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Comput. Ind. Eng. 2009, 56, 1309–1318. [Google Scholar] [CrossRef]
- Nouri, H.E.; Driss, O.B.; Ghédira, K. Solving the flexible job shop problem by hybrid metaheuristics-based multiagent model. J. Ind. Eng. Int. 2017, 14, 1–14. [Google Scholar] [CrossRef]
- Amin-Naseri, M.R.; Afshari, A.J. A hybrid genetic algorithm for integrated process planning and scheduling problem with precedence constraints. Int. J. Adv. Manuf. Technol. 2012, 59, 273–287. [Google Scholar] [CrossRef]
- Shao, X.; Li, X.; Gao, L.; Zhang, C. Integration of process planning and scheduling—A modified genetic algorithm-based approach. Comput. Oper. Res. 2009, 36, 2082–2096. [Google Scholar] [CrossRef]
- Leung, C.; Wong, T.; Mak, K.; Fung, R.Y.K. Integrated process planning and scheduling by an agent-based ant colony optimization. Comput. Ind. Eng. 2010, 59, 166–180. [Google Scholar] [CrossRef]
- Falih, A.; Shammari, A.Z.M. Hybrid constrained permutation algorithm and genetic algorithm for process planning problem. J. Intell. Manuf. 2020, 31, 1079–1099. [Google Scholar] [CrossRef]


| (Meta-) Heuristic Optimization | Evolutionary Inspired, i.e., | Genetic Algorithms (GA) Differential Evolution (DE) | |
| Trace Trajectory Inspired, i.e., | Tabu Search (TS) | ||
| Food-Hunting Inspired | Swarm based, i.e., | Artificial Colony Optimization (ACO) Particle Swarm Optimization (PSO) Pigeon based Optimization | |
| Predatory based, i.e., | Wolf based Optimization Whale based Optimization Bats based optimization | ||
| Breeding–Hunting Inspired, i.e., | Honey-Bee Mating Algorithm (HBMO) Hybrid behavior | ||
| Physical Behaviour Inspired, i.e., | Big-Band optimization Expansion optimization Simulated Annealing (SA) | ||
| Publication | Method | Coding | Search/Mating Strategy | Objective Function | Problem Perspective | |
|---|---|---|---|---|---|---|
| Cross-Over | Mutation | |||||
| Ahmadi et al. [51] | A Pareto based approach employing New version of non-dominated sorting genetic algorithm (NSGA-II) and non-dominated ranking genetic algorithm (NRGA) | Matrix permutation-based chromosome of three columns represented Gantt chart as (current job, operation, machine) | POX | modified Position Based Mutation (PBM) as well as Machine Based Mutation (MBM) | Multi-objective: make-span and stability measure | FJSSP/IPPS Multiple machines problem |
| Singh et al. [52] | Quantum behaved PSO | stochastic particle (operation, machine priority sequencing representation) | Particles updated based on masked procedure | Random position swapping mutation that happened governed by a condition | Minimize make-span | FJSSP Multiple machines problem |
| Li et al. [53] | Sequencing operation based Hybrid Artificial Bee Colony (ABC) | Two vectors of operation based coding: (position, operation, machine) combination | Random positioning | Multiple stage swapping based on random points | Minimize make-span | DFJSSP Multiple machines problem |
| Nouiri et al. [54] | Two stage of PSO | Two vector parts of process and corresponding assigned machine | Particles updated based on mathematical formulation | Multi-objective: Minimize make-span and stability measure simultaneously. | FJSSP, Generates predictive schedules insensitive to breakdowns [55]. | |
| Wu et al. [56] | Mathematical model and non-dominated sorting genetic algorithm (NSGA-II) | Row vector of positioned operations. | LOX | Random points swapping | Multi-objective:
| FJSSP |
| Che et al. [57] | mixed-integer linear programming (MILP) model based on position assignment | Mathematical representation | Pareto front considering Stochastic calculation that paid attention to machine idle period | Multi-objective:
| JSSP Single machine scheduling | |
| García-León et al. [40] | General local neighbour search based on a disjunction graph model | Two disjunction graph; operation- and machine- sequencing graph | Pareto front employing four search strategies and two neighbourhood structures based on semi-random three variable selected criteria. | Multi-objective based on criteria | FJSSP | |
| Mokhtari et al. [58] | Hybrid GA and SA | Matrix based mathematical model | Two cross-over: uniform- and position based- crossover are mixed as a masked crossover | Two mutations technique are mixed reverse sequence and swapping | Multi-objective:
| FJSSP Considering different paths of each machine |
| Dai et al. [59] | Modified GA based on mathematical model | Multi-layer encoding strings composed horizontally of: alternative process plan strategy positioned in job sequenced order, and scheduling plan gene-string | Multiple Single point cross-over | SA-based mutation operator | Multiple objective:
| IPPS |
| Li et al. [60] | Hybrid of HBMO and SA | Feature string | Single point cross-over | Adjacent swapping | Minimize energy through tool change time and travelling time (make-span) | JSSP Single job optimization, No precedence constraints |
| Defersha et al. [42] | Two stage GA | (job, operation) string in first stage and then Indirect (job, operation, machine) string | Three cross- over: (i) single-point randomly selected, (ii) job cross-over and (iii) assignment cross-over both are exchanged based on a probability | Operations swapping mutation, and assignment altering mutation | Minimize make-span | FJSSP |
| Meng et al. [61] | Mixed models of integer linear programming (MILP) | Mathematical representation | Sequenced stages of mathematical formulation of nine decision variables | Minimize energy consumption summation: idle, total and common | FJSSP Environmental awareness point of view | |
| Luo et al. [31] | Heterogeneous parallel GA with developed event driven strategy with a two level of parallelization | Modified operation based encoding (two paired patterns) | Random chosen point cross over | Different arbitrary genes randomly chosen to exchange values | Muti-objective into single:
| DJSSP |
| Min et al. [62] | Enhanced heuristic based on combination of GA, PSO and SA | two-layer horizontally encodes machine gene string and operation gene string | Cross over design based on PSO | Based on SA | Multi-objective optimization model:
| DJSSP Energy efficient perspective |
| Mahmoodjanloo et al. [63] | Mathematical model relying on two Mixed Integer-Linear Programming (MILP) | Mathematical Representation | Modified masked crossover based on rate factor | Two main strategies of: (i) Based on differential evolution and (ii) Multiple self-adaptive strategies based on indices | Minimize completion time (make-span) | FJSSP Reconfigurable machine tool included |
| Ambrogio et al. [64] | Mathematical model | Mathematical formulation based on three main decision making variables | Minimize consumption time as energy saving indicator | FJSSP | ||
| Deng et al. [65] | Timetable method of a local search algorithm applied with Nawaz-Enscore-Ham based heuristic | Two square matrices, operation matrix and corresponding machine matrix | - | - | Minimize Total flow time | JSSP |
| Li et al. [47] | Hybrid based of a genetic algorithm and variable neighbourhood search | Three strings: Job-Feature string indexes feature appearance, operation string insert alternative operation strategy and machine alternative operation strategy string | JOX, POX, POX respecting t feature, operation, machine strings. | Two-points swapping | Minimize make-span | FJSSP Precedence constraint included with a correctness step |
| Li et al. [15] | Discrete PSO based algorithm | Three strings: Job-Feature string indexes feature appearance, operation string insert alternative operation strategy and machine alternative operation strategy string | JOX, POX, POX respecting t feature, operation, machine strings. | Two-points swapping | Minimize make-span | FJSSP Precedence constraint included with a correctness step |
| Jing et al. [66] | Integrated optimization GA | Operation string | Single cut-point | Random swapping mutation | Multi-objective:
| FJSSP preventive maintenance scope |
| Cao et al. [39] | Heterogeneous earliest finish time (HEFT) adopting arbitrary directed acyclic graph (DAG) on Parallel CPU | DAG—Graph based | Two-cut points | Two-cut points | Minimize make-span | DJSSP Manipulate setup time |
| Lin et al. [67] | Developed GA based on incomplete Graph representation | Two-hand sides strings; process plan and sequence of operation, respectively. | Two crossover operators—one crossover per side; Process plan: random cut-points with orderbased generator.Operation sequence: masked | Two mutation operators: Random swapping based on two genes, and escalation based on random single gene. | Minimize Make-span | IPPS/DFJSSP |
| Zhang et al. [68] | Mathematical formulation included into a GA based | Array of layer-coded of (job, process plan strategy, assigned machine), and the gene position indicates the processing sequence | PMX based on job and process plan matching along the whole parent. | Two mutation strategies: Operation conditioned exchange Machine based on random selection | Minimize total energy consumption | IPPS Considered tool power profile of different machining parameters |
| Liu et al. [69] | Hybrid of mathematical model and GA based | Matrix of available machines by operation sequence | Random cut-point | Random swapping point | Minimize make-span/completion time respecting work load | DFJSSP Single machine—maintenance perspective |
| Yavari et al. [70] | Mixed-integer linear programming model (MILP Model) cooperated with GA based two local search windows. | Two strings; 1- jobs sequence string on a machines and 2- parts ordering string. | Single cut-point attached to the first string only | Random swapping point, attached to the first string only. | Minimize completion time, parts ordering and holding cost | JSSP Supply chain perspective |
| Zhou et al. [71] | A Pareto front explored by two multi-objective approached via three models of multi-agent structure: (i) NSGA II, and (ii) Strength Pareto searching algorithm. | Disjunction graph based | Single-cut point (node randomly selected) | Based on a probability, a selected root inherited from parents | Minimize three objectives:
| FJSSP Parallel computing |
| Lu et al. [72] | GA based | 1D-to-3D representation based on a job string and operation-machine matrix | Single point cross-over | Two genes swapping | Minimize cell make-span | DFJSSP New order arrival with transportation time is considered |
| Caldeira et al. [55] | Backtracking search based on GA with directed old population | Two vector representation: operation sequence and machine assignation | A similarity based POX (SPOX) | Dynamic mutation relying on rate factor | Multi-objective:
| DFJSSP Considering new job arrival |
| Wu et al. [73] | A Self-deterioration model and energy consumption model are optimized through a hybrid pigeon inspired followed by SA. | String of two tuples genes: job number—operation number | LOX | Swapping mutation | Multi-objective:
| DFJSSP Machine wearing included |
| Zheng et al. [41] | Integer programming model and Based on Non-dominated Sorting GA II (NSGA-II). | Chromosome of job routes and the corresponding sequence of operations | Exchange two selected operation gene between the parents | Two positions swapping | Bi-objective:
| FJSSP |
| Zhu et al. [74] | Multiple-independent micro-swarm of hierarch communication structure paired with constraints mathematical model | Two-vectors encode job sequence and process sequence | Multi-masked/conditioned cross-over | Three mutations techniques: insertion, swap and inversion. | Minimize interval grey make-span | FJSSP with job precedence constraints |
| Yang et al. [75] | Creating two phases of optimizations via prediction model and robustness model deploying learning machine and NSGA-II | Single long string of two parts; operation sequences of multiple jobs followed by machine assignment. [76] | Single point cross-over | Swapping mutation | Bi-objective:
| DFJSSP Machine breakdowns considered |
| Vela et al. [77] | Fuzzy uncertainty model combined with a schedule based a hybrid TS-GA | Disjunction graph model representation | JOX, GOX and GPMX | Insert, swap and partial inversion | Maximize due-date satisfaction | FJSSP |
| Zhang et al. [78] | Improved GA through enhancing the inter procedures behaviours, combined with a greedy operation. | Two arrays of machine selection and operation sequence. Each array is consisted of two parts, the chromosome length is the total number of operations | Machine selection chromosome had multiple point crossover, and operation sequence used POX cross-over | Machine selection used roulette-wheel, Operation sequence used adaptive neighbourhood search | Multi-objective:
| FJSSP |
| Samarghandi et al. [79] | GA based on mixed integer programming model, a local search is added to enhance the pool chromosomes | Job routing matrix | Random selected jobs to be inherited from each parent with a corresponding order | Reorder position of multiple points regarding a threshold value | Minimize make-span | JSSP |
| Tang et al. [80] | Hybrid of discrete PSO and SA, implementing two neighbourhood structures. | Two vectors: Operation scheduling vector and resource assignment vector | POX and Rand-point Preservation Crossover | Conditioned two elements exchange | Multi-objective:
| FJSSP Workers are included as a resources |
| Sotskov et al. [81] | Five heuristic algorithms split between job sequencing and machine assignation | Mixed graph model function at resource and precedence constraints creating a train timetable for a railroad | Minimize the make-span. | FJSSP Concerning on the case where the number of jobs is less than the total number of the available machines | ||
| Fanjul-Peyro [82] | Mixed Integer linear programming developed along three phases of assignment, sequencing and timing. | Three graph for resources; presents resources, setup resources and shared resources | Minimize the make-span. | FJSSP | ||
| Functions | |
|---|---|
| 1 | SA Initialization |
| current_solution ← initial solution | |
| best_solution ← initial_solution | |
| current_cost ← evaluate (current_solution) | |
| best_cost ← evaluate (best_solution) | |
| 2 | Searching Progress |
| T ← Tinit | |
| While (T > Tstopping) | |
| For i = 1 to iterations (T) | |
| new_solution ← Modified_Move (current_solution) | |
| new_cost ← evaluate (new_solution) | |
| Δcost ← new_cost—current_cost | |
| If (Δcost ≤ 0 or > random ()) /* accept new solution */ current_solution ← new_solution current_cost ← new_cost | |
| If new_cost < best_cost best_solution ← new_solution best_cost ← new_cost | |
| Else /* escape deadlock state */ current_solution ← best_solution current_cost ← best_solution |
| Parameters | Value |
|---|---|
| No. of islands | 8 |
| Sub-pop size | 70 |
| No. of emigrant chroms | 5 |
| No. of history chroms | 3 |
| Crossover probability | 0.6 |
| Mutation Probability | 0.2 |
| Case No. | Total No. of Jobs per Machines | E × Act Solution | GA | GA Li et al. [47] | PSO Li et al. [15] | DPSO | Adopted From | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Average | Average Convergent Generation | Best | Average | Average Convergent Generation | Best | Average | Average Convergent Generation | Best | Average | Average Convergent Generation | ||||
| 1 | 3 × 4 | 5 | 5 | 5.2 | 18 | 5 | 5 | 10 | 5 | 5 | 12.1 | 5 | 5 | 5 | Kacem et al. [89,90], and Zhang et al. [94] |
| 2 | 4 × 5 | 11 | 11 | 11.5 | 23 | 11 | 11 | 12 | 11 | 11 | 12.6 | 11 | 11 | 8 | |
| 3 | 8 × 8 | 14 | 14 | 14 | 27 | 14 | 14 | 12 | 14 | 14 | 11.6 | 14 | 14 | 9 | |
| 4 | 10 × 10 | 7 | 7 | 7.1 | 29 | 7 | 7 | 12.4 | 7 | 7 | 13.1 | 7 | 7 | 9 | |
| 5 | 15 × 10 | 11 | 11 | 13.1 | 39 | 11 | 11 | 19.1 | 11 | 11 | 20 | 11 | 11 | 15 | |
| 6 | 10 × 7 | 11 | 11 | 13.2 | 41 | 11 | 11 | 25.1 | 11 | 11 | 26.8 | 11 | 11 | 13 | |
| 7 | 6 × 8 | 148 | 152 | 154.6 | 68.1 | 148 | 149.7 | 24.4 | 148 | 150.9 | 31.4 | 148 | 149.1 | 18 | Based on Shao et al. [97] |
| 8 | 10 × 8 | 253 | 257 | 259.8 | 81.2 | 253 | 256.1 | 28.1 | 253 | 259.2 | 36.1 | 253 | 255.2 | 22.4 | |
| 9 | 15 × 8 | 288 | 305 | 305.8 | 89.6 | 288 | 290 | 29 | 288 | 291.9 | 38.4 | 288 | 289.5 | 23.7 | |
| 10 | 3 × 4 | 24 | 24 | 24.1 | 56.4 | 24 | 24.2 | 23.2 | 24 | 24.7 | 27.8 | 24 | 24.1 | 11.1 | Based on Naseri et al. [96] |
| 11 | 6 × 4 | 43 | 43 | 43.6 | 72.1 | 43 | 43.3 | 22.3 | 43 | 44.3 | 32.1 | 43 | 43.4 | 18.6 | |
| 12 | 8 × 4 | 54 | 55 | 57.1 | 79.3 | 54 | 54.3 | 56.1 | 54 | 55.2 | 36.3 | 54 | 54.3 | 19.1 | |
| 13 | 12 × 7 | 58 | 64 | 67.3 | 82.1 | 58 | 58.89 | 60.2 | 58 | 60.2 | 38.5 | 58 | 59.4 | 26.3 | |
| 14 | 1 × 15 | 377 | 377 | 377.1 | 61 | 377 | 377 | 21 | 377 | 377 | 22.1 | 377 | 377 | 11 | Based on Li et al. [15,47] |
| 15 | 1 × 5 | 222 | 222 | 222.3 | 45.1 | 222 | 222 | 18 | 222 | 222 | 19.8 | 222 | 222 | 8 | |
| 16 | 9 × 15 | 395 | 418 | 423.2 | 70.5 | 395 | 406.7 | 30.2 | 395 | 410.7 | 29.2 | 395 | 404.2 | 18.9 | |
| 17 | 17 × 15 | 455 | 473 | 481.5 | 90.1 | 455 | 469.9 | 40.1 | 455 | 472.9 | 39.1 | 455 | 466.8 | 28.5 | |
| Case No. | Total No. of Jobs per Machines | Reported Solution | GA + TS | DPSO + TS |
|---|---|---|---|---|
| 18 | 1 × 3 | 423 | 441 | 423 |
| 19 | 1 × 4 | 790 | 800 | 790 |
| 20 | 1 × 5 | 393 | 398 | 388 |
| 21 | 4 × 3 | 1089 | 1193 | 1089 |
| 22 | 2 × 3 | 510 | 522 | 510 |
| Ideal scenario of 3 × 4 | 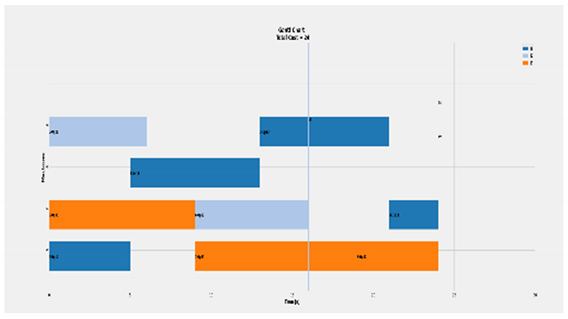 | Total Cost = 24 Actual Cost = 24 Jobs completion cost:  Machine usage as followed: 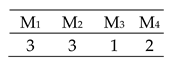 |
| Transmission and Tool change included of 3 × 4 |  | Efficiency = [100, 100, 100, 100]% Total Cost = 36 Actual Cost = 36 Jobs completion cost: 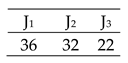 Machine usage as followed:  |
| Deterioration factor effect. Transmission and tool change cost included. (Complete Case) 3 × 4 | 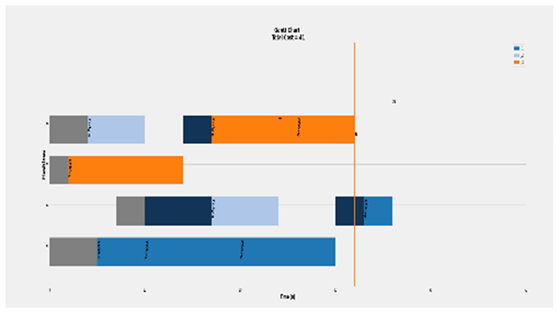 | Eff = [100, 100, 100, 100]% Total Cost = 41 Actual Cost = 36 Jobs completion cost: 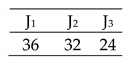 Machine usage as followed:  |
| Complete Case of 3 × 4 | 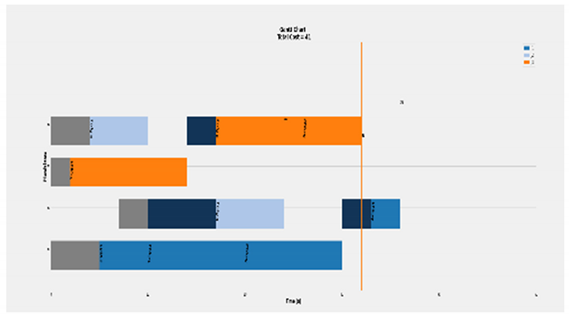 | Eff = [65, 92, 73, 68]% Total Cost = 61 Actual Cost = 38 Jobs completion cost:  Machine usage as followed:  |
| Complete Case of 3 × 4 |  | Eff = [85, 55, 79, 78]% Total Cost = 56 Actual Cost = 36 Jobs completion cost:  Machine usage as followed:  |
| Ideal scenario of 6 × 4 |  | Total Cost = 35 Actual Cost = 35 Jobs completion cost:  Machine usage as followed: 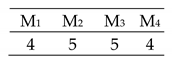 |
| Transmission and Tool change included of 6 × 4 |  | Eff = [100, 100, 100, 100]% Total Cost = 49 Actual Cost = 49 Jobs completion cost:  Machine usage as followed:  |
| Complete Case of 6 × 4 |  | Eff = [85, 55, 79, 78]% Total Cost = 102 Actual Cost = 53 Jobs completion cost:  Machine usage as followed:  |
| Deerioration snd tool change of 2 × 3 |  | Total Cost = 510 Actual Cost = 510 Jobs completion cost:  Machine usage as followed: 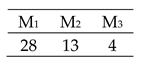 |
| Complete Case of 2 × 4 |  | Eff = [1, 1, 1, 1]% Total Cost = 793 Actual Cost = 641 Jobs completion cost:  Machine usage as followed:  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, M.A.; Abd-Elaziz, H.M. A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations. Processes 2021, 9, 1700. https://doi.org/10.3390/pr9101700
Awad MA, Abd-Elaziz HM. A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations. Processes. 2021; 9(10):1700. https://doi.org/10.3390/pr9101700
Chicago/Turabian StyleAwad, Mohammed A., and Hend M. Abd-Elaziz. 2021. "A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations" Processes 9, no. 10: 1700. https://doi.org/10.3390/pr9101700
APA StyleAwad, M. A., & Abd-Elaziz, H. M. (2021). A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations. Processes, 9(10), 1700. https://doi.org/10.3390/pr9101700





