Dynamic Optimization of Chemical Processes Based on Modified Sailfish Optimizer Combined with an Equal Division Method

Abstract

The optimal solution of the chemical dynamic optimization problem is the basis of automatic control operation in the chemical process, which can reduce energy consumption, increase production efficiency, and maximize economic benefit. In this paper, a modified sailfish optimizer (MSFO) combined with an equal division method is proposed for solving chemical dynamic optimization problems. Based on the basic sailfish optimizer, firstly, the tent chaotic mapping strategy is introduced to disturb the initialization of sailfish and sardine populations to avoid the loss of population diversity. Secondly, an adaptive linear reduction strategy of attack parameters is proposed to enhance the exploration and exploitation ability of sailfish. Thirdly, the updating formula of sardine position is modified, and the global optimal solution is used to attract all sardine positions, which can avoid the premature phenomenon of the algorithm. Eventually, the MSFO is applied to solve six classical optimization cases of chemical engineering to evaluate its feasibility. The experimental results are analyzed and compared with other optimization methods to prove the superiority of the MSFO in solving chemical dynamic optimization problems.

1. Introduction

With the aggravation of environmental and energy problems, reducing energy consumption, increasing production efficiency, and maximizing economic benefits in the chemical process have become the focus of industry and academia. However, the chemical production model has the characteristics of a complex structure, strong nonlinearity, and uncertainty. Srinivasan et al. [1] listed the optimization control of the chemical process as the category of dynamic optimization, so dynamic optimization technology has become an effective means to solve chemical process control problems.

The traditional methods to solve chemical dynamic optimization problems are control vector parameterization (CVP) [2], iterative dynamic programming method (IDP) [3,4], and intelligent optimization method. Among them, the meta-heuristic intelligent optimization algorithm, which is simple, easy to implement, and has a strong searching ability, has become the focus of scholars. The chemical dynamic optimization problem is transformed into an NLP problem by the discretization method, which has a similar form and characteristic to a static optimization problem. Therefore, many intelligent optimization methods suitable for chemical dynamic optimization have been put forward. Pham [5] introduced smoothing and rotation into a genetic algorithm to improve the diversity of the population and solved the chemical dynamic optimization problem. Chiou and Wang [6] introduced the migration strategy and acceleration mechanism to improve the convergence speed of the algorithm and proposed a hybrid differential evolution algorithm for chemical dynamic optimization. Zhang et al. [7] proposed a sequential ant colony algorithm for optimizing chemical dynamic problems. The adaptive Cuckoo algorithm for chemical optimization based on adaptive technology was introduced by Yuanbin et al. [8]. Jiang et al. [9] proposed an efficient multi-objective artificial raindrop algorithm to solve the dynamic optimization problem of chemical process. Shi et al. [10] combined the particle swarm optimization algorithm with the CVP method and proposed the PSO-CVP algorithm to solve the chemical optimization problem.

The sailfish optimizer (SFO) is a new meta-heuristic swarm intelligence optimization algorithm proposed by Shrivastva and Das [11] in 2019, which has been well applied in many fields. Ghosh et al. [12] proposed an improved binary sailfish optimizer (BSF) based on adaptive β-hill climbing to solve the feature selection problem. Li et al. [13] proposed novel discrete binary multi-objective SFO (MOSFO) with a GA, which was applied in the expert recommendation system. Hammouti et al. [14] present a modified sailfish optimizer (MSFO), the modification was to add a local search technique at the last stage of the SFO algorithm (ATK < 0.5), to solve the berth allocation problem. Li et al. [15] proposed an improved sailfish optimization algorithm (ISFO) for successful application in the hybrid dynamic economic emission scheduling of power systems.

In this paper, a modified sailfish optimizer called MSFO is proposed to solve the problems of population initialization dependence, population diversity reduction, low precision, and premature convergence in the SFO. Firstly, the tent chaotic mapping strategy is introduced to disturb the initialization of sailfish and sardine populations to avoid the decline of population diversity. Secondly, the linear decreasing attack parameters of sailfish are improved, and an adaptive linear decreasing attack parameters strategy is proposed to enhance the exploration and exploitation ability. Thirdly, the updating formula for sardine position is improved, and the global optimal solution is used to attract all sardine positions to avoid the premature defect of the algorithm. The modified sailfish optimizer (MSFO) is then combined with an equal separation and dispersion method to solve six classical dynamic optimization cases of chemical engineering. The experimental results show that MSFO is feasible and advantageous in solving dynamic optimization problems of chemical engineering.

The paper is organized as follows: Section 2 depicts the dynamic optimization problems and the equal division method. Section 3 briefly reviews the classic sailfish algorithm and its flow. Section 4 sets out the main contribution provided in this paper, which is the modified sailfish optimizer (MSFO). Eventually, verification of the optimization performance of MSFO is by carried out for six classical dynamic optimization cases of chemical engineering in Section 5.

2. Problem Description and Equal Division Method

2.1. DOP Description

The goal of the dynamic optimization problem (DOP) is to make the optimal control quantity continuously approach the current optimal operation quantity and to achieve the maximization of economic benefit in turn under the condition of satisfying the safety requirements and constraints [16]. The research object of dynamic optimization is generally a time-varying system, which is mathematically called a dynamic system. The dynamic model in industrial process is formulated as differential-algebraic equation (DAE) [17]. The differential equation is used to describe the dynamic characteristics of the system, such as the conservation of mass, momentum, and energy, and the algebraic equation is used to ensure the equilibrium between physics and thermodynamics. The standard forms of dynamic optimization problems (DOPs) are as follows:

$$\min J=\Phi [x(t_f),t_f]+{\displaystyle {\int }_{t_0}^{t_f}\phi [t,x(t),u(t)]dt}$$

(1)

$$\begin{array}{ll}s.t.& \dot{x}(t)=f[t,x(t),u(t)]\\ & x(t_0)=x_0\\ & u_{\min }\le u(t)\le u_{\max }\\ & t\in [t_{0,}{t}_f]\end{array}$$

(2)

where $x(t)$ is the state vector, and $x_0$ is the initial value of the state variable at time ($t_0$). $u(t)$, $J$ are the control vector and performance index. $f$, $\phi$ are constrained by differential equations and algebraic equations, respectively. $t_0$, $t_f$, are the initial time and terminal time; and $u_{\max }$, $u_{\min }$ are the lower and upper bounds of the control vector, respectively. To solve the dynamic optimization problem is to find the optimal control $u(t)(t\in [t_0,t_f])$) so that the performance index $J$ is the minimum when the process satisfies the constraints.

2.2. Equal Division Method

The direct method to solve the dynamic optimization problem is to transform the standard dynamic optimization problem into a finite parameter optimization problem or an NLP problem by means of numerical analysis. The main discrete method is control vector parameterization (CVP) [2], the core idea of which is to discretize the control variables in the time domain and then to approximate each part with a finite number of basis functions.

As shown in Figure 1, this paper divides the time ($t\in [t_0,t_f]$) domain of the standard dynamic optimization problem into N sub-time regions of length $d=(t_f-t_0)/N$ by using the method of piecewise constant in CVP. Meanwhile, the Runge–Kutta method is used to solve the value of each sub-time region (${\sigma }_i^k(k=1,2,3\cdots N)$). Finally, according to the theory of function approximation, the optimal control variables are obtained by linear combination approximation of each optimal result using the intelligent optimizer (MSFO) proposed in this paper.

3. Sailfish Optimizer

Studies have found that group hunting is one of the social behaviors in groups of arthropods, fish, birds, and mammals [11]. Compared with individual hunting, group hunting can save the energy consumption of hunters to achieve the goal of capturing prey. The sailfish optimizer is a new meta-heuristic algorithm based on a group-hunting-inspired simulation of sailfish attacking sardines alternatively. The variable of the problem is the position of the sailfish and sardines in the search space. SFO tries to move as many sailfish and sardines randomly as possible. Sailfish are used to save the current optimal solution, while sardines are used in the search space to find the best solution. The mathematical model of the algorithm is as follows:

Randomly initialize the population positions of sailfish and sardines, to each sailfish and sardine is assigned a randomized position $X_{SF(i)}^k$ and $X_{SD(j)}^k$, consecutively. Where $i\in \left\{sailfish\right\}$, $j\in \left\{sardlines\right\}$ and k is the number of iterations. Mathematically, the update position of sailfish shown in Equation (3):

$$X_{SF\left(i\right)}^{k+1}=X_{elite}^k-{\mu }_k\times \left(rand\left(0,1\right)\times \frac{X_{elite}^k+X_{injure}^k}{2}-X_{SF\left(i\right)}^k\right)$$

(3)

$${\mu }_k=2\times rand\left(0,1\right)\times Pd-Pd$$

(4)

$$Pd=1-\frac{NumSF}{NumSF+NumSD}$$

(5)

where $X_{SF\left(i\right)}^k$ is the previous position of the $i\mathrm{th}$ sailfish, and ${\mu }_k$ is a coefficient generated at $k\mathrm{th}$ iteration, which is derived from Equation (4). To preserve the optimal solution of each iteration, the sailfish and sardine with the best fitness value are called “elite” sailfish and “injured” sardine, respectively, and their position at iteration k is given $X_{eilte}^k$ and $X_{injure}^k$. $Pd$ is the density of prey sardines, which represents the number of prey in each iteration, given by Equation (5). NumSF and NumSD represent the population of sailfish and sardines, and the relationship is $NumSF=NumSD\times percent$, where percent represents the initial species of sailfish as a percentage of the sardine population.

A new position of the sardines at iteration k can be calculated as given in Equation (6):

$$X_{SD\left(j\right)}^{k+1}=rand\left(0,1\right)\times \left(X_{elite}^k-X_{SD\left(j\right)}^k+ATK\right)$$

(6)

$$ATK=A\times \left(1-\left(2\times iter\times \epsilon \right)\right)$$

(7)

$$\alpha =NumSD\times ATK$$

(8)

$$\beta =d\times ATK$$

(9)

where $X_{SD(j)}^k$ represents the previous position of the $j\mathrm{th}$ sardine. iter represents the number of current iterations. ATK is the sailfish’s attacking power, which is linearly decreased on each iteration as shown in Equation (7). When A = 4 and ε = 0.001, If ($ATK<0.5$), the number of sardines that update their position $(\alpha )$ and the number of variables of them $(\beta )$ are calculated as Equations (8) and (9). If ($ATK\ge 0.5$), then all sardines get updated.

In order to simulate the process of the sailfish catching sardines, if $f\left(S{D}_j\right)<f\left(S{F}_i\right)$, the position of this later is replaced by the position of the sardine j, as given by Equation (10).

$$X_{SF(i)}^k=X_{SD(j)}^k\begin{array}{c}\begin{array}{c}\begin{array}{c}\end{array}\end{array}\end{array}\begin{array}{c}\end{array}f\left(S{D}_j\right)<f\left(S{F}_i\right)$$

(10)

Figure 2 shows the specific implementation flow chart of the sailfish optimizer.

4. Modified Sailfish Optimizer (MSFO)

In the search space, the sailfish optimizer has a strong searching ability, but because of the complexity of dynamic optimization, in some cases, it will fall into local optimum, skip optimal solution, low precision, premature convergence, and so on. The main reason is that sailfish and sardine populations rely on initialization and the diversity of the late iteration is reduced, so the exploration and exploitation of the algorithm are insufficient. With a thorough investigation of sailfish optimizer and dynamic optimization, this paper proposes the following modification strategies to modify the performance of the algorithm.

4.1. Tent Chaos Initialization Policy

Chaotic mapping systems have stochastic behavior and nonlinear motion and both randomness and certainty [18]. Chaos theory is the study of dynamic systems. The interesting property of these systems is that when there is a minor change in the system, the whole system gets affected [19]. Common chaotic mapping systems are Gauss mapping, Chebyshev mapping, logistic mapping, tent mapping, etc. [20]. The study found that given an initial value of the chaotic system, the population of the meta-heuristic algorithm is initialized according to the relation of the chaotic mapping, and the chaotic sequence is generated, which can effectively keep the diversity of the population and overcome the premature problem of the classical optimization algorithm [21].

The population initialization of sailfish and sardines in the SFO algorithm is a stochastic strategy. It relies too much on the initialization of the population when searching for the optimal solution. To improve the global search ability of the algorithm and avoid the problem that the diversity of sailfish and sardine population decreases in later searches, we propose to initialize the population of sailfish and sardines by tent chaotic operator. The tent map is defined by the following equation [21]:

$$T_{i+1}=\{\begin{array}{c}\frac{T_i}{0.7},T_i\le 0.7\\ \frac{1-T_i}{0.3},T_i>0.7\end{array}$$

(11)

where $T_i$ is the sequence of $i\mathrm{th}$ iteration $(T_i\in (0,1))$. Figure 3 is the tent chaotic sequence distribution of $T_n$ with the initial value $T_0=0.9$ in 200 iterations.

Figure 3 shows that the tent map has small and unstable periods, so it can effectively improve the diversity of the population and avoid the disadvantage of the diversity loss of the population of sailfish and sardine late in the iteration. We initialize the sailfish and sardine populations using Equation (12):

$$\begin{array}{l}{X}_{SF\left(i+1\right)}=T_{\mathrm{i}+1}\times \left(X_{ub}-X_{lb}\right)+X_{lb}\\ X_{SD\left(j+1\right)}=T_{j+1}\times \left(X_{ub}-X_{lb}\right)+X_{lb}\end{array}$$

(12)

where $X_{SF\left(i+1\right)}$ and $X_{SD\left(j+1\right)}$ are the position values of individual sailfish and sardines. $X_{ub}$ and $X_{lb}$ are the upper and lower boundaries of the individual sailfish and sardines in all dimensions.

4.2. Adaptive Linear Decrease Attack Parameter

In the basic SFO algorithm, the sailfish attack value $ATK=A\times \left(1-\left(2\times itr\times \epsilon \right)\right)$ is a linear decreasing parameter that plays an important role in shifting sardines from the exploratory phase to the exploitation phase, where $\epsilon$ is a fixed value. As long as the dynamic optimization problem involves many local optimal values, sardines ($X_{SD\left(j\right)}^k$) can easily fall into local optimal when searching according to the basic attack parameter ATK, so it is difficult to find or approach the optimal solution. Accordingly, to solve the dynamic optimization problem and enhance the exploration and exploitation ability of sardines in the search space, we improved the attack parameter formula, Equation (7), based on the SFO algorithm and proposed the adaptive linear decrease attack parameter as Equation (13):

$$ATK=A-\left(A\times \left(\frac{iter}{T}\right)\right)$$

(13)

where $\frac{iter}{T}$ is the adaptive decreasing coefficient of the attack degree, which increases with the number of iterations. Figure 4 shows the linear decreasing contrast between the original attack parameters and the adaptive attack parameters proposed in this paper under 1000 iterations. Compared with the original attack parameters, the proposed attack parameters can keep a higher value when decreasing, so that sardines can conduct a longer global search in the search space, avoid local optimization, and better enhance the exploration and exploitation ability of the algorithm.

4.3. Modifying the Search Equation for Sardines

As shown in Figure 2, in the basic SFO algorithm flow, sardine populations determine their number of replacements based on the attack parameter ATK, thus balancing sardine exploration and exploitation capabilities. After Equation (6) uses the adaptive attack parameters proposed in this article, the accuracy of the optimal solution obtained is affected due to the complexity of the dynamic optimization problem and the individual sardines ($X_{elite}^k$) being updated around the current elite sailfish position ($X_{elite}^k$). Therefore, we modified the position updating formula of sardines and proposed the global optimal solution and the elite sardines’ ($X_{injured}^k$) attraction strategy. The proposed formula for updating sardine positions is as follows:

$$X_{SD\left(j\right)}^{k+1}=rand(0,1)\times ATK\times \left[X_{SD\left(j\right)}^k+\left(X_{injure}^k-X_{S\left(j\right)}^k\right)+\left(Gbest(k)-X_{SD\left(j\right)}^k\right)\right]$$

(14)

where $Gbest(k)$ is the global optimal solution recorded in iteration k. Using the current global optimal solution and the attraction of elite sardines to all sardines’ individual locations to provide a greedy search direction. The sardine populations can escape from the local optimum, avoid the premature phenomenon of the algorithm, further enhance the exploration and exploitation capacity of the algorithm, and improve the algorithm efficiency.

The pseudo-codes of the modified sailfish optimizer (MSFO) are given in the following table.

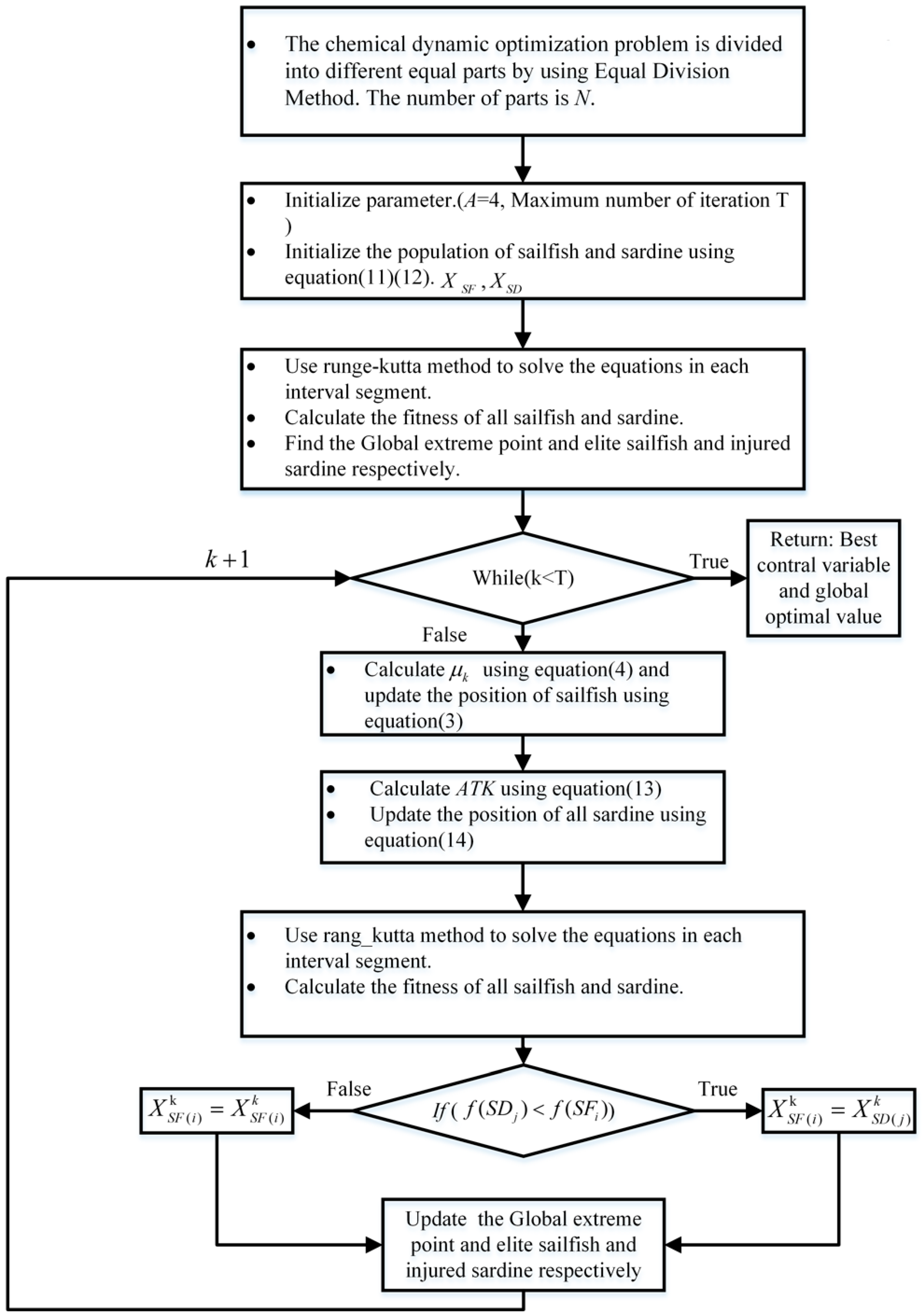
Algorithm 1 Pseudo-codes of the MSFO

Inputs: The population size Pop and maximum number of iterations T. Outputs: The global optimal solution. Initialize parameter (A = 4) and the population of sailfish and sardine using Equations (11) and (12). Calculate the objective fitness of each sailfish and sardine. Find the Global extreme point, elite sailfish, and injured sardine, respectively. while (k < T) do  for each sailfish Calculate ${\mu }_k$ using Equation (4) and update the position of sailfish using Equation (3) end for Calculate ATK using Equation (13)   for each sardine     Update the position of all sardines using Equation (14). end for Check and correct the new positions based on the boundaries of variables.   Calculate the fitness of all sailfish and sardine. Sort the moderate values of sailfish and sardines.     If the fitness of sardine is better than that of the sailfish     Replace a sailfish with an injured sardine using Equation (10).     Remove the hunted sardine from population.       Update the best sailfish and best sardine.     end if     Update the Global extreme point and elite sailfish and injured sardine, respectively. end while return global optimal solution.

4.4. Performance Analysis of Modified Sailfish Optimizer

To test the performance of the MSFO, we conducted numerical experiments for benchmark function testing. The operating system used in this experiment was Windows 10 Professional 64-bit, the experimental software was MATLAB R2020a, and the processor was Intel(R) Core (TM)i5-5257U.

4.4.1. Benchmark Functions

We have selected six well-known benchmark functions, as shown in

Table 1. Benchmark function.

Functions	Formulation	Rang	Dim	${\mathit{f}}_{\mathbf{min}}$
Sphere	$F1\left(x\right)={\displaystyle \sum _{i=1}^n{x}_i^2}$	[−100,100]	30	0
Schwefel	$F2\left(x\right)={\displaystyle \sum _{i=1}^N\left|x_i\right|+}{\displaystyle \prod _{i=1}^N\left|x_i\right|}$	[−10,10]	30	0
Rastrigin	$F3\left(x\right)={\displaystyle \sum _{i=1}^n\left[x_i^2-10\cos \left(2\pi x_i\right)+10\right]}$	[−5.12,5.12]	30	0
Ackley	$\begin{array}{l}F4\left(x\right)=-20\exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i^2}}\right)-\exp \left(\frac{1}{n}{\displaystyle \sum _{i=1}^n\cos \left(2\pi x_i\right)}\right)\\ +20+e\end{array}$	[−32,32]	30	0
Kowalik	$F5\left(x\right)={\displaystyle \sum _{i=1}^{11}{\left[a_i-\frac{x_1\left(b_i^2+b_i{x}_2\right)}{b_i^2+b_i{x}_3+x_4}\right]}^2}$	[−5,5]	4	0.00030
Six Hump Camel Back	$F6\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_3^4$	[−5,5]	2	−1.0316

, which can be broadly divided into unimodal functions (F1–F3) and multimodal functions (F4–F6). The solution space of the unimodal function problem contains a globally optimal solution, which can be used to examine the exploitation capability and optimization speed of the algorithm. The solution space of the multimodal function problem contains one or more global optimal solutions, which can be used to evaluate the ability to develop the algorithm and avoid the local optimal solution.

4.4.2. Parameter Settings

In order to prove the superiority of MSFO, we chose several famous meta-heuristic algorithms to compare, including the basic sailfish optimization algorithm (SFO) [11], particle swarm optimization algorithm (PSO) [22], and butterfly optimization algorithm (BOA) [23]. To obtain satisfactory results and ensure fairness, the number of the search population used in the experiment was 30 and the maximum number of iterations was 1000. The specific parameters of the relevant algorithms were as follows:

PSO: the learning factors $C_1$ and $C_2$ were 2 and the weight $\omega$ was 0.9.

BOA: the perceived form parameter c was 0.01, power exponent $\alpha$ was 0.1, the probability of conversion from global search to local search was 0.8.

SFO: initial attack value A was 4, sailfish ratio was 0.3.

MSFO: initial attack value A was 4, sailfish ratio was 0.2.

4.4.3. Statistical Result Comparison

In this section, each algorithm is run 50 times independently to avoid the randomness of the results.

Table 2. Test result benchmark functions.

Algorithm
Functions	Result	MSFO	SFO	PSO	BOA
F1	Best	6.8104 × 10−94	9.7670 × 10−16	1.6556 × 103	2.7743 × 100
	Worst	3.6275 × 10−54	1.0181 × 10−9	8.6603 × 103	7.0283 × 100
	Mean	8.4117 × 10−56	9.5079 × 10−11	4.8832 × 103	5.0551 × 100
	Std.	5.1736 × 10−55	1.9546 × 10−10	1.8340 × 103	9.6613 × 10−1
	Rank	1	2	4	3
F2	Best	2.7641 × 10−52	5.3076 × 10−7	3.4437 × 101	8.0016 × 10−2
	Worst	5.4745 × 10−27	1.8220 × 10−4	7.9924 × 102	1.2217 × 100
	Mean	1.5945 × 10−28	3.9648 × 10−5	3.5138 × 102	4.7870 × 10−1
	Std.	8.0045 × 10−28	3.9331 × 10−5	1.3872 × 103	2.6753 × 10−1
	Rank	1	2	4	3
F3	Best	0.0000 × 100	2.3124 × 10−10	2.1053 × 102	1.5309 × 102
	Worst	0.0000 × 100	2.5092 × 10−6	3.6692 × 102	2.3210 × 102
	Mean	0.0000 × 100	1.9599 × 10−7	2.9085 × 102	1.9280 × 102
	Std.	0.0000 × 100	4.36977 × 10−7	2.8042 × 101	1.7471 × 101
	Rank	1	2	4	3
F4	Best	8.8818 × 10−16	6.2225 × 10−8	8.3902 × 100	1.3961 × 101
	Worst	8.8818 × 10−16	2.8007 × 10−5	1.5680 × 101	1.9874 × 101
	Mean	8.8818 × 10−16	6.3357 × 10−6	1.2945 × 101	1.8706 × 101
	Std.	5.9765 × 10−31	5.2560 × 10−6	1.5215 × 100	1.0767 × 100
	Rank	1	2	3	4
F5	Best	3.1071 × 10−4	3.1082 × 10−4	1.2370 × 10−3	3.0955 × 10−4
	Worst	5.2036 × 10−4	5.7377 × 10−4	2.9944 × 10−2	3.5654 × 10−3
	Mean	3.6986 × 10−4	3.6003 × 10−4	1.1166 × 10−2	7.8221 × 10−4
	Std.	2.0186 × 10−4	5.7242 × 10−5	9.7893 × 10−3	5.2900 × 10−4
	Rank	1	2	3	4
F6	Best	−1.0316 × 100	−1.0316 × 100	−1.0316 × 100	−1.0316 × 100
	Worst	−1.0316 × 100	−9.9951 × 101	−1.0246 × 100	−1.0316 × 100
	Mean	−1.0316 × 100	−1.0306 × 100	−1.0294 × 100	−1.0316 × 100
	Std.	4.4860 × 100	4.5484 × 10−3	1.8578 × 10−3	4.4860 × 10−16
	Rank	1	3	4	2

shows the optimal values of Best, Worst, Mean, and Std. of variance for each algorithm. Rank is the result of sorting the best values according to each algorithm. From the experimental results, it can be seen that the MSFO optimization performance proposed in this paper is obviously superior to that of the other three algorithms in single peak test function (F1~F3) and multipeak function (F4~F8), and the optimization results are of the highest accuracy and the first rank. According to the results of variance, MSFO is the best among the three algorithms. Thus, the feasibility of three modified strategies in improving the performance of SFO algorithm is illustrated.

4.4.4. Convergence Trajectory Comparison

Figure 5 and Figure 6 show the convergence trajectories of four algorithms for optimizing unimodal and multimodal test functions. It can be seen from Figure 5 that MSFO converges to a more accurate optimal target value and converges faster than other methods when optimizing unimodal function(F1~F3). It can be observed from Figure 6 that in optimizing multimodal test function F4, MSFO effectively avoids the local minimum and finds the optimal target value. Therefore, it can be concluded that MSFO has a strong search ability to approximate the global optimal solution when optimizing functions with different characteristics.

4.4.5. Box Plot Analysis

Figure 7 plots the boxplot of four different algorithms running 50 iterations of the benchmark function independently, which can fully display the characteristic information of the target value (minimum, binary, quartile, median, and maximum). As can be seen from the graph, MSFO is not only better than the other three methods in the mean, minimum, and maximum but also in the range and standard deviation of the target value.

4.4.6. Wilcoxon p-Value Statistical Test

The Wilcoxon test is a classical nonparametric statistical hypothesis test, which is used to compare the performance of different methods and is expressed by p-value.

Table 3. The p-value test results of analysis over unimodal and multimodal benchmark functions.

Function	MSFO versus SFO	MSFO versus PSO	MSFO versus BOA
F1	7.0661 × 10−18	7.0661 × 10−18	7.0661 × 10−18
F2	7.0661 × 10−18	4.8495 × 10−18	4.8495 × 10−18
F3	3.3111 × 10−20	3.3111 × 10−20	3.3111 × 10−20
F4	3.3111 × 10−20	3.3111 × 10−20	3.3111 × 10−20
F5	0.0483	8.0196 × 10−6	5.3702 × 10−10
F6	8.4620 × 10−18	6.6308 × 10−20	0.0011

shows the P values of MSFO versus SFO, MSFO versus SFO, and MSFO versus BOA. As can be seen from Table 3, in the comparison of unimodal and multimodal test functions, the p-value is always less than 0.05, so it shows the superiority of MSFO in statistical differences.

5. Application MSFO to Dynamic Optimization Problems in Chemical Processes

In order to test the performance of MSFO in solving dynamic optimization problems, six classical chemical dynamic optimization problems were selected in this paper for testing. The concentration of the reaction product was used as a performance indicator to evaluate the MSFO algorithm in dealing with dynamic optimization problems in chemical processes. The experimental results were compared with those in the related literature.

5.1. Experimental Flow and Parameter Settings

The specific flow of solving chemical dynamic optimization problems using the proposed MSFO algorithm was as follows:

(1)

The chemical dynamic optimization problem was divided into different equal parts by using the equal division method. The number of parts was N.

(2)

Runge–Kutta Method was used for numerical solutions.

(3)

MSFO algorithm was used to optimize the chemical case.

The sailfish sardine position variables represented the optimal control variable, and its fitness value represented the production’s concentration. Each chemical test case was run independently 20 times. Specific experimental parameters were set as shown in

Table 4. Setting of experimental parameters.

Parameter	Quantity	Value
A	Initial attack value	4
percent	Sailfish ratio	0.2
Pop	Population	800
T	Maximum number of iterations	1000

, the specific flow chart of the experiment is shown in Figure 8.

5.2. Test Case and Analysis

5.2.1. Case 1: Benchmark Dynamic Optimization Problem

This case is a classic chemical dynamic optimization problem with an analytical solution, which is an unconstrained mathematical system. The case involves two state variables and has an analytical solution and a global optimum. Many researchers have tested this case to illustrate their approaches [24,25,26]. The mathematical model can be described as follows:

$$\min J(u)=x_2(t_f)$$

(15)

$$s.t.\{\begin{array}{l}\frac{d{x}_1}{dt}=u\\ \frac{d{x}_2}{dt}=x_1^2+u_1^2\\ x(0)={[1,0]}^T\\ -1\le u\le 0,t_f=1\end{array}$$

(16)

where $x_1$, $x_2$ are state variables, $u$ is the control vector, and $t_f$ is terminal time.

5.2.2. Case 2: Batch Reactor Consecutive Reaction

The schematic of a typical fed-batch reactor is presented in Figure 9 for illustration.

The objective is to find the optimal temperature profile that maximizes the target product B at the final time of an operation in a batch reactor, where reaction $A\to B\to C$ takes place. The mathematical model can be described as follows [25]:

$$\max J(T)=C_B(t_f)$$

(17)

$$s.t.\{\begin{array}{l}\frac{d{C}_A}{dt}=-4000\exp (\frac{-2500}{T})C_A\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}\begin{array}{ccc}& & \end{array}& \end{array}& \end{array}& & \end{array}\\ \frac{d{C}_B}{dt}=4000(\frac{-2500}{T})C_A^2-6.2\times {10}^5\exp (\frac{-5000}{T})C_B\\ C={[1,0]}^T\begin{array}{ccc}\begin{array}{cc}\begin{array}{cccc}\begin{array}{cc}\begin{array}{cccc}\begin{array}{cc}& \end{array}& & & \end{array}& \end{array}& & & \end{array}& \end{array}& & \end{array}\\ 298\le T\le 398,t_f=1\begin{array}{ccc}\begin{array}{cc}\begin{array}{cccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & & \end{array}& \end{array}& & \end{array}\end{array}$$

(18)

where $C_A,C_B$ are the concentration of A and B, respectively. $t_f$ is the final moment of reaction. T is the temperature.

5.2.3. Case 3: Parallel Reactions in Tubular Reactor

This case describes two parallel chemical reactions taking place $A\to B$ and $B\to C$ in a tubular reactor The reaction trajectory of the optimal control variable is to be determined such that the concentration of target product B is maximum. The problem is formulated as follows [27]:

$$\max J(t_f)=x_2(t_f)$$

(19)

$$s.t.\{\begin{array}{l}\frac{d{x}_1}{dt}=-[u(t)+0.5u^2(t)]x_1(t)\\ \frac{d{x}_2}{dt}=u(t)x_1(t)\\ x(0)={[1,0]}^T\\ 0\le u(t)\le 5,t_f^{}=1\end{array}$$

(20)

where $x_1(x)$ and $x_2(x)$ are the concentration of A and B, respectively. J is the performance index. $u(t)$ is the control variable. $t_f$ is terminal time.

5.2.4. Case 4: Catalyst Mixing Problem

This problem considers a plug flow reactor, packed with two catalysts. The objective is to obtain the optimal catalyst concentration profile that maximizes the yield of the intermediate product C for a fixed reactor length where the reaction $A\leftrightarrow B\to C$ occurs. The dynamic optimization problem of this problem can be described as follows [28]:

$$\max J(z_f)=1-x_A(z_f)-x_B(z_f)$$

(21)

$$s.t.\{\begin{array}{l}\frac{d{x}_A}{dz}=-u(z)[10\times x_B(z)-x_A(z)]\\ \frac{d{x}_B}{dz}=u(z)[10\times x_B(z)-x_A(z)]-[1-u(z)]\times x_B(z)\\ C(0)={[1,0]}^T\\ 0\le u(z)\le 1,z_f^{}=12m\end{array}$$

(22)

Denoting $x_A$, $x_B$ and J as the mole fractions of the substance A, B, and C. z is the pipe length of the tubular reactor. $u(z)$ is the mixing fraction of catalyst A.

5.2.5. Case 5: Plug Flow Tubular Reactor

This case study considers a plug flow reactor as studied by Reddy and Husain [29], Luus et al. [30] and Mekarapiruk and Luus [31] to find the optimal control trajectory of the normalized coolant flow rate $u(t)$ that maximizes the normalized concentration of the desired product. The mathematical statement is as follows:

$$\max J=x_1(t_f)$$

(23)

$$s.t.\{\begin{array}{l}\frac{d{x}_1}{dt}=\left(1-x_1\right)k_1-x_1{k}_2\\ \frac{d{x}_2}{dt}=300\left(\left(1-x_1\right)k_1-x_1{k}_2\right)-u\left(x_2-290\right)\\ k_1=1.7536\times {10}^5\times \exp \left(-\frac{1.1374\times {10}^4}{1.9872x_2}\right)\begin{array}{c}\end{array}\\ k_1=2.4885\times {10}^{10}\times \exp \left(-\frac{2.2748\times {10}^4}{1.9872x_2}\right)\\ x(0)={[0,380]}^T\\ 0\le u\le 0.5,t_f=5\\ x_2\le 460\end{array}$$

(24)

where $x_1$ denotes the normalized concentration of the desired product, $x_2$ is the temperature, and are rate constants. $t_f$ is terminal time.

5.2.6. Case 6: Fed Batch Bioreactor

This case study deals with the optimal production of a secreted protein in a fed-batch reactor. It was originally formulated by Park and Ramirez [32] in 1988. The objective is to maximize the secreted heterologous protein by a yeast strain in a fed-batch culture. The dynamic model accounts for host-cell growth, gene expression, and the secretion of expressed polypeptides. The mathematical statement is as follows:

$$\max J(t_f)=z_1{z}_5$$

(25)

$$s.t.\{\begin{array}{l}\frac{d{z}_1}{dt}=g_1(z_2-z_1)-\frac{u}{z_5}{z}_z\\ \frac{d{z}_2}{dt}=g_2{z}_3-\frac{u}{z_5}{z}_2\\ \frac{d{z}_3}{dt}=g_3{z}_3-\frac{u}{z_5}{z}_3\\ \frac{d{z}_4}{dt}=-7.3g_3{z}_3+\frac{u}{z_5}(20-z_4)\\ \frac{d{z}_5}{dt}=u\\ z_1(0)=0,z_2(0)=0,z_3(0)=1,z_4(0)=5,z_5(0)=1\\ g_1=\frac{4.75g_3}{0.12+g_3},g_2=\frac{z_4}{0.1+z_4}\exp (-5z_4),g_3=\frac{21.87z_4}{(z_4+0.4)(z_4+62.5)},t_f=15\end{array}$$

(26)

where $z_1$, $z_2$ are, respectively, the concentration of the secreted protein and the total protein. $z_3$ is the culture cell density, $z_4$ is the substrate concentration, $z_5$ is the holdup volume, u is the nutrient (glucose) feed rate, and J is the mass of protein produced. For final time $t_f=15$, and the following constraints on the control variable, $0\le u\le 2$. $g_1,g_2,g_3$ are protein secretion rate constants.

5.3. Results and Discussions

5.3.1. Analysis of the Experimental Results of Case 1

Table 5. Results of benchmark dynamic optimization by different methods.

Ref.	Method	N	Optimum
[24]	OCT	-	0.761594156
[25]	ACO-CP	-	0.76238
[26]	IACO-CVP	-	0.76160
[33]	IGA-CVP	-	0.761595
[34]	IWO-CVP	50	0.76159793
[34]	ADIWO-CVP	50	0.76159417
This work	MSFO	20	0.76165319
This work	MSFO	50	0.761594199

shows the analytical solution and the global optimum results of MSFO versus OTC, ACO-CP, IACO-CVP, IGA-CVP, IWO-CVP, and ADIWO-CVP in the benchmark dynamic optimization problem. The “~” in Table 5 means that the reference did not provide a value. Figure 10 is the optimal control variable trajectory with N = 20 and N = 50, Figure 11 is the optimal state variable trajectory, and Figure 12 is the iteration curve of the optimal result of the benchmark dynamic optimization problem.

In the open literature, the analytical solution and the global optimum is J = 0.761594156 by adopting classic optimal control theory (OCT) [24] for Case 1. Rajesh et al. [25] got a value of 0.76238 using the ant colony framework with control profile approximation (ACO-CP). Asgari and Pishvaie [26] obtained a value of 0.76160 using region reduction strategy and control vector parameterization with an ant colony optimization algorithm (IACO-CVP). Qian et al. [33] got a value of 0.761595 using a control vector parameterization method with an iterative genetic algorithm (IGA-CVP). Tian et al. [34] obtained values of 0.76159793 (N = 50) and 0.76159417 (N = 50) using control vector parameterization based invasive weed optimization (IWO-CVP) and control vector parameterization based adaptive invasive weed optimization (ADIWO-CVP).

The global optimum obtained by the MSFO after 20 independent runs was 0.76165319 (N = 20) and 0.761594199 (N = 50). Tian et al. [34] reached a value of 0.76165319 by control vector parameterization based adaptive invasive weed optimization (ADIWO-CVP), which is the best literature result close to the analytical result. The results of MSFO were close to the ADIWO-CVP and superior to those of other methods, which shows the validity of the proposed algorithm.

5.3.2. Analysis of the Experimental Results of Case 2

Table 6. Results of batch reactor optimization by different methods.

Ref.	Method	N	Optimum
[9]	MOARA	-	5.54 × 10−2
[10]	PSO-CVP	-	0.6105359
[34]	IWO-CVP	-	0.61079180
[35]	IACA	10	0.6100
[35]	IACA	20	0.6104
[36]	GA	-	0.61072
[36]	IKEA	10	0.6101
[36]	IKEA	20	0.610426
[36]	IKEA	100	0.610781–0.610789
[37]	CP-PSO	-	0.6107847
[37]	CP-APSO	-	0.6107850
[38]	IKBCA	10	0.6101
[38]	IKBCA	20	0.610454
[38]	IKBCA	100	0.610779–0.610787
[39]	ISOA	10	0.6101
[39]	ISOA	25	0.61053
[39]	ISOA	50	0.6107724
This work	MSFO	10	0.610118
This work	MSFO	25	0.610537
This work	MSFO	50	0.610771–0.610785

shows the optimal target product concentration results of MSFO and 10 different methods for optimizing batch reactor continuous reaction problem. The “~” in Table 6 means that the reference did not provide a value. Figure 13 is the optimal temperature control variable curve with N = 20 and N = 50, Figure 14 is the optimal state variable curve, and Figure 15 is the iteration curve for the optimal result.

In the Table 6, Jiang et al. [9] used the an efficient multi-objective artificial raindrop algorithm (MOARA) to obtain the value of 5.54 × 10⁻². Shi et al. [10] reached a value of 0.6105359 using optimal control strategies combined with PSO and control vector parameterization (PSO-CVP). Tian et al. [34] obtained a value of 0.61079180 using control vector parameterization based invasive weed optimization (IWO-CVP). Zhang and Chen [35] got values of 0.6100 (N = 10) and 0.6104 (N = 20) using iterative ant colony algorithm (IACA). Peng et al. [36] obtained values of 0.6101 (N = 10), 0.610426 (N = 20), and range 0.610781–0.610789 (N = 100) using an improved knowledge evolution algorithm (IKEA). Zhou and Liu [37] got values of 0.6107847 and 0.6107850 using control parameterization-based particle swarm approach (CP-PSO) and control parameterization-based adaptive particle swarm approach (CP-APSO). Liu et al. [38] obtained values of 0.6101 (N = 10), 0.610454 (N = 20), and range 0.610779–0.610787 (N = 100) using improved knowledge-based cultural algorithm (IKBCA). Xu et al. [39] proposed an improved seagull optimization algorithm combined with an unequal division method (ISOA) to obtain values of 0.6101 (N = 10), 0.61053 (N = 20), and 0.6107724 (N = 50).

As can be seen from the results in Table 6, as the number of partitions increases, so does the value of optimal target product concentration by MSFO optimizations. The optimal target product concentration obtained by the MSFO after 20 independent runs was 0.610118 (N = 10), 0.610537 (N = 25), 0.610771–0.610785 (N = 50). The optimal concentration of MSFO was close to that of Liu et al., while Liu et al. [38] achieved a value in the range of 0.610779–0.610787 (N = 100) using IKBCA, which is better than that of other methods in the literature. The result shows the feasibility and superiority of solving dynamic optimization problems with MSFO.

5.3.3. Analysis of the Experimental Results of Case 3

Table 7. Results of parallel reaction problems in tubular reactors by different methods.

Ref.	Method	N	Optimum
[28]	MCB	~	0.57353
[37]	CP-PSO	~	0.573543
[37]	CP-APSO	~	0.573544
[39]	ISOA	10	0.572226
[39]	ISOA	35	0.57348
[40]	CVP	~	0.56910
[40]	CVI	~	0.57322
[41]	CPT	~	0.57353
This work	MSFO	10	0.572143
This work	MSFO	40	0.573212–0.574831

shows the product concentration results of MSFO versus CP-PSO, CP-APSO, HSOA CVP, CVI, CPT, and MCB for optimization of parallel reactions in a tubular reactor problem. The “~” in Table 7 means that the reference did not provide a value. Figure 16 is the optimal control variable curve with N = 10 and N = 40, Figure 17 is the optimal state variable trajectory, and Figure 18 is the iteration curve of the optimal result.

As can be seen from the results in Table 7, Zhou and Liu [37] got values of 0.573543 and 0.573544 using the control parameterization-based particle swarm approach (CP-PSO) and control parameterization-based adaptive particle swarm qpproach (CP-APSO). Xu et al. [39] obtained values of 0.572226 (N = 10) and 0.57348 (N = 35) using improved seagull optimization algorithm (ISOA). Biegler [40] got values of 0.56910 (CVP) and 0.57322 (CVI) using successive quadratic programming and orthogonal collocation. Vassiliadis et al. [41] got a value of 0.57353 using CPT. Banga and Seider [28] obtained a value of 0.57353 using stochastic algorithms.

In this paper, the optimal target product concentration obtained by the MSFO after 20 independent runs was 0.572143 (N = 10); 0.573212–0.574831 (N = 40). Comparing the experimental results with other literature, it can be seen that the optimal concentration of the product obtained by the optimization of MSFO is not much difference in value compared with other methods in the literature.

5.3.4. Analysis of the Experimental Results of Case 4

Table 8. Results of catalyst mixing problem by different methods.

Ref.	Method	N	Optimum
[36]	IKEA	20	0.4757
[36]	IKEA	100	0.47761–0.47768
[39]	ISOA	40	0.47721
[42]	STA	5	0.47260
[42]	STA	10	0.47363
[42]	STA	15	0.47453
[42]	GA	5	0.47260
[42]	GA	10	0.47363
[42]	GA	15	0.47453
[43]	TDE	20	0.47527
[43]	TDE	40	0.47683
[44]	NDCVP-HGPSO	15	0.47771
This work	MSFO	20	0.47562
This work	MSFO	70	0.477544–0.47760

shows the optimal results of MSFO versus IKEA, HSOA, STA, GA, TDE, and NDCVP-HGPSO for the catalyst mixing problem. Figure 19 is the optimal control variable curve with N = 10 and N = 70, Figure 20 is the optimal state variable curve, and Figure 21 is the iteration curve of the optimal result.

In the open literature, Peng et al. [36] obtained values of 0.4757 (N = 10) and a range of 0.47761–0.47768 (N = 100) using an improved knowledge evolution algorithm (IKEA). Xu et al. [39] obtained a value of 0.47721 (N = 10) using improved seagull optimization algorithm (ISOA). Huang et al. [42] used a genetic algorithm (GA) to obtain values of 0.47260 (N = 5), 0.47363 (N = 10), and 0.47453 (N = 15) and proposed control vector parameterization with state transition algorithm (STA) to obtain values of 0.47260 (N = 5), 0.47363 (N = 10), and 0.47453 (N = 15). Angira and Santosh [43] obtained values of 0.47527 (N = 20) and 0.47683 (N = 40) using a trigonometric differential evolution approach (TDE). Chen et al. [44] reached the value of 0.47771 (N = 15) using nonuniform discretization-based control vector parameterization (NDCVP-HGPSO).

Experimental results show that the optimal solution of MSFO was 0.47562 when the number of partitions was N = 20, which is better than that of Angira et al. [43], who applied TDE to obtain values of 0.47527(N = 20) and Huang et al. [42], who applied STA to obtain values of 0.47453 (N = 15). When N = 70, the optimal solution of MSFO optimization was stable between 0.477544 and 0.4760, which is better than STA, TDE, GA, and ISOA but slightly worse than IKEA and NDCVP-HGPSO. The experimental results further demonstrate the ability of MSFO to solve dynamic optimization problems.

5.3.5. Analysis of the Experimental Results of Case 5

Table 9. Results of plug flow tubular reactor by different methods.

Ref.	Method	N	Optimum
[45]	IPSO	20	0.677219
[46]	SVTN	20	0.677389
[47]	Iterative dynamic programming (IDP)	10	0.67531
[48]	Combination mode method (CMM)	10	0.7226
[29]	Conjugate gradient method (CGM)	10	0.7227
[49]	Nonuniform control vector parameterization (NU-CVP)	20	0.77298
[50]	S-CVP	20	0.7234708
[50]	PWV-CVP	20	0.7234708
This work	MSFO	10	0.7226987
This work	MSFO	20	0.7234724

shows the optimal results of MSFO versus IPSO, SVTN, IDP, CMM, CGM, NOCVP, S-CVP, and PWV-CVP for plug flow tubular reactor optimization. Figure 22 is the optimal control trajectory of the normalized coolant flow rate with N = 10 and N = 70. Figure 23 is the optimal state variable curve, and Figure 24 is the iteration curve of the optimal result.

In the open literature, Zhang et al. [45] used iterative multi-objective particle swarm optimization-based control vector parameterization (IPSO) to obtain the value of 0.677219 (N = 20). Xiao and Liu [46] reached the value of 0.677389 (N = 20) using an effective pseudospectral optimization approach with sparse variable time nodes (SVTN). Luus [47] used iterative dynamic programming (IDP) to obtain the value of 0.67531 (N = 10). Ko [48] used combination mode method (CMM) to obtain the value of 0.67531 (N = 10). Reddy and Husain [29] got the value of 0.7227 (N = 10) using the conjugate gradient method (CGM). LEI et al. [49] reached the value of 0.77298 (N = 20) using a nonuniform control vector parameterization approach (NU-CVP). Wei, F.X. et al. [50] reached a value of 0.74708 by S-CVP and PWV-CVP, which was the best literature re sult.

The global optimum obtained by the MSFO after 20 independent runs was 0.7226987 (N = 10) and 0.7234794 (N = 20). When N = 20, MSFO was slightly better than the S-CVP and PWV-CVP, thus outperforming all the other approaches mentioned in this article.

5.3.6. Analysis of the Experimental Results of Case 6

Table 10. Results of plug flow tubular reactor by different methods.

Ref.	Method	N	Optimum
[8]	VSACS	10	32.18175–32.18246
[8]	VSACS	20	32.45614–32.45629
[8]	VSACS	100	32.81001–32.81224
[34]	PADIWO-CVP	~	32.68649
[34]	GADIWO-CVP	~	32.68720
[36]	IKEA	20	32.4225–32.6783
[38]	IKBCA	20	32.4556–32.4561
[38]	IKBCA	150	32.7114–32.7180
[43]	TDE	~	32.684494
[44]	NDCVP-HGPSO	~	32.68712
[51]	FIDP	~	32.47
[52]	DCM-PSO	10	32.68851327
[52]	DCM-PSO	20	32.68851335
This work	MSFO	10	32.18024–32.18197
This work	MSFO	20	32.45332–32.45446
This work	MSFO	100	32.69236–32.71112

shows the optimal results of MSFO versus VSACS, IKBCA, IKEA, TDE, NDCVP- HGPSO, FIDP, DCM-PSO, PADIWO-CVP, and GADIWO-CVP methods for optimizing the PR-b problem. The “~” in Table 10 means that the reference did not provide a value. Figure 25, Figure 26 and Figure 27 are the optimal control variable curves with N = 10, N = 20, and N = 100, and Figure 28 is the optimal state variable curve.

In the open literature, Yuanbin et al. [8] got values in the range of 0.28 to 0.9, 32.18175–32.18246 (N = 10), 32.45614–32.45629 (N = 20), and 32.81001–32.81224 (N = 100) using adaptive Cuckoo search algorithm (VSACS). Tian et al. [34] got values of 32.68649 and 32.68720 using control vector parameterization based adaptive invasive weed optimization. Peng et al. [36] used an improved knowledge evolution algorithm (IKEA) to obtain a value in range of 32.4225–32.6783 (N = 20). Liu et al. [38] obtained values in range of 32.4556–32.4561 (N = 20) and 32.7114–32.7180 (N = 150) using improved knowledge-based cultural algorithm (IKBCA). Angira and Santosh [43] used a trigonometric differential evolution approach (TDE) to obtain a value of 32.684494. Chen et al. [44] used nonuniform discretization-based control vector parameterization (NDCVP- HGPSO) to obtain a value of 32.68712. Tholudur and Ramirez [51] obtained a value of 32.47 using a modified iterative dynamic programming algorithm (FIDP). Wang and Li [52] obtained values 32.68851327 (N = 10) and 32.68851335 (N = 20) using a dynamic chaotic mutation based particle swarm optimization (DCM-PSO).

In this paper, the secreted heterologous protein obtained by the MSFO after 20 independent runs was in the range of 32.18024–32.18197 (N = 10), 32.45332–32.45446 (N = 20), and 32.69236–32.71112 (N = 100). The comparison results in Table 10 show that MSFO is obviously better than TDE, FIDP, PADIWO-CVP, and GADIWO-CVP, but there is a certain gap between MSFO, IKBCA, and VSACS. Because the test case involves many local extremum points, the optimization performance of the algorithm is required to be higher. Experimental results show that MSFO has certain advantages in solving dynamic optimization problems.

6. Conclusions

In this paper, a novel dynamic optimization method, integrating the equal division method into the modified sailfish optimizer, named MSFO, was proposed. Aiming at the reliance on population initialization of SFO optimizer, reduced population diversity in the later iterations, low solution accuracy, and premature convergence, the tent chaotic mapping strategy was introduced to initialize the sailfish and sardine population perturbations; an adaptive linear reduction attack parameter was proposed; the sardine position update formula was modified, and a modified sailfish optimizer (MSFO) was proposed. Through an equal division method, an infinite optimization problem of dynamic systems can be successively transformed into a finite-dimensional NLP, providing a calculable evaluation fitness function for the next optimization steps. Six chemical dynamic optimization cases were solved by MSFO. The experimental results showed that the MSFO had better optimization ability and the solution precision was satisfactory. Consequently, the proposed MSFO can be applied to a wider scope of real-life scenarios to solve DOPs.

The method of dividing the time domain into equal parts was used, which has the problems of a large amount of calculation and difficult calculation Thus, the next works will be to use the control variable method of unequal division of the dispersion of time-domain segmentation, combined with a modified sailfish optimizer to solve the chemical dynamic optimization problem.