DEM–FEM Coupling Simulation of the Transfer Chute Wear with the Dynamic Calibration DEM Parameters
Abstract
:1. Introduction
2. Numerical Methodology
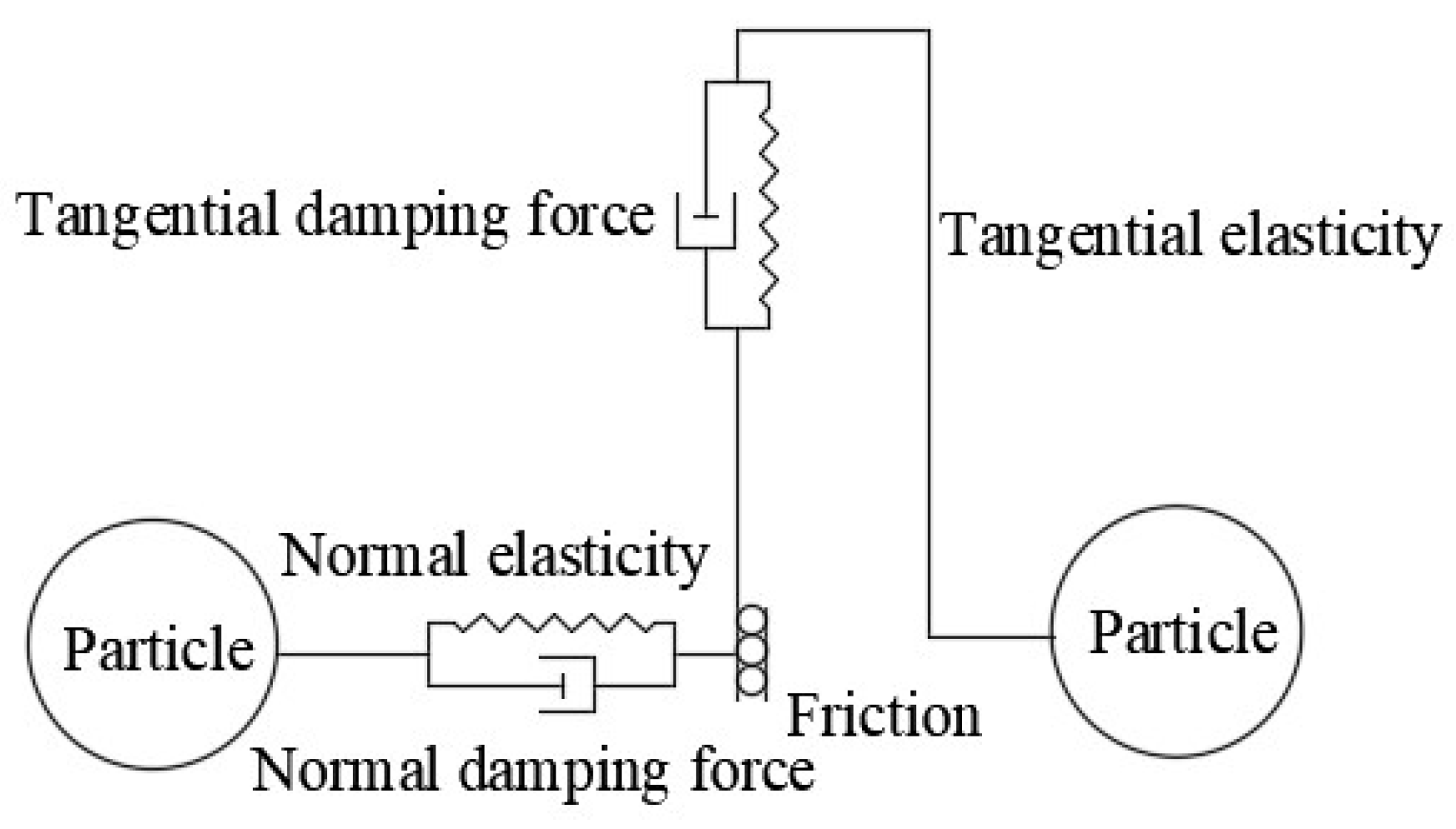
2.1. Discrete Element Method
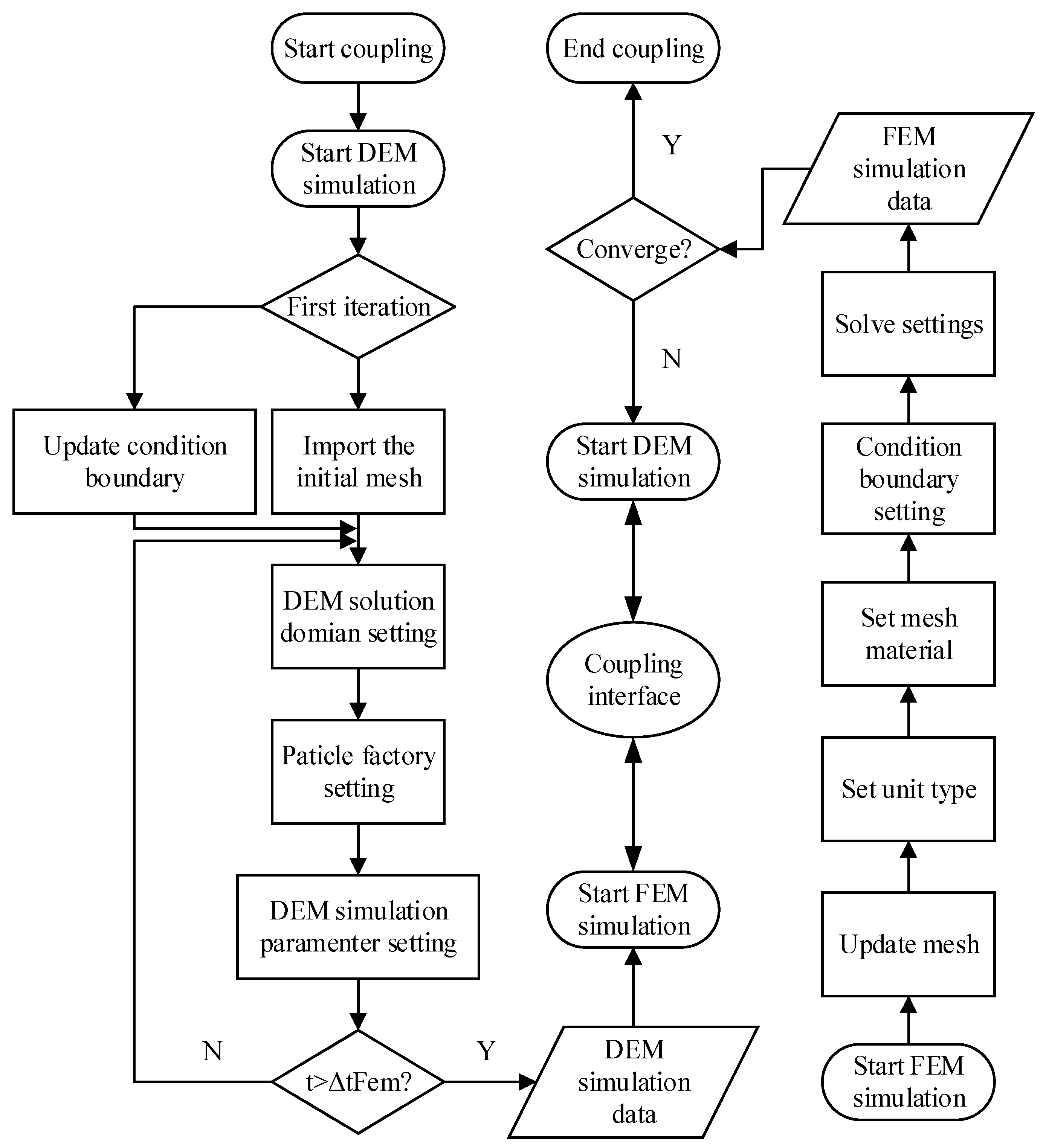
2.2. DEM–FEM Coupling Method
3. Simulation Model and Parameters
4. DEM Parameters Dynamic Calibration
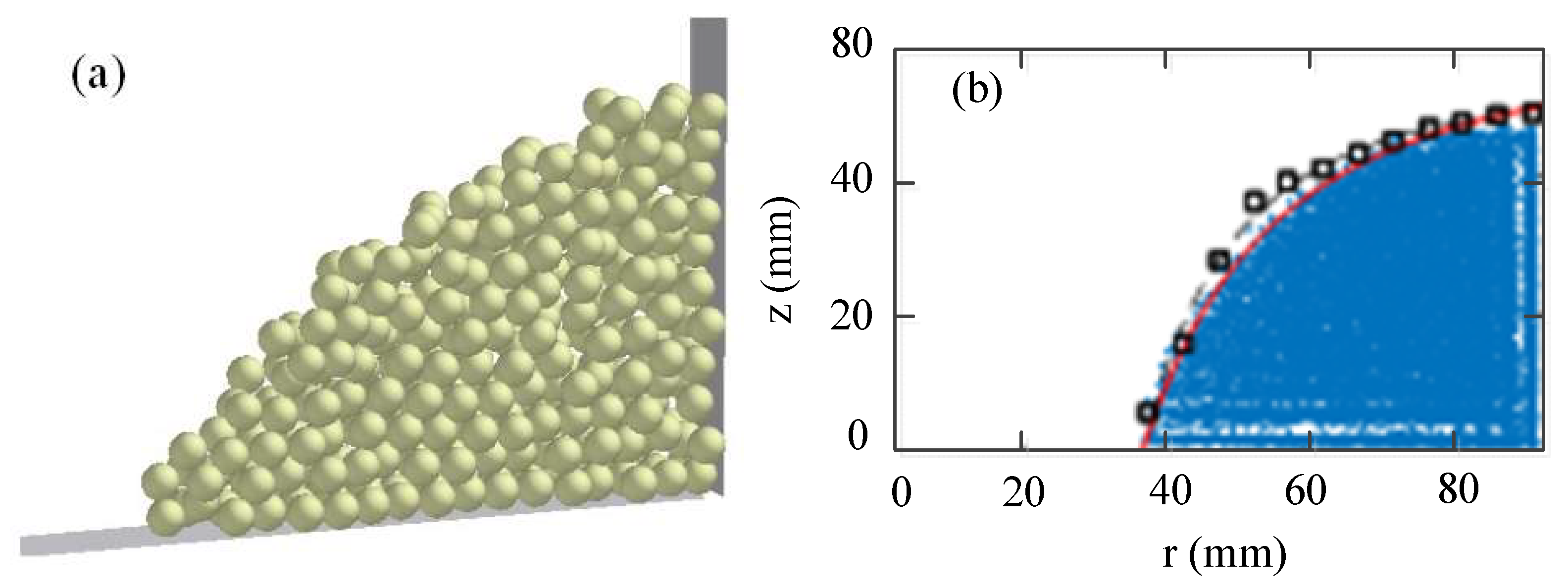
4.1. Friction Coefficient Calibration with Disc Tester
4.2. Wear Coefficient Calibration with the Wear Tester
5. Simulation Results
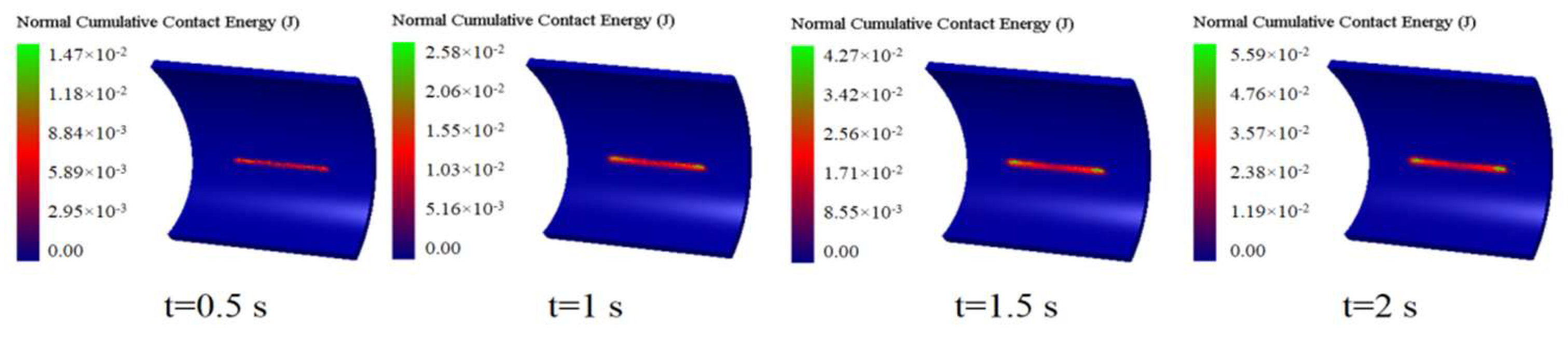
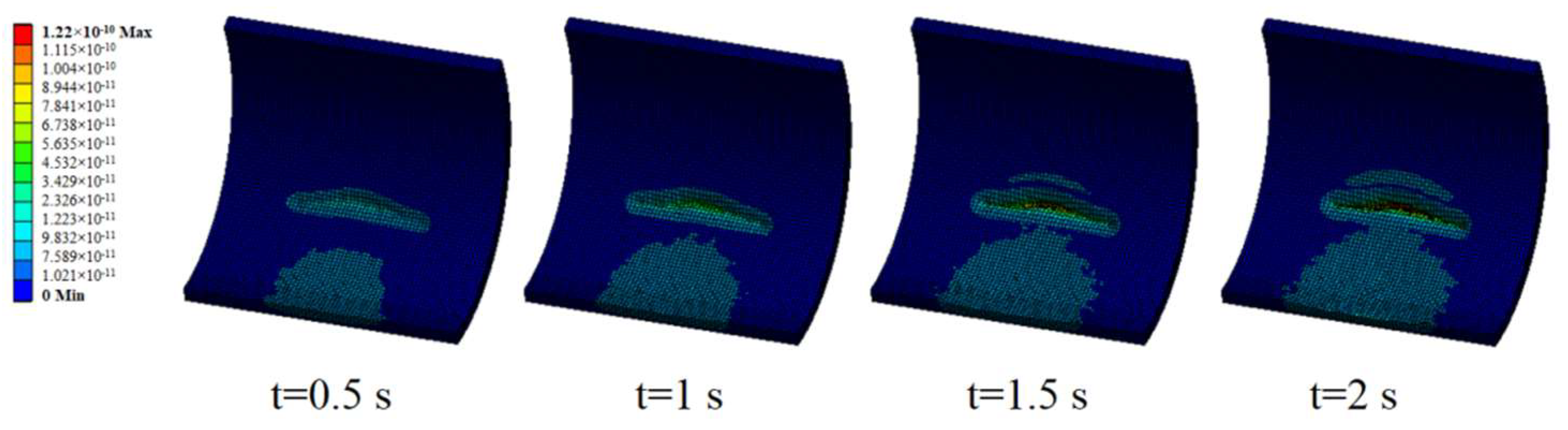
5.1. Chute Cumulative Contact Energy
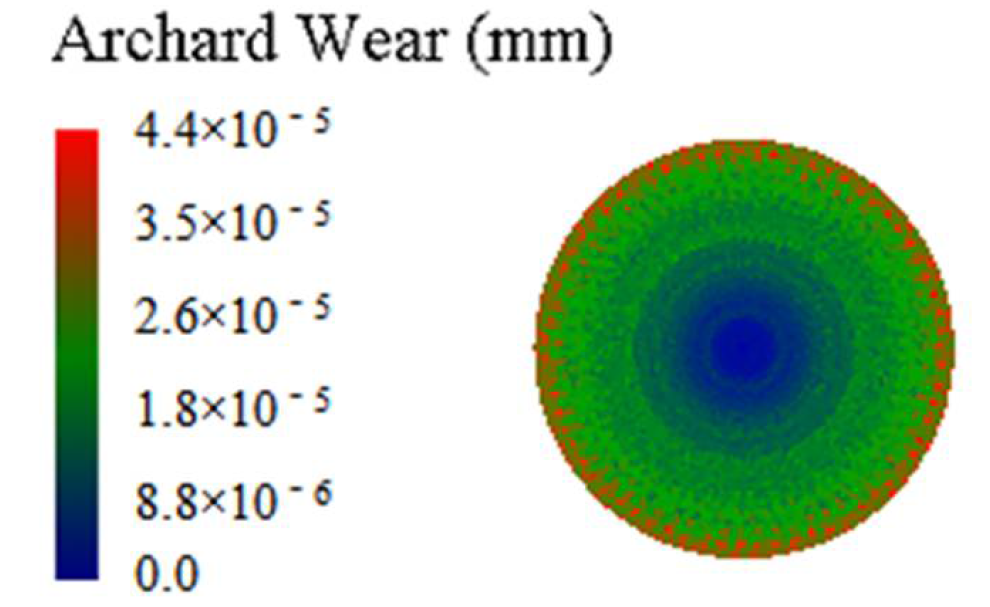
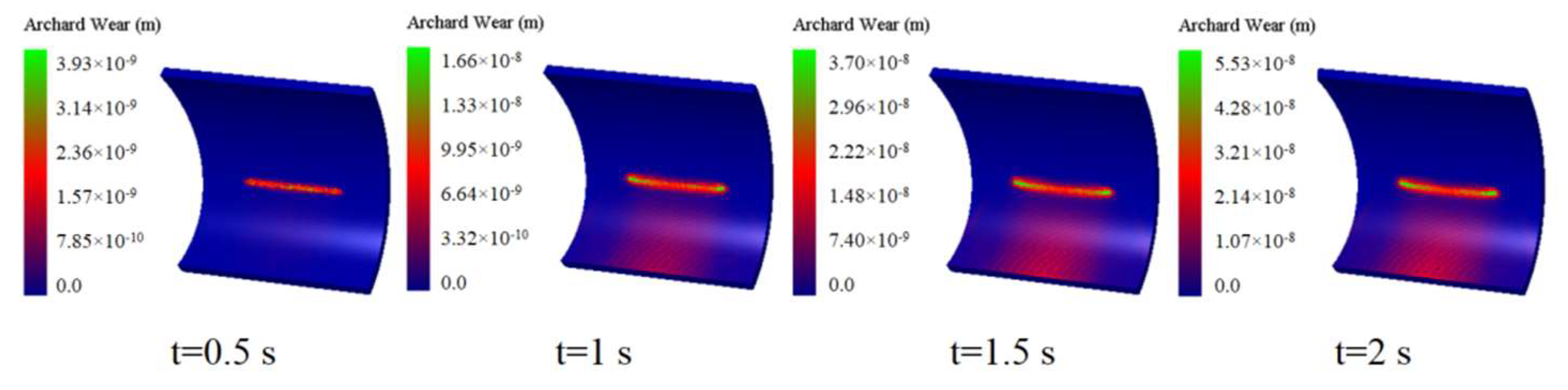
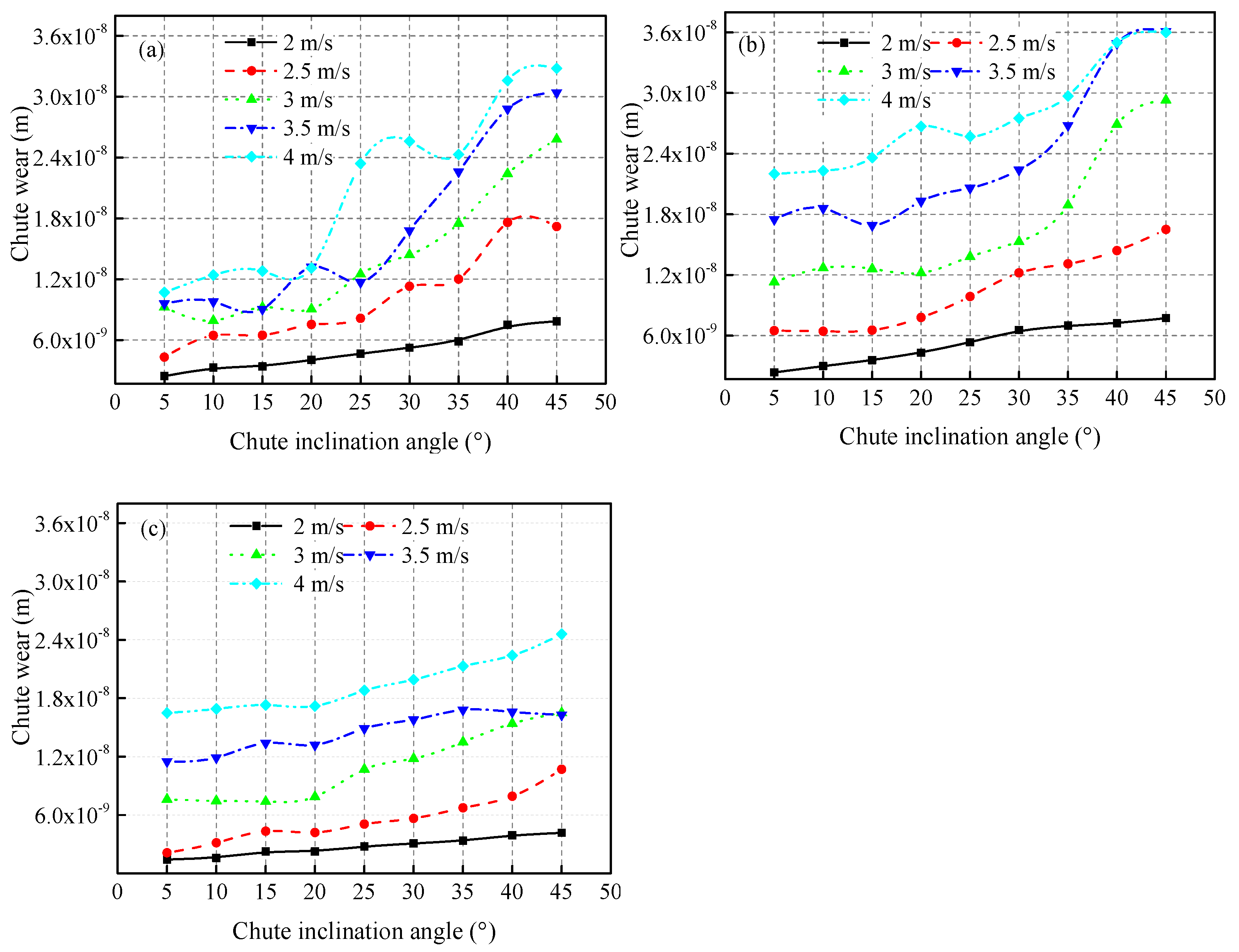
5.2. Chute Wear Volume
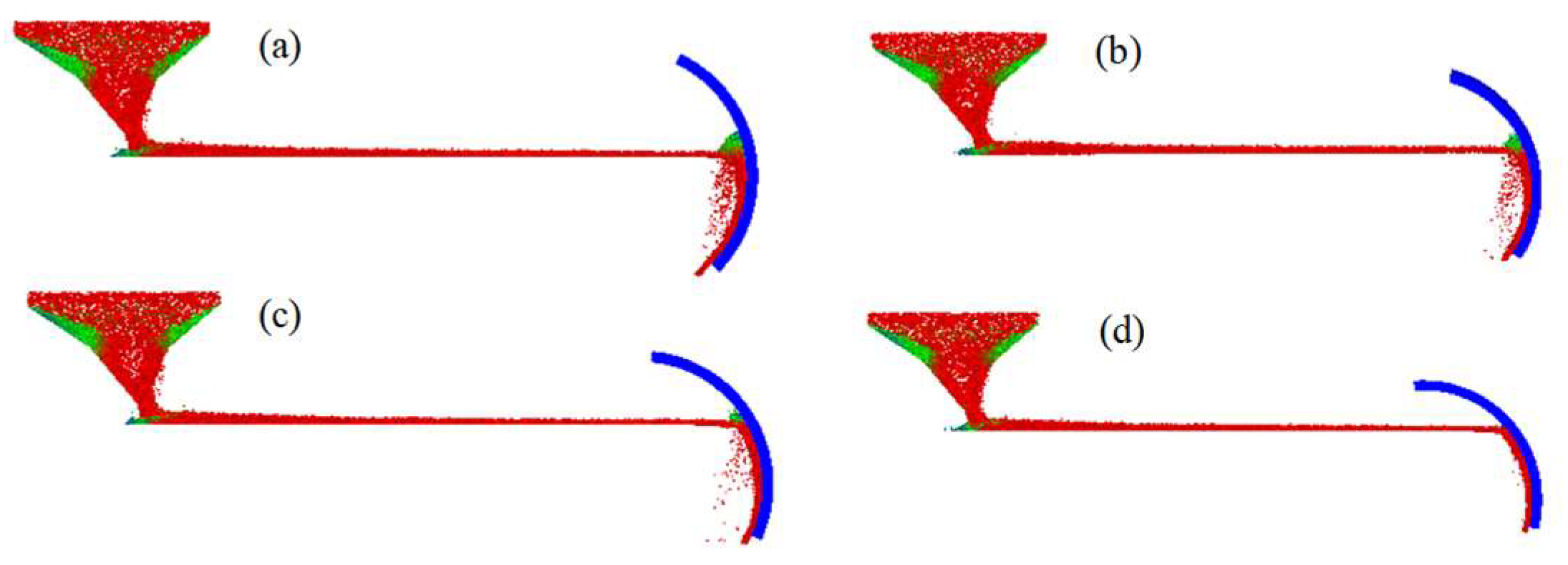
5.3. Shape Variables
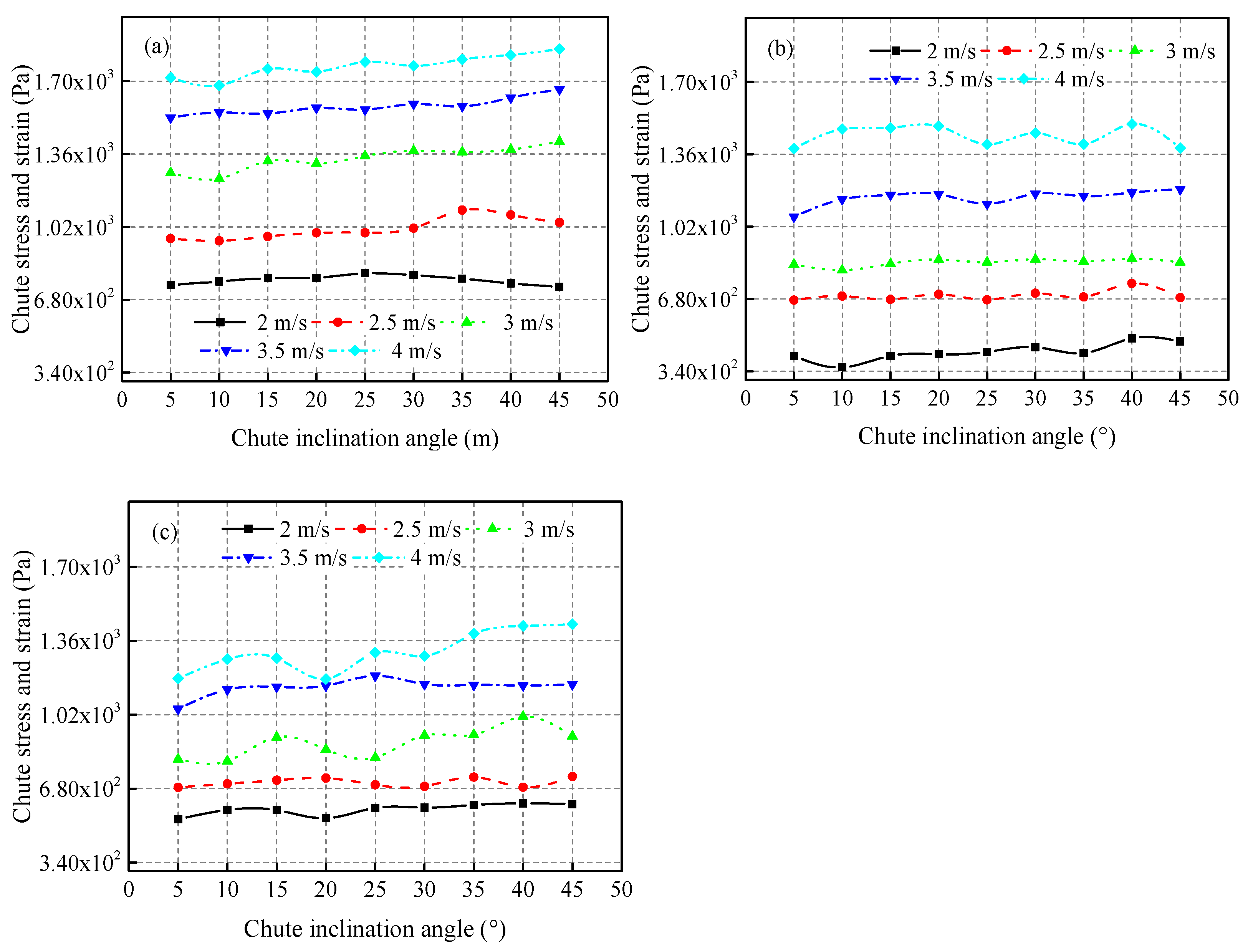
5.4. Chute Pressure
5.5. Practical Implications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Qin, Z.Y.; Zhao, Z.L.; Zhao, Y.J. Simulation and Analysis of Material Horizontal Vibration Conveying Based on DEM. Adv. Mater. Res. 2014, 941–944, 2268–2272. [Google Scholar] [CrossRef]
- Shimizu, Y.; Cundall, P. Numerical Simulations Of Bulk Handling in Screw Conveyors by Three-Dimensional DEM; Australasian Institute of Mining and Metallurgy: Brisbane, Australia, 2000; pp. 887–892. [Google Scholar]
- Zheng, Z.; Zhao, H.; Liu, P.; He, J. Maize straw cutting process modelling and parameter calibration based on discrete element method (DEM). INMATEH-Agric. Eng. 2021, 63, 461–468. [Google Scholar]
- Shen, J.; Roberts, A.; Wheeler, C. Dem simulations on gate loads and bin storage characteristics before discharge. Powder Technol. 2021, 383, 280–291. [Google Scholar] [CrossRef]
- Jia, W.; Markine, V.L.; Jing, G. Analysis of furnace slag in railway sub-ballast based on experimental tests and DEM simulations. Constr. Build. Mater. 2021, 288, 123114. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, X.; Zeng, Q.; Gao, K.; Jiang, K.; Zhou, J. Application of a screw conveyor with axial tilt blades on a shearer drum and investigation of conveying performance based on DEM. Particuology 2021. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, X.; Meng, W. Research on the axial velocity of the raw coal particles in vertical screw con-veyor by using the discrete element method. J. Mech. Sci. Technol. 2021, 35, 2551–2560. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Li, B.; Chen, J. Calibration of parameters of wheat required in discrete element method sim-ulation based on repose angle of particle heap. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2016, 32, 247–253. [Google Scholar]
- González-Montellano, C.; Ramírez-Gómez, Á.; Gallego, E.; Ayuga, F. Validation and experimental calibration of 3D discrete element models for the simulation of the discharge flow in silos. Chem. Eng. Sci. 2011, 66, 5116–5126. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle-structure interactions under impact conditions. Powder Technol. 2011, 212, 198–209. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, J.; Liao, T.; Hu, X.; Zhang, X. Performance Analysis of Ball Mill Liner Based on DEM-FEM Coupling. Lect. Notes Electr. Eng. 2020, 634, 3–10. [Google Scholar] [CrossRef]
- Xia, H.; Tong, X.; Li, Z.; Wu, X. DEM-FEM coupling simulations of the interactions between particles and screen surface of vibrating screen. Int. J. Min. Miner. Eng. 2017, 8, 250–263. [Google Scholar] [CrossRef]
- Perazzo, F.; Löhner, R.; Labbe, F.; Knop, F.; Mascaró, P. Numerical modeling of the pattern and wear rate on a structural steel plate using DEM. Miner. Eng. 2019, 137, 290–302. [Google Scholar] [CrossRef]
- Forsström, D.; Jonsén, P. Calibration and validation of a large scale abrasive wear model by coupling DEM-FEM: Local failure prediction from abrasive wear of tipper bodies during unloading of granular material. Eng. Fail. Anal. 2016, 66, 274–283. [Google Scholar] [CrossRef]
- Yuan, J.; Li, M.; Ye, F.; Zhou, Z. Dynamic characteristic analysis of vertical screw conveyor in variable screw section condition. Sci. Prog. 2020, 103, 0036850420951056. [Google Scholar] [CrossRef] [PubMed]
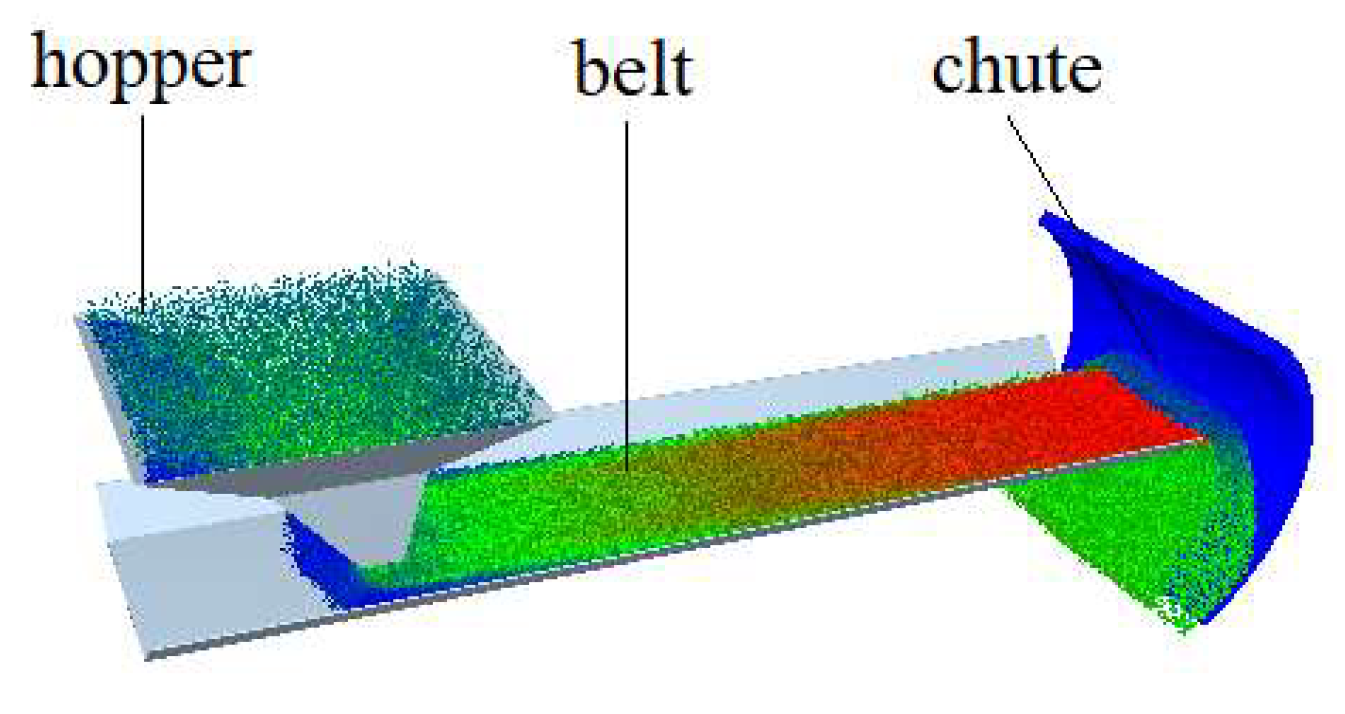
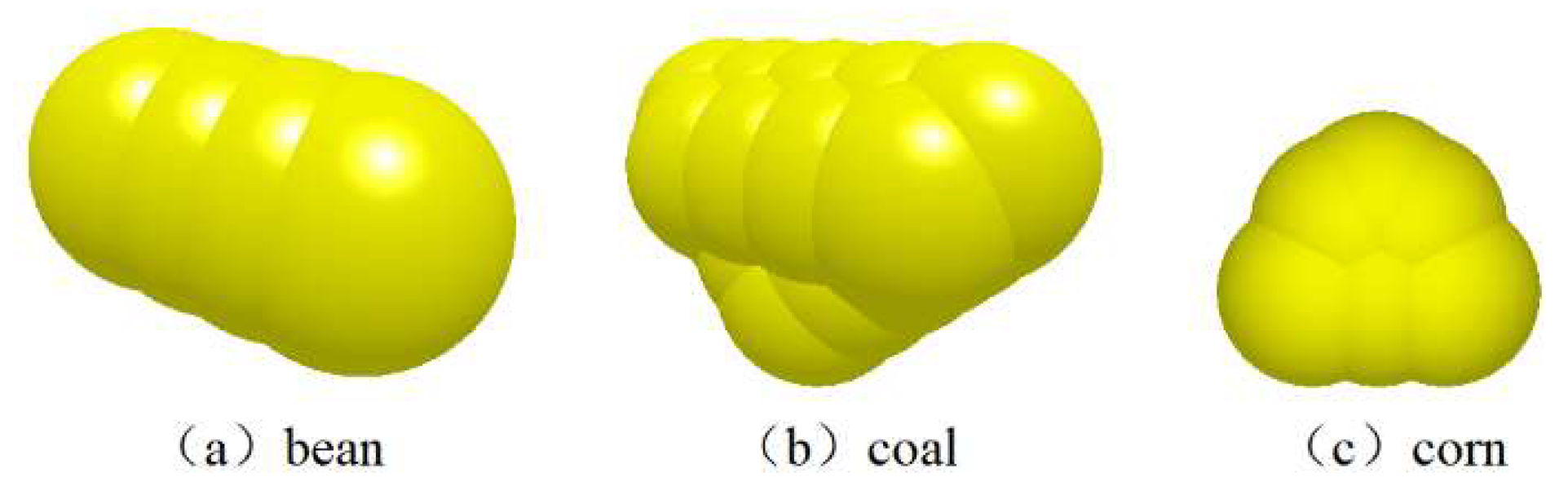







| Geometry | Hopper | Belt | Chute |
|---|---|---|---|
| Poisson’s ratio | 0.31 | 0.49 | 0.31 |
| Shear modulus (Pa) | 1 × 106 | 1 × 106 | 1 × 106 |
| Solids density (kg/m3) | 7800 | 2000 | 7800 |
| Properties | Coal | Bean | Corn |
|---|---|---|---|
| Solids density (kg/m3) | 1500 | 2000 | 780 |
| Poisson’s ratio | 0.3 | 0.25 | 0.438 |
| Shear modulus (Pa) | 1 × 106 | 1 × 106 | 1 × 106 |
| Coefficient of restitution | 0.2 | 0.1 | 0.1 |
| Coefficient of static friction μs,pp | 0.4~0.8 | 0.3~0.7 | 0.2~0.5 |
| Coefficient of rolling friction μr,pp | 0.01~0.04 | 0.01~0.06 | 0.02~0.04 |
| Coefficient of static friction μs,pg | 0.3~0.6 | 0.3~0.5 | 0.2~0.5 |
| Coefficient of rolling friction μr,pg | 0.01~0.03 | 0.01~0.05 | 0.01~0.02 |
| Properties | Coal | Bean | Corn |
|---|---|---|---|
| Coefficient of static friction μs,pp | 0.42 | 0.34 | 0.31 |
| Coefficient of rolling friction μr,pp | 0.012 | 0.009 | 0.008 |
| Coefficient of static friction μs,pg | 0.47 | 0.34 | 0.32 |
| Coefficient of rolling friction μr,pg | 0.018 | 0.015 | 0.016 |
| Particle Material | Coal | Bean | Corn |
|---|---|---|---|
| Coefficient of wear | 8.658 × 10−12 | 5.364 × 10−12 | 6.254 × 10−12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Qiang, Y.; Jiang, W.; Fu, X. DEM–FEM Coupling Simulation of the Transfer Chute Wear with the Dynamic Calibration DEM Parameters. Processes 2021, 9, 1847. https://doi.org/10.3390/pr9101847
Ye F, Qiang Y, Jiang W, Fu X. DEM–FEM Coupling Simulation of the Transfer Chute Wear with the Dynamic Calibration DEM Parameters. Processes. 2021; 9(10):1847. https://doi.org/10.3390/pr9101847
Chicago/Turabian StyleYe, Fangping, Yuezhang Qiang, Weijie Jiang, and Xiang Fu. 2021. "DEM–FEM Coupling Simulation of the Transfer Chute Wear with the Dynamic Calibration DEM Parameters" Processes 9, no. 10: 1847. https://doi.org/10.3390/pr9101847
APA StyleYe, F., Qiang, Y., Jiang, W., & Fu, X. (2021). DEM–FEM Coupling Simulation of the Transfer Chute Wear with the Dynamic Calibration DEM Parameters. Processes, 9(10), 1847. https://doi.org/10.3390/pr9101847






