Study on Dynamics of a Two-Stage Gear Transmission System with and without Tooth Breakage
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Dynamic Model
2.2. Time-Varying Stiffness
2.3. Model for Tooth Breakage
2.4. Meshing Error of Gear Pair
3. System Parameters
3.1. Geometric Parameters
3.2. Structure Parameters
4. Numerical Simulation
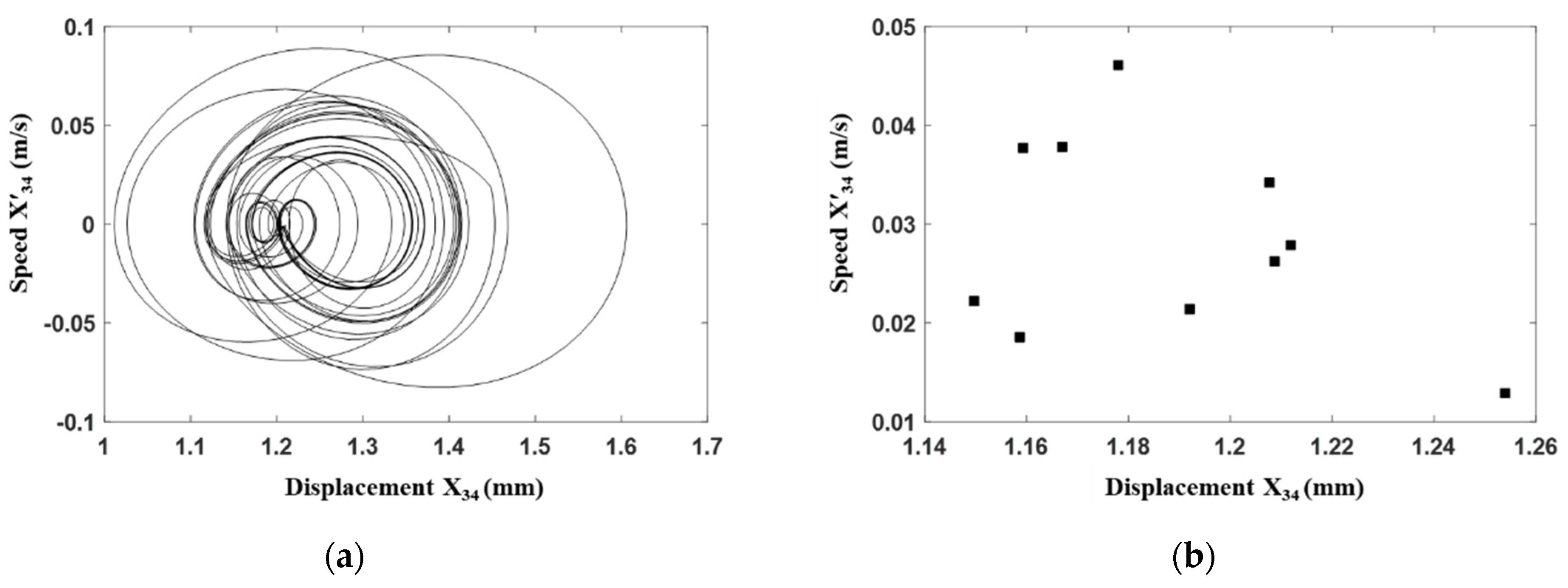
4.1. Bifurcation Analysis
4.2. Time-Frequency Characteristics
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, Q.; Cheng, Y. A gear pair model and its application in the software Adams. Acta Armamentaria 2003, 24, 509–512. [Google Scholar]
- Kahraman, A. Natural Modes of Planetary Gear Trains. J. Sound Vib. 1994, 173, 125–130. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, C. Natural Mode Analysis of Planetary Gear Trains. China Mech. Eng. 2004, 16, 1461–1465. [Google Scholar]
- Yuan, R.; Ji, M. Analysis of vibration characteristics of airplane planetary reducer. J. Aerosp. Power 1995, 10, 395–398. [Google Scholar]
- Vinayak, H.; Singh, R.; Padmanabhan, C. Linear dynamic analysis of multi-mesh transmissions containing external, rigid gears. J. Sound Vib. 1995, 185, 1–32. [Google Scholar] [CrossRef]
- Sun, Z.; Shen, Y.; Li, S. Study on dynamic behavior of encased differential gear train. J. Mech. Eng. 2002, 38, 44–48. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, Y. Vibration analysis of gears considering time-varying meshing stiffness and transfer error. J. Mech. Transm. 2002, 26, 5–8. [Google Scholar]
- Liu, M.; Shen, Y.; Dong, H. Research on numerical characters of the attractors in a nonlinear gear system. J. Mech. Eng. 2003, 39, 111–116. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system. J. Sound Vib. 1991, 146, 135–156. [Google Scholar] [CrossRef]
- Ji, J. Dynamics Research of a Two-Stage Gear System Based on the Analysis of Multi-Parameters Simulation; Lanzhou Jiaotong University: Lanzhou, China, 2015. [Google Scholar]
- Sun, Z.; Ji, L.; Shen, Y.; Chang, H. Influence of backlashes on torsional vibration of star gear train. J. Mach. Des. 2003, 20, 3–6. [Google Scholar]
- Su, C. Analysis of the nonlinear dynamic characteristics of single-stage gear transmission system. J. Lanzhou Univ. Technol. 2012, 38, 32–36. [Google Scholar]
- Tian, X. Dynamic Simulation for System Response of Gear Box Including Location Gear Faults; University of Alberta: Edmonton, AB, Canada, 2004. [Google Scholar]
- Zhou, J.; Dong, H. On Load Sharing Characteristic of Planetary Gear System Based on Nonlinear Dynamics. Mech. Sci. Technol. Aerosp. Eng. 2008, 27, 808–811. [Google Scholar]
- Qian, B.; Wu, S.; Zhou, G. Research on Dynamic Characteristics of Planetary Gear Sets. J. Syst. Simul. 2009, 21, 6608–6612. [Google Scholar]
- Zhu, E.; Wu, S.; Wang, X.; Deng, M.X.; Qian, B. Study on nonlinear dynamic model of planetary gear train sets with friction force. J. Vib. Shock. 2010, 29, 217–220. [Google Scholar]
- Choy, F.K.; Ruan, Y.F.; Tu, R.K.; Zakrajsek, J.J.; Townsend, D.P. Modal analysis of multistage gear systems coupled with gearbox vibrations. J. Sol. Energy Eng. 1991, 114, 486–497. [Google Scholar] [CrossRef] [Green Version]
- Zhennan, A.C.H. Analysis of the Influence of Pitting and Spalling on Torsional Mesh Stiffness of Gears. J. Vib. Meas. Diagn. 2008, 28, 354–357. [Google Scholar]
- Kuang, J.H.; Lin, A.D. The Effect of Tooth Wear on the Vibration Spectrum of a Spur Gear Pair. J. Vib. Acoust. 2001, 123, 311–317. [Google Scholar] [CrossRef]
- Chaari, F.; Fakhfakh, T.; Haddar, M. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness. Eur. J. Mech. A/Solids 2009, 28, 461–468. [Google Scholar] [CrossRef]
- Chaari, F.; Fakhfakh, T.; Haddar, M. Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking. J. Fail. Anal. Prev. 2006, 6, 73–78. [Google Scholar] [CrossRef]
- Panrey, A.; Tandon, N. Spur gear dynamic model including defects: A review. Shock. Vib. Dig. 2003, 35, 465–478. [Google Scholar]
- Parey, A.; Badaoui, M.E.; Guillet, F.; Tandon, N. Dynamic modelling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect. J. Sound Vib. 2006, 294, 547–561. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, H.; Yang, T.; Yang, J.; Guan, Z. Nonlinear Dynamic Characteristics of Gear System with Single-Tooth Fault. J. Vib. Acoust. 2010, 6, 654–656. [Google Scholar]
- Wang, Y.; Zheng, H.; Yang, T.; Guan, Z.; Yang, J. Nonlinear Dynamics Behavior of Gear System with Fault Parameters. J. Vib. Acoust. 2011, 31, 570–573. [Google Scholar]
- Ning, S.; Han, Z.; Li, Y.; Wu, X. Dynamics Simulation of the Tooth Root Crack Fault of Gear Transmission System. J. Mech. Transm. 2015, 64–67. [Google Scholar]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of spur gear dynamics and estimation of fault growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Zhang, Q.; Tang, L.; Zheng, H.; Yang, T. Parameters Determination and Simulation Analysis of Nonlinear Dynamic Model of GearTooth Fatigue Crack. J. Vib. Acoust. 2011, 31, 94–97. [Google Scholar]
- Su, X.; Wang, S. Study on the Experiment and Nonlinear Dynamics Mechanism of Gear Fault Evolution. J. Mech. Transm. 2015, 39, 19–24. [Google Scholar]
- Wan, Z.; Zi, Y.; Cao, H. Gear Crack Propagation Simulation and Analysis of Mesh Stiffness. Appl. Math. Mech. 2015, 36 (Suppl. S1), 14–20. [Google Scholar]
- Wang, X.; Wu, S.; Zhou, X.; Hu, J.C. Nonlinear dynamics analysis of gear transmission system with wear fault. J. Vib. Shock. 2013, 32, 37–43. [Google Scholar]
- Gao, H.; Li, Y.; Liu, J. Dynamic analysis of a spur gear system with tooth-wear faults based on dynamic back lash. J. Vib. Shock. 2014, 33, 221–226. [Google Scholar]
- Liu, C.; Wu, Y.; Zhen, C. Rolling Bearing Fault Diagnosis Based on Variational Mode Decomposition and Fuzzy C Means Clustering. Proc. CSEE 2015, 35, 3358–3365. [Google Scholar]
- Li, Z.; Zhu, M.; Chu, F.; Xiao, Y. Mechanical fault diagnosis method based on empirical wavelet transform. Chin. J. Sci. Instrum. 2014, 35, 2423–2432. [Google Scholar]
- Yuan, H.; Zhang, R.; Wang, H. Fault diagnosis of gear box based on HMM and improved distance measure. J. Vib. Shock. 2014, 33, 89–94. [Google Scholar]
- Zhu, W.; Feng, Z. Fault diagnosis of planetary gear box based on improved empirical wavelet transform. Chin. J. Sci. Instrum. 2016, 37, 2193–2201. [Google Scholar]
- Xu, Y.; Zhao, G.; Hou, S.; Zhang, J. DT-CWT Domain Correlation Filter and Its Application in Incipient Gear box Fault Diagnosis. J. Vib. Acoust. 2016, 138–144. [Google Scholar] [CrossRef]
- Zhang, S.; Li, P.; Hu, Y.; Wang, J.; Jiang, W. Application of multifractal approximate entropy and sub tractive FCM clusteringin gear box fault diagnosis. J. Vib. Shock. 2015, 34, 205–209. [Google Scholar]
- Gregory, R.W.; Harris, S.L.; Munro, R.G. Dynamic behavior of spur gears. Proc. Inst. Mech. Eng. 1963, 178, 207–226. [Google Scholar] [CrossRef]
- Kahraman, A.; Blankenship, G.W. Experiments on Nonlinear Dynamic Behavior of an Oscillator with Clearance and Periodically Time-Varying Parameters. J. Appl. Mech. 1997, 64, 217. [Google Scholar] [CrossRef]
- Kubur, M.; Kahraman, A.; Zini, D.M.; Kienzle, K. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: Model and experiment. J. Vib. Acoust. 2004, 126, 398–406. [Google Scholar] [CrossRef]
- Xiang, L.; Gao, N.; Tang, L.; Guo, P.F. Nonlinear dynamic features of wind turbine’s gear systems subjected to internal and external excitations. J. Vib. Shock. 2018, 37, 94–97. [Google Scholar]
- Gao, L.; Zhang, L.; Zhu, J.; Zhou, C. De-noising processing of gear box vibration signal based on wavelet analysis. CSCD 2010, 34, 50–52. [Google Scholar]
















| Gear | Zi | Modulus | Jzi (kg·mm2) |
|---|---|---|---|
| 1 | 25 | 2 | 84.2 × 10−6 |
| 2 | 60 | 2 | 3118.7 × 10−6 |
| 3 | 45 | 2 | 955.9 × 10−6 |
| 4 | 60 | 2 | 3118.7 × 10−6 |
| Parameters | G12 | G34 |
|---|---|---|
| Kzi (N/m) | 2.8 × 106 | 2.8 × 106 |
| e0 (μm) | 10 | 10 |
| er (μm) | 1 | 1 |
| Czi (N s/m) | 51.05 | 159.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, D.; Gao, S.; Liu, H. Study on Dynamics of a Two-Stage Gear Transmission System with and without Tooth Breakage. Processes 2021, 9, 2141. https://doi.org/10.3390/pr9122141
Fu D, Gao S, Liu H. Study on Dynamics of a Two-Stage Gear Transmission System with and without Tooth Breakage. Processes. 2021; 9(12):2141. https://doi.org/10.3390/pr9122141
Chicago/Turabian StyleFu, Deyi, Shiqiao Gao, and Haipeng Liu. 2021. "Study on Dynamics of a Two-Stage Gear Transmission System with and without Tooth Breakage" Processes 9, no. 12: 2141. https://doi.org/10.3390/pr9122141





