Abstract
Intelligent Transportation system are becoming an interesting research area, after Internet of Things (IoT)-based sensors have been effectively incorporated in vehicular ad hoc networks (VANETs). The optimal route discovery in a VANET plays a vital role in establishing reliable communication in uplink and downlink direction. Thus, efficient optimal path discovery without a loop-free route makes network communication more efficient. Therefore, this challenge is addressed by nature-inspired optimization algorithms because of their simplicity and flexibility for solving different kinds of optimization problems. NIOAs are copied from natural phenomena and fall under the category of metaheuristic search algorithms. Optimization problems in route discovery are intriguing because the primary objective is to find an optimal arrangement, ordering, or selection process. Therefore, many researchers have proposed different kinds of optimization algorithm to maintain the balance between intensification and diversification. To tackle this problem, we proposed a novel Java macaque algorithm based on the genetic and social behavior of Java macaque monkeys. The behavior model mimicked from the Java macaque monkey maintains well-balanced exploration and exploitation in the search process. The experimentation outcome depicts the efficiency of the proposed Java macaque algorithm compared to existing algorithms such as discrete cuckoo search optimization (DCSO) algorithm, grey wolf optimizer (GWO), particle swarm optimization (PSO), and genetic algorithm (GA).
1. Introduction
Intelligent transportation is the process of finding the optimal communication path for vehicle-to-vehicle (V2V) communication and vehicle-to-infrastructure (V2I) communication in IoT-based vehicular ad hoc networks (VANETs). The vehicle is considered to be the primary source of transmission, and the signal will be received by other vehicles within a specific radius (100–200 m) [1,2]. IoT-based senor components are typically used for information transfer between V2V communication and V2I communication. Furthermore, modern IoT-based sensors play a vital role in identifying location and speed, and authenticating a vehicle via on-board sensors. Effective routing can also consider scenarios such as road surface conditions [3,4], traffic conditions [1,5] and information transfer, among other nodes. Route optimization is a major hurdle in the VANET deployment model, because of its highly volatile network topology. Consequently, the development of a robust communication route has become a major problem for VANET implementation, and this serves as a motivation for the development of a novel method of approaching this problem.
Nature-inspired optimization algorithms (NIOAs) are effectively used in VANETs to find the optimal routes for communication. The optimization algorithms are designed well to solve large-scale optimization problems. However, the multi-dimensional search space made of multiple parameters limits the existing methods to determining the optimal routing path for communication. Thus, information sent via a non-optimal route may have a delay in communication. Consequently, optimization algorithms incorporate hybrid search strategies for solving the multi-dimensional search space. Eventually, major optimization algorithms have attained dominance in solving continuous optimization problems. However, frequent route updating in VANETs (i.e., discrete search space) has created a vital demand to evolve reliable and robust route optimization algorithms.
Most discrete optimization problems fall under the categories of NP-hard or NP-complete [6]. However, the optimization algorithm faces many hurdles when solving typical discrete optimization problems [7,8]. The problem space of a discrete optimization problem is represented as the set of all feasible solutions that satisfy the constraint and the fitness function that maps each element to the problem space. Thus, the discrete or combinatorial optimization problem searches for the optimal solution from a set of feasible solutions [6,9,10].
Thus, the existing optimization algorithms may be trapped with local optimal routes due to the robust nature of vehicle movement. However, many optimization algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), and cuckoo search optimization (CSO), have been converted from continuous space to discrete space to address this IoT-based route-discovery process [3,11]. Parameter tuning and conversion from continuous space to discrete space has made algorithms achieve poor convergence due to the imbalance between intensification and diversification. In addition, it also lacks selection and elitist procedure during the search process. In this paper, we propose a Java macaque optimization algorithm that has been copied from the behavior of Java macaques, which combines genetic and swarm behavior to achieve an efficient route-discovery process.
The novel contributions of this proposed intelligent approach are described as follows:
- We introduced a novel optimization algorithm based on the behavior of Java macaque monkeys for balancing a search operation. The balance is achieved by modeling the natural behavior of Java macaques in terms of multi-group behavior, multiple search agents, social hierarchy-based selection strategy, mating, male replacement, and learning process.
- A multi-group population with multiple search agents of male and female monkeys helps with the exploration of different search spaces and in maintaining diversity.
- This algorithm uses the dominance hierarchy-based mating process for exploring complex search spaces.
- To address communication issues in a multi-group population, Java monkeys have a unique behavior called male replacement.
- The exploitation phase of the proposed algorithm is achieved by the learning process.
- This algorithm uses the multileader approach for male and female search agents such as alpha male and female in each group, and maintains the global best male and female agents. Thus, the multileader approach assists in the smooth transition from exploration phase to exploitation phase [12]. Furthermore, the social hierarchical-based selection strategy improves the maintenance of both converged and diverse monkeys in each group, as well as in the population.
2. Related Work
Generally, IoT-based VANET communication failure factors are classified in terms of transmit power, signal strength, path loss, and frequency [1]. Various detailed surveys have been conducted using different nature-inspired algorithms for routing purposes [13]. Popular algorithms, such as the genetic algorithm (GA), have proved their capability for addressing communication, but the performance of GA lacks optimal route discovery due to its convergence in a local optimal route [1,9,14,15]. The ant colony optimization (ACO) algorithm was proposed in [16] to ensure the resolution of the dynamic routing protocol. However, the proposed algorithm has a better communication process for a lower number of attempts.In addition, ref. [17] proposed a hybrid ACO and PSO to reduce communication delay and reduce fast convergence. Thus, the incorporation of the PSO algorithm helps to maintain diversity among the solutions, which improves the exploration capability of ACO algorithms.
An alternative route-discovery algorithm was investigated using the modified lion algorithm (MLA) in [18], and it shows its dominant performance in terms of convergence and routing cost compared to traditional GA. Likewise, ref. [19] proposed a clustering algorithm based on the grey wolf optimization (GWO) algorithm. The clustering capability of GWO helps to reduce the overhead of a complex network. Furthermore, the bee life algorithm was proposed to enhance the quality of service in IoT-based VANET [20]. The author in [21] proposed an improved firefly algorithm for addressing delay and failing communication in multicast routing using the levy distribution. However, the levy distributes the delays when attaining a convergence solution. In [22], the fuzzy bacterial optimization zone-based routing protocol is presented, which finds a short and stable route for communication within a small environment.
Nature-inspired optimization algorithms depict efficiency in IoT-based vehicle ad hoc networks. However, the design conversion from continuous search to discrete search space reduces its performance over a dynamic complex network topology. Thus, [23] clearly illustrates the performance of the discrete bat algorithm (BA), firefly algorithm (FA), and PSO, showing their dominance over cuckoo search (CS). Therefore, optimal path discovery in VANET has a greater impact in vehicle information transfer from V2V and V2I communication in both uplink and downlink channels. Furthermore, a new optimization algorithm-based levy flight-based discrete cuckoo search model helps to find an optimal path in [24]. The investigation used the levy flight and random walk technique to enhance the exploration behavior of CSO, which helps in finding a loop-free optimal communication route. The authors in [25] introduced the enhanced harmony search optimization algorithm to configure a routing protocol using roulette wheel selection and tournament selection. Furthermore, the combination of ant colony optimization (ACO) and on-demand distance vector (AODV) is used to reduce congestion in VANET. Thus, the significance of ACO is further incorporated into the routing protocol in [26], and that establishes the optimal path in low-density networks, and demonstrates poor convergence in high-density networks.
However, the limitation of optimization algorithms is the maintenance of the optimal solution for the next generation, and increased convergence time when finding the optimal route discovery due to unbalanced exploration, exploitation and selection strategy. Therefore, in IoT-based VANET, communication via uplink and downlink direction is quite complicated due to a robust network topology and that makes the route-discovery process quite difficult [27,28]. During an emergency, an infrastructure pushes messages to all vehicles, which causes congestion in the network due to the computational complexity in the routing process. However, the routing process falls under the category of an NP-hard problem. In this work, a novel Java macaque optimization algorithm is proposed, which concentrates on the selection and randomization procedure to attain a balance between exploration and exploitation in the search process, which helps with the discovery of a loop-free optimal path.
3. Preliminaries and Background
A new route discovery for uplink and downlink direction has been determined using the Java macaque algorithm. Furthermore, the routing protocol incorporates three important mechanisms—the initialization phase, new route discovery, and the route maintenance phase.
3.1. Initialization Phase
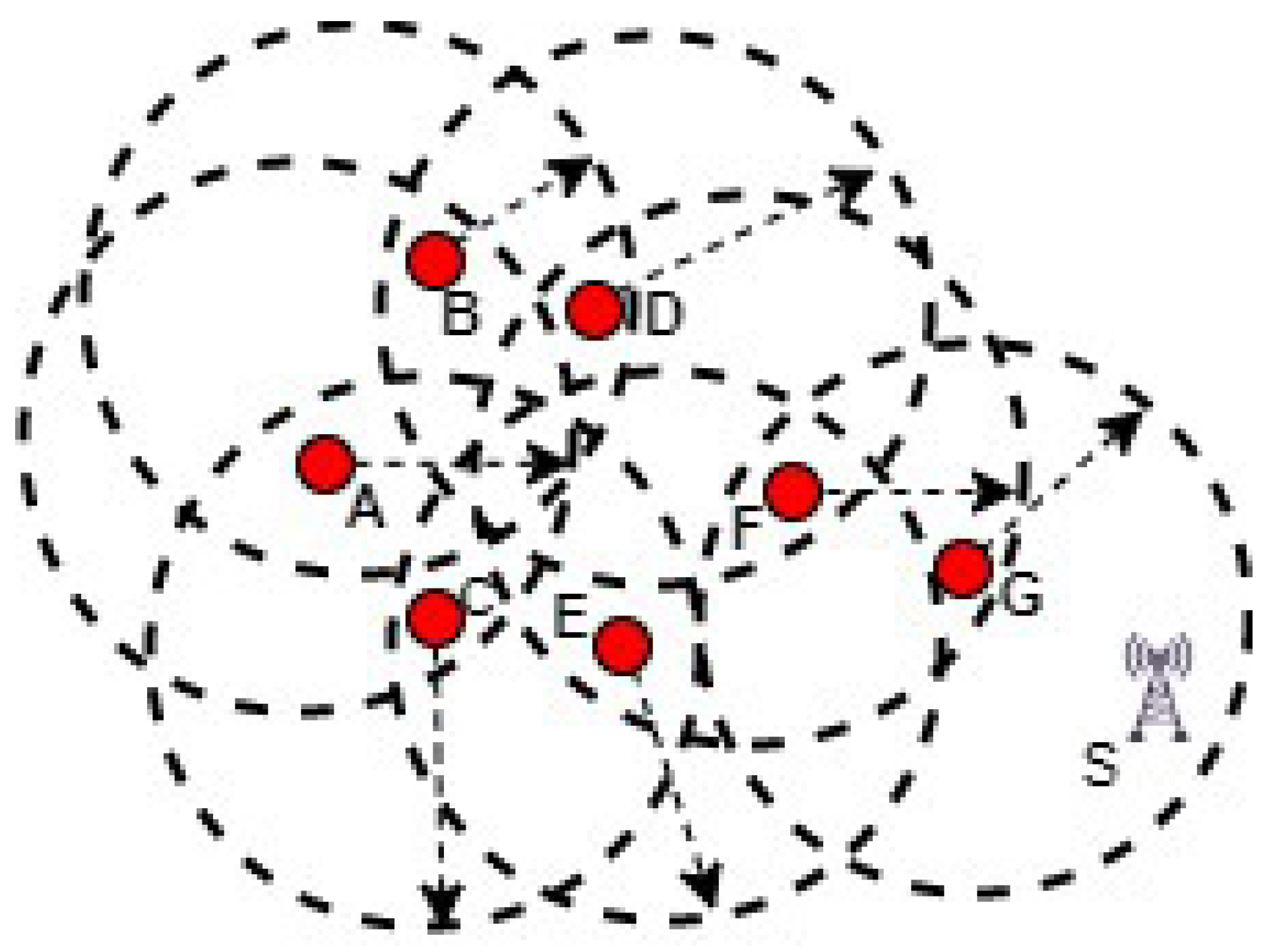
The initialization phase provides proper guidelines for vehicle registration in the IOT-based VANET infrastructure. Initially, the address of the infrastructure is not known to the new vehicle in the network, and it sends a broadcast message to connect with the infrastructure. In this network, let us assume that vehicles moving at an average speed of 20 km/h are only permitted to establish a communication with the infrastructure, which enhances network stability in VANET. The request-to-connect message is repeatedly broadcast by all the vehicles until it receives an acknowledgement message from the infrastructure. Thus, vehicle registration has been sequentially completed and updated in the routing table by the infrastructure services. As per [1,24], the request message consists of GPS location, speed, RSS (received signal strength), and appended GPS location. The initialization phase is clearly demonstrated in Figure 1.
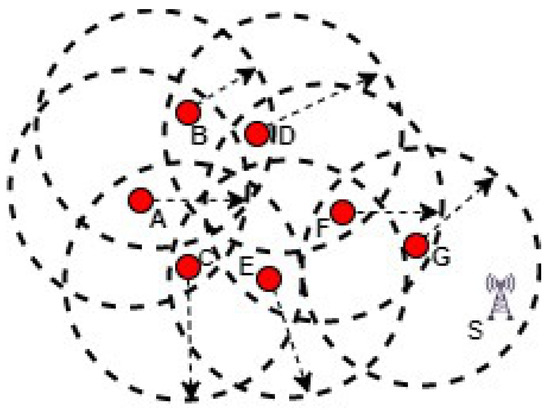
Figure 1.
Red dots represent vehicles, the black triangle S denotes the infrastructure, the arrows are the transmission range and links.
The initialization phase helps the infrastructure to locate the vehicle precisely in the VANET. However, vehicles in IoT-based environments dynamically modify their positions. Furthermore, the addition of new vehicles and the deletion of existing vehicles requires the updating of the routing table, and this initialization process establishes proper communication between the infrastructure which in due course enhances network stability for communication.
3.2. Route-Discovery Phase
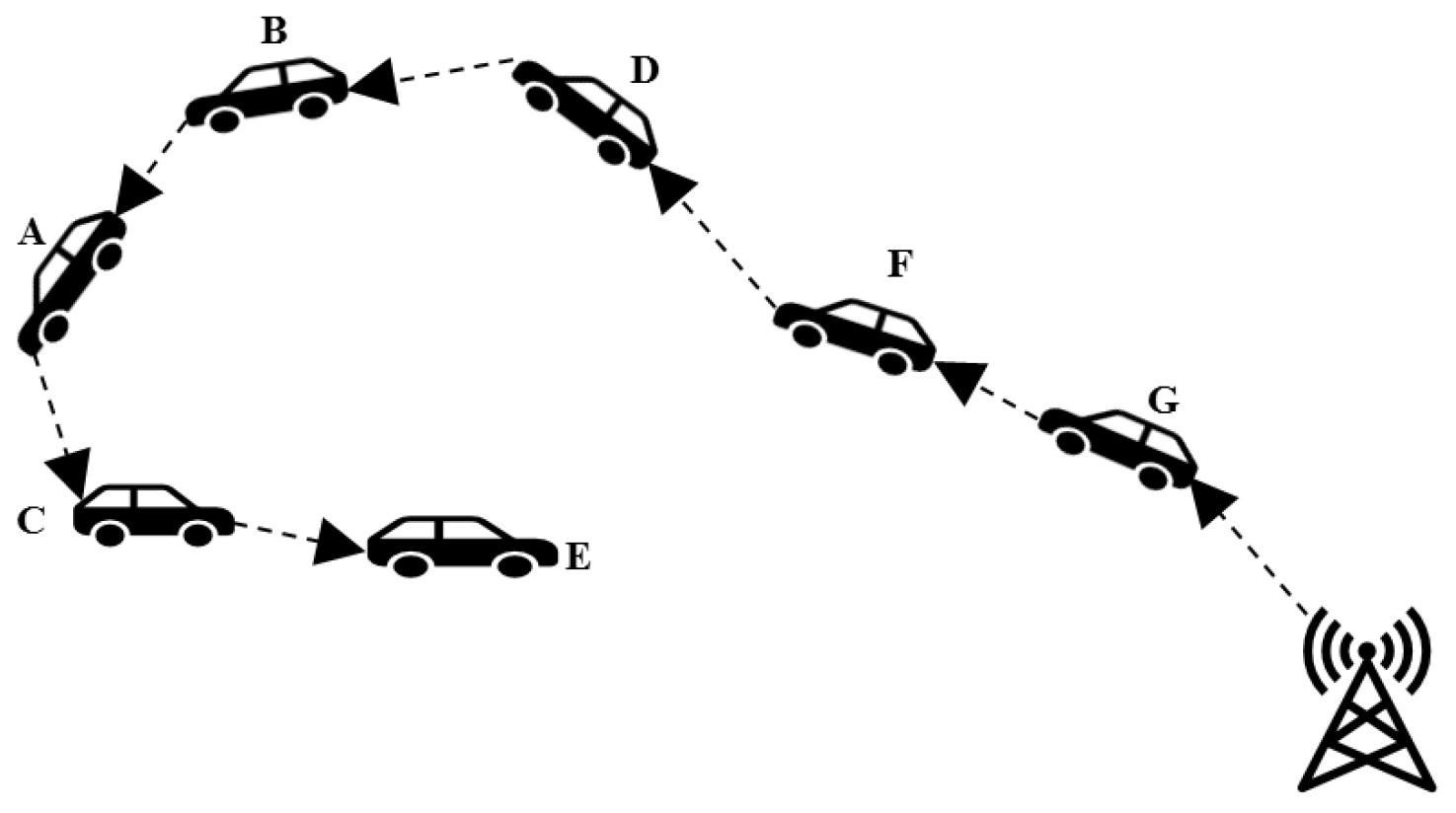
After completion of the route initialization process, the infrastructure uses the downlink communication to update the position of each vehicle. Furthermore, this downlink communication helps to maintain a loop-free optimal path for all vehicles. To achieve this efficient downlink communication between infrastructure and vehicle, the proposed Java macaque algorithm is efficiently used to find an optimal path. The optimal single route using Hamiltonian distance (I-G-F-D-B-A-C-E) helps to reduce the flooding message in VANET, and this is clearly shown in Figure 2. Thus, the single-route techniques enhance network stability and reduce the flooding message in VANET.
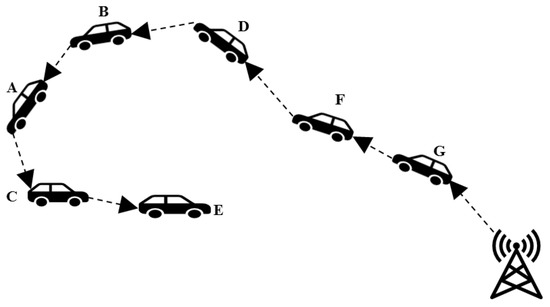
Figure 2.
Downlink route-discovery process from infrastructure to vehicle.
3.3. Route Maintenance Phase
In the dynamic changing network topology, the infrastructure continuously updates the routing table due to the addition and remove of vehicles. This activity involves an initialization and route-discovery process due to the addition of new vehicles. Furthermore, it monitors the current position of existing vehicles by sending messages; if the infrastructure does not receive the acknowledgement message from a particular vehicle, then that vehicle is discarded from the routing table, and a route-discovery process is initiated to ensure a single-route loop-free optimal path.
4. Algorithm Modeling for VANET
Behavioral analysis of the Java macaque monkey has been briefly described by Dinesh Karunanidy et al. in [29]. The significance of the Java macaque algorithm using the multi-population characteristic explores the search space in an efficient way, and that suits the solution of the routing problem in IoT-based VANET. However, it is a challenging task to solve NP-hard problems where the complexity of solving these problems exponentially increases in a dense network. However, the communication process is effectively addressed via male replacement and the optimal route is maintained using the learning process. Meanwhile, the dominance hierarchy-based selection process for mating helps to identify stable vehicles in the dynamic network (see Algorithms 1–7).
4.1. Population Initialization
The Java macaque algorithm is typically a population-based search technique that initially starts with population initialization. The initial population is generated using the random population seeding technique. Furthermore, individuals are generated with mapping () between the dimensional vector of the search space to the dimensional vector in the problem space . In the discrete optimization problem, the total number of vehicles is represented in the problem space and must be mapped to individuals.
where is an individual, represented as a tuple of a dimensional vector in the search space and the corresponding dimensional vector in the problem space . The initialization process starts with the minimum number of individuals in a group regarding the problem size. Then, the above process is repeated until g groups are created. Therefore, the total population at the initial stage is less than N individuals, and the actual number of individuals in each group is derived in .
| Algorithm 1 Initialization. |
|
| Algorithm 2 Classification of Population. |
|
4.2. Categorization of the Individuals
The individuals in each group are evaluated using the fitness function, where the individual must visit all cities with minimum distance. The route can be formulated as a graph , where E is the set of edges and is the set of vehicles, and the route should be loop-free at minimum distance. The reliability of the individual calculated from the equation as stated in [1,24] is as follows:
for and , where is the fitness value of individual with respect to total number of vehicles NOV in VANET. Furthermore, the distance between the two vehicle points is calculated using Euclidean distance.
Therefore, the individual with least distance is recognized as the best individual. and indicates the best individual from the male and female set in group i. Thus, and represents the local best individual in each group. Furthermore, the global best alpha male and female are selected from the set and in the population. Then, individuals are further subdivided into dominant{DS} and non-dominant{NDS} sets. Therefore, this determines the local best and global best individuals in the population.
4.3. Mating Process
Mating has become the most active part of the Java macaque algorithm. It performs an explorative search process of the problem space. A good search process has several advantages for the Java macaque algorithm, such as exploration and diversity maintenance.
| Algorithm 3 Mating Process. |
|
A special mating process has been used for handling a large search space. Parents are selected either from the dominant or non-dominant set, and perform the mating operation. New offspring generated from the mating process represent the natal code of the parents. To maintain crowding distance, the number of offspring generated by dominant parents are decided by , where A lies in the range 0.4 to 0.6, whereas the offspring generated by non-dominant parents is between . Finally, new individuals for the population are generated with crowding distance.
| Algorithm 4 Evaluate Maturity of Offspring. |
|
4.4. Male Replacement
The main idea of the male replacement process is the performance of an adaptive search process. First, the offspring , which attains sexual maturity (i.e., attain fitness value above ), becomes a stray male and similarly the offspring above becomes a member of female set. Secondly, the stray male performs an adaptive search to replace the dominant male from the other group.
| Algorithm 5 Male Replacement. |
|
This replacement increases the robustness of the algorithm for solving the large problem. In contrast, if the stray male fails to replace the appropriate dominant male, then he becomes a member of .
| Algorithm 6 Learning Process. |
|
4.5. Learning
The learning process is a mechanism that adapts the learning model for the enhancement of individual fitness. However, it increases individual fitness by exploiting the search space regarding problem space. The individual in the should improve its fitness value via learning and increase the probability of attaining a global optimum. Then, learning for discrete optimization is defined as:
where represents the set of individuals, is the feasible search space of the solution, is the fitness function, and is the learning rate of the individual between . Then, is the learning process .
where two values are randomly generated for i and j.
The learning rate differs regarding the problem domain. A new learning paradigm for solving the discrete optimization problem improves the individual using four different learning techniques—, and . The learning model depends on two variables which are also based on the learning rate . Then each individual undergoes different learning models and the best suitable model with the highest fitness value is selected for the current individual.
| Algorithm 7 JMAD: Java Macaque Algorithm for Discrete Optimization. |
|
5. Proposed Algorithm for Intelligent Route Discovery in IoT-Based VANET
The initial phase of the Java macaque algorithm is random population initialization with N individuals in g groups. The individuals are mapped regarding the search space of the problem. Then, the individuals are evaluated regarding the convergence of the optimization problem. Consequently, the local best individuals, known as ‘AlphaMale’ and ‘AlphaFemale’ are selected from the group. Furthermore, ‘GB-Alphamale’ and ‘GB-AlphaFemale’ global best individuals are selected from the set of alphamale and alphafemale.
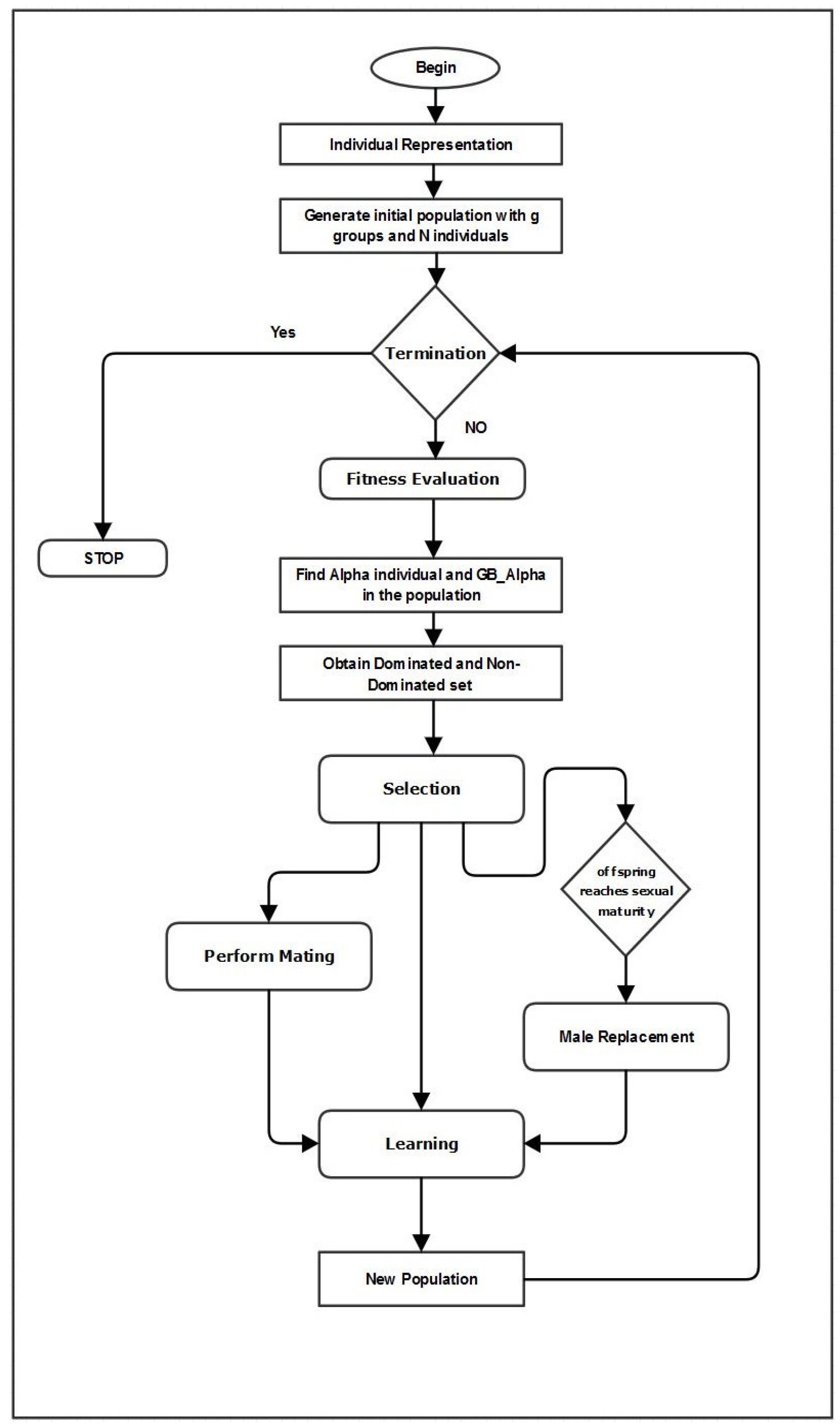
All the individuals in the group are further divided into dominant and non-dominant individuals based on fitness value. Then, the new offspring are generated during the mating process, where the selection of the mating individual is based on the dominance hierarchy. Then, the female offspring reaches sexual maturity and becomes the female individual in the natal group. However, the male offspring who attain sexual maturity are forced to leave the natal group, and are known as ‘Stray Male’. Therefore, the stray male must find an alternative group by replacing the dominant male, which is known as ‘Male Replacement’. Finally, the learning process is an important feature of the Java macaque algorithm, where individuals improve its fitness. Thus, the Java macaque algorithm is an optimization algorithm for a given problem . The individual is the one with dominant fitness using the search operation of the JMA from the search space regarding the problem space (see Figure 3).
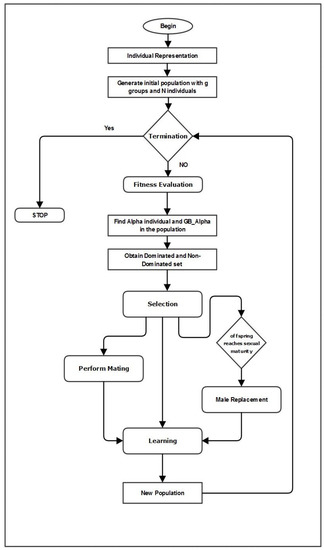
Figure 3.
Methodology Diagram.
6. Experimentation and Result Analysis
In this section, we present our works in two different subsections. Initially, we present our results regarding the parameter tuning of our proposed JMA algorithm. In the second subsection, we analyze the proposed algorithm with varying deployed vehicle densities, such as 10, 30, and 50 vehicle-density test cases. The obtained outcomes are evaluated using 1000 various Monto Carlo trails to ensure the efficacy of the algorithm. With the aid of 1000 Monto Carlo trails, average outcomes are measured and noted as mean results, whereas the worst and best results are taken out from one of the 1000 trails. In this work, the free space model is studied to simulate the obtained SNR in dB towards each incoming vehicle j. For ease of simplicity, the free space model is formulated as follows:
where is transmission energy of an individual communicating vehicle, is the processing frequency of the VANET, is specified as noise power at each communicating vehicle determined using the mathematical model namely Gaussian noise is noise adjustment, and is the Euclidean distance between i,n paired transmitting vehicles mathematically represented as
where and are coordinates of vehicles scattered in the deployment area R. The experimentation of the proposed model is carried out in MATLAB R2019a. The parameter setting of VANET is shown in Table 1.

Table 1.
Parameter settings for experimentation.
6.1. Dataset Creation
Vehicles are randomly scattered among deployment area A. The distance (D) between each vehicle is taken as 1 km within the area. Thus, the coordinates of each vehicle v is noted as
where and are arbitrary values created within the range 0 to 1 using uniform distribution function . We used Equation (7) to determine the vehicle positions for three different scenarios, namely low, medium, and high vehicle density; all vehicles in all three scenarios are deployed within specified area A.
6.2. Results Based on Parameter Tuning
The performance of our JMA algorithm is measured by three significant parameters, namely the probability of mating replacement , the population , and the estimated number of fitness function epochs. Generally, the number of fitness evaluations is measured classically, and controls the number of generations, as well as the computation time of the technique. The performance of route reliability is measured regarding increasing fitness evaluations. The results are obtained based on the medium number of vehicle density, and the vehicle speed is fixed as 20 km/h.
6.2.1. Route Reliability Results Based on the Probability of Mating Rate Parameter
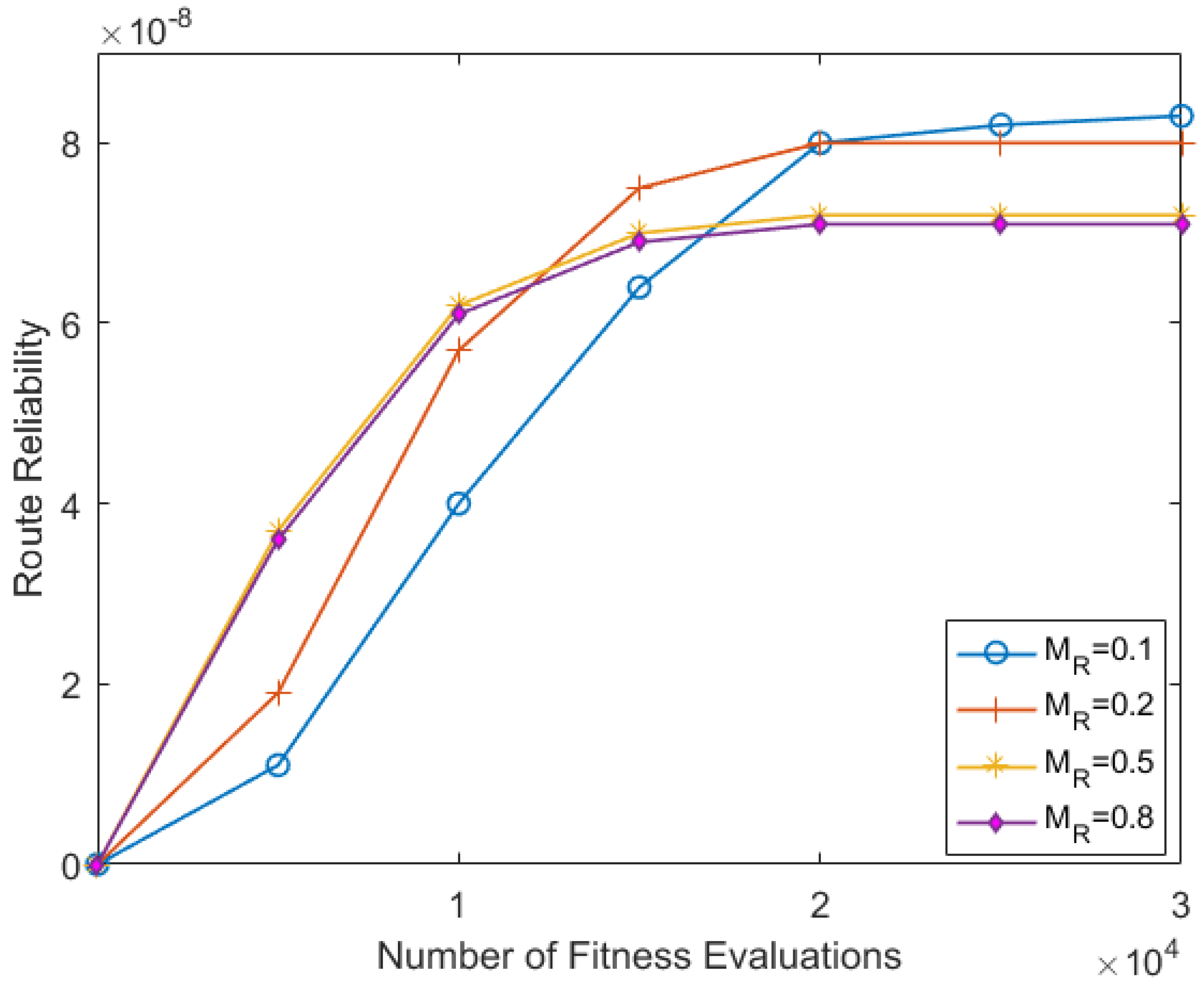
The results of significant route reliability scores aid delivery of efficacy of the proposed system by varying the probability of mating rate values, as shown in the figure insert. The obtained results are measured in three categories, namely best, mean, and worst based on 1000 Monte Carlo trails.
Figure 4 insert presents the mean values of the route reliability scores for varying values. The y-axis denotes the route reliability values based on the x-axis number of fitness evaluations. We categorized the number of fitness evaluations into three sections, namely fast-run (within range of 1–10,000 fitness evaluations), mean run range (within the range of 10,000–20,000 fitness evaluations), and long-run range (within the range of 20,000–30,000 fitness evaluations). In Figure 4, it can be seen that using higher values (i.e., converges the proposed JMA algorithm towards the best routing path compared with minimum values. However, in the mid-run range category it can be seen that outperforms the larger values when finding route reliability. On the other hand, the aid of smaller values in the long-run range outperforms than the larger values when determining the best routes. The results specify that the use of small values achieves better exploration in the JMA, whereas it avoids local optima and premature convergence problems. The outcome of the result concludes that the use of probability obtains satisfactory results compared with values. The best and worst route stability scores obtained over varying values are satisfactory in JMA. We noticed that again the value drastically provides the best route compared with values. Figure 4 shows that the best mean route is achieved late in the fast run and stays the same in the long-run range. Interestingly, Figure 4 shows that using achieves a better reliability score compared to the other values. The overall result shows that the use of outperforms the other values.
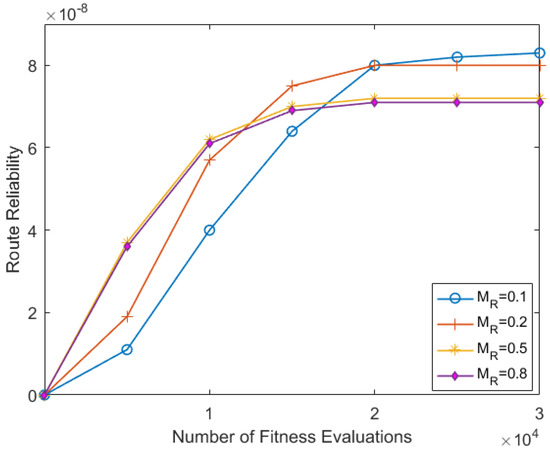
Figure 4.
Mating probability Rate —over 1000 Monte Carlo trails.
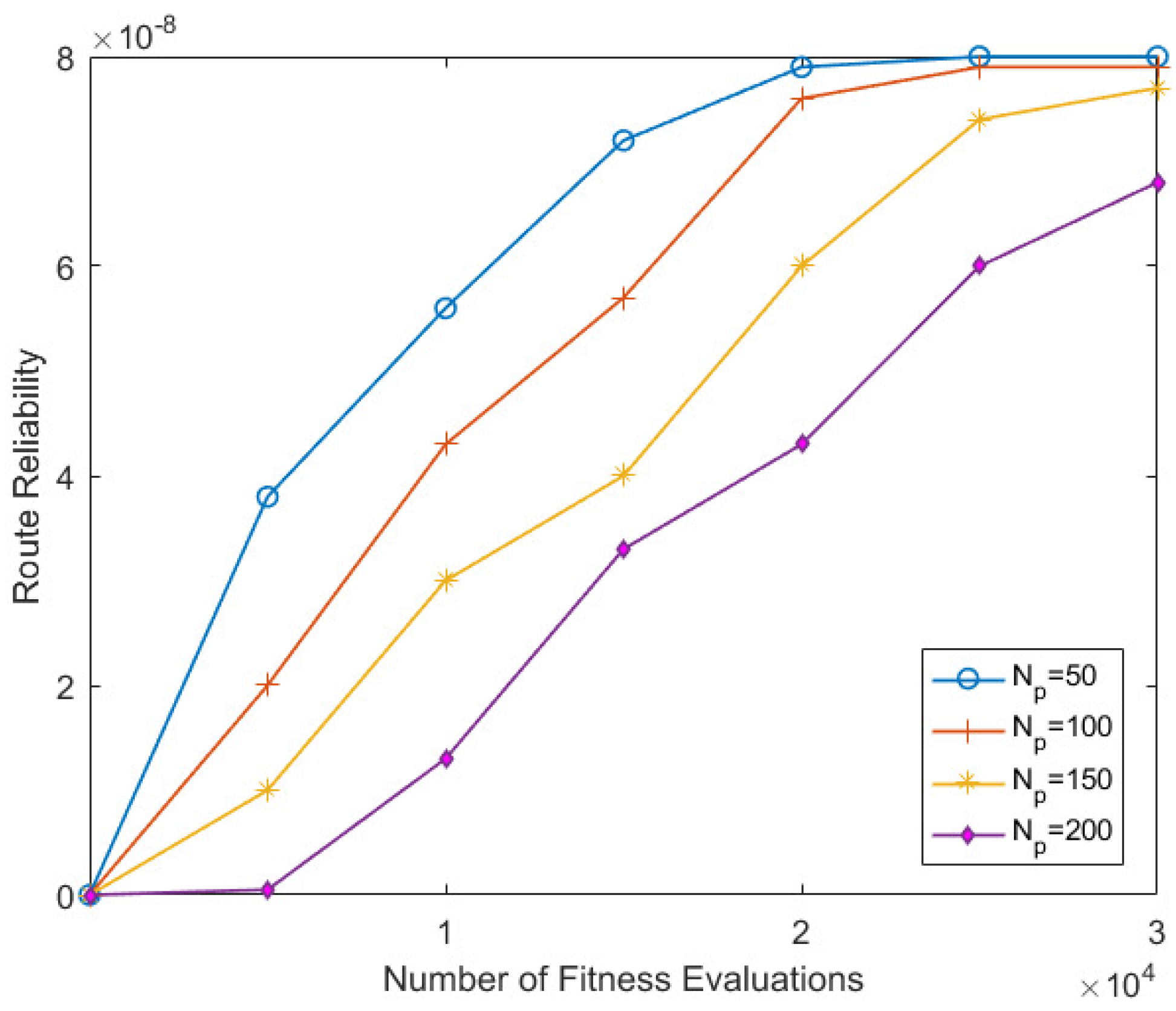
6.2.2. Route Reliability Results Based on Population Size POP Parameter
In this section, we analyzed the efficacy of the proposed JMA algorithm with varying population sizes POP; the results of route reliability are shown in Figure 5. Based on the above observations, we fixed to observe the efficacy of the JMA algorithm in varying population sizes. The population size achieves better scores in the fast-run range and stays the same until the long-run range. In realistic scenarios, due to high computational complexity and high demand on memory resources, it is difficult to prolong the long-run range, therefore obtaining the best result within fast-run and mid-run range ensures the efficacy of the algorithm. On the other hand, using a higher population size in metaheuristic algorithms does not achieve better accuracy. It can be easily observed in different batch computations over the computational process is achieved as , where is the total number of fitness computations. Therefore, it is clearly noticed that using higher value will minimize the total number of batch evaluations, thus result in a faster computation time that yields reduced route reliability scores. Based on this observation, we noticed that achieves more accurate results than different values.
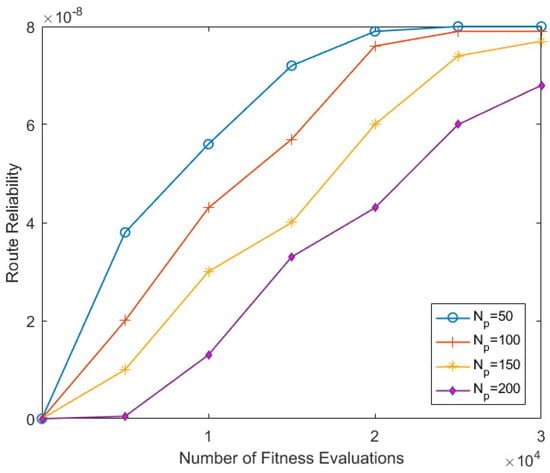
Figure 5.
Mean route reliability results achieved over 1000 Monte Carlo trails based on varying population size .
Figure 5 displays the best mean route reliability score using in the mid-range run, whereas a different value achieves the best score in the large-run range. In addition to that, Figure 5 shows the best mean route for population size over the set of worst routes. This route was determined in the fast- and mid-run ranges.
6.2.3. Mean Route Reliability Results Based on the Different Velocity Values
In this study, we measured the best route discovery based on varying vehicle speeds to ensure the performance of the JMA algorithm in various scenarios. Based on experimentation, we noticed that higher velocity rates achieve low-quality routes compared with the reduced velocity rates. In addition, we observed that velocity at 20 km/h for vehicles discovers the best route. This study clearly shows that topology becomes stable at lower velocity rates. In the next subsection, results are observed based on average mobility of 20 km/h. It is noticed that the reliability score will not be stable when there are fluctuations in velocity above 20 km/h. With this outcome, we stabilize vehicles in VANET that are fixed at a speed of 20 km/h, to process the routing of data.
6.3. Result Analysis under Various Vehicle-Density Ratios
In this study, we analyzed the route reliability performance using JMA compared to the cuckoo search (CS), genetic algorithm (GA) and particle swarm optimization (PSO) algorithms. The parameter settings of these techniques are shown in Table 2. In this study, we used three different test cases, namely low density (10 vehicles), medium density (30 vehicles), and high density (50 vehicles). In each test case, we provided the route reliability discovery graphs based on number of fitness evaluations.

Table 2.
Parameter configurations of the algorithms compared in our experimentations.
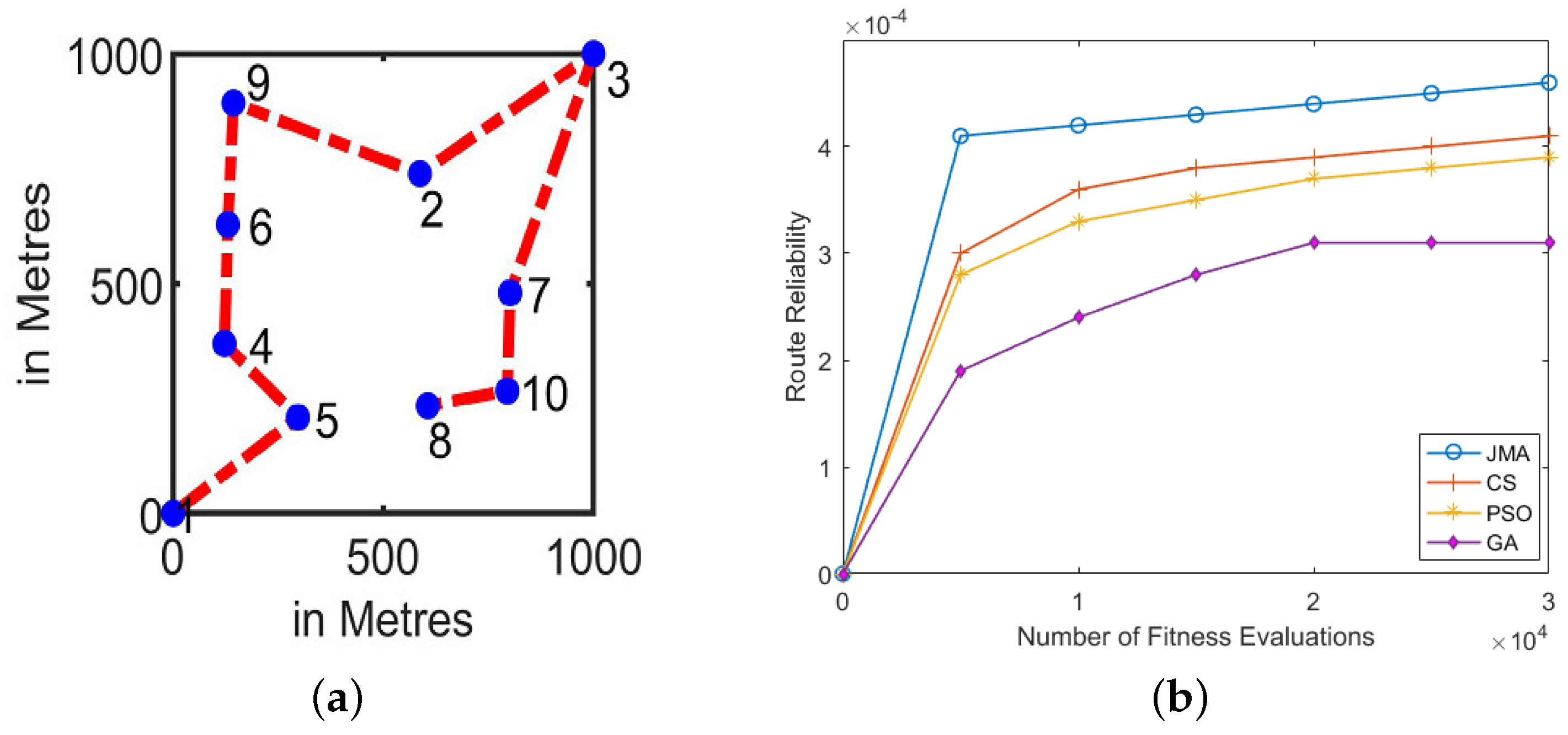
6.3.1. Test Case 1: Low Density (10 Vehicles)
In test case 1, we used low-density vehicles, which are arbitrarily scattered using uniform distribution in deployment area A. The case of V2I transmission was considered, in which a server is considered to be infrastructure, and aims to communicate the information towards all the vehicles in the VANET. However, this could lead to the dissemination of data towards accident scenarios or malicious road information in some realistic scenarios. In our experimentation, we fixed the server at location (0,0) to retain the best route, and to eradicate the use of the same nodes for manifold routes. Figure 6b displays the mean route-discovery performance achieved across 1000 Monte Carlo tracks. It shows that JMA discovers the best route path in whole run ranges. Comparison of the various algorithms shows that JMA finds the best route more reliability in the fast-run range compared with other algorithms, namely GA, Cuckoo, and PSO.
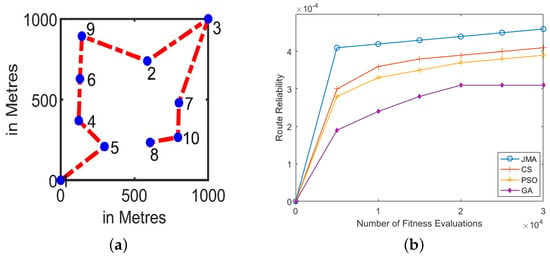
Figure 6.
Low Vehicular Density (10 vehicles). (a) Best route discovery achieved using JMA; (b) Mean route reliability results achieved across 1000 Monte Carlo trails.
The results for best route discovery of JMA is presented in Figure 6a. Here, we can clearly note that JMA finds the best route in the initial fast-run range and sustains the same for the long-run range. The CS algorithm can find the best route only in the mid-run range, and deviates from the best route in a course of iterations. Figure 6 shows the outcome of the worst route reliability for all algorithms. Here, JMA has achieved enhancements of 9.23%, 8.98%, and 7.24% compared with the GA, PSO and CS algorithms, respectively. Thus, the results show that the overall performance of JMA is satisfactory with a low-density vehicle rate.
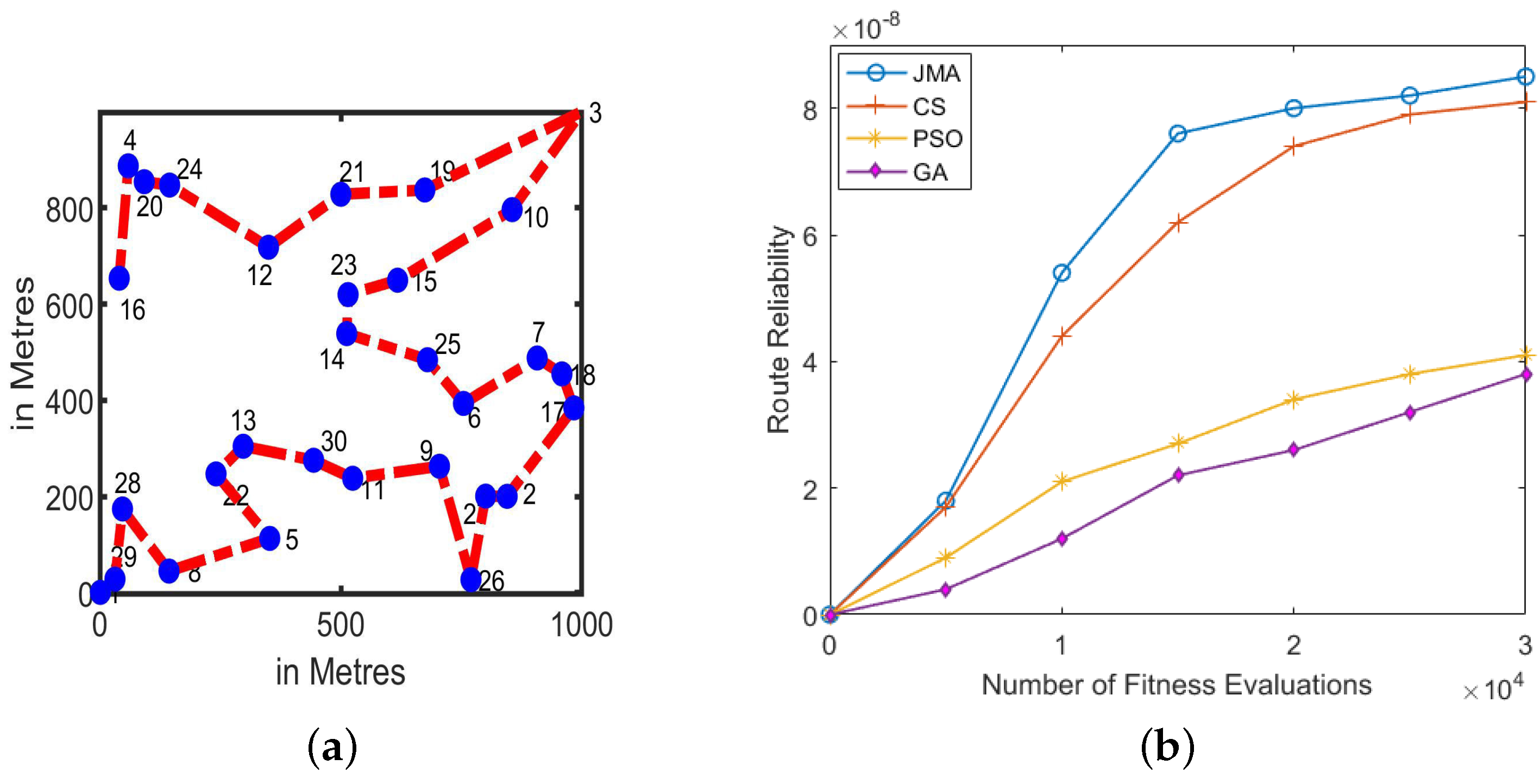
6.3.2. Test Case 2: Medium Density (30 Vehicles)
In this test case, 30 vehicles are considered, where each vehicle was arbitrarily scattered over deployment area A with a distance of 1 km. Generally, an increase in the number of vehicles increases the complexity of the route establishment process. The server is at the origin (0,0) to broadcast data to all vehicles in the VANET.
The best route results of medium-density vehicles are presented in Figure 7a. Figure 7b presents the mean route reliability scores of all algorithms. Here, JMA achieves best route reliability among all algorithms for most run ranges. The performance of JMA dominates the rest of the algorithm, whereas the rest of the compared algorithms provide poorer performance in most run ranges. Initially, PSO variants obtain the best route-discovery score, but later it fails to sustain the best route discovery over a course of iterations. Figure 7 provides the best route-discovery results of all algorithms, in which JMA achieves the best route in the fast-run range and sustains the same for the rest of the run ranges. Therefore, JMA achieved better route-discovery scores than the PSO, GA and cuckoo algorithms. Thus, the overall results for medium-density vehicles concludes that the overall performance of JMA achieves 13.45%, 10.26% and 9.38% better performance compared to the GA, PSO and CS algorithms, respectively.
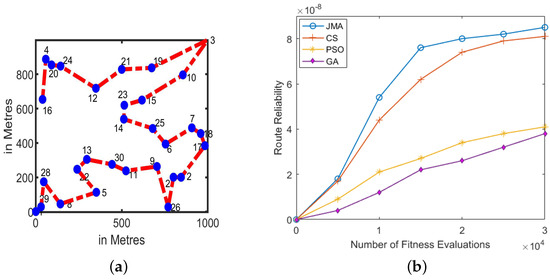
Figure 7.
Medium Vehicular Density (30 vehicles). (a) Best route discovery achieved using JMA; (b) Mean route reliability results achieved across 1000 Monte Carlo trails.
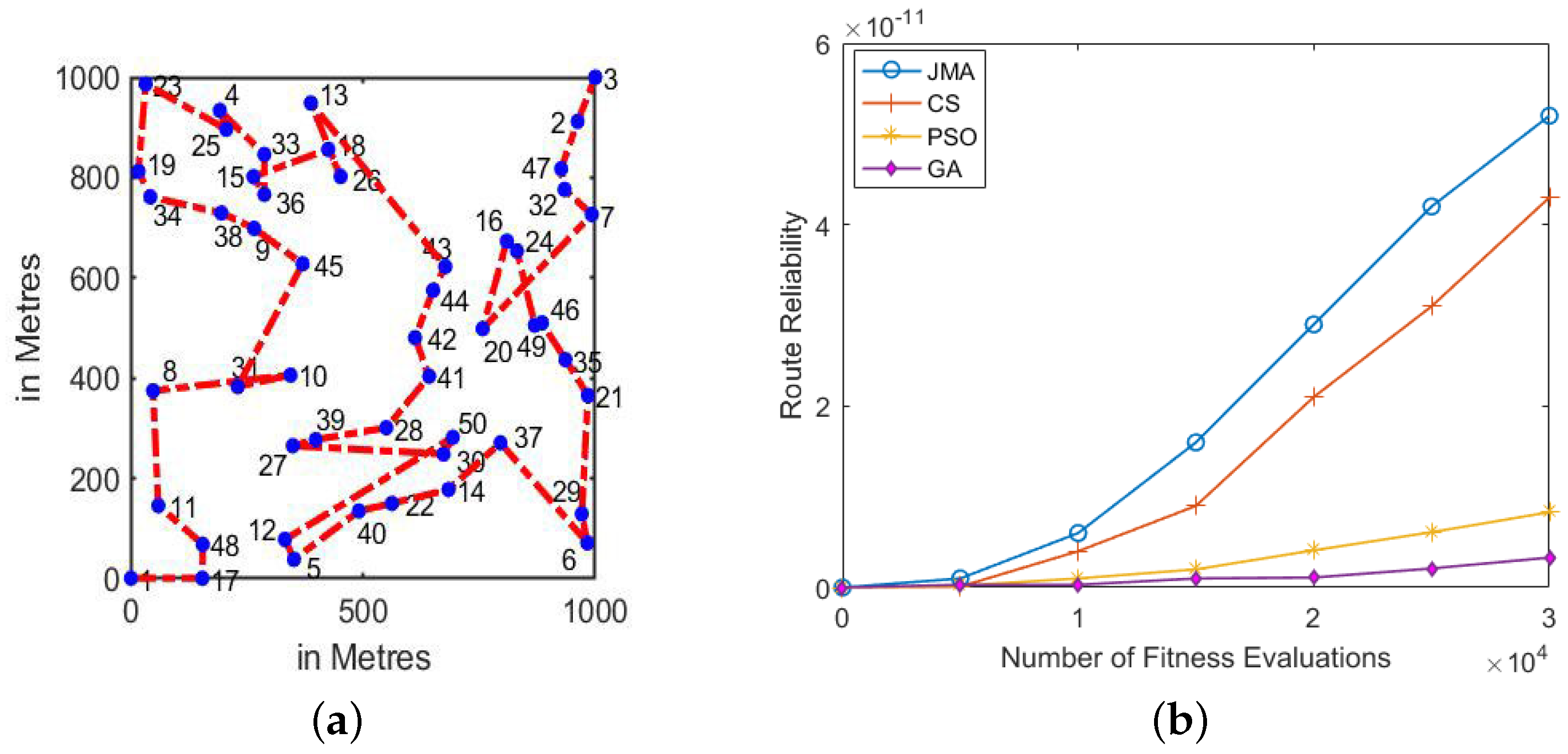
6.3.3. Test Case 3: High Density (50 Vehicles)
Fifty vehicles were arbitrarily scattered using uniform distribution among deployment area A within the 1 km square range. The server in VANET is at the origin (0,0) to disseminate data packets to all vehicles. The mean route reliability score is presented in Figure 8b. Here, we observed that JMA achieves the best route reliability in the fast-run range. However, compared algorithm starts to achieve the better routes in the late mid-run range, and fails to sustain the route in the long-run range. Figure 8a shows the best route discovery of JMA. Here, JMA converges slowly in the fast-run range, and later increases the convergence rate, sustains the best route score in late fast-run range, and retains the same until the long-run range.
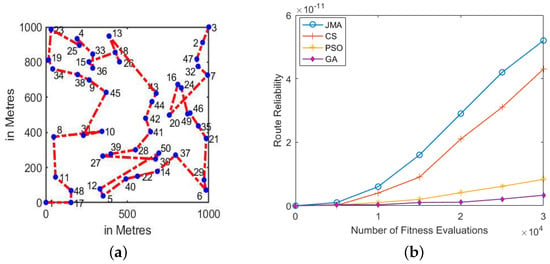
Figure 8.
High Vehicular Density (50 vehicles). (a) Best route discovery achieved using JMA; (b) Mean route reliability results achieved across 1000 Monte Carlo trails.
Thus, the overall results of high-density vehicles concludes that JMA achieved 32.65%, 24.56% and 21.43% better performance compared to the GA, PSO and cuckoo search algorithms, respectively. The outcome clearly shows the superiority of the proposed JMA compared GA, PSO, and CS algorithms.
6.4. Discussion of Outcomes
The overall experimentation results are discussed as follows:
- Based on parameter tuning experimentation, we found that the minimized values for the probability of mating rate provides better route discovery. Therefore, we suggest that the use of smaller values enhance the diversification of our proposed JMA and therefore eradicates local optima and premature convergence.
- Based on population size varying experimentation, we suggest that using population size achieves best route discovery reliability. However, maximizing population size will lead to high computation complexity rather than reduced complexity, as well as lower accuracy.
- Based on varying the velocity of vehicles, we suggest that using velocity of 20 km/h and lower will achieve the best reliable route discovery for the efficient transmission of information over the vehicles.
- Finally, JMA achieves the satisfactory performance over the all the different density scenarios. Among these three different scenarios, JMA provides the best results in low- and medium-density test cases, and kept the pace in high-density test cases.
7. Conclusions
In the last decade, various nature-inspired optimization algorithms have been proposed for route discovery in IoT-based VANETs. However, the existing algorithms have become stuck with local optimal solutions due to unsustainable selection strategies, parameter tuning, and exploitation maintenance. Thus, the proposed Java macaque algorithm based on the social behavior of Java macaque monkeys amply shows its efficiency in striking a balance between exploration and exploitation using dominance hierarchy-based selection, male replacement and the learning process which suits the solution of route discovery in dynamic network topology well. In experimentation, the performance of the proposed Java macaque algorithm clearly illustrates its efficiency over the existing algorithm in three different scenarios. Therefore, the natural behavior of Java macaque suits the solution of route problems in real-world IoT-based VANETs well.
For future work, the proposed algorithm should be fine-tuned to solve wide varieties of real-world problems, such as multi-objective engineering, image processing, and cloud computing domains. Furthermore, it could be extended to solve complex problems such as knapsack, scheduling, routing, and feature selection.
Author Contributions
Conceptualization, D.K., R.R. and A.D.; Methodology, R.S., I.A. and D.A.; Validation, H.H. and M.I; Formal Analysis, D.K. and R.R.; Investigation, I.A.; Resources, H.H.; Data Curation, D.A.; Writing—Original Draft, D.K., R.R. and A.D.; Writing—Review Editing, D.A. and I.A., Supervision, H.H.; Project Administration, I.A. and M.I. All authors have read and agreed to the published version of the manuscript.
Funding
The project was supported by University of Moncton, Canada.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| JMA | Java Macaque Algorithm |
| IoT | Internet of Things |
| VANETs | Vehicular Ad hoc Networks |
| DCSO | Discrete Cuckoo Search |
| GWO | Grey Wolf Optimization |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| NIOA | Nature-Inspired Optimization Algorithm |
| V2V | Vehicle-to-Vehicle |
| V2I | Vehicle-to-Infrastructure |
| ACO | Ant Colony Optimization |
| MLA | Modified Lion Algorithm |
| BA | Bat Algorithm |
| FA | Firefly Algorithm |
| AODV | Ad hoc On-demand Distance Vector |
| RSS | Received Signal Strength |
| Individual | |
| Feasible solution search space | |
| Problem space | |
| Learning rate of individual | |
| Number of population | |
| Male Replacement rate | |
| Different learning rate | |
| Population | |
| Number of Vehicle | |
| Group of Alpha Male | |
| Non-Dominant Set | |
| Dominant Set | |
| Group of Alpha Female | |
| Fitness value of individual | |
| Offspring individual | |
| Stray Male individual | |
| Eliminated Set |
References
- Bello-Salau, H.; Aibinu, A.; Wang, Z.; Onumanyi, A.; Onwuka, E.; Dukiya, J. An optimized routing algorithm for vehicle ad-hoc networks. Eng. Sci. Technol. Int. J. 2019, 22, 754–766. [Google Scholar] [CrossRef]
- Dua, A.; Kumar, N.; Bawa, S. A systematic review on routing protocols for vehicular ad hoc networks. Vehr. Commun. 2014, 1, 33–52. [Google Scholar] [CrossRef]
- Bello-Salau, H.; Aibinu, A.; Onwuka, E.; Dukiya, J.; Bima, M.; Onumanyi, A.; Folorunso, T. A new measure for analysing accelerometer data towards developing efficient road defect profiling systems. J. Sci. Res. Rep. 2015, 7, 108–116. [Google Scholar] [CrossRef]
- Babu, S.; Kumar, P.A.R. DTMR: An Adaptive Distributed Tree-based Multicast Routing Protocol for Vehicular Networks. Comput. Stand. Interfaces 2021, 79, 103551. [Google Scholar] [CrossRef]
- Sravya, A.; Dinesh, K.; Prasad, S. A Density based Deceptive data Detection in VANET. Int. J. Recent Technol. Eng. (IJRTE) 2019, 7, 136–140. [Google Scholar]
- Todosijević, R.; Mjirda, A.; Mladenović, M.; Hanafi, S.; Gendron, B. A general variable neighborhood search variants for the travelling salesman problem with draft limits. Optim. Lett. 2017, 11, 1047–1056. [Google Scholar] [CrossRef]
- Kyritsis, M.; Blathras, G.; Gulliver, S.; Varela, V.A. Sense of direction and conscientiousness as predictors of performance in the Euclidean travelling salesman problem. Heliyon 2017, 3, e00461. [Google Scholar] [CrossRef]
- Dinesh, K.; Subramanian, R.; Dweib, I.; Nandhini, M.; Mohamed, M.Y.N.; Rajakumar, R. Bi-Directional Self-Organization Technique for Enhancing the Genetic Algorithm. In Proceedings of the 6th International Conference on Information Technology: IoT and Smart City, Hong Kong, China, 29 December 2018–31 December 2019; pp. 251–255. [Google Scholar]
- Manicassamy, J.; Karunanidhi, D.; Pothula, S.; Thirumal, V.; Ponnurangam, D.; Ramalingam, S. GPS: A constraint-based gene position procurement in chromosome for solving large-scale multiobjective multiple knapsack problems. Front. Comput. Sci. 2018, 12, 101–121. [Google Scholar] [CrossRef]
- Hernández-Pérez, H.; Salazar-González, J.J.; Santos-Hernández, B. Heuristic algorithm for the split-demand one-commodity pickup-and-delivery travelling salesman problem. Comput. Operat. Res. 2018, 97, 1–17. [Google Scholar] [CrossRef]
- Kandali, K.; Bennis, L.; Bennis, H. A New Hybrid Routing Protocol Using a Modified K-Means Clustering Algorithm and Continuous Hopfield Network for VANET. IEEE Access 2021, 9, 47169–47183. [Google Scholar] [CrossRef]
- Apinantanakon, W.; Sunat, K.; Chiewchanwattana, S. A Cooperation of Multileader Fruit Fly and the Probabilistic Random Walk with Adaptive Normalization for Solving Solution of the Unconstrained Optimization Problems. Preprints 2018, 2018090495. [Google Scholar] [CrossRef]
- El Ouahmani, T.; Chehri, A.; Hakem, N. Bio-inspired routing protocol in VANET networks-a case study. Procedia Comput. Sci. 2019, 159, 2384–2393. [Google Scholar] [CrossRef]
- Oh, B.; Na, Y.; Yang, J.; Park, S.; Nang, J.; Kim, J. Genetic algorithm-based dynamic vehicle route search using car-to-car communication. Adv. Electr. Comput. Eng. 2010, 10, 81–86. [Google Scholar] [CrossRef]
- Aibinu, A.; Salau, H.B.; Rahman, N.A.; Nwohu, M.; Akachukwu, C. A novel clustering based genetic algorithm for route optimization. Eng. Sci. Technol. Int. J. 2016, 19, 2022–2034. [Google Scholar] [CrossRef]
- Oranj, A.; Alguliev, R.; Yusifov, F.; Jamali, S. Routing algorithm for vehicular ad hoc network based on dynamic ant colony optimization. Int. J. Electron. Elect. Eng. 2016, 4, 79–83. [Google Scholar] [CrossRef][Green Version]
- Jindal, V.; Bedi, P. An improved hybrid ant particle optimization (IHAPO) algorithm for reducing travel time in VANETs. Appl. Soft Comput. 2018, 64, 526–535. [Google Scholar] [CrossRef]
- Wagh, M.B.; Gomathi, N. Route discovery for vehicular ad hoc networks using modified lion algorithm. Alex. Eng. J. 2018, 57, 3075–3087. [Google Scholar] [CrossRef]
- Fahad, M.; Aadil, F.; Khan, S.; Shah, P.A.; Muhammad, K.; Lloret, J.; Wang, H.; Lee, J.W.; Mehmood, I. Grey wolf optimization based clustering algorithm for vehicular ad-hoc networks. Comput. Electr. Eng. 2018, 70, 853–870. [Google Scholar] [CrossRef]
- Bitam, S.; Mellouk, A. Bee life-based multi constraints multicast routing optimization for vehicular ad hoc networks. J. Netw. Comput. Appl. 2013, 36, 981–991. [Google Scholar] [CrossRef]
- Elhoseny, M. Intelligent firefly-based algorithm with Levy distribution (FF-L) for multicast routing in vehicular communications. Expert Syst. Appl. 2020, 140, 112889. [Google Scholar] [CrossRef]
- Mehta, K.; Bajaj, P.; Malik, L. Fuzzy bacterial foraging optimization zone based routing (FBFOZBR) protocol for VANET. In Proceedings of the 2016 International Conference on ICT in Business Industry & Government (ICTBIG), Indore, India, 18–19 November 2016; pp. 1–10. [Google Scholar]
- Masegosa, A.D.; Osaba, E.; Angarita-Zapata, J.S.; Laña, I.; Ser, J.D. Nature-inspired metaheuristics for optimizing information dissemination in vehicular networks. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 1312–1320. [Google Scholar]
- Bello-Salau, H.; Onumanyi, A.J.; Abu-Mahfouz, A.M.; Adejo, A.O.; Mu’Azu, M.B. New discrete cuckoo search optimization algorithms for effective route discovery in IoT-based vehicular ad-hoc networks. IEEE Access 2020, 8, 145469–145488. [Google Scholar] [CrossRef]
- Chandren Muniyandi, R.; Hasan, M.K.; Hammoodi, M.R.; Maroosi, A. An improved harmony search algorithm for proactive routing protocol in VANET. J. Adv. Transp. 2021, 2021, 6641857. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Thangavelu, M. An enhanced hybrid ant colony optimization routing protocol for vehicular ad-hoc networks. J. Ambient Intell. Hum. Comput. 2021, 1–32. [Google Scholar] [CrossRef]
- Afzal, K.; Tariq, R.; Aadil, F.; Iqbal, Z.; Ali, N.; Sajid, M. An Optimized and Efficient Routing Protocol Application for IoV. Math. Probl. Eng. 2021, 2021, 9977252. [Google Scholar] [CrossRef]
- Kudva, S.; Badsha, S.; Sengupta, S.; La, H.; Khalil, I.; Atiquzzaman, M. A scalable blockchain based trust management in VANET routing protocol. J. Parallel Distrib. Comput. 2021, 152, 144–156. [Google Scholar] [CrossRef]
- Karunanidy, D.; Amudhavel, J.; Datchinamurthy, T.S.; Ramalingam, S. A novel java macaque algorihtm for travelling salesman prolem. IIOAB J. 2017, 8, 252–261. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).