Change in Mixing Power of a Two-PBT Impeller When Emptying a Tank

Abstract

The paper presents research on the phenomenon of an increase in mixing power during the emptying of a tank with two 6-PBT45° axial impellers in operation, located on a common shaft, pumping the liquid to the bottom of the mixing tank. A large increase in mixing power took place when the free surface of the liquid was just above the upper edge of one of the impellers (h_p/D < 0.1). This increase was even more than 50% compared to the design power for a fully filled mixing vessel. Admittedly, high motor overload, while not very long, may damage it. The study investigated the instantaneous torques acting on the impeller shaft during the emptying of the tank and the velocity distributions in planes r-z. On their basis, the mechanism of the phenomenon observed was determined and correlation relationships were given that permitted the calculation of the numerical values of the power increase factors.

1. Introduction

Mixing in tanks is one of the most common processes used in the technologies of the chemical, biochemical, pharmaceutical, and related industries. One of the more interesting solutions in the construction of mixing systems in tanks is the use of several impellers placed on one shaft. These solutions are often used when mixing gas–liquid, liquid–solid, or gas–liquid–solid systems [1,2,3,4,5], and in many cases, they have an advantage over solutions with one impeller [2,6,7], despite the fact that a construction with several impellers is more complicated [8,9,10]. Systems with several impellers have higher hold-up values for the same mixing powers per unit volume of mixed liquid [2,11,12] or higher values of the volumetric mass transfer coefficient k_La [10,12,13,14]. Examples of industrial applications of systems with many impellers include the structures of fermenters, crystallizers, polymerizers, impellers with sewage aeration, and others [1,15,16,17,18].

1.1. Single-Pitched-Blade Turbine (PBT) Systems

For mixing fluids of single and multiphase systems in turbulent motion, impellers with relatively small diameters D/T = 0.25 ÷ 0.5 are usually used and the most frequently used types are PBT mixers with inclined blades (pitched-blade turbines) and the Rushton Turbine RT, i.e., disc-turbine impellers with blades located perpendicular to the plane of rotation and mounted on the internal disk. The first of these mainly produces an axial stream of the liquid in the impeller zone, and these are called axial impellers. The RT or flat-blade turbine (FBT) impellers are radial impellers as they generate a large radial stream of liquid thrown from the impeller zone onto the mixer wall. These impellers demand a high mixing power.

Determining the mixing power is a key element in the design of any process involving mechanical agitation as the energy needed to maintain continuous circulation of the liquid in the mixing tank. Finally, it may lead to homogenization of the mixing vessel contents, dispersion of two immiscible liquids, formation of a solid suspension, increased values of heat and mass transfer coefficients, and the obtaining of a high gas hold-up during aeration. The mixing power depends primarily on the type of impeller and the geometrical parameters of the impeller-mixer system. For pitched-blade turbines (PBT), O’Kane [19] investigated the effect of the width and number of blades on the mixing power. For a standard six-paddle impeller 6-PBT45° (D/T = 1/3, y₁/D = 1, and b/D = 0.2), they obtained a power number Po equal to 1.52. Shiue and Wong [20] gained a slightly higher Po equal to 1.74 for a four-paddle impeller 4-PBT45° pumping the liquid toward the bottom of the mixing tank (D/T = 0.325, H/T = 1, y₁/T = 0.5, and b/D = 0.231). For a flat-bottom tank, Chudacek [21] gave a value of Po = 1.63 for a six-PBT impeller (D/T = 1/3, H/T = 1, y₁/T = 1/3, and b/D = 0.2). Machon et al. [22] gave a value of Po = 1.72 for a six-PBT impeller with parameters D/T = 0.5, H/T = 1, and y₁/D = 0.5, although the authors did not provide width b of the impeller blades. Rewatkar et al. [23] investigated the influence on the mixing power of many geometrical parameters of PBT impellers, such as their diameter, width and blade inclination angle, the number of blades, and the height of the impeller suspension above the bottom y₁. The value of the number strongly depended on the manner of liquid flow in the impeller and increased with the decrease in the value y₁. For the standard layout, they obtained Po = 1.67, and they generalized all results in the form of a correlation Equation (1)

$$Po=0.653·T^{0.26}·{\left(\frac{T}{D}\right)}^{0.11}·{\left(\frac{y_1}{T}\right)}^{-0.23}·n_{}^{0.68}·{\alpha }^{1.82},$$

(1)

where the diameter of the tank T is expressed in meters.

1.2. Multiple PBT Systems

The number of tests on systems with two- or three-PBT impellers placed on a common shaft is much smaller. Bates et al. [24] found that for a system of two impellers, the total mixing power was less than twice the power of a single impeller, and it decreased as the distance between the impellers decreased. Armenante and Nagamine [25], who investigated the mixing power for a two-phase liquid–solid system using a low-slung bottom impeller (1/48 < y₁/D < 1/8), confirmed Bates et al.’s [24] research.

Armenante et al. conducted extensive research on the mixing power for clean liquid and aerated liquid in the turbulent range of mixing [26]. They found that the mixing power of the binary system was always significantly less than twice the power of a single impeller. This was found irrespective of whether the liquid was aerated. However, when the lower impeller was suspended close to the bottom and the upper impeller was further away from the lower impeller more than D, there was a throttling effect in the bottom of the impeller, and the power of the lower impeller increased. Reducing the distance between the two impellers reduced this effect and lowered the overall mixing power, as well as the power of the lower impeller. In turn, the results obtained by Armenante et al. [27] regarding the determination of the conditions for obtaining a stable suspension indicate that, contrary to intuition, the use of two or three axial-action PBT impellers does not have to be energetically beneficial. Even in most cases where the critical frequency of the impellers decreases with the number of impellers on the shaft, the total power of such a system is greater than that for a single impeller operating at a higher rotational frequency.

1.3. Emptying Vessels

In some cases, emptying the tanks must be done with a constantly operating impeller. This is most often the case when multi-phase liquid–liquid or liquid–solid systems are mixed, and must be kept in the form of a stable mixture at all times. Then, during emptying, the demand for mixing power may increase when the falling liquid surface is just above the impeller or in the area of the impeller. It is especially dangerous for impellers with a capacity of several dozen or more cubic meters of liquid. The first mention of this can be found in the work of Poul et al. [28], the second only in the work of Mazoch et al. [29]. A momentary increase in power may result in an overload of the motor, as the motor is usually selected for conditions when the entire mixing tank is filled with liquid. The mechanism of this phenomenon, as well as the magnitude of the observed increase in power, has not been thoroughly described in monographs devoted to mixing processes [30,31]. In certain works [32,33], it was found that the effect of increasing the mixing power when emptying the tank with the impeller working occurs only in the case of axial impellers and results from the change in axial circulation to radial circulation. As a result of the research carried out for the six-PBT impeller with different blade inclination angles α, it was confirmed that the power increase factor φ depends on the Froude number and the angle α according to the correlation equation developed by the authors (2) [33].

$$\phi =\frac{E{u}_{max}}{Eu}=0.61·F{r}^{0.285}·{\left(\sin \alpha \right)}^{-0.367},$$

(2)

As Equation (2) shows, in an extreme case, the mixing power may even double. The theoretical foundations of this phenomenon are presented in [34].

The aim of the present work is to investigate the increase in power and to analyze the mechanism of increasing the mixing power for the systems of two 6-PBT45° impellers mounted on one shaft.

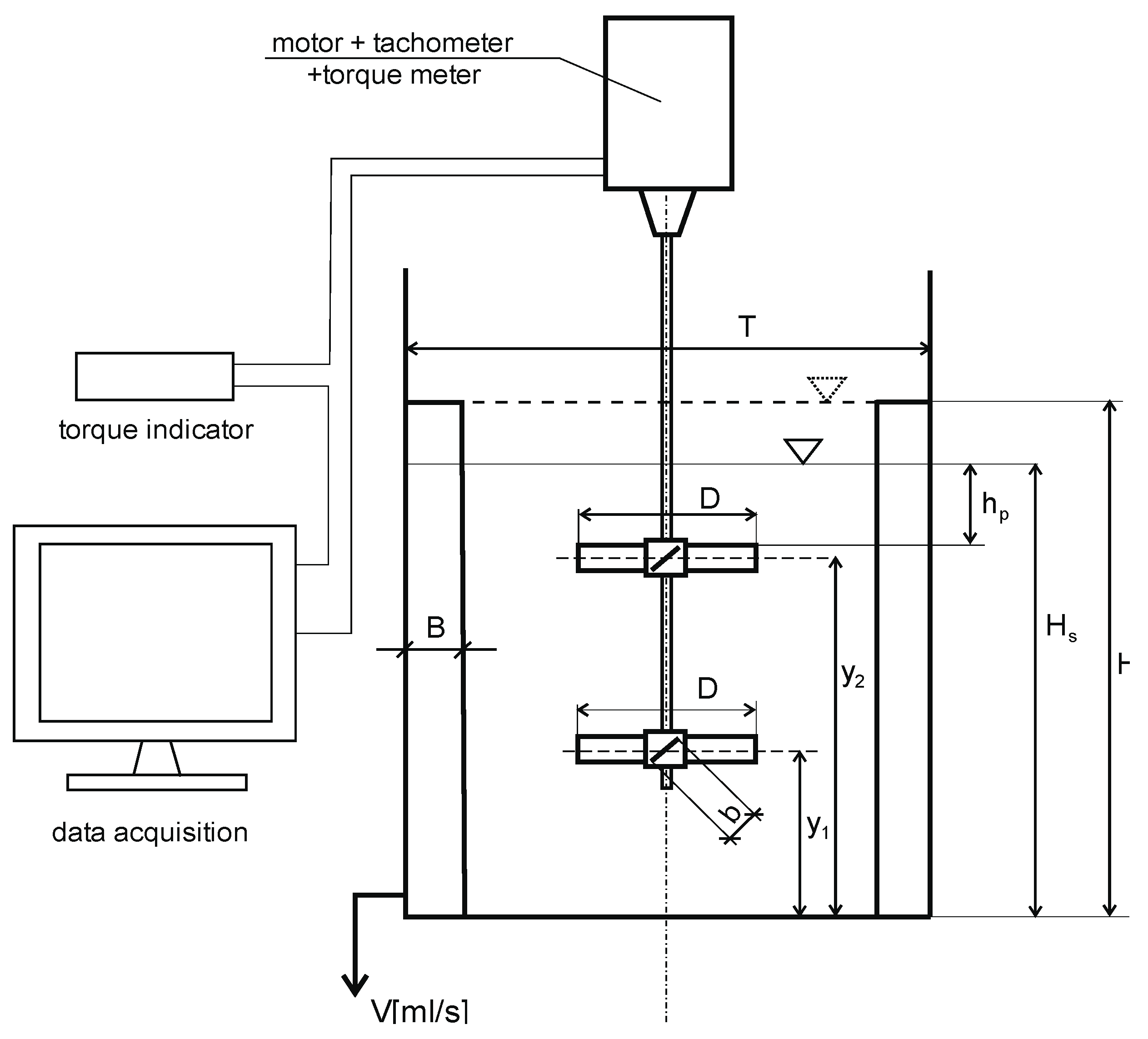
2. Materials and Methods

Tests of the torque of impellers during tank emptying were carried out in a flat-bottomed steel tank with a diameter T = 400 mm equipped with four standard baffles (B = 0.1 · D). Two six-blade impellers 6-PBT45° of diameter D = 133 mm and blade width b = 26.6 mm (b = 0.2 · D) were suspended at heights of y₁ = 1/3 · H and y₂ = 2/3 · H above the bottom of the tank. The tank was filled with water. Both impellers pumped the liquid toward the bottom of the mixing vessel. The diagram of the experimental equipment is shown in Figure 1.

The torque measurements were made with a IKA EURO-ST P CV meter.

During the measurements for a fully filled mixer, the meter software increased the rotational frequency of the stirrer within 30 min from N = 0.9 to 4.5 s⁻¹.

Measurement data were recorded with Labworldsoft 4.6 with an interval of 2 s. Thus, 900 measurements were obtained for each measurement series. This method of measuring power is widely used in laboratory conditions, not only in the case of impellers [35,36,37]. While torque measurements were made during the emptying of the mixer, a Verderflex 2010 peristaltic pump was used to pump out the water from the tank. Due to the practical invariability of the torque at the beginning of emptying the tank, the tank was filled with water up to the height H_s = 350 mm. Then, the impeller drive was started, and the torque meter and the peristaltic pump were turned on, which pumped the liquid out of the tank at a constant volume flow rate V = 7.73 cm³/s. This resulted in a linear descending speed of the free surface of the liquid equal to 0.125 mm/s. The measurement was terminated when the liquid level in the tank was approximately 10 mm below the lower edge of the lower mixing tank blades. The measurement time was approximately 45 min.

In turn, measurements of velocity distributions inside the impeller tank in the vertical r-z plane and the horizontal r-φ plane were carried out in a transparent glass vessel with a diameter of T = 292 mm.

The mixing system was geometrically similar to that shown in Figure 1. The impeller was additionally placed in a rectangular aquarium filled with distilled water. The LaVision PIV (Particle Image Velocimetry) system with a two-pulse laser with a maximum power of 135 mW was used to measure the velocity of the liquid in the mixer. The photos were taken with an ImagePro camera with a resolution of 2048 px × 2048 px. The Nikkor 1.8/50 lens, with aperture 5.6 ensuring maximum resolution, was used. The measurement area was in the vertical plane of symmetry between two baffles. The dimensions of the area were 240 mm × 120 mm with a thickness of 1 mm. For the presented configuration, the axial and radial velocity above and below the stirrers were determined for the rotational frequency of N = 2 s⁻¹ (120 min⁻¹). Each measuring point represents 200 double shots (time interval Δτ = 1000 µs), which were taken at a frequency of 2.7 Hz and then processed in the DaVis 7.2 program. Two-pass data processing was used with the final size of the analyzed field 32 px × 32 px without overlapping. Measurement parameters and details on how to measure velocity distributions can be found in the work of Heim and Stelmach [38].

3. Results and Discussion

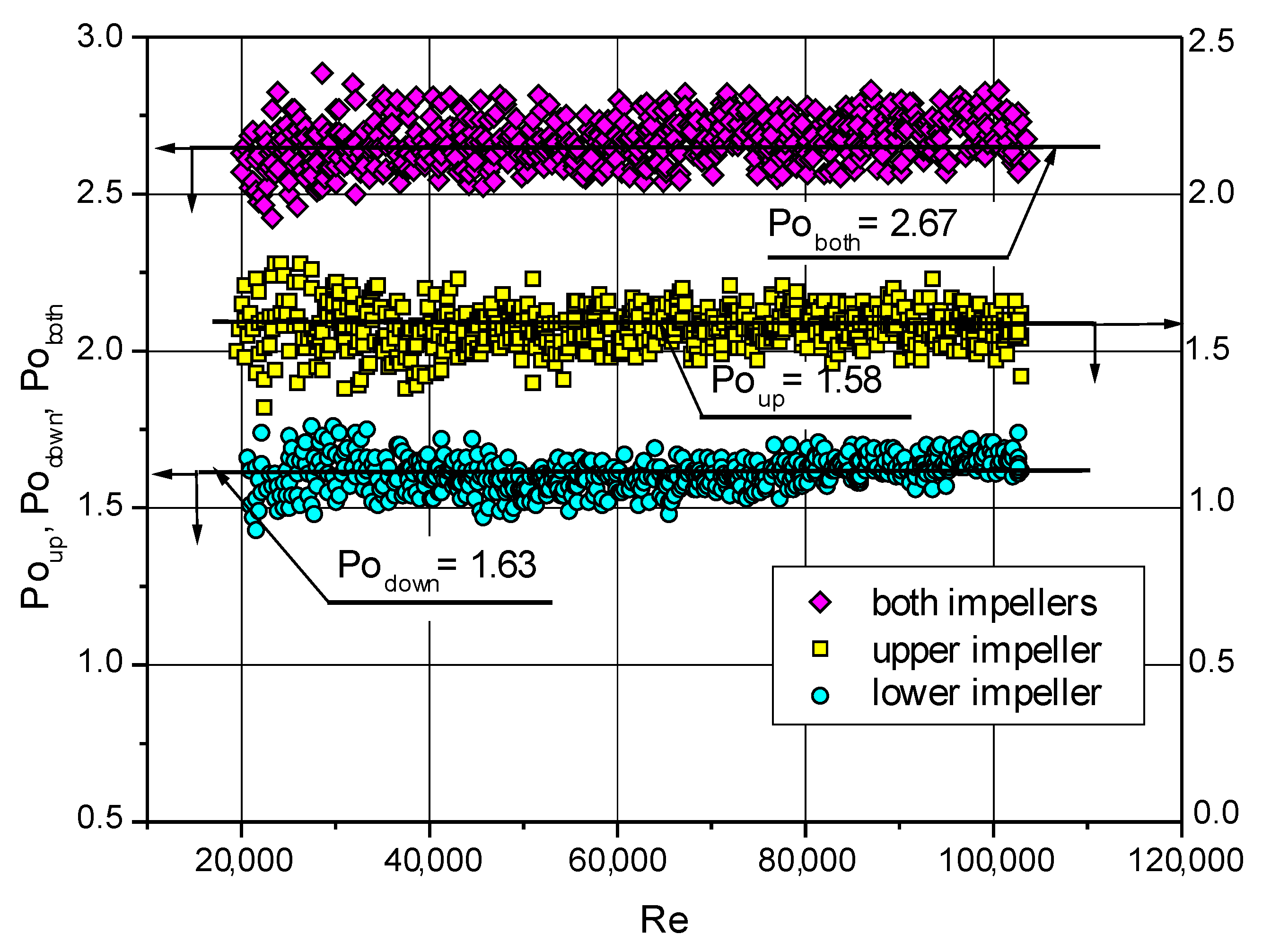
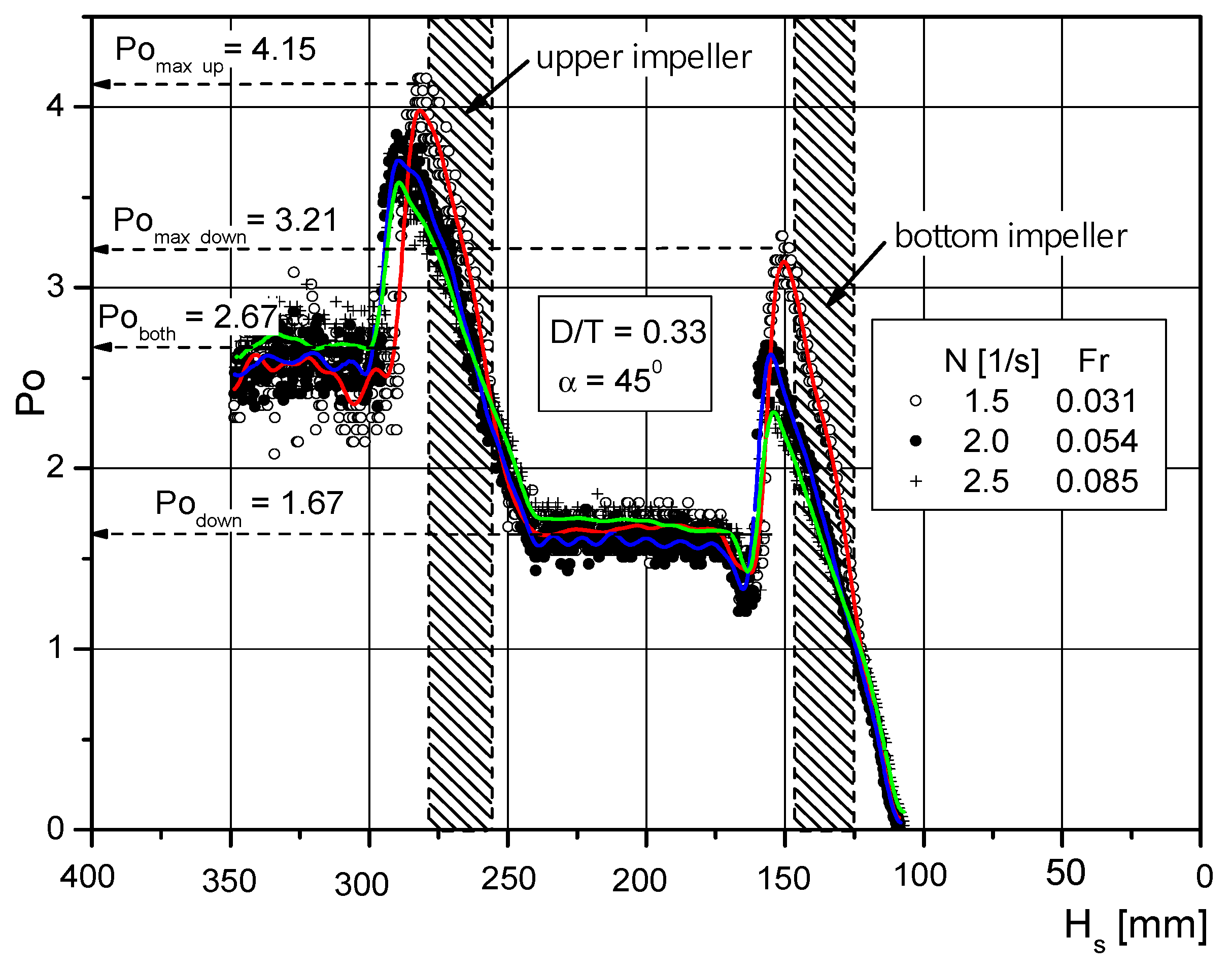
3.1. Mixing Power

The first stage of the research was to determine the mixing power demand for the tested impellers when the height of the liquid in the impeller was constant and equal to H = T = 400 mm. Stirring power was measured for the individual 6-PBT45° impellers in height y₁ = 1/3 · H or height y₂ = 2/3 · H and for both impellers placed on a common shaft at the same distances. The results obtained are shown in Figure 2. The significant dispersion of experimental points observed in Figure 2 resulted from the fact that the measured values of the instantaneous torque were read exactly every 2 s. Averaging the values of the power numbers Po was performed only after the end of each measurement series. The average measurement error for all measurements was ±6.8%.

For the upper single impeller, the value of the power number was obtained as Po_up = 1.58, while for a single lower impeller, a similar value 3.5% higher was obtained, Po_down = 1.63. The relation obtained of the Po value is consistent with the research of many authors [21,23,25,37].

Table 1. Comparison with other authors’ results for the agitator 6-PBT45° (D/T = 1/3, y₁/T = 1/3, b/D = 0.2) for turbulent mixing range.

Author	Po	Comments	Our Work
Machon et al., 1991 [22]	1.72	D/T = 0.5	1.63
Rewatkar et al., 1990 [23]	1.64	Equation (1)
Raghava Rao and Joshi, 1988 [39]	1.61
Chudacek et.al., 1985 [21]	1.63
Shiue and Wong, 1984 [20]	1.74	4-PBT45°, b/D = 0.23
O’Kane, 1974 [19]	1.52
Rushton et al., 1950 [40]	1.42	H/T = 0.92

shows a comparison of the Po_down value for the lower impeller with the results of other authors.

For the system of two impellers placed simultaneously, the value was obtained as Po_both = 2.67. Thus, for the distance between the impellers equal to D, the value obtained of the power number Po was lower by 17% than the sum of the values for a single upper and lower impeller (1.58 + 1.63 = 3.21). This is consistent with the studies of other authors who obtained similar results for the six-PBT impellers [24,25,26].

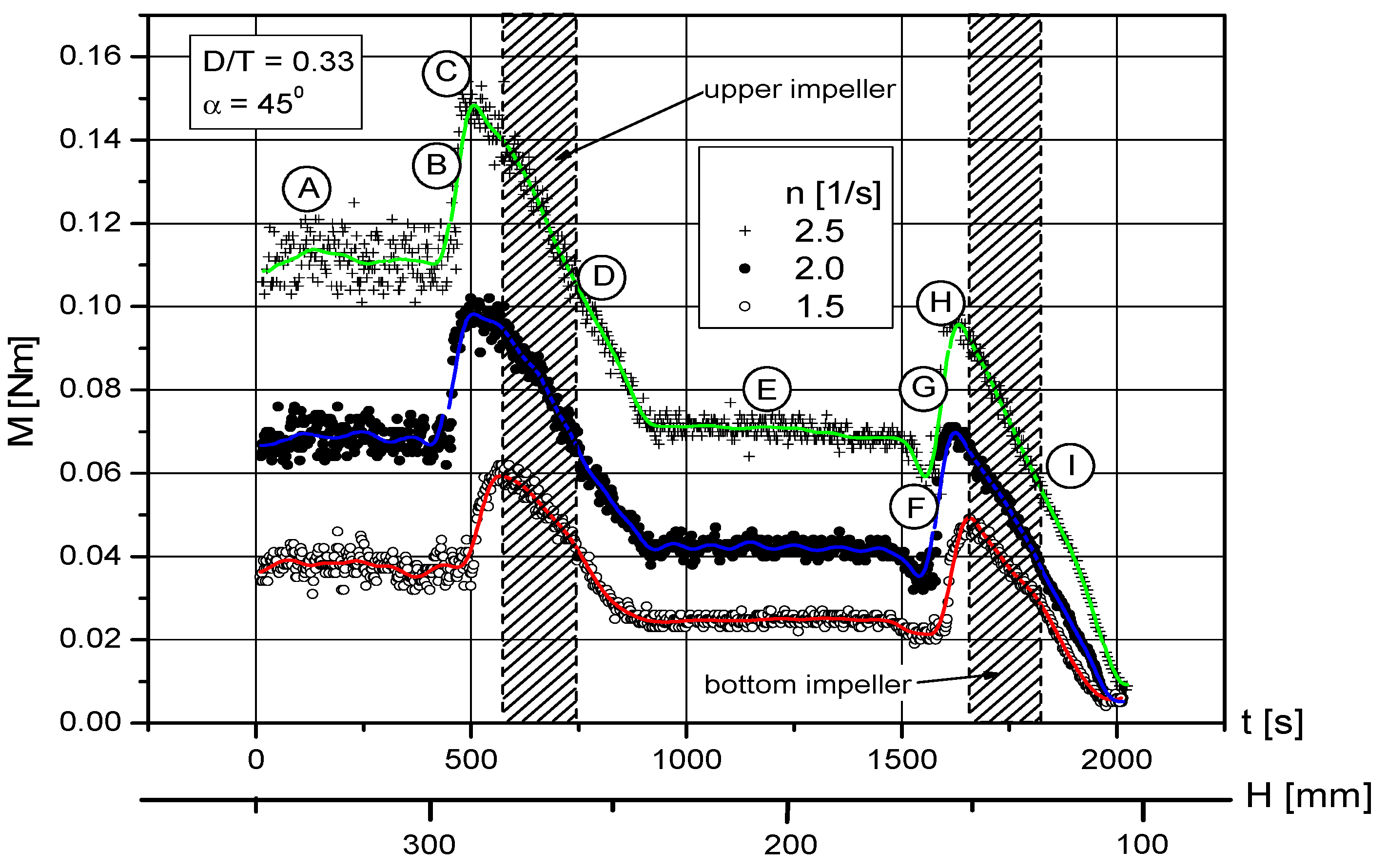
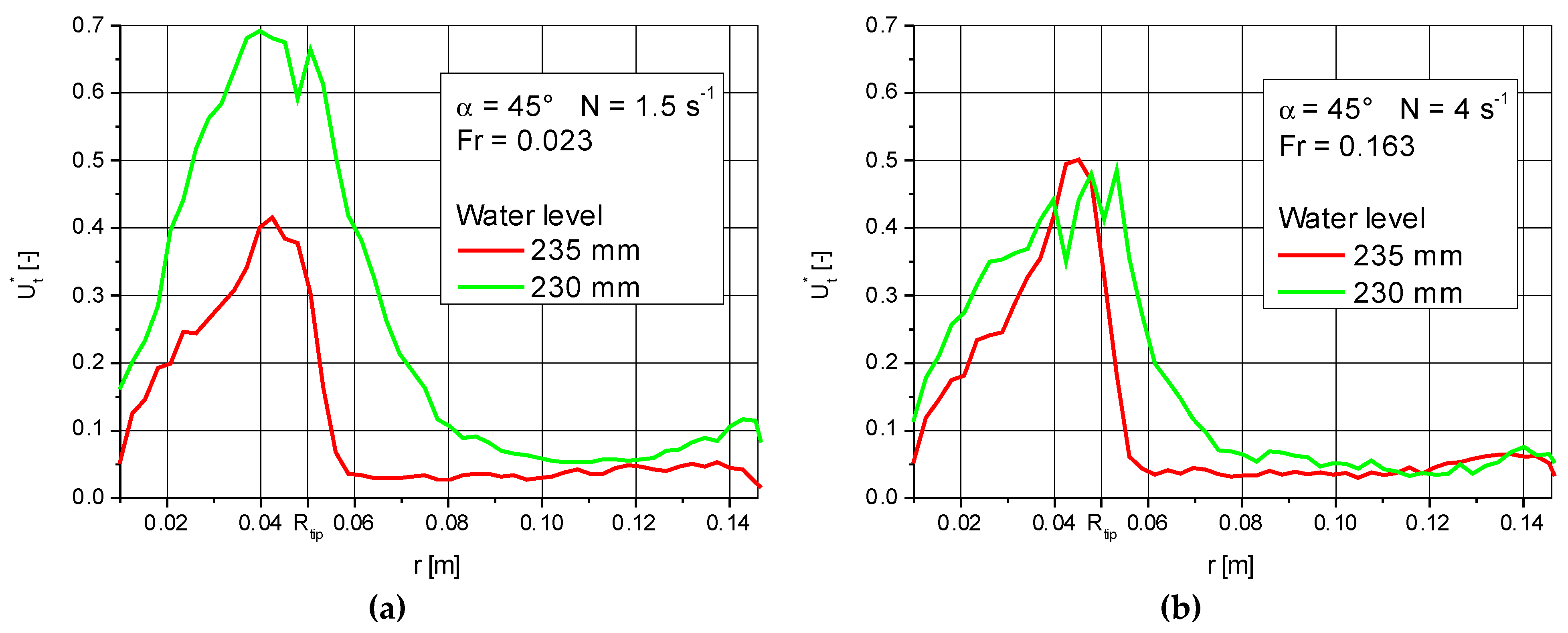
3.2. Pumping to the Bottom of the Mixing Tank

Two measurement programs were prepared in the study, the aim of which was to determine the mechanism and quantitative values related to the increase in mixing power during the process of emptying the tanks.

The first program concerned the determination of the mixing power in a mixing tank with a diameter of T = 400 mm for a system of two 6-PBT45° impellers pumping the liquid downward. The diagram of the measuring system is presented in Figure 1. The course of changes in the torque M [Nm] for three rotational frequencies of the impeller N = 1.5, 2.0, and 2.5 s⁻¹ is shown in Figure 3. The shaded areas in the figure indicate the areas of the upper and lower impeller. As the initial lowering of the liquid table caused practically no changes in the torque value, emptying the tank was started from the height of the free liquid surface from the bottom of the impeller equal to H_s = 350 mm.

In the second measurement program, the velocity distributions of the liquid in the mixing tank in the r-z plane for different levels of the free surface during emptying were determined. Measurements were made using a laser PIV system in the tank with a diameter of T = 293 mm, geometrically similar to the tank shown in Figure 1. The liquid level in the mixing tank was lowered every 10 mm from the height H_s = 290 mm to the level H_s = 100 mm. In total, 21 measurements of velocity distribution were made. The six key distributions from the point of view of the analyzed mechanism are presented in Figure 4.

Figure 3 shows the waveforms obtained of the torque changes over time for three rotational frequencies of the impeller. The instantaneous values of the torque were recorded with the time interval t = 2 s. From the analysis of Figure 3, the waveforms obtained were similar to each other and independent of the rotational frequency of the impellers. From the results of Figure 3, each of the runs can be divided into nine sub-areas.

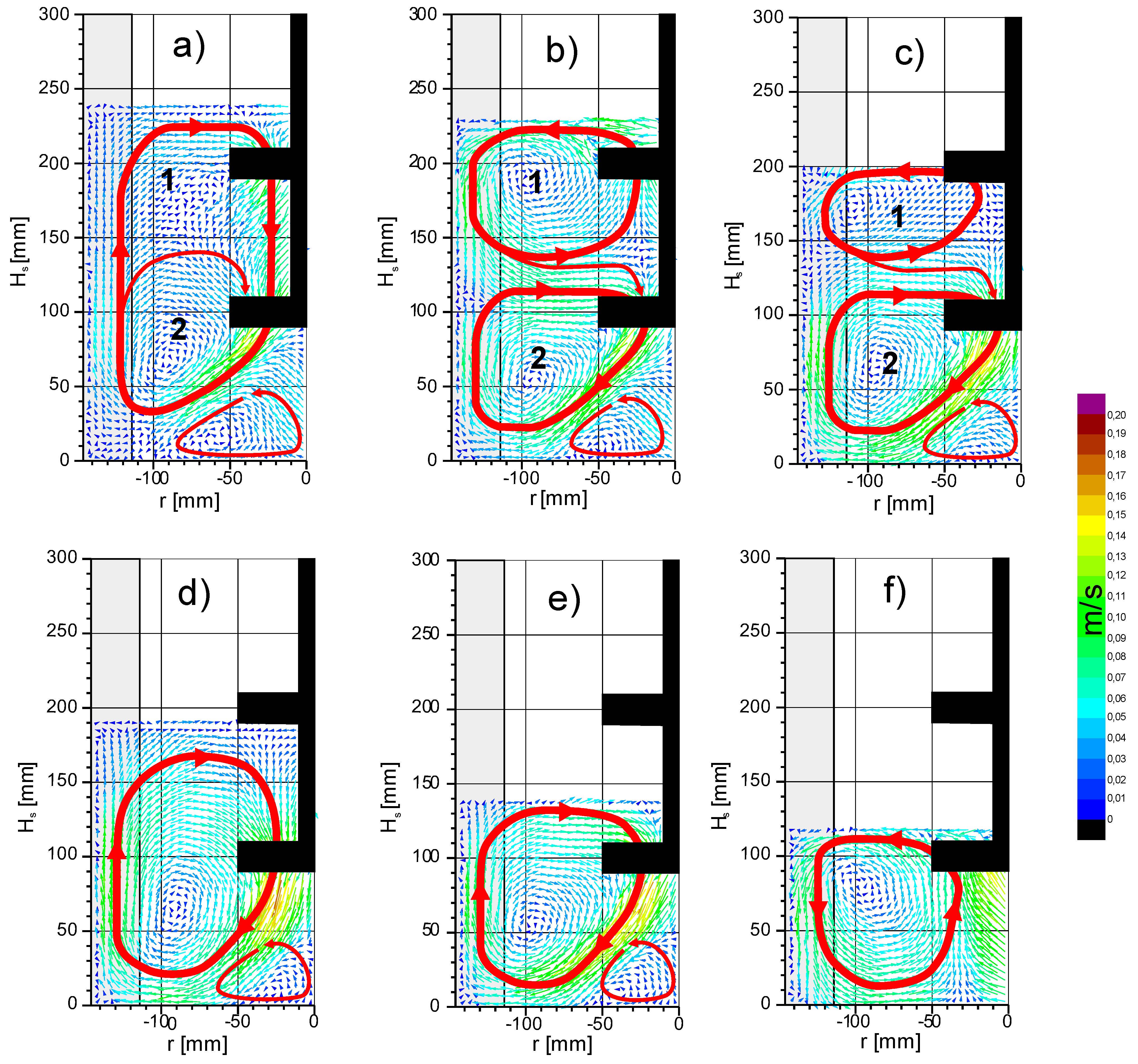
3.2.1. Area A—The Liquid Level in the Impeller Is Well Above the Edge of the Upper Impeller

Despite the systematic decrease in the amount of liquid in the impeller, the measurement points are arranged approximately on a horizontal straight line. The upper impeller in this H_s range works like a typical axial impeller, which results from the velocity distribution obtained (Figure 4a). For the liquid levels in the mixing tank up to H_s ≈ 240 mm (h_p/D > 0.10), the obtained circulation lines in Figure 4 were similar to each other. The main circulation loop 1 covered the entire area of the impeller with both impellers. There was a much smaller loop 2 between the impellers, being part of loop 1, with the direction of movement being clockwise in both loops. Just above the bottom, in the center of the tank, a small vortex formed in the opposite direction.

3.2.2. Area B—The Liquid Level Approaches the Top of the Upper Impeller

This is the key moment for this impeller. The ratio value is h_p/D ≈ 0.10 and the amount of liquid above the impeller is so small that the main circulation loop 1 (Figure 4a–c) only partially closes above the top impeller. The volumetric flow rate in loop 1 decreases in favor of the increase in flow in loop 2 associated with the operation of the bottom impeller. The stabilized axial flow of the liquid in the mixing tank changes rapidly. A smaller and smaller axial flow flows through the area of the upper impeller and, at a certain moment, the upper impeller will only eject the liquid from its area in the radial direction. For a relatively short time, the upper impeller will be able to generate only a radial and circumferential liquid stream, i.e., it will work as a radial impeller. This causes a rapid increase in the mixing power (Figure 3, area B), because the radial impellers have a two- and sometimes even three-times higher power consumption compared to the axial impellers [30,31,41]. The liquid, thrown by centrifugal force toward the wall of the impeller, had to flow from that moment to the bottom of the tank because the liquid was there only (Figure 4b). This changes the direction of rotation of loop 1 to the opposite of the original direction.

3.2.3. Area C—The Liquid Level Is Just Above the Top Impeller

The system reaches its maximum mixing power. The 6-PBT45° overhead impeller works as a radial and circumferential impeller. From the measurements of the velocity distributions presented in Figure 5a for a geometrically similar impeller–mixer system with a diameter of T = 292 mm, for the height of the liquid in the mixing tank H_s = 230 mm (h_p/D < 0.10), the maximum value of the dimensionless peripheral velocity was 1.75 times greater than in the case of only a slightly higher liquid level in the tank equal to H_s = 235 mm (h_p/D > 0.10). At this point, there was a very sharp increase in mixing power. It should be noted that for higher rotational frequencies of the impeller N = 4.5 s⁻¹, i.e., for higher values of Froude number Fr, the increase in the peripheral velocity of the liquid remains practically unchanged (Figure 5b).

3.2.4. Area D—The Liquid Level Is in the Impeller Zone

The overhead impeller is operated with only partial contact with the liquid. There is a gradual decrease in the torque M. As the liquid level drops below the lower level of the impeller blades, the mixing power of the entire system should theoretically decrease abruptly as the upper impeller should not be submerged further in the liquid. In fact, despite the presence of the baffles, a small funnel formed in the center of the impeller, and the rotating impeller continued to rotate inside the liquid for some time as the blade tips were still partially submerged in the liquid. Hence, a gradual flattening of the torque curve took place and its stabilization occurred only after the upper impeller had completely emerged from the liquid.

3.2.5. Area E—The Liquid Level Is Below the Upper Impeller

Only the lower impeller is loaded. It works like a typical axial impeller with one circulation nucleus (Figure 4d). After the upper impeller had completely emerged from the liquid, the situation returned to case A (Figure 3), i.e., the vortex of the secondary circulation was again turning clockwise. Although, the direction of rotation of the secondary circulation vortex was changed again, but without changing the torque, because the bottom impeller was still working and worked like an axial impeller. With a further decrease in the liquid level, the resistance of the lower impeller decreased slightly (the volume of the mixed liquid decreased).

3.2.6. Area F—The Liquid Level Is Near the Top of the Bottom Impeller

There is a visible, but not too large, temporary decrease in the torque M of the impeller (point F). It occurred for each rotational frequency of the impeller. The mechanism of this phenomenon is difficult to explain at the moment.

3.2.7. G and H Areas

The mechanism is repeated in accordance with the description for areas B and C. In this case, it is the key moment for the bottom impeller, because the change in the direction of the secondary circulation vortex to the opposite direction, i.e., clockwise direction, occurs at the value of h_p/D ≈ 0.1 for the lower impeller (Figure 4e,f).

3.2.8. Area I

The mechanism of the phenomenon is similar to that described for area D. With a further decrease in the liquid level in the mixing tank for h_p/D < 0.1 for the lower impeller, the small circulation vortex just above the bottom of the impeller practically disappears (Figure 4f), visible in all the previous drawings.

From the above description, it can be concluded that the increase observed in mixing power during the emptying of the tanks should be attributed to the double, temporary changes in the axial circulation of the liquid to the more energy-consuming circumferential–radial circulation in the moment when the liquid surface is just above the upper edges of the upper or the lower impeller.

The graphs of changes in the impeller torque and the instantaneous height of the liquid surface H_s presented in Figure 3 depended on the rotational frequency N of the impeller. This made the quantitative analysis of the observed phenomenon difficult. Therefore, Figure 6 shows the values of the dimensionless power numbers Po calculated on the basis of the torque value M in Figure 3.

As can be seen from Figure 6, if the lowering of the free surface of the liquid was significantly above the upper surface of the blades of the upper or lower impeller (h_p/D > 0.1), the values of the power numbers Po determined for individual rotational frequencies N of the impeller practically coincided and assumed the values from Table 1. These were either Po_both = 2.67 (above the upper impeller) or Po_down = 1.67 (above the lower impeller). However, they were significantly different for the areas just above the two impellers. It is easy to notice that the lower the rotational frequency of the impellers, the greater the increase in the value of Po power numbers in these areas, i.e., the lower the value of the Froude number. For the sake of clarity, Figure 6 presents the characteristic numerical values of the numbers Po only for the lowest rotational frequency of the impellers N = 1.5 s⁻¹. For the remaining rotational frequencies N, similar values are presented in

Table 2. Mixing power increase factors for reference value Po_both = 2.67 and P_down = 1.67

N [s−1]	Re	Fr	Pomax up	Pomax down	φup	φdown
1.5	26,500	0.0305	4.15	3.21	1.55	1.97
2.0	35,400	0.0542	3.81	2.72	1.43	1.63
2.5	44,200	0.0847	3.55	2.25	1.33	1.35
3.5	61,900	0.1660	3.17	1.79	1.19	1.07
4.5	79,600	0.2740	2.97	1.67	1.11	1.00

. It should be noted that when the direction of rotation of the secondary circulation vortex was changed for the upper impeller and N = 1.5 s⁻¹, there was a jump in the power number from Po = 2.67 to the maximum value equal to Po_{max up} = 4.15, i.e., the mixing power increased by over 55% compared to the power calculated at the design stage. This is a significant increase. Similar calculations were also performed for the remaining rotational frequencies N (Table 2). Such a large overload of the engine may damage it. Apart from the size of the engine overload, the possibility of it burning also depends on the duration of the overload. In turn, this depends on the speed of the liquid level decrease in the tank during emptying with the impeller working.

For the lower impeller and for the same rotational frequency N = 1.5 s⁻¹, the relative increase in mixing power was even greater, as the power number increased from Po = 1.63 to Po_{max down} = 3.21, so it almost doubled. However, from a practical point of view, this increase is not very important, because the drive motor is calculated for the variant with the operation of both impellers and, in this case, the motor overload will be (3.21−2.67)/2.67 = 0.176, i.e., 20.2%. It should be noted that the mixing power only for the lower impeller at the moment of its maximum increase is even greater than the mixing power for both impellers when the tank is fully filled. This indirectly proves the importance of the phenomenon observed.

It is easy to notice from Figure 6 that the higher the rotational frequency of the impellers, the smaller the increase in the mixing power. Figure 7 shows the results of similar measurements as in Figure 3, but for the two largest ones used in the research on the rotational frequency of the impellers N = 3.5 and 4.5 s⁻¹. For the upper impeller, in the case of emptying the tank for the first of the rotational frequencies, the maximum increase in the mixing power was 16%, and in the second case, it was only a 9% increase. For the lower impeller, the increases in both cases were even smaller. Generally, it can be stated that the higher the rotational frequencies of the impellers, i.e., the greater the values of Reynolds numbers and Froude numbers, the smaller the increases in mixing power.

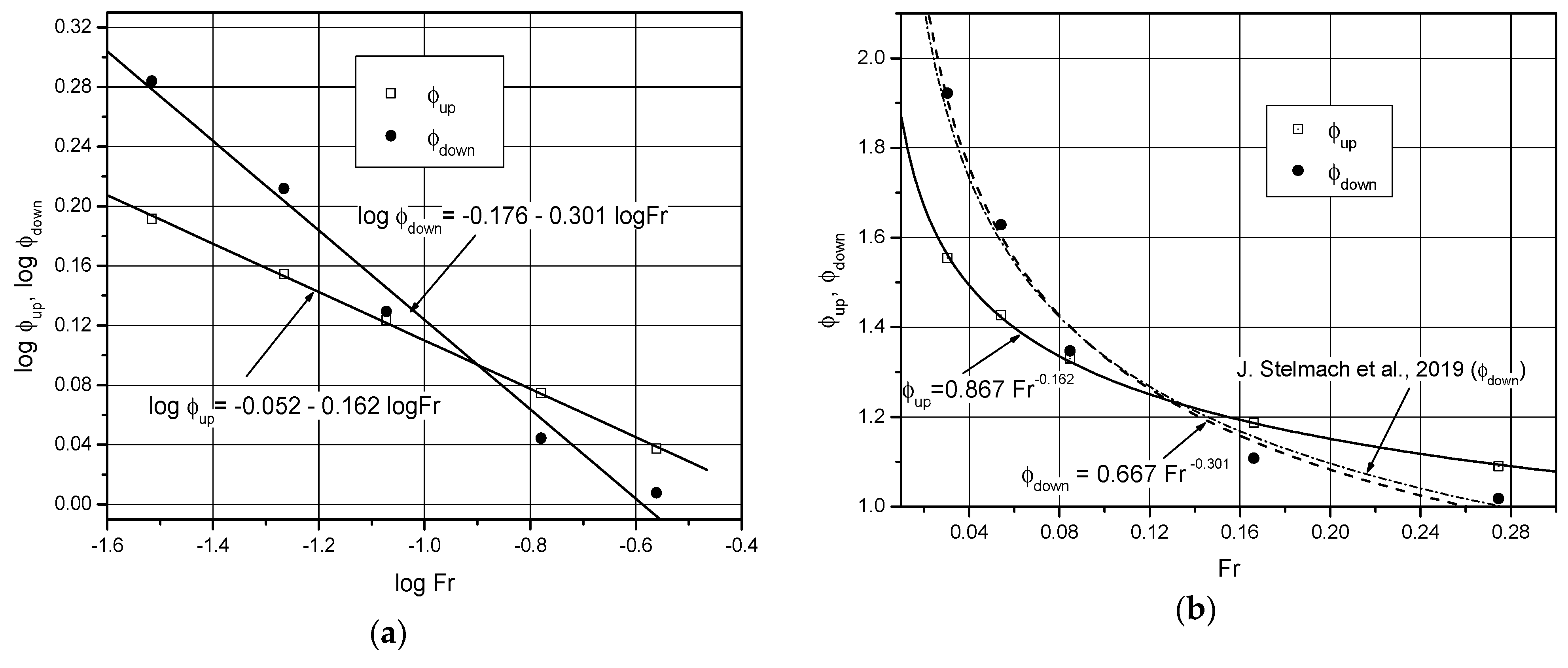
3.3. Determination of the Value of the Mixing Power Increase Factors

To quantify the amount of increase in mixing power, Equation (3) defines the power increase factor φ_up for the upper impeller as the ratio of the maximum power numbers Po_{max up} read from Figure 6 and Figure 7 to the initial power number Po_both = 2.67 for both impellers because at this point, the mixing system shows the highest mixing power. Similarly, Equation (4) defines the value of the coefficient φ_down for the lower impeller, where the reference value is the value Po_down = 1.63. The values of both factors are presented in Table 2.

$${\phi }_{up}=\frac{P{o}_{\max up}}{Po},$$

(3)

$${\phi }_{up}=\frac{P{o}_{\max down}}{Po},$$

(4)

As can be seen from the presented mechanism of increasing the mixing power during tank emptying, the liquid stream ejected by the centrifugal force from the impeller area plays a decisive role. Therefore, considering the values of the coefficients φ_up and φ_down, it was decided to connect the values of Froude numbers, which according to their definition, take into account the magnitude of this force.

Figure 8a shows the dependence of both power increase coefficients φ on the Froude number in a double logarithmic system. In both cases, the experimental points performed well on straight lines. In the case when only the lower impeller worked, the slope of the straight line was –0.301 and the correlation coefficient was R = 0.992. This means that the relationship φ_down = f(Fr) can be written in the form of Equation (5)

$${\phi }_{down}=0.667·F{r}^{-0.301},$$

(5)

For the upper impeller, when both impellers were working, the experimental points φ_up = f(Fr) in Figure 8a were also arranged on a straight line, but with a lower inclination coefficient of –0.162. This means we can express it as

$${\phi }_{up}=0.867·F{r}^{-0.162},$$

(6)

Despite this, for both identical working impellers, significantly different values of the slope coefficients φ were obtained, because the value of the power increase factor of the upper impeller was loaded with the influence of the working lower impeller. Hence, we observed an apparently smaller influence of the centrifugal force on the value of the coefficient φ_up.

Figure 8b shows the results of the φ value for both impellers in the normal system. For the case when only the lower impeller was working, the equation obtained (6) was in good agreement with the results obtained in our earlier work [33] for a single 6-PBT45° impeller placed in the middle of the mixing tank height.

The decrease in the power increase coefficients observed in Figure 8 with the increase in the Froude number can be interpreted in such a way that for high rotational frequencies of the impeller, the primary radial flow of liquid resulting from the centrifugal force is so large that the additional flow generated in the same direction, and resulting from the change in the liquid circulation method in the mixing tank, does not substantially change the value of the entire stream. This is confirmed by Figure 5b, where for a high rotational frequency of the impeller N = 4 s⁻¹, no significant increase in the dimensionless peripheral velocity was obtained. Therefore, only low rotational frequencies of the impellers, i.e., small primary streams (small centrifugal forces), can increase power factors φ even above 1.5.

According to the work in [33], the critical value of the Froude number, above which no increase in mixing power is observed, was Fr_cr ≈ 0.31. In this work, for the impeller located at a height of 1/3 · H from the bottom of the impeller, a similar value of Fr_cr ≈ 0.26 was obtained (Figure 8b).

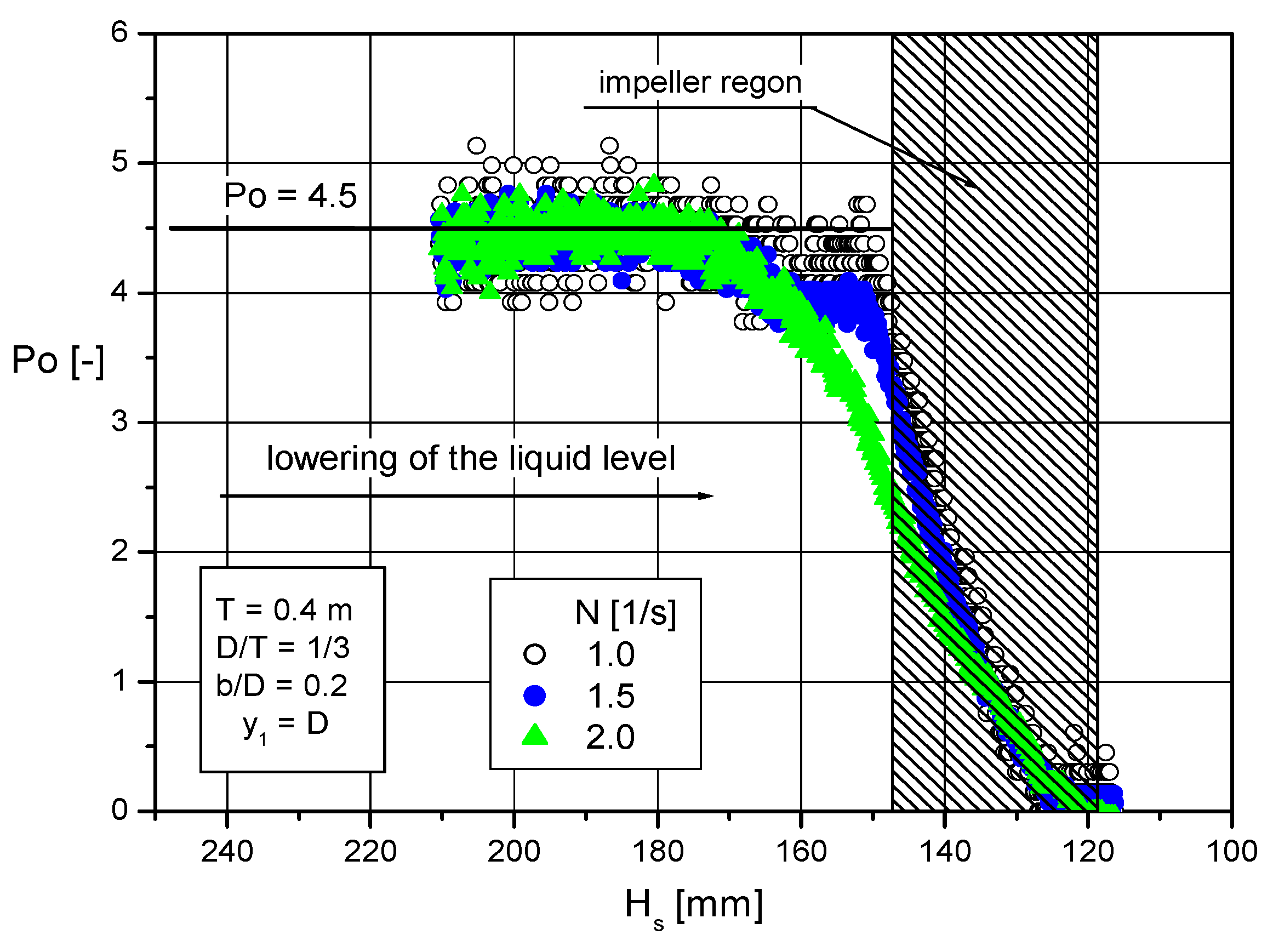
3.4. Radial Impellers

Figure 9 shows the change in torque for a single radial FBT (flat-blade turbine) impeller during tank emptying with the impeller running. The impeller was suspended in the liquid at a height of y₁ = D = 1/3 · H.

As shown in the analysis of Figure 9, despite the use of very low rotational frequencies of the impeller, i.e., small values of Froude numbers, no increase in mixing power was observed at any time of emptying the tank. Thus, an increase in mixing power only occurs with the axial action impeller. PIV methods that were used in this research are also widely used in different applications as in designing heat exchangers [42,43] and dryers [44,45,46,47,48].

4. Conclusions

• The phenomenon of the increase in mixing power when emptying the tanks with the impeller working occurs only in the case of impellers with axial action.
• The instantaneous increase in the mixing power for two working impellers placed on a common shaft and pumping the liquid toward the bottom of the mixer may be even more than 50% greater in relation to the calculated power. This could damage the engine.
• The increase in mixing power takes place when the direction of rotation of the vortices of the radial-axial circulation changes i.e., when the free surface of the liquid approaches the upper surface of the impeller blades.
• The smaller the rotational frequency of the impeller (i.e., the lower the Froude number), the greater the relative increase in mixing power when emptying the tank.
• Further research should be conducted toward the dependence of the mixing power increase factor on the value of the secondary circulation in the mixer, not on the type of the impeller. It will also be advisable to carry out appropriate numerical simulations.