Pore-Scale Simulations of Particles Migration and Deposition in Porous Media Using LBM-DEM Coupling Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Particle Governing Equations Based on DEM
2.1.1. Contact Force (Fc)
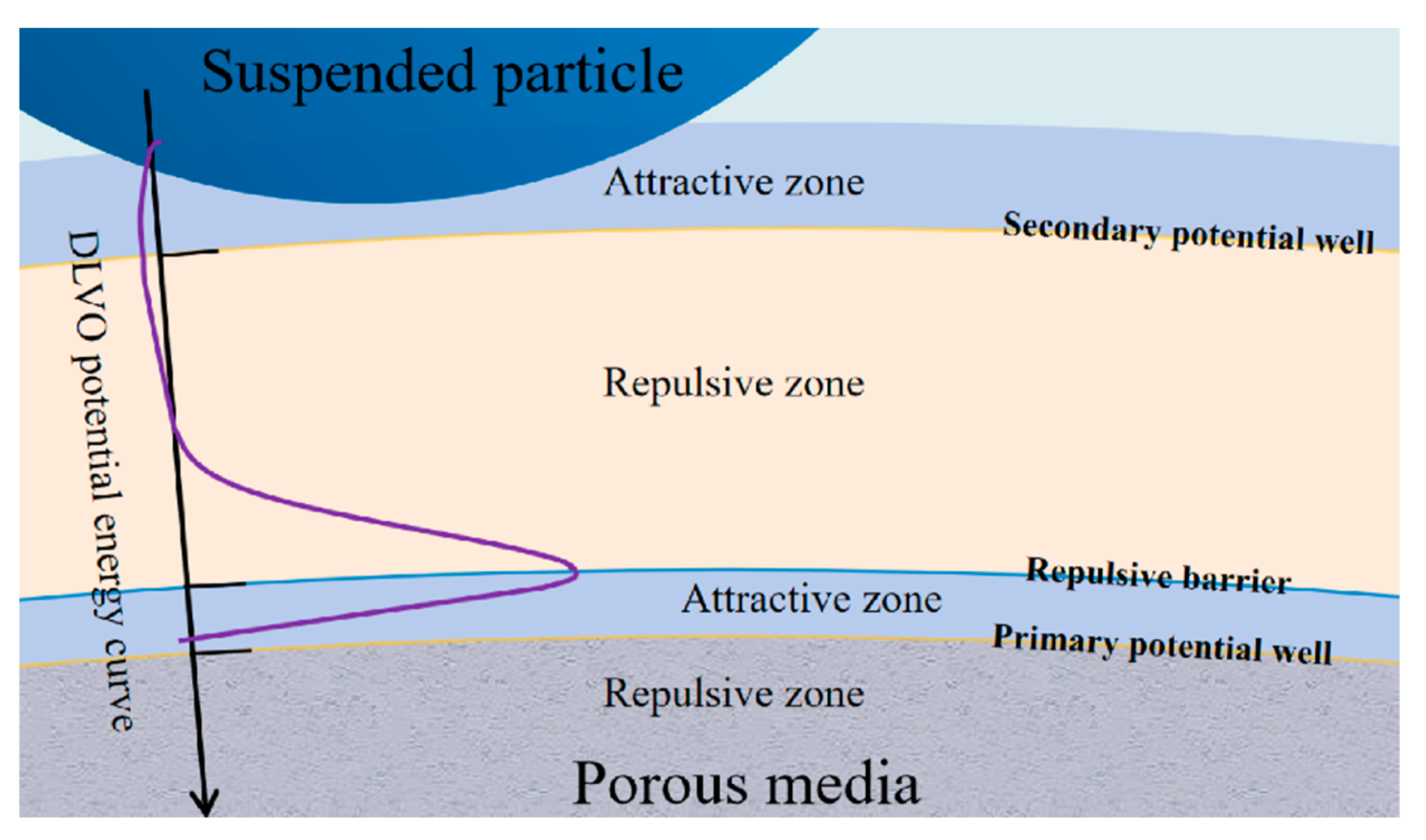
2.1.2. Long-Range Force
2.2. Fluid Governing Equations Based on LBM
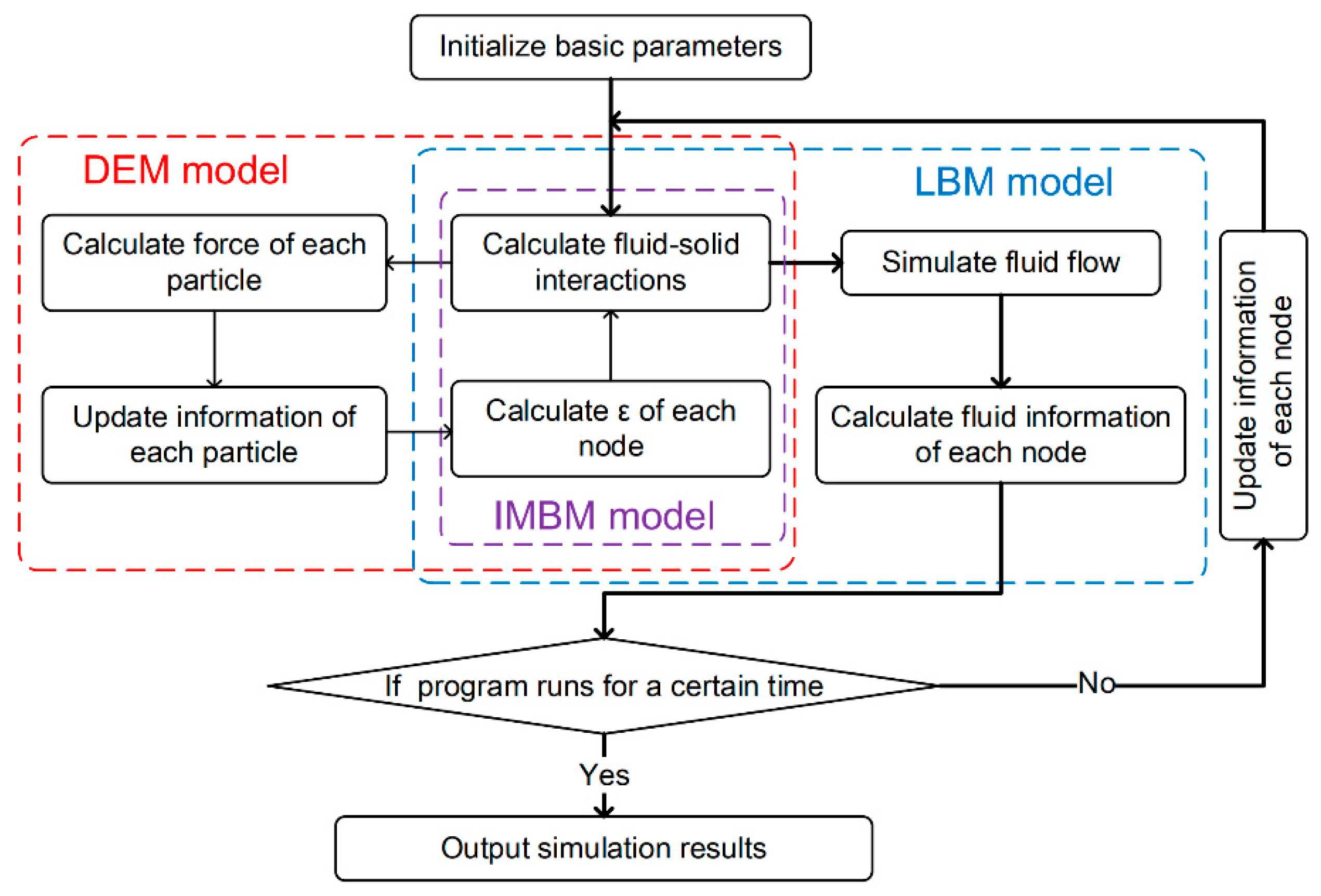
2.3. The LBM-DEM Coupled Method
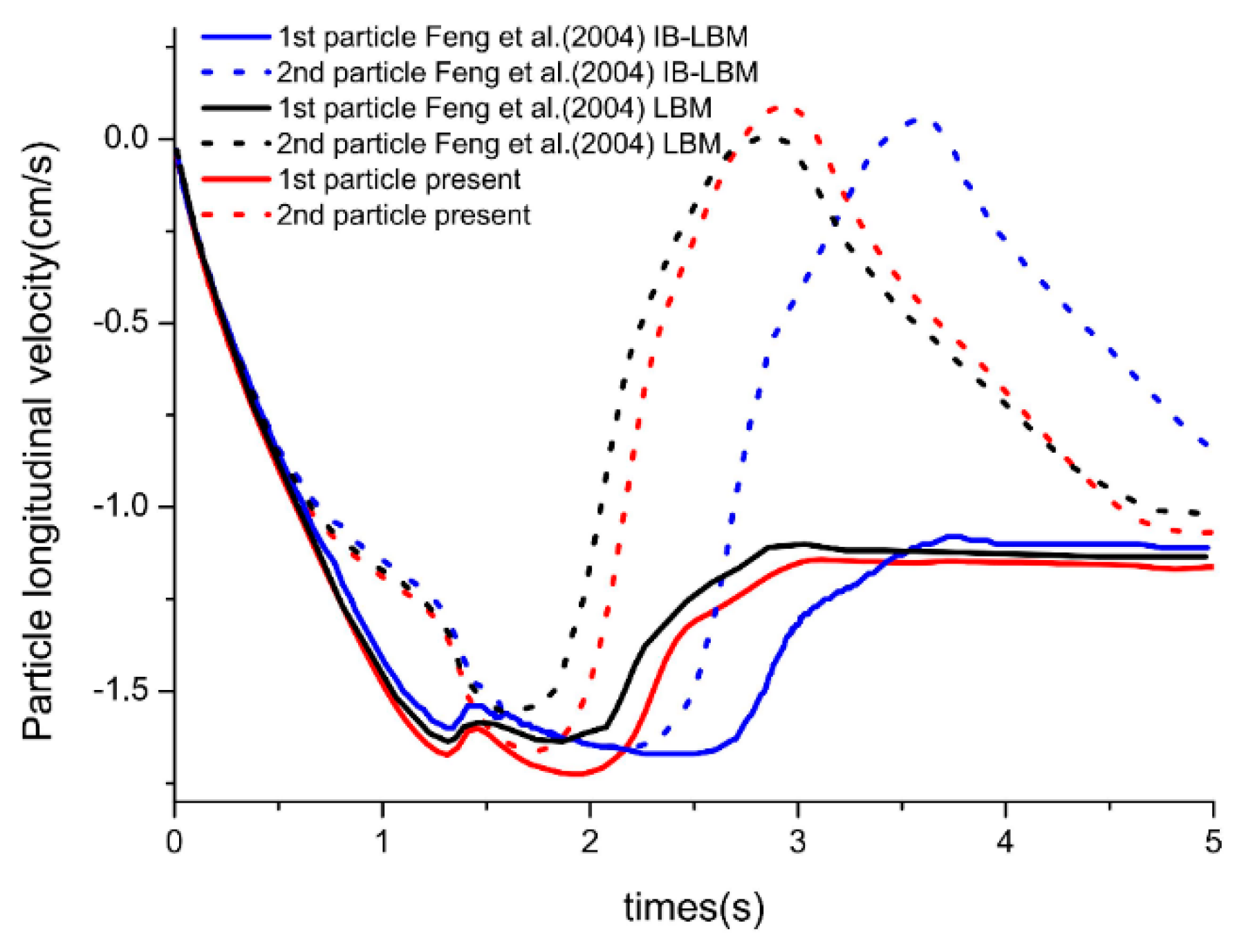
3. Model Verification
4. Results and Discussion
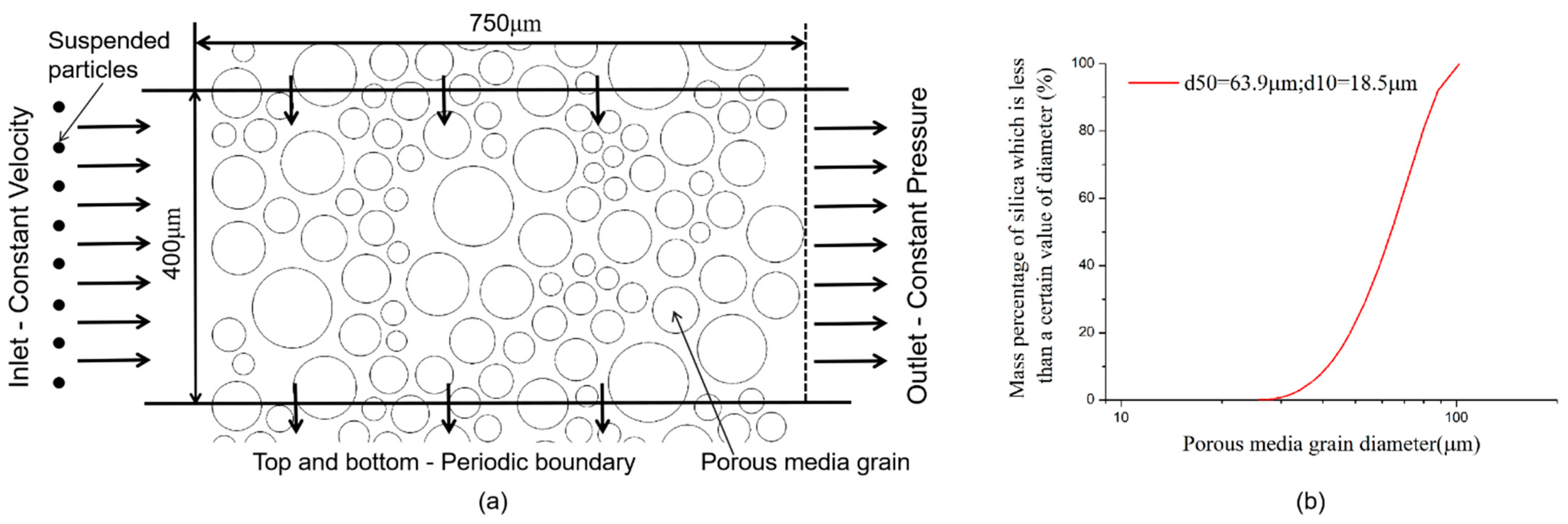
4.1. Simulation Method and Conditions
4.1.1. Data Processing
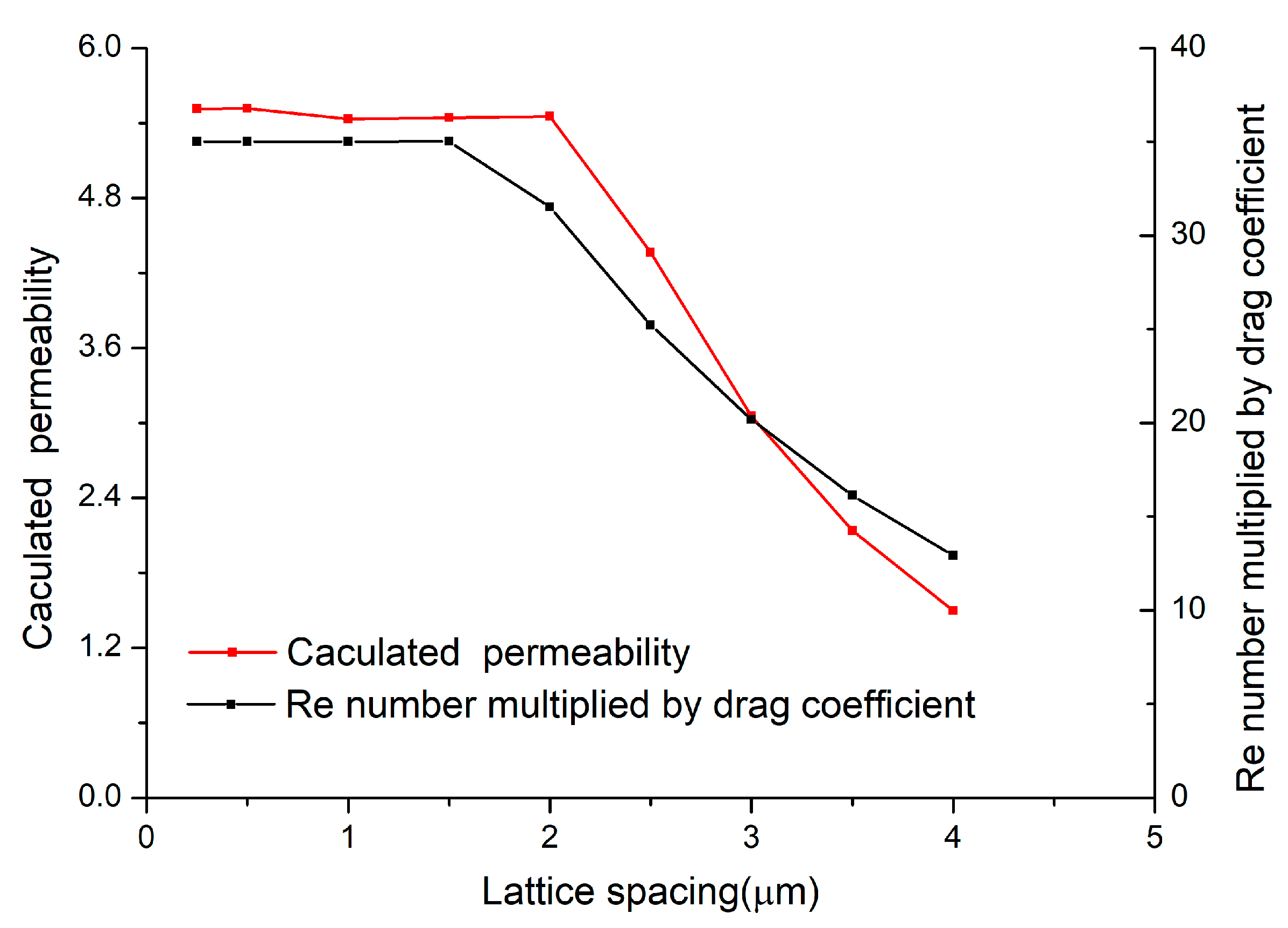
4.1.2. Grid-Independence Test
4.2. Analysis of Simulation Results
4.2.1. Coupling Effect of Flow Rate and Concentration
4.2.2. Coupling Effect of Flow Rate and pH
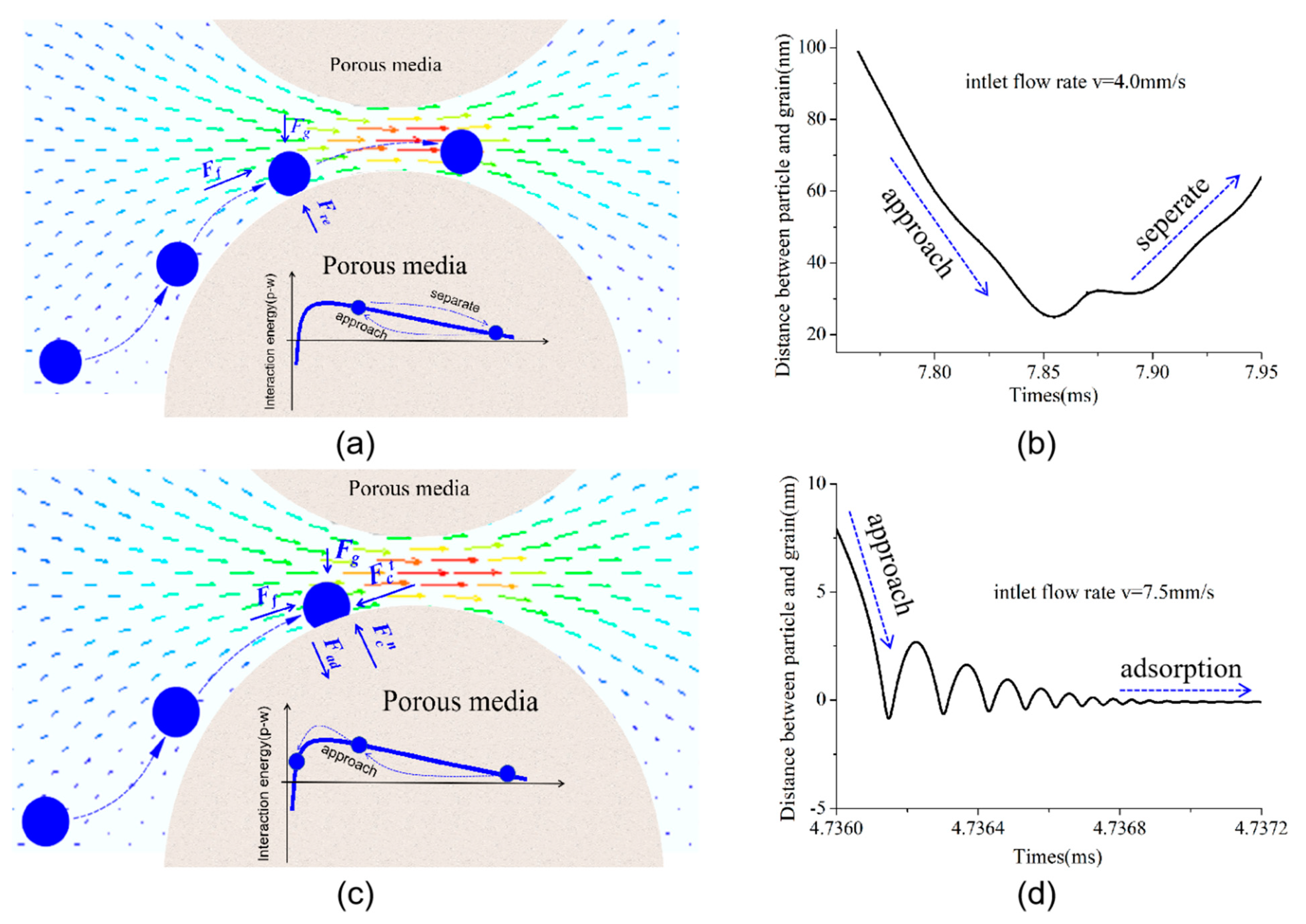
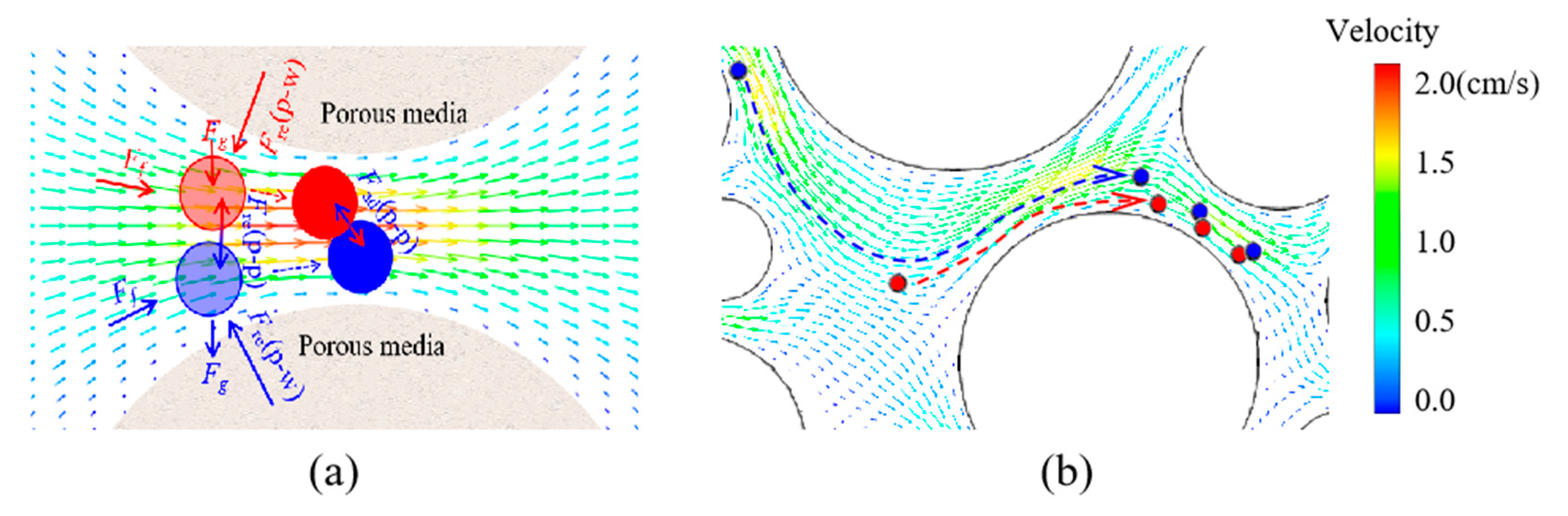
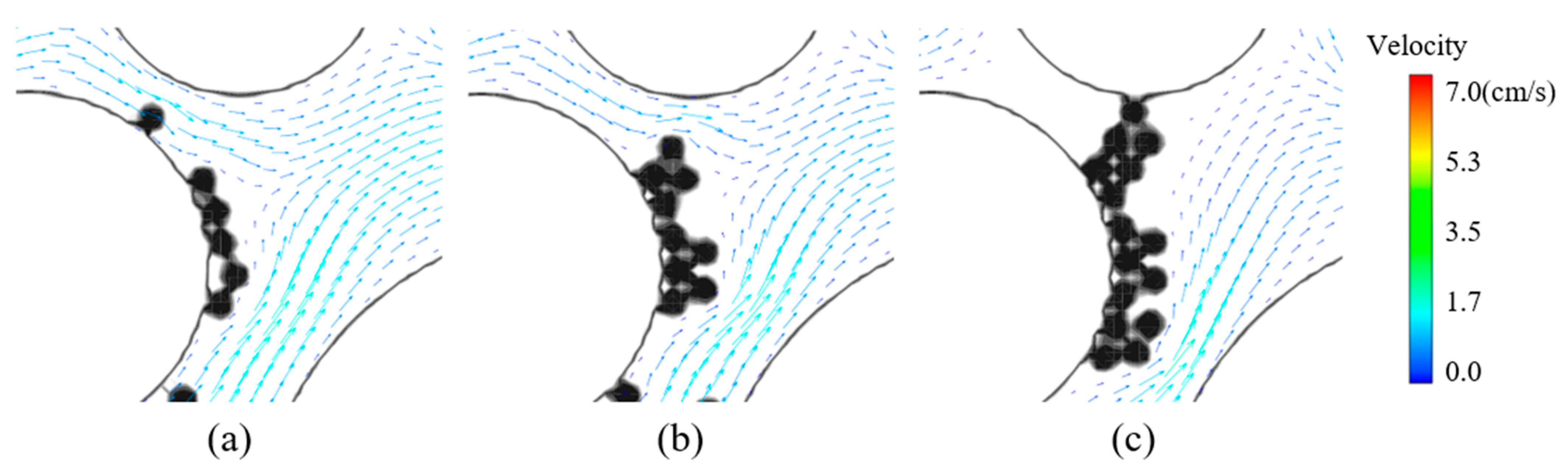
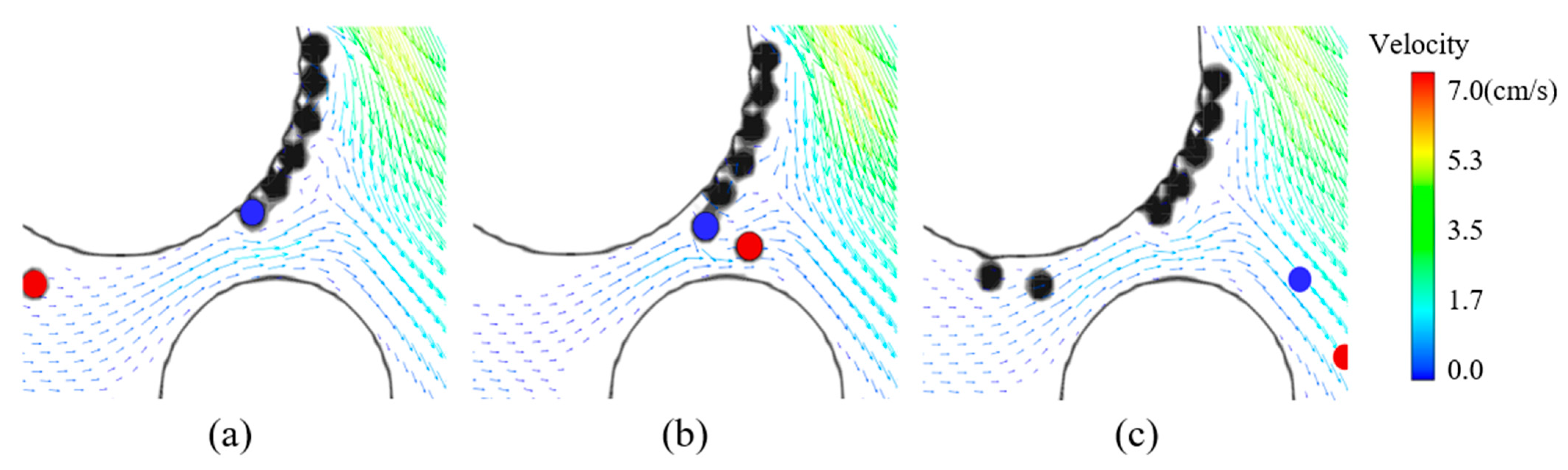
4.3. Particle Micro Deposition Behavior
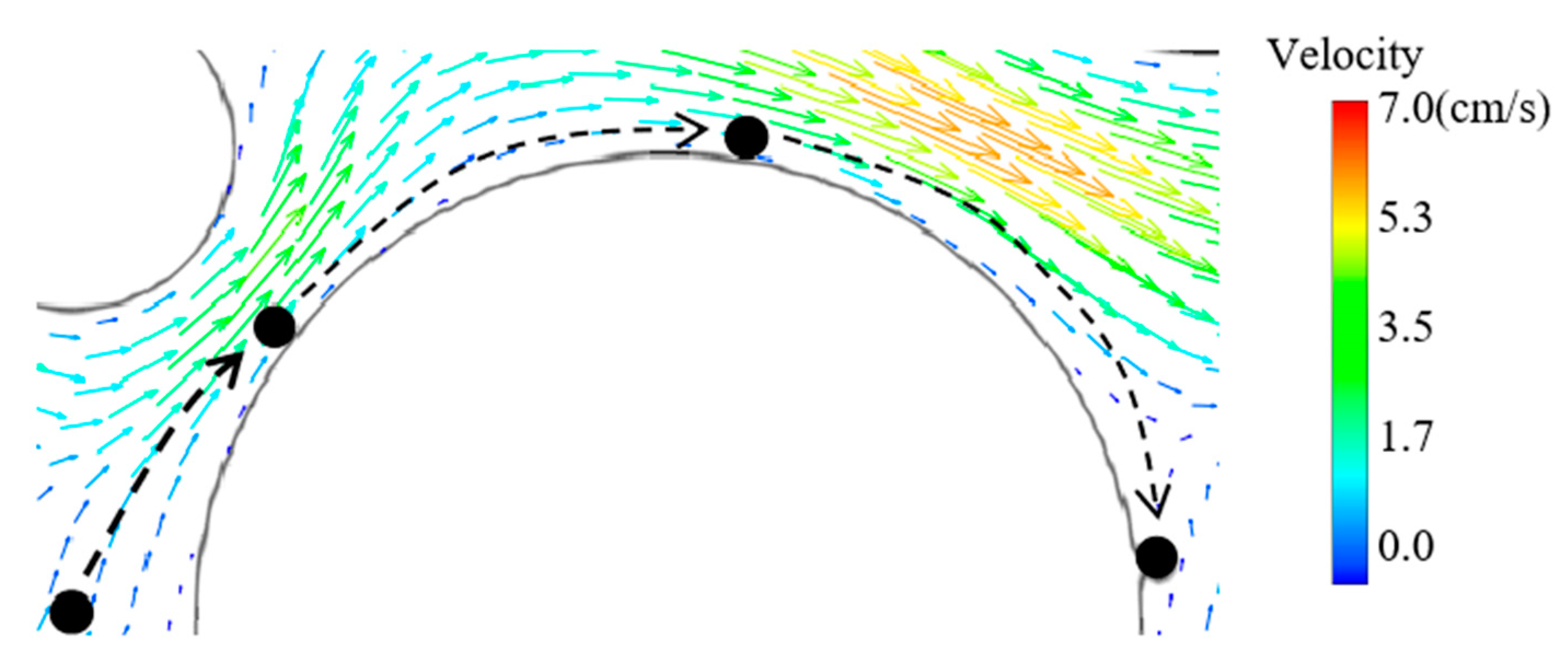
4.4. Dynamics of the Clogging Process and Resuspension
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| x | Position of particle/Grid coordinate |
| i, j | Particle index/Direction in LBM |
| t, ∆t | Time and Time step |
| vp,ωp | Velocity and angular velocity of particle |
| m, I | Mass of particle and moment of inertia |
| F, T | Force and torque on particles |
| Ff, Tf | Hydrodynamic force and torque induced by fluid flow |
| Fc, Tc | Contact forces and Torque resulting from the contact process |
| Fad, Fre | Adhesive force and repulsive force |
| Fg | Gravity force |
| n, t | Normal unit vectors and tangent unit vectors |
| n | Number |
| k | Stiffness constant |
| δ | Overlap length |
| σ | Coefficient of restitution |
| η | Damping constant |
| ζ | Friction coefficient |
| Vij | Relative velocity between particle i and j |
| r | Particle radius |
| Sij, hij | Center-to-center distance and surface distance between particle i and j |
| AH | Hamaker constant |
| εr, ε0 | Permittivity of vacuum and dielectric constant of the medium |
| R | Gas constant |
| F | Faraday constant |
| ψ | Zeta-potentials of the surface |
| z | Valence of the background electrolyte |
| κ | Reciprocal of Debye length |
| el | Electronic basic charge |
| NA | Avogadro constant |
| I | Ionic strength of solution |
| T | Temperature |
| T | Duration of the collision event |
| wilj | Surface adhesive energy |
| ci | Discrete lattice velocity |
| fi | Density distribution function |
| τBGK | Relaxation time |
| feq | Local equilibrium distribution function |
| wi | Weight factor |
| wi | Weight factor |
| ρf, ρlbm, ρ | Fluid density, fluid density in LBM and particle density |
| u | Fluid velocity |
| cs | Lattice sound velocity |
| P, ∆P | Pressure of the fluid and pressure drop |
| Ωis | Additional collision terms for nodes overlapping with solids |
| Bs | Weight coefficient |
| εs | Percentage of solids in lattice |
| Vin, Vp | Volume of injected liquid and volume of pore space |
| vin | Inlet flow rate |
| PV | Pore volume |
| k | Permeability |
| kr, k0 | Percentage of remaining permeability and initial permeability of porous media |
| μ | Viscosity of fluid |
| L | Length of the porous media |
| Cr | Normalized concentration |
| Cout, C0 | Volume concentrations in the effluent and volume concentrations in the influent |
| Mr | Percentage of particles retained |
References
- Rybach, L.; Sanner, B. Ground-Source Heat Pump Systems-The European Experience. Geo Heat Cent. Q. Bull. 2000, 21, 16–26. [Google Scholar] [CrossRef]
- Lund, J.; Sanner, B.; Rybach, L.; Curtis, R.; Hellström, G. Geothermal (ground-source) heat pumps a world overview. Geo Heat Cent. Q. Bull. 2004, 25, 1–10. [Google Scholar]
- Sharma, M.M.; Yortsos, Y.C. Fines Migration in Porous-Media. Aiche J. 1987, 33, 1654–1662. [Google Scholar] [CrossRef]
- Boek, E.S.; Hall, C.; Tardy, P.M.J. Deep Bed Filtration Modelling of Formation Damage Due to Particulate Invasion from Drilling Fluids. Transp. Porous Media 2012, 91, 479–508. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Caruso, N. Analytical Model for Fines Migration During Water Injection. Transp. Porous Media 2014, 101, 161–189. [Google Scholar] [CrossRef]
- Abdoli, S.M.; Shafiei, S.; Raoof, A.; Ebadi, A.; Jafarzadeh, Y.; Aslannejad, H. Water Flux Reduction in Microfiltration Membranes: A Pore Network Study. Chem. Eng. Technol. 2018, 41, 1566–1576. [Google Scholar] [CrossRef]
- McKinley, J.W.; Siegrist, R.L. Soil Clogging Genesis in Soil Treatment Units Used for Onsite Wastewater Reclamation: A Review. Crit. Rev. Environ. Sci. Technol. 2011, 41, 2186–2209. [Google Scholar] [CrossRef]
- Feng, Q.; Xu, S.; Wang, S.; Li, Y.; Gao, F.; Xu, Y. Apparent permeability model for shale oil with multiple mechanisms. J. Pet. Sci. Eng. 2019, 175, 814–827. [Google Scholar] [CrossRef]
- Guo, W.; Guo, X.; Chen, X.; Li, Y.; Li, Z.; An, Y.; Dai, W. Laboratory Evaluation of the Permeability Durability of Utilization of Oil Shale Waste as Fine Aggregate in Open Grade Friction Course in Seasonal Frozen Regions. Appl. Sci. 2020, 10, 419. [Google Scholar] [CrossRef] [Green Version]
- Fallah, H.; Fathi, H.B.; Mohammadi, H. The Mathematical Model for Particle Suspension Flow through Porous Medium. Geomaterials 2012, 2, 57–62. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Wen, D. Particle migration in a flow of nanoparticle suspensions. Powder Technol. 2005, 149, 84–92. [Google Scholar] [CrossRef]
- Alem, A.; Elkawafi, A.; Ahfir, N.-D.; Wang, H. Filtration of kaolinite particles in a saturated porous medium: Hydrodynamic effects. Hydrogeol. J. 2013, 21, 573–586. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Bai, B.; Jiang, S.C. Coupled effects of hydrodynamic forces and pore structure on suspended particle transport and deposition in a saturated porous medium. Rock Soil Mech. 2016. [Google Scholar] [CrossRef]
- Shen, C.Y.; Bradford, S.; Wang, Z.; Huang, Y.F.; Zhang, Y.L.; Li, B.G. DLVO Interaction Energies between Hollow Spherical Particles and Collector Surfaces. Langmuir 2017, 33, 10455–10467. [Google Scholar] [CrossRef] [PubMed]
- Ahfir, N.D.; Hammadi, A.; Alem, A.; Wang, H.Q.; Le Bras, G.; Ouahbi, T. Porous media grain size distribution and hydrodynamic forces effects on transport and deposition of suspended particles. J. Environ. Sci. 2017, 53, 161–172. [Google Scholar] [CrossRef]
- Bennacer, L.; Ahfir, N.D.; Alem, A.; Wang, H.Q. Coupled Effects of Ionic Strength, Particle Size, and Flow Velocity on Transport and Deposition of Suspended Particles in Saturated Porous Media. Transp. Porous Media 2017, 118, 251–269. [Google Scholar] [CrossRef]
- Liu, Q.S.; Cui, X.Z.; Zhang, C.Y.; Zhan, T. Effects of particle size on characteristics of transportation and deposition of suspended particles in porous media. Chin. J. Geotech. Eng. 2014, 36, 1777–1783. [Google Scholar] [CrossRef]
- Razzaghmanesh, M.; Borst, M. Investigation clogging dynamic of permeable pavement systems using embedded sensors. J. Hydrol. 2018, 557, 887–896. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Ye, X.; Zhang, X. Clogging of saturated porous media by silt-sized suspended solids under varying physical conditions during managed aquifer recharge. Hydrol. Process. 2018, 32, 2254–2262. [Google Scholar] [CrossRef]
- Li, X.; Mi, Z.; Tan, S.; Wang, R.; Wang, X. PIV study of velocity distribution and turbulence statistics in a rod bundle. Ann. Nucl. Energy 2018, 117, 305–317. [Google Scholar] [CrossRef]
- Reci, A.; Sederman, A.J.; Gladden, L.F. Experimental evidence of velocity profile inversion in developing laminar flow using magnetic resonance velocimetry. J. Fluid Mech. 2018, 851, 545–557. [Google Scholar] [CrossRef]
- Khan, M.S.; Karim, I.; Evans, G.M.; Doroodchi, E.; Joshi, J.B.; Mitra, S. Estimation of dispersion coefficient in a solid-liquid fluidised bed system. Powder Technol. 2020, 374, 560–576. [Google Scholar] [CrossRef]
- Peng, Z.; Joshi, J.B.; Moghtaderi, B.; Khan, M.S.; Evans, G.M.; Doroodchi, E. Segregation and dispersion of binary solids in liquid fluidised beds: A CFD-DEM study. Chem. Eng. Sci. 2016, 152, 65–83. [Google Scholar] [CrossRef]
- Poletto, V.G.; De Lai, F.C.; Junqueira, S.L.M. CFD-DEM simulation of mud cake formation in heterogeneous porous medium for lost circulation control. J. Braz. Soc. Mech. Sci. Eng. 2020, 42. [Google Scholar] [CrossRef]
- Trofa, M.; D′Avino, G.; Sicignano, L.; Tomaiuolo, G.; Greco, F.; Maffettone, P.L.; Guido, S. CFD-DEM simulations of particulate fouling in microchannels. Chem. Eng. J. 2019, 358, 91–100. [Google Scholar] [CrossRef]
- Zhang, H.; Li, T.; Huang, Z.; Kuang, S.; Yu, A. Investigation on vertical plug formation of coarse particles in a non-mechanical feeder by CFD-DEM coupling method. Powder Technol. 2018, 332, 79–89. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, C.; Zhang, L. Simulating Progression of Internal Erosion in Gap-Graded Sandy Gravels Using Coupled CFD-DEM. Int. J. Geomech. 2020, 20. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Wang, R.; Tian, R.; Sun, Q.; Ma, Y. Numerical simulation of flow behavior of particles in a porous media based on CFD-DEM. J. Pet. Sci. Eng. 2018, 171, 140–152. [Google Scholar] [CrossRef]
- Han, K.; Feng, Y.T.; Owen, D.R.J. Numerical simulations of irregular particle transport in turbulent flows using coupled LBM-DEM. CMES Comput. Model. Eng. Sci. 2007, 18, 87–100. [Google Scholar] [CrossRef]
- Fan, J.; Luu, L.-H.; Noury, G.; Philippe, P. DEM-LBM numerical modeling of submerged cohesive granular discharges. Granul. Matter 2020, 22. [Google Scholar] [CrossRef]
- Najuch, T.; Sun, J. Analysis of two partially-saturated-cell methods for lattice Boltzmann simulation of granular suspension rheology. Comput. Fluids 2019, 189, 1–12. [Google Scholar] [CrossRef]
- Su, T.C.; O′Sullivan, C.; Yasuda, H.; Gourlay, C.M. Rheological transitions in semi-solid alloys: In-situ imaging and LBM-DEM simulations. Acta Mater. 2020, 191, 24–42. [Google Scholar] [CrossRef]
- Cui, X.L.; Li, J.; Chan, A.; Chapman, D. Coupled DEM-LBM simulation of internal fluidisation induced by a leaking pipe. Powder Technol. 2014, 254, 299–306. [Google Scholar] [CrossRef]
- Montella, E.P.; Toraldo, M.; Chareyre, B.; Sibille, L. Localized fluidization in granular materials: Theoretical and numerical study. Phys. Rev. E 2016, 94, 14. [Google Scholar] [CrossRef] [Green Version]
- Parvan, A.; Jafari, S.; Rahnama, M.; Apourvari, S.N.; Raoof, A. Insight into particle retention and clogging in porous media; a pore scale study using lattice Boltzmann method. Adv. Water Resour. 2020, 138. [Google Scholar] [CrossRef]
- Zhou, K.; Hou, J.; Sun, Q.C.; Guo, L.L.; Bing, S.X.; Du, Q.J.; Yao, C.J. A Study on Particle Suspension Flow and Permeability Impairment in Porous Media Using LBM-DEM-IMB Simulation Method. Transp. Porous Media 2018, 124, 681–698. [Google Scholar] [CrossRef]
- Noble, D.R.; Torczynski, J.R. A lattice-Boltzmann method for partially saturated computational cells. Int. J. Mod. Phys. C 1998, 9, 1189–1201. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. Discrete Numerical-Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Crowe, C.T.; Sommerfield, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781439840504. [Google Scholar]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian Numerical Simulation of Plug Flow of Cohesionless Particles in a Horizonal Pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Rettinger, C.; Ruede, U. A coupled lattice Boltzmann method and discrete element method for discrete particle simulations of particulate flows. Comput. Fluids 2018, 172, 706–719. [Google Scholar] [CrossRef] [Green Version]
- Vigil, G.; Xu, Z.H.; Steinberg, S.; Israelachvili, J. Interactions of Silica Surfaces. J. Colloid Interface Sci. 1994, 165, 367–385. [Google Scholar] [CrossRef]
- Liang, Y.; Hilal, N.; Langston, P.; Starov, V. Interaction forces between colloidal particles in liquid: Theory and experiment. Adv. Colloid Interface Sci. 2007, 134–135, 151–166. [Google Scholar] [CrossRef]
- Peng, Z.B.; Doroodchi, E.; Evans, G. DEM simulation of aggregation of suspended nanoparticles. Powder Technol. 2010, 204, 91–102. [Google Scholar] [CrossRef]
- Yang, H.T.; Balhoff, M.T. Pore-network modeling of particle retention in porous media. Aiche J. 2017, 63, 3118–3131. [Google Scholar] [CrossRef]
- Abbasfard, H.; Evans, G.; Moreno-Atanasio, R. Effect of van der Waals force cut-off distance on adhesive collision parameters in DEM simulation. Powder Technol. 2016, 299, 9–18. [Google Scholar] [CrossRef]
- Mihajlovic, M.; Roghair, I.; Annaland, M.V.S. On the numerical implementation of the Van der Waals force in Soft-Sphere Discrete Element Models for gas-solid fluidization. Chem. Eng. Sci. 2020, 226. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface Energy and the Contact of Elastic Solids. Procrsoclonda 1971, 324, 301–313. [Google Scholar] [CrossRef] [Green Version]
- Hong, C.W. From Long-Range Interaction to Solid-Body Contact Between Colloidal Surfaces During Forming. Jeuroceramsoc 1998, 18, 2159–2167. [Google Scholar] [CrossRef]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann-Equation to Simulate Lattice-Gas Automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.H.; Cha, L.M.; Dai, C.L.; Zhao, G.; Wang, S. Effect of particle size and concentration on the migration behavior in porous media by coupling computational fluid dynamics and discrete element method. Powder Technol. 2020, 360, 704–714. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Fan, W.; Li, Q.; Huo, M.X.; Wang, X.Y.; Lin, S.S. Transport of bacterial cell (E. coli) from different recharge water resources in porous media during simulated artificial groundwater recharge. Front. Environ. Sci. Eng. 2020, 14, 13. [Google Scholar] [CrossRef]
- Bergstrom, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar] [CrossRef]
- Chen, X.; Cai, Q.; Wu, Z. Experimental and theoretical study of coupled influence of flow velocity increment and particle size on particle retention and release in porous media. Water Sci. Eng. 2017, 10, 236–245. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, P.; Tian, Y.; Shen, C.; Li, Z.; Peng, P.; Jin, C. Investigation for Synergies of Ionic Strength and Flow Velocity on Colloidal-Sized Microplastic Transport and Deposition in Porous Media Using the Colloidal-AFM Probe. Langmuir 2020, 36, 6292–6303. [Google Scholar] [CrossRef]
- Hou, J.; Xu, X.; Lan, L.; Miao, L.; Xu, Y.; You, G.; Liu, Z. Transport behavior of micro polyethylene particles in saturated quartz sand: Impacts of input concentration and physicochemical factors. Environ. Pollut. 2020, 263. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Ye, X.; Du, X.; Zhang, X.; Cui, R. Study on the migration characteristics of suspended particles in porous media during different concentration of suspension. Water Resour. Hydropower Eng. 2019, 50, 25–31. [Google Scholar] [CrossRef]
- Shen, C.; Li, B.; Wang, C.; Huang, Y.; Jin, Y. Surface Roughness Effect on Deposition of Nano- and Micro-Sized Colloids in Saturated Columns at Different Solution Ionic Strengths. Vadose Zone J. 2011, 10, 1071–1081. [Google Scholar] [CrossRef]
- Kuznar, Z.A.; Elimelech, M. Direct microscopic observation of particle deposition in porous media: Role of the secondary energy minimum. Colloids Surf. A Physicochem. Eng. Asp. 2007, 294, 156–162. [Google Scholar] [CrossRef]
- Agbangla, G.C.; Bacchin, P.; Climent, E. Collective dynamics of flowing colloids during pore clogging. Soft Matter 2014, 10, 6303–6315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, C.; Ren, C.L.; Emelko, M.B. Concurrent Modeling of Hydrodynamics and Interaction Forces Improves Particle Deposition Predictions. Environ. Sci. Technol. 2016, 50, 4401–4412. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, S.C.; Chen, S.-C.; Segets, D.; Pui, D.Y.H. Predicting collision efficiencies of colloidal nanoparticles in single spherical and fibrous collectors using an individual particle tracking method. Sep. Purif. Technol. 2019, 222, 202–213. [Google Scholar] [CrossRef]
- Abdelfatah, E.; Kang, K.; Pournik, M.; Shiau, B.J.B.; Harwell, J. Mechanistic study of nanoparticles deposition and release in porous media. J. Pet. Sci. Eng. 2017, 157, 816–832. [Google Scholar] [CrossRef]
- Sefrioui, N.; Ahmadi, A.; Omari, A.; Bertin, H. Numerical simulation of retention and release of colloids in porous media at the pore scale. Colloids Surf. A Physicochem. Eng. Asp. 2013, 427, 33–40. [Google Scholar] [CrossRef] [Green Version]





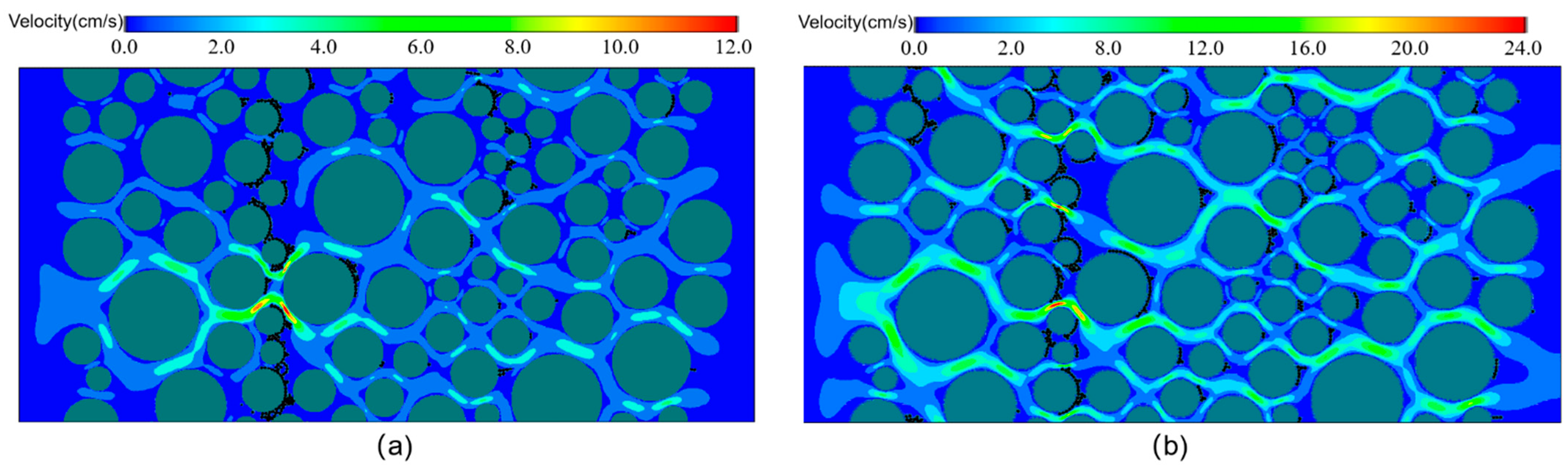
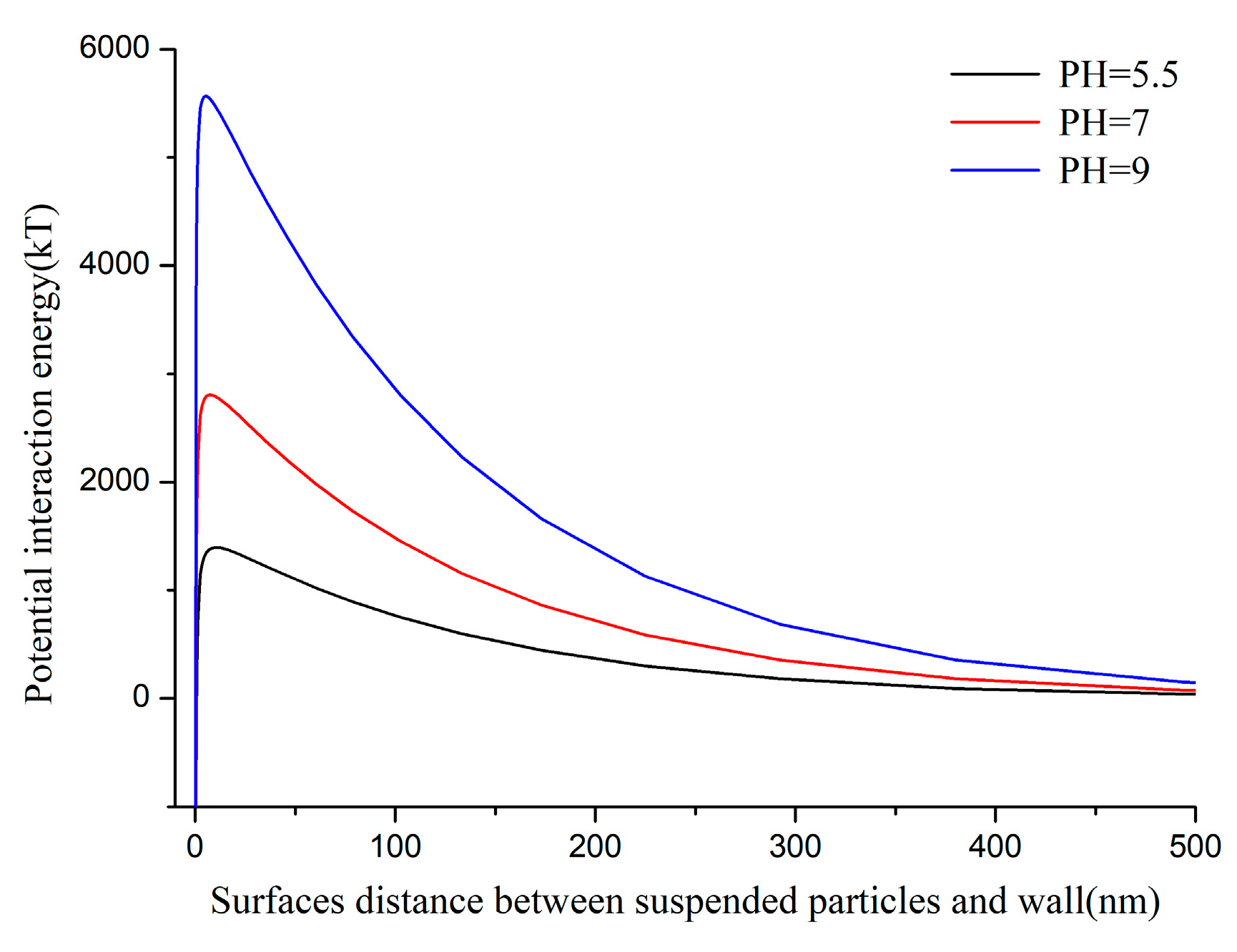
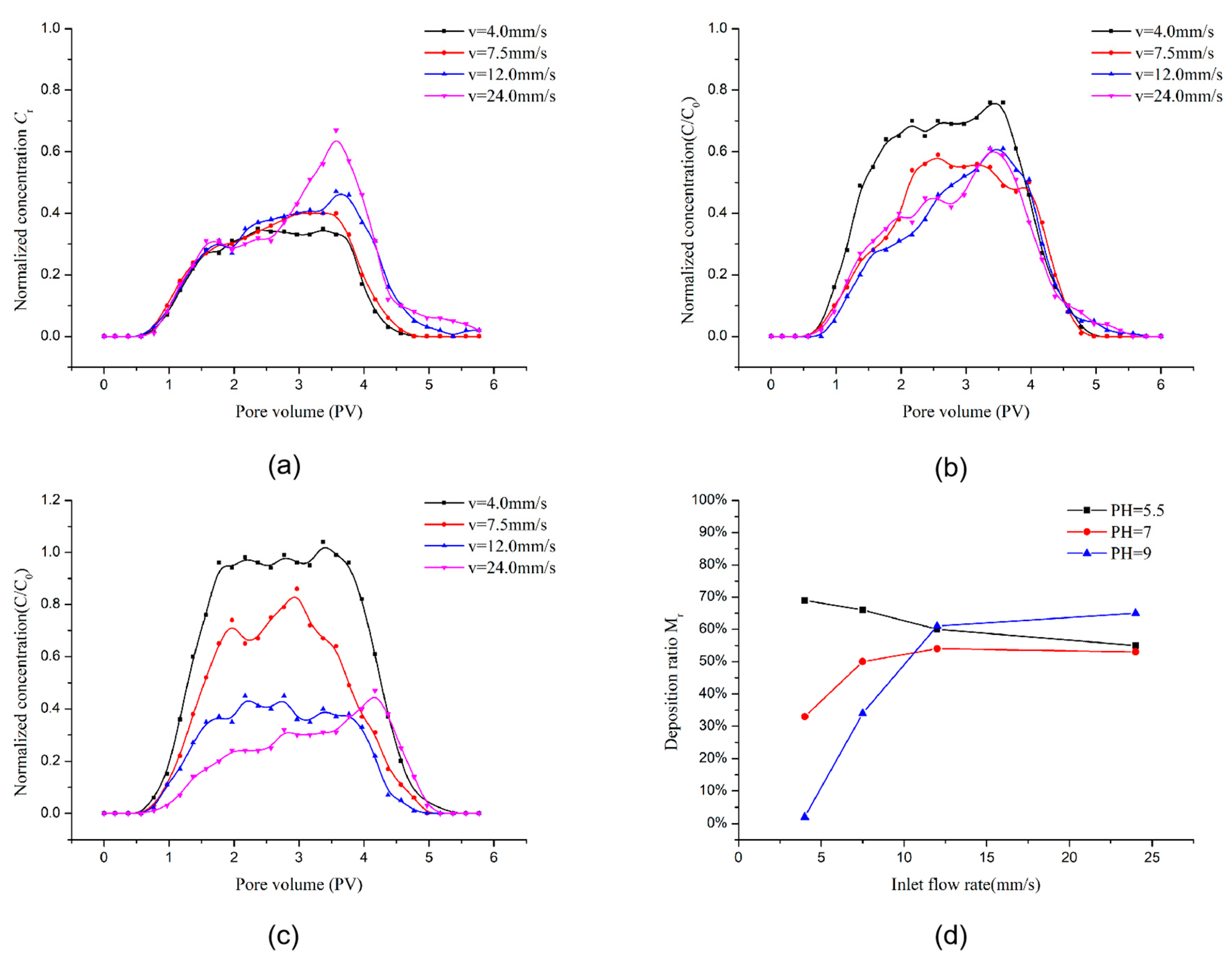
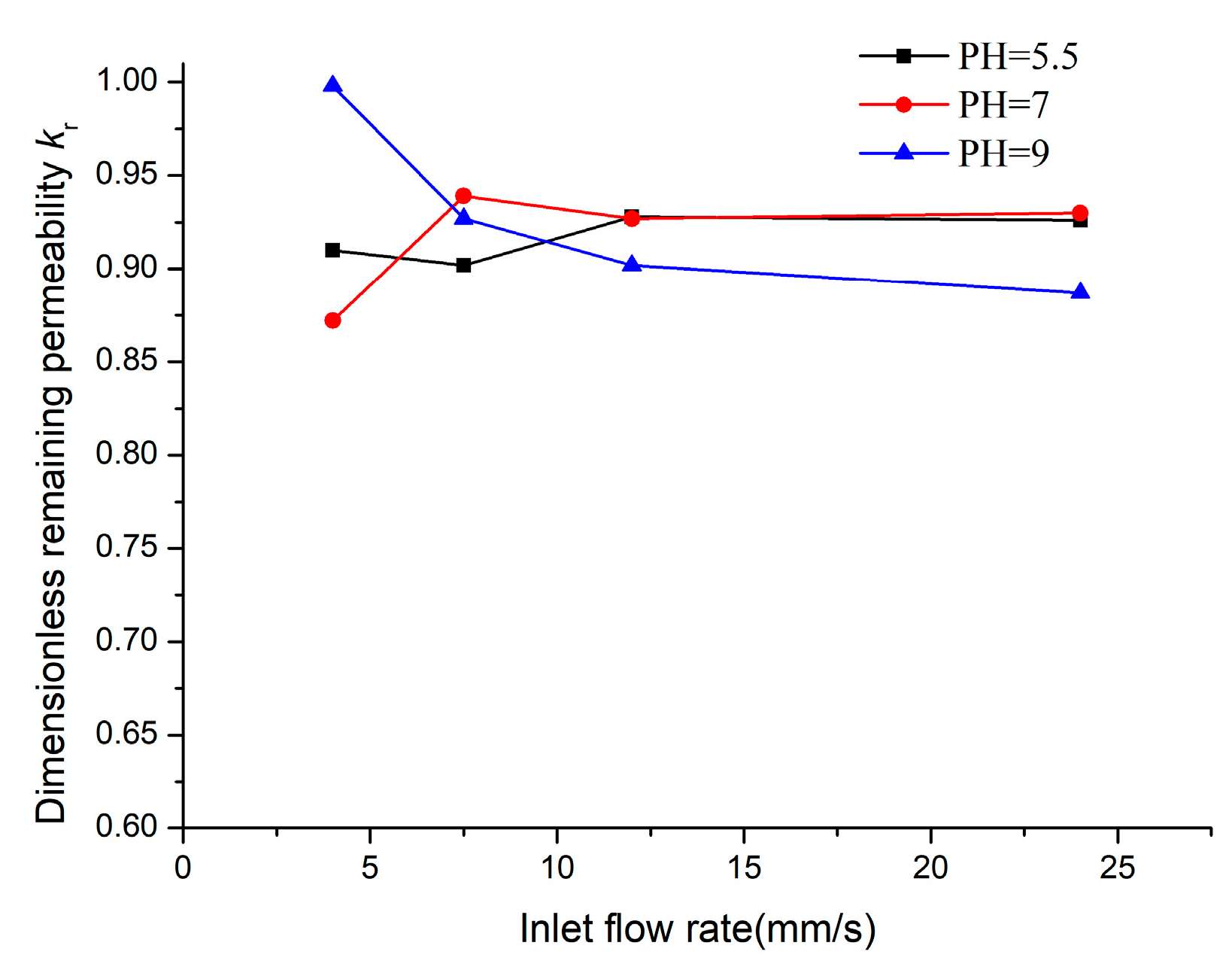


| LBM and Fluid Paraments | DEM and Particle Paraments | ||
|---|---|---|---|
| Lattice spacing, ∆x | 1 × 10−6 m | Normal stiffness kn | 2 × 106 N/m |
| LBM time step, ∆t | 5 × 10−8 s | Tangential stiffness kt | 0.8 × kn |
| Relation time, τBGK | 0.65 | Coefficient of restitution, σ | 0.8 |
| Fluid density (H2O), ρf | 1 × 103 kg/m3 | Friction coefficient, ζ | 0.5 |
| Fluid density in LBM, ρlbm | 1 | Particle density, ρ | 2.6 × 103 kg/m3 |
| Ionic valence, z | 1 | Hamaker constant [54], AHwall-p | 0.9 × 10−20 J |
| Temperature, T | 280 K | Hamaker constant, AHp-p | 2.9 × 10−20 J |
| Fluid viscosity, μf | 1 × 10−3 Pa∙s | DEM Time step, ∆tdem | 5 × 10−8 s/5 × 10−10 s |
| Ionic strength, I | 5 mM | Surface adhesive energy, wilj | 1 mJ/m2 |
| Diameter of particle, dp | 4 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Chen, L.; Gong, Y.; Wang, S. Pore-Scale Simulations of Particles Migration and Deposition in Porous Media Using LBM-DEM Coupling Method. Processes 2021, 9, 465. https://doi.org/10.3390/pr9030465
Zhou Y, Chen L, Gong Y, Wang S. Pore-Scale Simulations of Particles Migration and Deposition in Porous Media Using LBM-DEM Coupling Method. Processes. 2021; 9(3):465. https://doi.org/10.3390/pr9030465
Chicago/Turabian StyleZhou, Yanjie, Liping Chen, Yanfeng Gong, and Shilin Wang. 2021. "Pore-Scale Simulations of Particles Migration and Deposition in Porous Media Using LBM-DEM Coupling Method" Processes 9, no. 3: 465. https://doi.org/10.3390/pr9030465





