Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy
Abstract
:1. Introduction
- By modifying the form of the production functions, NSNVC P systems adopt a new variable consumption strategy, in which the values of the variables involved will have a prescribed consumption rate without all being set to 0 after a production function execution.
- In addition to assigning a threshold to each production function to control the firing of the neurons, polarizations of the neurons, where the production functions are located, are also used to control production function executions in NSNVC P systems. Therefore, both the polarization and the threshold can control the execution of a production function.
- The proposed NSNVC P systems also introduce postponement features and multiple synaptic channels to reduce the complexity and the number of computing units, i.e., neurons, of the systems.
2. NSNVC P Systems
2.1. The Definition of NSNVC P Systems
- represents the set of channel labels.
- represents neurons with the form , for . The specifics of a neuron are given below.
- (a)
- refers to the initial charge of neuron , where +, 0 and − indicate the positive, neutral and negative polarizations, respectively.
- (b)
- is a finite set of channel labels of neuron , indicating its synaptic channels. A synaptic channel of neuron may involve one or more synapses connecting neuron to other neurons and a synapse may be involved in a number of synaptic channels.
- (c)
- is the set of variables in neuron .
- (d)
- is the set of initial values of the variables in neuron .
- (e)
- represents a finite set of production functions associated with neuron . The form of a production function is , where ; is the channel label indicating the synaptic channel of neuron associated with the function; is used to distinguish the production functions contained in neuron ; is the consumption rate of the variables when the production function . executes; refers to the threshold at which the production function can execute; and indicates the postponement future of the production function. If , the form of production function is simplified to .
- with is the set of synapses among the neurons with their channel labels, where means that neuron connects to neuron via synaptic channel . If a synapse connects from neuron to neuron , neuron is called a presynaptic neuron of neuron and neuron is called a postsynaptic neuron of neuron .
- indicates the input neuron.
- indicates the output neuron.
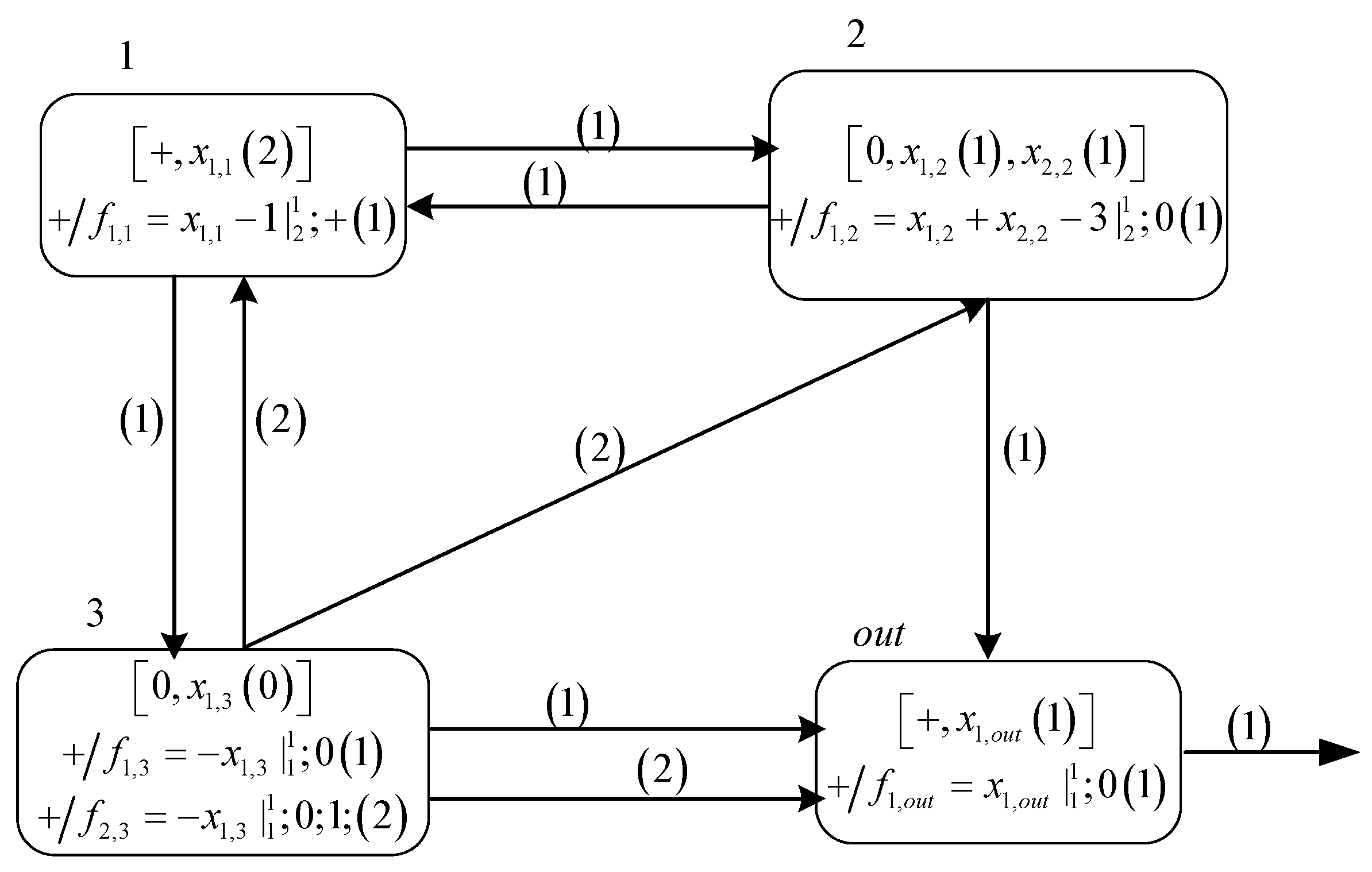
- Comparison stage: Only when neuron contains just charge and the current values of the variables involved in the production function are all equal to the threshold , i.e., , the production function can apply. Otherwise, the production function cannot apply.
- Production stage: If production function can be applied at time , then its production value is calculated based on the current values of the variables .
- Distribution stage: The distribution of the production value and a charge is based on the repartition protocol, which is stated in the following. The production value and the charge are transmitted to all postsynaptic neurons of neuron through synaptic channel at time . If , the transmission happens immediately at time . If , then neuron is dormant, i.e., cannot fire nor receive new production values, at time . At time , neuron becomes active again and the transmission occurs. In particular, the value received by neuron will be immediately passed to its variables, which will increase or decrease the values of the variables.
- Multiple positive, neutral and negative charges will degenerate to a single charge of the same kind.
- A positive charge plus a negative charge will produce a neutral charge.
- A positive or negative charge will not change after a neutral charge is added to it.
2.2. An Illustrative Example
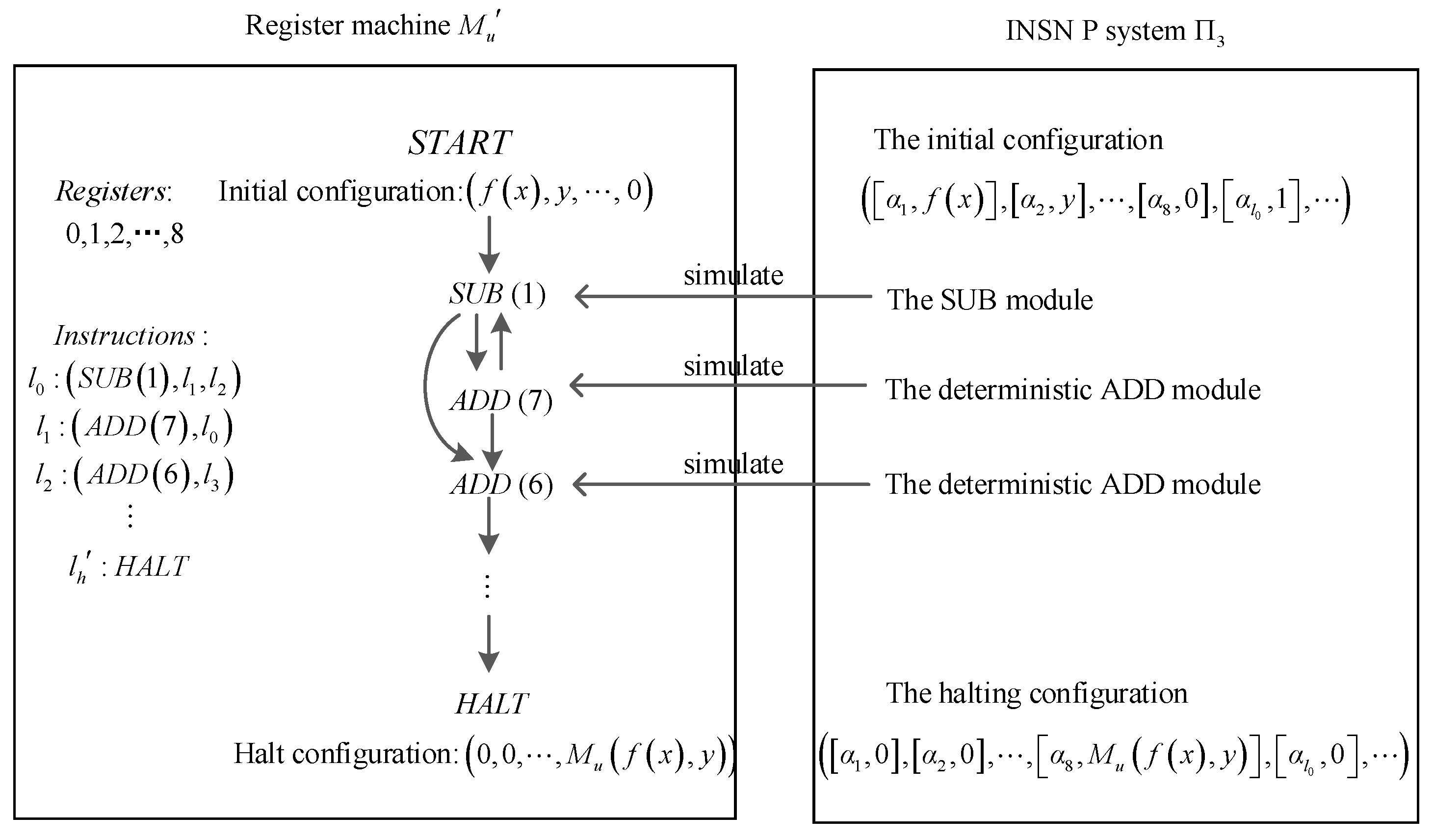
3. Turing Universality of NSNVC P Systems as Number Generating/Accepting Devices
- is the number of registers.
- represents a limited set of instruction labels.
- correspond to the START and HALT instruction labels, respectively.
- is a set of labeled instructions. The instructions in have the following three forms:
- (a)
- ADD instructions , whose function is to add 1 to the value in register , and move non-deterministically to one of the instructions with labels and ;
- (b)
- SUB instructions , whose function is to subtract 1 from the value of register , and then go to the instruction marked by if the number stored in is nonzero, or go to the instruction marked by otherwise;
- (c)
- The HALT instruction , whose function is to terminate the operation of the register machine.
3.1. NSNVC P Systems as Number Generating Devices
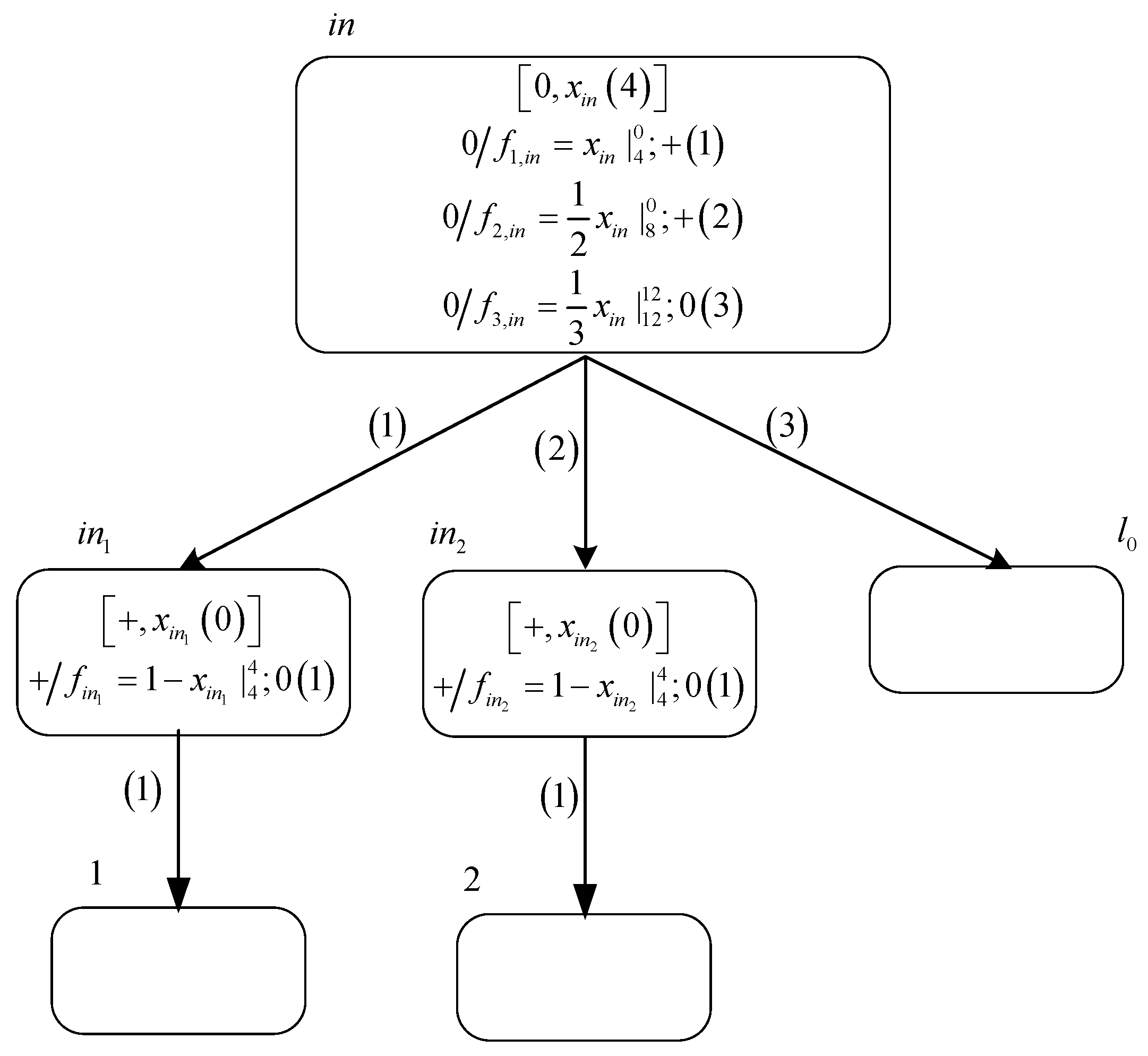
3.1.1. Module ADD—Simulating an ADD Instruction
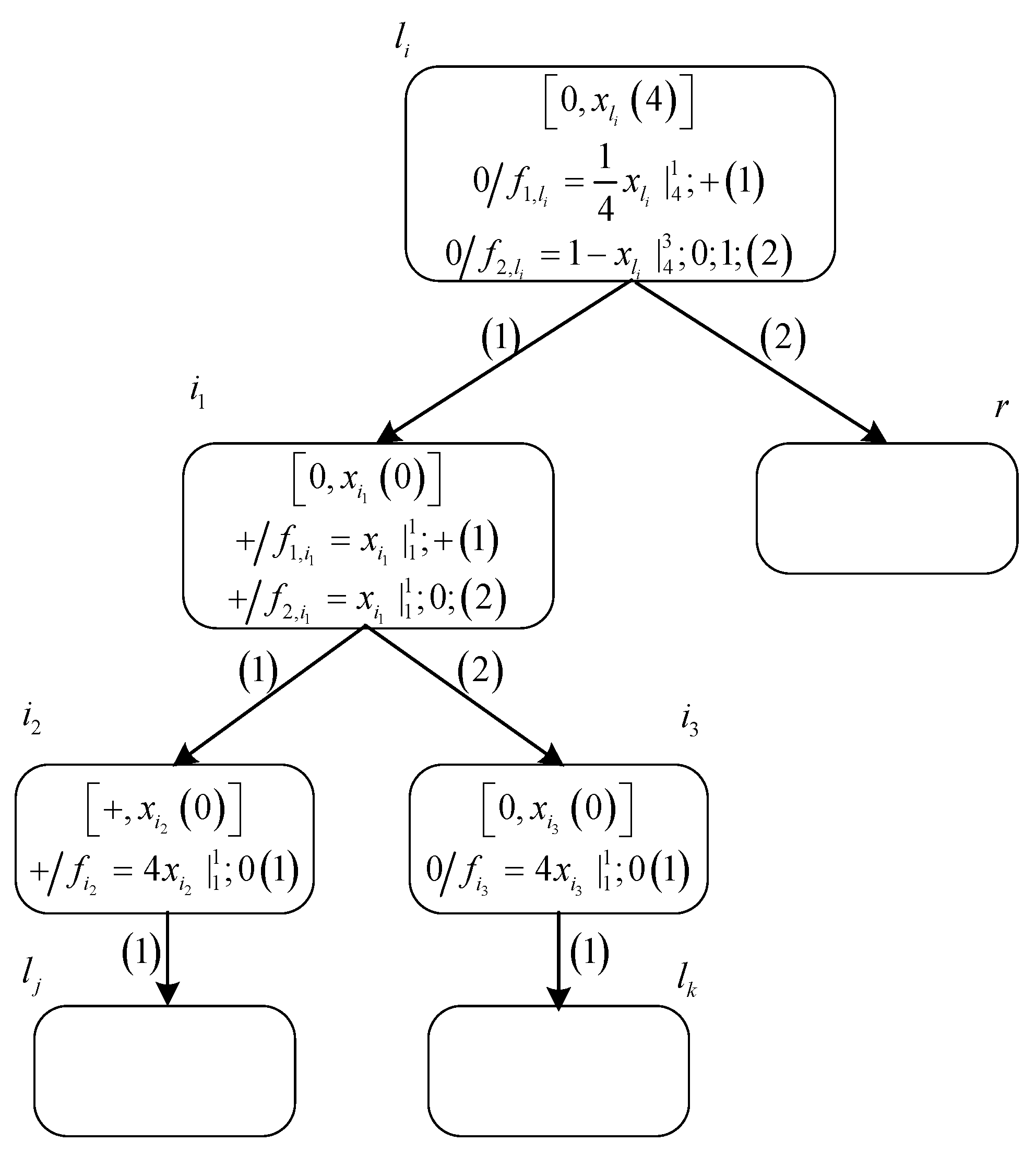
- If production function is selected for execution at time , then neuron sends a positive charge and a value of 1 to neuron . As a result, the polarization of neuron becomes positive and variable gets a value of 1. Therefore, the configuration of system at time becomes . At time , production function satisfies the execution condition, so that neuron transmits a value of 4 to neuron , causing system to start simulating the instruction with label in .
- If production function is selected for execution at time , neuron sends a value of 1 to neuron . Therefore, the configuration of system at time becomes . At time , neuron transmits a value of 4 to neuron , causing system to start simulating the instruction with label in .
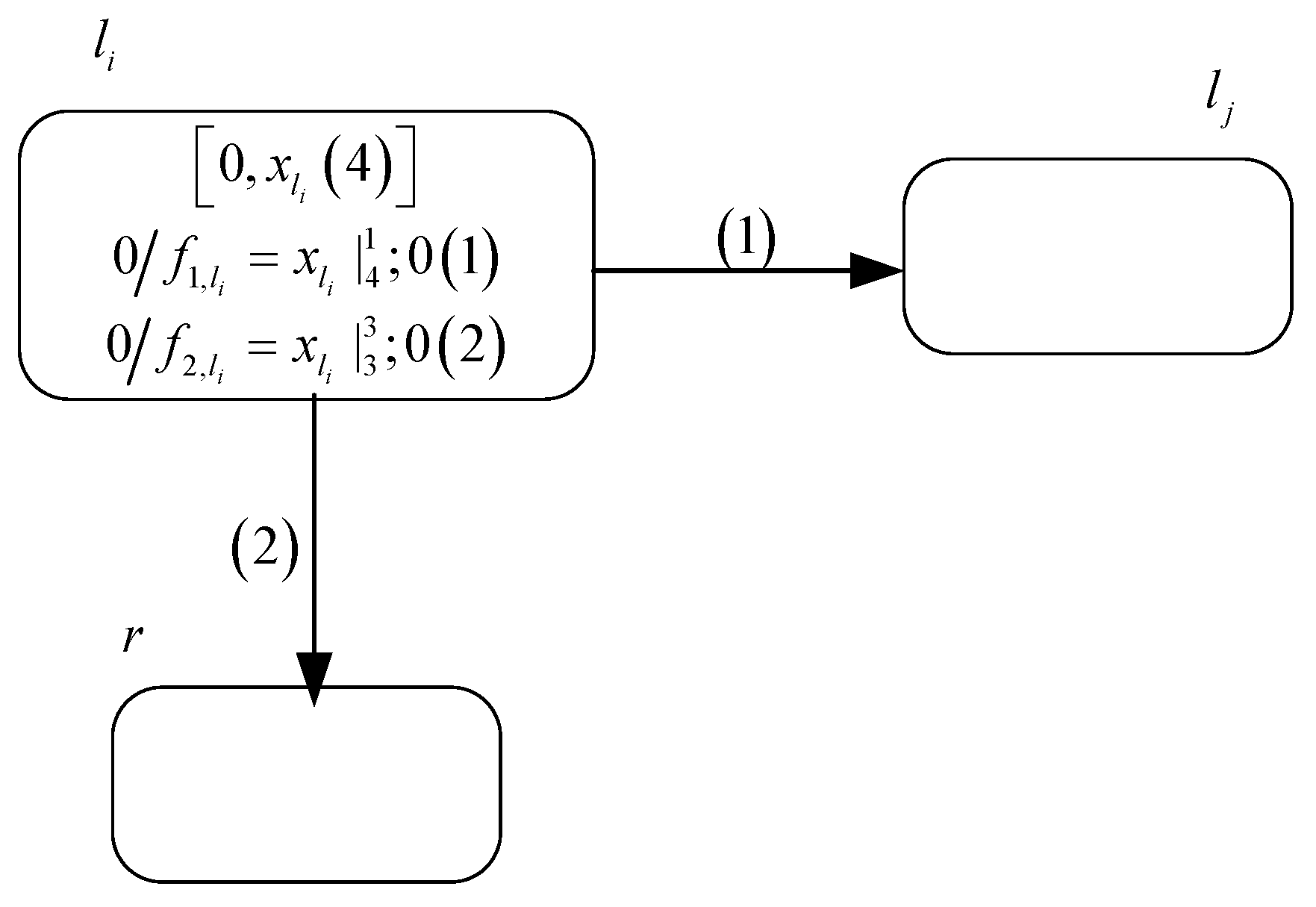
3.1.2. Module SUB—Simulating an SUB Instruction
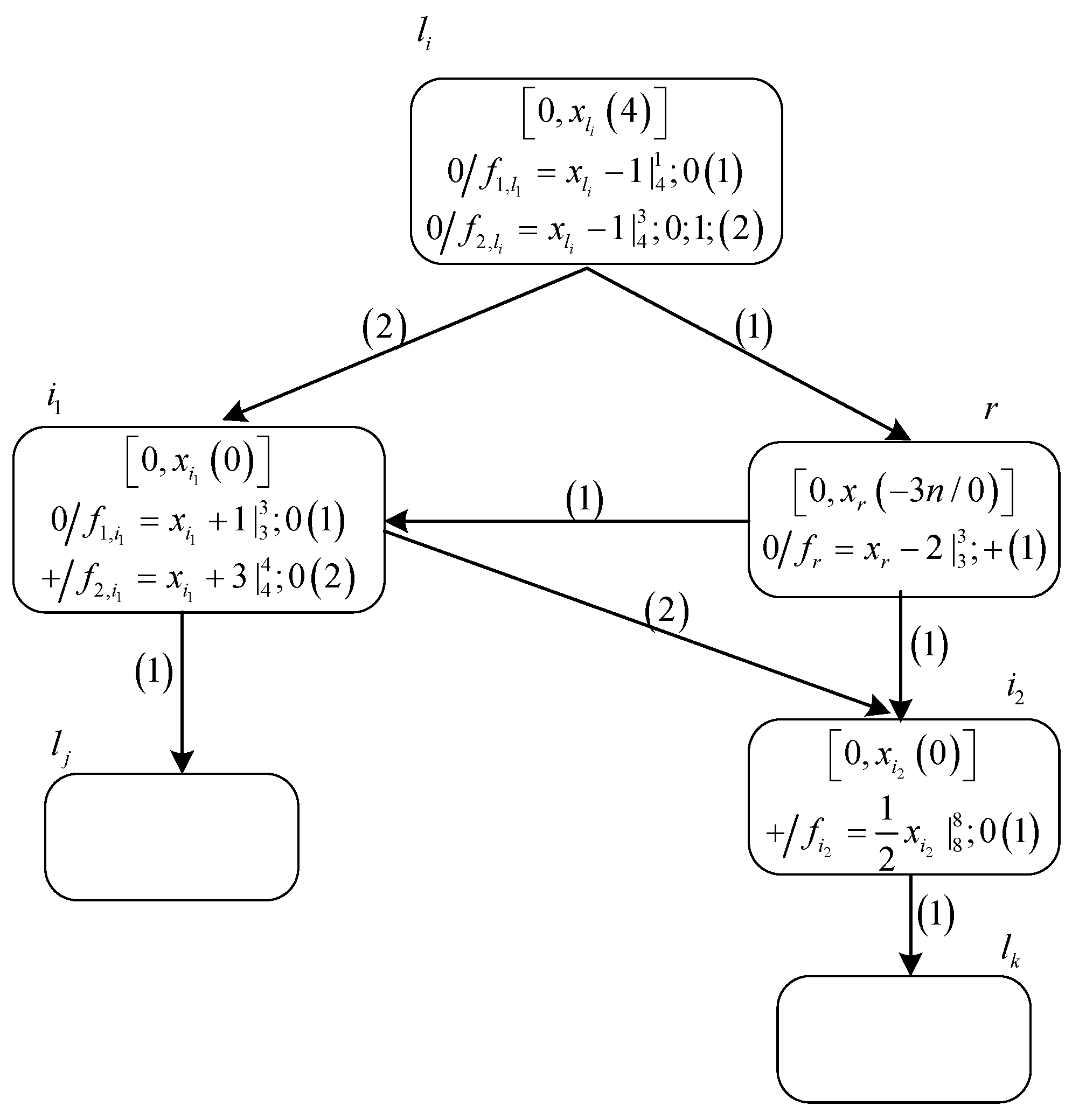
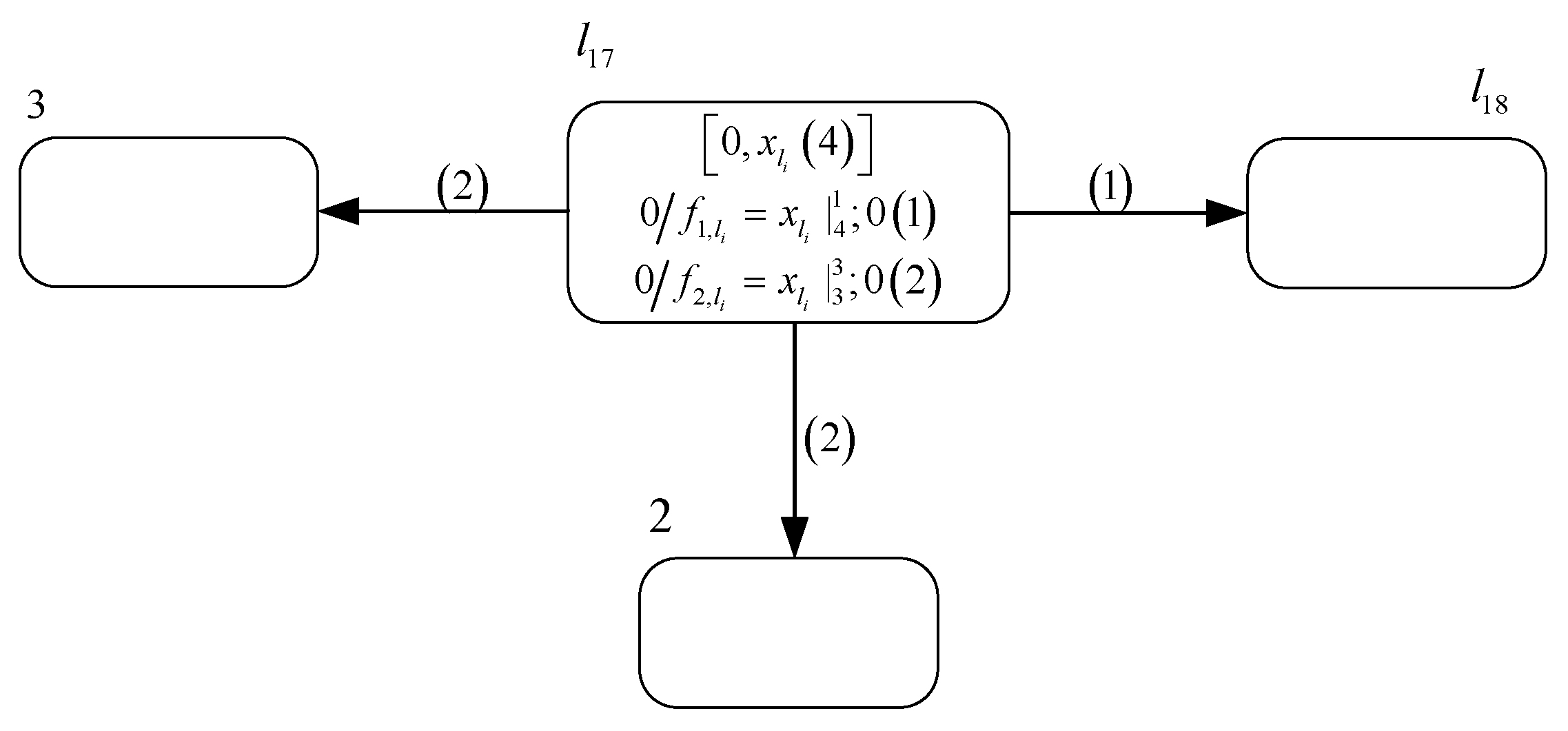
- One situation is that the value of variable , i.e., the number stored in register , is 0 at time . Production function satisfies the threshold condition after variable receives a value of 3. At time , with the execution of this production function, neuron transmits a positive charge and a value of 1 to neurons and , respectively. Since production function has a postponement feature, neuron sends a value of 3 to neuron at time . After production functions and execute, the polarization of neuron becomes positive, and the value of variable becomes 4. Therefore, production function executes at time . Then, neuron transmits a value of 7 to neuron via synaptic channel . Consequently, the polarization of neuron becomes positive and the value of variable accumulates to 8, causing neuron to transmit a value of 4 to neuron . Since neuron receives a value of 4, system starts to simulate instruction .
- The other situation is that the value of variable is − with at time , i.e., the value stored in register is greater than 0. After getting a value of 3 from neuron , the value of variable becomes , which does not satisfy the threshold condition of production function . Thus, neuron will not fire at time . However, due to the execution of production function , variable receives a value of 3 from neuron at time , causing production function to execute at time . Ultimately neuron receives a value of 4 from neuron , leading system to start simulating instruction .
3.1.3. Module FIN—Simulating a HALT Instruction
3.2. NSNVC P Systems as Number Accepting Devices
4. Turing Universality of NSNVC P Systems for Computing Functions
- 25 neurons associated with 25 instruction labels;
- 9 neurons associated with 9 registers;
- auxiliary neurons for 14 SUB modules;
- 3 neurons in the INPUT module;
- 2 neurons in the OUTPUT module.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Gong, F.; Liu, X. Spiking neural P systems with white hole neurons. IEEE Trans. NanoBiosci. 2016, 15, 666–673. [Google Scholar] [CrossRef] [PubMed]
- Ionescu, M.; Păun, G.; Yokomori, T. Spiking neural P systems. Fund. Inform. 2006, 71, 279–308. [Google Scholar]
- Păun, G. Spiking neural P systems with astrocyte-like control. J. UCS 2007, 13, 1707–1721. [Google Scholar]
- Pan, L.; Wang, J.; Hoogeboom, H. Spiking neural P systems with astrocytes. Neural Comput. 2012, 24, 805–825. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Păun, G. Spiking neural P systems with anti-spikes. Int. J. Comput. Commun. Control 2009, 4, 273–282. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Păun, A.; Zhang, Z.; Pan, L. Spiking neural P systems with polarizations. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3349–3360. [Google Scholar]
- Song, T.; Pan, L.; Păun, G. Spiking neural P systems with rules on synapses. Theoret. Comput. Sci. 2014, 529, 82–95. [Google Scholar] [CrossRef]
- Peng, H.; Yang, J.; Wang, J.; Wang, T.; Sun, Z.; Song, X.; Luo, X.; Huang, X. Spiking neural P systems with multiple channels. Neural Netw. 2017, 95, 66–71. [Google Scholar] [CrossRef]
- Song, X.; Wang, J.; Peng, H.; Ning, G.; Sun, Z.; Wang, T.; Yang, F. Spiking neural P systems with multiple channels and anti-spikes. Biosystems 2018, 169, 13–19. [Google Scholar] [CrossRef]
- Wang, J.; Hoogeboom, H.; Pan, L.; Păun, G.; Pérez-Jiménez, M. Spiking neural P systems with weights. Neural Comput. 2010, 22, 2615–2646. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Zhang, X.; Song, T.; Pan, L. Spiking neural P systems with thresholds. Neural Comput. 2014, 26, 1340–1361. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Pérez-Jiménez, M.J.; Riscos-Núñez, A. Dynamic threshold neural P systems. Knowl. Based Syst. 2019, 163, 875–884. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J. Coupled Neural P Systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1672–1682. [Google Scholar] [CrossRef]
- Cavaliere, M.; Ibarra, O.H.; Păun, G.; Egecioglu, O.; Ionescu, M.; Woodworth, S. Asynchronous spiking neural P systems. Theor. Comput. Sci. 2009, 410, 2352–2364. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Pan, L.; Păun, G. Asynchronous spiking neural P systems with local synchronization. Inf. Sci. 2013, 219, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Peng, H.; Wang, J.; Ning, G.; Sun, Z. Small universal asynchronous spiking neural P systems with multiple channels. Neurocomputing 2020, 378, 1–8. [Google Scholar] [CrossRef]
- Cabarle, F.G.C.; Adorna, H.N.; Jiang, M.; Zeng, X. Spiking neural P systems with scheduled synapses. IEEE Trans. Nanobiosci. 2017, 16, 792–801. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Păun, G.; Zhang, G.; Neri, F. Spiking neural P systems with communication on request. Int. J. Neural Syst. 2017, 27, 1750042. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Liu, X. Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules. Processes 2020, 8, 1281. [Google Scholar] [CrossRef]
- Kong, Y.; Zheng, Z.; Liu, Y. On string languages generated by spiking neural P systems with astrocytes. Fundam. Inform. 2015, 136, 231–240. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, X.; Pan, L. On string languages generated by spiking neural P systems with exhaustive use of rules. Nat. Comput. 2008, 7, 535–549. [Google Scholar] [CrossRef]
- Cabarle, F.; Adorna, H.; Pérez-Jiménez, M.; Song, T. Spiking neuron P systems with structural plasticity. Neural Comput. Appl. 2015, 26, 1905–1917. [Google Scholar] [CrossRef]
- Peng, H.; Chen, R.; Wang, J.; Song, X.; Wang, T.; Yang, F.; Sun, Z. Competitive spiking neural P systems with rules on synapses. IEEE Trans. NanoBiosci. 2017, 16, 888–895. [Google Scholar] [CrossRef]
- Ren, Q.; Liu, X.; Sun, M. Turing Universality of Weighted Spiking Neural P Systems with Anti-spikes. Comput. Intell. Neurosci. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Păun, G.; Păun, R. Membrane computing and economics: Numerical P systems. Fundam. Inform. 2006, 73, 213–227. [Google Scholar]
- Zhang, Z.; Su, Y.; Pan, L. The computational power of enzymatic numerical P systems working in the sequential mode. Theor. Comput. Sci. 2018, 724, 3–12. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, Z.; Wu, T.; Xu, J. Numerical P systems with production thresholds. Theor. Comput. Sci. 2017, 673, 30–41. [Google Scholar] [CrossRef]
- Liu, L.; Yi, W.; Yang, Q.; Peng, H.; Wang, J. Numerical P systems with Boolean condition. Theor. Comput. Sci. 2019, 785, 140–149. [Google Scholar] [CrossRef]
- Díaz-Pernil, D.; Peña-Cantillana, F.; Gutiérrez-Naranjo, M.A. A parallel algorithm for skeletonizing images by using spiking neural P systems. Neurocomputing 2013, 115, 81–91. [Google Scholar] [CrossRef]
- Xiang, M.; Dan, S.; Ashfaq, K. Image Segmentation and Classification Based on a 2D Distributed Hidden Markov Model. Proc. Int. Soc. Opt. Eng. 2008, 6822, 51. [Google Scholar]
- Zhang, G.; Gheorghe, M.; Li, Y. A membrane algorithm with quantum-inspired subalgorithms and its application to image processing. Natural Comput. 2012, 11, 701–717. [Google Scholar] [CrossRef]
- Buiu, C.; Vasile, C.; Arsene, O. Development of membrane controllers for mobile robots. Inf. Sci. 2012, 187, 33–51. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G. Design and implementation of membrane controllers for trajectory tracking of nonholonomic wheeled mobile robots. Integr. Comput. Aided Eng. 2016, 23, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Xiong, G.; Shi, D.; Zhu, L.; Duan, X. A new approach to fault diagnosis of power systems using fuzzy reasoning spiking neural P systems. Math. Probl. Eng. 2013, 2013, 211–244. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Zhang, G.; Zhao, J.; He, Z.; Wang, J.; Pérez-Jiménez, M.J. Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems. IEEE Trans. Power Syst. 2014, 30, 1182–1194. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Ming, J.; Shi, P.; Pérez-Jiménez, M.J.; Yu, W.; Tao, C. Fault diagnosis of power systems using intuitionistic fuzzy spiking neural P systems. IEEE Trans. Smart Grid. 2018, 9, 4777–4784. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Shi, P.; Pérez-Jiménez, M.J.; Riscos-Núñez, A. An extended membrane system with active membrane to solve automatic fuzzy clustering problems. Int. J. Neural Syst. 2015, 26, 1650004. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Shi, P.; Wang, J.; Riscos-Núñez, A.; Pérez-Jiménez, M.J. Multiobjective fuzzy clustering approach based on tissue-like membrane systems. Knowl. Based Syst. 2017, 125, 74–82. [Google Scholar] [CrossRef]
- Han, L.; Xiang, L.; Liu, X.; Luan, J. The K-medoids Algorithm with Initial Centers Optimized Based on a P System. J. Inf. Comput. Sci. 2014, 11, 1765–1774. [Google Scholar] [CrossRef]
- Wu, T.; Pan, L.; Yu, Q.; Tan, K.C. Numerical Spiking Neural P Systems. IEEE Transact. Neural Netw. Learn. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Peng, H.; Li, B.; Wang, J. Spiking neural P systems with inhibitory rules. Knowl. Based Syst. 2020, 188, 105064. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, T.; Xu, F. Simplified and yet Turing universal spiking neural P systems with polarizations optimized by anti-spikes. Neurocomputing 2020, 414, 255–266. [Google Scholar] [CrossRef]
- Jiang, S.; Fan, J.; Liu, Y.; Wang, Y.; Xu, F. Spiking Neural P Systems with Polarizations and Rules on Synapses. Complexity 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Korec, I. Small universal register machines. Theor. Comput. Sci. 1996, 168, 267–301. [Google Scholar] [CrossRef] [Green Version]
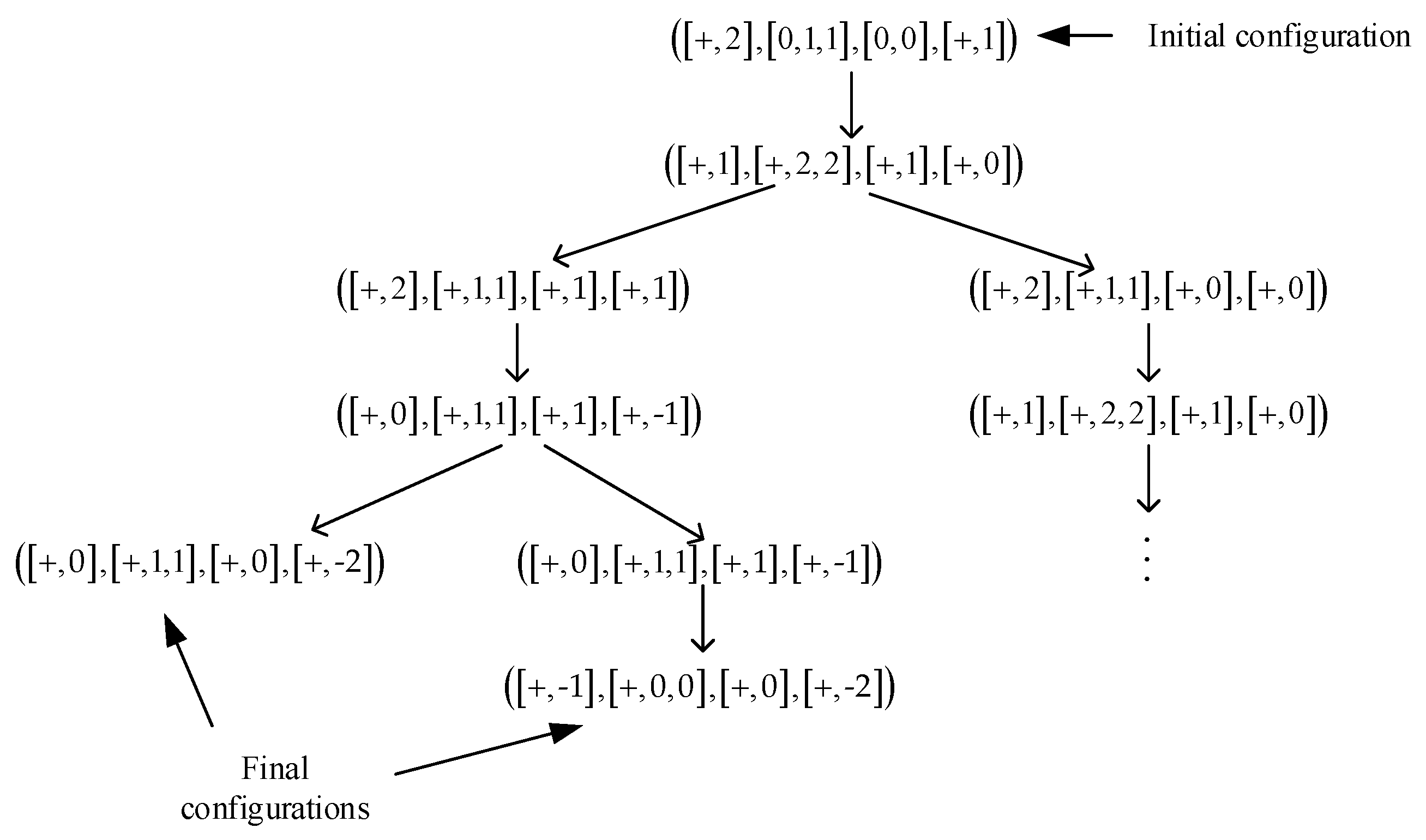

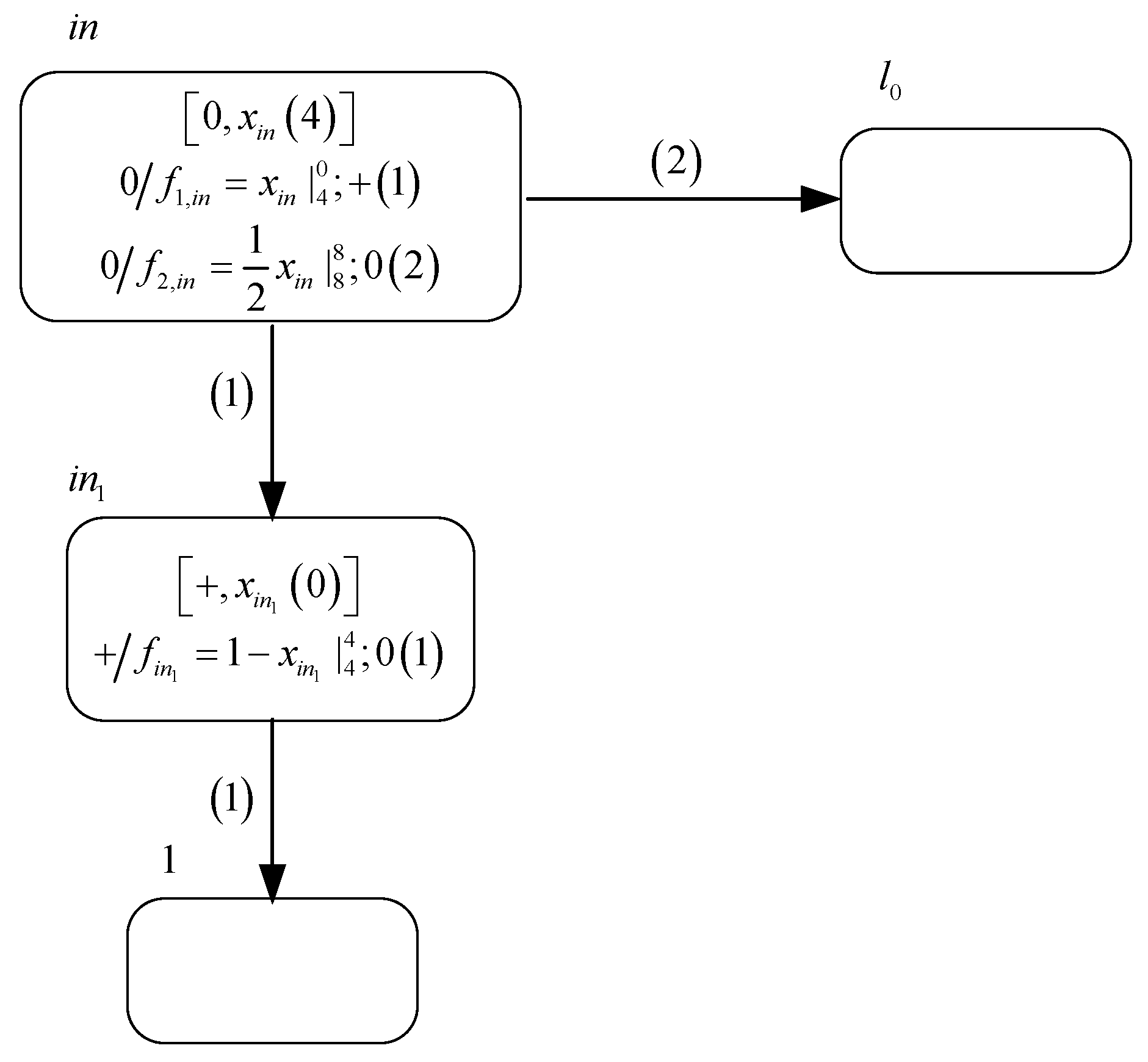



| System | Full Name |
|---|---|
| SNP systems [3] | Spiking neural P systems |
| PSN P systems [7] | Spiking neural P systems with polarizations |
| SNP-MC systems [17] | Small universal asynchronous spiking neural P systems with multiple channels |
| NP systems [37] | Numerical P systems |
| NSN P systems [41] | Numerical spiking neural P systems |
| SNP-IR systems [42] | Spiking neural P systems with inhibitory rules |
| PASN P systems [43] | Simplified and yet Turing universal spiking neural P systems with polarizations optimized by anti-spikes |
| PSNRS P systems [44] | Spiking neural P systems with polarizations and rules on synapses |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Liu, X.; Sun, M.; Ren, Q. Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy. Processes 2021, 9, 549. https://doi.org/10.3390/pr9030549
Yin X, Liu X, Sun M, Ren Q. Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy. Processes. 2021; 9(3):549. https://doi.org/10.3390/pr9030549
Chicago/Turabian StyleYin, Xiu, Xiyu Liu, Minghe Sun, and Qianqian Ren. 2021. "Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy" Processes 9, no. 3: 549. https://doi.org/10.3390/pr9030549
APA StyleYin, X., Liu, X., Sun, M., & Ren, Q. (2021). Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy. Processes, 9(3), 549. https://doi.org/10.3390/pr9030549








