Abstract
In this work, a new algorithm is proposed for a unique representation for simple and multiple joint planar kinematic chains (KCs) having any degree of freedom (DOF). This unique representation of KCs enhances the isomorphism detection during the structural synthesis process of KCs. First, a new concept of joint degree is generated for all joints of a given KC based on joint configuration. Then, a unified loop array (ULA) is obtained for each independent loop. Finally, a unified chain matrix (UCM) is established as a unique representation for a KC. Three examples are presented to illustrate the proposed algorithm procedures and to test its validity. The algorithm is applied to get a UCM for planar KCs having 7–10 links. As a result, a complete atlas database is introduced for 7–10-link non-isomorphic KCs with simple or/and multiple joints and their corresponding unified chain matrix.
1. Introduction
The structural synthesis of kinematic chains (KCs) usually starts with an enumeration of all candidates of KCs. During that, KCs should be represented in such a way to facilitate the synthesis process. The structural representation of KCs may be classified into graphical or numerical methods. Then, isomorphism detection is to be performed to exclude isomorphic KCs. Consequently, many techniques are available for isomorphism detection in KCs with either simple or multiple joints.
The matrix representation for the structural synthesis of both single and two degrees of freedom of simple-jointed chains was used by Mruthyunjaya and Balasubramanian [1,2,3]. They also used the characteristic polynomial of the degree matrix of the corresponding graph to detect the isomorphism of simple-jointed KCs up to 10 links with one, two and three degrees of freedom (DOF). Jin-Kui and Wei-Qing [4] proposed the concept of a link’s adjacent-chain table to detect the topological relationships between links and isomorphism in KCs. Summation polynomials for isomorphism detection in single freedom and multi-DOF planar KCs were introduced by Shende and Rao [5]. A computer-aided method, based on the concept of multiplicity distance, was presented by Yadav et al. [6] for detecting isomorphism among planar binary KCs. Rao et al. [7,8] used fuzzy logic and chain loop string to investigate isomorphism among planar KCs with simple joints. The concept of eigenvalues and eigenvectors of an adjacent matrix was developed for the detection of graph isomorphism [9,10,11].
A stratified representation to enumerate planar simple-jointed KCs that does not require isomorphism testing on the final set of KCs was proposed by Butcher and Hartman [12]. Pucheta and Cardona [13] offered a systematic technique to find topological alternatives for certain kinematic problems based on graph theory, the initial graph concept and a combinatorial analysis in a non-isomorphic way. New two basic loop operations for the topological structure analysis of KCs and isomorphism identification were proposed by Huafeng Ding and Huang [14,15,16]. New concepts of the perimeter loop, maximum perimeter degree sequence, perimeter topological graph and canonical perimeter graph were presented for isomorphism identification of KCs. Hasan and Khan [17] used a weighted physical connectivity matrix (WPCM) and characteristic polynomial to detect distinct mechanisms in all types of simple-jointed one DOF planar KCs up to ten links. Dargar et al. [18,19] proposed the first adjacency chain link string [FACLS] and the second adjacency chain link string [SACLS] as a composite identification number of KCs of single or multi-DOF with simple or multiple joints. Then extended adjacency link value (EALV) and link total loop size (TLS) were developed to detect distinct mechanisms of simple-jointed KCs. Galán-Marín et al. [20] designed a multivalued neural network to enable a simplified formulation of the graph isomorphism problem.
A technique of adding sub-chains to get the identification code and formation code of a topological structure was presented by Deng et al. [21]. Then, isomorphic structures could be eliminated according to the certain DOF and link-joining properties of planar closed-chain mechanisms. Ding et al. [22,23,24,25] established a whole atlas database of two DOF 11-link KCs and one DOF planar KCs with 6, 8, 10, 12 and 14 links. The concept of bicolor graphs in graph theory was adopted to represent the topological structures of multiple-joint KCs, and a characteristic number of strings was proposed to detect isomorphism. The whole families of multiple-joint KCs with up to 16 links were synthesized. A new method using incident matrices was developed by Yang et al. [26] to identify the isomorphism of topological graphs. Rizvi et al. [27,28,29] used a unique chain code based on the degree of links as an identifier of a KC to detect isomorphism in all types of KCs of single or multi-DOF with simple joints. Then, a fuzzy similarity index was proposed to identify isomorphism in planer KCs. Moreover, some tests were presented for KCs of one DOF, with 8, 9 and 10 links having two DOF. The link identification number (LIN) and chain identification number (CIN) were obtained from adjacency matrices of KCs for isomorphism detection. Ping Yang [30,31,32] proposed a Dividing and Matching Algorithm (DMA) and a hybrid immune genetic algorithm model for the isomorphism identification in KCs.
A loop analysis was investigated by Pozhbelko [33] to obtain a unified structure theory for open, closed and mixed KCs with simple and multiple joints. Ding et al. [34,35] used contracted graphs to synthesize the whole set of planar non-fractionated KCs with up to six independent loops. Characteristic codes of topological graphs of KCs were presented to increase the efficiency of isomorphism identification. By transforming multiple links into multiple joints, planar non-fractionated KCs with two multiple joints were generated from KCs with one multiple joint. Therefore, a family of planar KCs with two multiple joints was established. Venkata et al. [36] suggested “net distance” to test isomorphism in planar KCs and geared KCs. This technique was applied to 8, 10 and 12-link KCs with one DOF and 15-link KCs with four DOF. Eleashy [37] proposed the Joint Sorting Code (JSC) and Kinematic Chain Structural Matrix (KCSM) to solve the problem of isomorphism in planar eight-bar KCs with up to three prismatic pairs. Yang et al. [38] presented a vertex degree and edge weight as a reliable method for the synthesis and isomorphism detection of KCs with prismatic pairs. Therefore, revolute-prismatic (RP) chains with 6–14 links were established.
The concepts of link connectivity number and entropy neglecting tolerance and clearance were proposed by Rai and Punjabi [39,40] for detecting isomorphism among simple-joint KCs of single and multi-DOF. Then, a maximum binary code was presented based on links labeling to detect isomorphism in simple and multiple-joint KCs and epicyclic gear trains with 4–6 links. A molecular topological index was proposed by Deng et al. [41] to identify isomers in KCs as used in organic chemistry. Therefore, the adjacency identification index, which fits for the isomorphism detection of KCs, was detected. This method was applied to all 230 ten-bar one DOF KCs. Li et al. [42] used a combinatorial graph to represent geared linkage kinematic chains (GLKCs). Then, the powers of a combinatorial matrix were used to detect isomorphism in GLKCs. Chu. et al. [43,44] introduced a new representation for mechanisms using a double color graph (DCG) that was applied for the structural synthesis of planar 10-link three DOF simple and multiple-joint KCs.
From the above literature, isomorphism detection is still a challenge in the mechanism synthesis process. Graphical and numerical techniques were investigated. The best of these techniques include complicated mathematical concepts based on link-adjacency matrices or their modifications. In this work, a simple method is presented for the unique representation of KCs that facilitate isomorphism detection among KCs. This paper will be discussed in four main parts: (1) basic definitions, (2) algorithm procedures, (3) examples to validate the algorithm and (4) results and conclusion.
2. Basic Definitions
Definition 1.
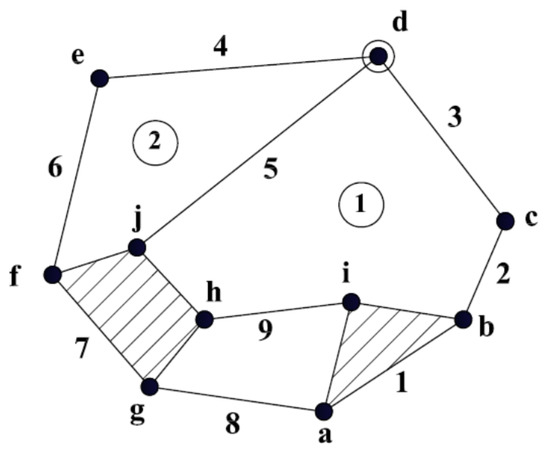
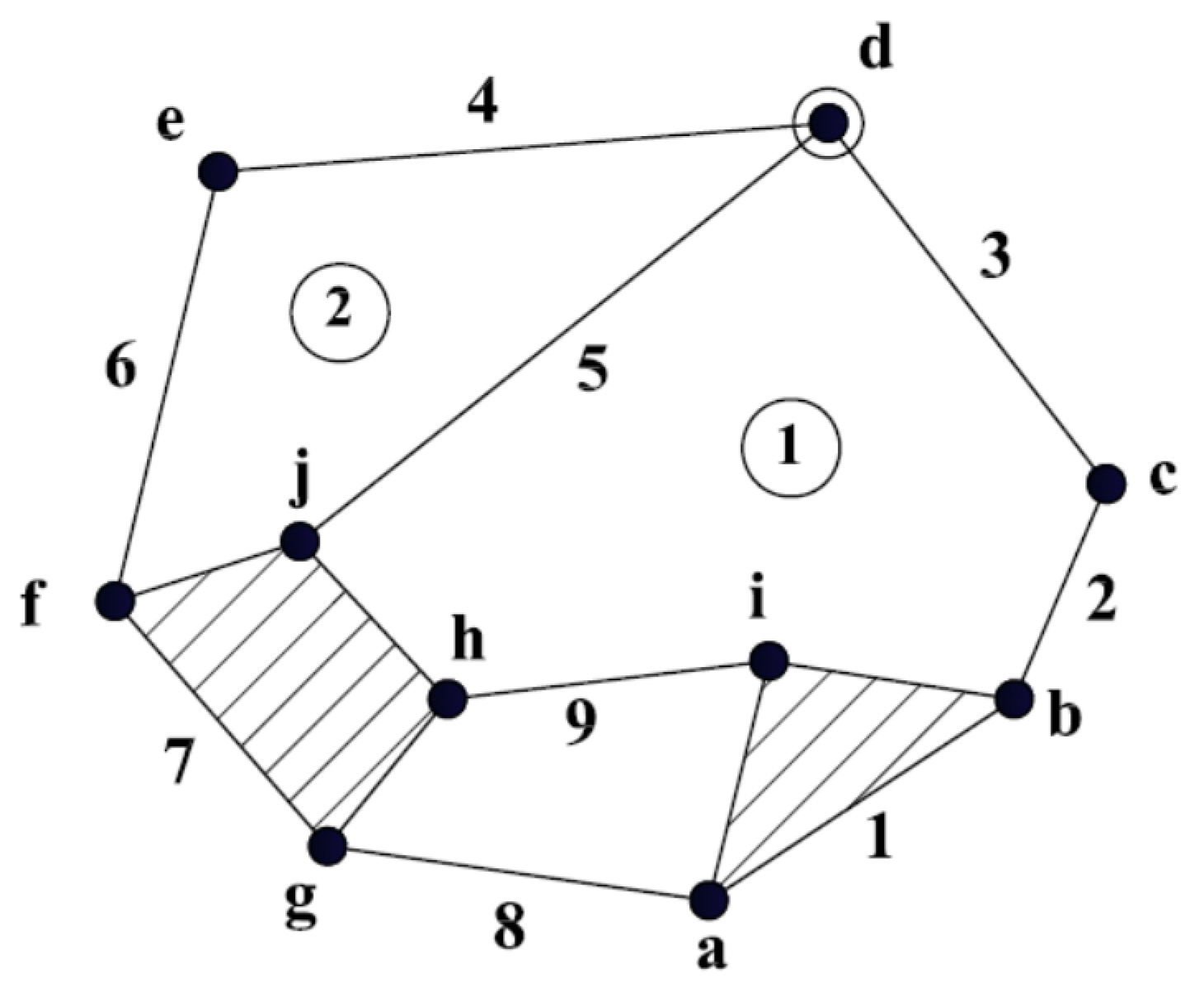
Topological structure of KCs: a schematic representation of KCs that include (1) the number and type of joints. (2) Number and type of links (such as binary, ternary, quaternary or quinary links). (3) Connection relations among these joints and links, as shown in Figure 1. These KCs may have open or closed loops. Topological graphs of KCs can be categorized into planar and nonplanar graphs. A planar graph can be drawn in the plane without edge crossing, whereas a nonplanar graph contains at least one edge crossing [45]. In this work, the KCs of planar graphs with closed loops were considered, as shown in Figure 1.

Figure 1.
Topological structure of a 9-link planar kinematic chain with simple and multiple joints.
Definition 2.
Simple and Multiple joints: a simple joint is formed when two links are connected together. As shown in Figure 1, joints a–c,e–j) are simple joints. Multiple joints are formed when more than two links are connected together. Joint (d) in Figure 1 is a multiple joint that connects three binary links—namely, links 3–5.
Definition 3.
Independent loop: any closed path through a KC in which no link or joint is encountered more than once. Moreover, an independent loop should not contain internal loops or link crossing. For the KC shown in Figure 1, loop (1) is formed by the connection of links (1, 2, 3, 5, 7 and 9). In other words, loop (1) is formed by joints (b–d,h–j) So that, loop of a KC represents the connectivity among its links.
Definition 4.
Loop Joint size: number of simple or multiple joints forming a loop in a KC. For the KC shown in Figure 1, loop (1) has six joints.
3. Proposed Algorithm Steps
The proposed method for the generation of a unique representation of a KC depends on (1) the number of independent loops that form a KC and (2) the joint configuration. The algorithm can be summarized in the following steps:
Step 1 Modified Link Assortment Array (LAA):
Number and type of links forming a KC with specified DOF are defined as a link assortment [46]. The modified link assortment array (LAA) of a N-link KC with any -DOF KC is given by:
where N, NB, NT, NQ and NP are the number of total, binary, ternary, quaternary and quinary links in the KC, respectively.
LAA = [N, NB, NT, NQ, NP]
Step 2 Joint Assortment Array (JAA)
Type and number of joints connecting different links in a KC are defined as a joint assortment array [47]. The joint assortment array (JAA) of an N-link KC with any DOF is given by:
where Jt, S and M are the total number of joints, number of simple joints and number of multiple joints in the KC, respectively.
JAA = [Jt, S, M]
Definition 5.
Degree of Freedom (F) of a planar KC: describes the relation between F (DOF), N (number of links) and J (number of simple joints). Therefore, referring to the Grübler equation, the DOF is given by [48].
F = 3(N − 1) − 2
Step 3 Independent loop
Definition 6.
Independent loop: the inner loop of a KC inside which there is no other closed loop. Planar KCs satisfy the equation
2 L = N − F − 1
Step 4 Joint Degree (JD)
Joints between links in a KC may be simple or multiple. The joint symbol can be detected according to type of connected link at this joint.
Definition 7.
Joint Symbol: an abbreviation code derived from the first letters of links types that are connected at the considered joint.
Definition 8.

Joint Degree (JD): a numerical value for each joint in a KC that can be generated based on joint type and its connectivity. Table 1 indicates joint degrees for simple and multiple joints with the most commonly used types of connection. Hence, all joints in the considered KC can be defined by their degrees. As illustrated in Table 1, joints are classified into simple and multiple joints formed by three links and multiple ones formed by four links.

Table 1.
Joint degree (JD) for simple and multiple joints according to their connectivity.
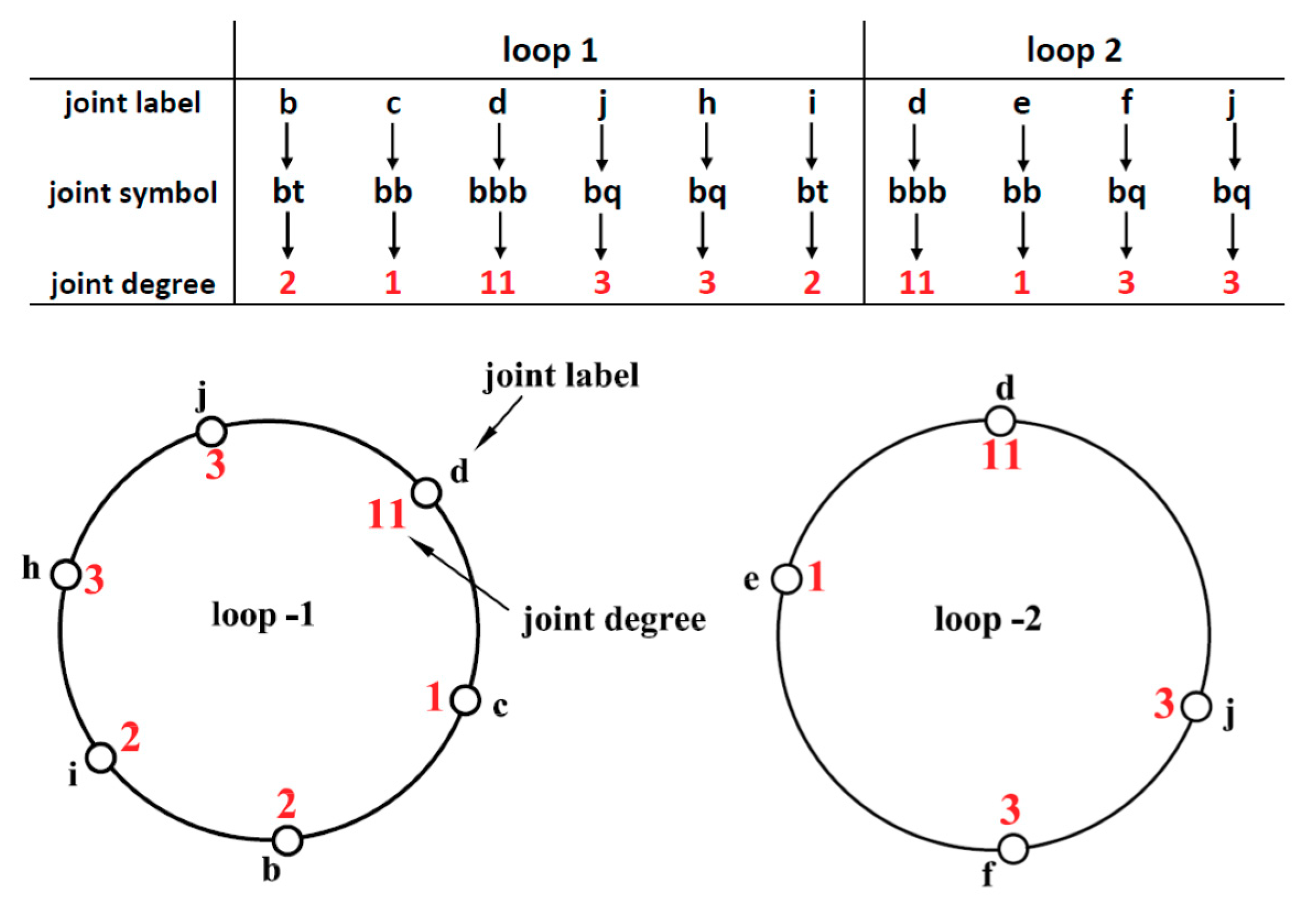
For the KC shown in Figure 1, the loops (1 and 2) can be analyzed to generate their joint symbols and joint degrees. This will be based on the values of joint degrees (JD) extracted from Table 1, as shown in Figure 2.
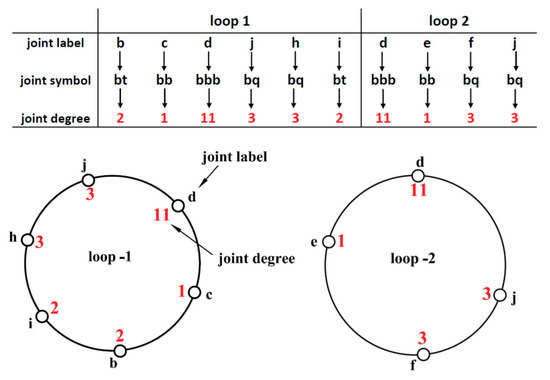
Figure 2.
Generation of joint degrees for loops (1 and 2) for the 9-link kinematic chain shown in Figure 1.
Step 5 Joint Degree Array (JDA):
Definition 9.
Joint Degree Array (JDA): is an initial array for a certain loop in a KC. The elements of JDA are represented by joint degrees of joints forming the considered loop. Therefore, Joint Degree Array (JDA) for a loop-i that has joints (a, b, c, d, …) is given by:
JDA (i) = [JD a, JD b, JD c, ……]
Joint degrees sequence in JDA is usually in a clockwise direction starting from any joint degree. Therefore, the same loop may have more than one JDA depending on the starting joint. For loop (1) in KC shown in Figure 2, JDA can be expressed as [11,1,2,2,3,3] starting from joint “d” or [2,2,3,3,11,1] starting from joint “b”, etc. However, the arrangement of joint degrees inside the array must be unified to ensure that a similar loop must generate the same array.
Step 6 Unified Loop Array (ULA):
In order to enhance the reliability of the joint degree array, it is important to have a unified loop joint degree array regardless the starting joint. In other words, each loop should have a unique array. A MATLAB code [49] was established to rearrange the elements of the joint degree array to start from a specific joint degree and continue in a specific loop direction. This arrangement depends on the concept of the “master joint” and “neighbor joint”, as described below.
Definition 10.
Master joint: a joint that has the least joint degree (JD) in a certain loop. Generally, each loop may contain single master joint or multiple master joints.
Case 1: Single master joint:
For a given loop, all joint degrees can be determined according to the Table 1. If there is a single master joint, a unified loop array, “ULA” can be generated as follows:
- Select the master joint in the given loop.
- Compare joint degrees of the 1st neighbor joints on both sides of the master joint and select the least value.
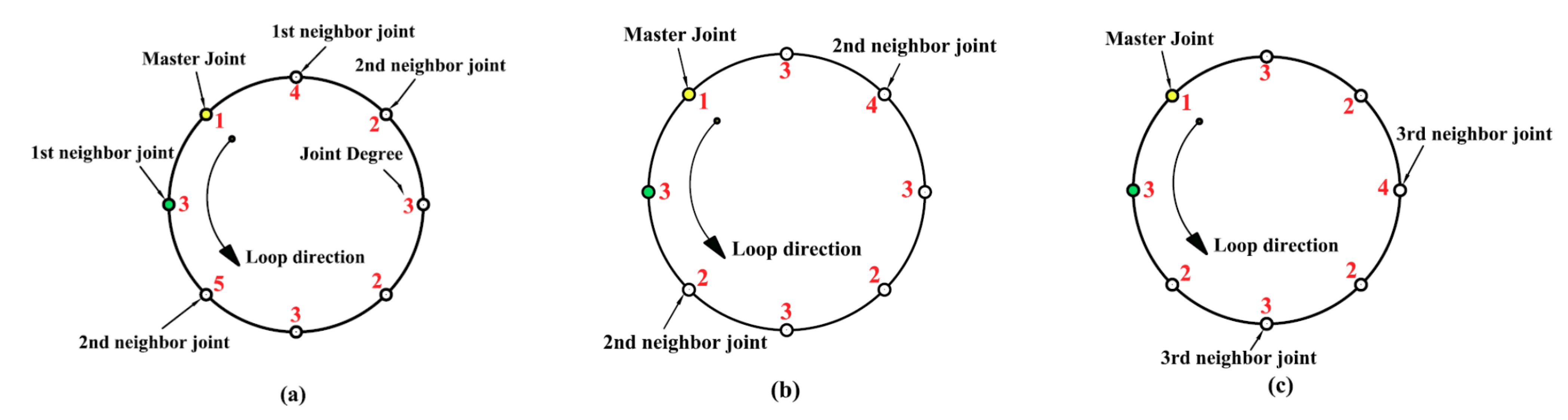
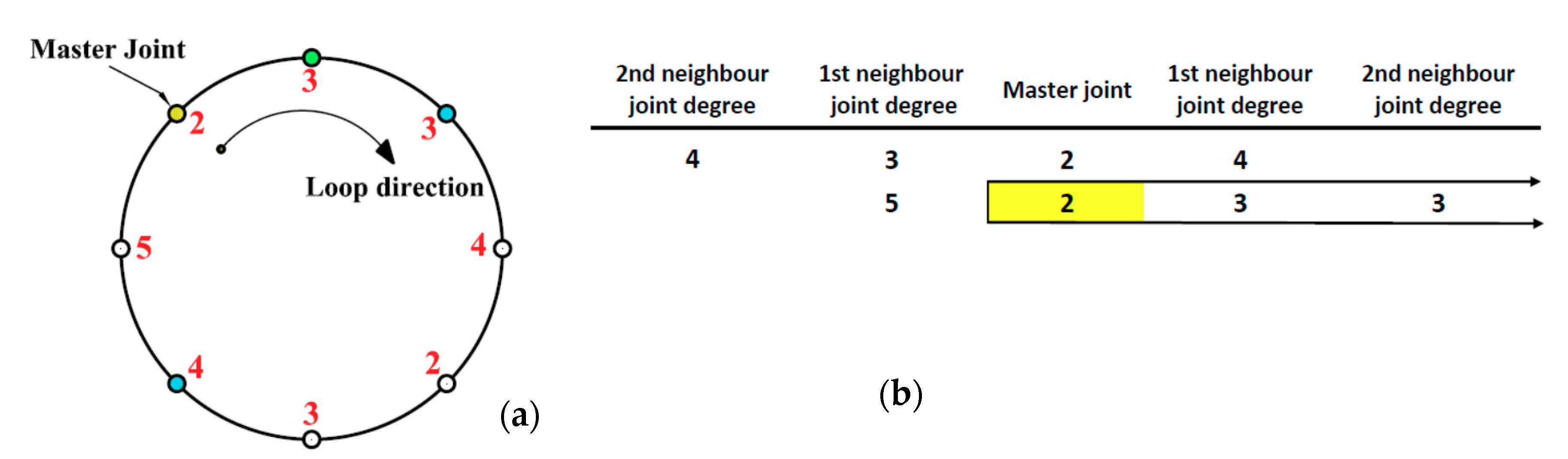
- ULA starts from the master joint and continues in the direction of the selected neighbor joint. In Figure 3a, the shown loop has a single master joint of JD = 1. The least 1st neighbor joint has JD = 3. Therefore, the given loop has ULA = [1 3 5 3 2 3 2 4].
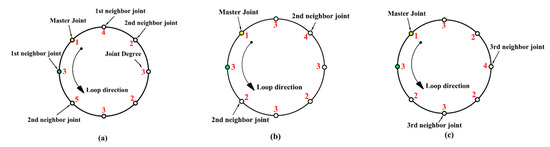 Figure 3. Examples for loops that have a single master joint. (a) non equal 1st neighbor joint degrees. (b) equal 1st neighbor joint degrees. (c) equal 1st and 2nd neighbor joint degrees.
Figure 3. Examples for loops that have a single master joint. (a) non equal 1st neighbor joint degrees. (b) equal 1st neighbor joint degrees. (c) equal 1st and 2nd neighbor joint degrees. - If the 1st neighbor joint degrees are similar, then compare between the 2nd neighbor joints. Therefore, the ULA will be continued in direction of the least 2nd neighbor joint degree starting from the master joint. In Figure 3b, the given loop has ULA = [1 3 2 3 2 3 4 3].
- If the 2nd neighbor joint degree is similar, then compare between the 3rd neighbor joints and so on. Then, “ULA” will be continued in direction of the least 3rd neighbor joint degree starting from the master joint. In Figure 3c, the given loop has ULA = [1 3 2 3 2 4 2 3].
Case 2: Multiple master joints
For a given loop, all joint degrees can be determined according to Table 1. In this case, multiple master joints can be detected in the same loop so that the ULA can be generated as follows:
- Check each master joint for its 1st-neighbor joint degrees.
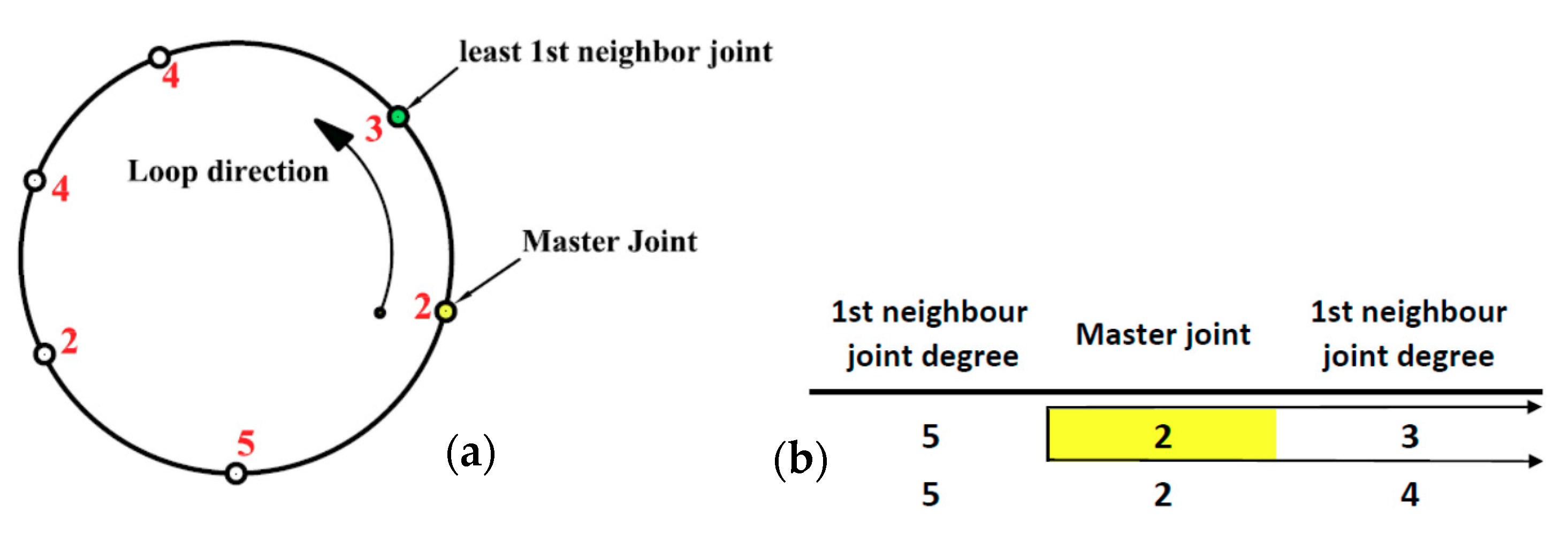
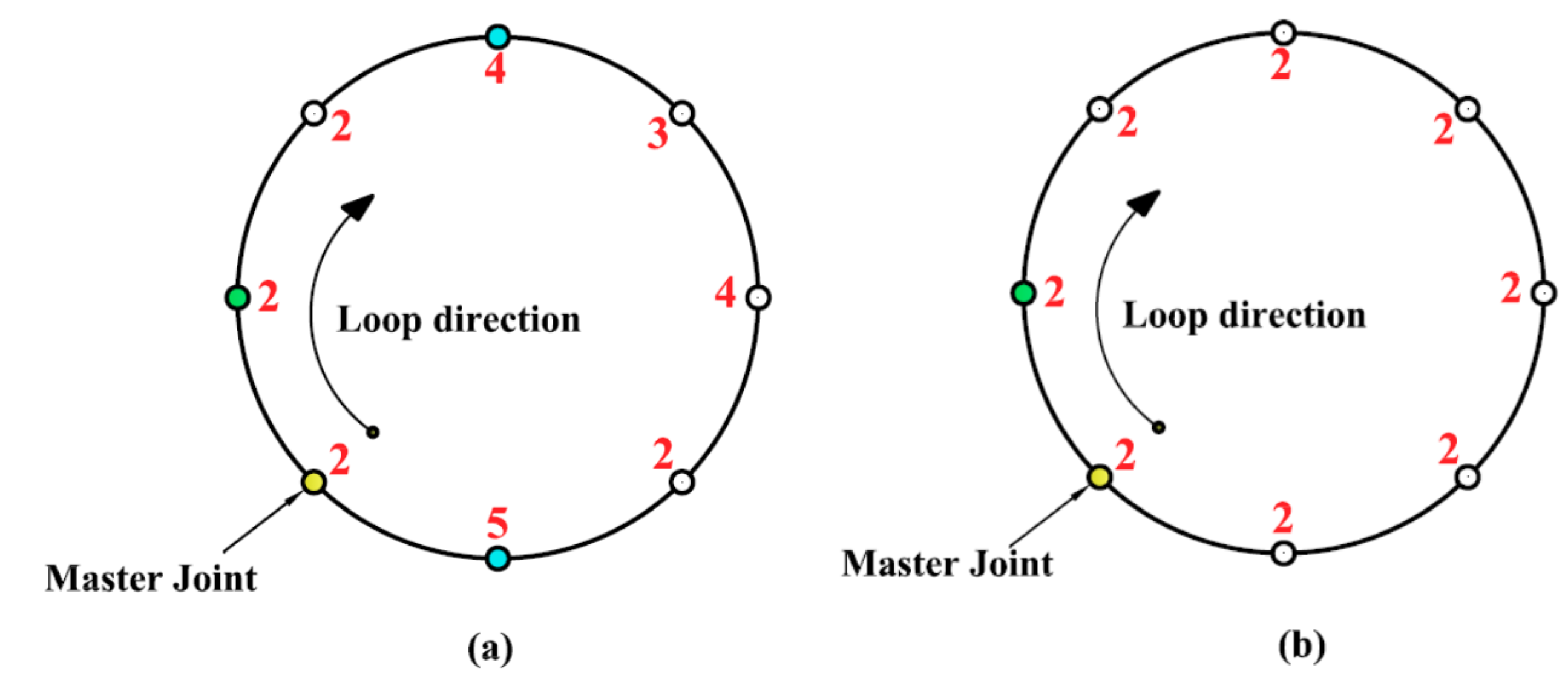
- If there is one master joint that has the least 1st-neighbor joint degree, then the ULA for this loop will be continued in direction of that least 1st-neighbor joint degree starting from its associated master joint. In Figure 4, the given loop has a master joint of JD = 2 (indicated by yellow in Figure 4), and its 1st-neighbor joint has JD = 3, which is the least value of joint degrees among all 1st-neighbor joints for all master joints. Hence, ULA = [2 3 4 4 2 5].
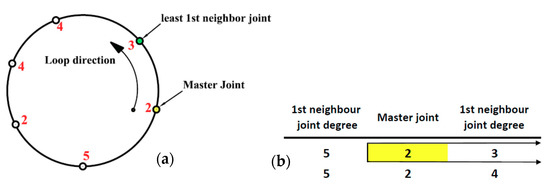 Figure 4. Generation of ULA. (a) loop with two master joints with distinct 1st-neighbor joint degrees. (b) Comparison between master joint neighbors.
Figure 4. Generation of ULA. (a) loop with two master joints with distinct 1st-neighbor joint degrees. (b) Comparison between master joint neighbors. - If the least 1st-neighbor joint degrees are equal in all master joints, check each master joint for its 2nd-neighbor joint degree and select the least 2nd-neighbor joint degree. Hence, the ULA will be continued in the direction of the least 2nd-neighbor joint degree starting from its associated master joint, indicated by yellow in Figure 5, therefore, the given loop has ULA = [2 3 3 4 2 3 4 5].
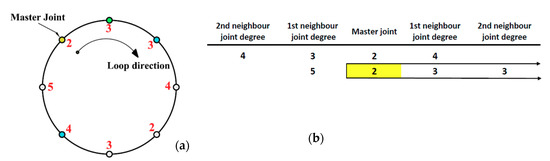 Figure 5. Generation of the ULA. (a) loop with two master joints with similar 1st-neighbor joint degrees. (b) Comparison between master joint neighbors.
Figure 5. Generation of the ULA. (a) loop with two master joints with similar 1st-neighbor joint degrees. (b) Comparison between master joint neighbors. - If the least 2nd-neighbor joint degrees are equal in all master joints, check each master joint for its 3rd-neighbor joint degree and select the least 3rd-neighbor joint degree. Hence, the ULA will be continued in direction of the least 3rd-neighbor joint degree starting from its associated master joint, indicated by yellow in Figure 6, therefore, the given loop has ULA = [2 3 2 4 3 4 2 5].
 Figure 6. Generation of the ULA. (a) loop with multiple master joints. (b) Comparison between multiple master joint neighbors.
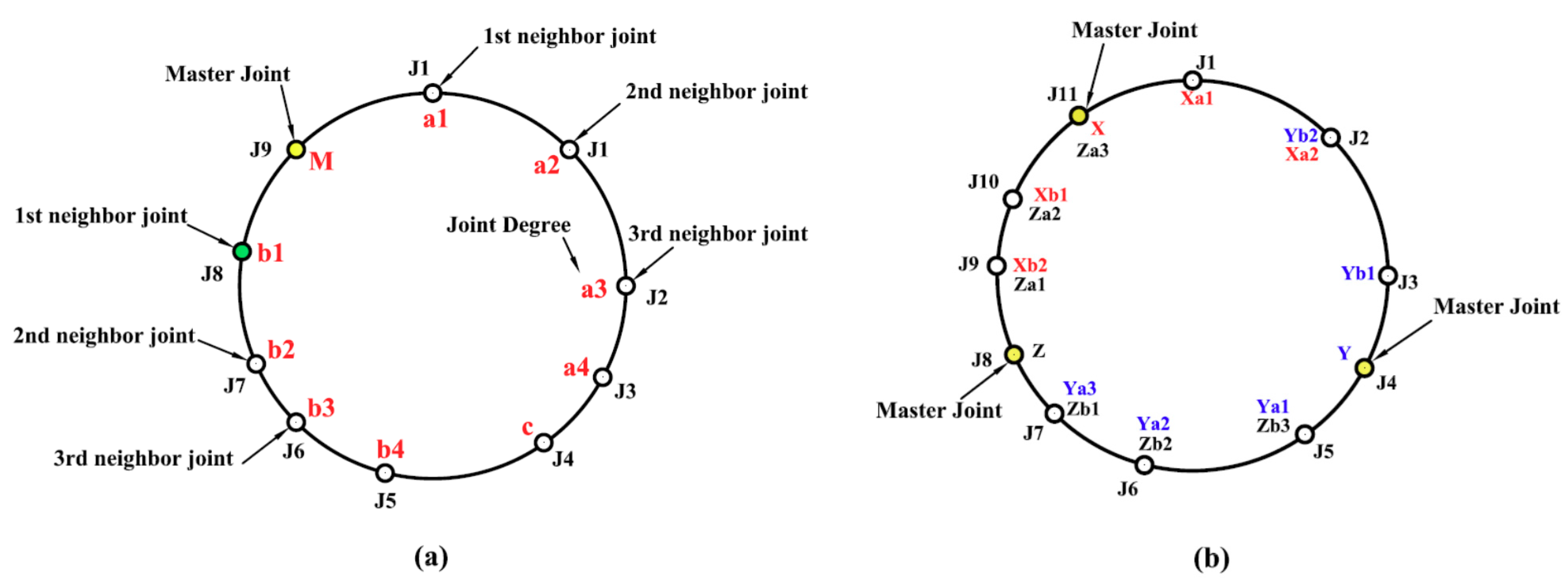
Figure 6. Generation of the ULA. (a) loop with multiple master joints. (b) Comparison between multiple master joint neighbors. - If there exist multiple consequent master joints, check the 1st-neighbor joint degree of the first and last master joints. If they are equal, check the 2nd-neighbor joint degree for the first and the last master joints. Therefore, the ULA will be continued in the direction of the least neighbor joint degree starting from the outmost master joint. As shown in Figure 7a, the given loop has ULA = [2 2 2 4 3 4 2 5].
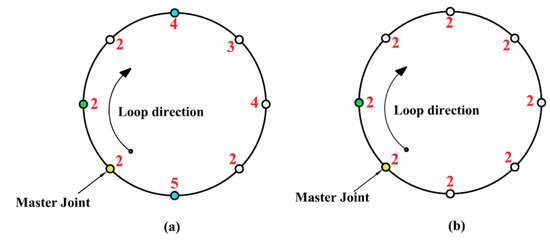 Figure 7. Schematic diagram for a given loop (a) has multiple consequent master joints. (b) has unified master joint degrees.
Figure 7. Schematic diagram for a given loop (a) has multiple consequent master joints. (b) has unified master joint degrees. - If all joints in a certain loop are master joints, then the ULA will start from any joint degree and continue in a clockwise direction. As shown in Figure 7b, the given loop has ULA = [2 2 2 2 2 2 2 2].
Moreover, all previous steps are included in the developed MATLAB code to obtain the unified loop array for a given loop. General rules for both cases of single and multiple master joints, as illustrated in Figure 8, are utilized to establish the MATLAB code, as shown in Algorithms 1 and 2.
| Algorithm 1. Code structure for determining the unified loop array, ULA, for single master joints. |
| L = [J2, J4, J7, J1, J5,…….] // initial loop array M = min (J2, J4, J7, J1, J5,……….) Mid array = [b4, b3, b2, b1, M, a1, a2, a3, a4] case: a1 < b1, ULA = [M,a1,a2,a3,……b1] case: b1 < a1; ULA = [M,b1,b2,b3,……,a1] case: a1 = b1, case: a2 < b2; ULA = [M,a1,a2,……,b1] case: b2 < a2; ULA = [M,b1,b2,……,a1] case a2 = b2; case: a3 < b3; ULA = [M,a1,a2,………,b1] case: b3 < a3; ULA = [M,b1,b2,………, a1] case: a3 = b3; case: a4 < b4; ULA = [M,a1,a2,………,b1] case: b4 < a4; ULA = [M,b1,b2,………, a1] case: a4 = b4; ULA = [M,a1,a2,………,b1] or ULA = [M,b1,b2,………, a1] |
| Algorithm 2. Code structure for determining the unified loop array, ULA, for multiple master joints. |
| L = [J2, J4, J7, J1, J5,…….] // initial loop array Mo = min (J2, J4, J7, J1, J5,……….) Mo = X, Y, Z X: Xmin = min (Xa1, Xb1) Y: Ymin = min (Ya1, Yb1) Z: Zmin = min (Za1, Zb1) M = min (Xmin, Ymin, Zmin) |
| case: M = Xmin, Xmin = Xb1; ULA = [X, Xb1, Xb2,……Xa1] case: M = Ymin; Ymin = Ya1; ULA = [Y, Ya1, Ya2,……, Yb1] case: M = Zmin; Zmin = Zb1; ULA = [Z, Zb1, Zb2,……, Za1] case: M = Xmin = Xb1 & M = Ymin = Ya1; case: Xb2 < Ya2; ULA = [X, Xb1,Xb2,…… Xa1] case: Ya2 < Xb2; ULA = [Y, Ya1, Ya2,……Yb1] case: Xb2 = Ya2; case: Xb3 < Ya3; ULA = [X, Xb1,Xb2,……,Xa1] case: Ya3 < Xb3; ULA = [Y, Ya1, Ya2,……,Yb1] case: Xb3 = Ya3; ULA = [X, Xb1,Xb2,……,Xa1] or, ULA = [Y, Ya1, Ya2,……,Yb1] |
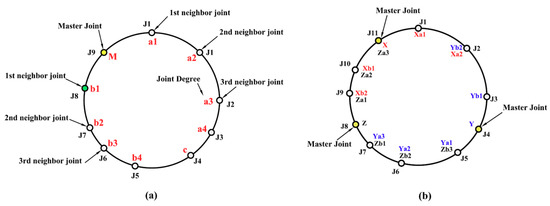
Figure 8.
General schematic diagram for a given loop has (a) a single master joint and (b) multiple master joints.
Step 7 Unified chain matrix (UCM)
After generating the ULA for all loops, the whole chain can be represented by the unified chain matrix.
Definition 11.
Unified chain matrix: a unique V × K matrix representing a given KC where V is the number of loops forming the considered KC, and K is the number of joints in the largest loop size.
However, the first row represents the ULA for the 1st loop, and the second row represents the ULA for the 2nd loop, etc. Any missing elements are represented as zero elements in the unified chain matrix.
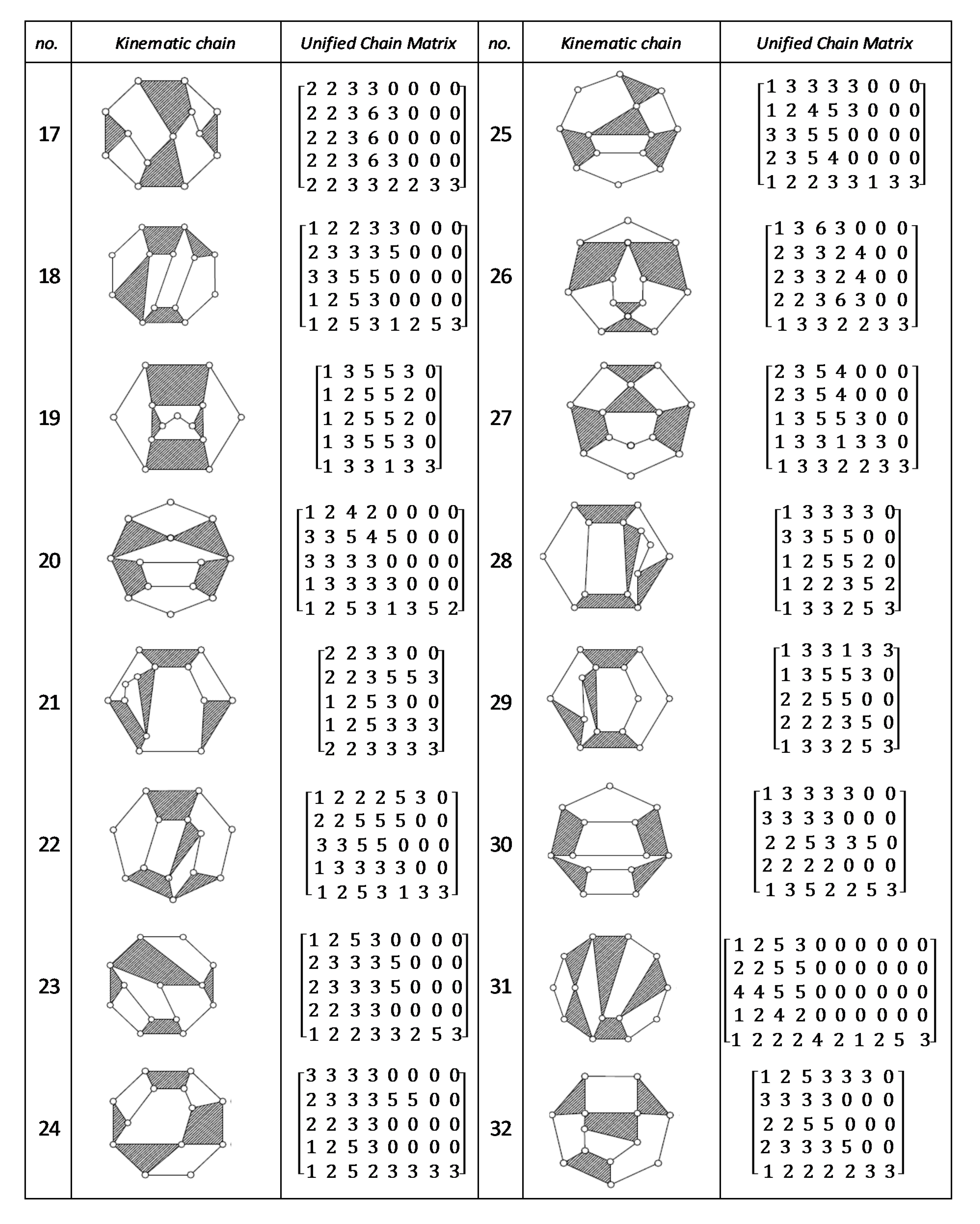
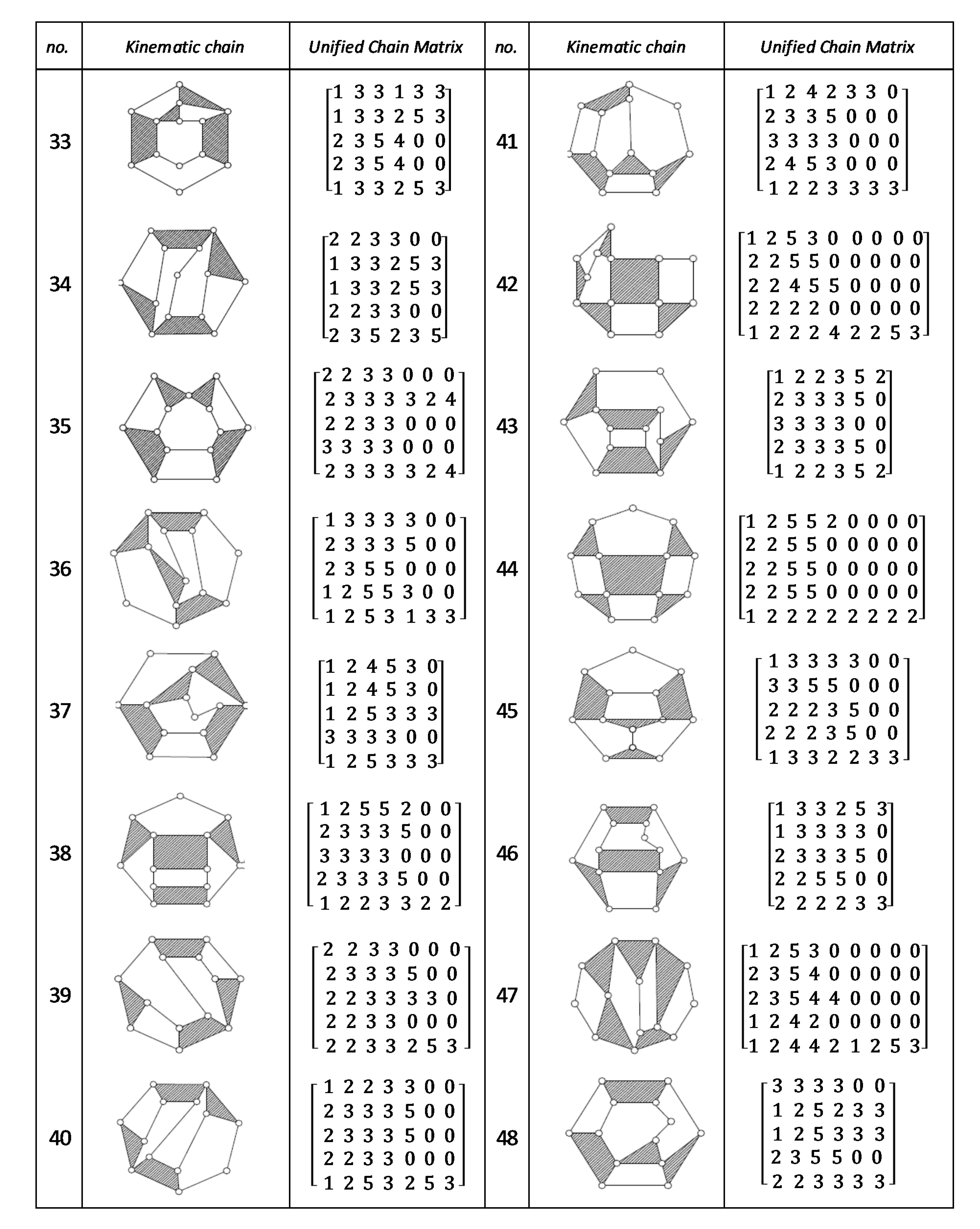
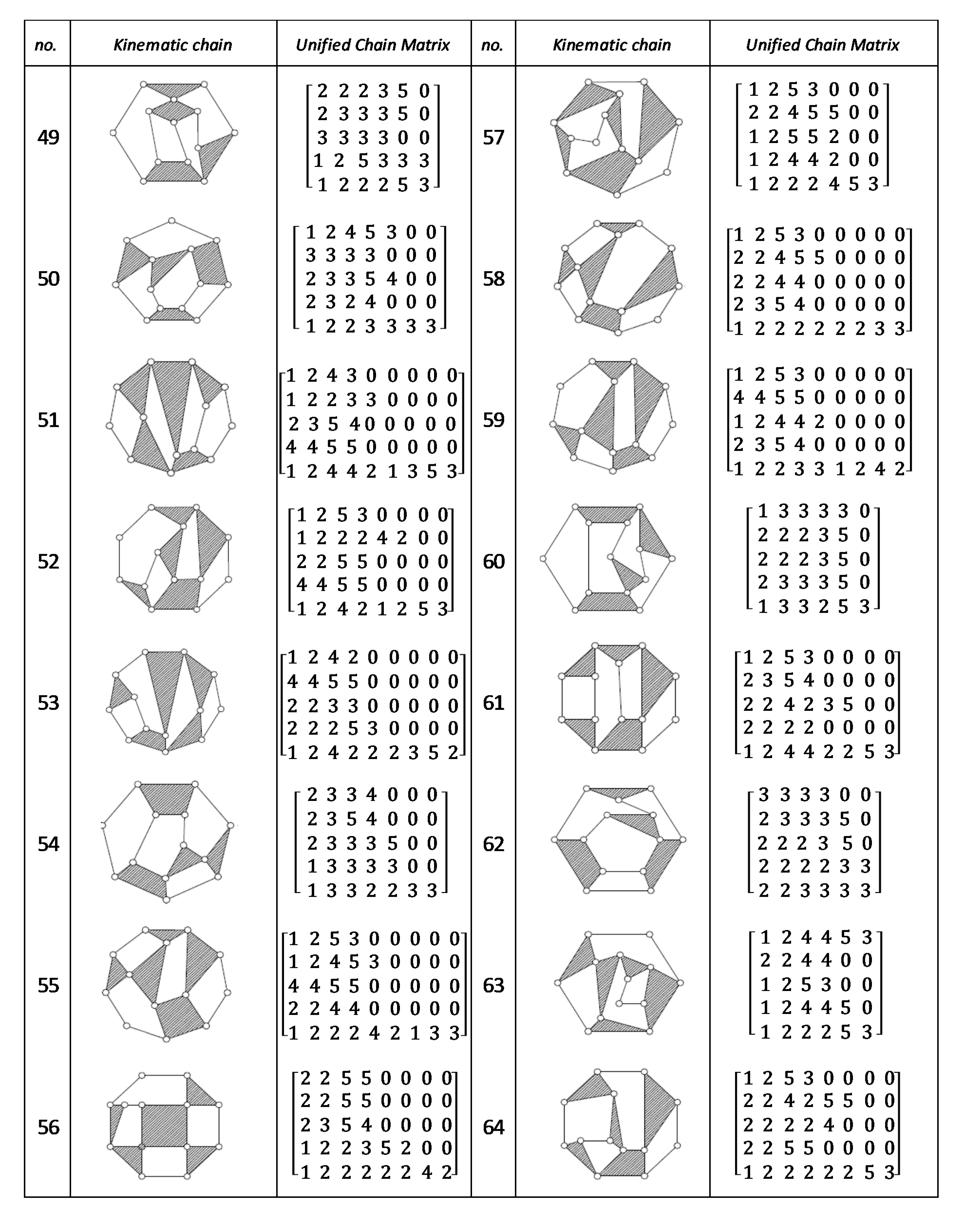
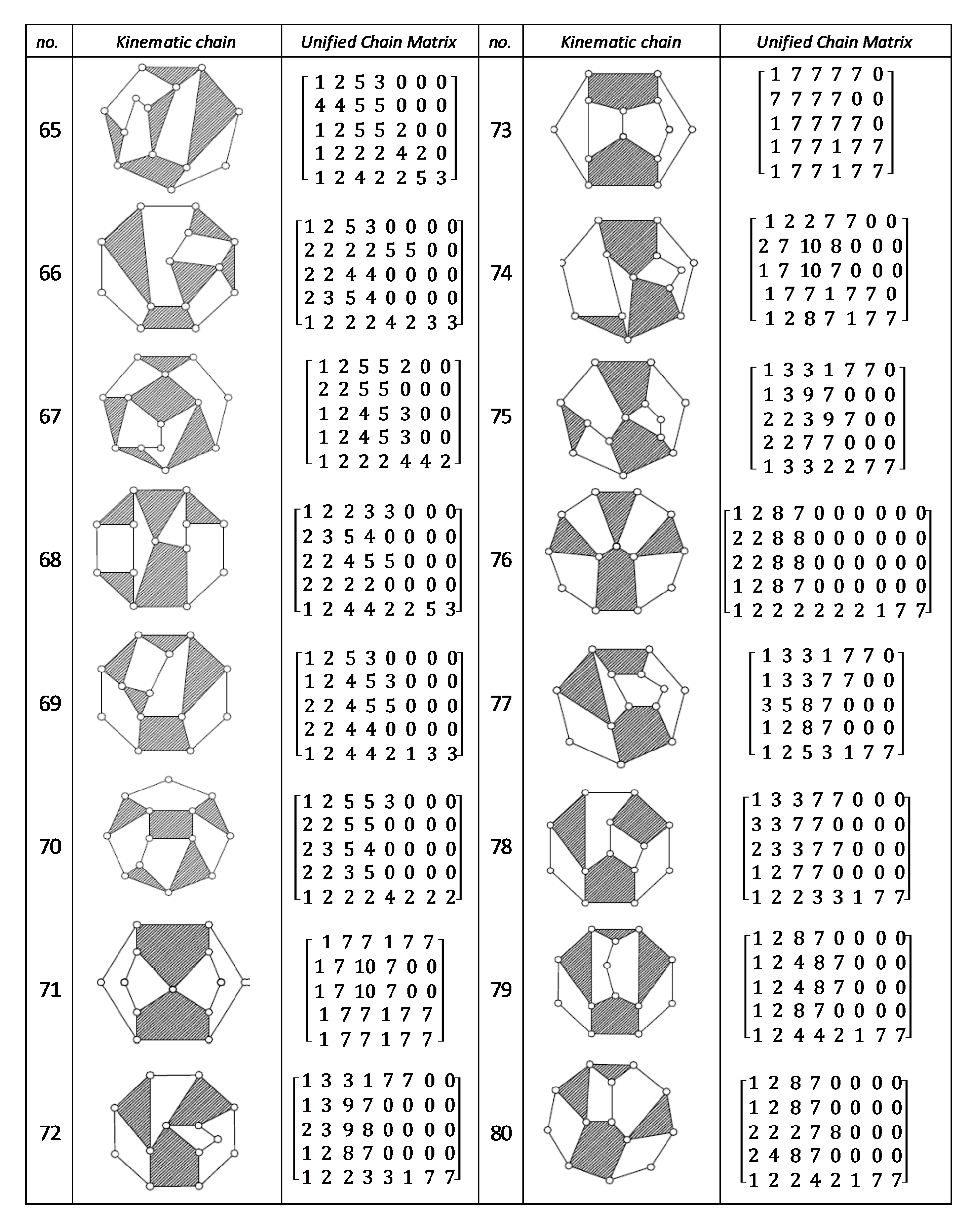
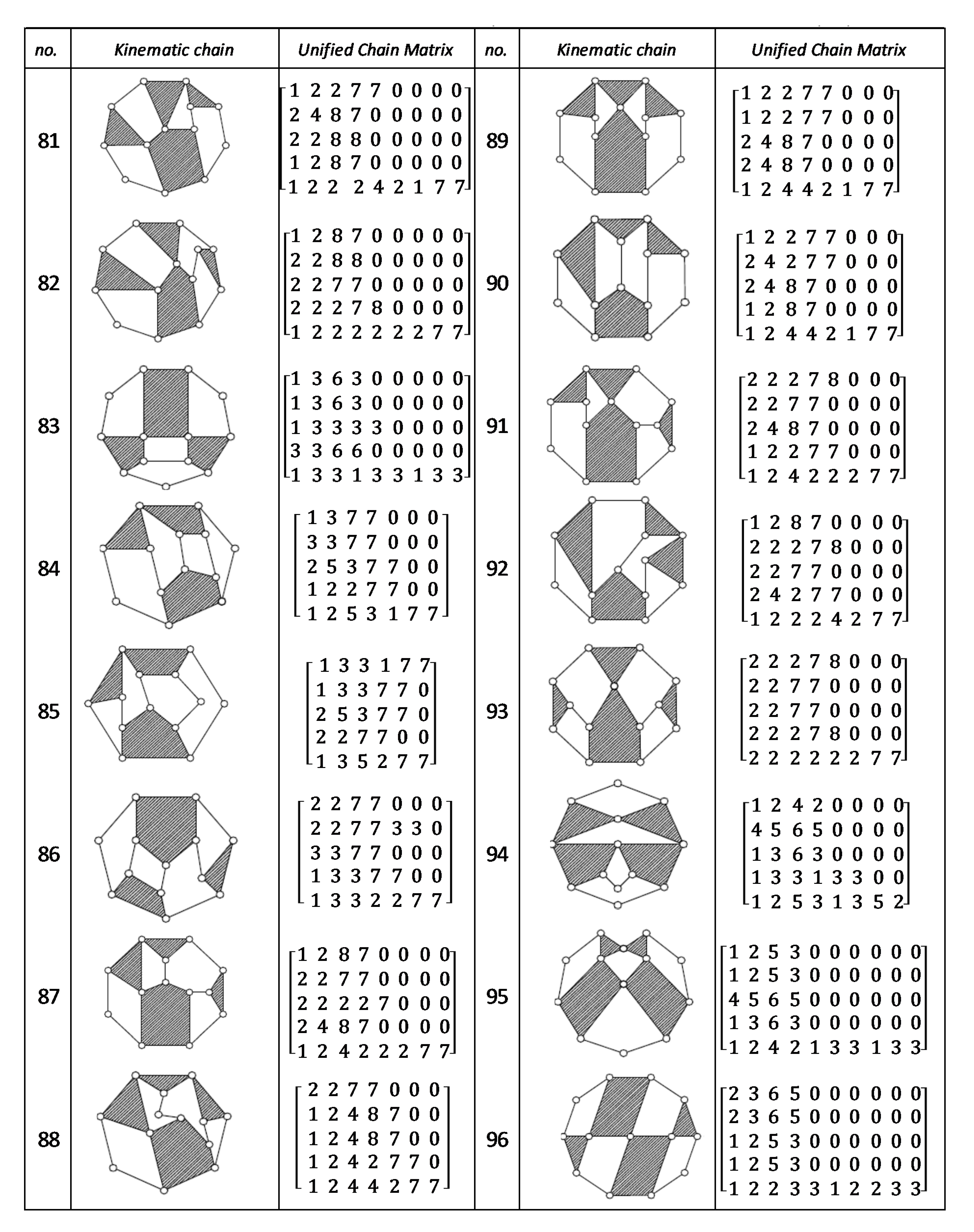
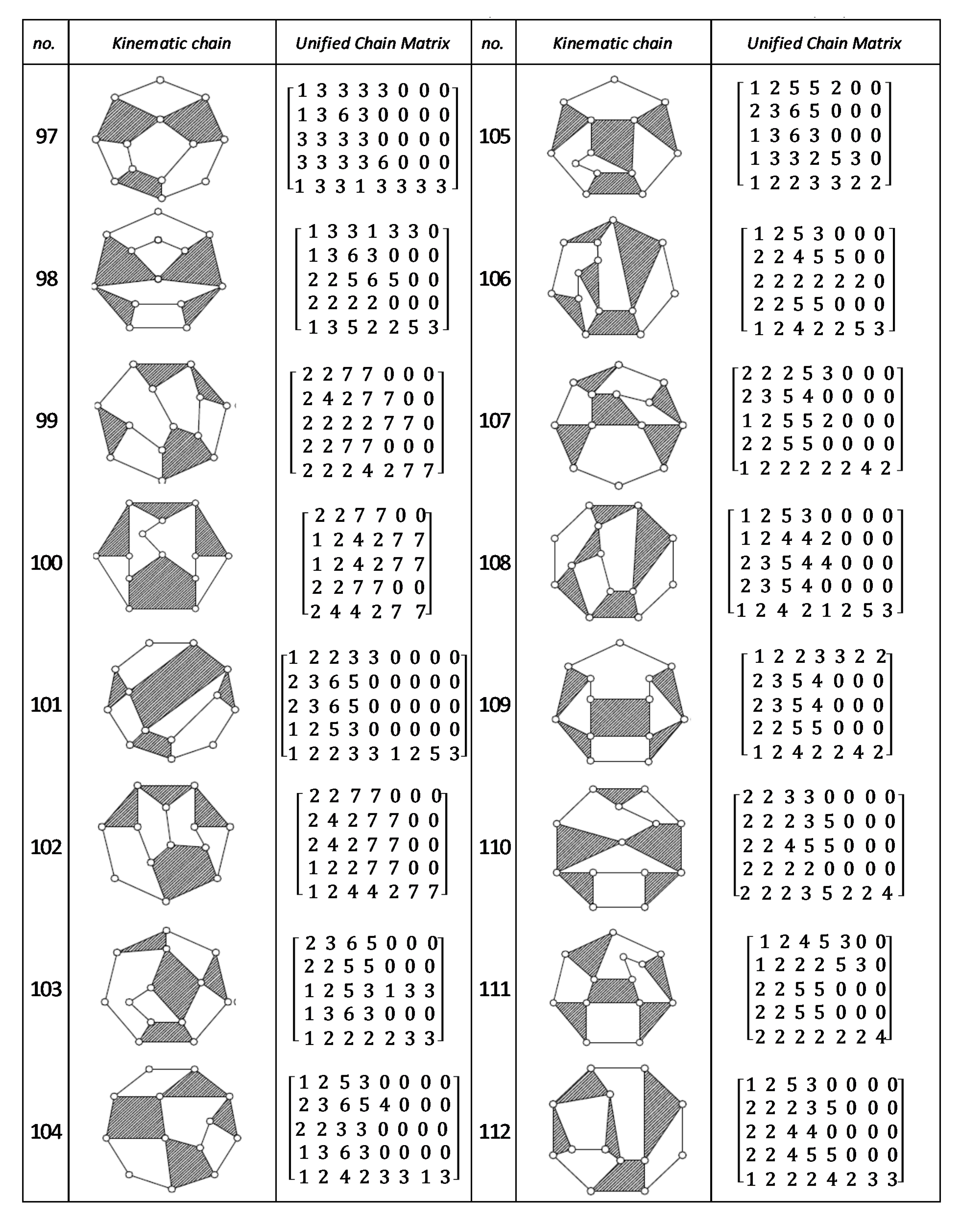
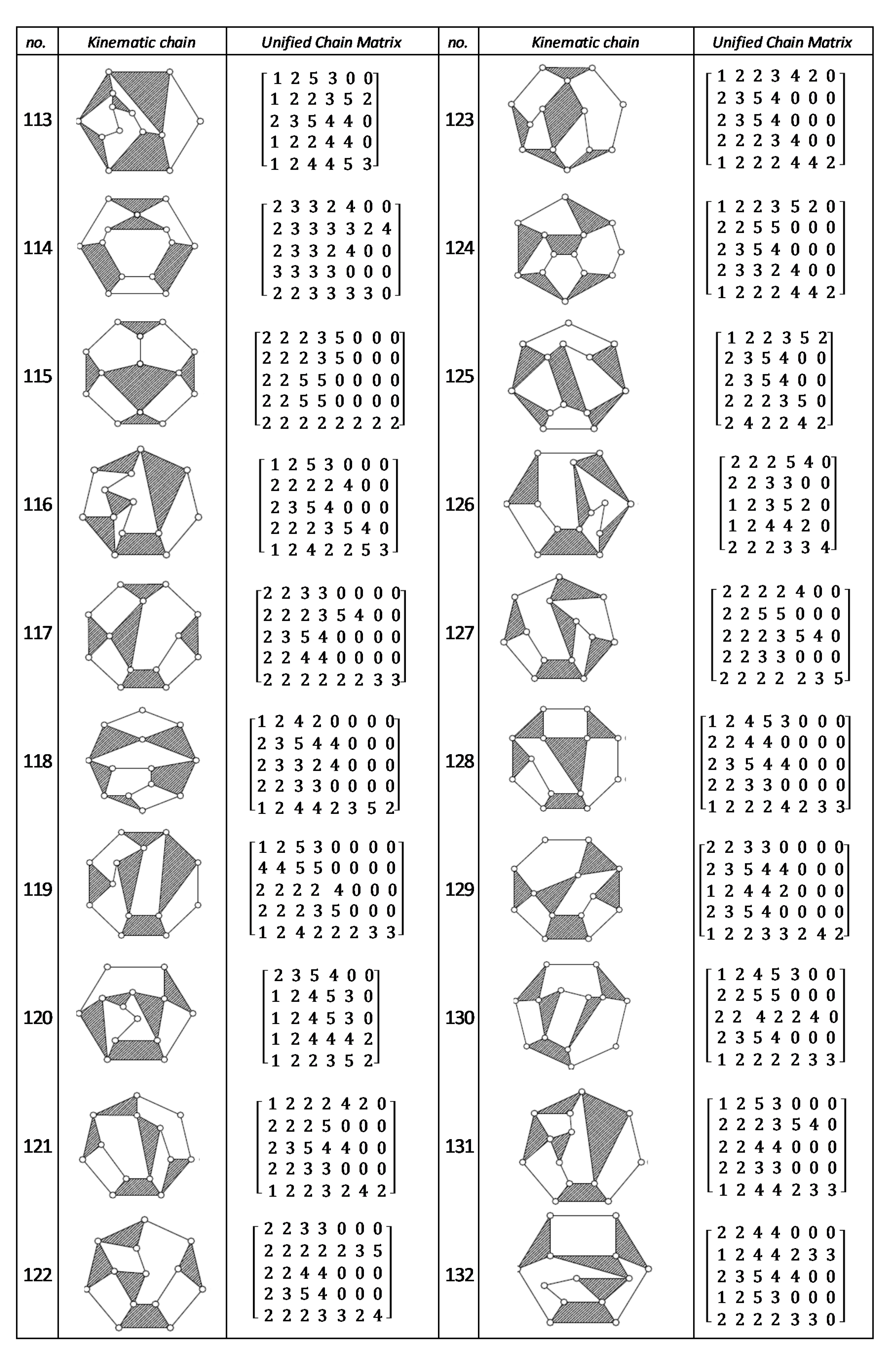
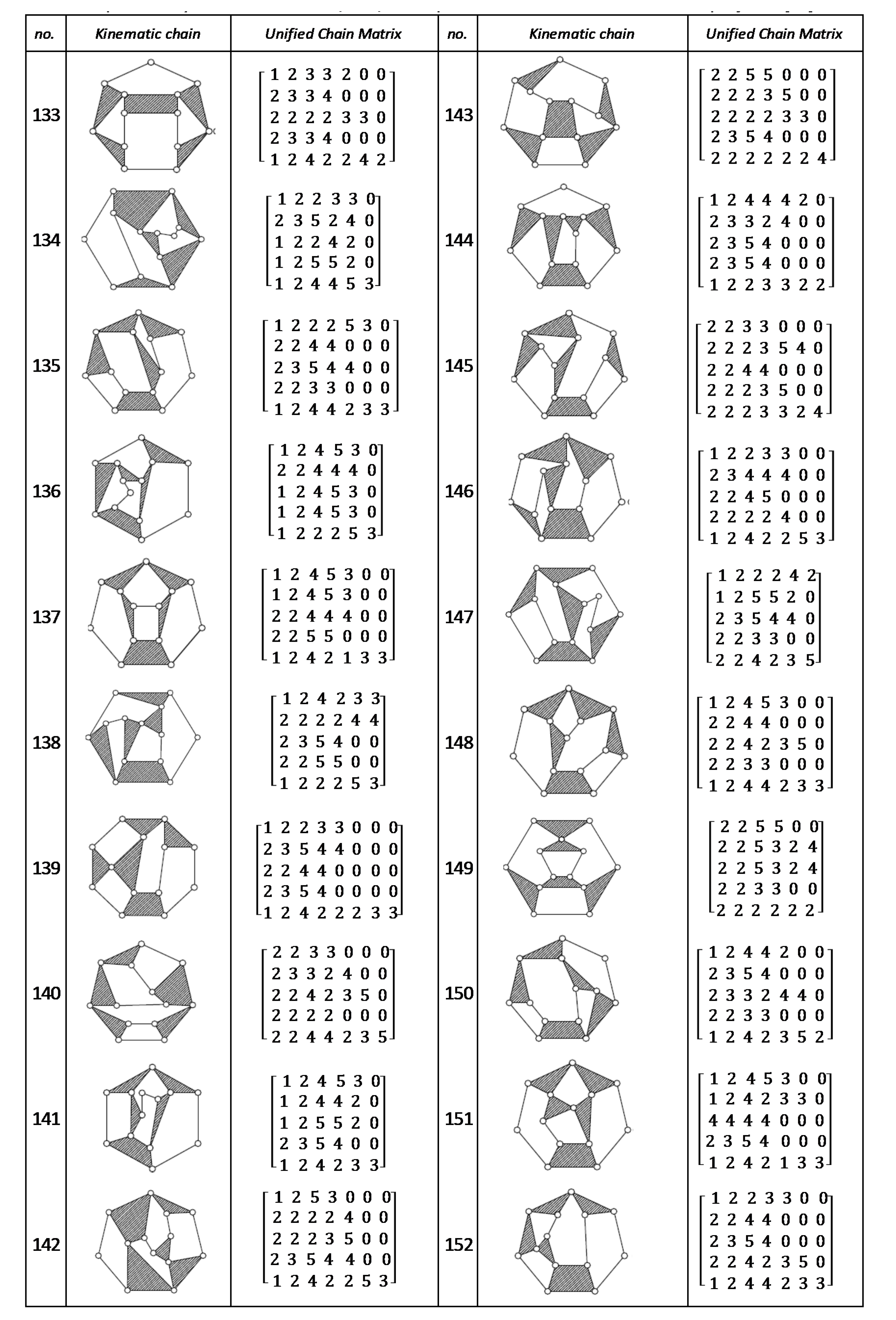
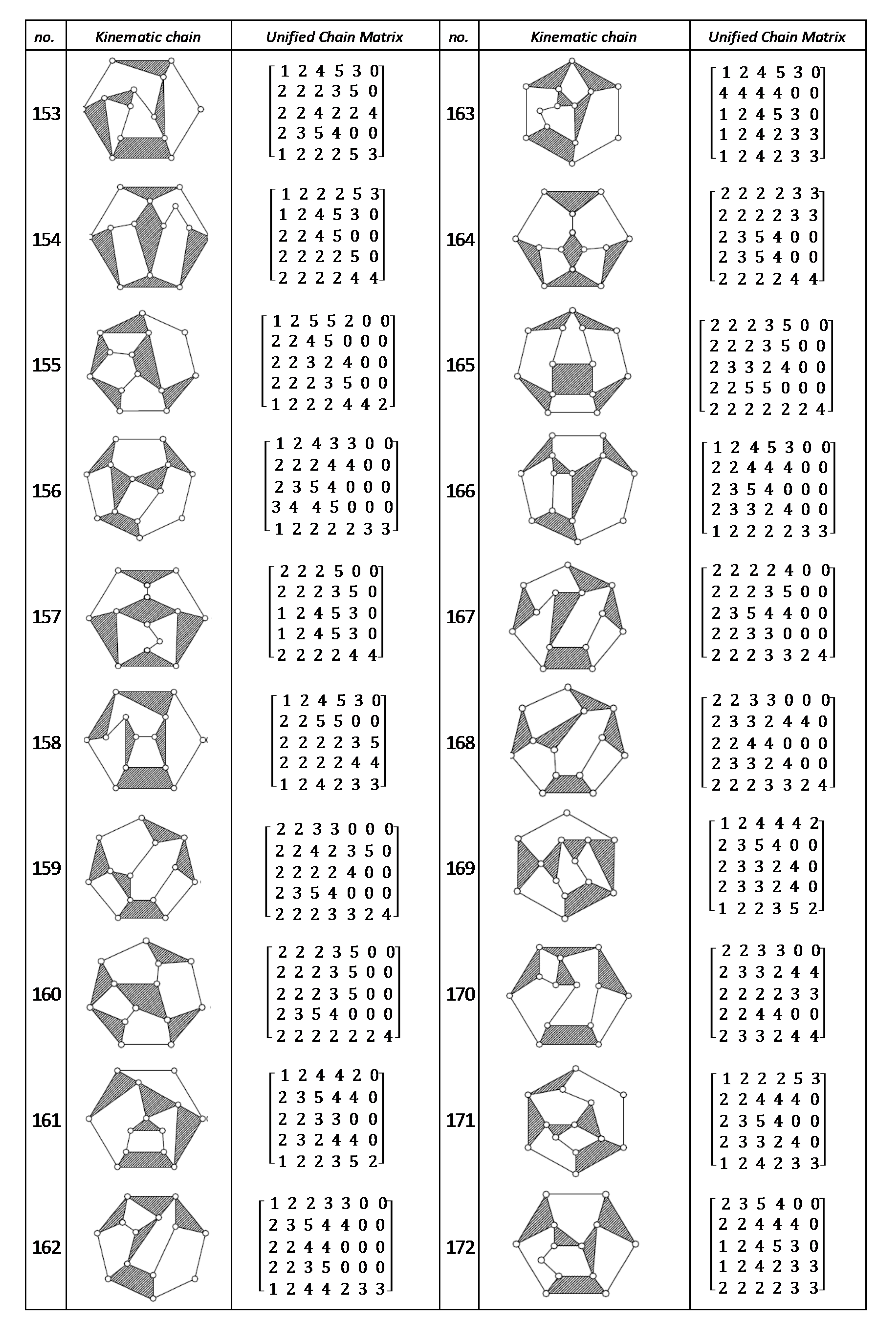
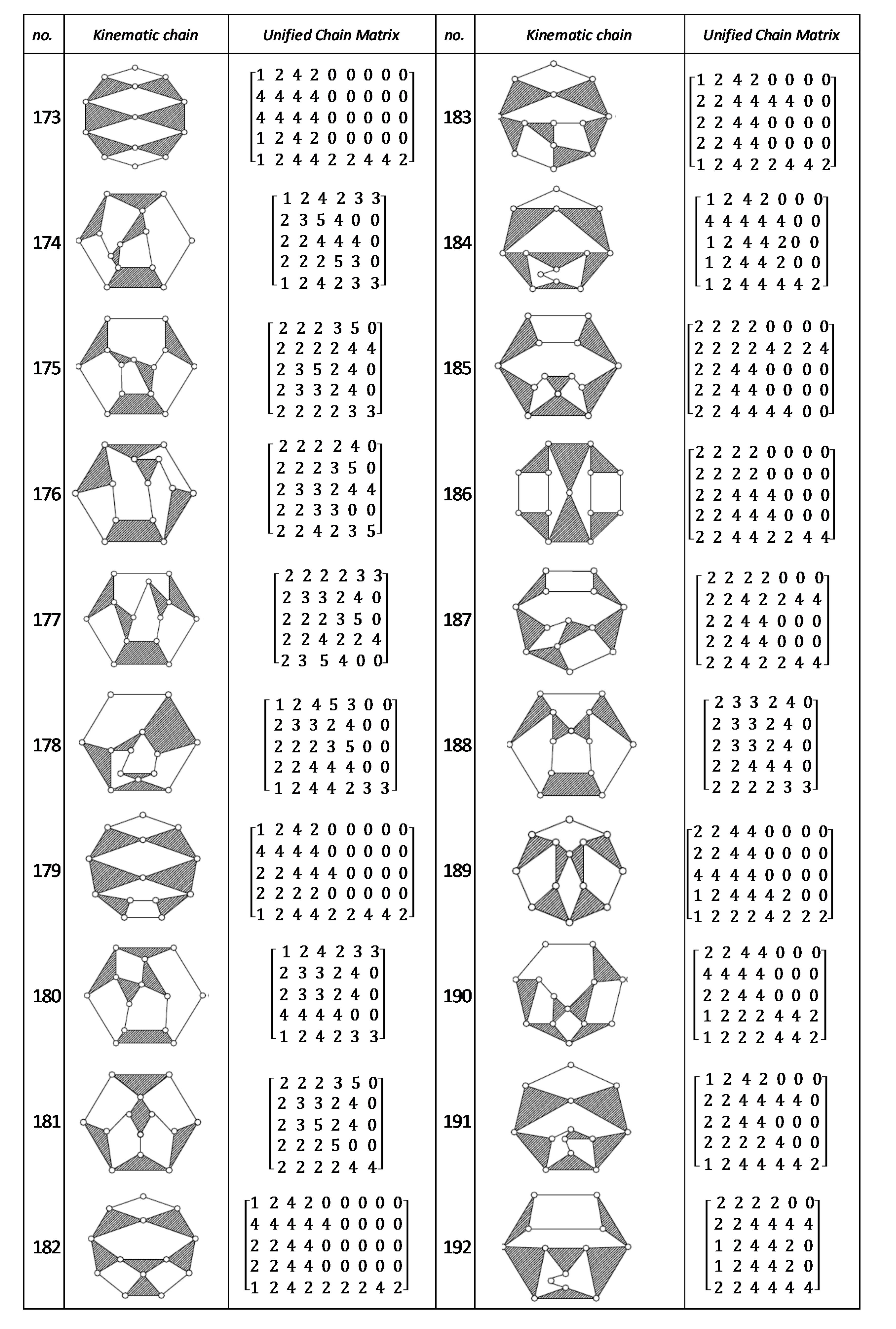
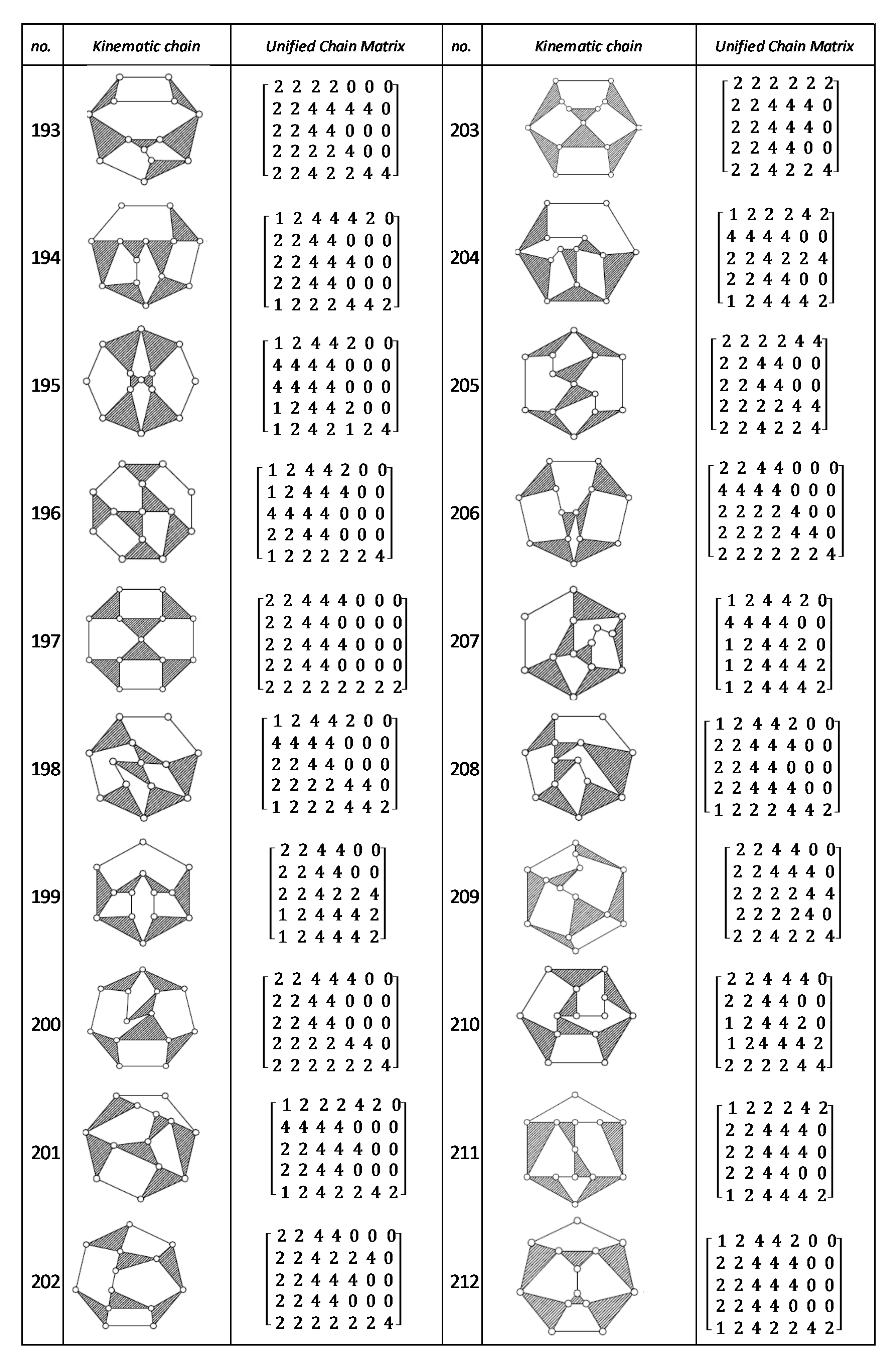
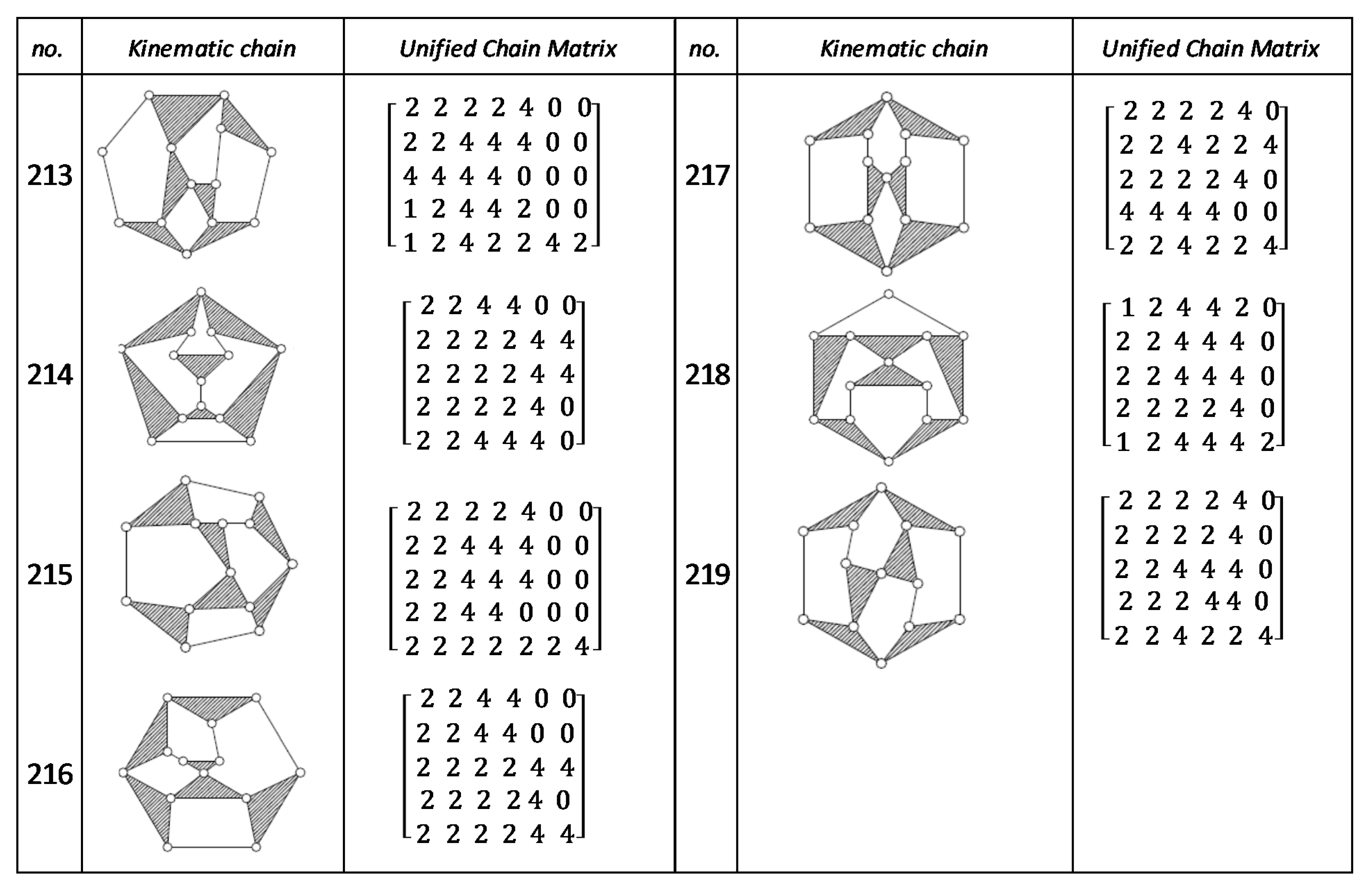
Using the unified chain matrix, a complete atlas database is established for planar 7, 8, 9 and 10-links KCs with simple and multiple joints (given in Appendix A).
Step 8 Isomorphism Detection
Isomorphism detection is the most important step in the structural synthesis of KCs. Isomorphic KCs are structurally identical chains that should be detected so as not to duplicate the enumeration or synthesis results. A reliable isomorphism detection process can be carried out using the UCM.
Definition 12.
Isomorphic KCs: Two KCs are said to be isomorphic if each row in the UCM of the first KC has a corresponding row in the UCM of the second KC, regardless of the row’s order.
Therefore, the previous algorithm can be applied to any planar KC. Different configurations of a KC should generate the same UCM. In other words, all configurations are isomorphic KCs.
4. Algorithm Validation Tests
In this section, some examples are given to illustrate the algorithm clearly with more detail and to test its validity. The selected examples present KCs with different DOF and different types of joints, either simple or multiple.
4.1. Example One: 11-Link KCs of Two DOF with Simple Joints
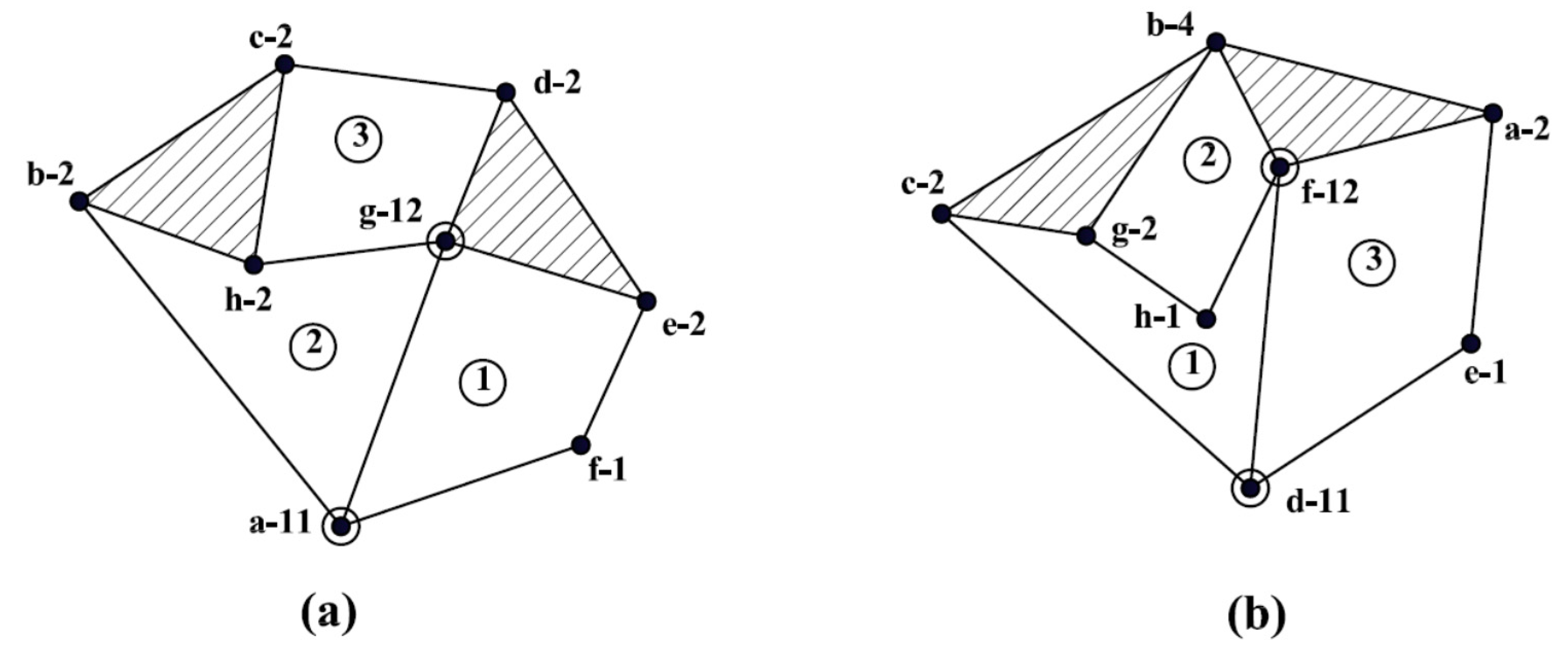
Consider a pair of 11-link simple-joint KCs with two DOF, shown in Figure 9a,b.
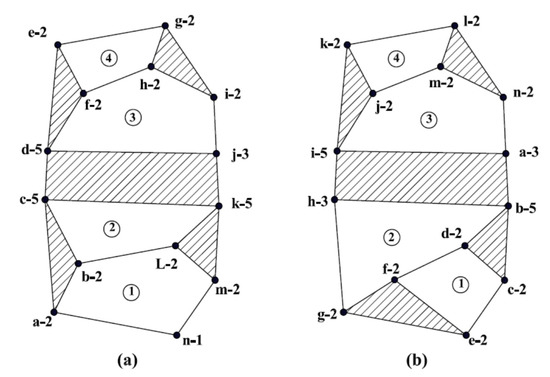
Figure 9.
Two 11-link kinematic chains with simple joints. (a) Kinematic chain: a. (b) kinematic chain: b.
The link assortment array (LAA) and joint assortment array (JAA) for KCs shown in Figure 9a,b are illustrated in Table 2.

Table 2.
Link Assortment Array and Joint Assortment Array for kinematic chains in Figure 9.
The joint degree for all joints of each KC can be determined according to Table 1 based on the joint type and its associated connected links. The joint degrees for the KCs shown in Figure 9a,b are listed in Table 3. Furthermore, Figure 9 illustrates all the joint labels and their corresponding joint degrees.

Table 3.
Values of Joint degrees for kinematic chains in Figure 9a,b.
The number of independent loops for each KC is IL = J − N + 1 = 14 − 11 + 1 = 4. Therefore, there are four independent loops besides the peripheral loop. Hence, both KCs have five loops. The joint degrees are then detected for each loop. However, the initial joint degree array (JDA) for each loop can be obtained. Then, the unified loop array (ULA) for each loop is generated, as shown in Table 4, using the MATLAB code.

Table 4.
Unified Loop Array for KC in Figure 9a,b.
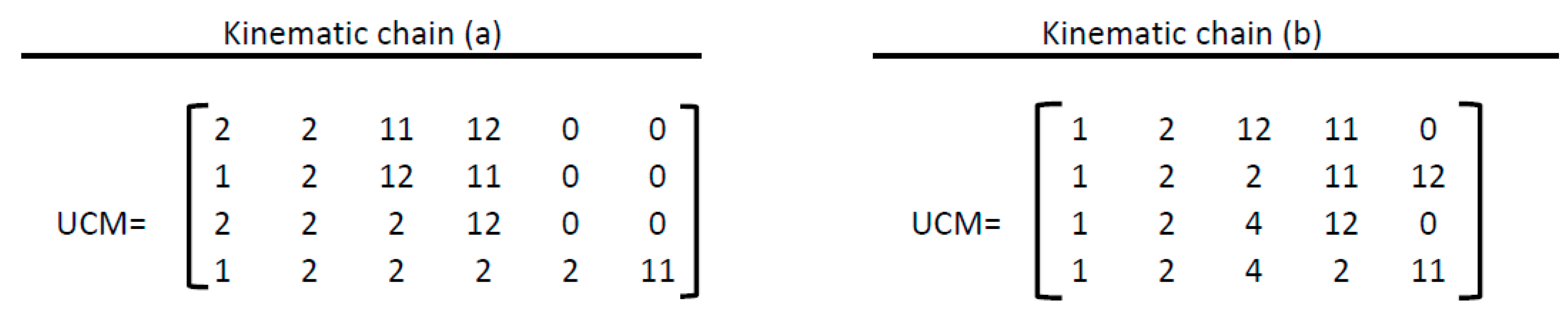
The unified chain matrix for each KC is derived as shown in Figure 10. However, there is no complete correspondence in both matrices. Therefore, the two KCs in Figure 9a,b are not isomorphic.

Figure 10.
Unified chain matrix for the kinematic chain in Figure 9a,b.
4.2. Example Two: Eight-Link KCs of One DOF with Two Multiple Joints
Consider a pair of eight-link KCs of one DOF with one multiple joint, shown in Figure 11a,b.
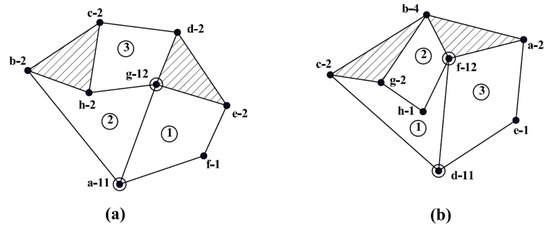
Figure 11.
Two 8-link kinematic chains with simple and multiple joints. (a) kinematic chain: a. (b) kinematic chain: b.
The link assortment array (LAA) and joint assortment array (JAA) for the KCs shown in Figure 11a,b are illustrated in Table 5.

Table 5.
Link Assortment Array and Joint Assortment Array for kinematic chains in Figure 11a,b.
The joint degree for all joints of each KC can be determined according to Table 1 based on the joint type and its associated connected links. The joint degrees for the KCs shown in Figure 11a,b are listed in Table 6. Furthermore, Figure 11 illustrates all the joint labels and their corresponding joint degrees.

Table 6.
Values of Joint degrees for kinematic chains in Figure 11a,b.
The number of independent loops for each KC is IL = J − N + 1 = 10 − 8 + 1 = 3. Therefore, there are three independent loops besides the peripheral loop. Hence, both KCs have four loops. The joint degrees are then detected for each loop. However, the initial joint degree array (JDA) for each loop can be obtained. Then, the unified joint array (ULA) for each loop is generated, as shown in Table 7.

Table 7.
Unified Joint Degree Array for KCs in Figure 11a,b.
The unified chain matrix for each KC is derived as shown in Figure 12. However, there is no complete correspondence in both matrices. Therefore, the two KCs in Figure 11a,b are not isomorphic.
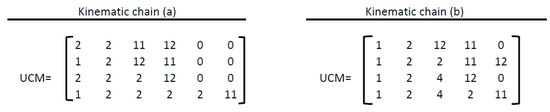
Figure 12.
Unified chain matrix for the kinematic chain in Figure 11a,b.
4.3. Example Three: 15-Link KCs of Four DOF with Simple Joints
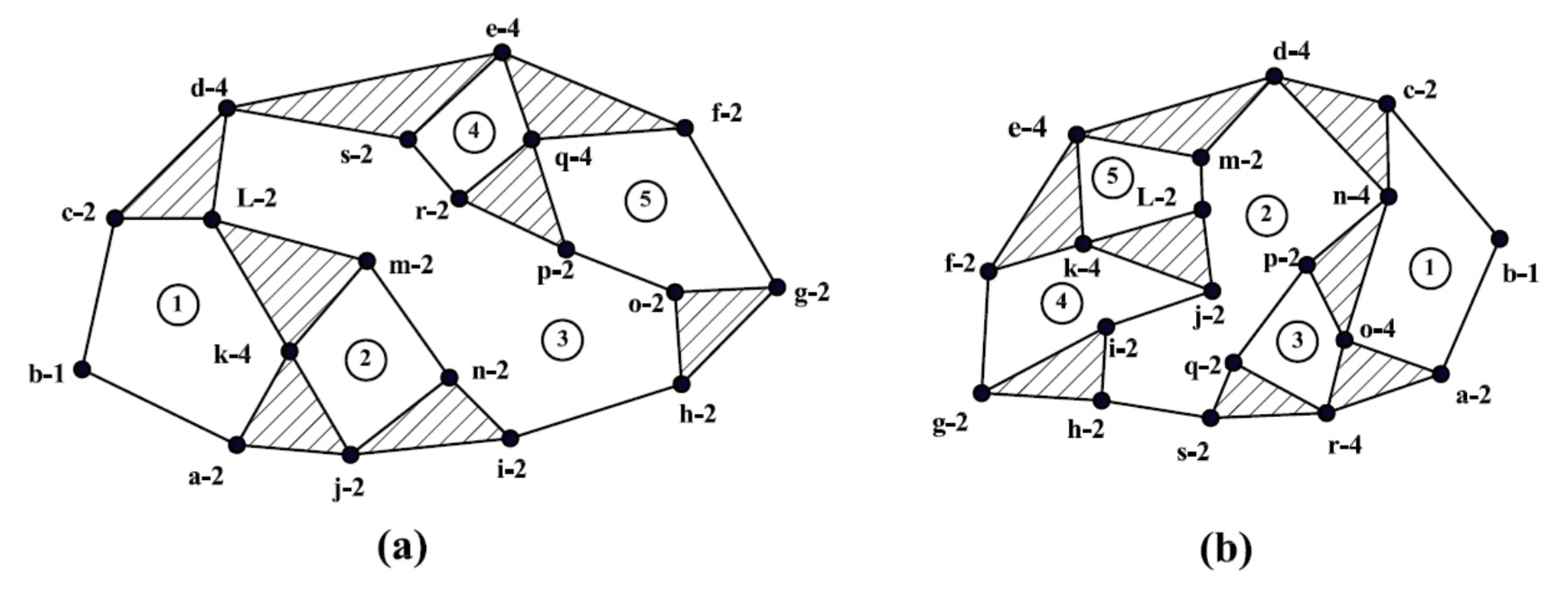
Consider a pair of 15-link simple joints KCs with four DOF, shown in Figure 13a,b.
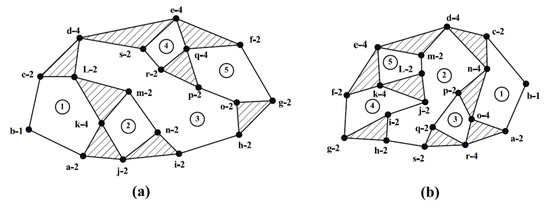
Figure 13.
15-links kinematic chains with simple joints. (a) kinematic chain: a. (b) kinematic chain: b.
The link assortment array (LAA) and joint assortment array (JAA) for the KCs shown in Figure 13a,b are illustrated in Table 8. Furthermore, Figure 13 illustrates all the joint labels and their corresponding joint degrees.

Table 8.
Link Assortment Array and Joint Assortment Array for kinematic chains in Figure 13.
The joint degree for all joints of each KC can be determined according to Table 1 based on the joint type and its associated connected links. The joint degrees for the KCs shown in Figure 13a,b are listed in Table 9. Furthermore, Figure 13 illustrates all the joint labels and their corresponding joint degrees.

Table 9.
Values of Joint degrees for kinematic chains in Figure 13a,b.
The number of independent loops for each KC is IL = J − N + 1 = 19 − 15 + 1 = 5. Therefore, there are five independent loops besides the peripheral loop. Hence, both KCs have six loops. The joint degrees are then calculated for each loop. However, the initial joint degree array (JDA) for each loop can be obtained. Then, the unified joint array (ULA) for each loop is generated, as shown in Table 10.

Table 10.
Unified Loop Array for KCs in Figure 13a,b.
The unified chain matrix for each KC is generated as shown in Figure 14. However, each row in the unified joint degree matrix of Figure 14a has a corresponding row in the unified joint degree of Figure 14b. Therefore, the two KCs in Figure 13 are isomorphic.

Figure 14.
Unified chain matrix for the kinematic chains in Figure 13a,b.
5. Results
The proposed algorithm was successfully applied to detect isomorphic KCs during the structural synthesis of the mechanisms. Two or more KCs are said to be isomorphic if they have the same UCM. For any planar KC with single or multiple DOF, a unified chain matrix can be obtained based on the independent loop and unified loop array. The ULA are generated for each independent loop based on the joint degree concept using the developed MATLAB code. The proposed method was applied to the most common planar KCs of 7–10 links with simple or multiple joints. As a result, a complete atlas for 7–10 links of KCs and their corresponding UCM was constructed up to five independent loops. The selected types of KCs are various in DOF and a number of multiple joints to ensure the algorithm validity. Almost all of the presented KCs have no edge crossing that facilitate independent loop detection. Three examples were presented for the generation of the unified chain matrix and isomorphism detection in 8, 11 and 15-link KCs. The examples and constructed atlas verified that using the UCM is a simple and effective tool in the isomorphism detection process. The developed atlas is presented in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 (given in Appendix A). The detailed results are listed below:
- ◾
- 18 eight links of one DOF KCs with two multiple joints
- ◾
- 22 eight links of one DOF KCs with one multiple joint
- ◾
- five seven links of two DOF KCs with one and two multiple joints
- ◾
- 40 nine links of two DOF KCs with simple joints
- ◾
- four seven links of two DOF KCs with simple joints
- ◾
- 83 nine links of two DOF KCs with one multiple joint
- ◾
- 16 eight links of one DOF KCs with simple joints
- ◾
- 219 ten links of one DOF KCs (without edge crossing) with simple joints
6. Conclusions
A new method to represent planar KCs was developed in this paper. The joint degree (JD) was introduced to represent all joints in a KC. Then, a MATLAB code was established to obtain the unified loop array (ULA) for each independent loop. Therefore, a unified chain matrix was generated to represent the considered KC. The proposed method was successfully tested for all KCs up to five independent loops. This algorithm was applied to planar KCs having single or multiple DOF with either simple or multiple joints. A complete atlas database was introduced for non-isomorphic 7, 8, 9 and 10-link KCs with simple or/and multiple joints with their corresponding UCM. Furthermore, isomorphic KCs can be easily identified using UCM. Some examples were presented for isomorphism detection in planar KCs. It was proven that the proposed method is a reliable approach to represent and detect isomorphism among KCs having closed planar graphs without edge crossing. In future works, KCs with edge crossing should be investigated. The proposed algorithm can also be extended to be applied for geared and spatial KCs. A MATLAB graphical user interface may be developed, including all algorithm steps, to facilitate the input and output data for users.
Author Contributions
Conceptualization, M.H., J.W.H. and H.E.; methodology, M.H., J.W.H. and H.E.; software, M.H. and H.E.; validation, M.H., J.W.H. and H.E.; formal analysis, M.H. and H.E.; investigation, M.H., J.W.H. and H.E.; resources, M.H. and H.E.; data curation, M.H. and H.E.; writing—original draft preparation, M.H. and H.E.; writing—review and editing, M.H., J.W.H. and H.E.; visualization, M.H., J.W.H. and H.E.; supervision, M.H. and H.E.; project administration, M.H., J.W.H. and H.E. and funding acquisition, M.H., J.W.H. and H.E. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 20NANO-B156177-01).
Data Availability Statement
Available upon needed from the corresponding author.
Acknowledgments
The authors are grateful to Taif University (Taif, KSA) and Mansoura University (Mansoura, Egypt) and Future University in Egypt (Cairo, Egypt) for providing all the required facilities to carry out the present research.
Conflicts of Interest
The authors declared no conflicts of interest.
Appendix A
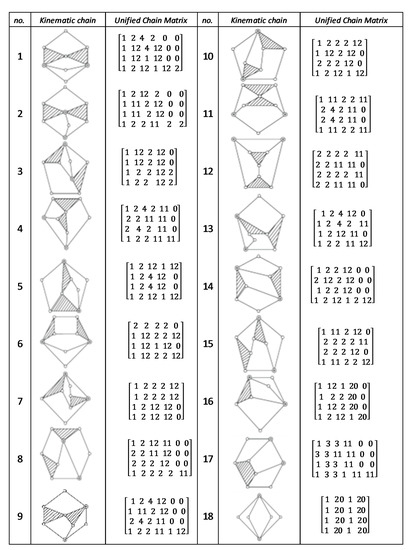
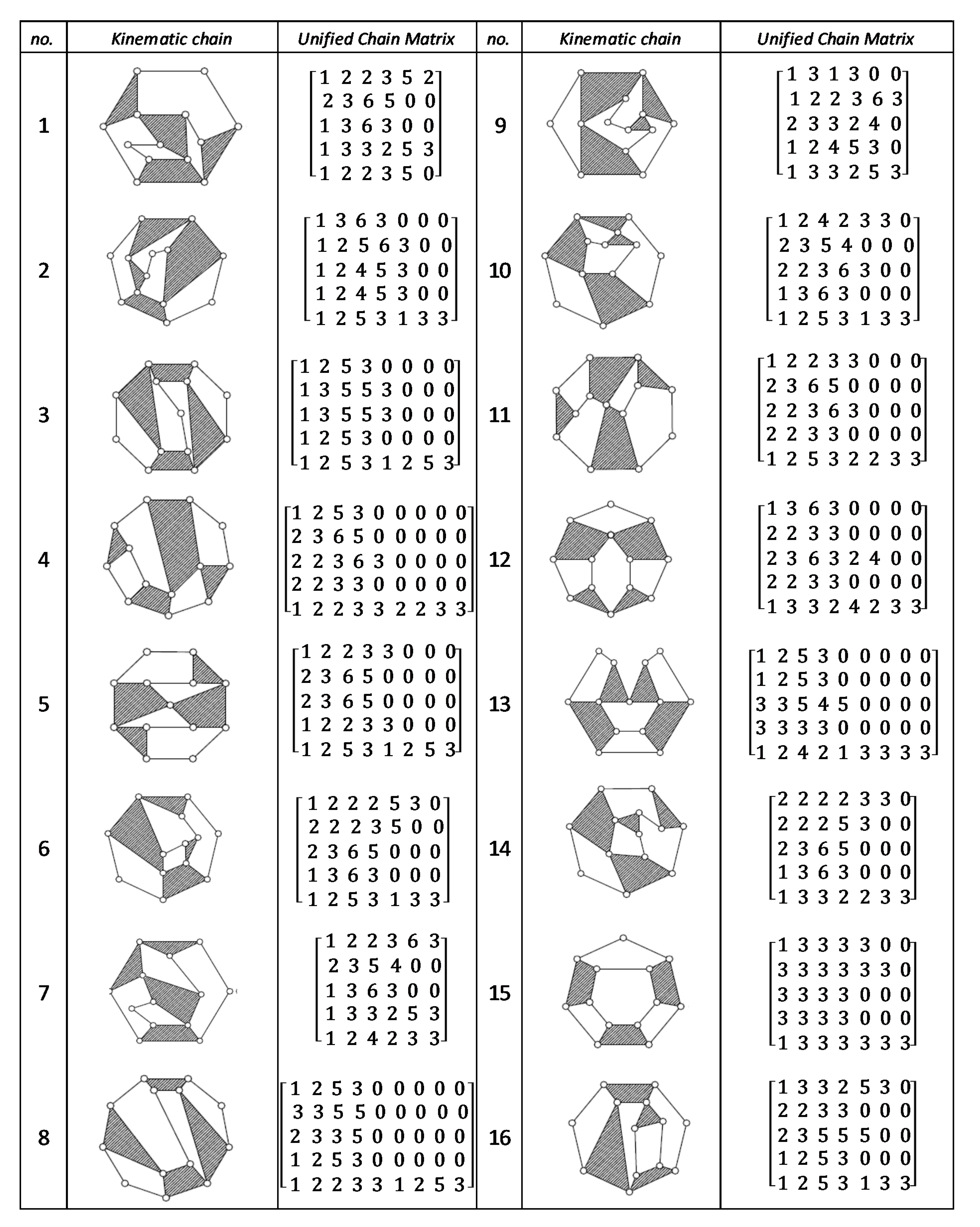
Figure A1.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with 2 multiple joints [25].
Figure A1.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with 2 multiple joints [25].
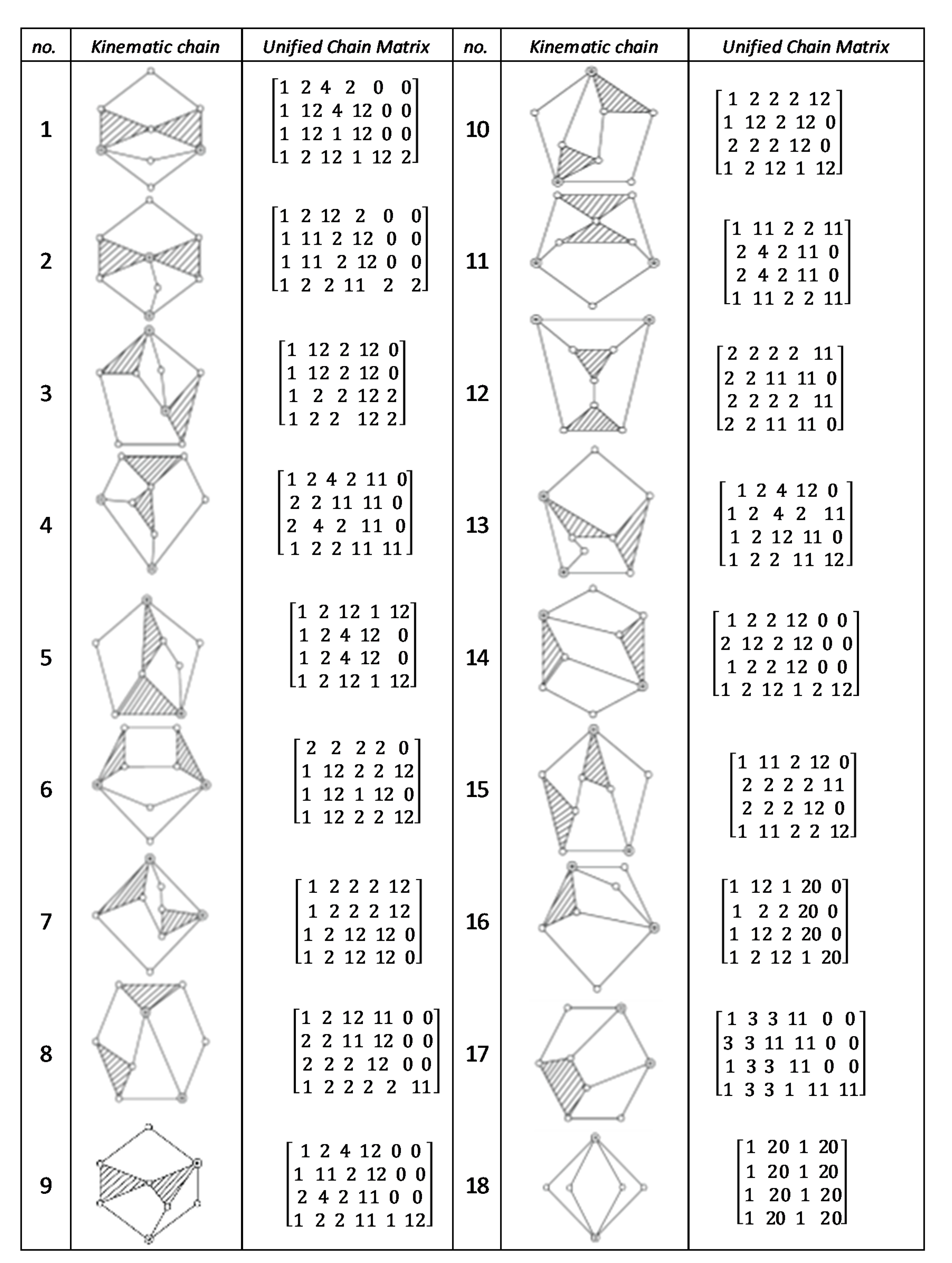
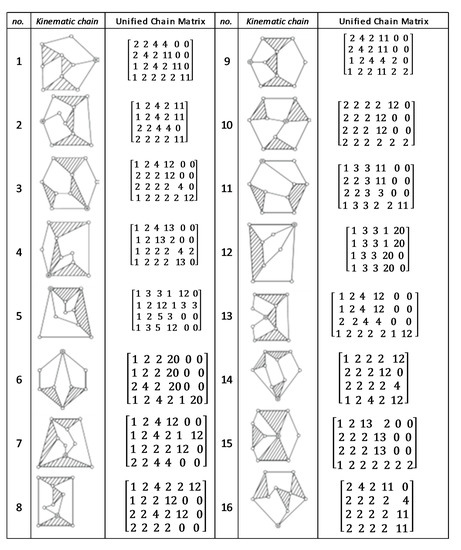
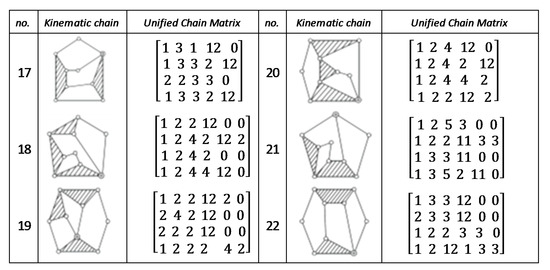
Figure A2.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with 1 multiple joint [25].
Figure A2.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with 1 multiple joint [25].
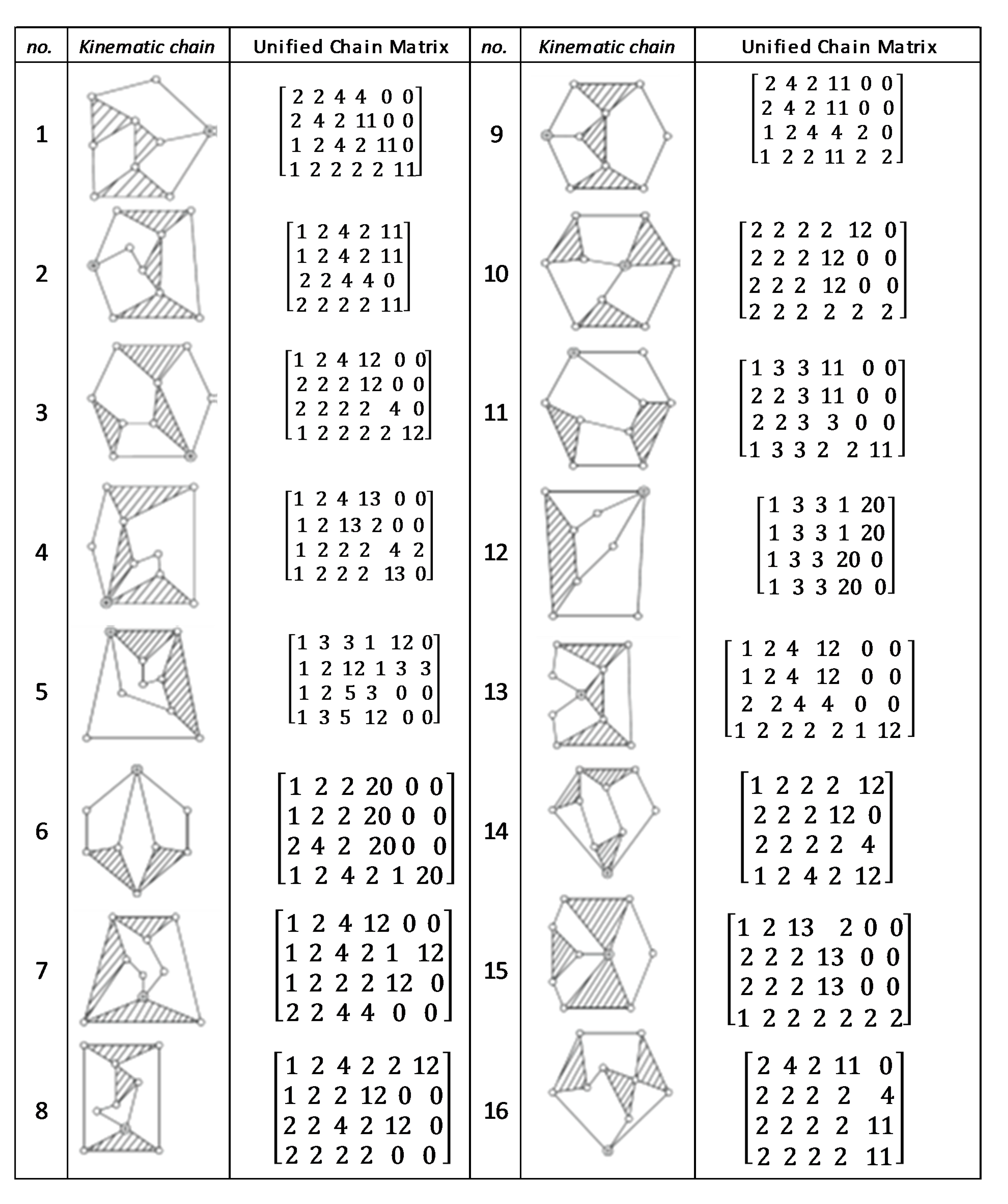
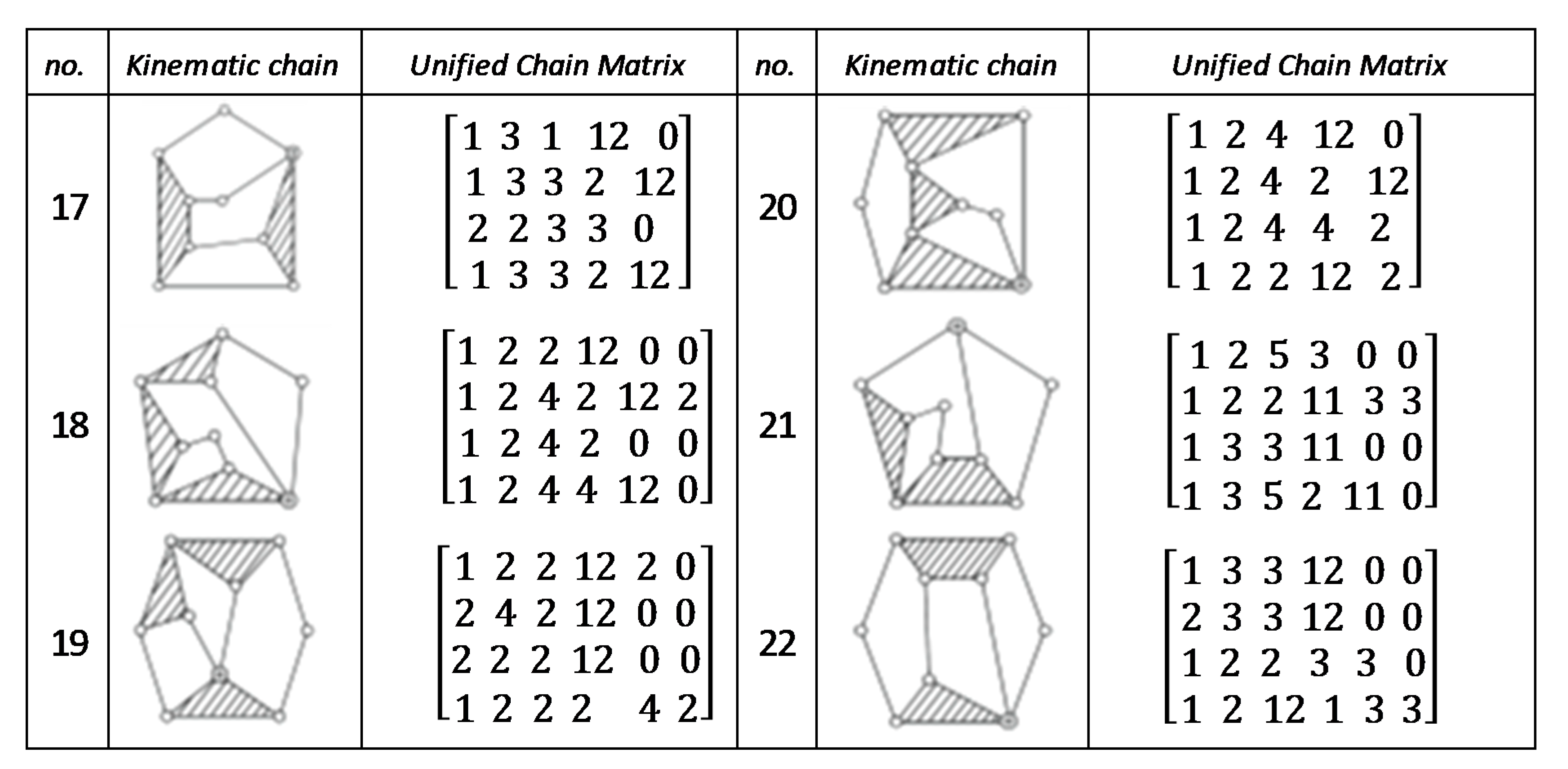
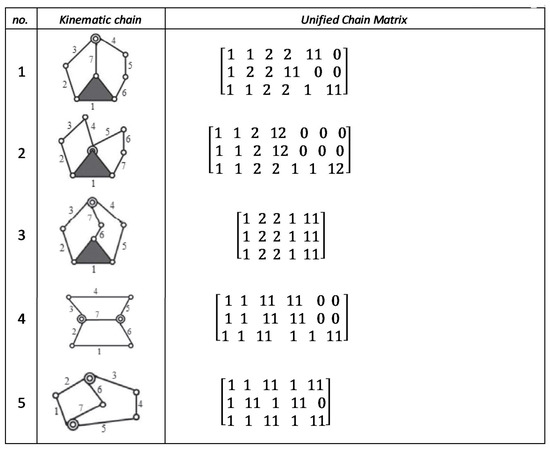
Figure A3.
Unified chain matrix, UCM, for all 7 links 2-DOF KCs with 1, 2 multiple joints [40].
Figure A3.
Unified chain matrix, UCM, for all 7 links 2-DOF KCs with 1, 2 multiple joints [40].
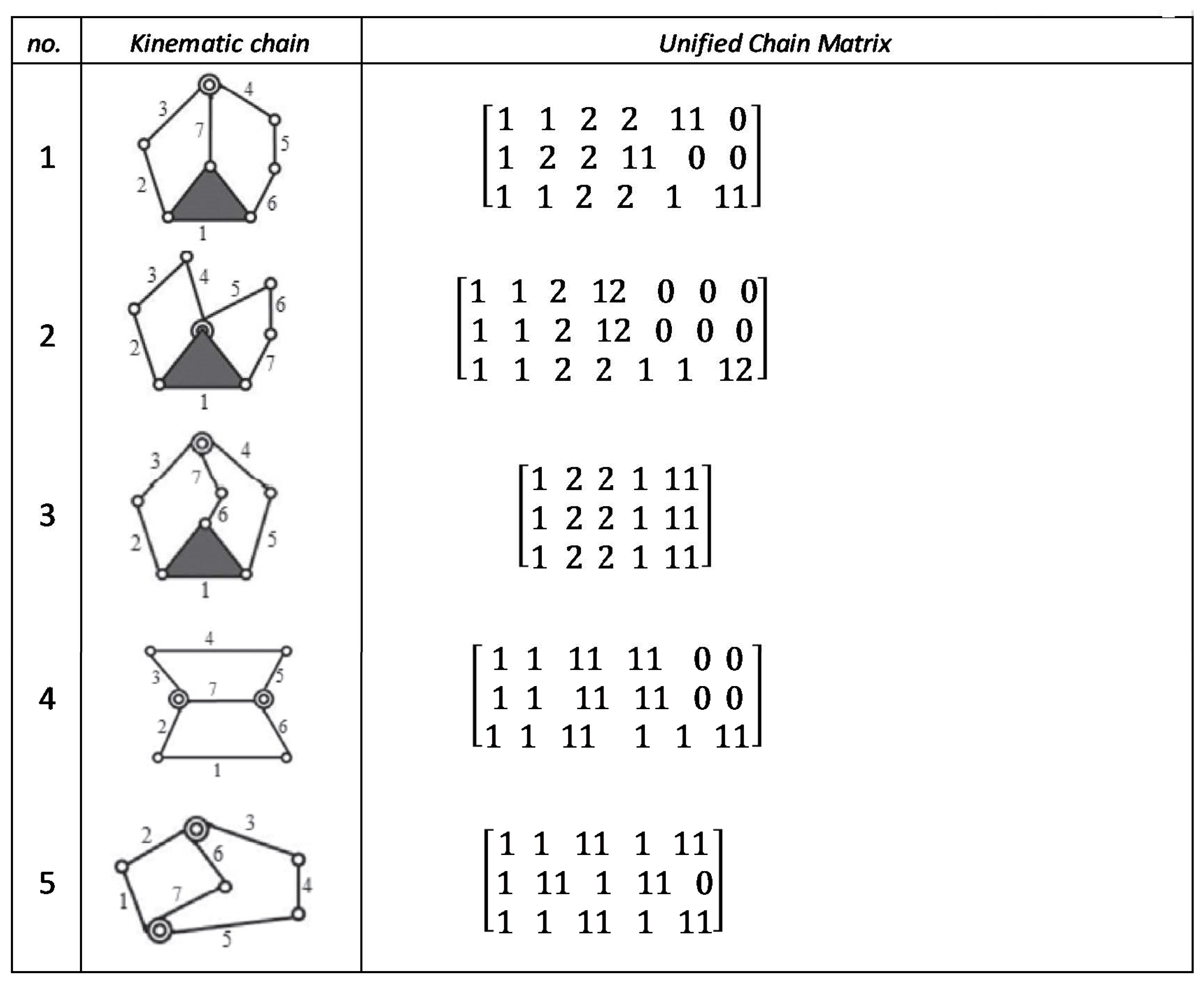

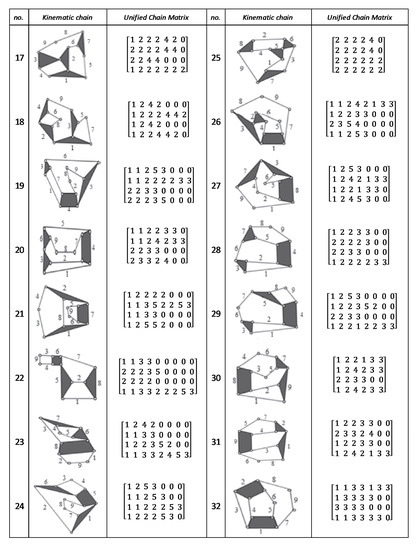
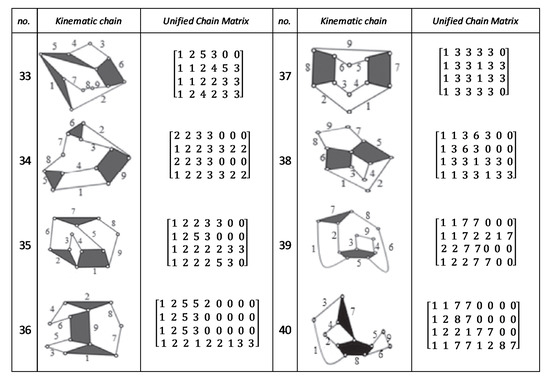
Figure A4.
Unified chain matrix, UCM, for all 9 links and 2-DOF KCs with simple joints [40].
Figure A4.
Unified chain matrix, UCM, for all 9 links and 2-DOF KCs with simple joints [40].

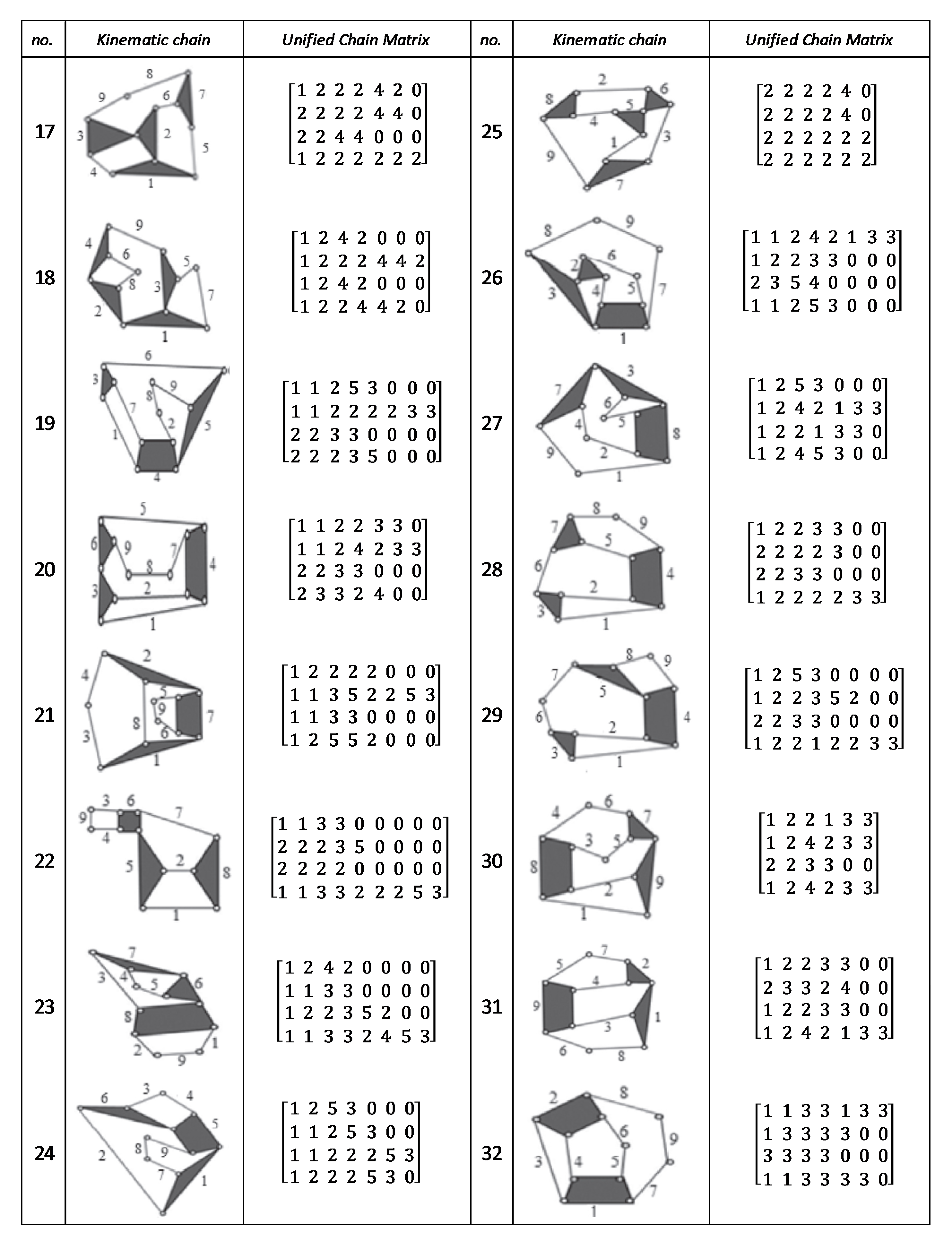
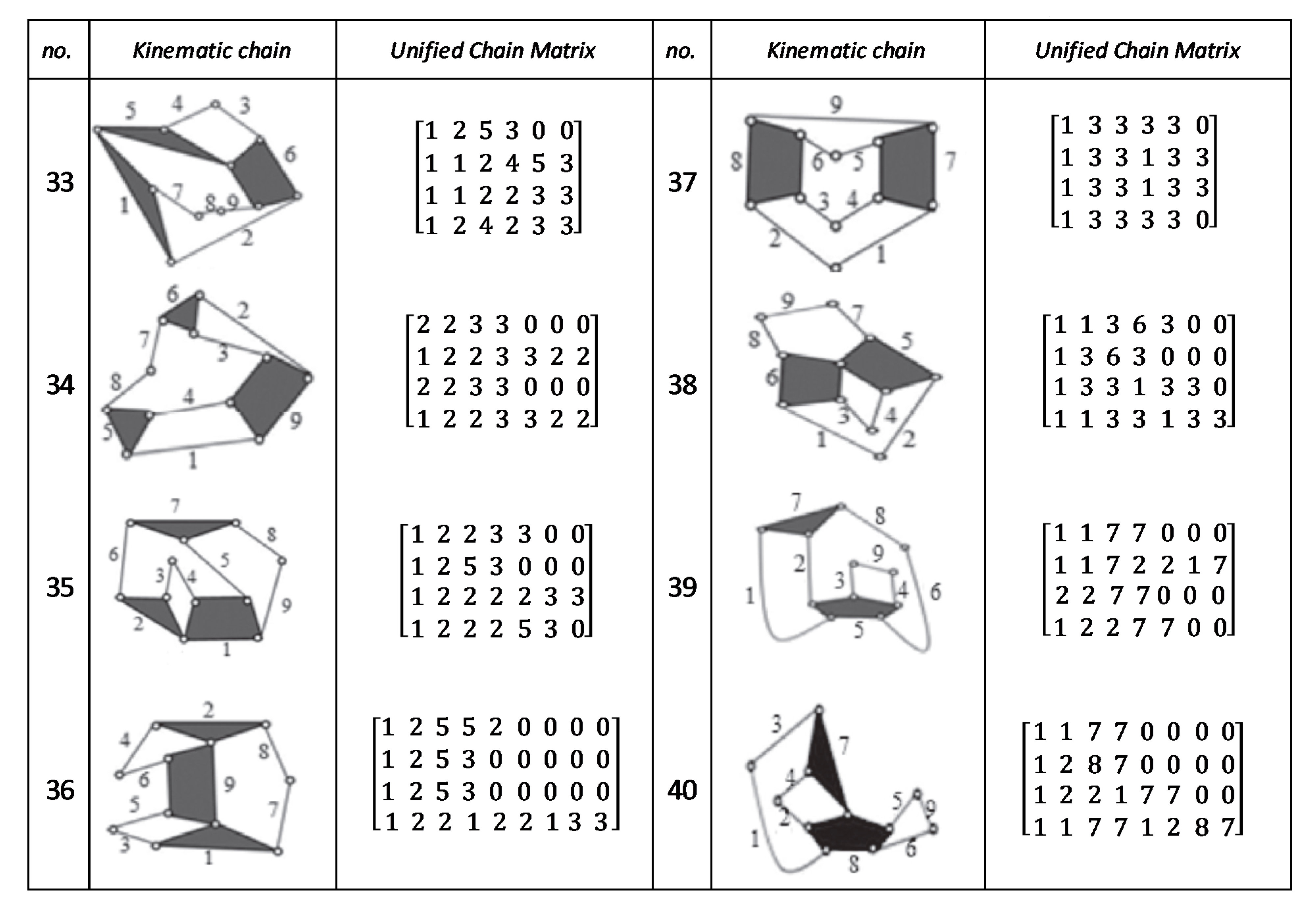
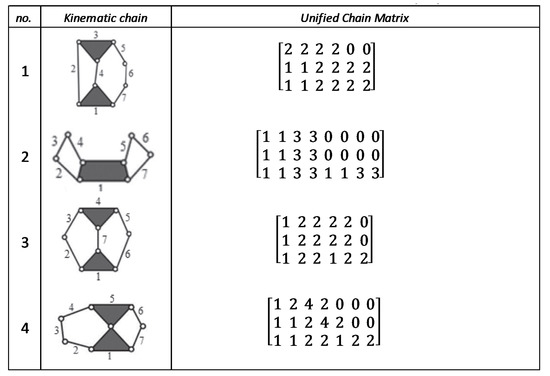
Figure A5.
Unified chain matrix, UCM, for all 7 links 2-DOF KCs with simple joints [40].
Figure A5.
Unified chain matrix, UCM, for all 7 links 2-DOF KCs with simple joints [40].
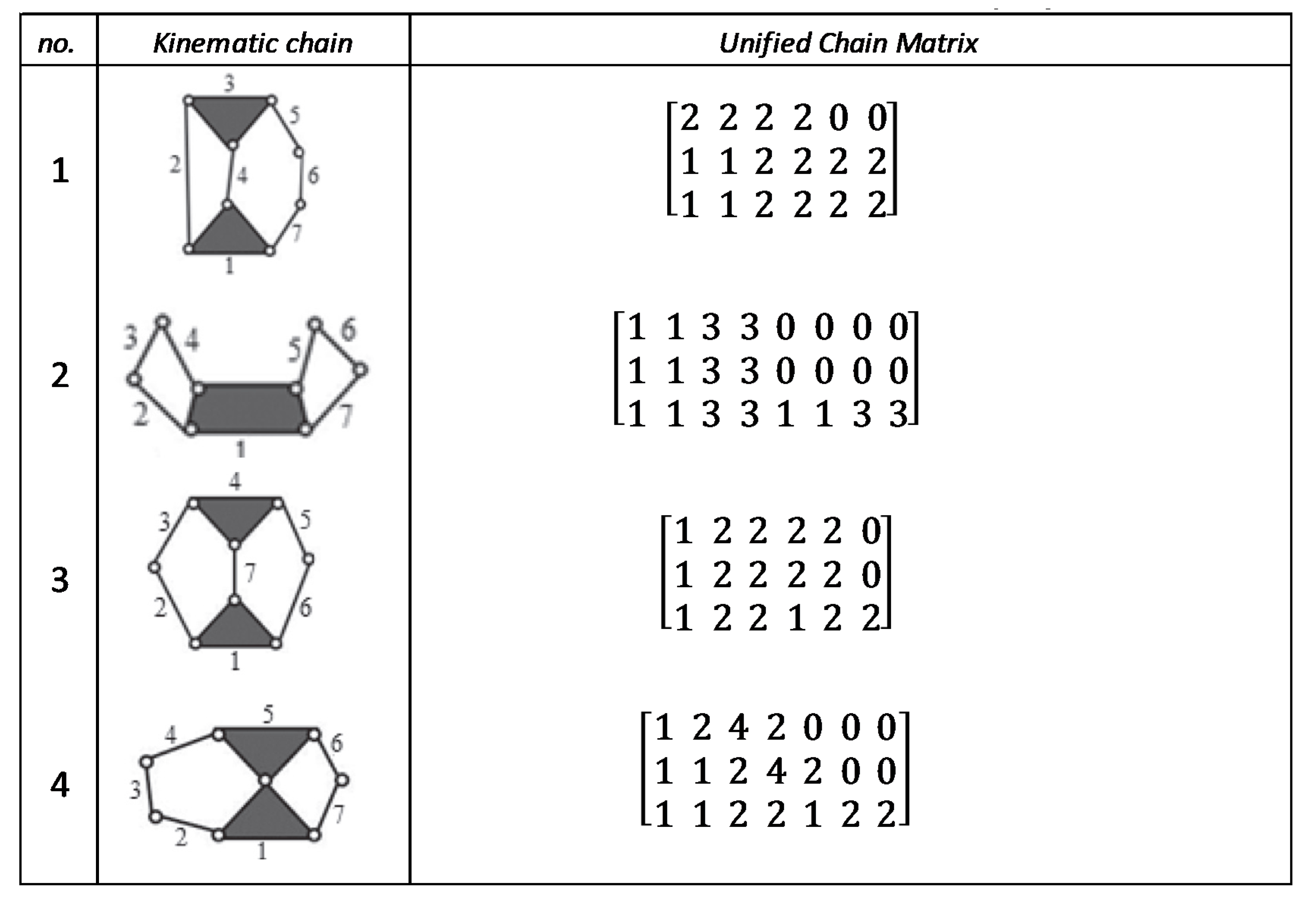
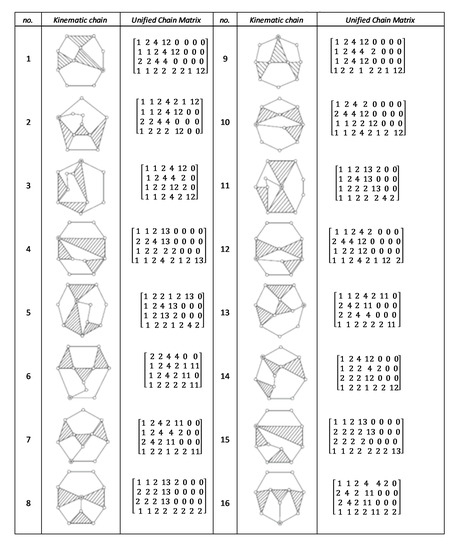
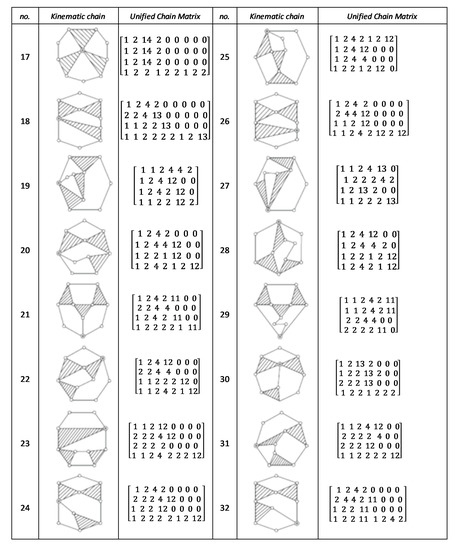
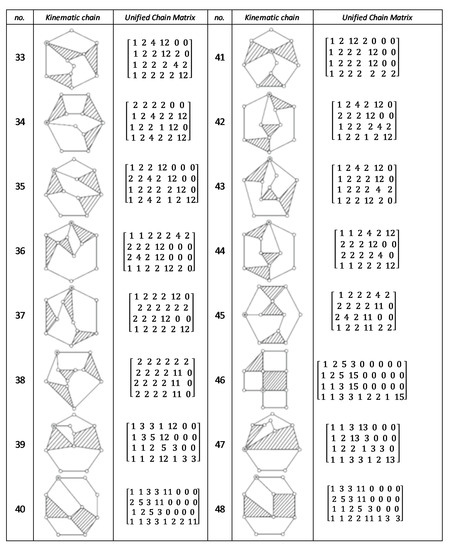
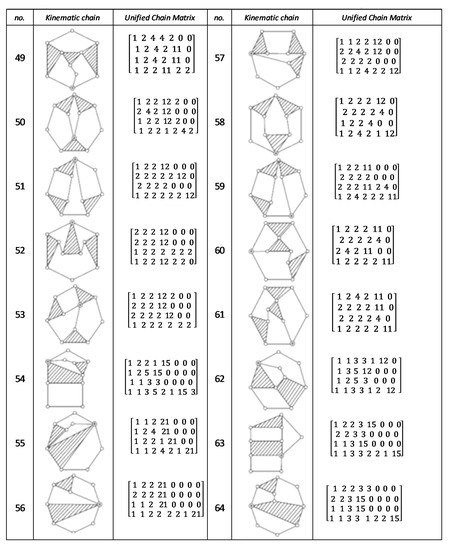
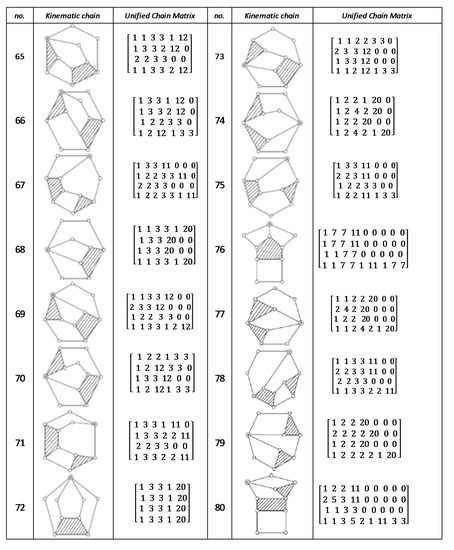
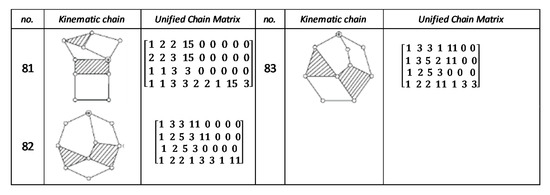
Figure A6.
Unified chain matrix, UCM, for all 9-links of 2-DOF KCs with 1-multiple joint [25].
Figure A6.
Unified chain matrix, UCM, for all 9-links of 2-DOF KCs with 1-multiple joint [25].
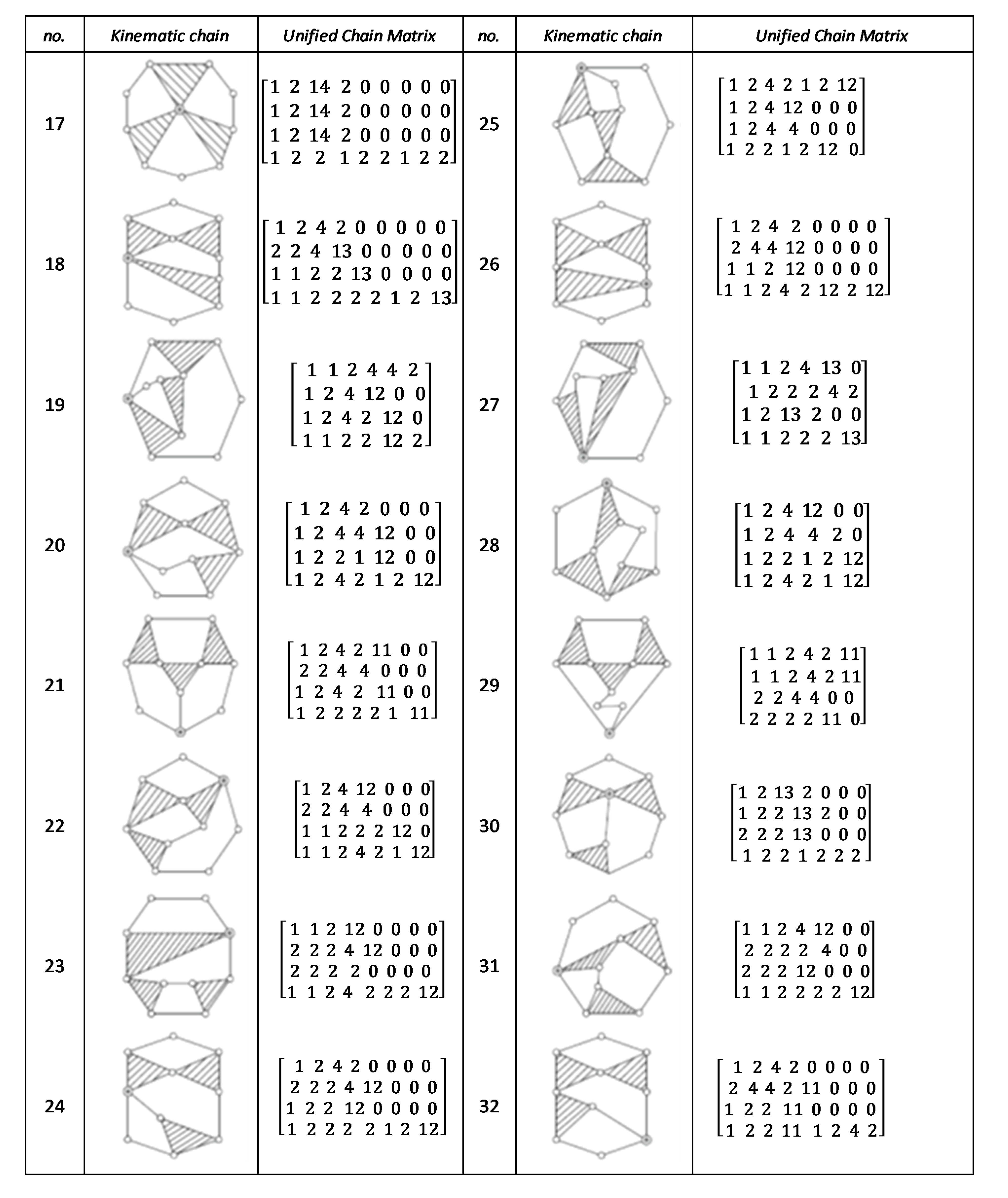
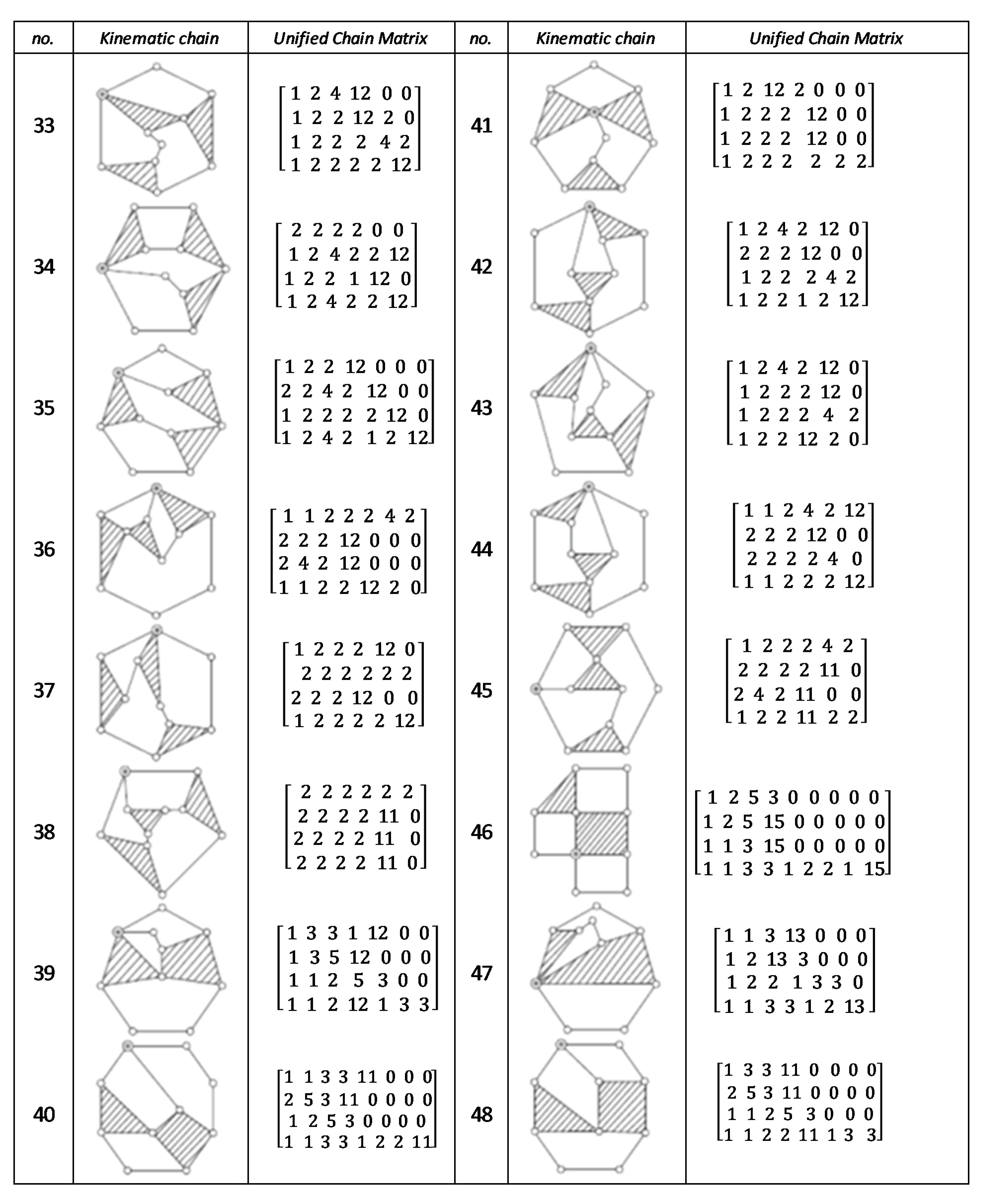
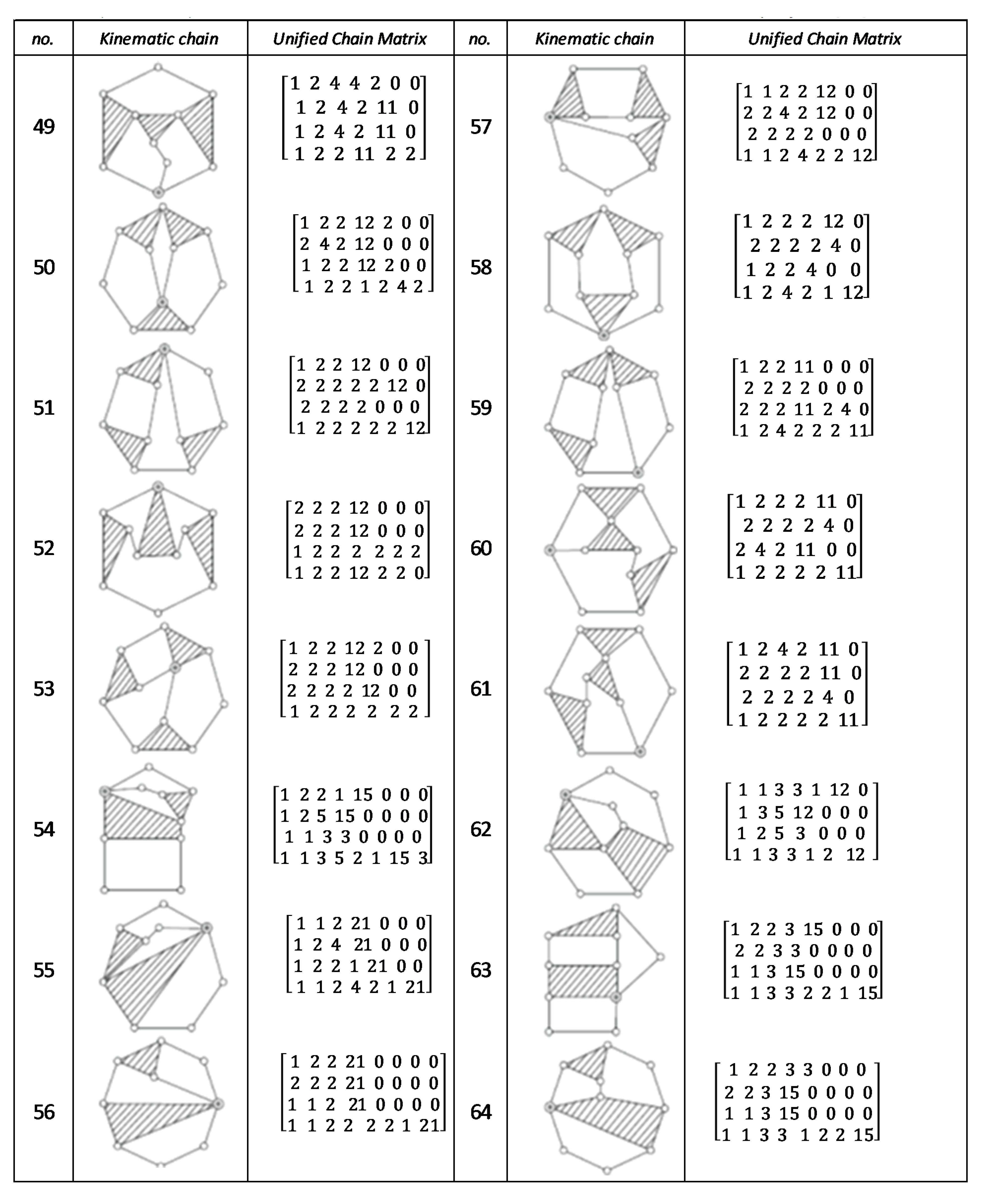
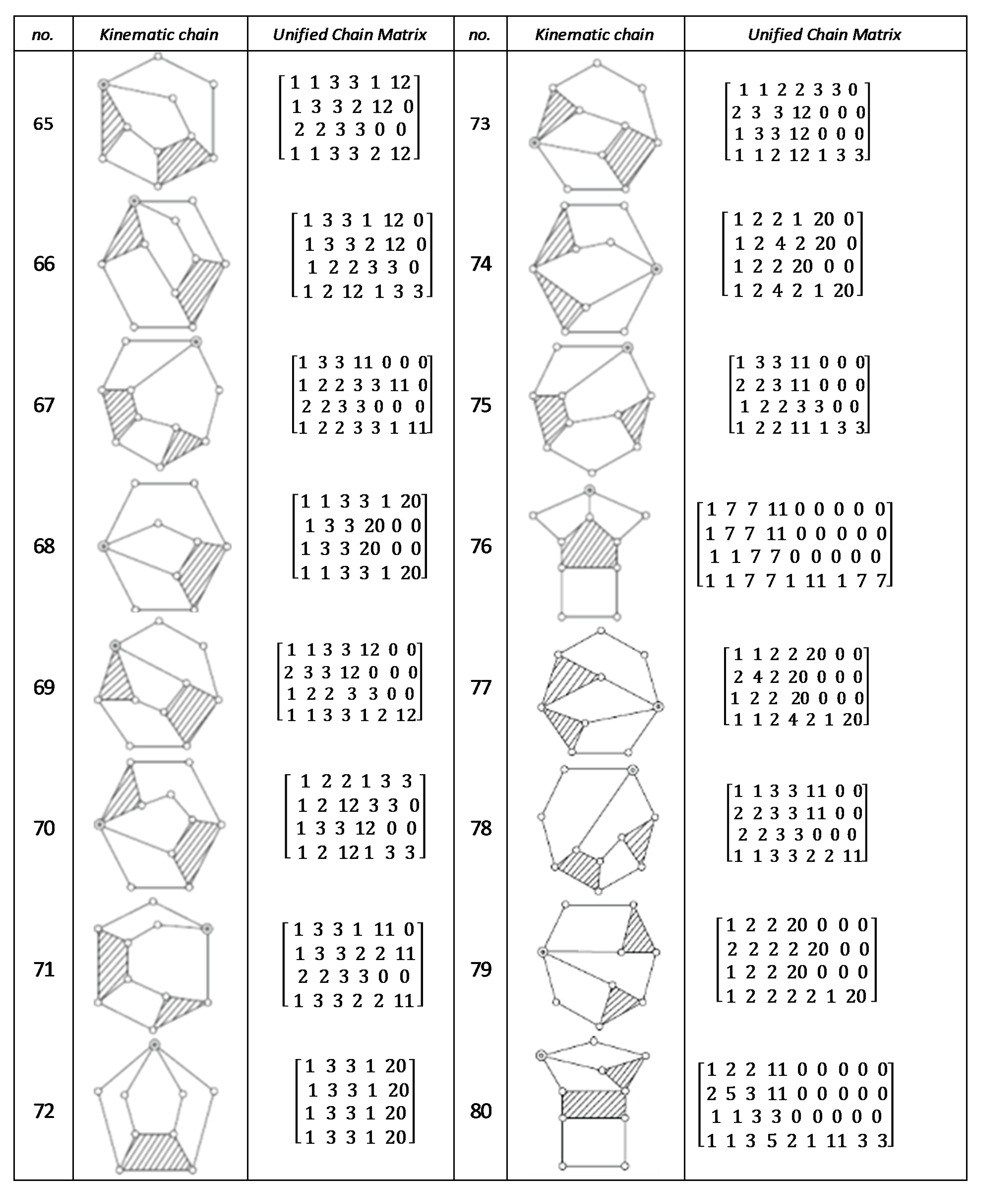
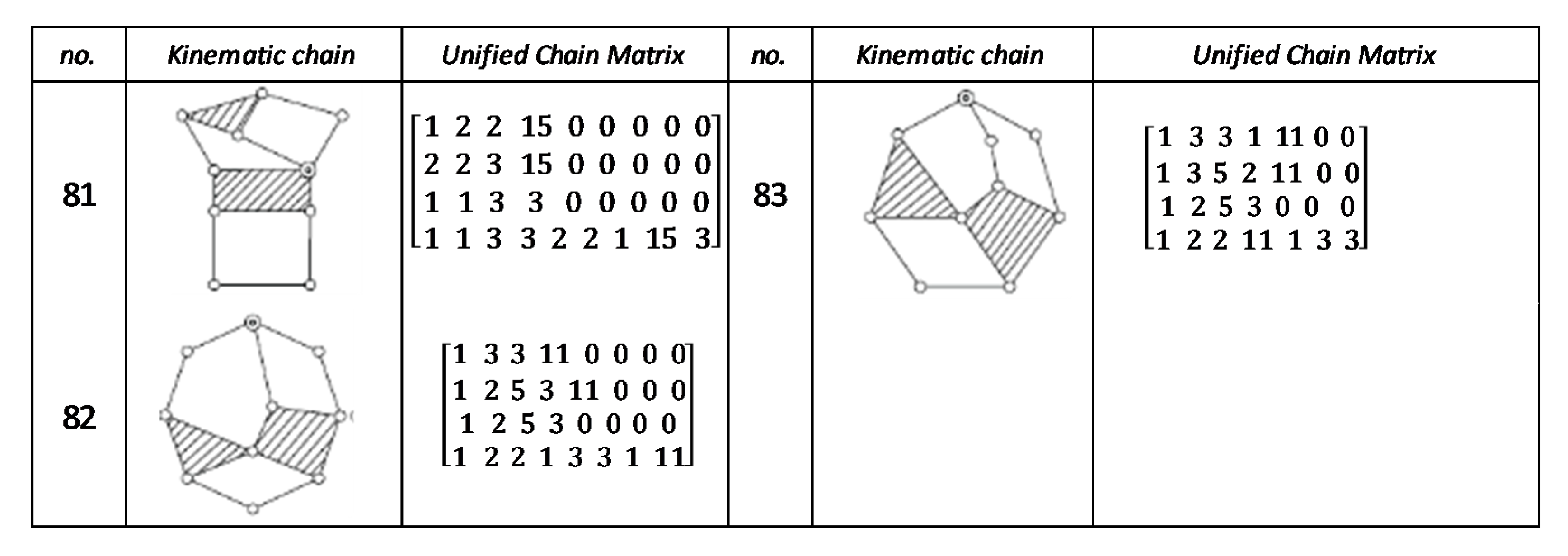
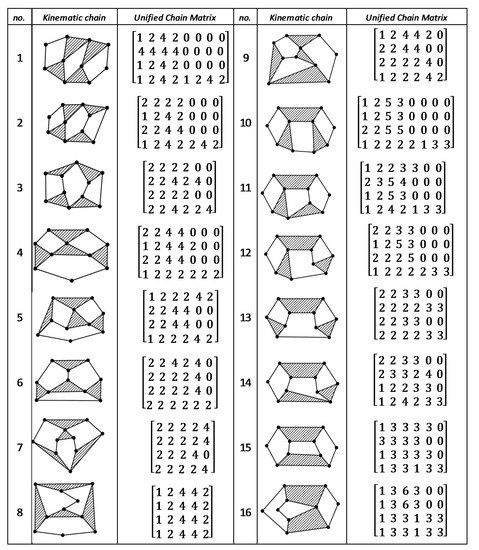
Figure A7.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with simple joints [37].
Figure A7.
Unified chain matrix, UCM, for all 8 links 1-DOF KCs with simple joints [37].
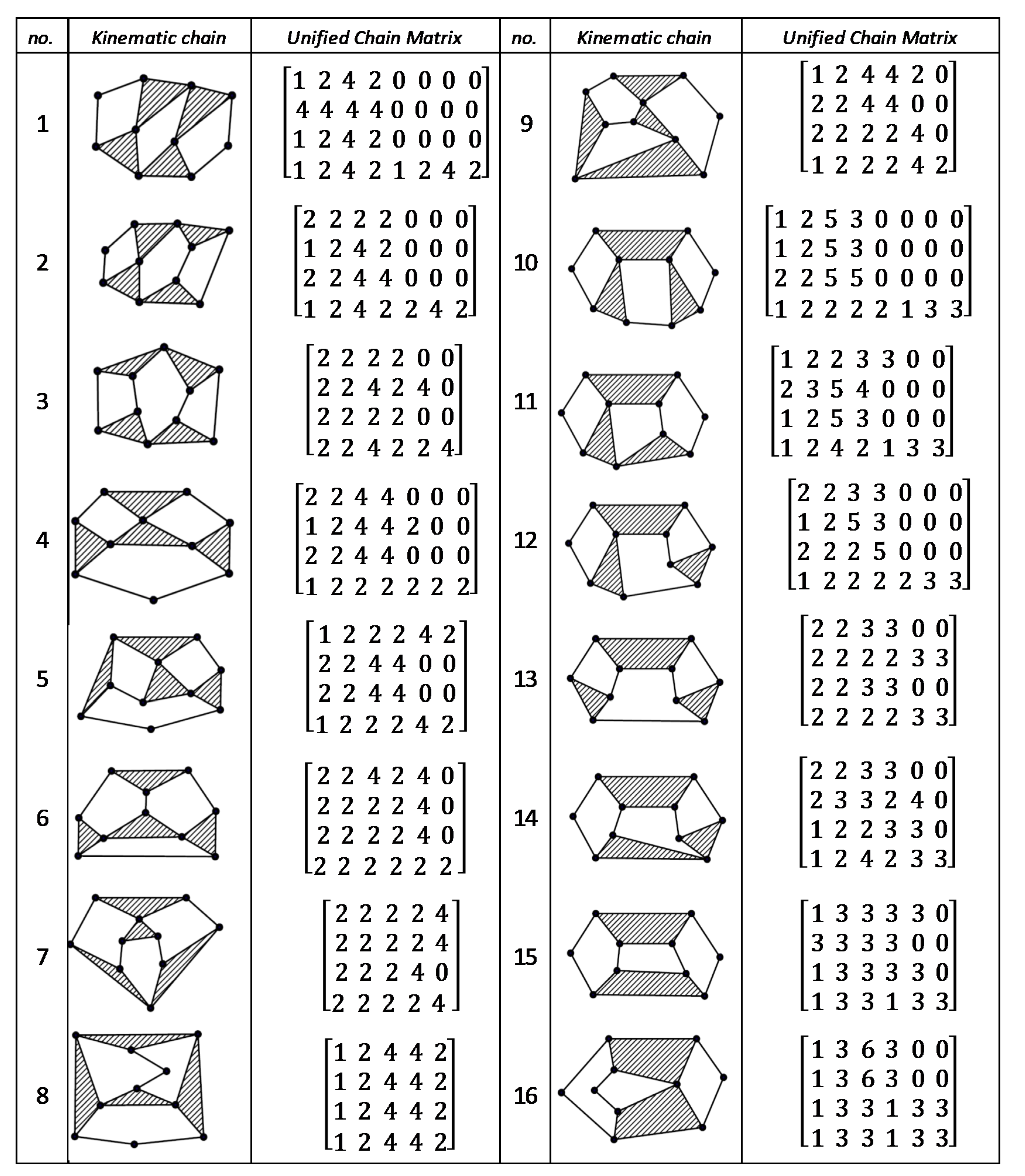
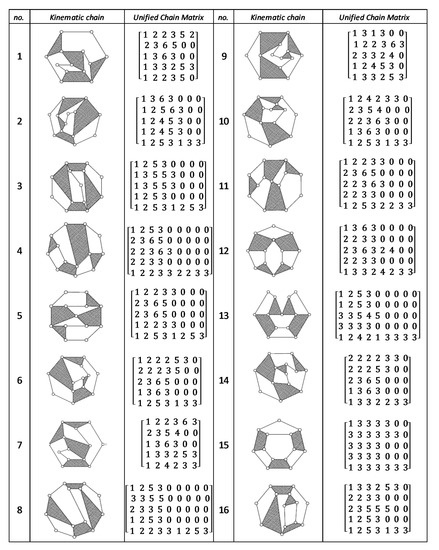
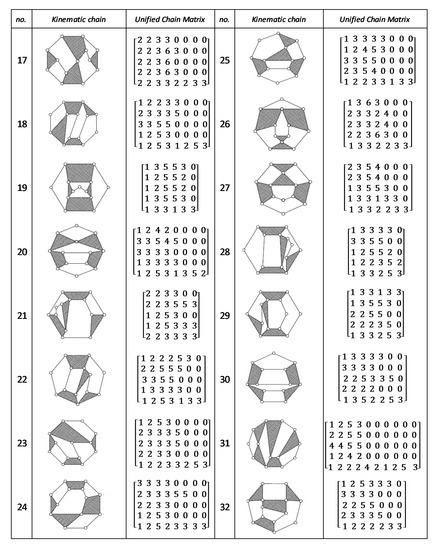
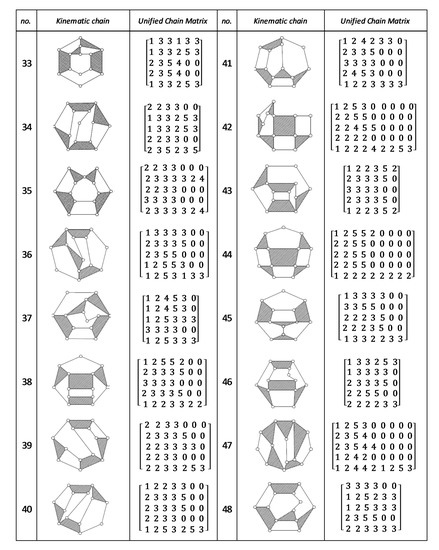
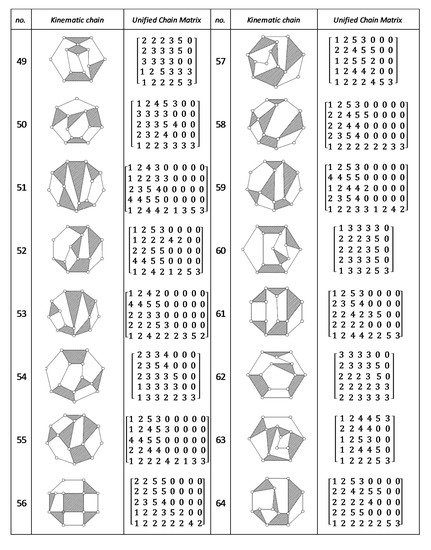
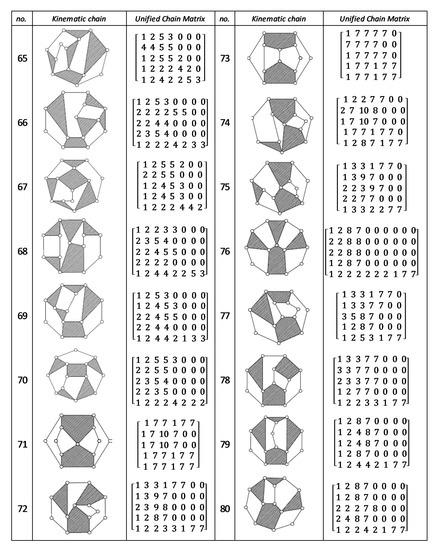
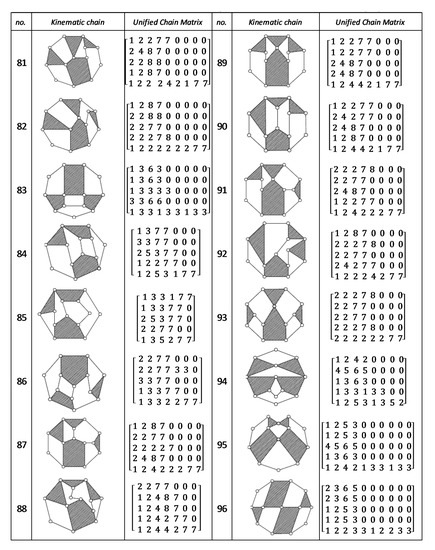
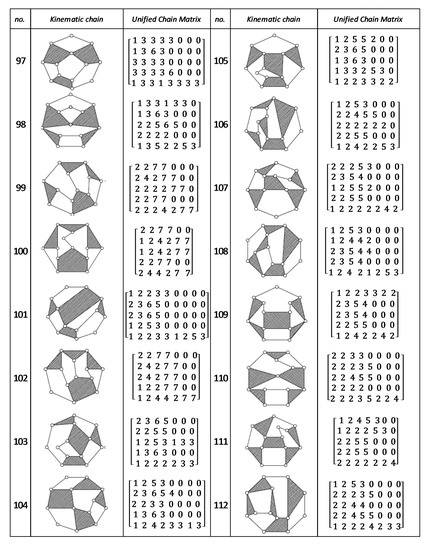
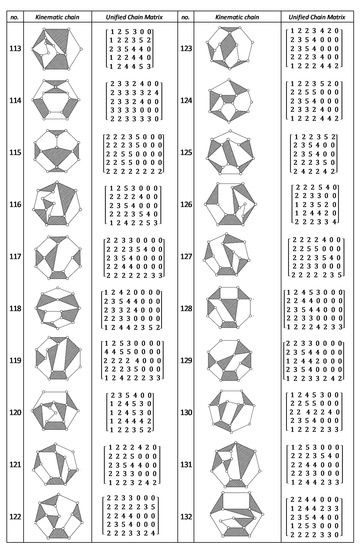
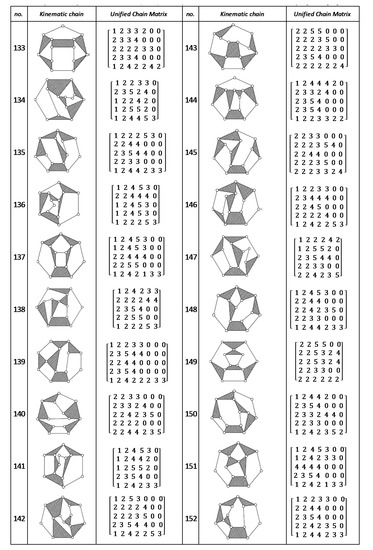
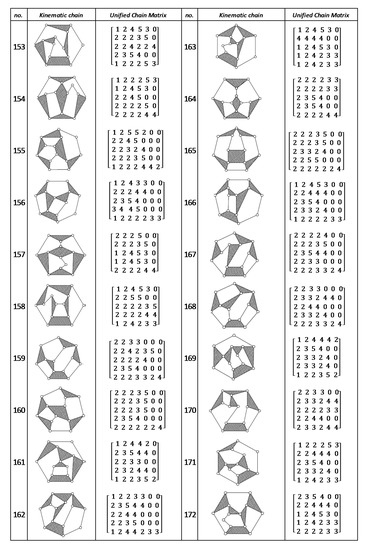
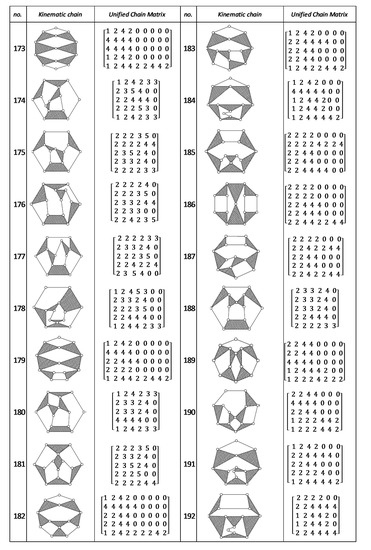
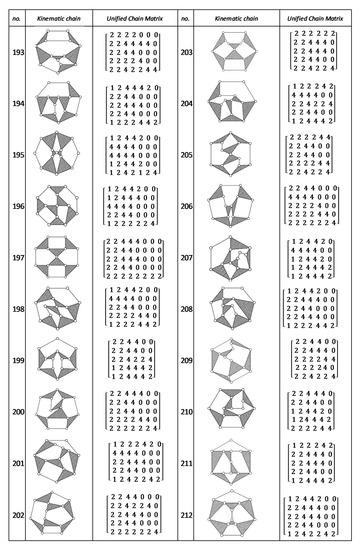
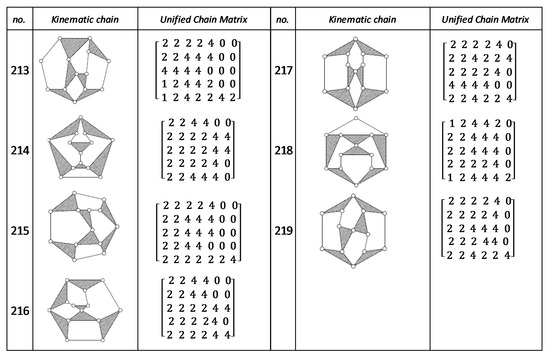
Figure A8.
Unified Joint matrix, UJM, for all planar 10 links and 1-dof KCs with simple joints [41].
Figure A8.
Unified Joint matrix, UJM, for all planar 10 links and 1-dof KCs with simple joints [41].
References
- Mruthyunjaya, T. A computerized methodology for structural synthesis of kinematic chains: Part 1—Formulation. Mech. Mach. Theory 1984, 19, 487–495. [Google Scholar] [CrossRef]
- Mruthyunjaya, T. A computerized methodology for structural synthesis of kinematic chains: Part 2—Application to several fully or partially known cases. Mech. Mach. Theory 1984, 19, 497–505. [Google Scholar] [CrossRef]
- Mruthyunjaya, T.; Balasubramanian, H. In quest of a reliable and efficient computational test for detection of isomorphism in kinematic chains. Mech. Mach. Theory 1987, 22, 131–139. [Google Scholar] [CrossRef]
- Jin-Kui, C.; Wei-Qing, C. Identification of isomorphism among kinematic chains and inversions using link′s adjacent-chain-table. Mech. Mach. Theory 1994, 29, 53–58. [Google Scholar] [CrossRef]
- Shende, S.; Rao, A. Isomorphism in kinematic chains. Mech. Mach. Theory 1994, 29, 1065–1070. [Google Scholar] [CrossRef]
- Yadav, J.; Pratap, C.; Agrawal, V. Computer aided detection of isomorphism among binary chains using the link-link multiplicity distance concept. Mech. Mach. Theory 1996, 31, 873–877. [Google Scholar] [CrossRef]
- Rao, A. Application of fuzzy logic for the study of isomorphism, inversions, symmetry, parallelism and mobility in kinematic chains. Mech. Mach. Theory 2000, 35, 1103–1116. [Google Scholar] [CrossRef]
- Rao, A.C.; Pathapati, V.V.N.R.P.R. Loop Based Detection of Isomorphism Among Chains, Inversions and Type of Freedom in Multi Degree of Freedom Chain. J. Mech. Des. 1999, 122, 31–42. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, C.; Yang, Y.; Wang, Y. A new method to mechanism kinematic chain isomorphism identification. Mech. Mach. Theory 2002, 37, 411–417. [Google Scholar] [CrossRef]
- And, P.R.H.; Zhang, W.J.; And, Q.L.; Wu, F.X.; He, P.R.; Li, Q. A New Method for Detection of Graph Isomorphism Based on the Quadratic Form. J. Mech. Des. 2003, 125, 640–642. [Google Scholar] [CrossRef]
- Cubillo, J.; Wan, J. Comments on mechanism kinematic chain isomorphism identification using adjacent matrices. Mech. Mach. Theory 2005, 40, 131–139. [Google Scholar] [CrossRef]
- Butcher, E.A.; Hartman, C. Efficient enumeration and hierarchical classification of planar simple-jointed kinematic chains: Application to 12- and 14-bar single degree-of-freedom chains. Mech. Mach. Theory 2005, 40, 1030–1050. [Google Scholar] [CrossRef]
- Pucheta, M.; Cardona, A. An automated method for type synthesis of planar linkages based on a constrained subgraph isomorphism detection. Multibody Syst. Dyn. 2007, 18, 233–258. [Google Scholar] [CrossRef]
- Ding, H.; Huang, Z. The Establishment of the Canonical Perimeter Topological Graph of Kinematic Chains and Isomorphism Identification. J. Mech. Des. 2006, 129, 915–923. [Google Scholar] [CrossRef]
- Ding, H.; Huang, Z. A new theory for the topological structure analysis of kinematic chains and its applications. Mech. Mach. Theory 2007, 42, 1264–1279. [Google Scholar] [CrossRef]
- Ding, H.; Huang, Z. Isomorphism identification of graphs: Especially for the graphs of kinematic chains. Mech. Mach. Theory 2009, 44, 122–139. [Google Scholar] [CrossRef]
- Hasan, A.; Khan, R.A. Isomorphism and Inversions Of Kinematic Chains Up To Ten Links Using Degrees Of Freedom Of Kinematic Pairs. Int. J. Comput. Methods 2008, 5, 329–339. [Google Scholar] [CrossRef]
- Dargar, A.; Khan, R.A.; Hasan, A. Application of link adjacency values to detect isomorphism among kinematic chains. Int. J. Mech. Mater. Des. 2010, 6, 157–162. [Google Scholar] [CrossRef]
- Dargar, A.; Hasan, A.; Khan, R. Some new codes for isomorphism identification among kinematic chains and their inversions. Int. J. Mech. Robot. Syst. 2013, 1, 49. [Google Scholar] [CrossRef]
- Galán-Marín, G.; López-Rodríguez, D.; Mérida-Casermeiro, E. A New Multivalued Neural Network for Isomorphism Identification of Kinematic Chains. J. Comput. Inf. Sci. Eng. 2010, 10, 011009. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, F.; Tao, J. Adding sub-chain method for structural synthesis of planar closed kinematic chains. Chin. J. Mech. Eng. 2012, 25, 206–213. [Google Scholar] [CrossRef]
- Ding, H.; Cao, W.; Kecskeméthy, A.; Huang, Z. Complete Atlas Database of 2-DOF Kinematic Chains and Creative Design of Mechanisms. J. Mech. Des. 2012, 134, 031006. [Google Scholar] [CrossRef]
- Ding, H.; Hou, F.; Kecskeméthy, A.; Huang, Z. Synthesis of the whole family of planar 1-DOF kinematic chains and creation of their atlas database. Mech. Mach. Theory 2012, 47, 1–15. [Google Scholar] [CrossRef]
- Ding, H.; Yang, W.; Huang, P.; Kecskeméthy, A. Automatic Structural Synthesis of Planar Multiple Joint Kinematic Chains. J. Mech. Des. 2013, 135, 091007. [Google Scholar] [CrossRef]
- Ding, H.; Zhao, J.; Huang, Z. Unified structural synthesis of planar simple and multiple joint kinematic chains. Mech. Mach. Theory 2010, 45, 555–568. [Google Scholar] [CrossRef]
- Yang, F.; Deng, Z.; Tao, J.; Li, L. A new method for isomorphism identification in topological graphs using incident matrices. Mech. Mach. Theory 2012, 49, 298–307. [Google Scholar] [CrossRef]
- Rizvi, S.; Hasan, D.A.; Khan, R.A. A New Method Based on the Comparison of the Unique Chain Code to Detect Isomorphism among Kinematic Chains. J. Eng. Res. 2014, 1, 16–21. [Google Scholar]
- ShaneHaiderRizvi, S.; Hasan, A.; Khan, R.A. A New Concept to Detect Isomorphism in Kinematic Chains using Fuzzy Similarity Index. Int. J. Comput. Appl. 2014, 86, 30–33. [Google Scholar] [CrossRef][Green Version]
- Rizvi, S.S.H.; Hasan, A.; Khan, R. An efficient algorithm for distinct inversions and isomorphism detection in kinematic chains. Perspect. Sci. 2016, 8, 251–253. [Google Scholar] [CrossRef][Green Version]
- Zeng, K.; Fan, X.; Dong, M.; Yang, P. A fast algorithm for kinematic chain isomorphism identification based on dividing and matching vertices. Mech. Mach. Theory 2014, 72, 25–38. [Google Scholar] [CrossRef]
- Yang, P.; Zeng, K.; Li, C.; Yang, J.; Wang, S. An improved hybrid immune algorithm for mechanism kinematic chain isomorphism identification in intelligent design. Soft Comput. 2014, 19, 217–223. [Google Scholar] [CrossRef]
- Liu, H.; Shi, S.; Yang, P.; Yang, J. An Improved Genetic Algorithm Approach on Mechanism Kinematic Structure Enumeration with Intelligent Manufacturing. J. Intell. Robot. Syst. 2018, 89, 343–350. [Google Scholar] [CrossRef]
- Pozhbelko, V. A unified structure theory of multibody open-, closed-, and mixed-loop mechanical systems with simple and multiple joint kinematic chains. Mech. Mach. Theory 2016, 100, 1–16. [Google Scholar] [CrossRef]
- Ding, H.; Huang, P.; Yang, W.; Kecskeméthy, A. Automatic generation of the complete set of planar kinematic chains with up to six independent loops and up to 19 links. Mech. Mach. Theory 2016, 96, 75–93. [Google Scholar] [CrossRef]
- Ding, H.; Yang, W.; Zi, B.; Kecskeméthy, A. The family of planar kinematic chains with two multiple joints. Mech. Mach. Theory 2016, 99, 103–116. [Google Scholar] [CrossRef]
- Kamesh, V.V.; Rao, K.M.; Rao, A.B.S. An Innovative Approach to Detect Isomorphism in Planar and Geared Kinematic Chains Using Graph Theory. J. Mech. Des. 2017, 139, 122301. [Google Scholar] [CrossRef]
- Eleashy, H. A new atlas for 8-bar kinematic chains with up to 3 prismatic pairs using Joint Sorting Code. Mech. Mach. Theory 2018, 124, 118–132. [Google Scholar] [CrossRef]
- Yang, W.; Ding, H.; Kecskeméthy, A. Automatic synthesis of plane kinematic chains with prismatic pairs and up to 14 links. Mech. Mach. Theory 2019, 132, 236–247. [Google Scholar] [CrossRef]
- Rai, R.K.; Punjabi, S. Kinematic chains isomorphism identification using link connectivity number and entropy neglecting tolerance and clearance. Mech. Mach. Theory 2018, 123, 40–65. [Google Scholar] [CrossRef]
- Rai, R.K.; Punjabi, S. A new algorithm of links labelling for the isomorphism detection of various kinematic chains using binary code. Mech. Mach. Theory 2019, 131, 1–32. [Google Scholar] [CrossRef]
- Deng, T.; Xu, H.; Tang, P.; Liu, P.; Yan, L. A novel algorithm for the isomorphism detection of various kinematic chains using topological index. Mech. Mach. Theory 2020, 146, 103740. [Google Scholar] [CrossRef]
- Li, T.-J.; Cao, W.-Q.; Chu, J.-K. The Topological Representation and Detection of Isomorphism among Geared Linkage Kinematic Chains. In Proceedings of the Volume 1A: 25th Biennial Mechanisms Conference, Atlanta, GA, USA, 13–16 September 1998. [Google Scholar]
- Chu, J.; Cao, W.; Yang, T. Type Synthesis of Baranov Truss with Multiple Joints and Multiple-Joint Links. In Proceedings of the Volume 1A: 25th Biennial Mechanisms Conference, Atlanta, GA, USA, 13–16 September 1998. [Google Scholar]
- Chu, J.; Zou, Y.; He, P. The structural synthesis of planar 10-link, 3-DOF simple and multiple joint kinematic chains. Int. J. Biomechatron. Biomed. Robot. 2013, 2, 150. [Google Scholar] [CrossRef]
- Yang, W.; Ding, H.; Kecskeméthy, A. A new method for the automatic sketching of planar kinematic chains. Mech. Mach. Theory 2018, 121, 755–768. [Google Scholar] [CrossRef]
- Ding, H.; Hou, F.; Kecskeméthy, A.; Huang, Z. Synthesis of a complete set of contracted graphs for planar non-fractionated simple-jointed kinematic chains with all possible DOFs. Mech. Mach. Theory 2011, 46, 1588–1600. [Google Scholar] [CrossRef]
- Rizk, R.; Awad, M. Mechanism, Machine, Robotics and Mechatronics Sciences; Springer International Publisher: New York, NY, USA, 2019. [Google Scholar]
- Tsai, L.-W. Mechanism Design: Enumeration of Kinematic Structures According to Function. J. Mech. Des. 2000, 122, 583. [Google Scholar] [CrossRef]
- Pratap, R. Getting Started with MATLAB; updated for Version 7.8; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).