Development of a Mathematical Model and Validation for Methane Production Using Cow Dung as Substrate in the Underground Biogas Digester
Abstract
:1. Introduction
- It involves the mathematical model for methane production on an hourly basis as opposed to the majority of mathematical models that predict methane production in daily intervals;
- It expands on the impact of additional meteorological factors (ambient temperature, relative humidity, and global solar irradiance) on methane production, as opposed to other popular methane production models that focus only on the impact of ambient temperature as a meteorological factor;
- It demonstrates the simultaneous variability of the inputs to the desired output by the employment of the 3D mesh plots and the potential outcomes of the desired output in the “if scenario” (which is what would have been the output, if other possible inputs were obtained which were not determined by the trained data used in the development of the mathematical models).
Biogas Production Potential in South Africa
2. Experimental Section
2.1. Substrate Preparation
2.2. Experimental/Methane Production Setup
2.3. Development, Consideration and Techniques of the Mathematical Model and Its Validation
2.4. Parameters Used for Establishing a Customized General Model for Methane Production
- Relative pH (pHr): This is the ratio of the absolute pH to the neutral pH (pHn) of 7.00. pH of 7 promises to be the desired pH for optimum biogas production;
- Relative I (Ir): This is the ratio of the absolute global solar irradiance to the maximum global irradiance to the maximum global irradiance (Imax) of 1360 W/m2. This variable is necessary because of the black nature of the material used for the fabrication, which contributes to retaining the heat inside the digester which enhances methane production;
- Relative RH (RHr): This is the ratio of the absolute, relative humidity to the maximum relative humidity (RHmax) of 100%;
- Ambient temperature: This is the surrounding temperature in the vicinity of the digesters (Tam);
- Gas temperature: This is the temperature in the vicinity of methane produced inside the digesters (Tg);
- Slurry bottom temperature: This is the temperature of the slurry at a lower level within the digesters (Tb);
- Slurry top temperature: This is the temperature of the slurry at an upper level within the digesters (Tt).
2.5. Derivation of the Mathematical Model
- (i)
- Step 1: Import the processed data into a data array;
- (ii)
- Step 2: Create a fitted model;
- (iii)
- Step 3: Locate and remove outliers;
- (iv)
- Step 4: Simplify the model;
- (v)
- Step 5: Predict the response (output).
3. Results and Discussion
3.1. Mathematical Model for the Methane Volume in the Biogas Digester
3.2. Effect of the Variables on the Model
3.3. Validation of the Mathematical Model for Methane Production
3.4. Model Sensitivity
4. Suggestion for Future Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Statement of Novelty
Nomenclature
| FHIT | Fort Hare Institute of Technology |
| R2 | Determination of coefficient |
| pHr | Relative pH |
| Ir (W/m2) | Relative global horizontal irradiance |
| RHr (%) | Relative humidity |
| I (W/m2) | Global horizontal irradiance |
| Tg (°C) | Gas temperature |
| C/N | Carbon/nitrogen |
| Tt (°C) | Slurry top temperature |
| ADM1 | Anaerobic digestion model no. 1 |
| AD | Anaerobic digestion |
| Tam (°C) | Ambient temperature |
| RMSE | Root means square error |
| Tb (°C) | Slurry bottom temperature |
| ANN | Artificial neural network |
| IA | Index of agreement |
| CH4 (mL/gVS) | Methane |
| HDPE | High-density polyethylene plastic |
References
- Manjusha, C.; Sajeena, B. Mathematical modelling and stimulation of anaerobic digestion of solid waste. Procedia Technol. 2016, 24, 654–660. [Google Scholar] [CrossRef] [Green Version]
- Ahring, B.K. Biomethanation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Deublein, D.; Steinhauser, A. Biogas from Waste and Renewable Resources—An Introduction; WileyVCH Verlag GmbH & Co, KGaA: Weinheim, Germany, 2003. [Google Scholar]
- Wu, C.F.J.; Hamada, M. Experiment: Planning, Analysis and Parameter Design Optimization, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bush, R.R.; Mosteller, F. A mathematical model for simple learning. In Selected Papers of Frederick Mosteller; Springer: New York, NY, USA, 2006; pp. 221–234. [Google Scholar]
- Enitan, A.M.; Adeyemo, J.; Swalaha, F.M.; Kumari, S.; Bux, F. Optimization of biogas generation using anaerobic digestion models and computational intelligence approaches. Rev. Chem. Eng. 2017, 33, 309–335. [Google Scholar] [CrossRef]
- Lauwers, J.; Appels, L.; Thompson, I.P.; Degreve, J.; van Impe, J.F.; Dewil, R. Mathematical modelling of anaerobic digestion of biomass and waste: Power and limitations. Progress. Energy Combust. Sci. 2013, 39, 383–402. [Google Scholar] [CrossRef] [Green Version]
- Theuerl, S.; Herrmann, C.; Heiermann, M.; Grundmann, P.; Landwehr, N.; Kreidenweis, U.; Prochnow, A. The future agricultural biogas plant in Germany: A vision. Energy Rev. 2019, 12, 396. [Google Scholar] [CrossRef] [Green Version]
- Kundu, K.; Sharma, S.; Sreekrishnan, T.R. Influence of process parameters on anaerobic digestion microbiome in bioenergy production: Towards an improved understanding. Bioenergy Resour. 2017, 102, 5045–5063. [Google Scholar] [CrossRef]
- Yang, H.; Deng, L.; Liu, G.; Yang, D.; Liu, Y.; Chen, Z. A model for methane production in anaerobic digestion of swine waste water. Water Resour. 2016, 102, 464–474. [Google Scholar]
- Deng, L.; Yang, H.; Liu, G.; Lei, Y. Kinetic of temperature effect and its significance to the heating strategy for anaerobic digestion of swine wastewater. Appl. Energy 2014, 134, 349–355. [Google Scholar] [CrossRef]
- Addario, M.D.; Temizel, I.; Edes, N.; Onay, T.T.; Demirel, B.; Copty, N.K.; Ruggeri, B. Development of Fuzzy logic model to predict the effects of ZnO nanoparticles on methane production from stimulated landfill. J. Environ. Chem. Eng. 2017, 5, 5944–5953. [Google Scholar] [CrossRef]
- Rieke, C.; Stollenwerk, D.; Dahmen, M.; Pieper, M. Modelling and optimization of a biogas plant for a demand driven energy supply. Energy 2018, 145, 657–664. [Google Scholar] [CrossRef]
- Girault, R.; Rousseau, P.; Steyer, J.P.; Bernet, N.; Beline, F. Combination of batch experiments with continuous reactor data for ADM1 calibration: Application to anaerobic digestion of pig slurry. Water Sci. Technol. 2011, 63, 2575–2582. [Google Scholar] [CrossRef]
- Batstone, D.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.; Pavlostathis, S.; Rozzi, A.; Sanders, W.; Siegrist, H.; Vavilin, V. The anaerobic digestion model no 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar]
- Delgadilo-Mirquez, L.; Machado-Higuera, M. Mathematical modelling and simulation of biogas production from organic waste. Int. J. Eng. Model. Simul. 2018, 10, 97–102. [Google Scholar] [CrossRef]
- Edwiges, T.; Frare, L.; Alino, J.; Lins, L.; Flotats, X.; Sarolli, M. Use of mathematical models to fast predict biochemical methane potential of fruit and vegetable waste. In Proceedings of the AD15—15th World Congress on Anaerobic Digestion, Beijing, China, 17–20 October 2017. [Google Scholar]
- Biswas, J.; Chowdhury, R.; Bhattacharya, P. Mathematical modelling for the prediction of biogas generation characteristics of an anaerobic digester based on food/vegetable residues. Biomass Bioenergy 2007, 31, 80–86. [Google Scholar] [CrossRef]
- Zareei, S.; Khodaei, J. Modelling and optimisation of biogas production from cow manure and maize straw using an adaptive neuro-fuzzy inference system. Renew. Energy 2017, 114, 423–427. [Google Scholar] [CrossRef]
- da Silva, I.S. South Africa’s biogas market potential worth R10-bn. Moon of the South News from Africa. 2013. Available online: http://moonofthesouth.com/South-Africa-biogas-market/ (accessed on 14 March 2021).
- Okudoh, V.; Trois, C.; Workneh, T.; Schmidt, S. The potential of cassava biomass and applicable technologies for sustainable biogas production in South Africa: A review. Renew. Sustain. Energy Rev. 2014, 39, 1035–1052. [Google Scholar] [CrossRef]
- Marrison, C.I.; Larson, E.D. A preliminary analysis of the biomass energy production potential in Africa in 2025 considering projected land needs for food production. Biomass Bioenergy 1996, 10, 337–351. [Google Scholar] [CrossRef]
- Lynd, L.R.; Weimer, P.J.; van Zyl, W.H.; Pretorius, I.S. Microbial cellulose utilization: Fundamentals and biotechnology. Microbiol. Mol. Biol. Rev. 2002, 66, 506–577. [Google Scholar] [CrossRef] [Green Version]
- von-Blottniz, H.; Melamu, R.; Aboyade, A.; Abraham, D.; Niyobuhungiro, R.; Paetz, C. Biogas Potential in South Africa: And What a Small Team at UCT Is Researching in That Regard; von Blottnitz, H., Ed.; University of Cape Town Publisher: Cape Town, South Africa, 2013. [Google Scholar]
- AGAMA Biogas. Integrated Biogas Solutions: Green Energy Solutions for Africa Energy; Legal Framework; AGAMA Energy: Cape Town, South Africa, 2008. [Google Scholar]
- Mukumba, P.; Makaka, G.; Mamphweli, S.; Simon, M.; Meyer, E. An insight into the status of biogas digesters technologies in South Africa with reference to the Eastern Cape Province. Fort Hare Pap. 2012, 19, 5–29. [Google Scholar]
- Nape, K.M.; Magama, P.; Moeletsi, M.E.; Tongwane, P.; Nakana, P.M.; Mliswa, V.K.; Motsepa, M.; Madikiza, S. Introduction of household bio digester in rural farming household of Maluti-a-Phofung Municipality South Africa. J. Energy South. Afr. 2019. [Google Scholar] [CrossRef] [Green Version]
- Obileke, K.; Mamphweli, S.; Meyer, E.; Makaka, G.; Nwokolo, N.; Onyeaka, H. Comparative study on the performance of aboveground and underground fixed dome biogas digesters. Chem. Eng. Technol. 2020, 43, 68–74. [Google Scholar] [CrossRef]
- Mukumba, P. Modelling of the Performance of a Batch Biogas Digester Fed with Selected Types of Substrates. Ph.D. Thesis, University of Fort Hare, Alice, South Africa, 2013. [Google Scholar]
- Tangwe, S. Demonstration of Residential Air Source Heat Pump Water Heater in South Africa: System Monitoring and Modelling. Ph.D. Thesis, University of Sunderland, Sunderland, UK, 2018. [Google Scholar]
- Ukpai, P.A.; Nnabuchi, M.N. Comparative study of biogas production from cow dung, cow pea and cassava peeling using 45 litres biogas digester. Adv. Appl. Sci. Res. 2012, 3, 1864–1869. [Google Scholar]
- Mukumba, P.; Makaka, G.; Mamphweli, S.; Misi, S. A possible design and justification for a biogas plant at Nyazura Adventist High School, Rusape, Zimbabwe. J. Energy South. Afr. 2013, 24, 12–20. [Google Scholar] [CrossRef]
- Wang, S.; Ma, F.; Ma, W.; Wang, P.; Zhao, G.; Lu, X. Influence of temperature on biogas production efficiency and microbial community in a two-phase anaerobic digestion system. Water 2019, 11, 133. [Google Scholar] [CrossRef] [Green Version]
- Rameshprabu, R.; Unpaprom, Y. Effect of temperature on the performance of biogas production from Duckweed. Chem. Res. J. 2016, 1, 58–66. [Google Scholar]
- İnce, E.İ.; Önkal, M.; Engin, G. Comparison of thermophilic and mesophilic anaerobic treatment for potato processing wastewater using a contact reactor. Glob. NEST J. 2017, 9, 318–326. [Google Scholar]
- Ukpai, P.A.; Agbo, P.E.; Nnabuchi, M.N. The effect of temperature on the rate of digestion and biogas production using cow dung, cow pea and cassava peeling. Int. J. Sci. Eng. Res. 2015, 6, 1255–1260. [Google Scholar]
- Uzodinma, E.O.U.; Onwuka, N.D. Optimum mesophilic temperature of biogas production from blends of agro-based waste. Trends Appl. Sci. 2007, 2, 39–44. [Google Scholar]
- Budiyano, I.; Syaichurrozi, S.; Sumardiono, S. Biogas production from bioethanol waste: The effect of pH and urea addition to biogas production rate. Waste Technol. 2013, 1. [Google Scholar] [CrossRef]
- Dobre, P.; Nicolae, F.; Matei, F. Main factors affecting biogas production—An overview. Rom. Biotechnol. Lett. 2014, 19, 9283–9296. [Google Scholar]
- Yan, T.; Mayne, C.S.; Gordon, F.G.; Porter, M.G.; Agnew, R.E.; Patterson, D.C.; Ferris, C.P.; Kilpatrick, D.J. Mitigation of enteric methane emissions through improving efficiency of energy utilization and productivity in lactating dairy cows. J. Dairy Sci. 2010, 93, 2630–2638. [Google Scholar] [CrossRef]
- Ellis, J.L.; Kebreab, E.; Odongo, N.E.; McBride, B.W.; Okine, E.K.; France, J. Prediction of methane production from daily and beef cattle. J. Dairy Sci. 2007, 90, 3456–3467. [Google Scholar] [CrossRef] [PubMed]
- Ramin, M. Predicting Methane Production in Daily Cows. Ph.D. Thesis, Swedish University of Agricultural Science, Uppsala, Sweden, 2013. [Google Scholar]


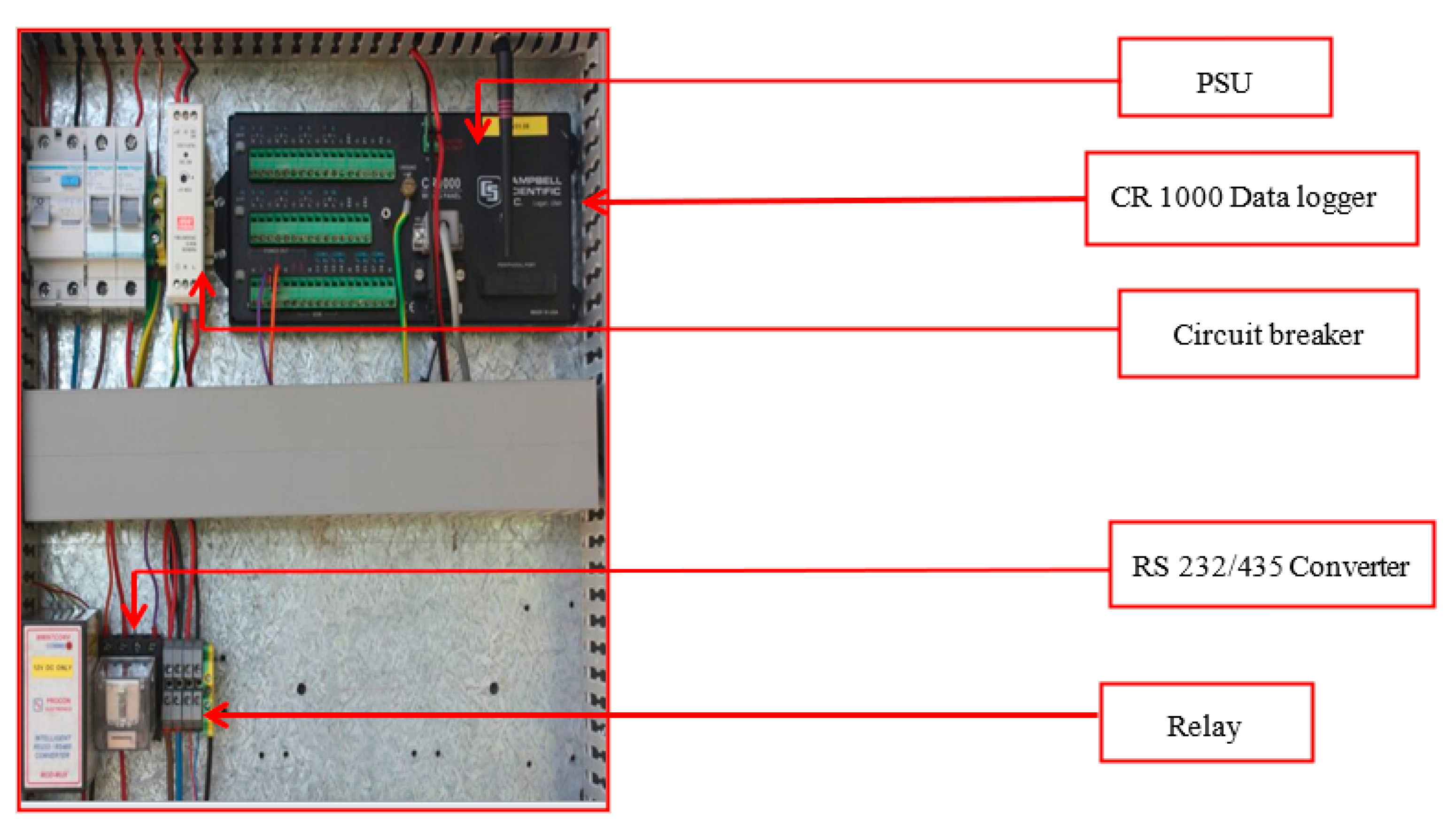

| Biomass | Estimated Energy Value | References |
|---|---|---|
| Cropped biomass | 1350 PJ | [22] |
| Solid waste (Landfill areas) | 5000 GW/h | [23] |
| Wastewater in municipal water plant | 9000 GW/h | [24] |
| Farm/homesteads | 5–10 kW thermal energy | [24] |
| Breweries | 50 kW to 5 MWth on industrial scale | [24] |
| Silage wastes | 5–10 MWth | [24] |
| Cow dung | - | - |
| Province | Biogas Reactor Type | Volume of Biogas Reactor (m3) | Purpose of the Energy | References |
|---|---|---|---|---|
| Free State | Floating drum | 10 | Cooking | [25,26] |
| Free State | Ball-balloon | 6–12 | - | [27] |
| Western Cape | Floating drum | 11 | Cooking | [25,26] |
| Western Cape | Floating drum | 1 | Cooking | [25,26] |
| Western Cape | Floating drum | 6 | Cooking | [25,26] |
| Eastern Cape | Fixed dome | 2.15 | Research | [28] |
| Eastern Cape | Fixed dome | 1 | Research | [29] |
| Properties of Cow Dung | Measurement of Cow Dung Used | Uncertainty Reported | Actual Values | Test Method Used |
|---|---|---|---|---|
| pH | 50 g | ±0.02 | 7.83 at 30 °C | Hydrogen-Electrode method |
| Total solids (TS) | 50 g | ±5.0 g/L | 130,800 g/L | APHA 2005 method |
| Volatile solids (VS) | 50 g | ±5.0 g/L | 110,476 g/L | APHA 2005 method |
| Chemical oxygen demand (COD) | 0.2 mL | ±2.0 g/L | 42,583 g/L | Calorimetric method |
| Calorific value | - | ±0.02 MJ/g | 27.00 MJ/g | Direct method |
| Model Parameter | Ranges of Measured Data Used | Equipment Used |
|---|---|---|
| Methane | 0.03–0.24 m3 | NDIR methane sensor |
| Carbon dioxide | 0.1–0.15 m3 | NDIR carbon dioxide sensor |
| pH | 6.83–7.20 | pH digital meter |
| Slurry top temperature | 11–22 °C | K-type thermocouple |
| Slurry bottom temperature | 10–35 °C | K-type thermocouple |
| Gas temperature | 11–22 °C | K-type thermocouple |
| Ambient temperature | 10–22 °C | K-type thermocouple |
| Relative humidity | 53.5–90.4% | Hygrometer |
| Global horizontal irradiance | 52–341 W/m2 | CMP pyrometer |
| Lump Input Parameter | Constant Name | Constant Symbol | Constant Value | Desired Output (mL/gVS) | Determination Coefficient (r2) |
|---|---|---|---|---|---|
| Forcing constant | A | 2.90 × 10−5 | CH4 volume | r2 = 0.955 | |
| Scaling constant | B | 2.81 × 10−10 | |||
| Scaling constant | C | 6.70 × 10−6 |
| Type of Model | Substrate Used | Input Predictor Used | Effect on Methane Production | Determination of Coefficient (R2) | Design Orientation | References |
|---|---|---|---|---|---|---|
| Empirical model | Cow dung | pH, RH, I, and temperature (Tg, Ts and Tamb ) | Increase in the input predictor corresponds to an increase in the volume of methane and decrease in the input predictor, resulting in a rise in the volume of methane produced | 0.962 | Large scale digester | Present study |
| Non-linear model | Organic waste | Organic loading rate and volatile fatty acid | Increase in the input parameters (organic matter and volatile fatty acid) corresponds to an increase in the volume of methane production | - | Pilot scale digester | [16] |
| Mechanistic model | Food/vegetable residues | Slurry, carbohydrate, and protein concentration | Methane production is significantly dependent on the input predictor | - | Pilot scale digester | [18] |
| Empirical method | Swine water | Organic loading rate and temperature | - | 0.97–099 | Pilot scale | [10] |
| Mechanistic model | Solid waste | pH and volatile fatty acid | Increase in the input parameters (organic matter and volatile fatty acid) corresponds to an increase in the volume of methane production | - | Pilot scale digester | [1] |
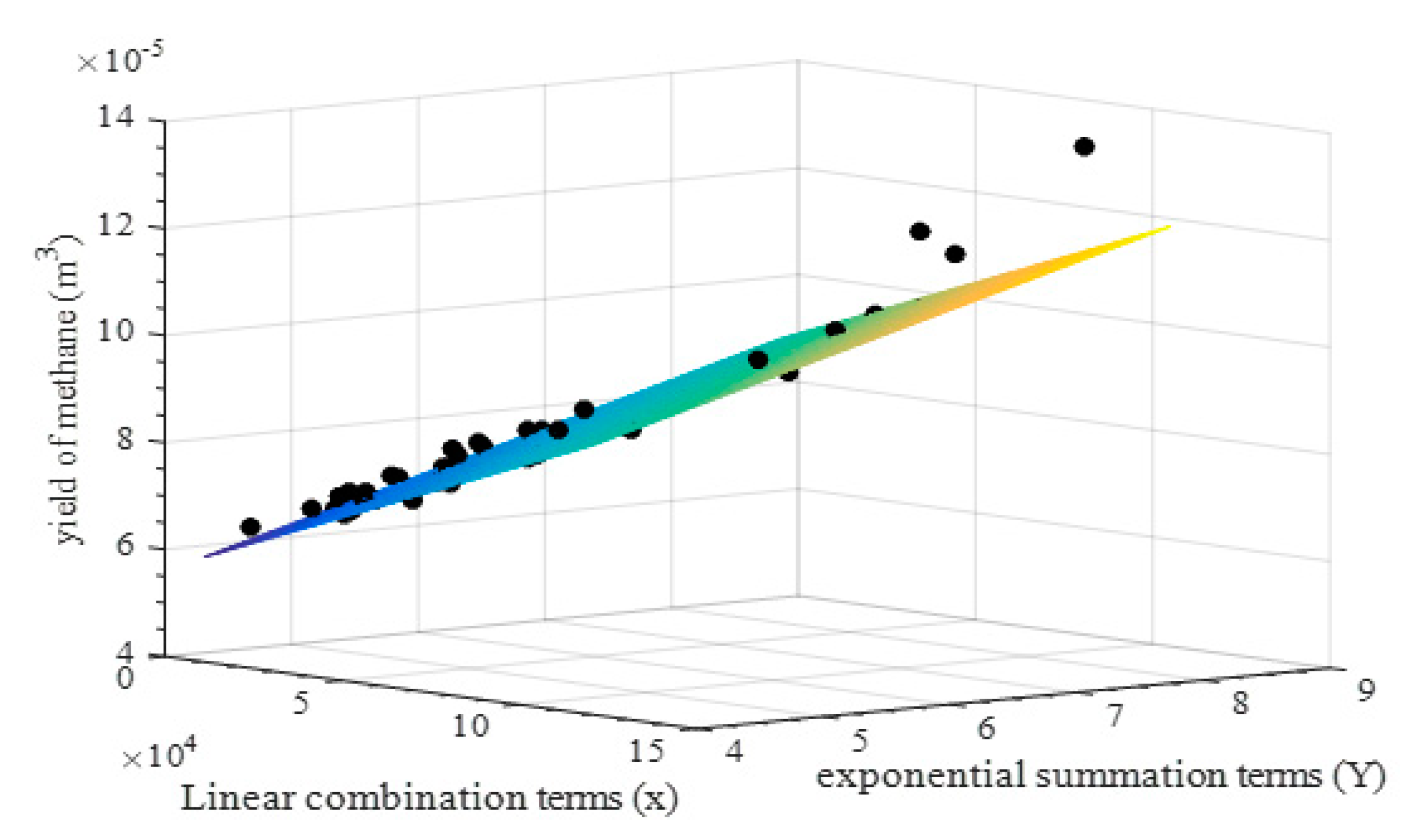
| Observations | Input (x) | Input (Y) | Calculated CH4 (mL/gVS) | Predicted CH4 (mL/gVS) |
|---|---|---|---|---|
| 1 | 21,800 | 4.36 | 6.42 × 105 | 6.43 × 105 |
| 6 | 5100 | 7.03 | 8.34 × 105 | 7.75 × 105 |
| 11 | 3330 | 6.96 | 8.13 × 105 | 7.66 × 105 |
| 16 | 429 | 6.69 | 7.70 × 105 | 7.39 × 105 |
| 21 | 625 | 6.34 | 7.76 × 105 | 7.16 × 105 |
| 26 | 451 | 5.83 | 7.91 × 105 | 6.82 × 105 |
| 31 | 89.72 | 6.57 | 7.87 × 105 | 7.31 × 105 |
| 36 | 560.99 | 6.92 | 8.35 × 105 | 7.55 × 105 |
| 40 | 5910 | 6.27 | 8.66 × 105 | 7.27 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obileke, K.; Mamphweli, S.; Meyer, E.L.; Makaka, G.; Nwokolo, N. Development of a Mathematical Model and Validation for Methane Production Using Cow Dung as Substrate in the Underground Biogas Digester. Processes 2021, 9, 643. https://doi.org/10.3390/pr9040643
Obileke K, Mamphweli S, Meyer EL, Makaka G, Nwokolo N. Development of a Mathematical Model and Validation for Methane Production Using Cow Dung as Substrate in the Underground Biogas Digester. Processes. 2021; 9(4):643. https://doi.org/10.3390/pr9040643
Chicago/Turabian StyleObileke, KeChrist, Sampson Mamphweli, Edson L. Meyer, Golden Makaka, and Nwabunwanne Nwokolo. 2021. "Development of a Mathematical Model and Validation for Methane Production Using Cow Dung as Substrate in the Underground Biogas Digester" Processes 9, no. 4: 643. https://doi.org/10.3390/pr9040643
APA StyleObileke, K., Mamphweli, S., Meyer, E. L., Makaka, G., & Nwokolo, N. (2021). Development of a Mathematical Model and Validation for Methane Production Using Cow Dung as Substrate in the Underground Biogas Digester. Processes, 9(4), 643. https://doi.org/10.3390/pr9040643








