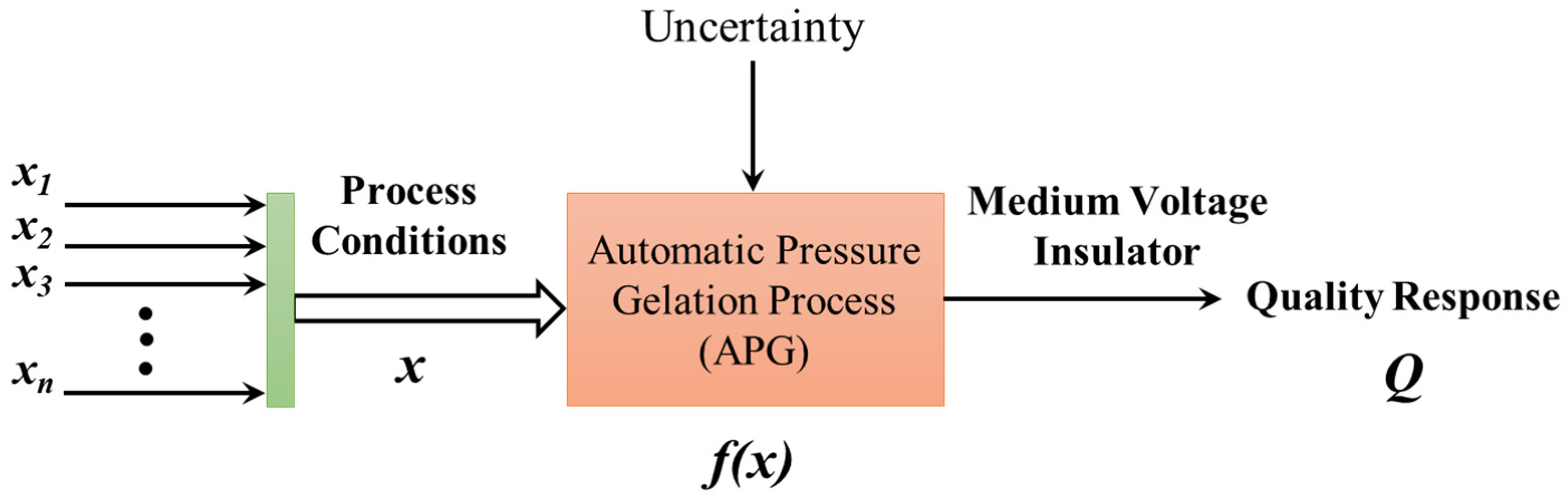
3.1. Knowledge-Informed Optimization Strategy
Since the operational cost of the APG is relatively high, the number of batches on quality control of medium voltage insulators has a significant impact on the economy of the quality control process. The rapidity, therefore, is of paramount importance for the quality control of medium voltage insulators. It is necessary to reduce the number of iterative experiments in the quality optimization process as much as possible, thus reducing the cost of quality control. Even though in the optimization framework, as shown in
Figure 2, the MFO method has excellent performance on quality control of a type of batch processes with lower operational cost. As the scenario is slightly different for the APG, the traditional MFO, however, faces the relatively high optimization price challenge.
Up to the present, there is no method superior to the MFO that exists to address this challenge. Considering that the MFO still has its advantages in the medium voltage insulators’ quality control, a possible way to promote quality control efficiency is to revise the conventional MFO method. Under the framework of MFO, the optimization method is the key. Consequently, it is critical to further enhance the optimization method’s efficiency under the existing optimization framework. During the optimization, a series of iterative process information, which contains process knowledge, will be generated dynamically. In traditional optimization methods, most of this knowledge is discarded or not used effectively. If this knowledge can be extracted and utilized effectively, it is possible to further enhance the optimization method’s efficiency. It is feasible to reduce the optimization number and improve the quality control efficiency for a type of batch process with relatively high operation cost by mining the process knowledge generated during the optimization. Based on the knowledge-informed idea, different knowledge-informed optimization strategies for SPSA had already been formulated. It was verified that appreciable improvement could be achieved.
The simplex search method, as a gradient-free optimization strategy, is different from SPSA. Even though the simplex search method’s principle is quite different from SPSA, the basic idea of the knowledge-informed optimization strategy for both of them is similar. Like SPSA, a certain amount of process knowledge will be generated during the iterative process of the simplex search optimization. The simplex search takes each simplex, which consists of n + 1 points, as an iteration point. It determines its current search direction and the step size only according to the current simplex information at each iteration. The knowledge of the historical sequential simplices, such as simplex sequences, centroids, and historical reflection points, is completely discarded. However, the historical knowledge can be utilized to enhance the optimization method’s efficiency if appropriate mechanisms could be built according to the characteristics of the simplex search. For the quality control of medium voltage insulators, this knowledge can be used to improve the simplex search method. Therefore, the knowledge-informed quality control strategy for the simplex-search-based MFO is promising. The framework of the knowledge-informed quality optimization via the simplex search method is shown in
Figure 3. Stem from the above-mentioned knowledge-informed idea, this section discusses a kind of knowledge-informed simplex search method based on historical quasi-gradient estimations in-depth. A feasible implementation mechanism of the GK-SS strategy was put forward.
3.2. Basic Principles of Simplex Search Methodology
As a gradient-free multivariate optimization method, the simplex search method is a direct search method for nonlinear optimization. This method is formulated based on a concept of simplex, which is a geometric object that is a convex hull of
n + 1 points—not lying in the same hyperspace—in
n-dimensional Euclidean space
(
n is the dimension of the optimization problem understudy) [
26]. This method’s origin can be traced back to the idea of evolutionary operation (EVOP), which was proposed by Box in 1957 [
27]. Considering how EVOP might be automatic, Spendley et al. proposed the original idea of the sequential simplex search [
28]. To further improve this method’s efficiency, Nelder and Mead made the simplex search method have the capability to adapt itself to the local landscape [
29]. Due to its simplicity and effectiveness, the Nelder-Mead simplex search method becomes widely used in industrial quality improvement areas. As a result, the Nelder-Mead simplex search (called simplex search by default) is the baseline method in this project. The procedure of the simplex search method, as can be seen in
Figure 4, is detailed as follows:
Step 1: Methodology initialization.
The initial process conditions are preset as
, which represents the 1st iteration point of the optimization. As each process condition has a different operating range, each is scaled into the same range [0, 100] to facilitate the optimization. The scaled initial conditions are represented as
. Meanwhile, the coefficients of the methodology,
, are set at this stage.
is the reflection coefficient,
is the contraction coefficient,
is the expansion coefficient,
is the shrink coefficient. Set the coefficients according to the suggestion of Nelder and Mead [
29].
Step 2: Initial simplex construction.
As shown in
Figure 5, a particular sequential perturbation strategy is proposed to construct a feasible initial simplex. Set the simplex iteration number
s = 0, and set the first vertex
. The construction rule for other
n vertices is expressed as below:
where
is a column vector, which has 1 in the
kth element and zeros in the other elements,
represents the (
k+1)th iteration point of the optimization;
is the perturbation coefficient that should be set according to the range of all the process conditions, which has a range of (5, 50). After the perturbation, the initial simplex is constructed as
. Experiments are then conducted to obtain the corresponding quality responses vector
, where
F represents the function response for each simplex vertex.
Step 3: Simplex Sorting.
The simplex iteration number s is updated as
s =
s + 1. The vertices in the current simplex
are sorted according to their corresponding quality responses
. The sorted simplex may be denoted as
, which has the following characteristics:
Thus, is the vertex with the best response, is the vertex with the next-to-the-worst response, is the vertex with the worst response.
Step 4: Reflection.
The reflection operation would be carried out to obtain the reflection point
according to the following expression:
is the centroid of all the vertices except
, which is expressed as:
Experiment to evaluate the quality response at the reflection point. If , which means that the performance of the process conditions along the reflection direction may be promising, the expansion operation should be executed; hence, the procedure would go to Step 5. If , which means that the performance of the process conditions along the reflection direction may be neutral, the current reflection point should be accepted, and the worst vertex would be substituted by the reflection point; thus, the procedure would go the Step 8. If , which means that the performance of the process conditions along the reflection direction may be gloomy, the contraction operation should be conducted, the procedure would go to Step 6.
Step 5: Expansion.
The expansion operation would be carried out to obtain the expansion point
according to the following expression:
Then, experiment to evaluate the quality response at the expansion point. If , the expansion is successful, thus would be replaced by . Otherwise, the worst vertex would be substituted by the reflection point. At last, the procedure would go to Step 8.
Step 6: Contraction.
The contraction operation could be categorized into two types, viz. (i) inside contraction, (ii) outside contraction. Generally, the contraction point
could be calculated according to the following formula:
where
, the reference point for contraction, maybe
or
. The choice of
depends on the contraction types.
Case 1: When , this is inside contraction.
In this case, , ; conduct experiments to evaluate the quality response . If , the contraction is accepted.
Case 2: When , this is outside contraction.
In this case, , ; conduct the experiments to evaluate the quality response . If , the contraction is accepted.
If the contraction is accepted in the above cases, replace with and go to Step 8. Otherwise, the contraction is refused, then go to Step 7 for a shrink operation.
Step 7: Shrink.
The shrink operation could be expressed as:
All the vertices, except the best vertex, are sequentially updated and substituted by the new vertices generated based on Equation (9). The quality responses of the updated vertices are obtained and updated via experiments.
Step 8: Termination.
Since the simplex search is utilized for the quality control, the method would be terminated when the maximum iteration number is achieved or the quality response of the best vertex is satisfied within a preset quality tolerance.
3.3. Basic Ideas for Knowledge-Informed Simplex Search Methodology Based on Quasi-Gradient Estimations
Considering the genesis and the development process of the simplex search method, it, to some extent, can be regarded as a particular type of knowledge-informed strategy. Different knowledge fusion mechanisms accompany the development of the simplex search method. To achieve more effective integration of process knowledge with the simplex search method, it is necessary to attain some inspiration from its development. This method was initially proposed by Spendley et al. in 1962 [
28]. Moreover, its origins can be dated back to Box’s EVOP strategy in 1955 [
29]. The basic philosophy of the EVOP method is that the improvement of the industrial process is very similar to the biological evolution process. At the current working point, EVOP continuously sets a series of controlled, slight process parameter variants and observes their responses to find the direction of progressive improvement of the process parameters iteratively. Each advancement of EVOP relies on the knowledge of the current working point and a series of controlled variants at its vicinity, reflecting an intrinsic characteristic of a knowledge-informed mechanism. However, the final optimization operation is still determined by the operation engineers in combination with their experience. To realize the automation of the EVOP, Spendley devised a sequential simplex-design-based optimization methodology, which inherits the basic principle of the EVOP. Under Box’s EVOP methodology, the execution and the search direction of the optimization operation are determined by the operator or the manager. Hence, it is a hybrid optimization strategy relying on both operation knowledge and experience. However, with Spendley’s method, the optimization operation could be determined entirely by the current simplex. The optimization, therefore, gets rid of the constraint of the operator’s experience and becomes automatic and more efficient. However, the iteration of the simplices relies only on the reflection operations in Spendley’s method. The reflection point will substitute the worst vertex, discarded from the current simplex, to form a new simplex. It is a mirror-symmetric reflection that the size of simplices remains unchanged in the optimization process. From the perspective of iterative optimization, the size of the simplex determines the optimal step size. As a result, the optimal step size of the method is kept unchanged. Hence, this is a fixed step size optimization strategy, which seriously restricts its optimization performances. Considering Spendley’s method’s rigidity, Nelder and Mead proposed a revised simplex method that can adapt itself to the optimization’s local landscape. The Nelder-Mead method still follows the idea of sequential simplex design, but it adds additional operations, such as expansion and contraction. These additional operations are conducted depending on the local landscape’s different scenarios; thus, the methodology could adapt to the process landscape. Hence, the revised method becomes a variable-step-size method with the step size of the simplices that could be adjusted dynamically according to the state of the optimization process. This method could contract to the optimal settings more efficiently. The Nelder-Mead method’s significant improvement can be attributed to the deep mining and utilization of knowledge information in the current iteration simplex. This method essentially utilizes the relationships between the reflection points and their subsequent operation points and the present simplex vertices’ knowledge information to realize the step size’s dynamic adjustment. To sum up, the method’s efficiency attribute to the utilization of iteration knowledge and the simplex search method’s development process reveals that making full use of the historical information generated during the optimization process can effectively improve optimization efficiency. Then, from the perspective of using iterative process knowledge to improve the efficiency of MFO, where is the next improvement direction of the simplex search method?
From the idea of knowledge-informed optimization, the traditional simplex search method is reviewed. It does not make full use of the historical iterative information of the optimization process. Some other historical knowledge information generated during the iteration of simplices has been ignored before. Only part of the knowledge is utilized. All the knowledge can be classified into two types according to their relationships with the current simplex. The classification of the knowledge is shown in
Figure 6. The first dimension represents the knowledge within the current simplex, while the second dimension contains the historical knowledge outside the current simplex.
The traditional simplex search method only utilizes the first dimension knowledge, and excellent optimization performance is achieved with an appropriate knowledge integration mechanism. Then, could the iteration knowledge in the second dimension be utilized to facilitate the optimization process? The answer must be yes. However, the critical question lies in how to dig, define, and finally use this iteration knowledge. The fusion mechanism of the iteration knowledge, including knowledge digging, definition, and utilization, is central to knowledge-informed strategy.
The genesis and essential characteristics of the simplex search method are analyzed to find sufficient knowledge that can be used to facilitate performance improvement. The simplex search method is widely regarded as a gradient-free algorithm. However, as pointed out by Spendley, the original EVOP method is essentially a rudimentary steepest descend optimization strategy that senses the steepest descend direction and climbs down. As a sequential-simplex-design EVOP strategy, Spendley’s method is a kind of steepest-descend method. Its direction is estimated from the simplex’s centroid through the hyperface. The hyperface is opposite to the vertex with the worst response. The advance direction is determined by a rough gradient estimation at the current simplex, as
, in essence. For the Nelder-Mead method, the optimization direction is determined by the exact mechanism. The steepest descend direction, which deviates from the actual gradient, is determined solely by the current simplex knowledge. In a sense, this method is still not out of the gradient algorithm’s scope, which could be treated as a special case. The calculation strategy of the operations can be generalized to reveal the essence further. According to the basic principle of the simplex search, the reflection operation could be reviewed and correspondingly transformed into a different form:
The expansion operations could be revised as below:
The contraction operations could be revised as below:
Hence, the inside contraction and the outside contraction would be transformed into a similar form as below:
From the above equivalent formula, except for shrink operation, other operations of the simplex search method attempt to find a new vertex in a unified way, which can be concluded as below:
where
can be viewed as the step size of the method, which can be adjusted dynamically according to the current optimization status estimated by the knowledge of the current simplex. According to the general settings,
is set to {2, 1, 0.5, −0.5} corresponding to the expansion, reflection, outside contraction, and inside contraction. It is obvious that
, in fact, plays the role of the step size. According to the unified iteration strategy, it can be seen that the simplex search method has a mechanism similar to the gradient-based methods. Thus, the vector from the centroid to the worst point is defined as quasi-gradient estimation, which is a rough estimation of the gradient at the centroid of the simplex. The quasi-gradient estimation can be expressed as follows:
Correspondingly, the iteration strategy of the simplex search method can be represented as below:
Like the gradient-based method, each simplex during the optimization can be viewed as an iteration point. Hence, the simplex search method with rough gradient estimation behaves like a gradient-based method. Like the SPSA, although the quasi-gradient estimations at every simplex iterations are rough estimations, the method could statistically find the steepest descend route. Thus, its efficiency can be guaranteed. We had proposed a knowledge-informed SPSA based on historical gradient approximations (GK-SPSA) in our previous work. The basic idea of the GK-SPSA lies that if we can appropriately make use of the historical gradient estimation information, then the gradient estimations’ accuracy may be improved to enhance the efficiency of the optimization method. Considering their similarity, the iterative quasi-gradient estimations generated during the simplex search optimization may also be gathered and utilized. This knowledge certainly carries some degree of information on the gradients’ tendency that it may be used to compensate for the gradient estimations at each simplex iteration. Once the gradient estimations’ accuracy could be improved, the simplex search method’s efficiency would be enhanced accordingly. A schematic diagram of the gradient estimation compensation mechanism can be seen in
Figure 7.
Based on the aforementioned knowledge-informed idea, a revised simplex search method, which incorporates the historical quasi gradient estimations to facilitate the optimization, was proposed. The different optimization mechanisms of the traditional simplex search and the revised method are illustrated in
Figure 8. The revised method utilizes the historical quasi-gradient estimations to compensate for the search direction moderately at each simplex iteration. Like the knowledge-informed SPSA, the revised method was named knowledge-informed simplex search method based on historical quasi gradient estimations (GK-SS for short). This method is a typical knowledge-informed optimization strategy. An implementation scheme for the GK-SS is proposed and illustrated in detail in the following subsection.
3.4. An Implementation Scheme of Knowledge-Informed Simplex Search Method
According to the traditional simplex search method principles, GK-SS’s implementation scheme is formulated and detailed based on the above knowledge-informed idea. In this mechanism, the simplex operations should be performed along the compensated search direction, which is different from the traditional method.
The simplex search method’s iteration strategy was reformulated from the steepest-descent characteristics of the traditional simplex search just discussed above. An intermediate quantity that has an apparent mathematical meaning was revealed and formulated. This quantity represents a search direction determined by each simplex, which, in a sense, is the approximate gradient information of the current simplex. Thus, this quantity of the current simplex is called the estimated quasi-gradient for current simplex (EGCS). The definition of the EGCS could be expressed as Equation (15), where represents the EGCS at the sth simplex.
With the above formula Equations (15) and (16), we construct a kind of quasi-gradient estimation information equivalent to the gradient approximation of the gradient-based strategies for the gradient-free simplex search method. In the traditional simplex search procedure, this kind of information does not exist explicitly. After each simplex is formed and sorted in the GK-SS, the EGCS of the current simplex would first be calculated before the corresponding simplex operations are conducted. Then, it can be recorded into a sequence in an orderly manner. The EGCS sequence, which grows with the simplices’ iteration, stores the historical quasi-gradient estimations generated by each simplex.
The EGCS provides a potential link between gradient-free methods and the gradient-based methods. The EGCS, however, is a slightly rough estimation of the gradient at the current simplex due to the operation rule. To integrate the historical knowledge to compensate the gradient estimation accuracy at the current simplex, a new compensated composite gradient for the current simplex (CCG) is defined as follows:
where
is the
sth compensated composite gradient (CCG) at the
sth simplex,
is the CCG at the (
s−1)th simplex,
is the CCG at the 1st simplex.
is a gradient compensation coefficient at the sth simplex, reflecting the gradient information’s current weights. According to Equation (17), the CCG at the current simplex is determined by all the historical EGCS generated during the previous optimization process. The historical EGCSs of the simplices nearing the current simplex plays a more critical role for the CCG at the current simplex. Considering that the credibility of the EGCS of the neighboring simplex is higher than that far away from the current simplex, the proposed mechanism is reasonable.
On the other hand, according to the simplex search method’s characteristics, the accuracy of CCG will gradually improve with the simplex iterations’ development. Hence, the coefficient should not be a fixed constant. Contrarily, it should be a parameter that changes dynamically with the iteration of the simplices. Therefore, a dynamic mechanism for the coefficient can be formed as follows:
where
is an upper limit that a CCG can be approached, which is set to 0.5 by default,
is the initial deviation between
and its lower limit, which is set to 0.2 by default, and
is an exponential coefficient, which counts on the iteration number effects on the accuracy of CCG. The coefficient
represents the tendency of the cumulative effect of the historical quasi-gradient estimations at each simplex on compensated gradients.
From Equation (17), the CCG at the
sth simplex is a linear combination of the previous CCG at the (
s−1)th simplex and the EGCS at the
sth simplex. The historical gradient estimations generated by each simplex are integrated into the revised simplex search method through the above mechanism. The CCG is utilized to substitute the implicit EGCS, as shown in Equation (16), in the traditional simplex search method’s operations. The historical quasi-gradient estimations are gained iteratively and stored sequentially. The ratio relationship of the EGCS on the synthesis of the CCG at each iteration is showcased in
Figure 9.
With the CCG, the original reflection operation, as shown in Equation (5), would be substituted as below:
where
is the reflection coefficient that is kept unchanged.
The expansion operation would be revised accordingly as follows:
Correspondingly, the outside contraction is:
Moreover, the inside contraction is:
The flowchart of the GK-SS is illustrated in
Figure 10. As shown in the figure, except for the reflection, expansion, and contraction operations, the other operations and the GK-SS’s basic procedures are the same as the traditional method. It is natural since these operations are the key to the simplex search method. Therefore, the revised simplex operation could provide an appropriate mechanism for the fusion of historical simplex information.
This GK-SS scheme provides a feasible way from a gradient view, which is relatively peculiar for a gradient-free method, for the fusion of the knowledge generated during the optimization process. The primary mechanism of the GK-SS conforms to the GK-SPSA in the search direction compensation. Using knowledge of historical equivalent gradient information generating during the iteration of the simplices, more accurate search directions could be obtained during the optimization. Thus, the optimization efficiency would be enhanced.