A Chance Constrained Programming Approach for No-Wait Flow Shop Scheduling Problem under the Interval-Valued Fuzzy Processing Time
Abstract
1. Introduction
2. Problem Formulation
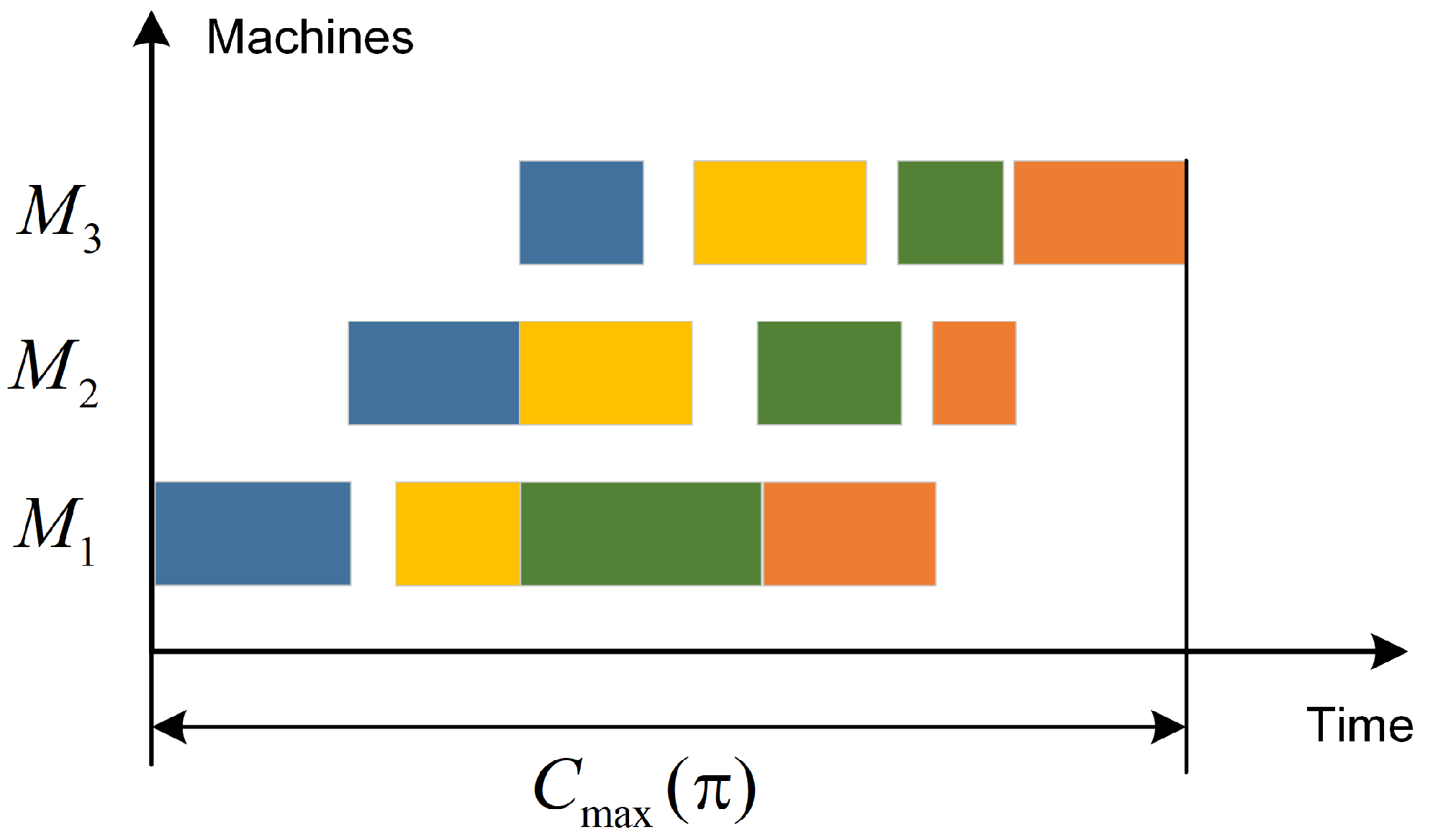
2.1. Problem Description
2.2. Mathematical Formulation
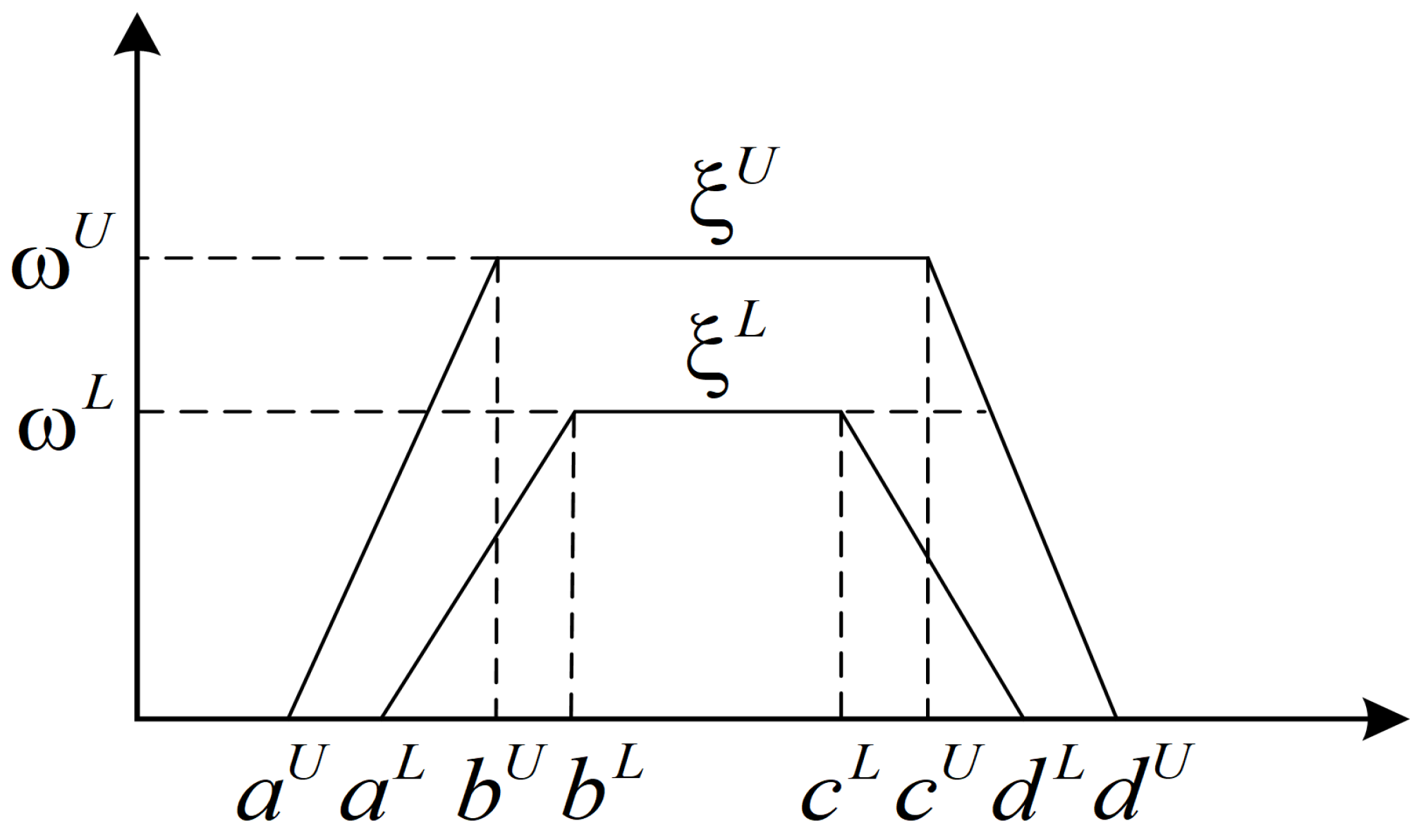
2.3. Interval-Valued Fuzzy Set
2.4. Robust NWFSP under Moment Uncertainty
3. Solution Method
3.1. Initial Solution
3.2. Neighborhood Search
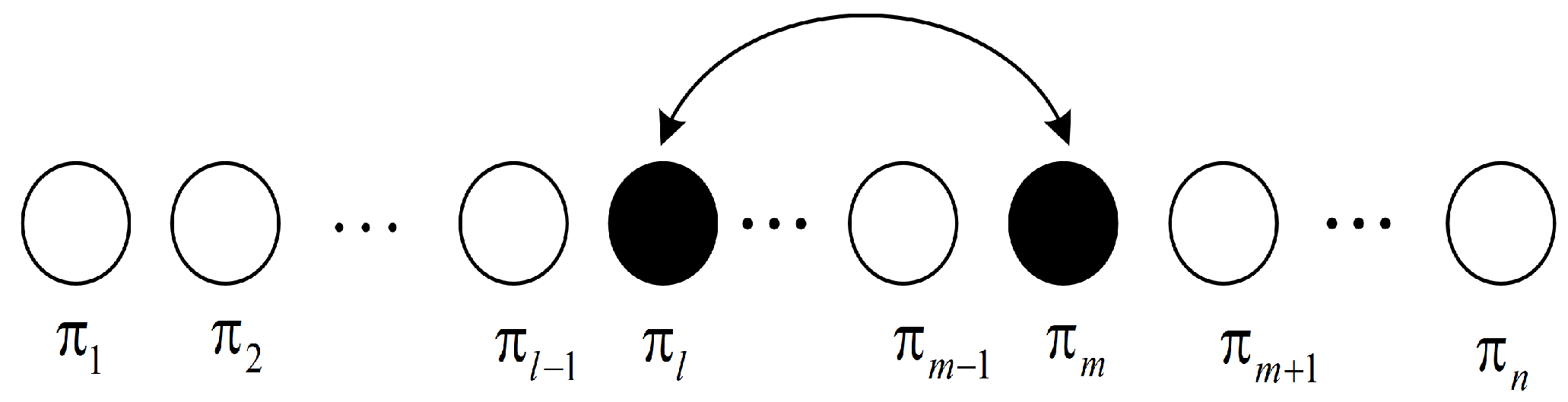
3.2.1. Swap
3.2.2. Reversion
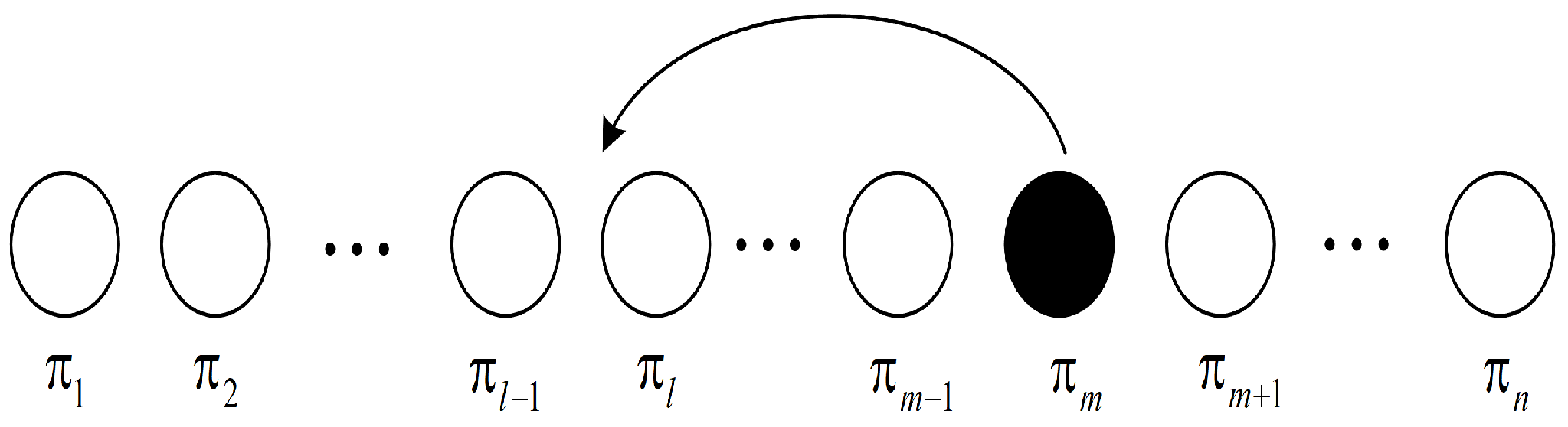
3.2.3. Insertion
3.3. Acceptance and Stop Criteria
3.4. Algorithm Framework
| Algorithm 1: Simulated Annealing Algorithm (SAA) |
| 1 (Initial solution): Generate an initial schedule using the NEH algorithm; |
| 2 Set the temperature |
| 3 Set initial iteration ; |
| 4 Set maximum number of inner iterations ; |
| 5While the termination condition is not met do |
| 6While do |
| 7 Update iteration: |
| 8 (Neighborhood search): Use the neighborhood search method that hybridizes the swap, reversion, and insertion to improve sequence in the previous step. |
| 9 (Acceptance): Set with the probability of |
| 10 |
| 11 where . |
| 12end While |
| 13end While |
| 14Output: The best solution found. |
4. Numerical Experiments
4.1. Experimental Setup
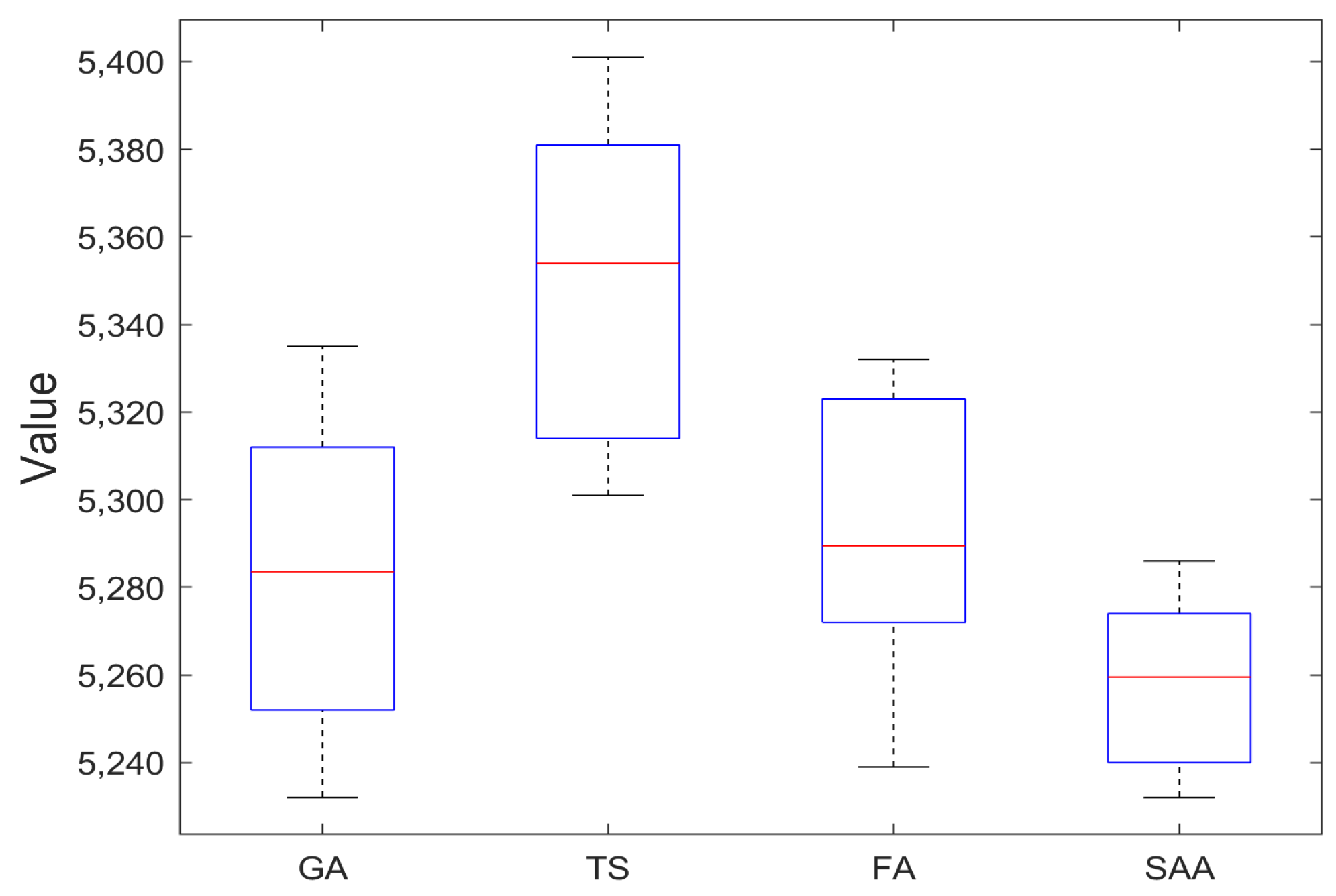
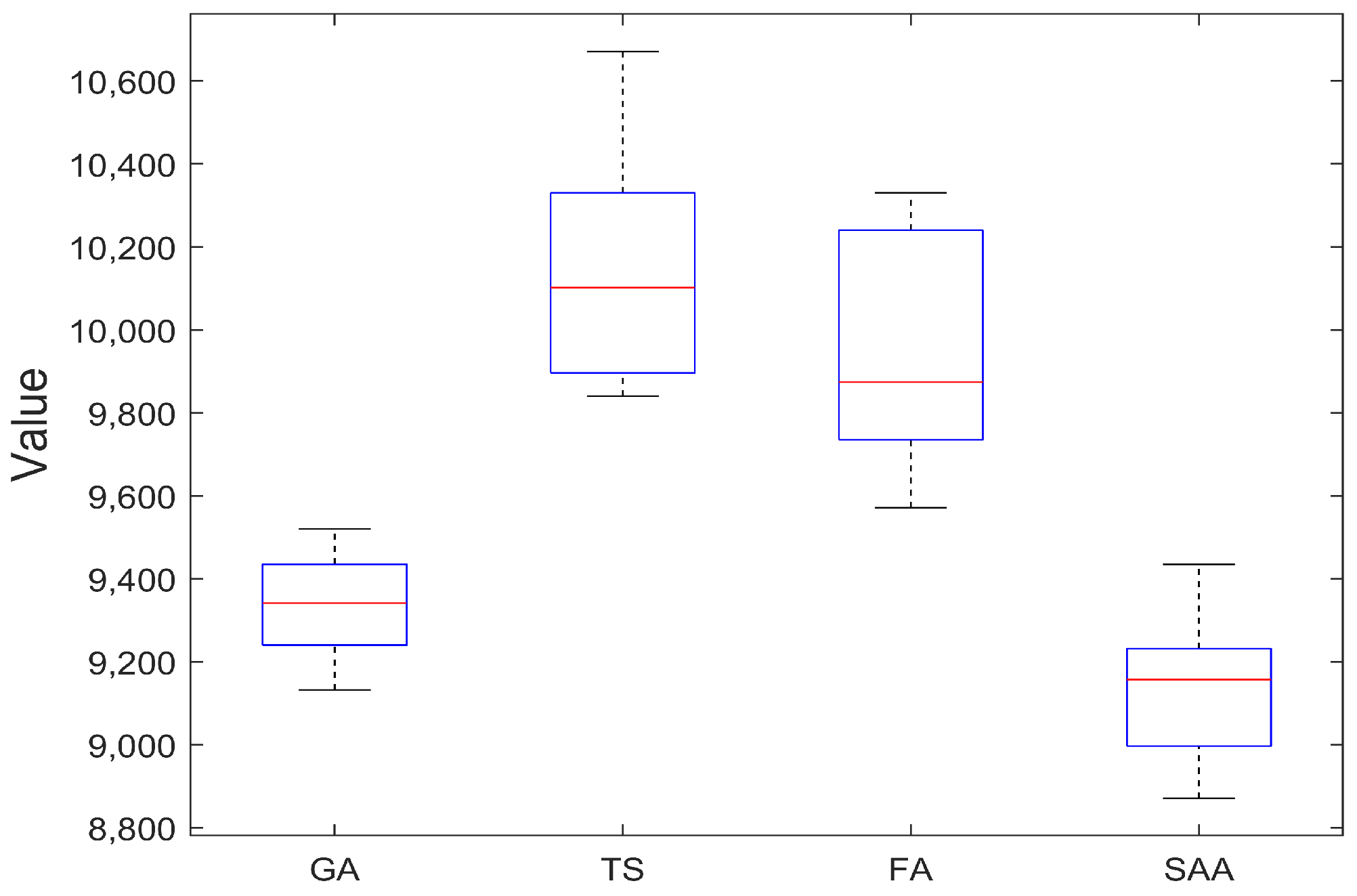
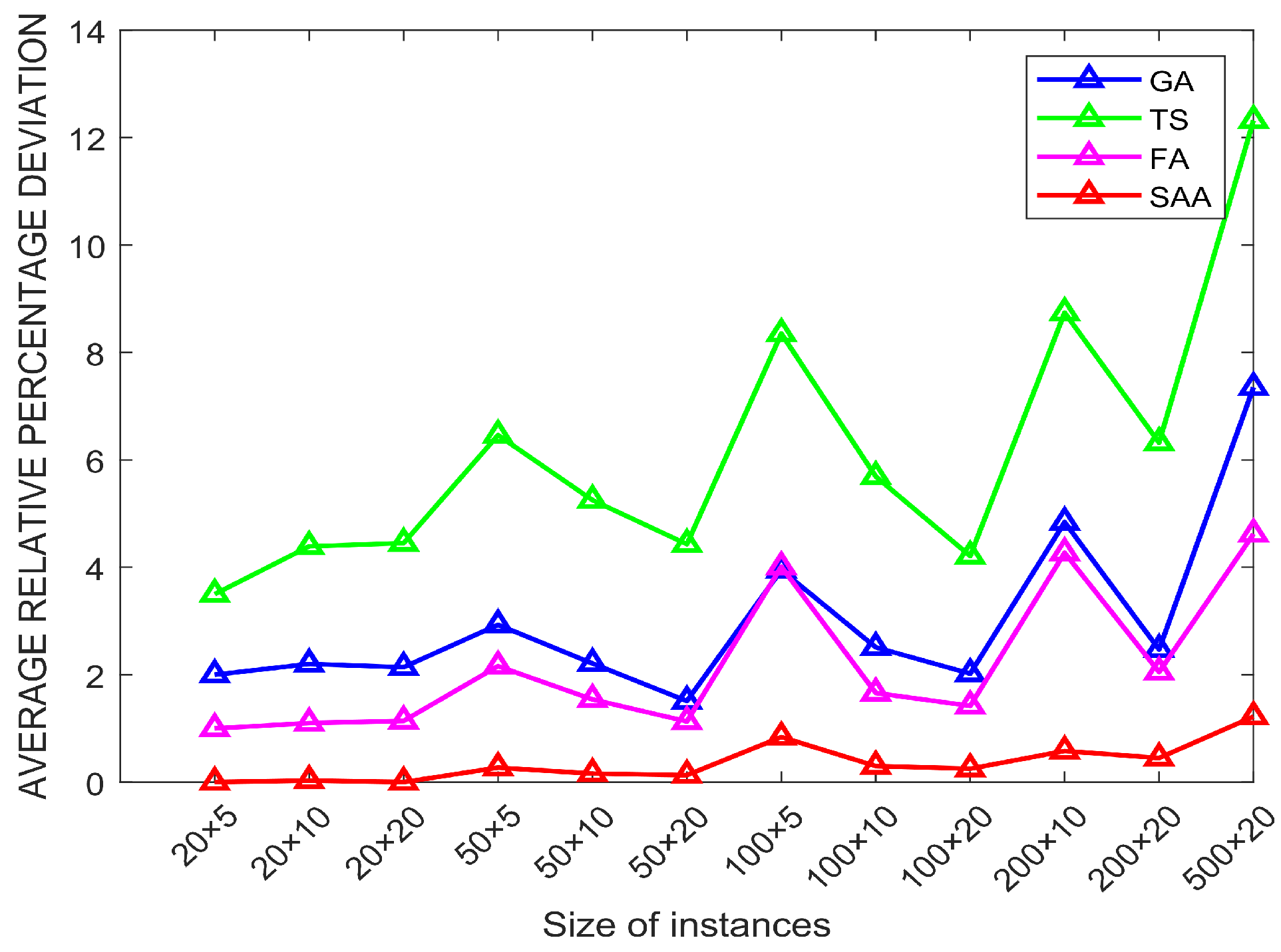
4.2. Comparison with Other Algorithms
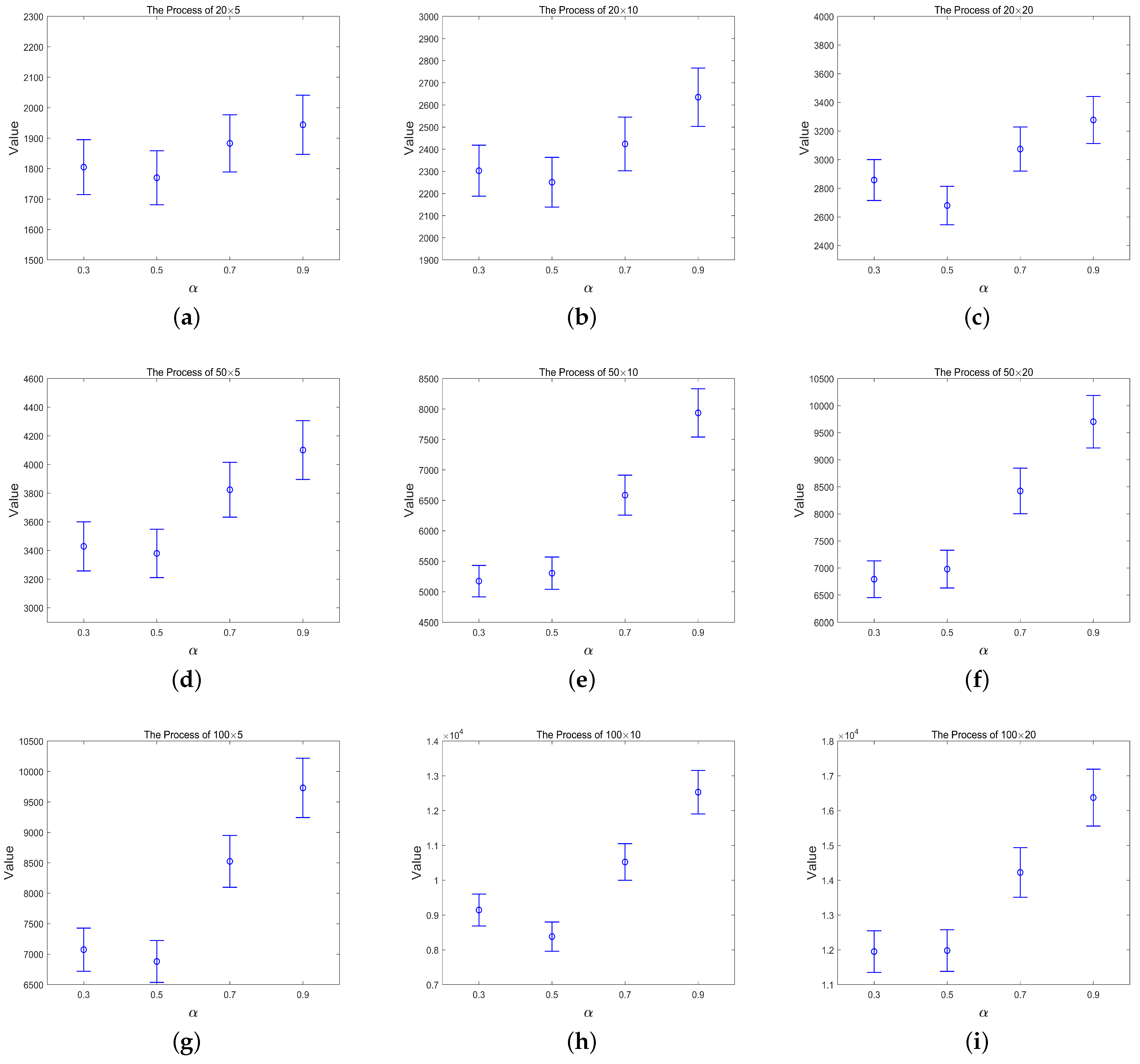
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems, 4th ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Chien, C.-F.; Dauzère-Pérès, S.; Ehm, H.; Fowler, J.W.; Jiang, Z.; Krishnaswamy, S.; Lee, T.E.; Moench, L.; Uzsoy, R. Modelling and analysis of semiconductor manufacturing in a shrinking world: Challenges and successes. Eur. J. Ind. Eng. 2011, 5, 254–271. [Google Scholar] [CrossRef]
- Huang, R.-H.; Yang, C.-L.; Huang, Y.-C. No-wait two-stage multiprocessor flow shop scheduling with unit setup. Int. J. Adv. Manuf. Technol. 2009, 44, 921–927. [Google Scholar] [CrossRef]
- Nagano, M.S.; Da Silva, A.A.; Lorena, L.A.N. A new evolutionary clustering search for a no-wait flow shop problem with set-up times. Eng. Appl. Artif. Intell. 2012, 25, 1114–1120. [Google Scholar] [CrossRef]
- Wang, Z.; Xing, W.; Bai, F. No-wait flexible flowshop scheduling with no-idle machines. Oper. Res. Lett. 2005, 33, 609–614. [Google Scholar] [CrossRef]
- Agnetis, A. Scheduling no-wait robotic cells with two and three machines. Eur. J. Oper. Res. 2000, 123, 303–314. [Google Scholar] [CrossRef]
- Shabtay, D. The just-in-time scheduling problem in a flow-shop scheduling system. Eur. J. Oper. Res. 2012, 216, 521–532. [Google Scholar] [CrossRef]
- Allahverdi, A. A survey of scheduling problems with no-wait in process. Eur. J. Oper. Res. 2016, 255, 665–686. [Google Scholar] [CrossRef]
- Schrijver, A. Combinatorial Optimization: Polyhedra and Efficiency, 1st ed.; Springer: Heidelberg, Germany, 2003. [Google Scholar]
- Ding, J.-Y.; Song, S.; Gupta, J.N.D.; Zhang, R.; Chiong, R.; Wu, C. An improved iterated greedy algorithm with a Tabu-based reconstruction strategy for the no-wait flowshop scheduling problem. Appl. Soft Comput. 2015, 30, 604–613. [Google Scholar] [CrossRef]
- Baoding, L.; Yian-Kui, L. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar] [CrossRef]
- Röck, H. The Three-Machine No-Wait Flow Shop is NP-Complete. Assoc. Comput. Mach. 1984, 31, 336–345. [Google Scholar] [CrossRef]
- Sahni, S.; Cho, Y. Complexity of Scheduling Shops with No Wait in Process. Math. Oper. Res. 1979, 4, 448–457. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Fatih, T.M.; Liang, Y.-C. A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem. Comput. Oper. Res. 2008, 35, 2807–2839. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, H.; Zhang, Y.; Ma, W.; Zhang, C. A discrete Water Wave Optimization algorithm for no-wait flow shop scheduling problem. Expert Syst. Appl. 2018, 91, 347–363. [Google Scholar] [CrossRef]
- Allahverdi, A.; Aydilek, H.; Aydilek, A. No-wait flowshop scheduling problem with two criteria; total tardiness and makespan. Eur. J. Oper. Res. 2018, 269, 590–601. [Google Scholar] [CrossRef]
- Temİz, İ.; Erol, S. Fuzzy branch-and-bound algorithm for flow shop scheduling. J. Intell. Manuf. 2004, 15, 449–454. [Google Scholar] [CrossRef]
- Han, Y.; Gong, D.; Jin, Y.; Pan, Q.-K. Evolutionary multi-objective blocking lot-streaming flow shop scheduling with interval processing time. Appl. Soft Comput. 2016, 42, 229–245. [Google Scholar] [CrossRef]
- Daniels, R.L.; Kouvelis, P. Robust scheduling to hedge against processing time uncertainty in single-stage production. Manag. Sci. 1995, 41, 363–376. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Noori-Darvish, S.; Mahdavi, I.; Mahdavi-Amiri, N. A bi-objective possibilistic programming model for open shop scheduling problems with sequence-dependent setup times, fuzzy processing times, and fuzzy due dates. Appl. Soft Comput. 2012, 12, 1399–1416. [Google Scholar] [CrossRef]
- Liu, G.-S.; Zhou, Y.; Yang, H.-D. Minimizing energy consumption and tardiness penalty for fuzzy flow shop scheduling with state-dependent setup time. J. Clean. Prod. 2017, 147, 470–484. [Google Scholar] [CrossRef]
- Shao, Z.; Shao, W.; Pi, D. Effective heuristics and metaheuristics for the distributed fuzzy blocking flow-shop scheduling problem. Swarm Evol. Comput. 2020, 59, 100747. [Google Scholar] [CrossRef]
- Long, J.; Sun, Z.; Pardalos, P.M.; Bai, Y.; Zhang, S.; Li, C. A robust dynamic scheduling approach based on release time series forecasting for the steelmaking-continuous casting production. Appl. Soft Comput. 2020, 92, 106271. [Google Scholar] [CrossRef]
- Kundu, P.; Majumder, S.; Kar, S.; Maiti, M. A method to solve linear programming problem with interval type-2 fuzzy parameters. Fuzzy Optim. Decis. Mak. 2019, 18, 103–130. [Google Scholar] [CrossRef]
- Lu, C.-C.; Lin, S.-W.; Ying, K.-C. Minimizing worst-case regret of makespan on a single machine with uncertain processing and setup times. Appl. Soft Comput. 2014, 23, 144–151. [Google Scholar] [CrossRef]
- Ashtiani, B.; Haghighirad, F.; Makui, A.; Montazer, G.L. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar] [CrossRef]
- Allahverdi, A.; Aydilek, H.; Aydilek, A. Single machine scheduling problem with interval processing times to minimize mean weighted completion time. Comput. Oper. Res. 2014, 51, 200–207. [Google Scholar] [CrossRef]
- Yao, J.-S.; Lin, F.-T. Constructing a fuzzy flow-shop sequencing model based on statistical data. Int. J. Approx. Reason. 2002, 29, 215–234. [Google Scholar] [CrossRef]
- Aydilek, H.; Allahverdi, A. A polynomial time heuristic for the two-machine flowshop scheduling problem with setup times and random processing times. Appl. Math. Model. 2013, 37, 7164–7173. [Google Scholar] [CrossRef]
- Pereira, J. The robust (minmax regret) single machine scheduling with interval processing times and total weighted completion time objective. Comput. Oper. Res. 2016, 66, 141–152. [Google Scholar] [CrossRef]
- Dorfeshan, Y.; Tavakkoli-Moghaddam, R.; Mousavi, S.M.; Vahedi-Nouri, B. A new weighted distance-based approximation methodology for flow shop scheduling group decisions under the interval-valued fuzzy processing time. Appl. Soft Comput. 2020, 91, 106248. [Google Scholar] [CrossRef]
- Gupta, J.N.D.; Stafford, E.F. Flowshop scheduling research after five decades. Eur. J. Oper. Res. 2006, 169, 699–711. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-Constrained Programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. OMEGA 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. On the NEH heuristic for minimizing the makespan in permutation flow shops. OMEGA 2007, 35, 53–60. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Osman, I.H.; Potts, C.N. Simulated annealing for permutation flow-shop scheduling. OMEGA 1989, 17, 551–557. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: Common pitfalls and guidelines to avoid them. Appl. Soft Comput. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- Ahmadizar, F.; Zarei, A. Minimizing makespan in a group shop with fuzzy release dates and processing times. Int. J. Adv. Manuf. Technol. 2013, 66, 2063–2074. [Google Scholar] [CrossRef]
- Ben-Daya, M.; Al-Fawzan, M. A tabu search approach for the flow shop scheduling problem. Eur. J. Oper. Res. 1998, 109, 88–95. [Google Scholar] [CrossRef]
- Udaiyakumar, K.C.; Chandrasekaran, M. Application of Firefly Algorithm in Job Shop Scheduling Problem for Minimization of Makespan. Procedia Eng. 2014, 97, 1798–1807. [Google Scholar] [CrossRef][Green Version]


| Factors | Value |
|---|---|
| Number of jobs (n) | 20/50/100/200/500 |
| Number of machines (m) | 5/10/20 |
| Processing time for each operation () | [1,99] |
| TCT constraint value (T) | Value of NEH solution |
| GA | TS | FA | SAA | |||||
|---|---|---|---|---|---|---|---|---|
| ARPD | SD | ARPD | SD | ARPD | SD | ARPD | SD | |
| 20, 5 | 2.00 | 1805.1 | 3.50 | 4.42 | 1.00 | 1.01 | 0.00 | 0.00 |
| 20, 10 | 2.20 | 1.65 | 4.39 | 4.81 | 1.10 | 1.07 | 0.03 | 0.02 |
| 20, 20 | 2.14 | 2.07 | 4.45 | 3.95 | 1.14 | 1.20 | 0.00 | 0.00 |
| 50, 5 | 2.93 | 3.04 | 6.46 | 6.01 | 2.16 | 2.19 | 0.27 | 0.19 |
| 50, 10 | 2.21 | 2.65 | 5.25 | 5.27 | 1.54 | 1.23 | 0.16 | 0.09 |
| 50, 20 | 1.51 | 2.72 | 4.43 | 4.89 | 1.13 | 1.65 | 0.13 | 0.13 |
| 100, 5 | 3.95 | 4.07 | 8.35 | 8.02 | 4.01 | 3.83 | 0.84 | 0.40 |
| 100, 10 | 2.51 | 2.98 | 5.69 | 4.92 | 1.66 | 1.21 | 0.30 | 0.33 |
| 100, 20 | 2.02 | 3.11 | 4.21 | 4.11 | 1.42 | 1.56 | 0.25 | 0.27 |
| 200, 10 | 4.84 | 5.83 | 8.74 | 8.05 | 4.27 | 3.86 | 0.58 | 0.62 |
| 200, 20 | 2.47 | 3.74 | 6.32 | 6.23 | 2.05 | 2.11 | 0.45 | 0.57 |
| 500, 20 | 7.35 | 8.21 | 12.32 | 12.11 | 4.62 | 4.63 | 1.22 | 1.39 |
| Average | 3.21 | 3.48 | 6.36 | 6.06 | 2.11 | 2.13 | 0.35 | 0.33 |
| GA | TS | FA | SAA | |||||
|---|---|---|---|---|---|---|---|---|
| Best | Mean | Best | Mean | Best | Mean | Best | Mean | |
| 20, 5 | 1778.3 | 1778.3 | 1778.3 | 1778.3 | 1778.3 | 1778.3 | 1778.3 | 1778.3 |
| 20, 10 | 2201.5 | 2303.7 | 2235.2 | 2363.2 | 2211.4 | 2363.4 | 2224.5 | 2331.2 |
| 20, 20 | 2658.5 | 2858.3 | 2674.3 | 2898.2 | 2736.7 | 2904.8 | 2703.5 | 2882.6 |
| 50, 5 | 3382.8 | 3428.9 | 3432.4 | 3504.3 | 3412.1 | 3503.6 | 3407.2 | 3488.6 |
| 50, 10 | 5043.2 | 5273.6 | 5173.6 | 5364.2 | 5120.4 | 5322.6 | 5100.2 | 5323.3 |
| 50, 20 | 6542.4 | 6793.3 | 6631.4 | 6923.4 | 6633.6 | 6921.7 | 6631.6 | 6882.9 |
| 100, 5 | 6738.2 | 7074.2 | 6926.7 | 7372.2 | 6831.8 | 7252.4 | 6821.2 | 7286.1 |
| 100, 10 | 8810.1 | 9143.5 | 8982.6 | 9431.6 | 9013.4 | 9433.8 | 8963.6 | 9393.5 |
| 100, 20 | 10,730.4 | 11950.4 | 11,432.6 | 12,651.7 | 11,341.4 | 12,763.7 | 10,865.8 | 12,473.7 |
| 200, 10 | 15,542.3 | 16,327.7 | 15,934.9 | 17,352.3 | 16,023.6 | 17,121.7 | 15,863.5 | 16,929.5 |
| 200, 20 | 20,842.1 | 21,536.3 | 21,163.5 | 22,316.4 | 21,545.8 | 22,383.4 | 21,342.5 | 22,237.8 |
| 500, 20 | 48,242.6 | 49,717.1 | 49,135.7 | 51,256.4 | 49,438.4 | 51,753.3 | 49,320.1 | 51,642.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Jiang, A.; Ge, D.; Zheng, X.; Gao, F. A Chance Constrained Programming Approach for No-Wait Flow Shop Scheduling Problem under the Interval-Valued Fuzzy Processing Time. Processes 2021, 9, 789. https://doi.org/10.3390/pr9050789
Sun H, Jiang A, Ge D, Zheng X, Gao F. A Chance Constrained Programming Approach for No-Wait Flow Shop Scheduling Problem under the Interval-Valued Fuzzy Processing Time. Processes. 2021; 9(5):789. https://doi.org/10.3390/pr9050789
Chicago/Turabian StyleSun, Hao, Aipeng Jiang, Dongming Ge, Xiaoqing Zheng, and Farong Gao. 2021. "A Chance Constrained Programming Approach for No-Wait Flow Shop Scheduling Problem under the Interval-Valued Fuzzy Processing Time" Processes 9, no. 5: 789. https://doi.org/10.3390/pr9050789
APA StyleSun, H., Jiang, A., Ge, D., Zheng, X., & Gao, F. (2021). A Chance Constrained Programming Approach for No-Wait Flow Shop Scheduling Problem under the Interval-Valued Fuzzy Processing Time. Processes, 9(5), 789. https://doi.org/10.3390/pr9050789






