Simulation of Shear-Thickening Liquid Transfer between U-Shaped Cell and Flat Plate
Abstract
:1. Introduction
2. Ink Properties and Model Parameters
3. Numerical Methods
4. Results and Discussion
4.1. The Effect of Substrate Wettability
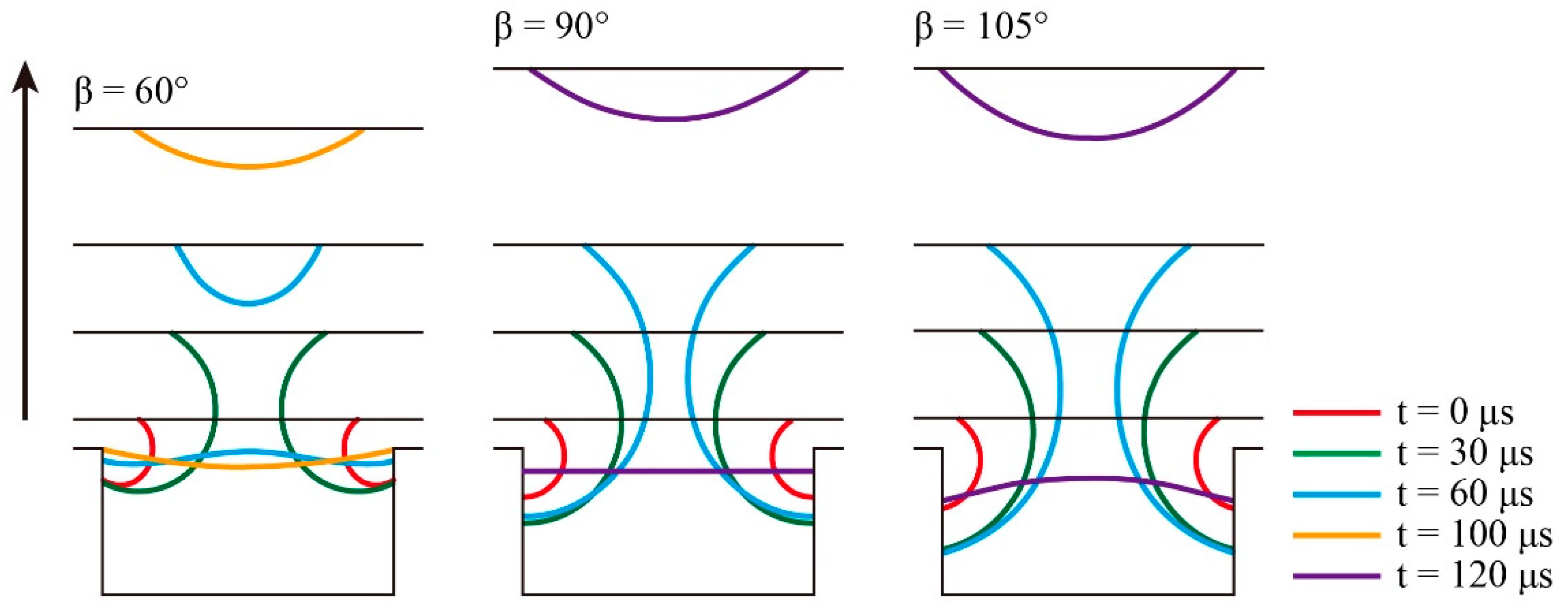
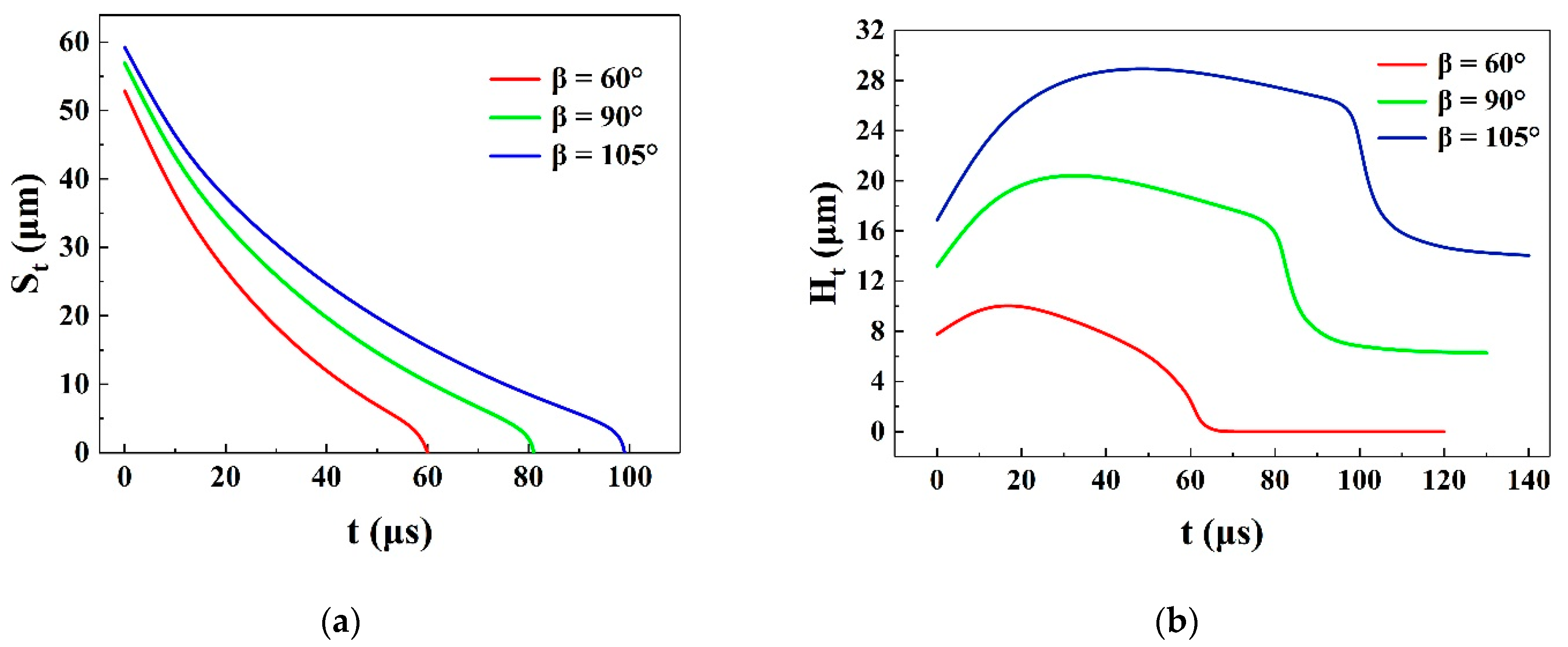
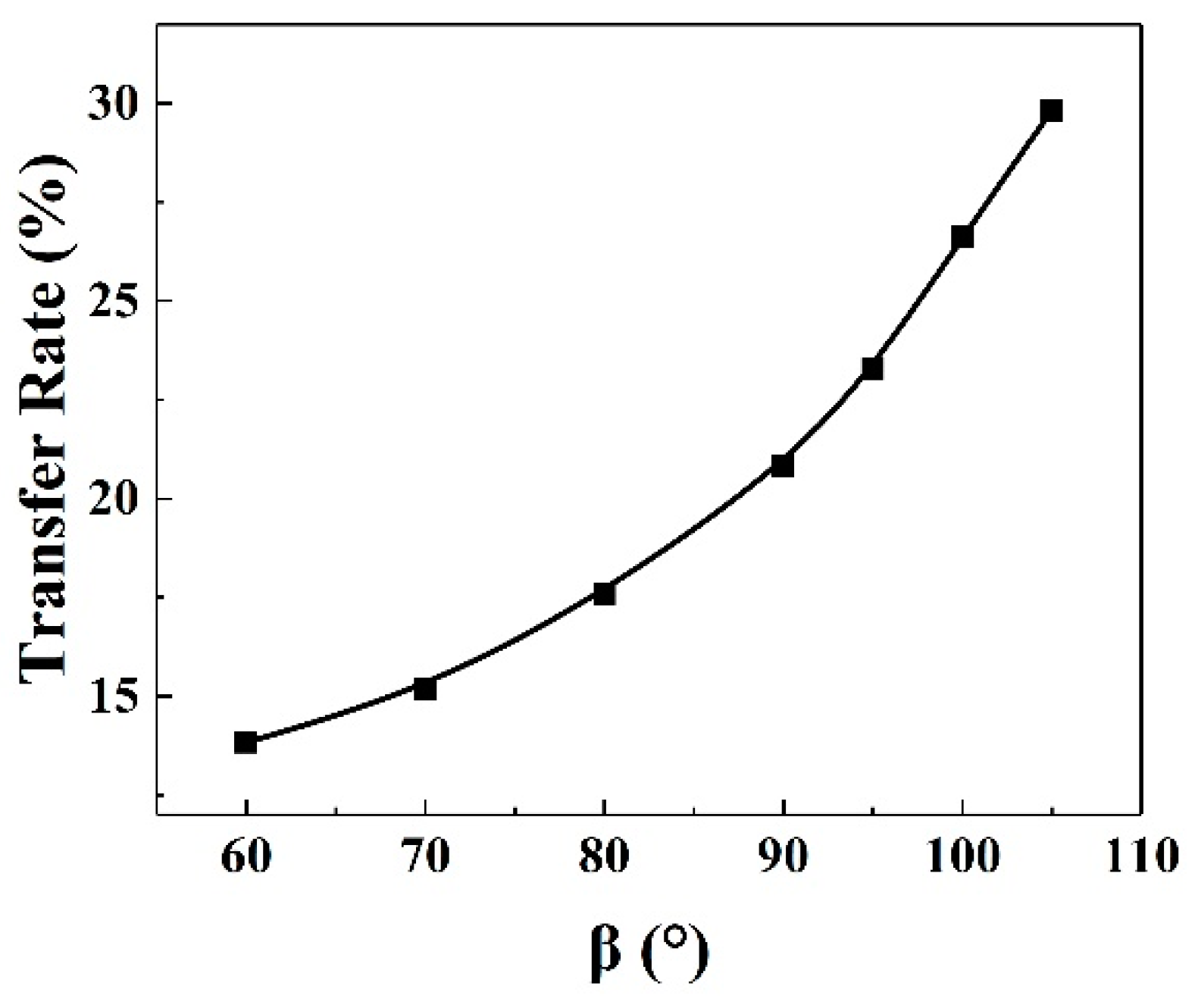
4.2. The Effect of Cell Contact Angle
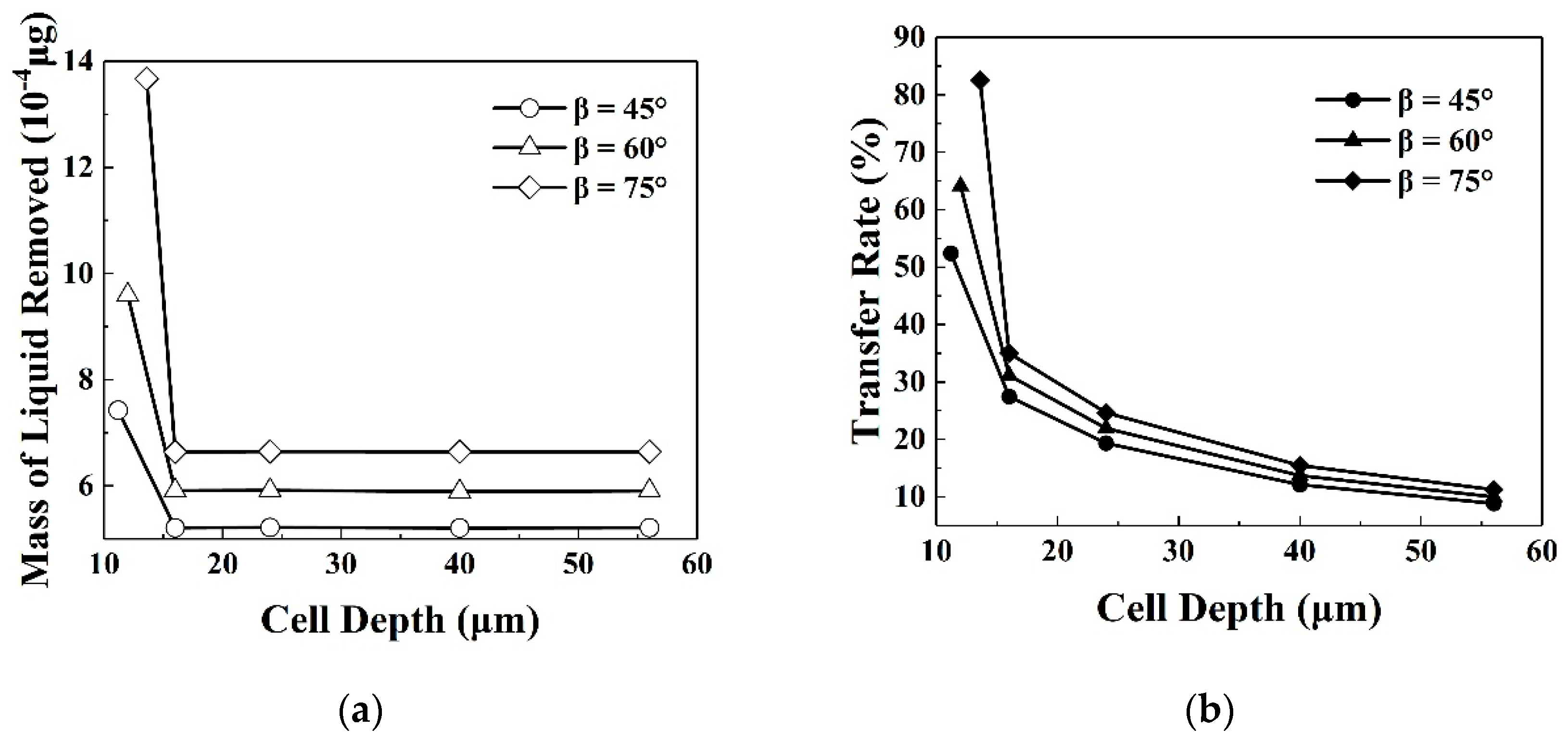
4.3. Shallow Printing Plate Effect
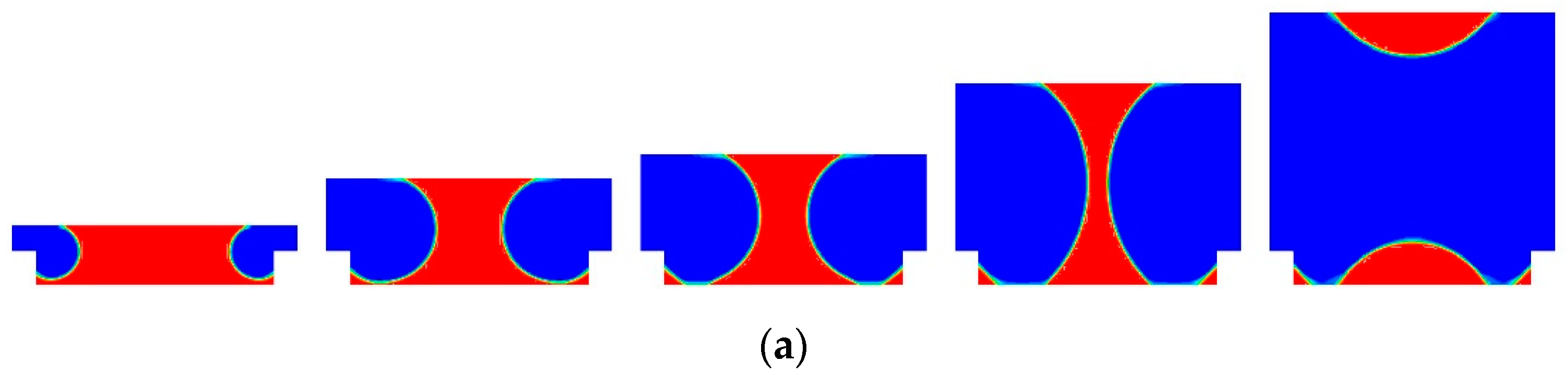
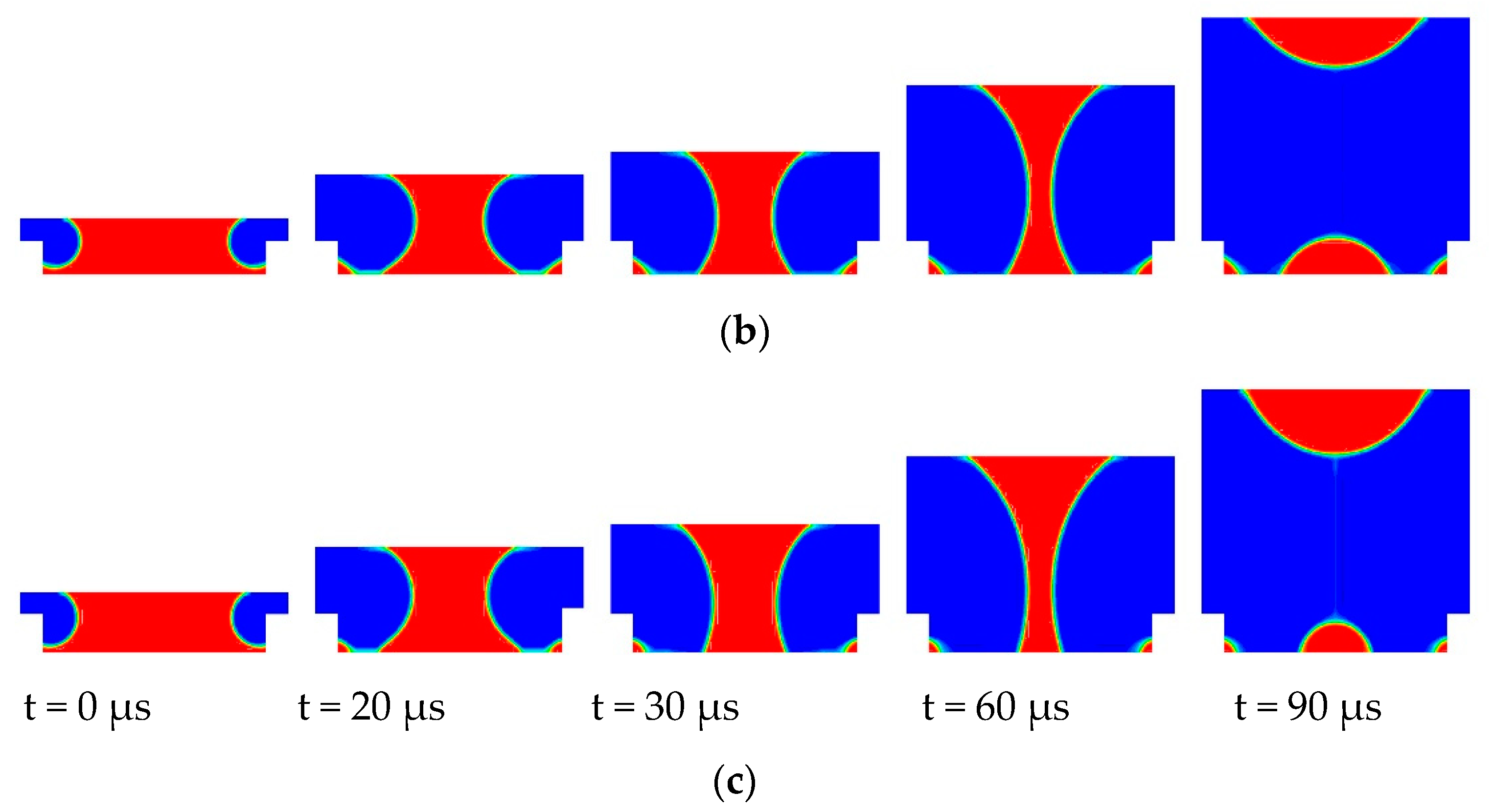
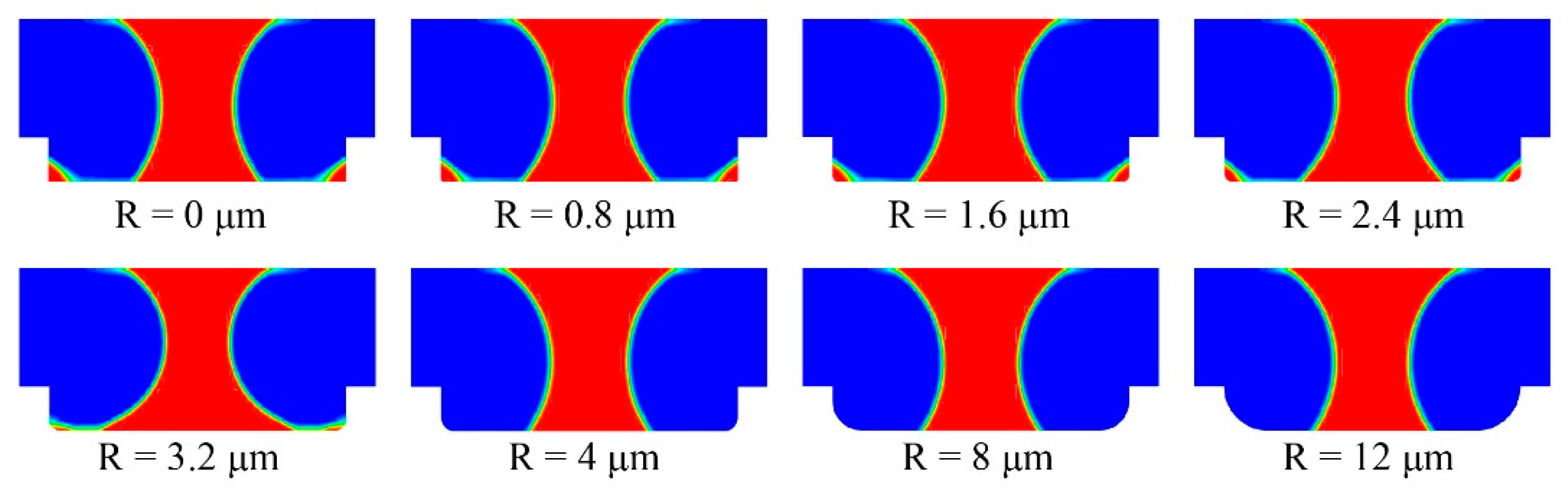
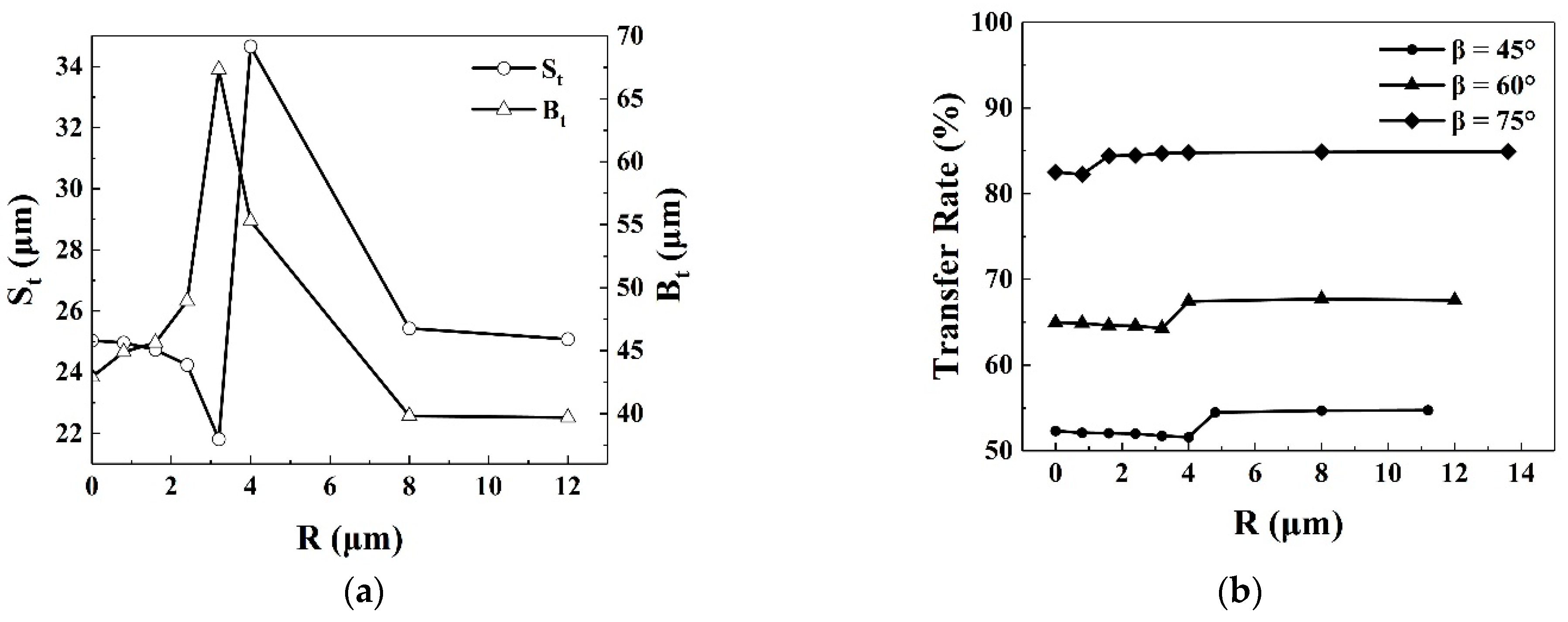
4.4. Cell Shape Optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameter | Define |
| PLIC | Piecewise Linear Interface Construction |
| VOF | Volume of Fluid |
| VOC | Volatile organic compounds |
| shear rate | |
| shear stress | |
| α | The contact angles of the liquid with the upper plate |
| β | The contact angles of the liquid with the cell wall |
| h | cell depth |
| St | The thickness of the thinnest part of the liquid filament |
| Ht | The depth of the contact line on the cell wall |
| Bt | The width of the contact line at the bottom of the cell |
| R | The corner radius of the cell |
References
- Hansuebsai, A.; Nawakitwong, S. Printability Analysis of Compostable Films by Flexographic Water Based Ink. Key Eng. Mater. 2020, 5925. [Google Scholar] [CrossRef]
- Xiaofang, W.; Zhao, L.; Jianming, S. Analysis of the current status and application of environmentally friendly water-based inks. Sci. Technol. Eng. 2017, 17, 167–175. [Google Scholar] [CrossRef]
- Gong, Y.; Huang, B.Q.; Wei, X.F. Comprehensive Research into the Influence of Resin on Properties of Environmentally Friendly Water-Based Ink. Appl. Mech. Mater. 2014, 525, 15–22. [Google Scholar] [CrossRef]
- Li, W.W.; Li, L.H.; Mo, L.X.; Hu, X.W.; Leng, X.; Fang, H.; Li, W.B.; Li, S.K. Progress of Printing RFID Antenna Using Water-Based Conductive Ink. Adv. Mater. Res. 2012, 380, 137–140. [Google Scholar] [CrossRef]
- Xiulan, X.; Yana, W. Research Progress in Water-based Inks. China Print. Packag. Res. 2011, 3, 1–8. [Google Scholar]
- Zhou, X.; Li, Y.; Fang, C.; Li, S.; Cheng, Y.; Lei, W.; Meng, X. Recent Advances in Synthesis of Waterborne Polyurethane and Their Application in Water-based Ink: A Review. J. Mater. Sci. Technol. 2015, 31, 708–722. [Google Scholar] [CrossRef]
- Sico, G.; Montanino, M.; Prontera, C.T.; Mauro, A.D.G.D.; Minarini, C. Gravure printing for thin film ceramics manufacturing from nanoparticles. Ceram. Int. 2018, 44. [Google Scholar] [CrossRef]
- Schfer, J.; Roisman, I.V.; Sauer, H.M.; Drsam, E. Millisecond fluid pattern formation in the nip of a gravure printing machine. Colloids Surf. A Physicochem. Eng. Asp. 2019, 575, 222–229. [Google Scholar] [CrossRef]
- Campana, D.M.; Ubal, S.; Giavedoni, M.D.; Saita, F.A.; Carvalho, M.S. Three dimensional flow of liquid transfer between a cavity and a moving roll. Chem. Eng. Sci. 2016, 149, 169–180. [Google Scholar] [CrossRef]
- Kim, K.; Nam, T.; Na, Y. A numerical study of the ink transfer process for roll-to-roll printing applications. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2496–2509. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Yang, T.Y.; Suhonen, R.; Välimäki, M.; Maaninen, T.; Kemppainen, A.; Jeon, N.J.; Seo, J. Gravure-Printed Flexible Perovskite Solar Cells: Toward Roll-to-Roll Manufacturing. Adv. Sci. 2019, 6, 1802094. [Google Scholar] [CrossRef] [Green Version]
- Pudas, M.; Hagberg, J.; Leppävuori, S. Printing parameters and ink components affecting ultra-fine-line gravure-offset printing for electronics applications. J. Eur. Ceram. Soc. 2004, 24, 2943–2950. [Google Scholar] [CrossRef]
- Wu, J.T.; Carvalho, M.S.; Kumar, S. Emptying of Gravure Cavities containing Shear-thinning and Shear-thickening Liquids. J. Non-Newton. Fluid Mech. 2019, 268, 46–55. [Google Scholar] [CrossRef]
- Dodds, S.; Carvalho, M.D.S.; Kumar, S. Stretching and slipping of liquid bridges near plates and cavities. Phys. Fluids 2009, 21, 4–366. [Google Scholar] [CrossRef]
- Ahmed, D.H.; Sung, H.J.; Kim, D.S. Simulation of non-Newtonian ink transfer between two separating plates for gravure-offset printing. Int. J. Heat Fluid Flow 2011, 32, 298–307. [Google Scholar] [CrossRef]
- Khandavalli, S.; Lee, J.A.; Pasquali, M.; Rothstein, J.P. The effect of shear-thickening on liquid transfer from an idealized gravure cell. J. Non-Newton. Fluid Mech. 2015, 221. [Google Scholar] [CrossRef]
- Kapur, N.; Hewson, R.; Sleigh, P.A. A review of gravure coating systems (Fundamental coating research). Convert. e-Print 2011, 1, 56–60. [Google Scholar]
- Yin, X.; Kumar, S. Flow visualization studies in scaled-up gravure grooves and cells. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, East Rutherford, NJ, USA, 23–25 November 2003. [Google Scholar]
- Chuang, H.K.; Lee, C.C.; Liu, T.J. An Experimental Study on the Pickout of Scaled-up Gravure Cells. Int. Polym. Process. J. Polym. Process. Soc. 2013, 23, 216–222. [Google Scholar] [CrossRef]
- Davarpanah, A.; Zarei, M.; Valizadeh, K.; Mirshekari, B. CFD design and simulation of ethylene dichloride (EDC) thermal cracking reactor. Energy Sour. Part A Recovery Util. Environ. Effects 2019, 41, 1573–1587. [Google Scholar] [CrossRef]
- Daryayehsalameh, B.; Nabavi, M.; Vaferi, B. Modeling of CO2 capture ability of [Bmim][BF4] ionic liquid using connectionist smart paradigms. Environ. Technol. Innov. 2021, 22, 101484. [Google Scholar] [CrossRef]
- Hsu, T.W.; Hsieh, C.M.; Tsai, C.Y.; Ou, S.H. Coupling VOF/PLIC and Embedding Method for Simulating Wave Breaking on a Sloping Beach. J. Mar. Sci. Technol. 2015, 23, 498–507. [Google Scholar] [CrossRef]
- Valizadeh, K.; Farahbakhsh, S.; Bateni, A.; Zargarian, A.; Zarei, M. A parametric study to simulate the non-Newtonian turbulent flow in spiral tubes. Energy Sci. Eng. 2019, 8, 134–149. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.T.; Francis, L.F.; Carvalho, M.S.; Kumar, S. Cavity filling with shear-thinning liquids. Phys. Rev. Fluids 2020, 5, 054003. [Google Scholar] [CrossRef]
- Lee, J.A.; Rothstein, J.P.; Pasquali, M. Computational study of viscoelastic effects on liquid transfer during gravure printing. J. Non-Newton. Fluid Mech. 2013, 199, 1–11. [Google Scholar] [CrossRef]
- Zhang, X. Dynamics of drop formation in viscous flows. Chem. Eng. Sci. 1999, 26, 1759–1774. [Google Scholar] [CrossRef]
- Powell, C.A.; Guthrie, J.T. Computational simulation of the printing of Newtonian liquid from a trapezoidal cavity. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 338–355. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Dezhi, D.; Tong, A.Y. An analytical interface reconstruction algorithm in PLIC-VOF method for 2D polygonal unstructured meshes. Int. J. Numer. Methods Fluids 2018. [Google Scholar] [CrossRef]
- Özkan, F.; Wenka, A.; Hansjosten, E.; Pfeifer, P.; Kraushaar-Czarnetzki, B. Numerical investigation of interfacial mass transfer in two phase flows using the VOF method. Eng. Appl. Comput. Fluid Mech. 2015, 10, 100–110. [Google Scholar] [CrossRef]
- Phan, H.N.; Lee, J.H. Flood Impact Pressure Analysis of Vertical Wall Structures using PLIC-VOF Method with Lagrangian Advection Algorithm. J. Comput. Struct. Eng. Inst. Korea 2010, 23, 675–682. [Google Scholar]
- Huang, W.X.; Lee, S.H.; Sung, H.J.; Lee, T.M.; Kim, D.S. Simulation of liquid transfer between separating walls for modeling micro-gravure-offset printing. China Print. Packag. Study 2008, 29, 1436–1446. [Google Scholar] [CrossRef]
- Ghadiri, F.; Ahmed, D.H.; Sung, H.J.; Shirani, E. Non-Newtonian ink transfer in gravure–offset printing. Int. J. Heat Fluid Flow 2011, 32, 308–317. [Google Scholar] [CrossRef]
- Chen, W.; Lai, W.; Wang, Y.; Wang, K.; Lin, S.; Yen, Y.; Hocheng, H.; Chou, T. Ultrafast Laser Engraving Method to Fabricate Gravure Plate for Printed Metal-Mesh Touch Panel. Micromachines 2015, 6, 1483–1489. [Google Scholar] [CrossRef] [Green Version]
- Hennig, G.; Selbmann, K.H.; Brockelt, A. Laser Engraving in Gravure Industry. In Workshop on Laser Applications in Europe; Gries, W., Pearsall, T.P., Eds.; SPIE: Bellingham, WA, USA, 2006; Volume 6157. [Google Scholar]
- Wu, S.; Xing, J.; Dong, L.; Zhu, H. Multi-Objective Optimization of Microstructure of Gravure Cell Based on Response Surface Method. Processes 2021, 9, 403. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Rubio-Hernández, F.; Velázquez-Navarro, J. Shear-thickening behavior of Aerosil® R816 nanoparticles suspensions in polar organic liquids. Rheol. Acta 2009, 48, 699–708. [Google Scholar] [CrossRef]
- Wagner, N.J.; Russel, W.B. Nonequilibrium statistical mechanics of concentrated colloidal dispersions: Hard spheres in weak flows with many-body thermodynamic interactions. Phys. A Stat. Mech. Appl. 1989, 155, 475–518. [Google Scholar] [CrossRef]
- Manica, R.; Bortoli, A. Simulation of sudden expansion flows for power-law fluids. J. Non-Newton. Fluid Mech. 2004, 121, 35–40. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Nourazar, S.S.; Campo, A. Analytical solution for two-phase flow between two rotating cylinders filled with power law liquid and a micro layer of gas. J. Mech. Sci. Technol. 2014, 28, 1849–1854. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Rubio-Hernández, F.J.; Sevilla, A. An apparent viscosity function for shear thickening fluids. J. Non-Newton. Fluid Mech. 2011, 166, 321–325. [Google Scholar] [CrossRef]
- Hizir, F.E.; Hardt, D.E. Phase-field modeling of liquids splitting between separating surfaces and its application to high-resolution roll-based printing technologies. Phys. Fluids 2017, 29, 052007. [Google Scholar] [CrossRef] [Green Version]
- Grüßer, M.; Waugh, D.G.; Lawrence, J.; Langer, N.; Scholz, D. On the Droplet Size and Application of Wettability Analysis for the Development of Ink and Printing Substrates. Langmuir 2019, 35, 12356–12365. [Google Scholar] [CrossRef] [PubMed]
- Popelka, A.; Khanam, P.N.; AlMaadeed, M.A. Surface modification of polyethylene/graphene composite using corona discharge. J. Phys. D Appl. Phys. 2018, 51, 105302. [Google Scholar] [CrossRef]
- Rocca-Smith, J.R.; Karbowiak, T.; Marcuzzo, E.; Sensidoni, A.; Piasente, F.; Champion, D.; Heinz, O.; Vitry, P.; Bourillot, E.; Lesniewska, E.; et al. Impact of corona treatment on PLA film properties. Polym. Degrad. Stab. 2016, 132, 109–116. [Google Scholar] [CrossRef]
- Chun, J.; Wang, J.-X.; Xu, C.; Wen, R.-F.; Lan, Z.; Ma, X.-H. Theoretical model of maximum spreading diameter on superhydrophilic surfaces. Acta Phys. Sin. 2021. [Google Scholar] [CrossRef]
- Kang, H.W.; Sung, H.J.; Lee, T.-M.; Kim, D.-S.; Kim, C.-J. Liquid transfer between two separating plates for micro-gravure-offset printing. J. Micromech. Microeng. 2008, 19, 015025. [Google Scholar] [CrossRef] [Green Version]


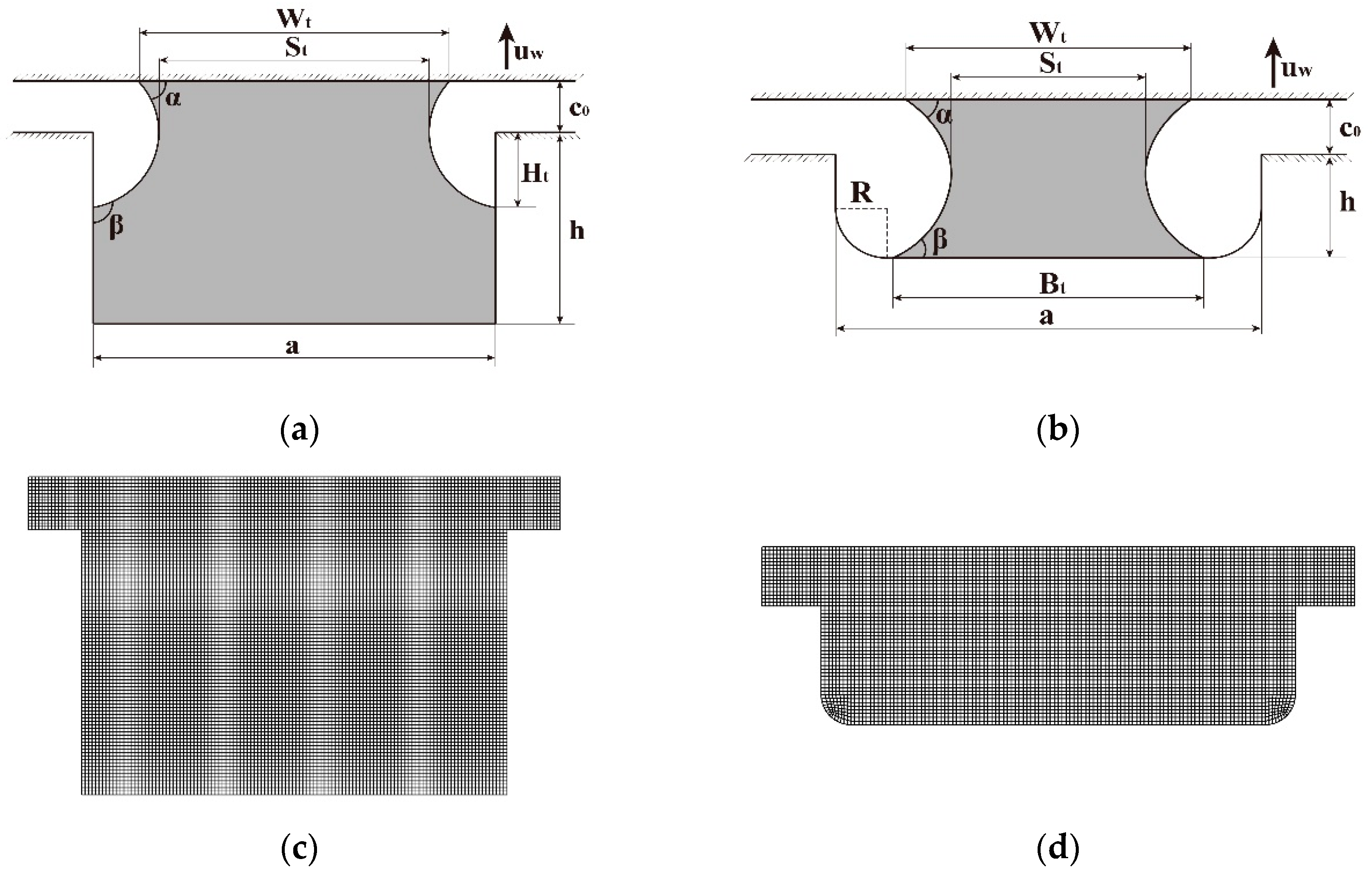

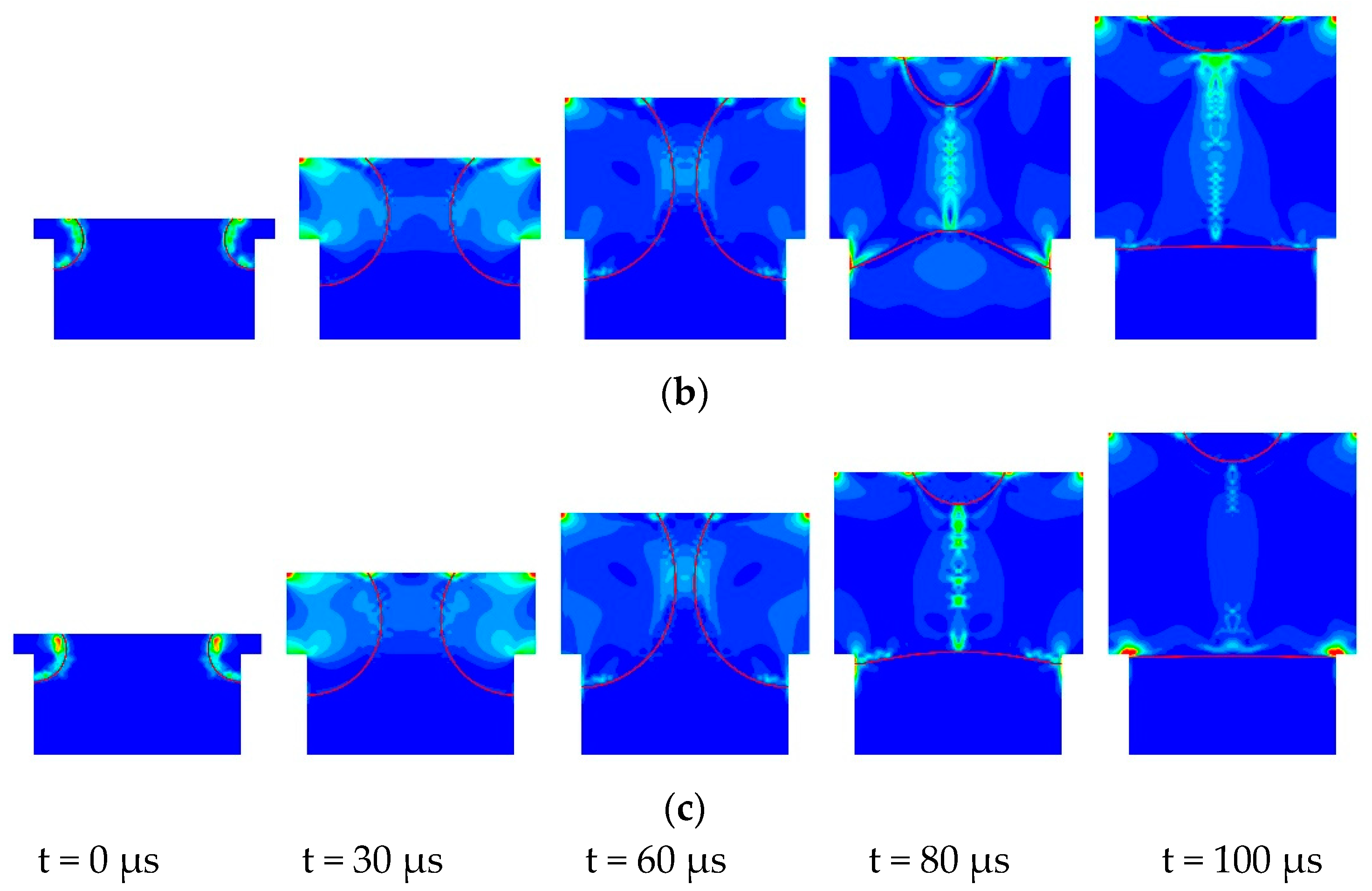
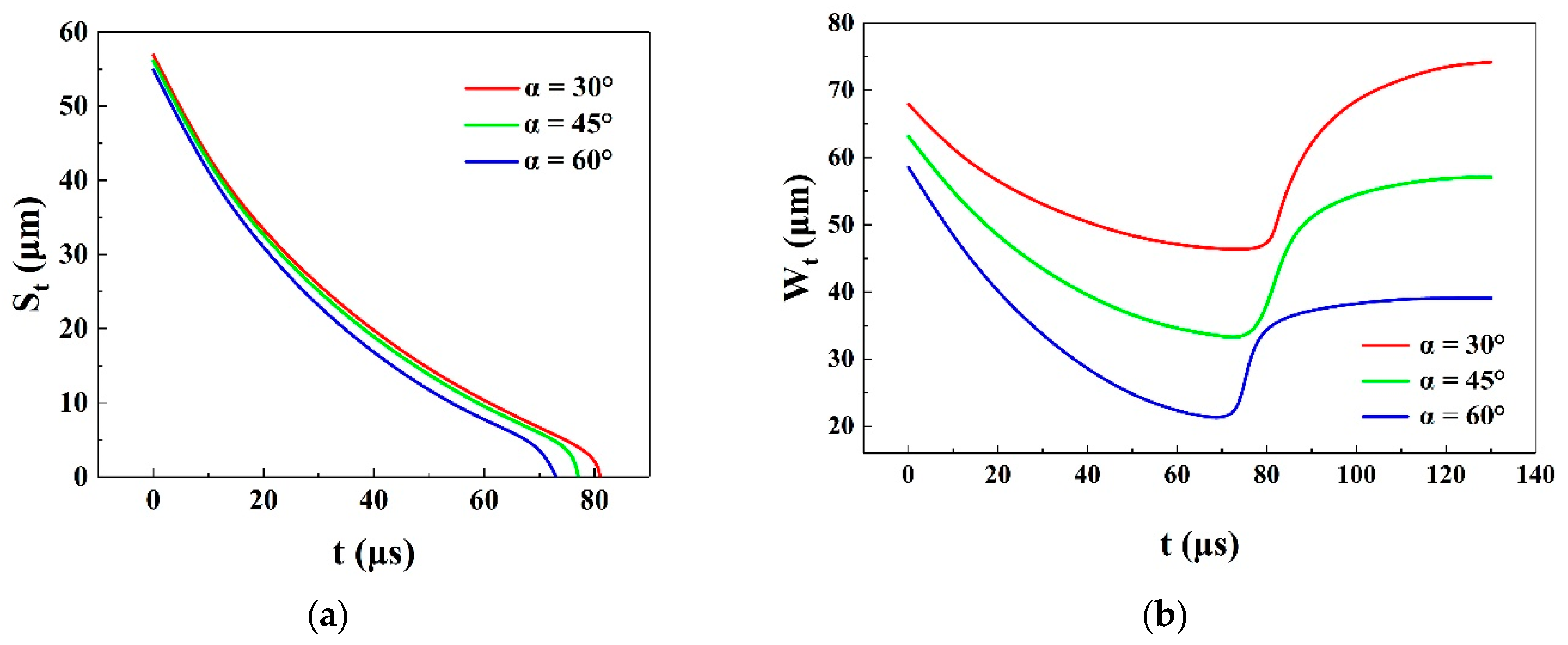
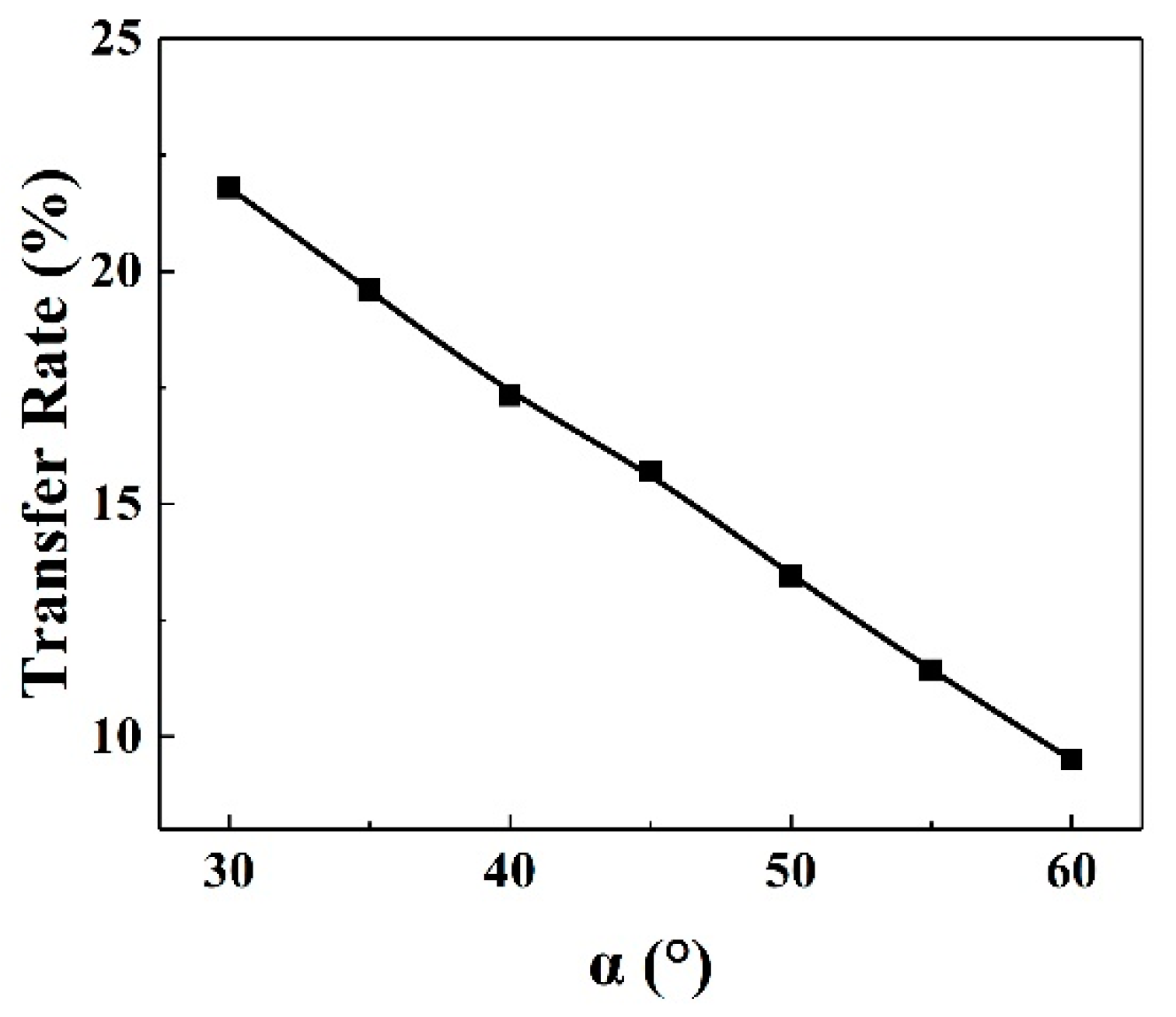

| Parameters | Date |
|---|---|
| Liquid density | 1000 kg m−3 |
| Liquid surface tension | 1 N m−1 |
| Initial liquid viscosity | 0.08 Pa·s |
| Air density | 1.22 kg m−3 |
| Air viscosity | 1.8 × 10−5 Pa·s |
| Parameters | Date |
|---|---|
| Cell open width, a | 80 μm |
| Cell depth, h | 40 μm |
| Initial distance between cell and upper plate, c0 | 8 μm |
| Upper plate move speed, uw | 1 m/s |
| Calculation time step | 2 × 10−8 s |
| The Cell Contact Angle, β (°) | The Cell Depth, h (μm) | Mass of Residual Liquid, (10−6 μg) |
|---|---|---|
| 45 | 11.2 | 71.4482 |
| 60 | 12 | 61.6148 |
| 75 | 13.6 | 46.6314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Xing, J.; Wu, S.; Guan, X.; Zhu, H. Simulation of Shear-Thickening Liquid Transfer between U-Shaped Cell and Flat Plate. Processes 2021, 9, 838. https://doi.org/10.3390/pr9050838
Dong L, Xing J, Wu S, Guan X, Zhu H. Simulation of Shear-Thickening Liquid Transfer between U-Shaped Cell and Flat Plate. Processes. 2021; 9(5):838. https://doi.org/10.3390/pr9050838
Chicago/Turabian StyleDong, Ling, Jiefang Xing, Shuang Wu, Xiaomin Guan, and Hongjuan Zhu. 2021. "Simulation of Shear-Thickening Liquid Transfer between U-Shaped Cell and Flat Plate" Processes 9, no. 5: 838. https://doi.org/10.3390/pr9050838
APA StyleDong, L., Xing, J., Wu, S., Guan, X., & Zhu, H. (2021). Simulation of Shear-Thickening Liquid Transfer between U-Shaped Cell and Flat Plate. Processes, 9(5), 838. https://doi.org/10.3390/pr9050838






