Parameter Estimation of a Countershaft Brake for Heavy-Duty Vehicles with Automated Mechanical Transmission
Abstract
:1. Introduction
2. AMT Dynamic Analysis
3. TB Analysis
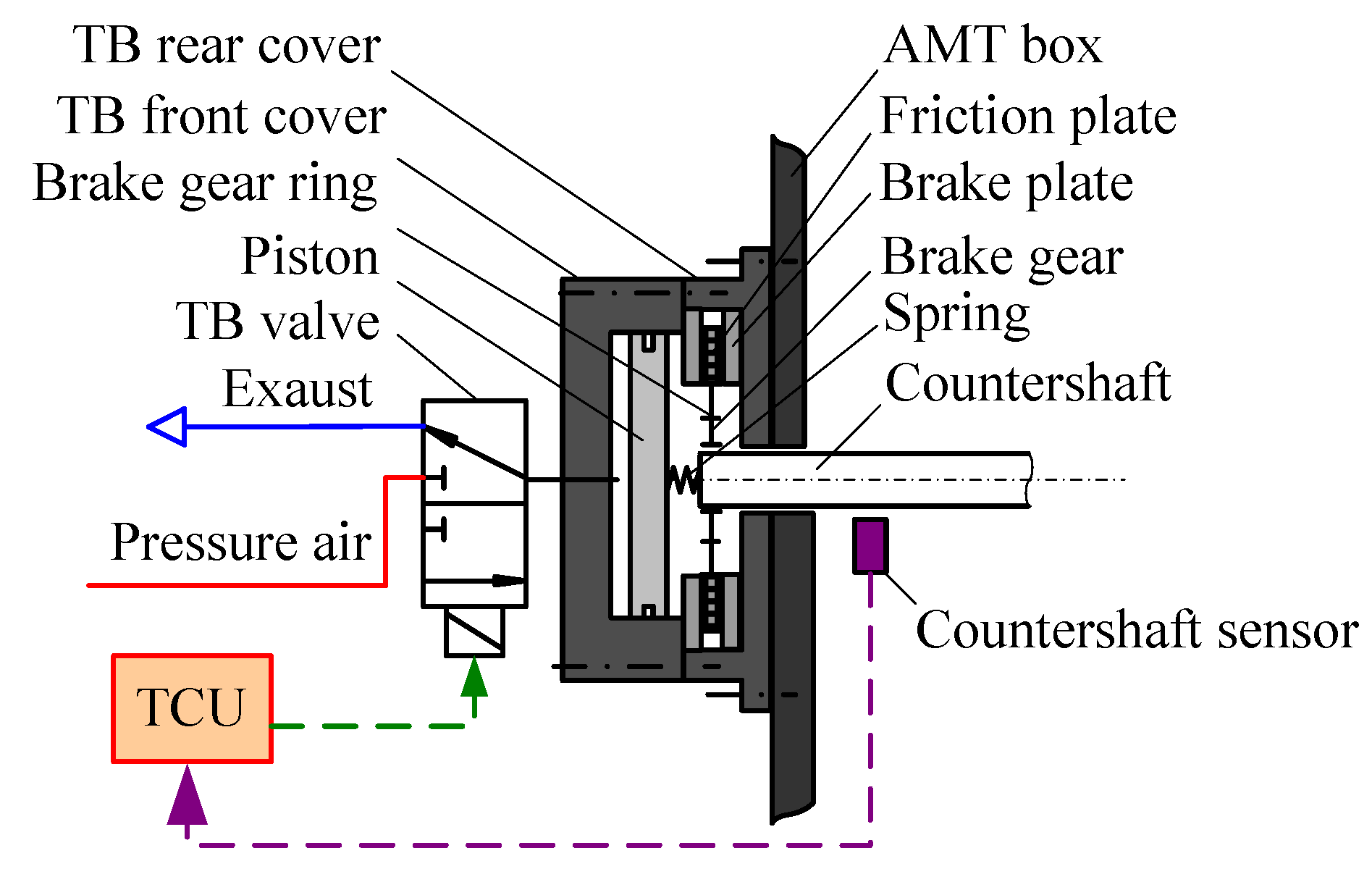
3.1. TB Model
3.2. Synchronous Shifting Condition
3.3. TB Control Flow
4. Estimation Method of TB Characteristic Parameters
4.1. Estimation Method of AMT Equivalent Resistance Torque
4.1.1. A. Estimation Algorithm
4.1.2. Flow of Identification Process
4.2. Estimation Method of TB Torque
4.2.1. Observation Model of TB Torque
4.2.2. Identification Method of TB Torque Based on the RLSM
4.3. Estimation Accuracy and Braking Intensity
4.3.1. Estimation Accuracy
4.3.2. Braking Intensity
4.4. Identification Process of TB Characteristic Parameters
5. Experimental Results
5.1. Estimation Results without TB Action
5.2. Estimation Results with TB Action
5.3. Result Analysis
5.3.1. Linear Interpolation of Braking Intensity
5.3.2. Desired Speed Algorithm
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mo, W.; Wu, J.; Walker, P.D.; Zhang, N. Shift characteristics of a bilateral Harpoon-shift synchronizer for electric vehicles equipped with clutchless AMTs. Mech. Syst. Signal Process. 2021, 148, 107166. [Google Scholar] [CrossRef]
- Mo, W.; Walker, P.D.; Tian, Y.; Zhang, N. Dynamic analysis of unilateral harpoon-shift synchronizer for electric vehicles. Mech. Mach. Theory 2021, 157. [Google Scholar] [CrossRef]
- Chen, B.; Guo, J.; Yan, M.F.; Wang, F.; Liu, F. Study on a Ni-P-nano TiN composite coating for significantly improving the service life of copper alloy synchronizer rings. Appl. Surf. Sci. 2020, 504. [Google Scholar] [CrossRef]
- Barathiraja, K.; Devaradjane, G.; Jibin, P.; Rakesh, S.; Gajanan, J. Analysis of automotive transmission gearbox synchronizer wear due to torsional vibration and the parameters influencing wear reduction. Eng. Fail. Anal. 2019, 105, 427–443. [Google Scholar] [CrossRef]
- Barathiraja, K.; Devaradjane, G.; Bhattacharya, A.; Sivakumar, V.; Yadav, V. Automotive Transmission Gearbox Synchronizer Sintered Hub Design. Eng. Fail. Anal. 2020, 107. [Google Scholar] [CrossRef]
- Eckert, J.J.; Santiciolli, F.M.; Yamashita, R.Y.; Correa, F.C.; Silva, L.C.A.; Dedini, F.G. Fuzzy gear shifting control optimization to improve vehicle performance, fuel consumption and engine emissions. IET Control Theory Appl. 2019, 13, 2658–2669. [Google Scholar] [CrossRef]
- Lin, S.; Li, B. Shift force optimization and trajectory tracking control for a novel gearshift system equipped with electromagnetic linear actuators. IEEE-ASME Trans. Mechatron. 2019, 24, 1640–1650. [Google Scholar] [CrossRef]
- Myklebust, A.; Eriksson, L. Modeling, observability, and estimation of thermal effects and aging on transmitted torque in a heavy duty truck with a dry clutch. IEEE-ASME Trans. Mechatron. 2015, 20, 61–72. [Google Scholar] [CrossRef]
- Gao, B.; Lu, X.; Chen, H.; Lu, X.; Li, J. Dynamics and control of gear upshift in automated manual transmissions. Int. J. Veh. Des. 2013, 63, 61–83. [Google Scholar] [CrossRef]
- Gao, B.; Chen, H.; Ma, Y.; Sanada, K. Design of nonlinear shaft torque observer for trucks with Automated Manual Transmission. Mechatronics 2011, 21, 1034–1042. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.; Sun, J. Optimal clutch pressure control in shifting process of automatic transmission for heavy-duty mining trucks. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, H.; Cao, D.; Chen, H. System modeling and pressure control of a clutch actuator for heavy-duty automatic transmission systems. IEEE Trans. Veh. Technol. 2016, 65, 4865–4874. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.; Yang, J.; Zhang, W. Optimizing automatic transmission double-transition shift process based on multi-objective genetic algorithm. Appl. Sci. 2020, 10, 217794. [Google Scholar] [CrossRef]
- Nakazawa, T.; Hattori, H.; Tarutani, I.; Yasuhara, S.; Inoue, T. Influence of pin profile curve on continuously variable transmission (CVT) chain noise and vibration. Mech. Mach. Theory 2020, 154. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Song, Z.; Liu, S. A Consequent-pole PM magnetic-geared double-rotor machine with flux-weakening ability for hybrid electric vehicle application. IEEE Trans. Magn. 2019, 55. [Google Scholar] [CrossRef]
- Onumata, Y.; Zhao, H.; Wang, C.; Morina, A.; Neville, A. Interactive Effect between Organic Friction Modifiers and Additives on Friction at Metal Pushing V-Belt CVT Components. Tribol. Trans. 2018, 61, 474–481. [Google Scholar] [CrossRef]
- Zhao, Z.; Lei, D.; Chen, J.; Li, H. Optimal control of mode transition for four-wheel-drive hybrid electric vehicle with dry dual-clutch transmission. Mech. Syst. Signal Process. 2018, 105, 68–89. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; He, L.; Wu, C.; Hedrick, J.K. Estimation of Torques Transmitted by Twin-Clutch of Dry Dual-Clutch Transmission during Vehicle’s Launching Process. IEEE Trans. Veh. Technol. 2017, 66, 4727–4741. [Google Scholar] [CrossRef]
- Schoeftner, J.; Ebner, W. Simulation model of an electrohydraulic-actuated double-clutch transmission vehicle: Modelling and system design. Veh. Syst. Dyn. 2017, 55, 1865–1883. [Google Scholar] [CrossRef]
- Bóka, G.; Lovas, L.; Márialigeti, J.; Trencséni, B. Engagement capability of face-dog clutches on heavy duty automated mechanical transmissions with transmission brake, Proceedings of the Institution of Mechanical Engineers. Part D J. Automob. Eng. 2010, 224, 1125–1139. [Google Scholar] [CrossRef]
- Li, W.; Gong, G.; Liu, J.; Zhang, Y.; Yang, H. Simulation of electro-hydraulic system for train brake based on pressure control of high frequency solenoid valve. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 340–348. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, Y.; Shi, Y.; Wang, Z.; Ma, X.; Song, E. Experimental research of dynamic response of high speed solenoid valve for common rail injecto. Harbin Gongcheng Daxue Xuebao/J. Harbin Eng. Univ. 2018, 39, 74–79. [Google Scholar] [CrossRef]
- Gao, Q.; Zhu, Y.; Luo, Z.; Bruno, N. Investigation on adaptive pulse width modulation control for high speed on/off valve. J. Mech. Sci. Technol. 2020, 34, 1711–1722. [Google Scholar] [CrossRef]
















| Signal | Mean |
|---|---|
| AMT input shaft’s equivalent moment of inertia | |
| Rotational torque of AMT input shaft | |
| AMT input shaft’s angular speed | |
| AMT output shaft’s equivalent moment of inertia | |
| Rotational torque of AMT output shaft | |
| AMT output shaft’s angular speed |
| Speed(rpm) | Duty Ratio | TB Torque (N·m) | Braking Intensity |
|---|---|---|---|
| 700 | 60% | −4.00 | 1.55 |
| 70% | −7.10 | 1.97 | |
| 80% | −20.58 | 3.83 | |
| 100% | −21.36 | 3.94 | |
| 750 | 60% | −2.72 | 1.39 |
| 70% | −5.03 | 1.69 | |
| 80% | −15.82 | 3.18 | |
| 100% | −17.05 | 3.35 | |
| 800 | 60% | −1.63 | 1.22 |
| 70% | −3.25 | 1.45 | |
| 80% | −10.34 | 2.42 | |
| 100% | −12.76 | 2.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, L. Parameter Estimation of a Countershaft Brake for Heavy-Duty Vehicles with Automated Mechanical Transmission. Processes 2021, 9, 1036. https://doi.org/10.3390/pr9061036
Li Y, Li L. Parameter Estimation of a Countershaft Brake for Heavy-Duty Vehicles with Automated Mechanical Transmission. Processes. 2021; 9(6):1036. https://doi.org/10.3390/pr9061036
Chicago/Turabian StyleLi, Yunxia, and Lei Li. 2021. "Parameter Estimation of a Countershaft Brake for Heavy-Duty Vehicles with Automated Mechanical Transmission" Processes 9, no. 6: 1036. https://doi.org/10.3390/pr9061036





