Study on the Aerodynamic Performance of Floating Offshore Wind Turbine Considering the Tower Shadow Effect
Abstract
:1. Introduction
2. Model and Numerical Methods
2.1. Governing Equations and Turbulent Model
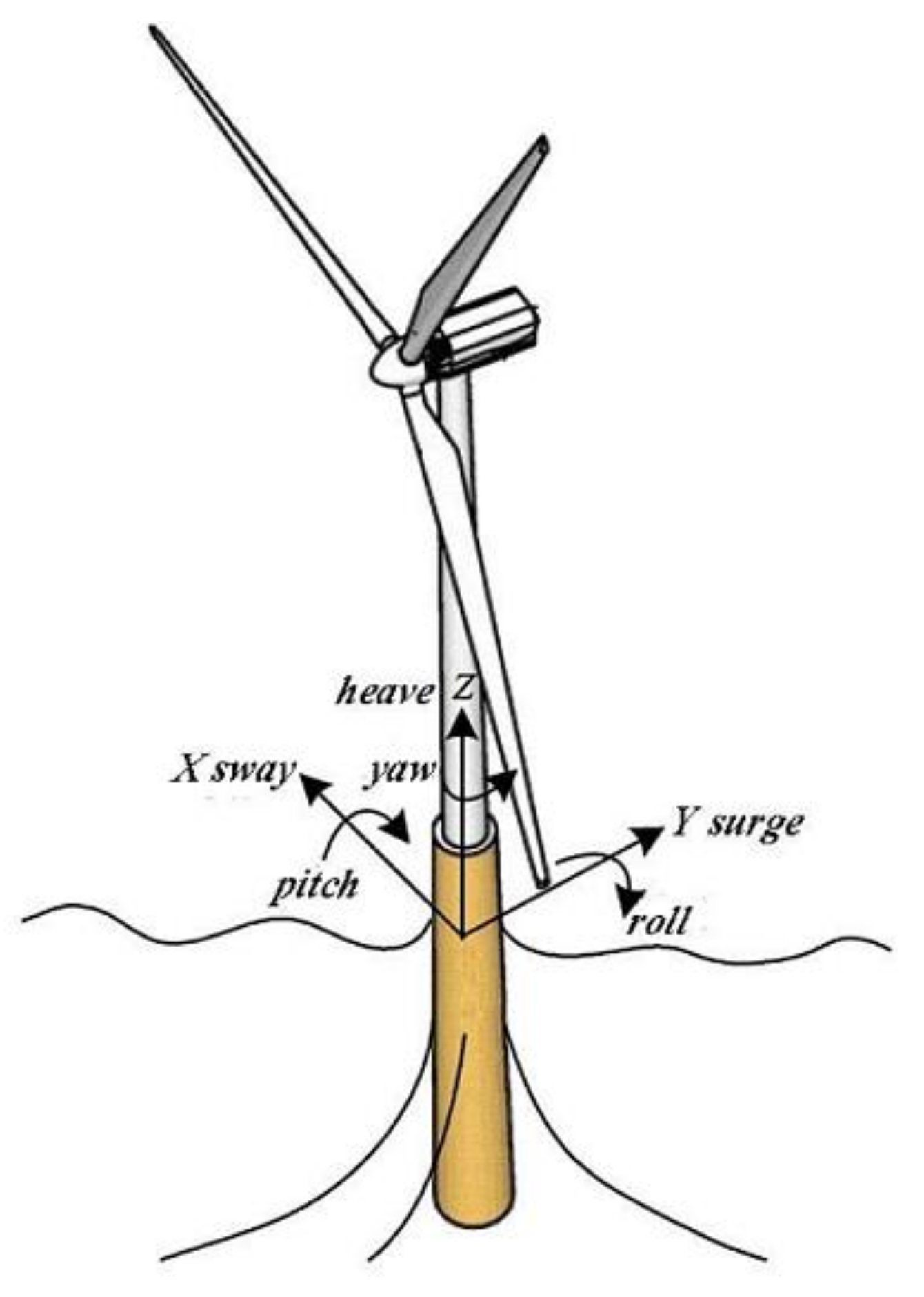
2.2. Floating Foundation
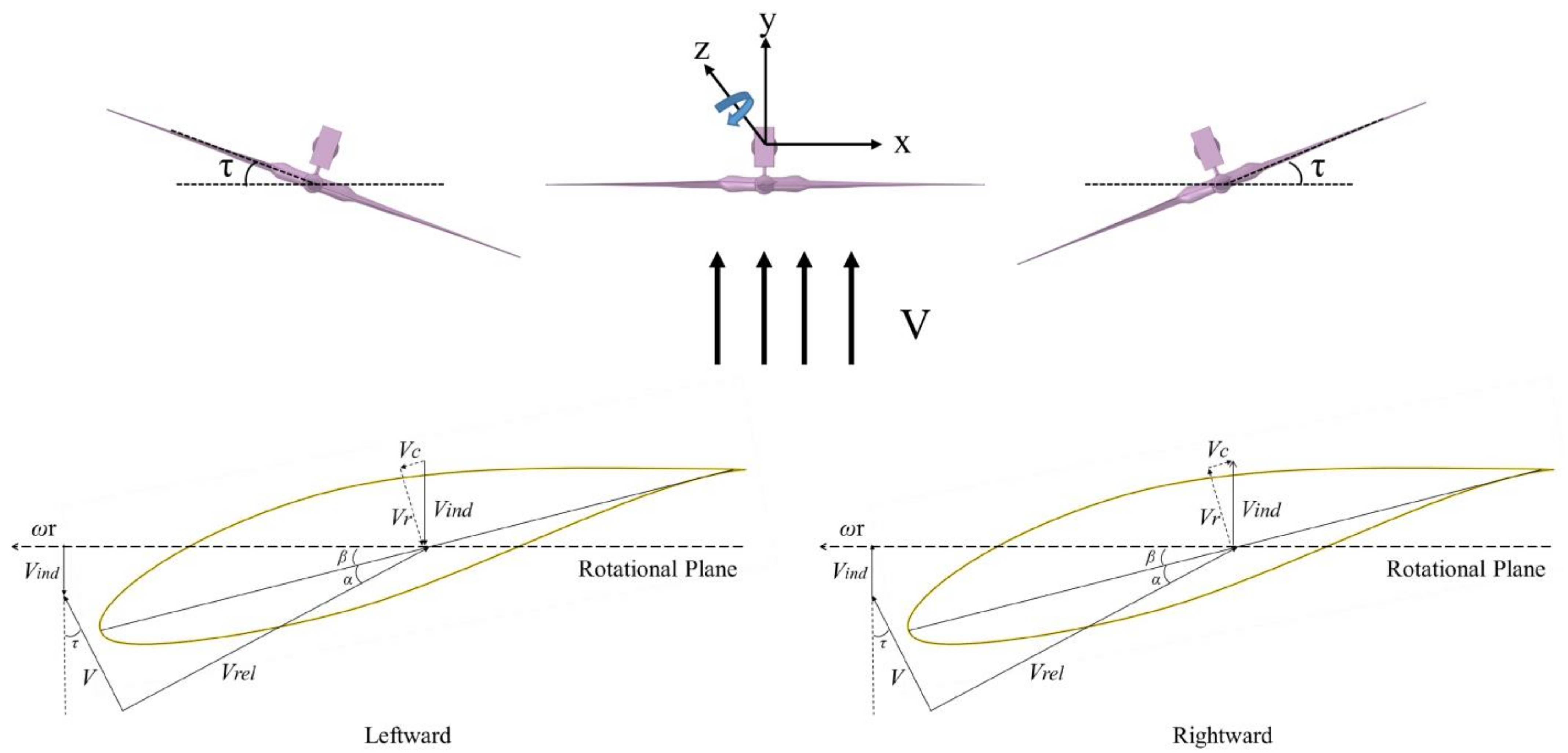
2.3. Wind Turbine Model
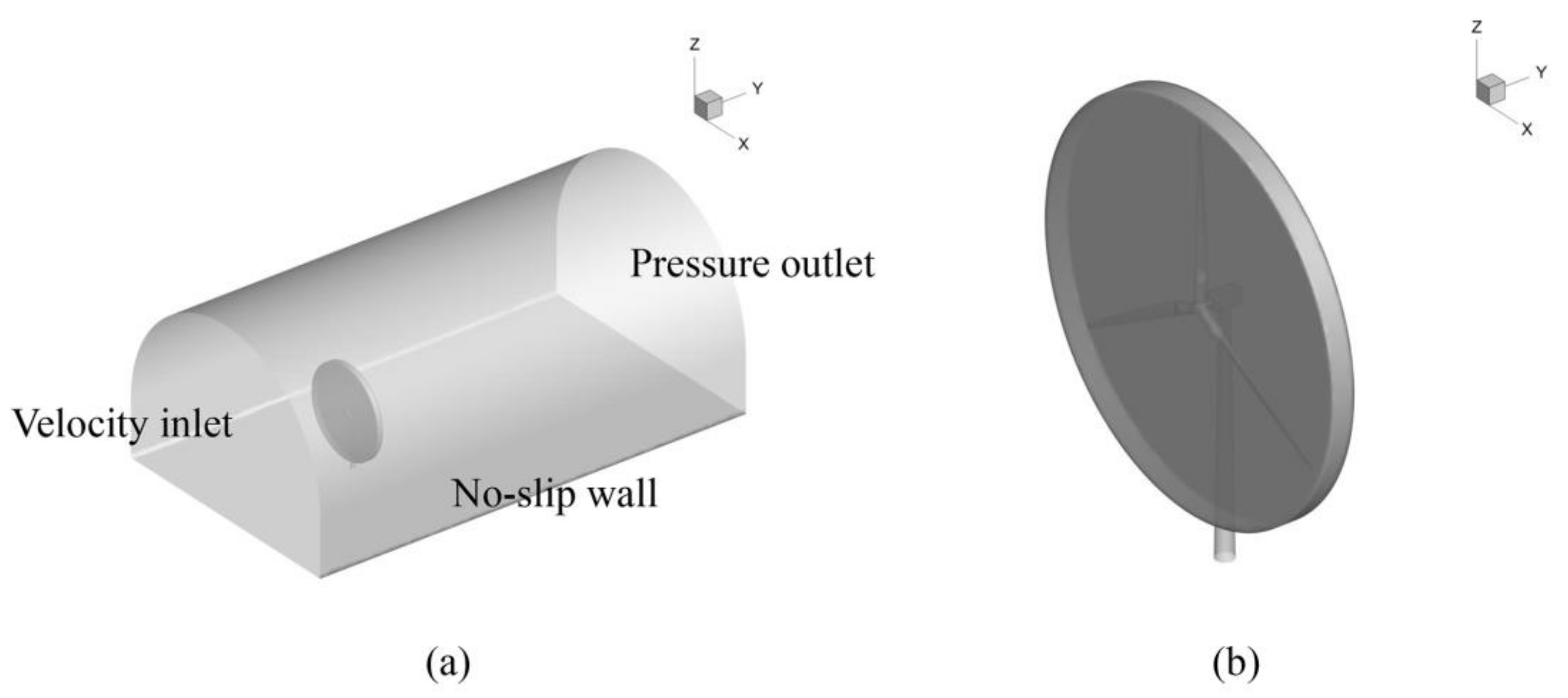
2.4. Flow Field and Boundary Conditions
2.5. Computational Mesh
2.6. Computational Methods
3. Numerical Model Verification
3.1. Model Grid Independence Verification
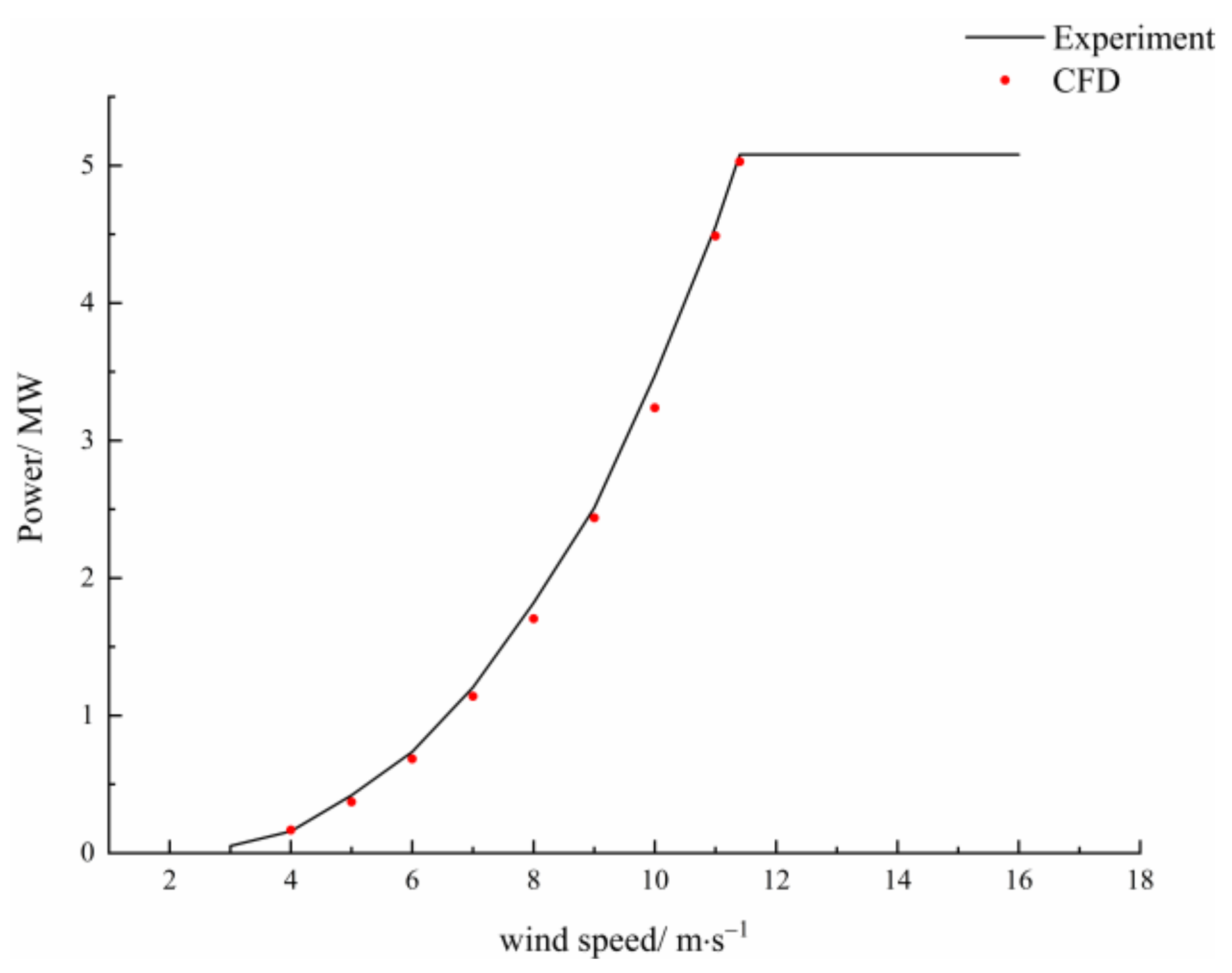
3.2. Model Power Verification
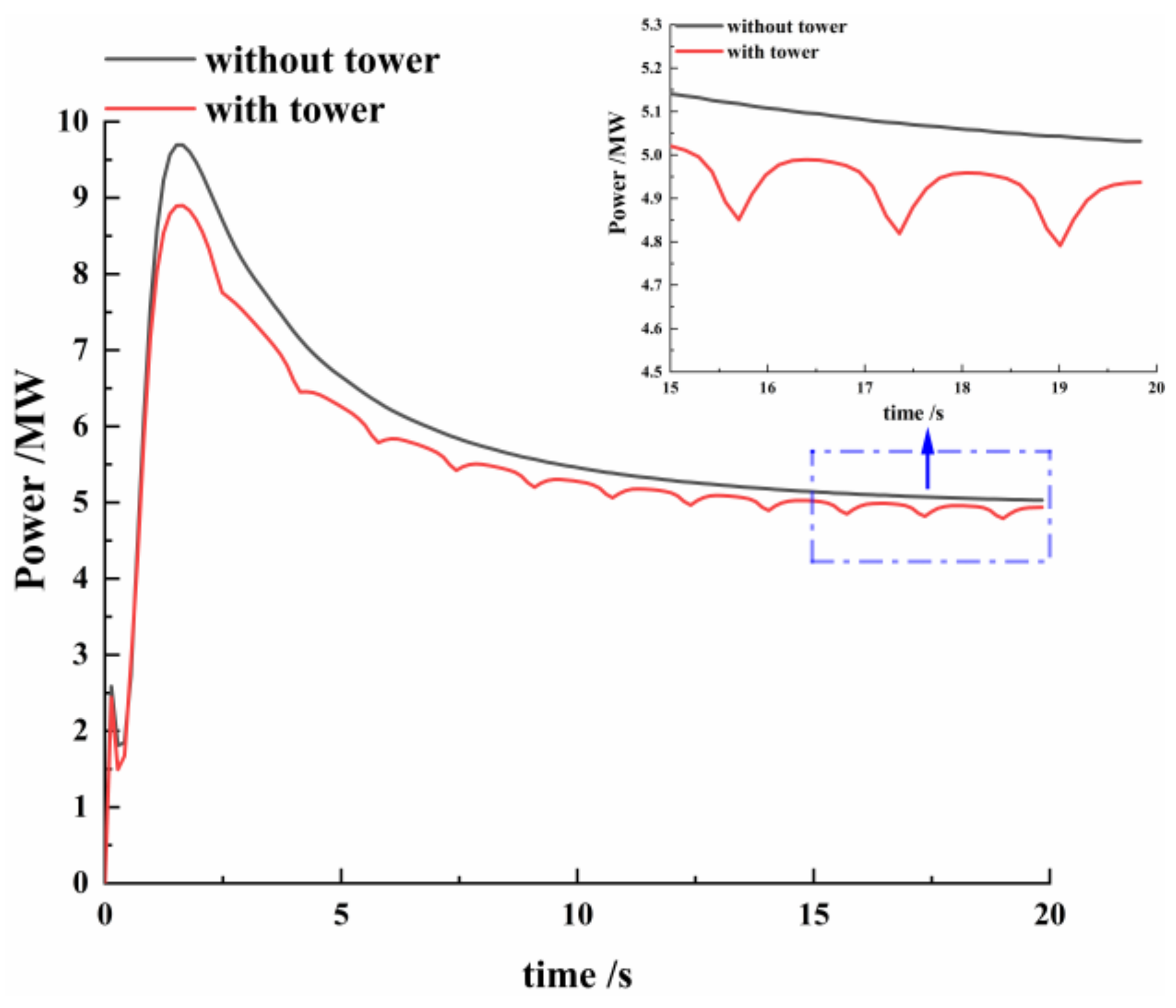
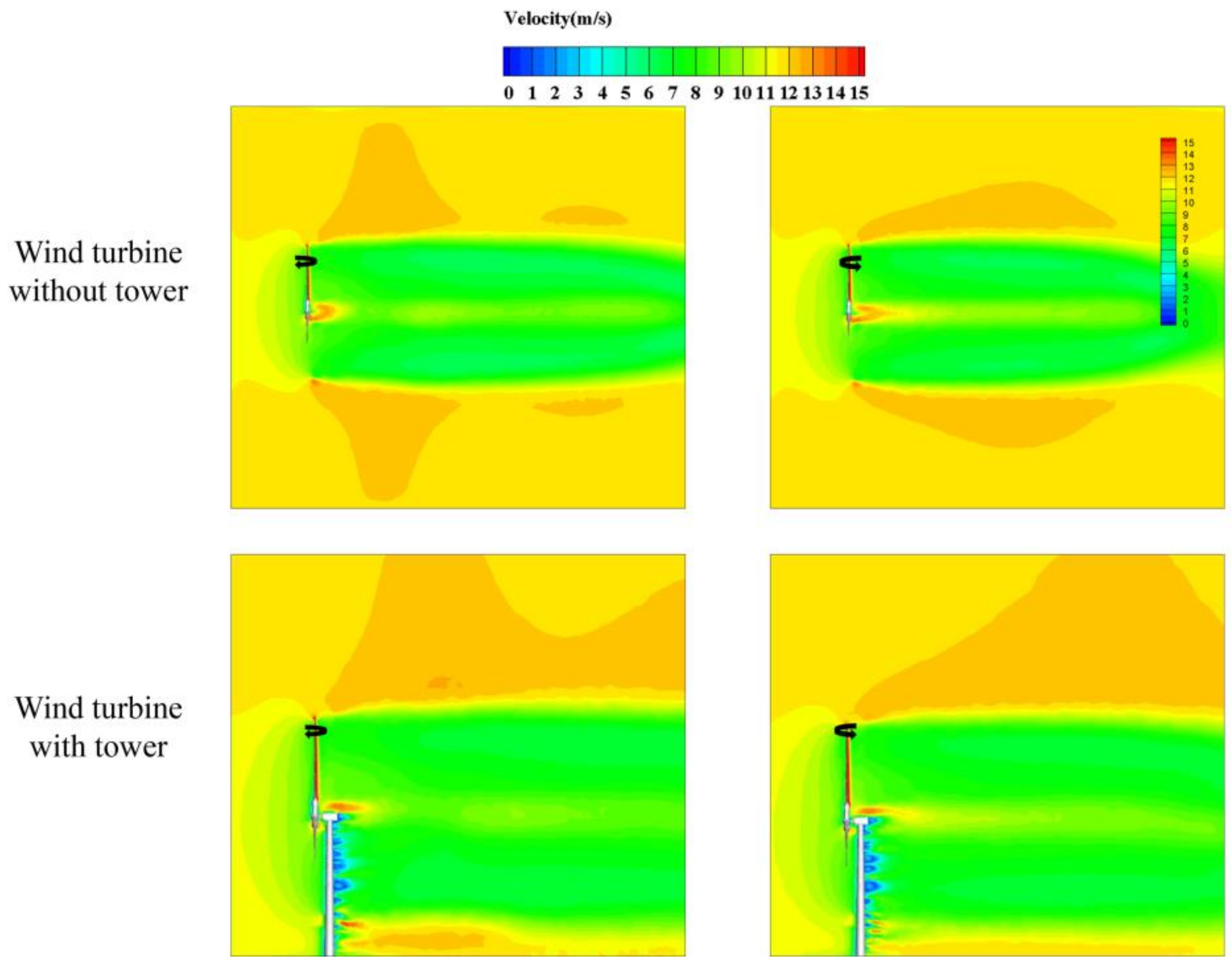
3.3. Validation Considering the Tower under the Unsteady Condition
4. Results and Discussion
4.1. Unsteady Aerodynamic Analysis under Surge Motion
4.1.1. Total Performance Analysis
4.1.2. Distribution of Pressure on the Blade Surface
4.1.3. Near Flow Field of Each Section of Blade
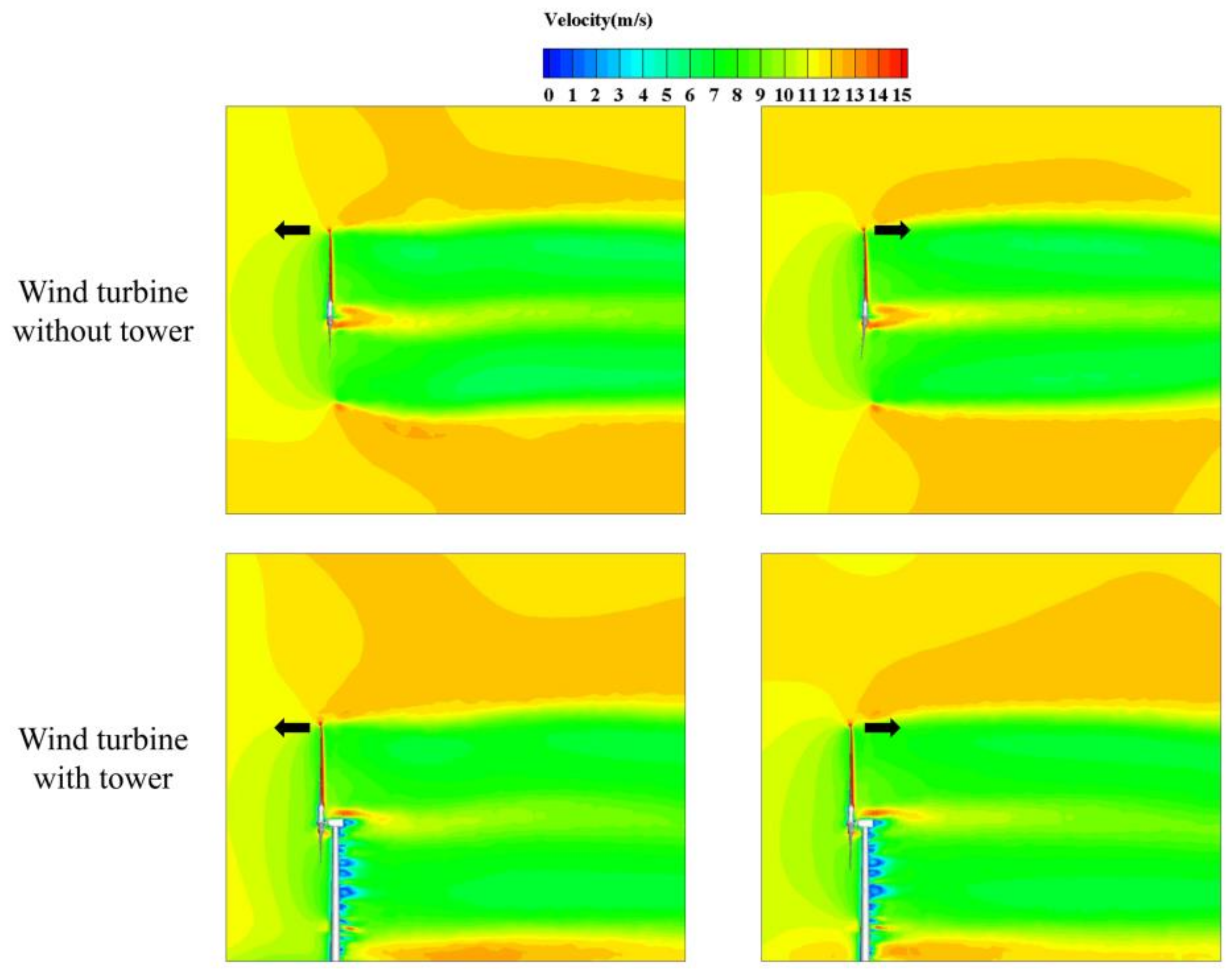
4.1.4. Wake Field behind the Wind Turbine
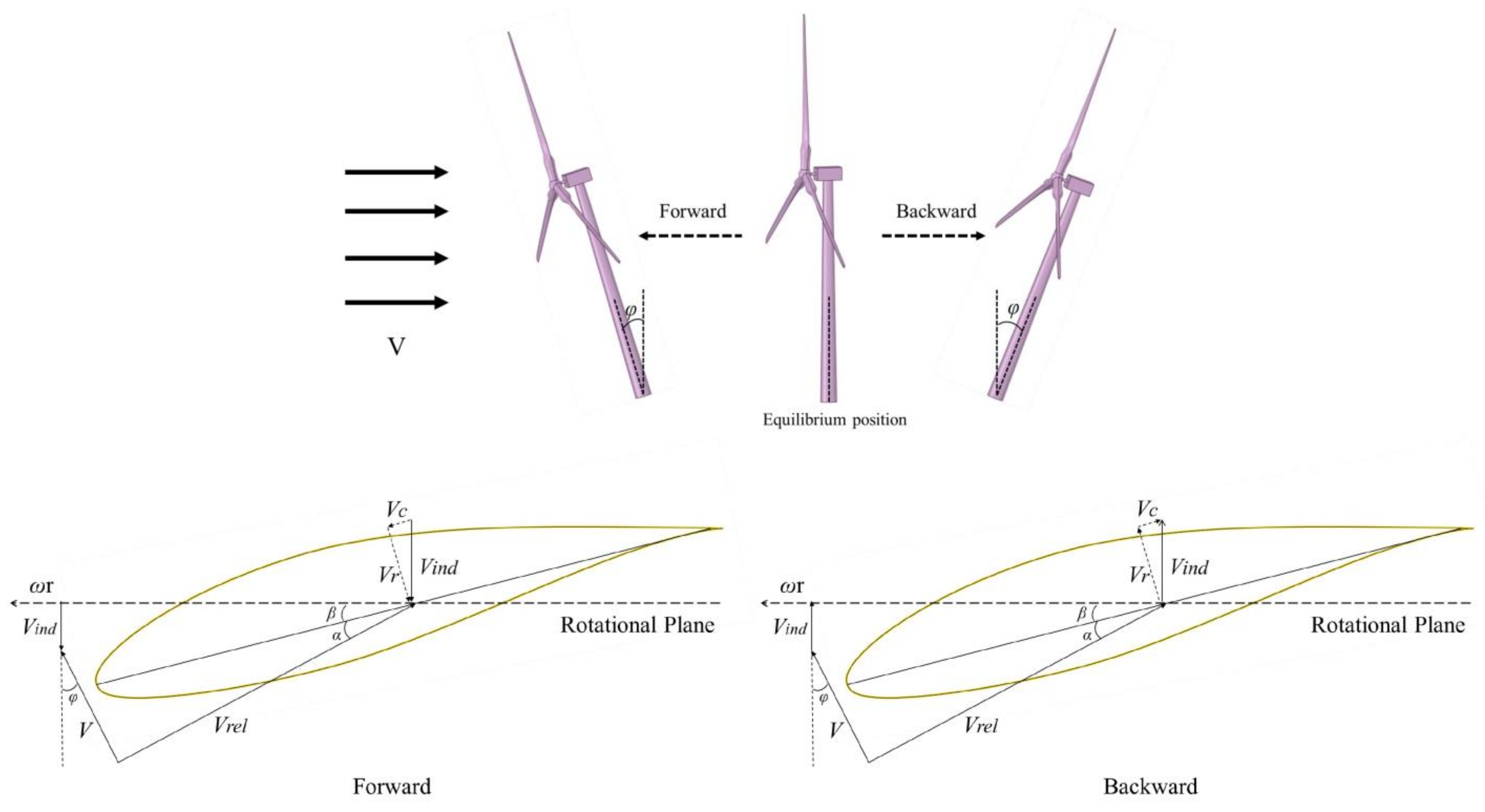
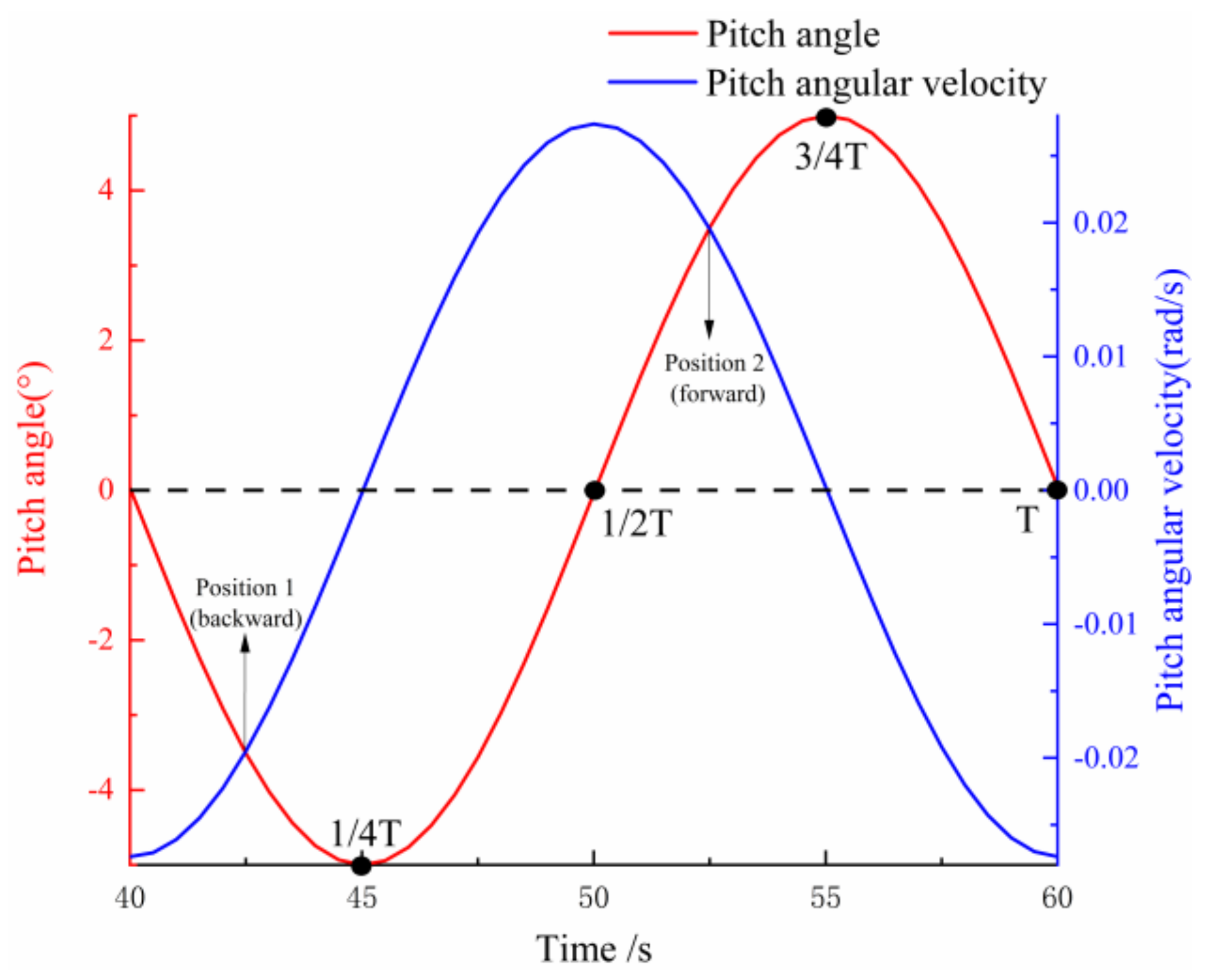
4.2. Unsteady Aerodynamic Analysis under Pitch Motion
4.2.1. Total Performance Analysis
4.2.2. Distribution of Pressure on the Blade Surface
4.2.3. Near Flow Field of Each Section of Blade
4.2.4. Wake Field behind the Wind Turbine
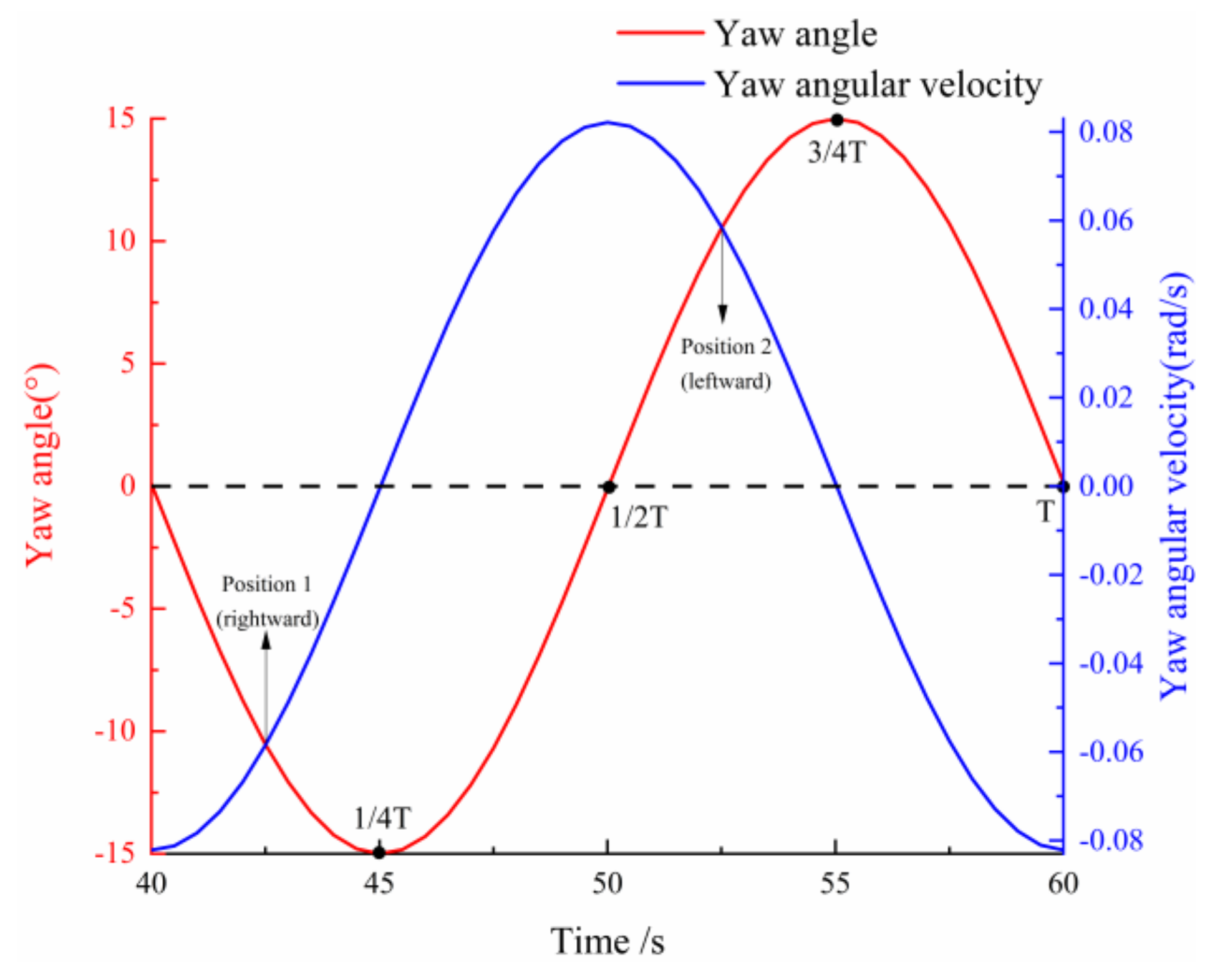
4.3. Unsteady Aerodynamic Analysis under Yaw Motion
4.3.1. Total Performance Analysis
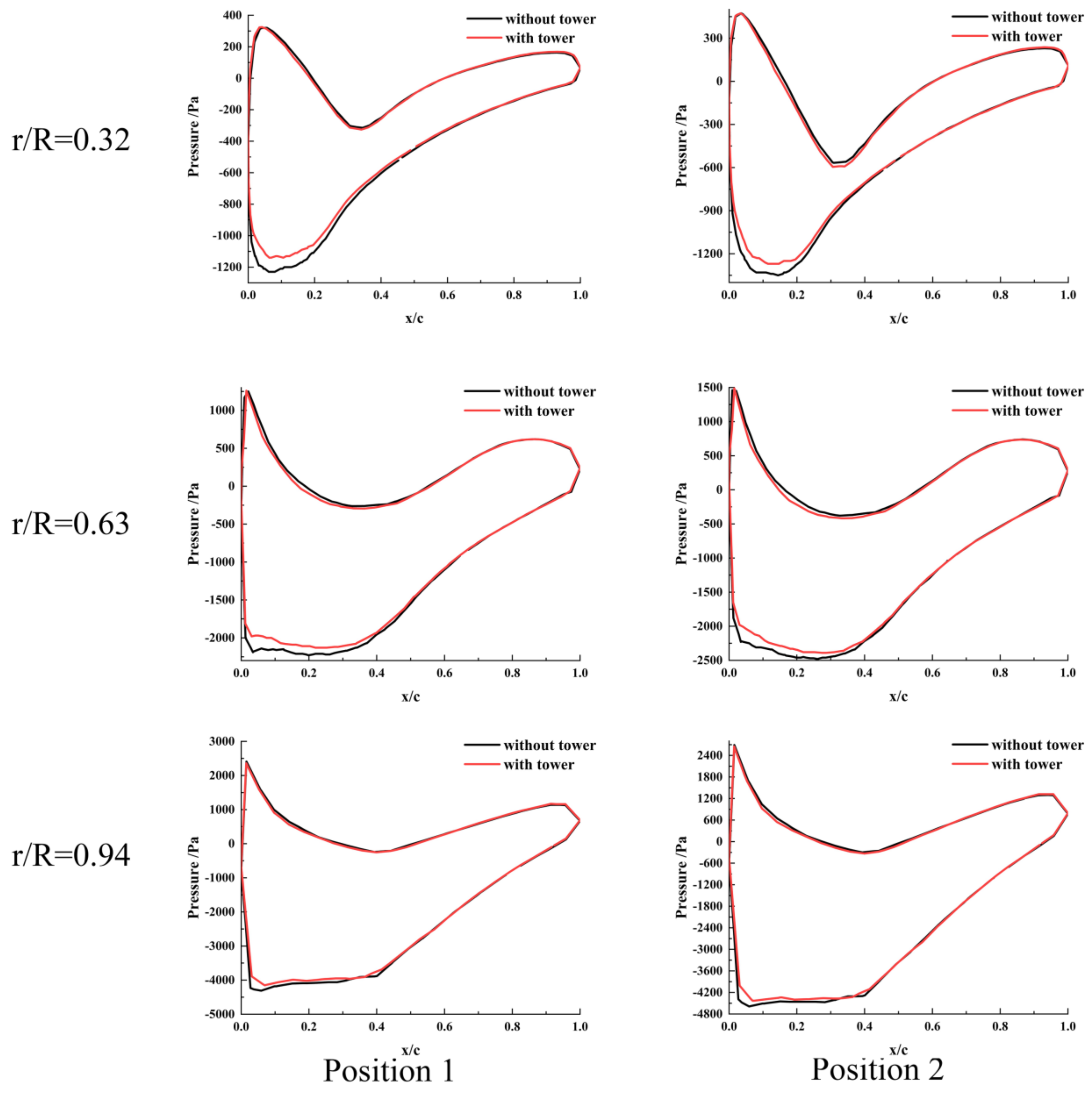
4.3.2. Distribution of Pressure on the Blade Surface
4.3.3. Near Flow Field of Each Section of Blade
4.3.4. Wake Field behind the Wind Turbine
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FOWT | Floating Offshore Wind Turbine |
| CFD | Computational Fluid Dynamic |
| 6-DOF | Six Degrees-of-Freedom |
| BEM | Blade Element Momentum |
| FVM | Free Vortex Method |
| UDF | User-Defined Function |
| RANS | Reynolds-Averaged Navier–Stokes equations |
| V | Incoming Wind Speed |
Nomenclature
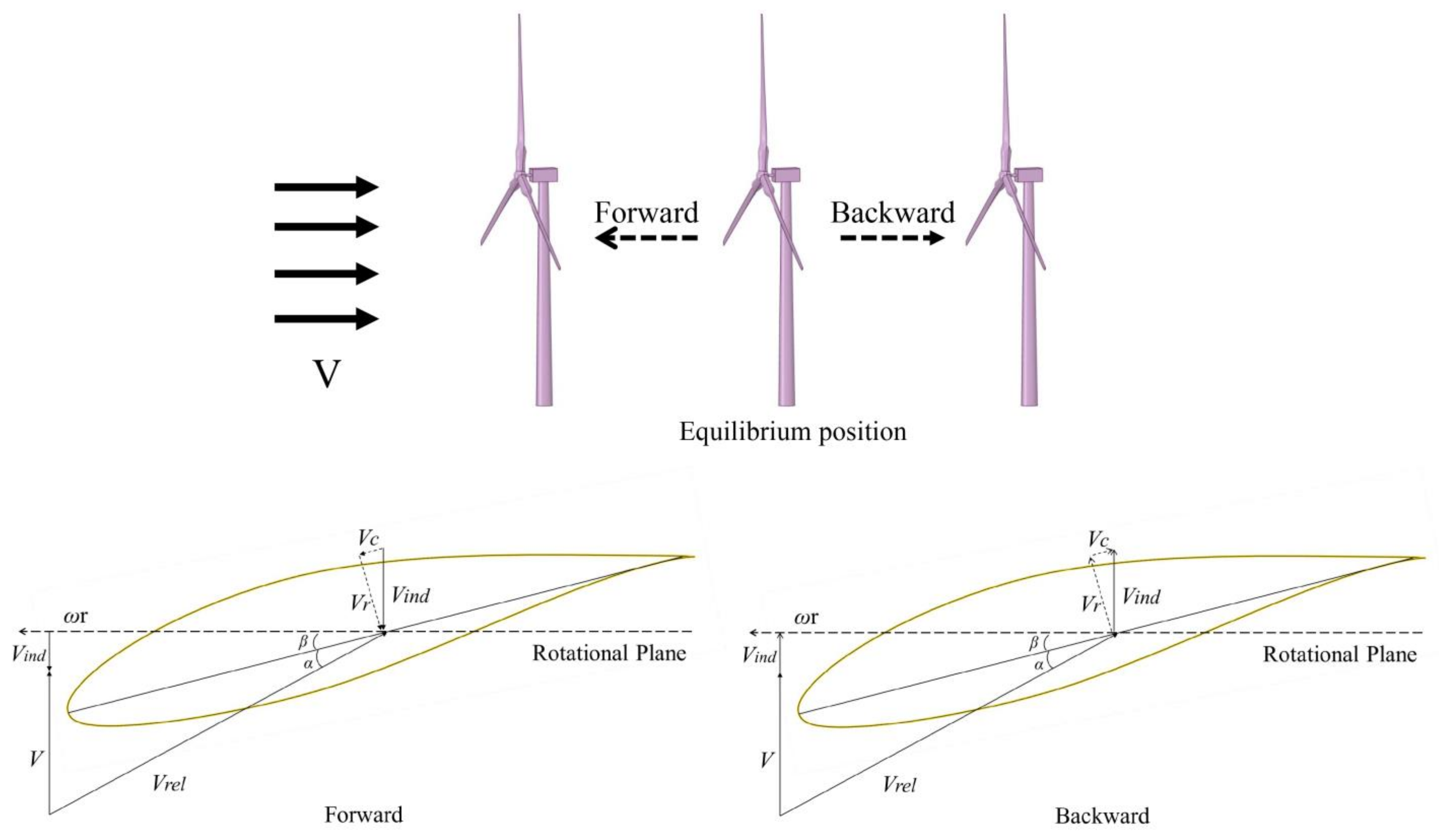
| VS | the relative inflow velocity under surge motion |
| VP | the relative inflow velocity under pitch motion |
| VY | the relative inflow velocity under yaw motion |
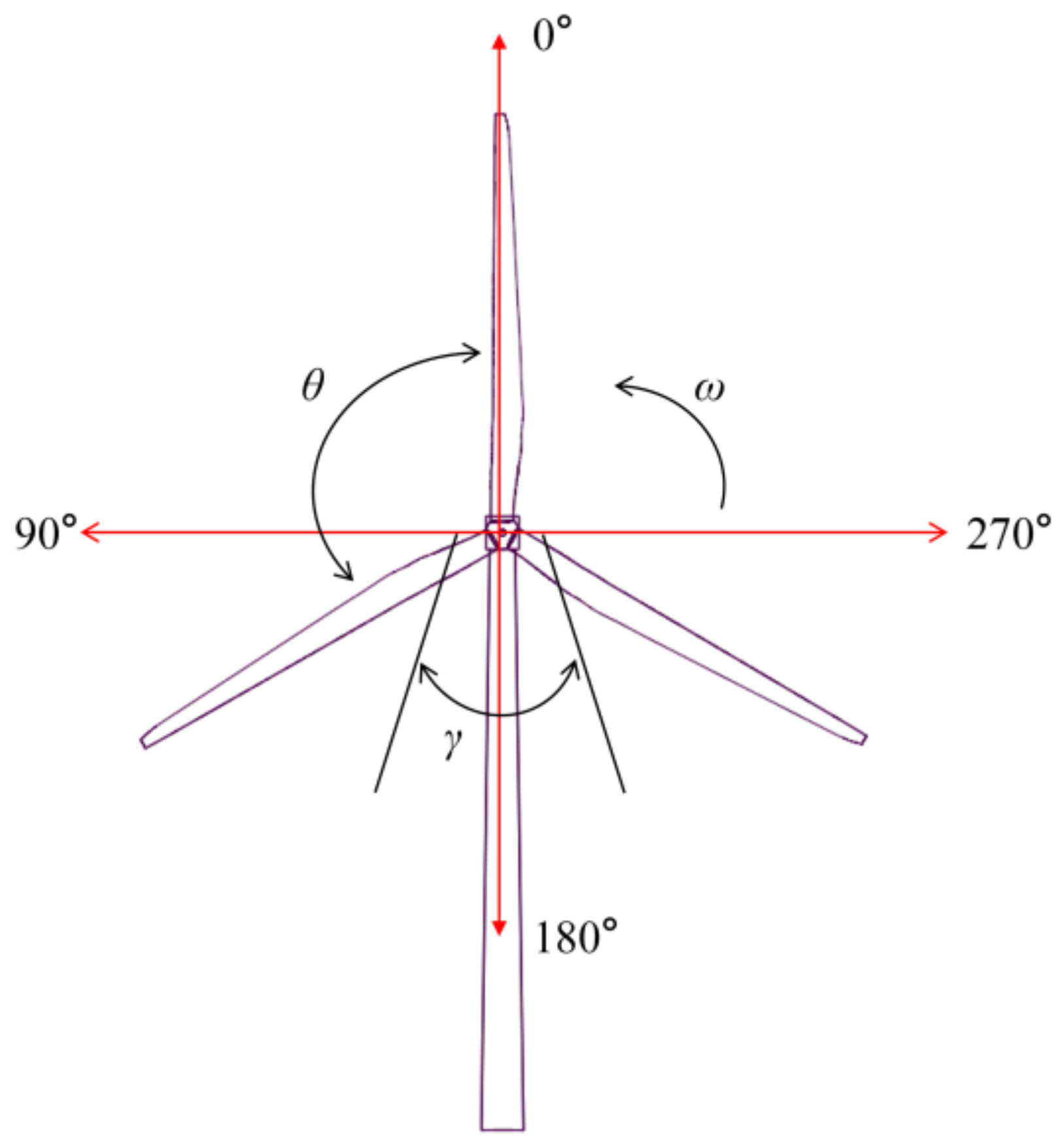
| θ | the angle between two blades |
| γ | the influence area of the tower shadow effect |
| ω | the rotational speed of the wind turbine |
| Vind | the induced velocity of platform motion |
| Vrel | the relative velocity |
| As | surge amplitude |
| Ap | pitch amplitude |
| Ay | yaw amplitude |
References
- Cheng, P.; Huang, Y.; Wan, D.C. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Shen, X.; Hu, P.; Chen, J.E.; Zhu, X.C.; Du, Z.H. The unsteady aerodynamics of floating wind turbine under platform pitch motion. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 1019–1036. [Google Scholar] [CrossRef]
- Wu, X.N.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.G.; Adcock, T.; Jiang, Z.Y.; Gao, Z.; Lin, Z.L.; et al. Foundations of offshore wind turbines: A review. Renew. Sustain. Energ. Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Gu, R.R.; Pan, P.; Zhu, J. Unsteady aerodynamics simulation of a full-scale horizontal axis wind turbine using CFD methodology. Energy Convers. Manag. 2016, 112, 146–156. [Google Scholar] [CrossRef]
- Sebastian, T.; Lackner, M. Analysis of the Induction and Wake Evolution of an Offshore Floating Wind Turbine. Energies 2012, 5, 968–1000. [Google Scholar] [CrossRef] [Green Version]
- De Vaal, J.B.; Hansen, M.O.L.; Moan, T. Effect of wind turbine surge motion on rotor thrust and induced velocity. Wind Energy 2014, 17, 105–121. [Google Scholar] [CrossRef]
- Ma, Z.; Li, W.; Ren, N.A.X.; Ou, J.P. The typhoon effect on the aerodynamic performance of a floating offshore wind turbine. J. Ocean Eng. Sci. 2017, 2, 279–287. [Google Scholar] [CrossRef]
- Farrugia, R.; Sant, T.; Micallef, D. A study on the aerodynamics of a floating wind turbine rotor. Renew. Energy 2016, 86, 770–784. [Google Scholar] [CrossRef]
- Wen, B.R.; Dong, X.J.; Tian, X.L.; Peng, Z.K.; Zhang, W.M.; Wei, K.X. The power performance of an offshore floating wind turbine in platform pitching motion. Energy 2018, 154, 508–521. [Google Scholar] [CrossRef]
- Wen, B.R.; Tian, X.L.; Dong, X.J.; Peng, Z.K.; Zhang, W.M. On the power coefficient overshoot of an offshore floating wind turbine in surge oscillations. Wind Energy 2018, 21, 1076–1091. [Google Scholar] [CrossRef]
- Salehyar, S.; Li, Y.; Zhu, Q. Fully-coupled time-domain simulations of the response of a floating wind turbine to non-periodic disturbances. Renew. Energy 2017, 111, 214–226. [Google Scholar] [CrossRef]
- Lin, L.; Wang, K.; Vassalos, D. Detecting wake performance of floating offshore wind turbine. Ocean Eng. 2018, 156, 263–276. [Google Scholar] [CrossRef]
- Tran, T.; Kim, D.; Song, J. Computational Fluid Dynamic Analysis of a Floating Offshore Wind Turbine Experiencing Platform Pitching Motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The aerodynamic interference effects of a floating offshore wind turbine experiencing platform pitching and yawing motions. J. Mech. Sci. Technol. 2015, 29, 549–561. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The platform pitching motion of floating offshore wind turbine: A preliminary unsteady aerodynamic analysis. J. Wind Eng. Ind. Aerodyn. 2015, 142, 65–81. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.T.; Kim, D.H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renew. Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
- Chen, J.H.; Hu, Z.Q.; Wan, D.C.; Xiao, Q. Comparisons of the dynamical characteristics of a semi-submersible floating offshore wind turbine based on two different blade concepts. Ocean Eng. 2018, 153, 305–318. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.-H.K.; Vinh-Tan, N. Aerodynamic simulations of offshore floating wind turbine in platform-induced pitching motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, D.C. Investigation of Interference Effects Between Wind Turbine and Spar-Type Floating Platform Under Combined Wind-Wave Excitation. Sustainability 2020, 12, 246. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Duan, L.; Han, Z.L.; Zhao, Y.S.; Yang, H. Numerical analysis of aerodynamic performance of a floating offshore wind turbine under pitch motion. Energy 2020, 192, 116621. [Google Scholar] [CrossRef]
- Fang, Y.; Li, G.; Duan, L.; Han, Z.L.; Zhao, Y.S. Effect of surge motion on rotor aerodynamics and wake characteristics of a floating horizontal-axis wind turbine. Energy 2021, 218, 119519. [Google Scholar] [CrossRef]
- Chen, Z.W.; Wang, X.D.; Guo, Y.Z.; Kang, S. Numerical analysis of unsteady aerodynamic performance of floating offshore wind turbine under platform surge and pitch motions. Renew. Energy 2021, 163, 1849–1870. [Google Scholar] [CrossRef]
- Chen, Z.W.; Wang, X.D.; Kang, S. Effect of the Coupled Pitch-Yaw Motion on the Unsteady Aerodynamic Performance and Structural Response of a Floating Offshore Wind Turbine. Processes 2021, 9, 290. [Google Scholar] [CrossRef]
- Sivalingam, K.; Martin, S.; Wala, A.A.S. Numerical Validation of Floating Offshore Wind Turbine Scaled Rotors for Surge Motion. Energies 2018, 11, 2578. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Lee, S.; Lee, S. Influence of blade-tower interaction in upwind-type horizontal axis wind turbines on aerodynamics. J. Mech. Sci. Technol. 2011, 25, 1351–1360. [Google Scholar] [CrossRef]
- Quallen, S.; Tao, X. An Investigation of the Blade Tower Interaction of a Floating Offshore Wind Turbine. In Proceedings of the 25th International Offshore and Polar Engineering Conference, Big Island, HI, USA, 21 June 2015. [Google Scholar]
- Ke, S.T.; Wang, T.G.; Ge, Y.J.; Tamura, Y. Aerodynamic loads and aeroelastic responses of large wind turbine tower-blade coupled structure in yaw condition. Struct. Eng. Mech. 2015, 56, 1021–1040. [Google Scholar] [CrossRef]
- Noyes, C.; Qin, C.; Loth, E.; Schreck, S. Measurements and predictions of wind turbine tower shadow and fairing effects. J. Wind Eng. Ind. Aerodyn. 2018, 179, 297–307. [Google Scholar] [CrossRef]
- Zhang, J.; Zhen, G.; Xing, Z.; Liang, G.; Hu, D. Dynamic analysis of offshore wind turbine blades under the action of wind shear and fluctuating wind. J. Vibroeng. 2018, 20. [Google Scholar] [CrossRef]
- Li, Z.W.; Wen, B.R.; Dong, X.J.; Peng, Z.K.; Qu, Y.G.; Zhang, W.M. Aerodynamic and aeroelastic characteristics of flexible wind turbine blades under periodic unsteady inflows. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104057. [Google Scholar] [CrossRef]
- Wu, W.M.; Liu, X.F.; Dai, Y.J.; Li, Q.Y. An in-depth quantitative analysis of wind turbine blade tip wake flow based on the lattice Boltzmann method. Environ. Sci. Pollut. Res. 2020, 13. [Google Scholar] [CrossRef]
- Regodeseves, P.G.; Morros, C.S. Unsteady numerical investigation of the full geometry of a horizontal axis wind turbine: Flow through the rotor and wake. Energy 2020, 202, 117674. [Google Scholar] [CrossRef]
- Burmester, S.; Vaz, G.; el Moctar, O. Towards credible CFD simulations for floating offshore wind turbines. Ocean Eng. 2020, 209, 107237. [Google Scholar] [CrossRef]
- Chen, D.; Gao, P.; Huang, S.S.; Fan, K.; Zhuang, N.; Liao, Y.D. Dynamic response and mooring optimization of spar-type substructure under combined action of wind, wave, and current. J. Renew. Sustain. Energy 2017, 9, 063307. [Google Scholar] [CrossRef]
- Wang, X.D.; Ye, Z.L.; Kang, S.; Hu, H. Investigations on the Unsteady Aerodynamic Characteristics of a Horizontal-Axis Wind Turbine during Dynamic Yaw Processes. Energies 2019, 12, 3124. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2007.
- Hu, D.M.; Ji, S.Q.; Wu, Z.X. Study on Aerodynamic Performance of Offshore Floating Wind Turbine with Fusion Winglets. J. Sol. Energy Eng. Trans. ASME 2020, 142, 051007. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5MW Reference Wind Turbine for Offshore System Development; Office of Scientific & Technical Information Technical Reports; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009.
- Wen, B.R.; Wei, S.; Wei, K.X.; Yang, W.X.; Peng, Z.K.; Chu, F.L. Power fluctuation and power loss of wind turbines due to wind shear and tower shadow. Front. Mech. Eng. 2017, 12, 321–332. [Google Scholar] [CrossRef] [Green Version]


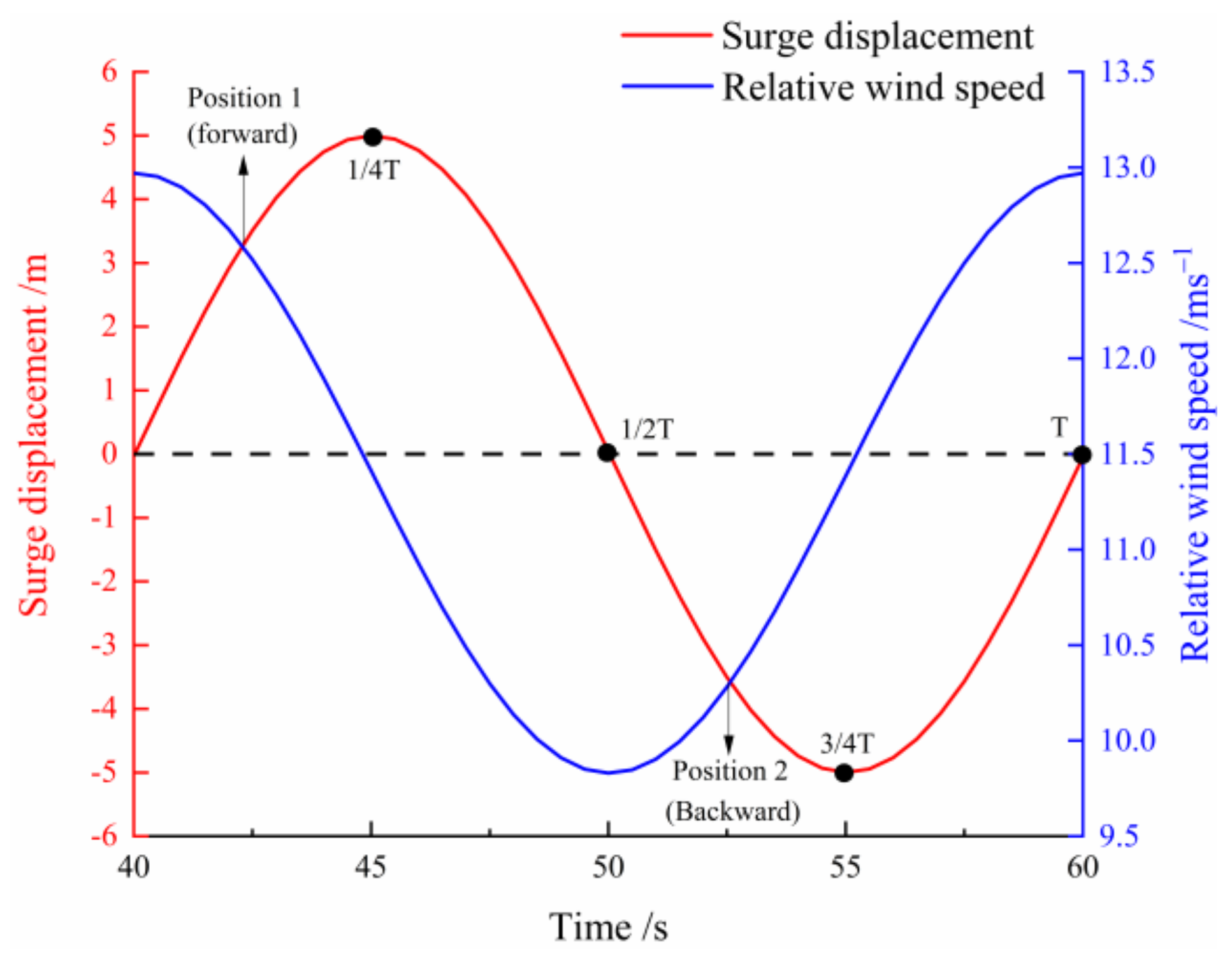





| Conditions | Motion | Displacement | Amplitude | Frequency |
|---|---|---|---|---|
| 1 | surge | −5–5 m | / | 0.05 Hz |
| 2 | pitch | / | −5–5° | 0.05 Hz |
| 3 | yaw | / | −15–15° | 0.05 Hz |
| Cells Number (Million) | 2.86 | 4.77 | 6.71 | 8.50 | 10.08 | Reference Value |
|---|---|---|---|---|---|---|
| Torque (N m) | 3.54 × 106 | 3.82 × 106 | 3.90 × 106 | 3.98 × 106 | 4.03 × 106 | 4.01 × 106 |
| Relative error (%) | 11.72 | 4.74 | 2.74 | 0.75 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, D.; Deng, L.; Zeng, L. Study on the Aerodynamic Performance of Floating Offshore Wind Turbine Considering the Tower Shadow Effect. Processes 2021, 9, 1047. https://doi.org/10.3390/pr9061047
Hu D, Deng L, Zeng L. Study on the Aerodynamic Performance of Floating Offshore Wind Turbine Considering the Tower Shadow Effect. Processes. 2021; 9(6):1047. https://doi.org/10.3390/pr9061047
Chicago/Turabian StyleHu, Danmei, Liwei Deng, and Li Zeng. 2021. "Study on the Aerodynamic Performance of Floating Offshore Wind Turbine Considering the Tower Shadow Effect" Processes 9, no. 6: 1047. https://doi.org/10.3390/pr9061047
APA StyleHu, D., Deng, L., & Zeng, L. (2021). Study on the Aerodynamic Performance of Floating Offshore Wind Turbine Considering the Tower Shadow Effect. Processes, 9(6), 1047. https://doi.org/10.3390/pr9061047





