Fundamental Understanding of Tea Growth and Modeling of Precise Tea Shoot Picking Based on 3-D Coordinate Instrument
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Testing Apparatus
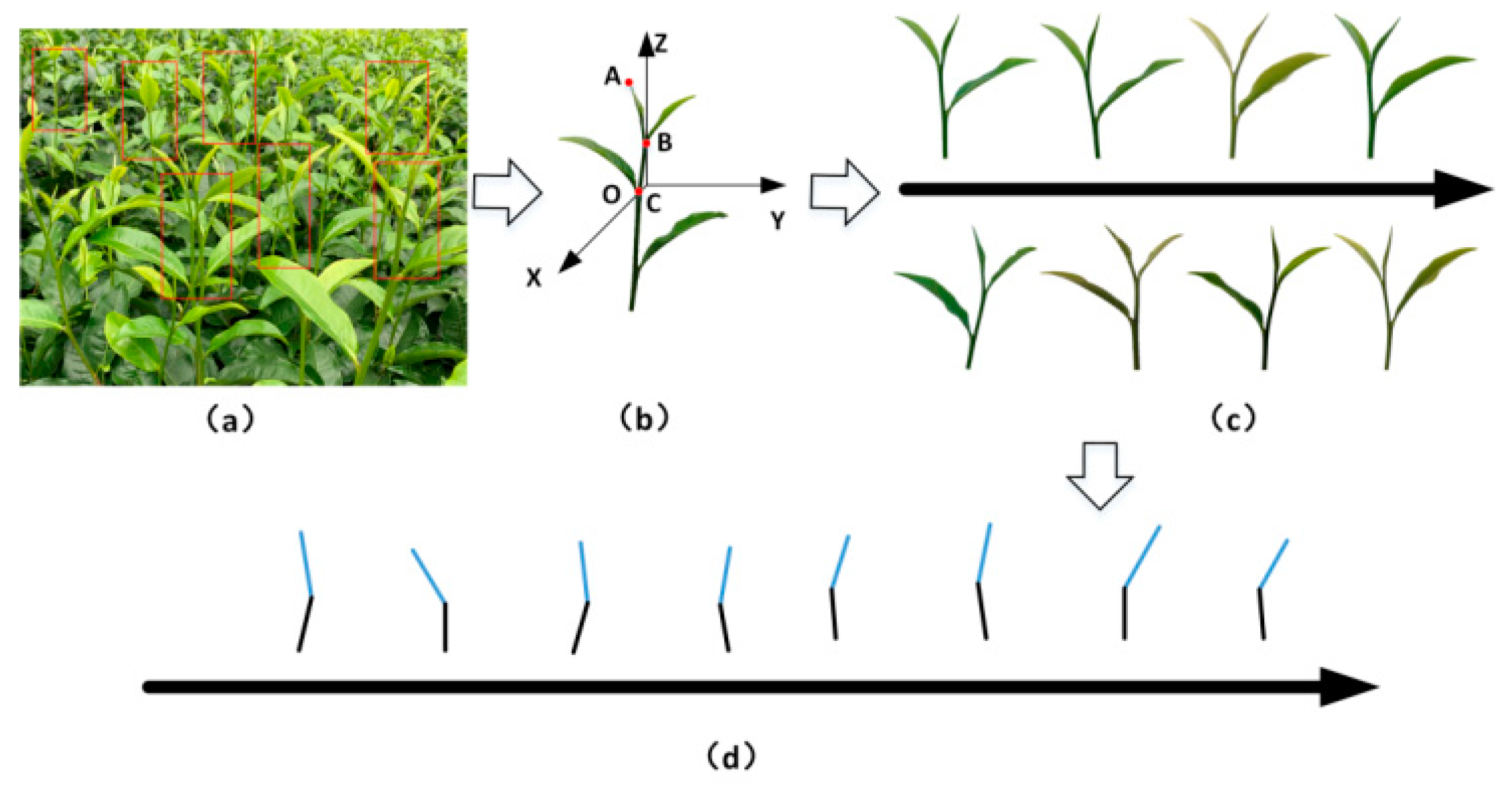
2.3. Data Acquisition
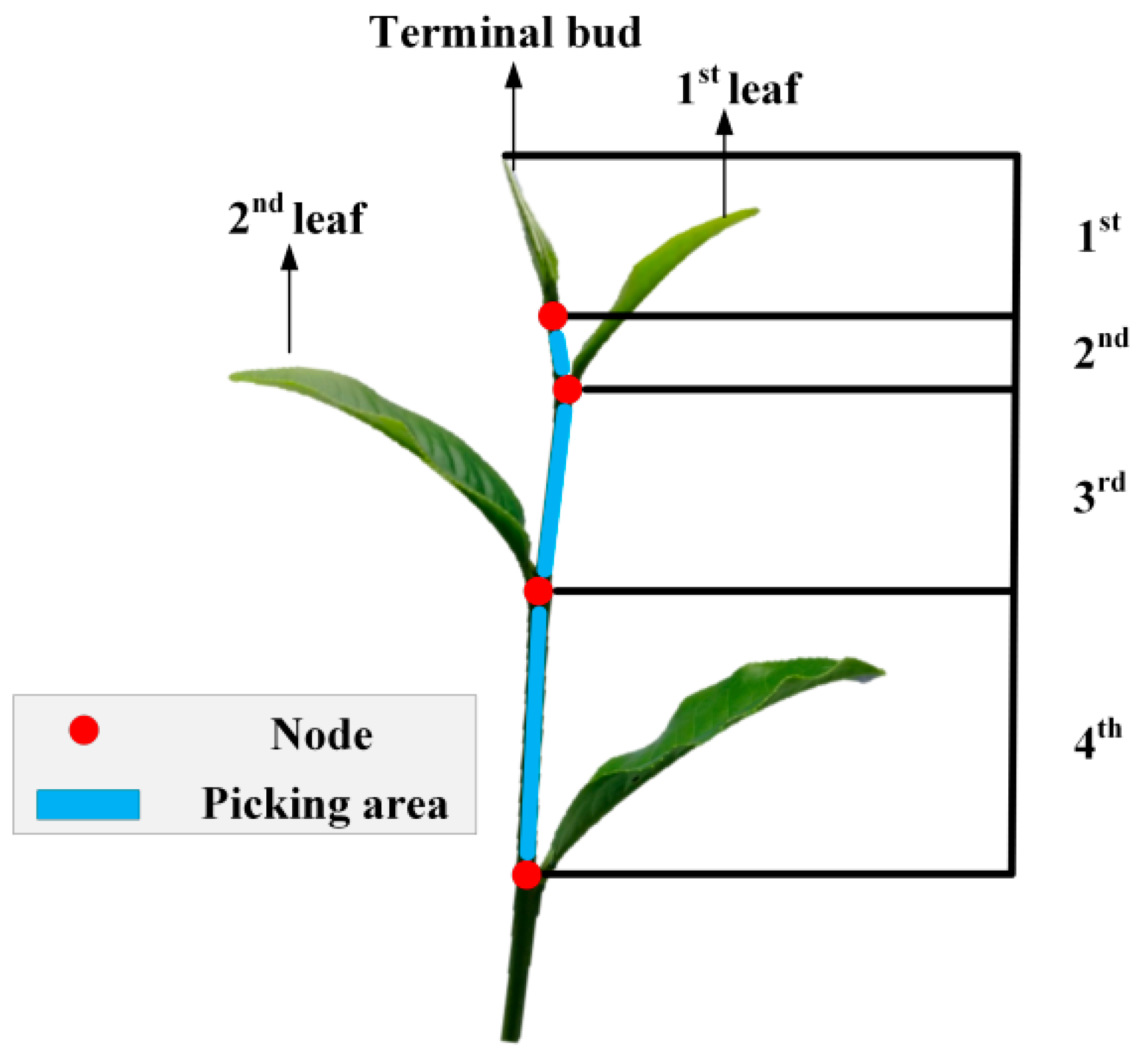
2.4. Biometric Analysis
2.5. Experimental Plan
3. Model Establishment
3.1. Key Parameters for Mathematical Model of Precision Tea Picking
3.2. Multivariate Least Squares Linear Regression Analysis to Analyze Parameters
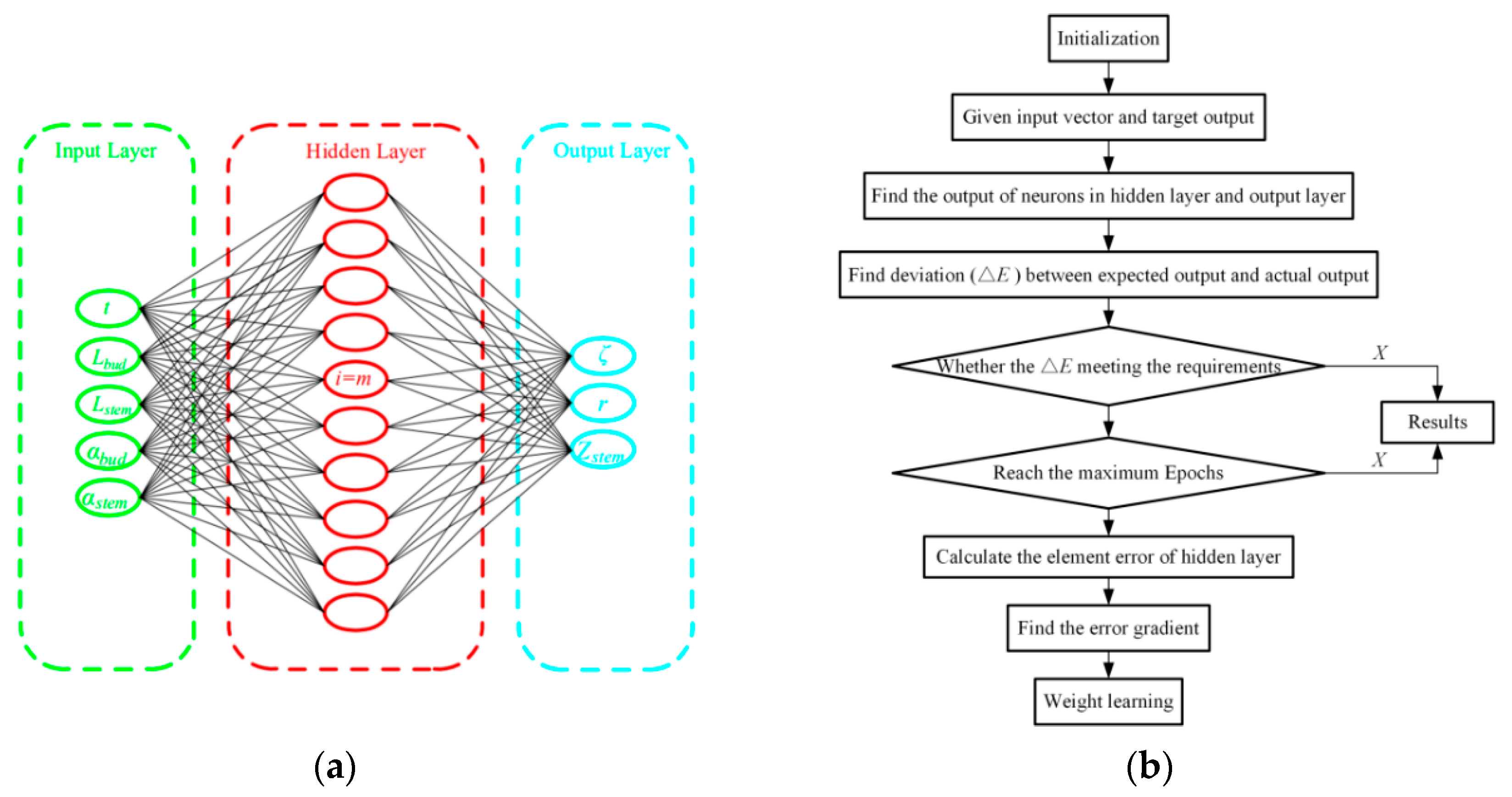
3.3. ANN Modeling for Precise Tea Picking Prediction
3.3.1. Input and Output Layer Neurons
3.3.2. Hidden Layer Neurons
3.3.3. Transfer and Train Function
3.3.4. Physical Structure of Model
3.3.5. Key Training Parameters of the ANN Model
3.3.6. Statistical Analysis
4. Results and Discussion
4.1. Variation Rules for Lbud, Lstem, and ξ with Growth Time for Different Periods
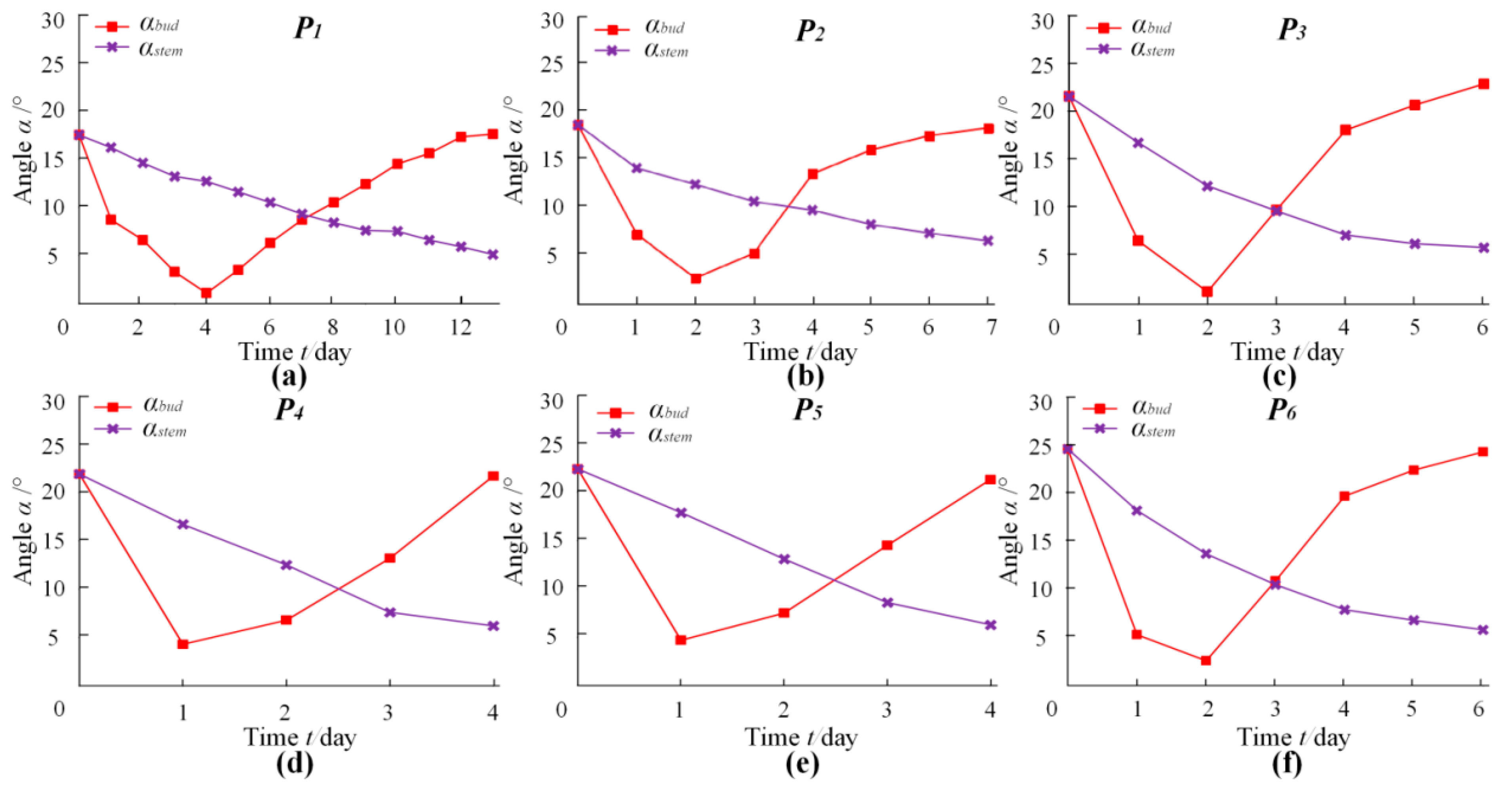
4.2. Variation Rules for αbud and αstem with Growth Time for Different Periods
4.3. Changes in Tea Growth Cycle with Time
4.4. Analysis of Prediction Results of the Established ANN Model
4.4.1. Number of Hidden Layers and Momentum Coefficient
4.4.2. Training Results of the ANN Model
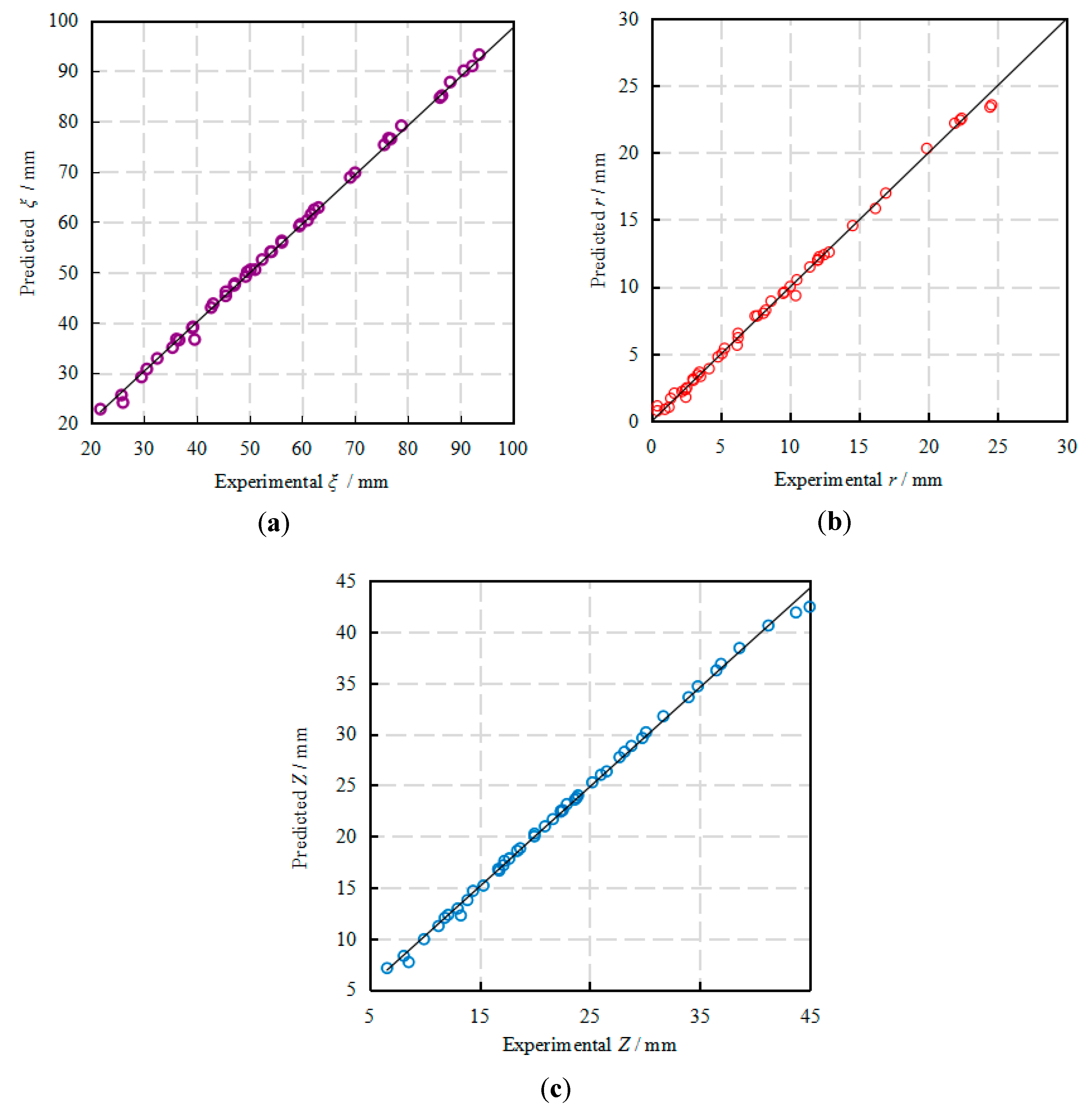
4.4.3. Validation of the Established ANN Model
4.4.4. Application of the Established ANN Model
5. Conclusions
- (1)
- A detailed growth cycle diagram including the transition period, budding period, and germination period of the tea growth was presented in this study.
- (2)
- The growth characteristics of the tea shoots were investigated and the growth cycle for periods P1, P2, P3, P4, P5, and P6 were determined to be 13, 7, 6, 4, 4, and 6 d, respectively, which can help in guiding the production of tea picking.
- (3)
- Considering the key growth parameters (Lbud, Lstem, αstem, and αbud) as the input neurons and the picking indexes (ξ, r, and Zstem) as the output neurons, a 5-2-12-3 ANN model was established.
- (4)
- The best performance for predicting ξ, r, and Zstem was found with 16 training epochs, where the MSE value was 0.0923 × 10−4, and the R values for the training, test, and validation data were 0.99976, 0.99871, and 0.99857, respectively. The established ANN model demonstrated excellent prediction performance and can be used to predict the picking indexes of tea shoots.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shevchuk, A.; Jayasinghe, L.; Kuhnert, N. Differentiation of black tea infusions according to origin, processing and botanical varieties using multivariate statistical analysis of lc-ms data. Food Res. Int. 2018, 109, 387–402. [Google Scholar] [CrossRef]
- Yang, C.; Kim, S.; Yang, G.; Lee, M.; Liao, J.; Chung, J. Inhibition of carcinogenesis by tea: Bioavailability of tea polyphenols and mechanisms of actions. Proc. Soc. Exp. Biol. Med. 2010, 220, 213–217. [Google Scholar]
- Khan, N.; Mukhtar, H. Multitargeted therapy of cancer by green tea polyphenols. Cancer Lett. 2008, 269, 269–280. [Google Scholar] [CrossRef]
- Murase, T.A.; Nagasawa, J.; Suzuki, T.; Hase, I. Tokimitsu. Beneficial effects of tea catechins on diet-induced obesity: Stimulation of lipid catabolism in the liver. Int. J. Obes. Relat. Metab. Disord. 2002, 26, 1459–1464. [Google Scholar] [CrossRef]
- Baruah, P. Types of tea, value addition and product diversification of Indian tea. Proc. First Int. Conf. Tea Sci. Dev. 2015, 7, 151–159. [Google Scholar]
- Takashi, N.S.H. Study on temperature and growth of tea plants (4th report). Growth of young tea plants in temperature and summer. Tea Trial Res. Rep. 1962, 1, 28–40. [Google Scholar]
- Nakayama, T.; Sanui, G. Morphological study on tea shoot development (2nd report). Differentiation and development of lateral shoots in summer. Tea Res. Rep. 1965, 23, 1–5. [Google Scholar]
- Nakayama, T. Vertical distribution of tea buds in a scissors-picking tea plantation. Tea Giken 1967, 35, 40–44. [Google Scholar]
- Harada, T.N.S. Morphological study on tea bud development. Tea Res. Rep. 1960, 23, 1–5. [Google Scholar]
- Stephens, W.; Othieno, C.O.; Carr, M.K.V. Climate and weather variability at the tea research foundation of kenya. Agric. For. Meteorol. 1992, 61, 219–235. [Google Scholar] [CrossRef]
- Koichi, K. The effects of autumn to spring on the sprouting and plucking seasons minimum temperature and precipitation. Chakenh 1988, 6, 22–37. [Google Scholar]
- Takezawa, N.K.K. Prediction of the germination period of the first tea by nonparametric DVR method. Agric. Weather 1994, 50, 221–224. [Google Scholar]
- Takayuki, N. Tea-side shoot development model starting from the pruning period. Jpn. Crop Sci. J. 1999, 68, 433–439. [Google Scholar]
- Jayasinghe, H.A.S.L.; Suriyagoda, L.D.B.; Karunarathne, A.S.; Wijeratna, M.A. Modelling shoot growth and yield of ceylon tea cultivar tri-2025 (camellia sinensis (l.) o. kuntze). J. Agric. Sci. 2018, 156, 200–214. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, S.; Wu, C.; Yang, S.; Zhu, J. Field experiments and model simulation based evaluation of rice yield response to projected climate change in southeastern China. Sci. Total Environ. 2020, 761, 143206. [Google Scholar] [CrossRef]
- Joshi, V.R.; Kazula, M.J.; Coulter, J.A.; Naeve, S.L.; Garcia, A. In-season weather data provide reliable yield estimates of maize and soybean in the us central corn belt. Int. J. Biometeorol. 2021, 65, 489–502. [Google Scholar] [CrossRef]
- Jwmp, A.; Cags, B.; Jeo, A. Temperature-based prediction of harvest date in winter and spring cereals as a basis for assessing viability for growing cover crops. Field Crops Res. 2021, 264. [Google Scholar] [CrossRef]
- Bernotas, G.; Scorza, L.C.T.; Hansen, M.F.; Hales, I.J.; Halliday, K.J.; Smith, L.N. A photometric stereo-based 3d imaging system using computer vision and deep learning for tracking plant growth. GigaScience 2019, 8, giz056. [Google Scholar] [CrossRef]
- Bengocheaguevara, J.M.; Andujar, D.; Sanchezsardana, F.L. A Low-Cost Approach to Automatically Obtain Accurate 3D Models of Woody Crops. Sensors 2017, 18, 30. [Google Scholar] [CrossRef]
- Golbach, F.G.; Kootstra, S.; Damjanovic, G.; Otten, R.V.; Zedde, D. Validation of plant part measurements using a 3d reconstruction method suitable for high-throughput seedling phenotyping. Mach. Vis. Appl. 2016, 2, 663–680. [Google Scholar] [CrossRef]
- Li, Y.; Fan, X.; Mitra, N.J.; Chamovitz, D.; Cohen-Or, D.; Chen, B. Analyzing growing plants from 4d point cloud data. Acm Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Cabo, C.; Pozo, S.D.; Rodríguez-Gonzálvez, P.; Ordóez, C.; González-Aguilera, D. Comparing terrestrial laser scanning (tls) and wearable laser scanning (wls) for individual tree modeling at plot level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Whitfield, D.M.; Connor, D.J. Architecture of individual plants in a field-grown tobacco crop. Funct. Plant Biol. 1980, 7, 415–433. [Google Scholar] [CrossRef]
- Sinoquet, H.; Stephan, J.; Sonohat, G.; Lauri, P.E.; Monney, P. Simple equations to estimate light interception by isolated trees from canopy structure features: Assessment with three-dimensional digitized apple trees. New Phytol. 2007, 175, 94–106. [Google Scholar] [CrossRef]
- Wu, S.G.; Bao, F.S.; Xue, E.Y. A Leaf Recognition Algorithm for Plant Classification Using Probabilistic Neural Network. IEEE 7th Interantional Symposium on Signal Processing and Information Technology. Cairo 2007, 11–16. [Google Scholar] [CrossRef]
- Guo, W.W.; Xue, H. Crop yield forecasting using artificial neural networks: A comparison between spatial and temporal models. Math. Probl. Eng. 2014, 22, 1–7. [Google Scholar] [CrossRef]
- Kucukonder, H.; Boyaci, S.; Akyz, A. A modeling study with an artificial neural network: Developing estimationmodels for the tomato plant leaf area. Turk. J. Agric. For. 2016, 40, 203–212. [Google Scholar] [CrossRef]
- Hu, J.; Xin, P.; Zhang, S. Model for tomato photosynthetic rate based on neural network with genetic algorithm. Int. J. Agric. Biol. Eng. 2019, 12, 179–185. [Google Scholar] [CrossRef]
- Green, T.R.; Salas, J.D.; Martinez, A. Relating crop yield to topographic attributes using spatial analysis neural networks and regression. Geoderma 2006, 139, 23–37. [Google Scholar] [CrossRef]
- Tang, P.; Shen, D.; Xu, Y.; Zhang, X.; Shi, J.; Yin, J. Effect of Fermentation Conditions and Plucking Standards of Tea Leaves on the Chemical Components and Sensory Quality of Fermented Juice. J. Chem. 2018, 1–7. [Google Scholar] [CrossRef]
- Wang, F.L. Scientific picking of high-quality tea. New Countrys. 1994, 4, 13. [Google Scholar]
- Liu, X.X.; Wang, J.L.; Zhao, H.F.; Hu, H.J.; Duan, X.Y. The physical and chemical difference of open surface leaf and clip leaf. Tea Commun. 2011, 38, 11–13. [Google Scholar]
- Dai, A.; Zhou, X.; Liu, X.; Liu, J.; Zhang, C. Model of drying process for combined side-heat infrared radiation and convection grain dryer based on bp neural network. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2017, 48, 351–360. [Google Scholar]
- Vogl, T.; Mangis, P.J.K. Accelerating the convergence of the back-propagation method. Biol. Cybern. 1988, 59, 257–263. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Rafiee, S.; Madadlou, A. The use of artificial neural network to predict exergetic performance of spray drying process: A preliminary study. Comput. Electron. Agric. 2012, 88, 32–43. [Google Scholar] [CrossRef]
- Reed, R.D.; Marks, R.J. Neural smithing-supervised learning in feedforward artificial neural networks. Pattern Anal. Appl. 2001, 4, 73–74. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Chokphoemphun, S. Moisture content prediction of paddy drying in a fluidized-bed drier with a vortex flow generator using an artificial neural network. Appl. Therm. Eng. 2018, 145, 630–636. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, M.; Wang, X.; Wu, W.; Ma, B. Modeling and optimization for konjac vacuum drying based on response surface methodology (RSM) and artificial neural network (ANN). Processes 2020, 8, 1430. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Huang, J.; Li, C. Application of artificial neural network for prediction of key indexes of corn industrial drying by considering the ambient conditions. Appl. Sci. 2020, 10, 5659. [Google Scholar] [CrossRef]
- Mariotti, B.; Maltoni, A.; Jacobs, D.F.; Tani, A. Tree shelters affect shoot and root system growth and structure in quercus robur during regeneration establishment. Eur. J. For. Res. 2015, 134, 641–652. [Google Scholar] [CrossRef]
- Vanderzande, S.; Hias, N.; Edge-Garza, D.; Costes, E.; Davey, M.W.; Keulemans, J. Sylleptic branching in winter-headed apple (malus×domestica) trees: Accession-dependent responses and their relationships with other tree architectural characteristics. Tree Genet. Genomes 2016, 12, 87. [Google Scholar] [CrossRef]
- Velisevich, S.N.; Bender, O.G.; Goroshkevich, S.N. The influence of scion donor tree age on the growth and morphogenesis of siberian stone pine grafts. New For. 2020, 1–19. [Google Scholar] [CrossRef]
- Fang, C.; Huang, J.; Cuan, K.; Zhuang, X.; Zhang, T. Comparative study on poultry target tracking algorithms based on a deep regression network. Biosyst. Eng. 2020, 190, 176–183. [Google Scholar] [CrossRef]








| Variety | Period | Quantity | Massive Content | Purpose |
|---|---|---|---|---|
| Yinghong #9 | P1 | 50 | A/B/C Coordinates in space | Calculate and test |
| P2 | 50 | |||
| P3 | 50 | |||
| P4 | 50 | |||
| P5 | 50 | |||
| P6 | 50 |
| Batch | Date | Lbud (mm) | Lstem (mm) | αbud (°) | αstem (°) | ξ (mm) | r (mm) | Zstem (mm) |
|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 15.911 | 6.955 | 18.555 | 18.555 | 21.764 | 4.796 | 6.594 |
| 3 | 19.773 | 10.305 | 7.105 | 15.105 | 29.571 | 2.446 | 9.949 | |
| 8 | 25.946 | 17.416 | 9.216 | 9.816 | 42.772 | 4.155 | 17.161 | |
| 14 | 32.508 | 25.341 | 17.941 | 5.441 | 56.154 | 10.014 | 25.227 | |
| P2 | 1 | 18.549 | 9.055 | 19.457 | 19.069 | 26.048 | 6.179 | 8.558 |
| 3 | 21.801 | 14.806 | 2.526 | 13.440 | 36.180 | 0.960 | 14.400 | |
| 6 | 33.273 | 22.635 | 16.763 | 8.739 | 54.231 | 9.596 | 22.372 | |
| 8 | 35.461 | 28.310 | 18.806 | 6.059 | 61.720 | 11.431 | 28.152 | |
| P3 | 1 | 27.506 | 13.302 | 23.366 | 23.693 | 37.431 | 10.909 | 12.181 |
| 4 | 42.984 | 25.688 | 11.811 | 11.528 | 67.243 | 8.797 | 25.169 | |
| 7 | 57.781 | 38.868 | 23.877 | 7.332 | 91.386 | 23.388 | 38.868 | |
| P4 | 1 | 30.245 | 18.385 | 23.959 | 23.297 | 44.524 | 12.281 | 16.886 |
| 3 | 45.614 | 30.053 | 9.231 | 14.682 | 74.095 | 7.317 | 29.071 | |
| 5 | 60.926 | 44.659 | 24.222 | 7.675 | 99.821 | 24.996 | 44.259 | |
| P5 | 1 | 32.740 | 18.670 | 25.609 | 25.907 | 46.317 | 14.151 | 16.793 |
| 3 | 48.366 | 30.453 | 10.355 | 16.374 | 76.795 | 8.693 | 29.217 | |
| 5 | 65.725 | 44.785 | 24.351 | 8.940 | 104.119 | 27.099 | 6.959 | |
| P6 | 1 | 28.317 | 14.933 | 27.547 | 26.629 | 38.455 | 13.095 | 13.348 |
| 4 | 43.784 | 27.475 | 13.030 | 12.549 | 69.475 | 9.871 | 26.818 | |
| 7 | 58.019 | 41.701 | 26.684 | 8.696 | 93.060 | 26.054 | 41.221 |
| Parameters of ANN Model | Range |
|---|---|
| Number of hidden layers | 1–3 |
| Number of neurons | 4–12 |
| Momentum coefficient | 0.1–0.4 |
| Number of training epochs | 300–1500 |
| Number of Hidden Layers | Number of Neurons | MSE for Momentum Coefficient (×10−4) | |||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | ||
| 1 | 5 | 0.8436 | 2.6269 | 2.0539 | 1.2984 |
| 7 | 1.2836 | 3.0167 | 2.0646 | 0.7428 | |
| 9 | 0.7960 | 3.0572 | 0.3638 | 2.8964 | |
| 11 | 8.0043 | 1.3594 | 2.2788 | 1.2983 | |
| 2 | 5 | 1.4782 | 1.3235 | 2.1980 | 1.2382 |
| 7 | 1.7443 | 0.2820 | 0.2846 | 0.0330 | |
| 9 | 9.5166 | 6.3066 | 0.8140 | 2.400 | |
| 11 | 4.9811 | 0.9080 | 3.3092 | 1.1428 | |
| 3 | 5 | 9.0875 | 2.9099 | 3.2776 | 1.4205 |
| 7 | 2.6697 | 2.5437 | 1.0459 | 2.4660 | |
| 9 | 0.1390 | 0.1032 | 0.1285 | 0.2722 | |
| 11 | 2.9457 | 1.4802 | 2.1811 | 0.5287 | |
| Weight | Matrix |
|---|---|
| Parameter | Statistical Values for Picking Indexes | ||
|---|---|---|---|
| ξ | r | Zstem | |
| Determination coefficient (R2) | 0.99679 | 0.99994 | 0.99978 |
| Mean square error (MSE) | 1.35183 | 0.12726 | 0.27117 |
| Mean absolute error (MAE) | 0.41474 | 0.03799 | 0.13437 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Han, C.; Wu, W.; Xu, J.; Zhang, Q.; Chen, M.; Hu, Z.; Zheng, Z. Fundamental Understanding of Tea Growth and Modeling of Precise Tea Shoot Picking Based on 3-D Coordinate Instrument. Processes 2021, 9, 1059. https://doi.org/10.3390/pr9061059
Wang X, Han C, Wu W, Xu J, Zhang Q, Chen M, Hu Z, Zheng Z. Fundamental Understanding of Tea Growth and Modeling of Precise Tea Shoot Picking Based on 3-D Coordinate Instrument. Processes. 2021; 9(6):1059. https://doi.org/10.3390/pr9061059
Chicago/Turabian StyleWang, Xiaoming, Chongyang Han, Weibin Wu, Jian Xu, Qingzhao Zhang, Ming Chen, Zhibiao Hu, and Zefeng Zheng. 2021. "Fundamental Understanding of Tea Growth and Modeling of Precise Tea Shoot Picking Based on 3-D Coordinate Instrument" Processes 9, no. 6: 1059. https://doi.org/10.3390/pr9061059
APA StyleWang, X., Han, C., Wu, W., Xu, J., Zhang, Q., Chen, M., Hu, Z., & Zheng, Z. (2021). Fundamental Understanding of Tea Growth and Modeling of Precise Tea Shoot Picking Based on 3-D Coordinate Instrument. Processes, 9(6), 1059. https://doi.org/10.3390/pr9061059







