Investigations of Gas–Particle Two-Phase Flow in Swirling Combustor by the Particle Stokes Numbers
Abstract
:1. Introduction
2. Modeling and Governing Equations
2.1. Continuity and Momentum Equations
2.2. Momentum Transfer between Gas and Particle Phases
2.3. Reynolds Stress Transport Equations of Gas and Particle Phases
2.4. Particle Temperature Equation Coupled with Kinetic Frictional Stress Model
3. Computational Method and Experimental Setting
3.1. Experimental Setting
3.2. Numerical Algorithms
4. Results and Discussion
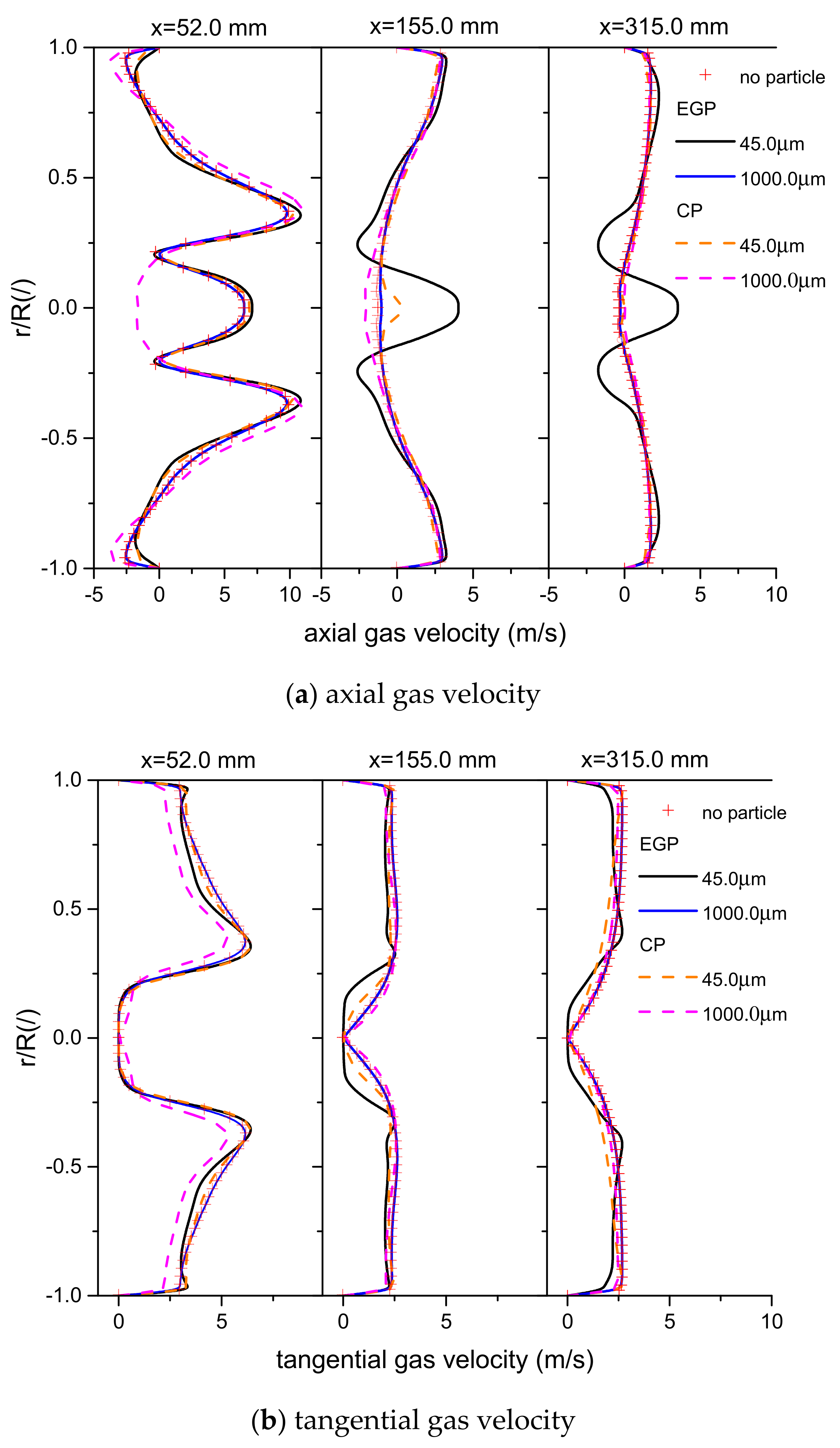
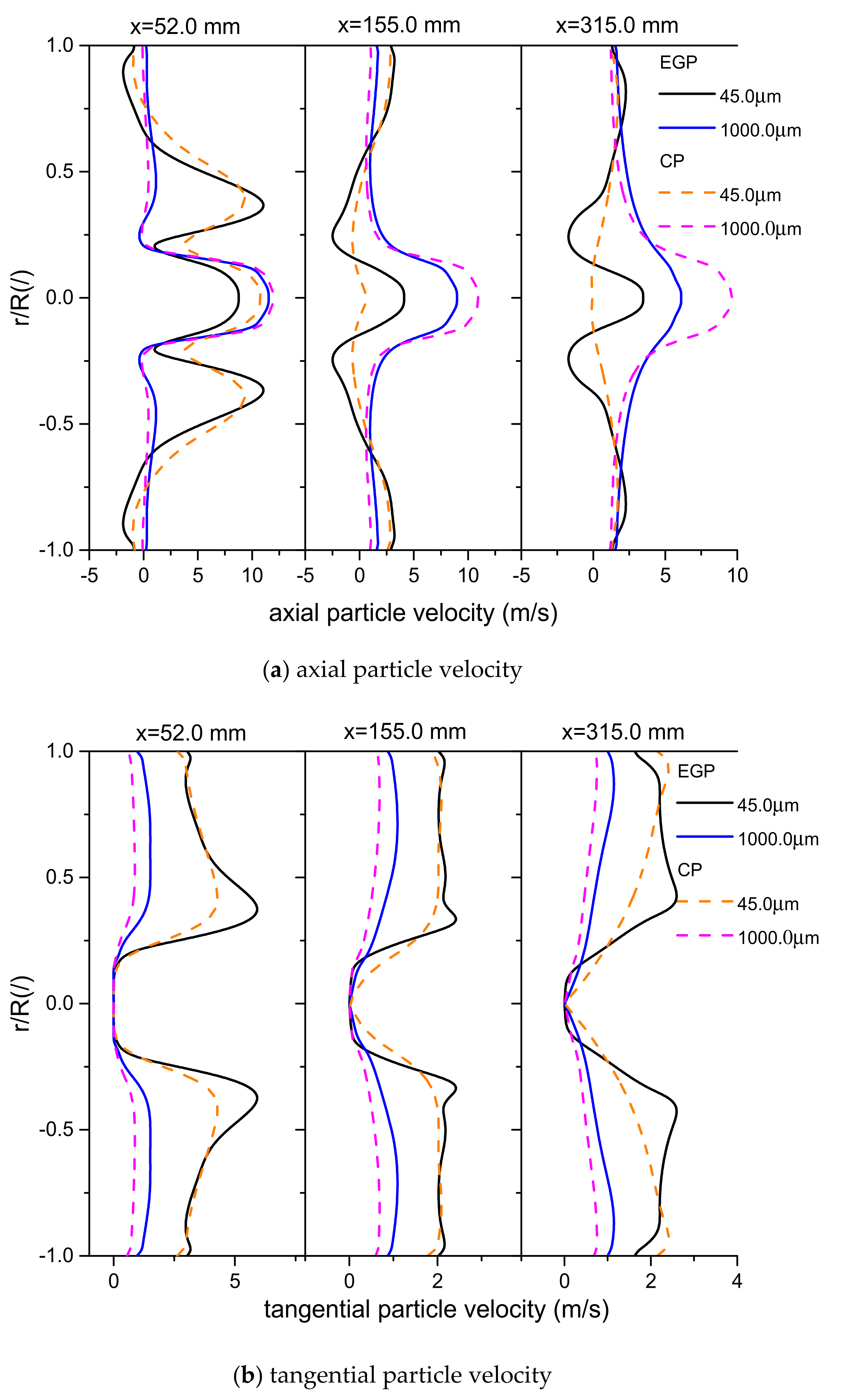
4.1. Experimental Validations for Gas and Particle Velocity
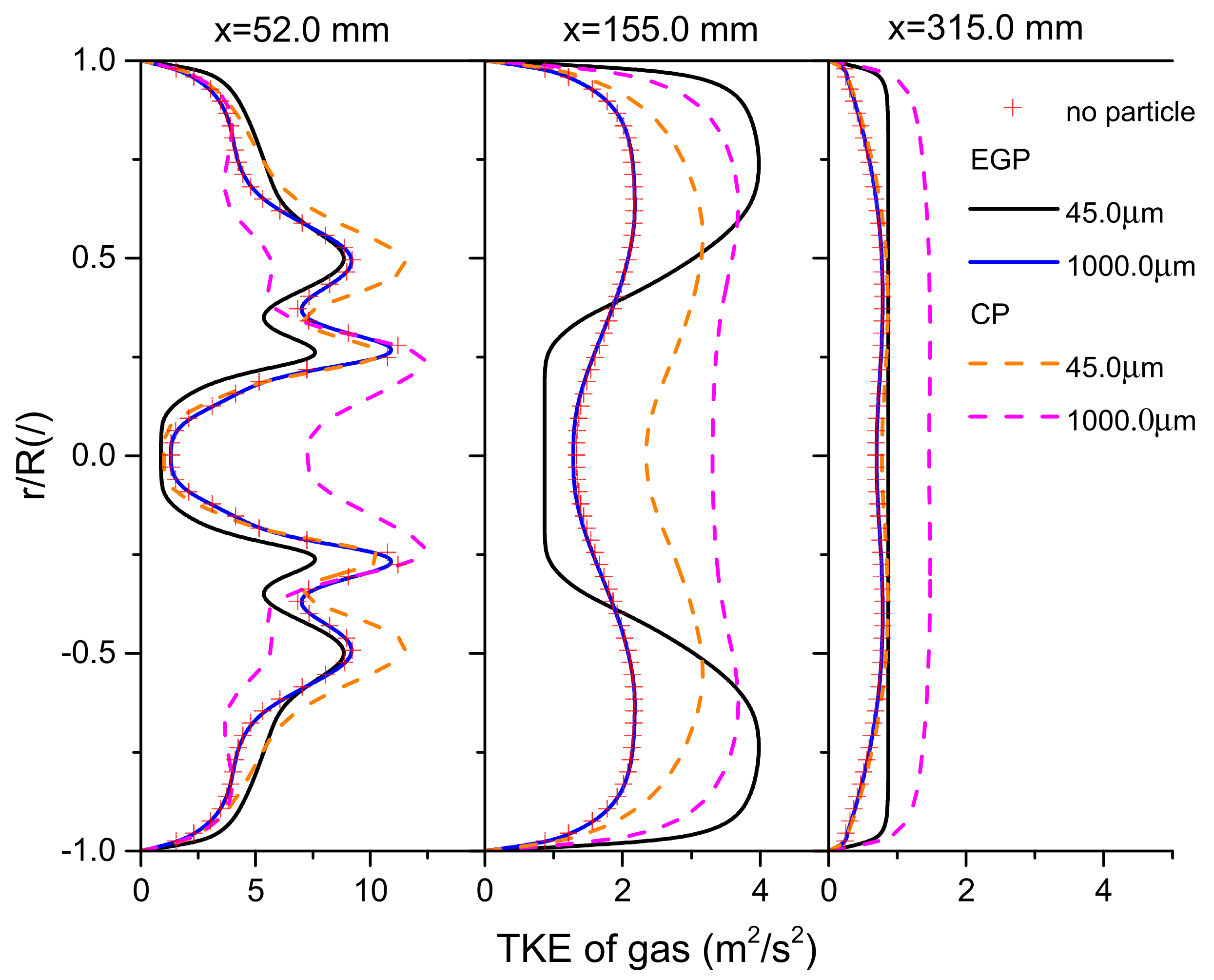
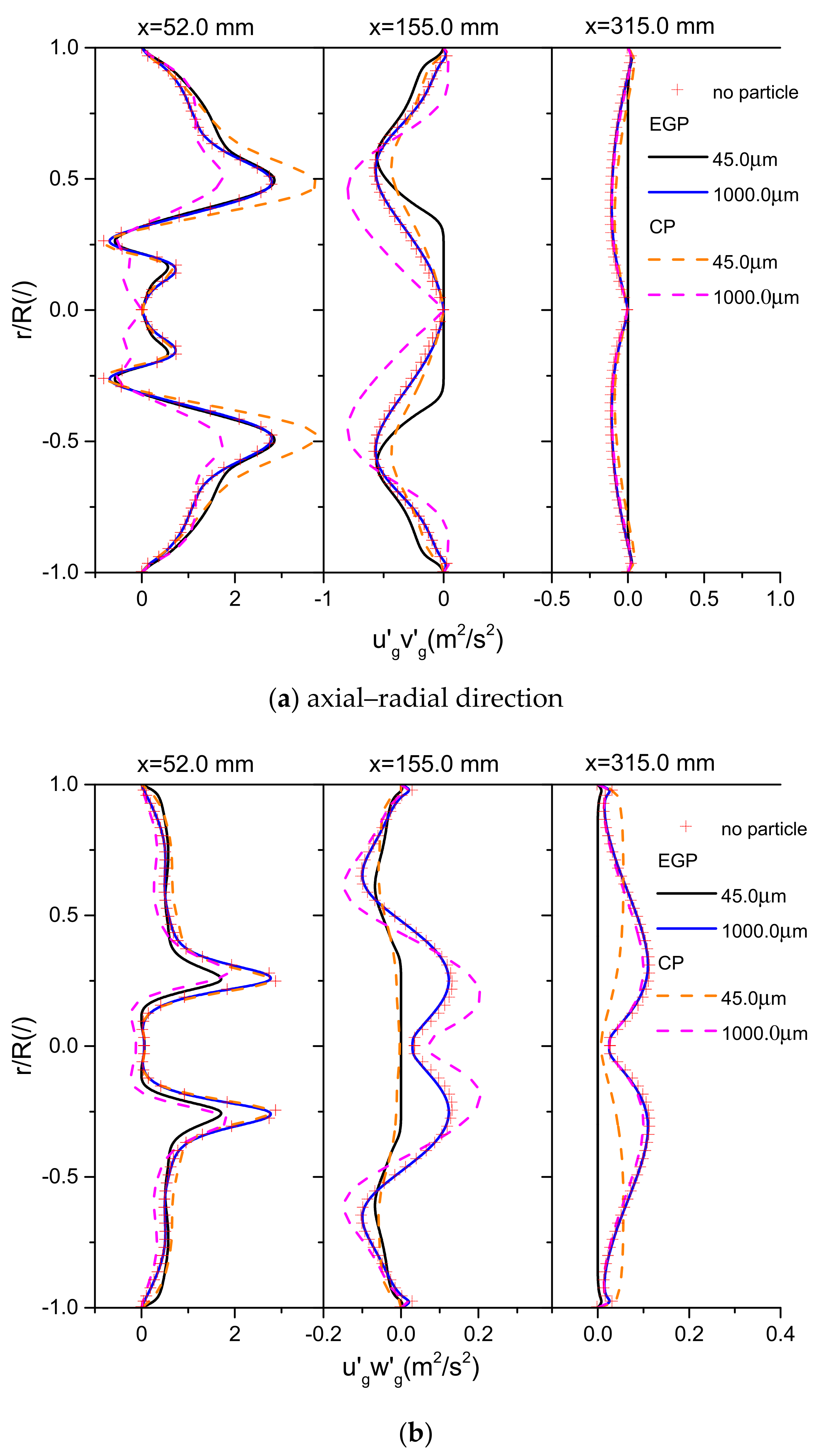
4.2. Gas Turbulence Modulations
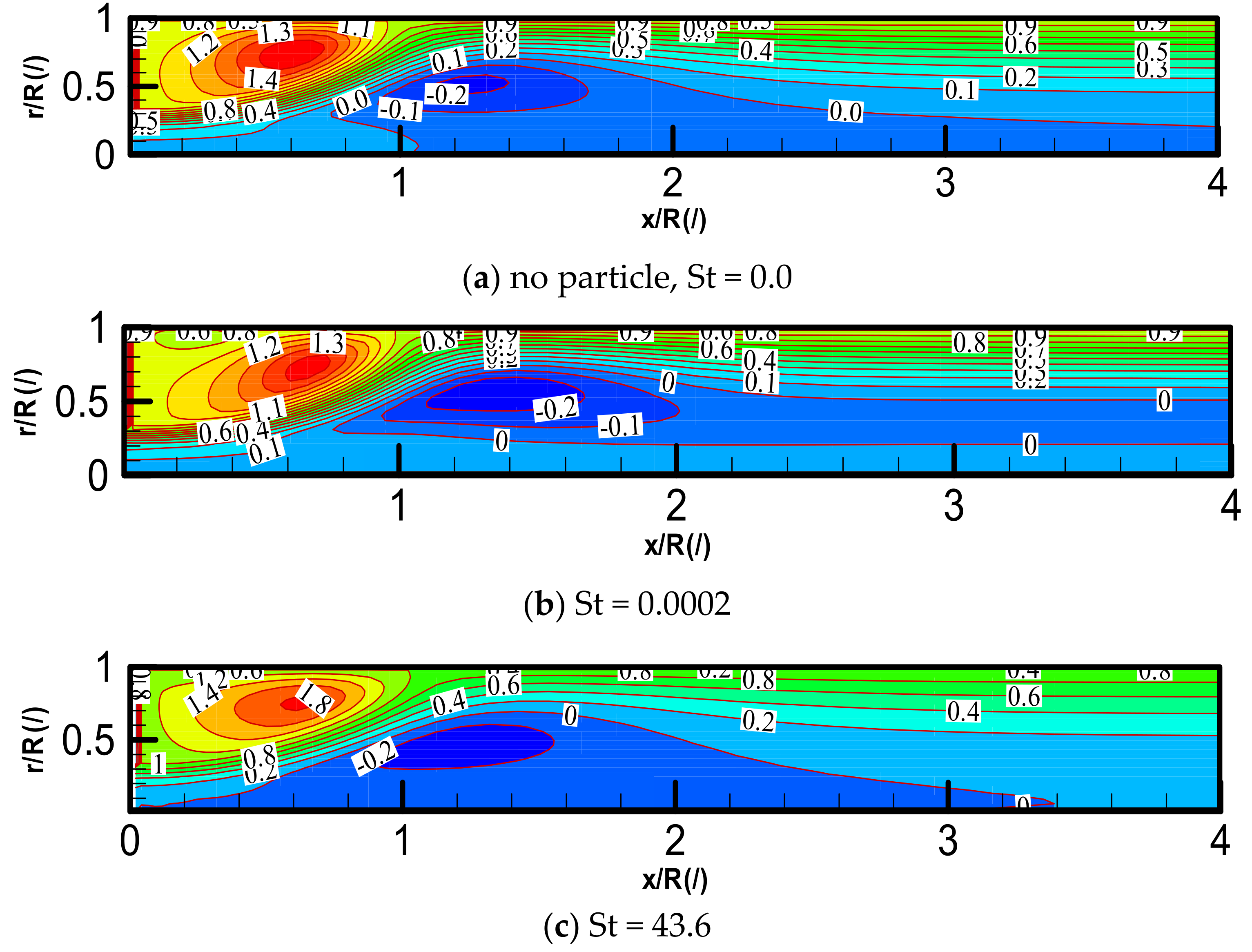
4.3. Effects of St Number on the Distributions of Gas and Particle Velocity
4.4. Effects of St Number on the Distributions of Gas and Particle Fluctuation Velocity
4.5. Effects of St Number on Turbulence Kinetic Energy (TKE)
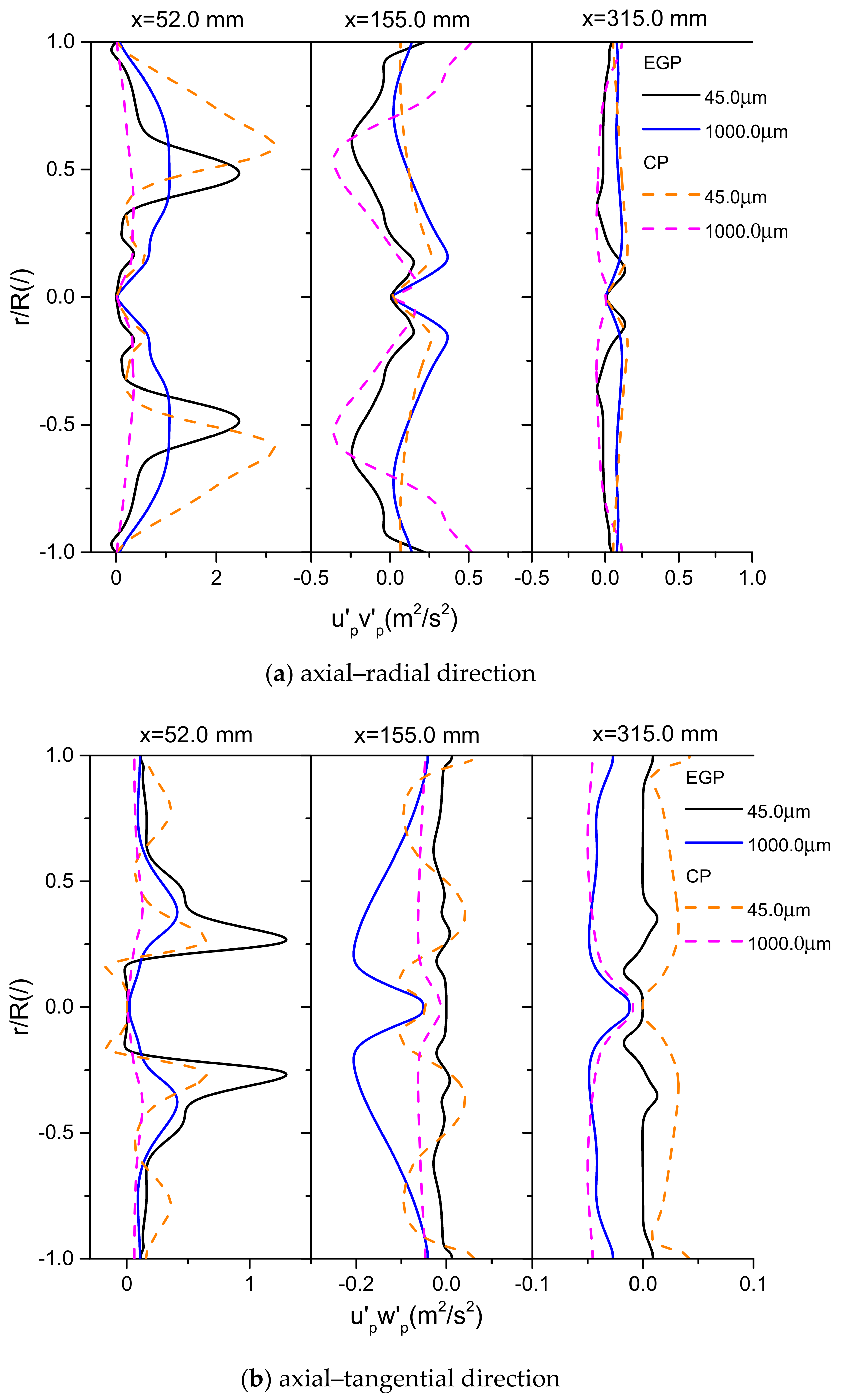
4.6. Effects of St Number on the Reynolds Shear Stresses of Gas and Particle Dispersions
4.7. Effects of St Number on the Tensor Stress Invariants
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CD | Drag coefficient, (dimensionless) |
| dp | Diameter of particle, (m) |
| D | Diffusion term, (dimensionless) |
| e | Restitution coefficient of particle, (dimensionless) |
| ew | Restitution coefficient of wall, (dimensionless) |
| g | Gravitational acceleration, (m/s2) |
| g0 | Radial distribution function, (dimensionless) |
| I | Unit tensor, (dimensionless) |
| kg | Turbulent kinetic energy of gas, (m2/s2) |
| kp | Turbulent kinetic energy of particle, (m2/s2) |
| p | Thermodynamic pressure, (Pa) |
| pp | Particle pressure term, (Pa) |
| pfp | Frictional particle pressure term, (Pa) |
| P | Transport production term, (dimensionless) |
| Q | Flow rates of gas and particle, (g/s) |
| Rep | The Reynolds numbers of particle, (dimensionless) |
| s | Swirling numbers of gas, (dimensionless) |
| St | Stokes numbers of particle, (dimensionless) |
| t | Time, (s) |
| T | Transport interaction terms, (dimensionless) |
| ug | Gas phase velocity, (m/s) |
| up | Particle phase velocity, (m/s) |
| Greek Alphabets | |
| αg | Volume fraction of gas, (dimensionless) |
| αp | Volume fraction of particle, (dimensionless) |
| αp,max | Maximum volume fraction of particle, (dimensionless) |
| βgp | Drag coefficient between gas–particle, (dimensionless) |
| γ | Dissipation rate of particle collision, (kg/ms3) |
| λ | Tensor eigenvalues, (dimensionless) |
| δ | Kronecker Delta symbol, (dimensionless) |
| ρg | Gas phase density, (kg/m3) |
| ρp | Particle phase density, (kg/m3) |
| εg | Turbulent energy dissipation rate of gas, (m2/s3) |
| εp | Turbulent energy dissipation rate of particle, (m2/s3) |
| μg | Gas phase dynamic viscosity, (Pa.s) |
| μp | Particle phase shear viscosity, (Pa.s) |
| τg | Gas stresses, (Pa) |
| τp | Particle stresses, (Pa) |
| ξs | Bulk viscosity of particle phase, (Pa.s) |
| θ | Granular temperature, (m2/s2) |
| Π | Pressure-strain, (dimensionless) |
| ϕ | lending function, (dimensionless) |
| Superscripts | |
| ′ | Fluctuations of gas and particle |
| ¯ | Averaged symbol |
| Subscripts | |
| an | Annular diameter |
| i,j,k | Space |
| in | Inlet |
| f | Friction, or flow |
| g,p | Gas phase, particle phase |
| l | Laminar flow |
| L | Length of geometry |
| o | Outer diameter |
| r | Relaxation time of particle |
References
- Gupta, A.; Lilley, D.G.; Syred, N. Swirl Flows; Abacus Press: Tunbridge Wells, UK, 1984. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Description; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Crowe, C.; Sommerfeld, M.S.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Liu, Y.; Zhang, L.; Chen, Z.Y.; Zhou, L.X. Numerical investigation on mixture particle dispersion characteristics in swirling particle-laden combustion chamber. Int. Commun. Heat Mass Transf. 2020, 117, 104720. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.Y.; Zhang, Y.J.; Zhou, L.X. Hydrodynamic modeling of swirling binary mixture gasp-article flows using a second order moment turbulence model. ACS Omega 2020, 5, 31490–31501. [Google Scholar] [CrossRef]
- Cabeza, C.; Sarasua, G.; Mart, A.C. Influence of coaxial cylinders on the vortex breakdown in a closed flow. Eur. J. Mech. B-Fluids 2010, 29, 201–207. [Google Scholar] [CrossRef] [Green Version]
- Eaton, J.K. Experiments and simulations on turbulence modification by dispersed particles. Appl. Mech. Rev. 1994, 47, 44–48. [Google Scholar] [CrossRef]
- Gui, N.; Fan, J.R.; Chen, S. Numerical study of particle-vortex interaction and turbulence modulation in swirling jets. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2010, 82, 056323. [Google Scholar] [CrossRef]
- Yan, J.; Gui, N.; Xie, G.N.; Gao, J.S. Direct numerical simulation of particle-laden swirling flows on turbulence modulation. Math. Problem Eng. 2014, 3, 1–12. [Google Scholar] [CrossRef]
- Yan, J.; Gui, N.; Xie, G.N.; Gao, J.S. Direct numerical simulation and visualization of biswirling jets. Math. Problem Eng. 2014, 6, 193731. [Google Scholar] [CrossRef]
- Wang, G.; Richter, D.H. Modulation of the turbulence regeneration cycle by inertial particles in planar Couette flow. J. Fluid Mech. 2019, 861, 901–929. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhang, H.Q.; Wang, X.L. Large eddy simulation of particle-laden turbulent flows over a backward-facing step considering two-phase two-way coupling. Adv. Mech. Eng. 2013, 325, 1–11. [Google Scholar]
- Apte, S.V.; Mahesh, K.; Moin, P.; Oefelein, J.C. Large-eddy simulation of swirling particle-laden flows in a coaxial-jet combustor. Int. J. Multiph. Flow 2003, 29, 1311–1333. [Google Scholar] [CrossRef]
- Joseph, C.; Oefelein, V.; Drozda, G. Large eddy simulation of swirling particle laden flow in model axisymmetric combustor. Proc. Combust. Inst. 2007, 3, 2291–2299. [Google Scholar]
- Brauner, T.; Jones, W.P.; Marquis, A.J. LES of the cambridge stratified swirl burner using a sub-grid pdf approach. Flow Turbul. Combust. 2016, 96, 965–985. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhou, L.X.; Xu, C.X. Numerical simulation of instantaneous flow structure of swirling, and non-swirling coaxial jet particle laden turbulence flows. Phys. A Statical Mech. Its Appl. 2010, 389, 5380–5389. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, H.L.; Liu, W.T. Model and simulation of gas-solid flow with wide size distributions in circulating fluidized bed. J. Chem. Ind. Eng. 2003, 54, 106–1071. [Google Scholar]
- Syred, N. A review of oscillation mechanisms and the role of the processing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–116. [Google Scholar] [CrossRef]
- Elghobashi, S. Direct numerical simulation of turbulent flows laden with droplets or bubbles. Ann. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef] [Green Version]
- Anagnostopoulos, J.S.; Bergeles, G.C. Discrete-phase effects on the flow field of a droplet-laden swirling jet with recirculation: A numerical study. Int. J. Heat Fluid Flow 1992, 13, 141–150. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Ando, A.; Qiu, H.H. Swirling, particle-laden flows through a pipe expansion. J. Fluids Eng. 1992, 114, 648–656. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Reese, J.M. Gas turbulence modulation in a two-fluid model for gas-solid flows. AIChE J. 2003, 49, 3048–3065. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, T.; Eaton, J.K. Classification of turbulence modification by dispersed spheres using a novel dimensionless number. Phys. Rev. Lett. 2008, 101, 114502. [Google Scholar] [CrossRef] [Green Version]
- Pakhomov, M.A.; Terekhov, V.I. Numerical simulation of turbulent swirling gas-dispersed flow behind a sudden tube expansion. Thermophyics Aeromech. 2015, 22, 597–608. [Google Scholar] [CrossRef]
- Kim, S.D.; Kim, C.H. Axial dispersion characteristics of three phase fluidized beds. J. Chem. Eng. Jpn. 1983, 16, 172–178. [Google Scholar] [CrossRef] [Green Version]
- Asif, M.; Petersen, J.N. Particle dispersion in a binary solid-liquid fluidized bed. AIChE J. 1993, 39, 1465–1471. [Google Scholar] [CrossRef]
- Galvin, K.P.; Swann, R.; Ramirez, W.F. Segregation and dispersion of a binary system of particles in a fluidized bed. AIChE J. 2006, 52, 3401–3410. [Google Scholar] [CrossRef]
- Khan, M.S.; Mitra, S.; Ghatage, S.V.; Doroodchi, E.; Evans, G.M. Segregation and dispersion studies in binary solid liquid fluidized beds a theoretical and computational study. Powder Technol. 2020, 314, 400–411. [Google Scholar] [CrossRef]
- Zhou, L.X. Two-fluid turbulence modeling of swirling gas-particle flows—A review. Powder Technol. 2017, 314, 253–263. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.J.; Zhou, L.X. Numerical study on bubble-liquid two-phase turbulent hydrodynamics in extremely narrow shape bioreactor. Int. Commun. Heat Mass Transf. 2019, 108, 104286. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Zhou, L.X. Effects of swirling flow on ultralight-particle dispersion characteristics in coaxial jet combustor. Energy Sci. Eng. 2019, 7, 3220–3233. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Jiang, L.X.; Zhang, Y.J. Hydrodynamic modeling of turbulence modulation by particles in a swirling gas-particle two-phase flow. ACS Omega 2021, 6, 10106–10118. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Zhang, Y.J.; Zhou, L.X. Effects of sparger holes on gas-liquid hydrodynamics in bubble column. Chem. Eng. Technol. 2020, 43, 307–316. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, L.X.; Zhang, Y.J. Numerical Simulation of bubbles-liquid two-phase turbulent in shallow bioreactor. Energies 2019, 12, 2269. [Google Scholar] [CrossRef] [Green Version]
- Gore, R.A.; Crowe, C.T. Effect of particle size on modulation in turbulent intensity. Int. J. Multiph. Flow 1989, 15, 279–298. [Google Scholar] [CrossRef]
- Elghobashi, S.E. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Qiu, H.H. Detailed measurements in a swirling particulate two-phase flow by a phase Doppler anemometer. Int. J. Heat Fluid Flow 1991, 12, 20–28. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Qiu, H.H. Characterization of particle-laden, confined swirling flows by a phase-doppler anemometer. Int. J. Heat Fluid Flow 1993, 19, 1093–1127. [Google Scholar]
- Lu, H.L.; Gidaspow, D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar]
- Johnson, P.C.; Nott, P.; Jackson, P. Frictional-collisional equations of motion for participate flows and their application to chutes. J. Fluid Mech. 1990, 210, 501–535. [Google Scholar] [CrossRef]
- Koch, D.L. Kinetic theory for monodisperse gas-solids suspension. Phys. Fluid 1990, 2, 1711–1723. [Google Scholar] [CrossRef]
- Mohanarangam, K.; Tu, J.Y. Two-fluid model for particle-turbulence interaction in a backward facing step. AIChE J. 2007, 53, 2254–2264. [Google Scholar] [CrossRef]
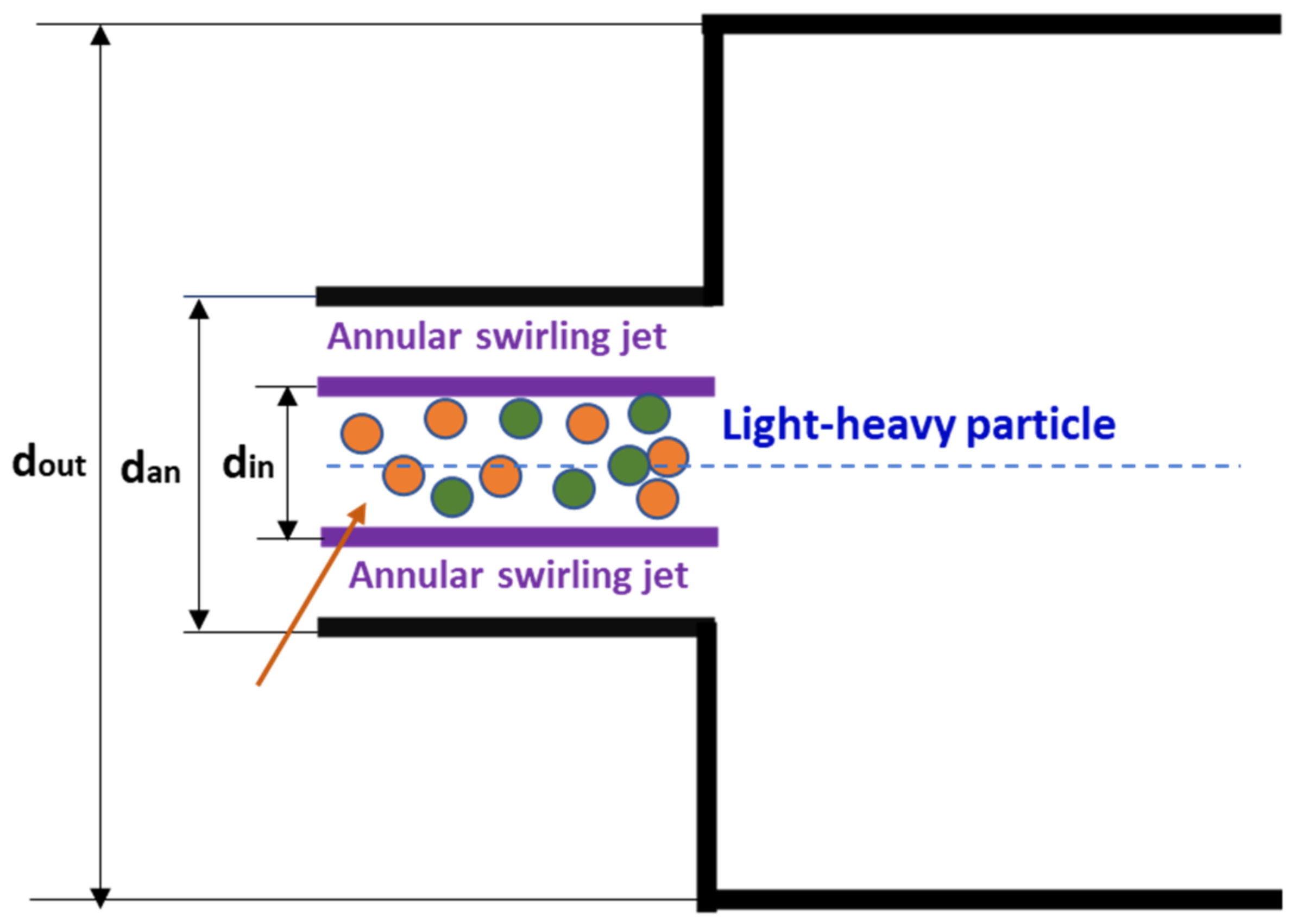
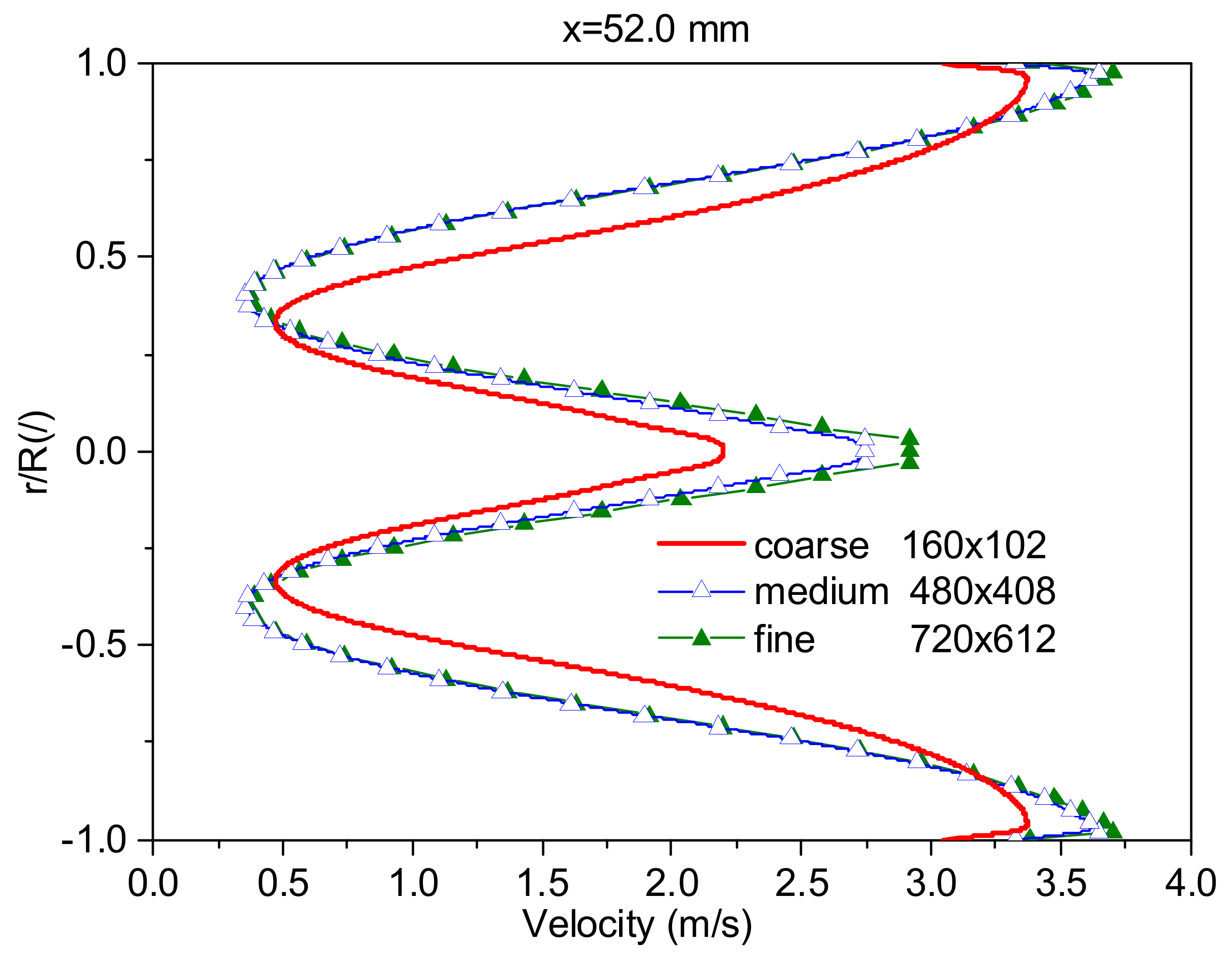






| Parameters of Gas and Particle | Unit | Value |
|---|---|---|
| Diameter of EGP and CP, dp | μm | 45/1000 |
| 45/1000 | ||
| Density of EGP and CP, ρp | kg/m3 | 21.9, 8900 |
| Diameter of glass particle, dpg | μm | 45 |
| Density of glass particle, ρpg | kg/m3 | 2500 |
| Density of gas, ρg | kg/m3 | 1.225 |
| Viscosity of gas, μg | Pa.s | 1.8 × 10−5 |
| Wall restitution coefficient, ew | - | 0.99 |
| Particles restitution coefficient, e | - | 0.90 |
| Sphericity of particle, φ | - | 0.98 |
| Diameter of inner tube, djn | mm | 32 |
| Diameter of annular jet, dan | mm | 64 |
| Diameter of chamber, do | mm | 194 |
| Length of test section, L | mm | 960 |
| Ratios of particle loadings, η | - | 0.034 |
| Swirling number of gas flow, s | - | 0.47 |
| Primary flow rates, Qs | g/s | 9.9 |
| Flow rate in annular jet, Qan | g/s | 38.3 |
| Inlet Reynolds number, Rein | - | 26,200 |
| Copper Stokes numbers St, dp = 45, 160, 1000 μm | - | 0.087, 43.6 |
| EGP Stokes numbers of St, dp = 45, 1000 μm | - | 0.0002, 0.11 |
| Glass particle Stokes number St, dp = 45 μm | - | 0.025 |
| Predictions | Experiment Data | |
|---|---|---|
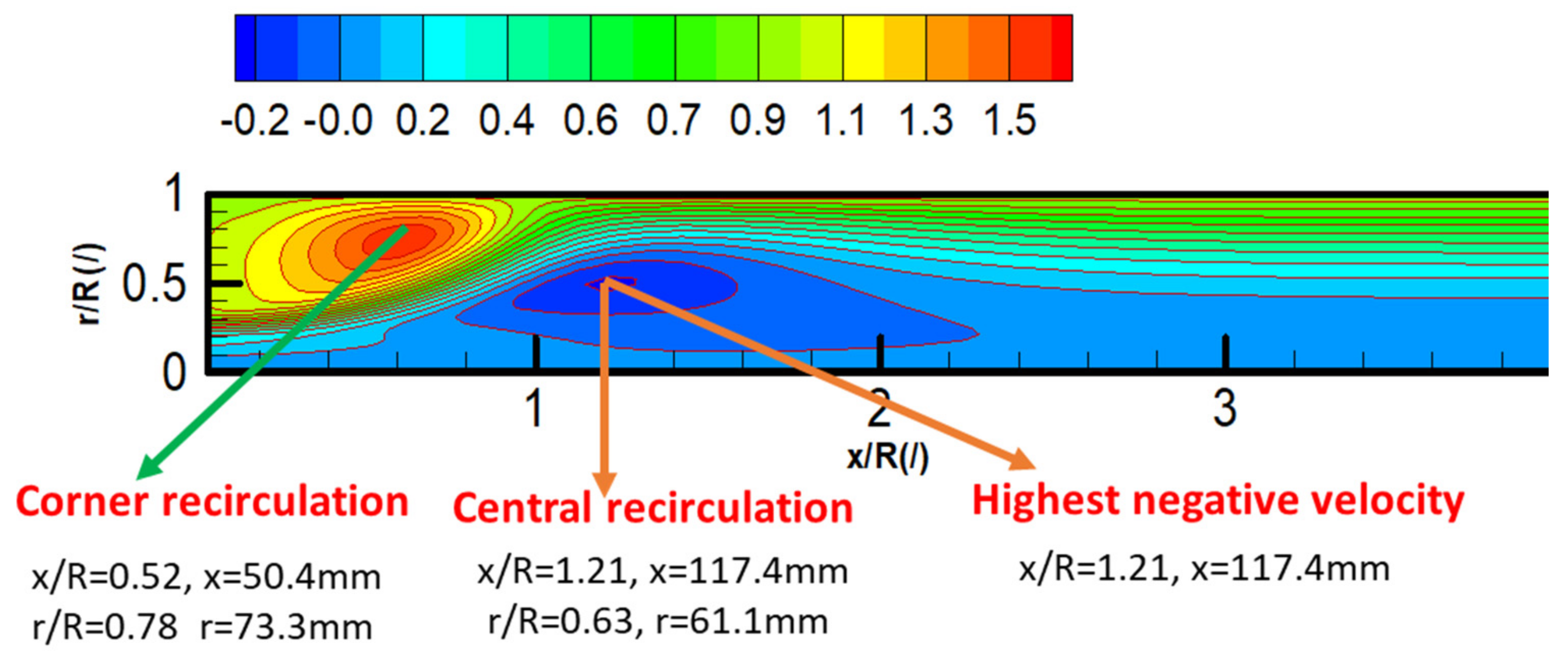
| Primary jetting regions, (x, r) | (50.4 mm, 73.3 mm) | (52.5 mm, -) |
| Secondary circulation zone, (x,r) | (117.4 mm, 61.1 mm) | (112.5 mm, -) |
| Reattachment position, (x,r) | (53.5 mm, 93.5 mm) | (52.5 mm, -) |
| The relative errors, % | 4.8 |
| EGP | CP | |||
|---|---|---|---|---|
| Stokes number | 0.0002 | 0.11 | 0.087 | 43.6 |
| Followability | Excellent | Good | Excellent | Worse |
| Second recirculation | Entrained | Entrained | Entrained | Entrained |
| Length of circulation region | Elongated | Elongated | Elongated | Elongated |
| Preferential accumulation | Increased | Increased | Increased | Decreased |
| Vortex formation | Help | Help | Unsensitive | Damage |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, G. Investigations of Gas–Particle Two-Phase Flow in Swirling Combustor by the Particle Stokes Numbers. Processes 2021, 9, 951. https://doi.org/10.3390/pr9060951
Liu Y, Li G. Investigations of Gas–Particle Two-Phase Flow in Swirling Combustor by the Particle Stokes Numbers. Processes. 2021; 9(6):951. https://doi.org/10.3390/pr9060951
Chicago/Turabian StyleLiu, Yang, and Guohui Li. 2021. "Investigations of Gas–Particle Two-Phase Flow in Swirling Combustor by the Particle Stokes Numbers" Processes 9, no. 6: 951. https://doi.org/10.3390/pr9060951
APA StyleLiu, Y., & Li, G. (2021). Investigations of Gas–Particle Two-Phase Flow in Swirling Combustor by the Particle Stokes Numbers. Processes, 9(6), 951. https://doi.org/10.3390/pr9060951






