A Computational Fluid Dynamic Study of Developed Parallel Stations for Primary Fans
Abstract
:1. Introduction
2. Methodology
3. Computational Domain
3.1. Symmetrical Branches
3.2. Overlapped Branches
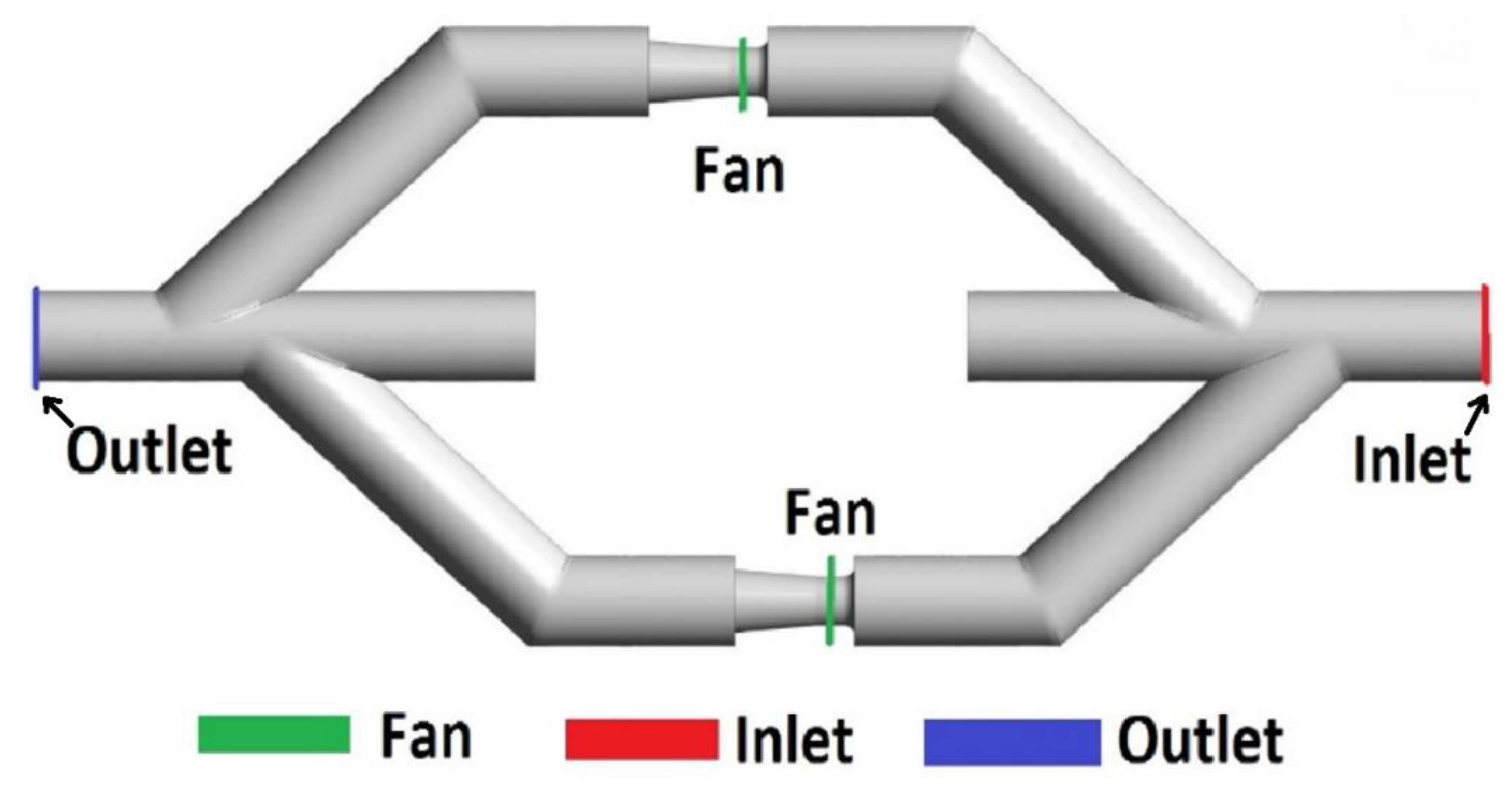
3.3. Run Around
4. Boundary Conditions
5. Set up and Initial Conditions
5.1. Obtaining the Operational Point
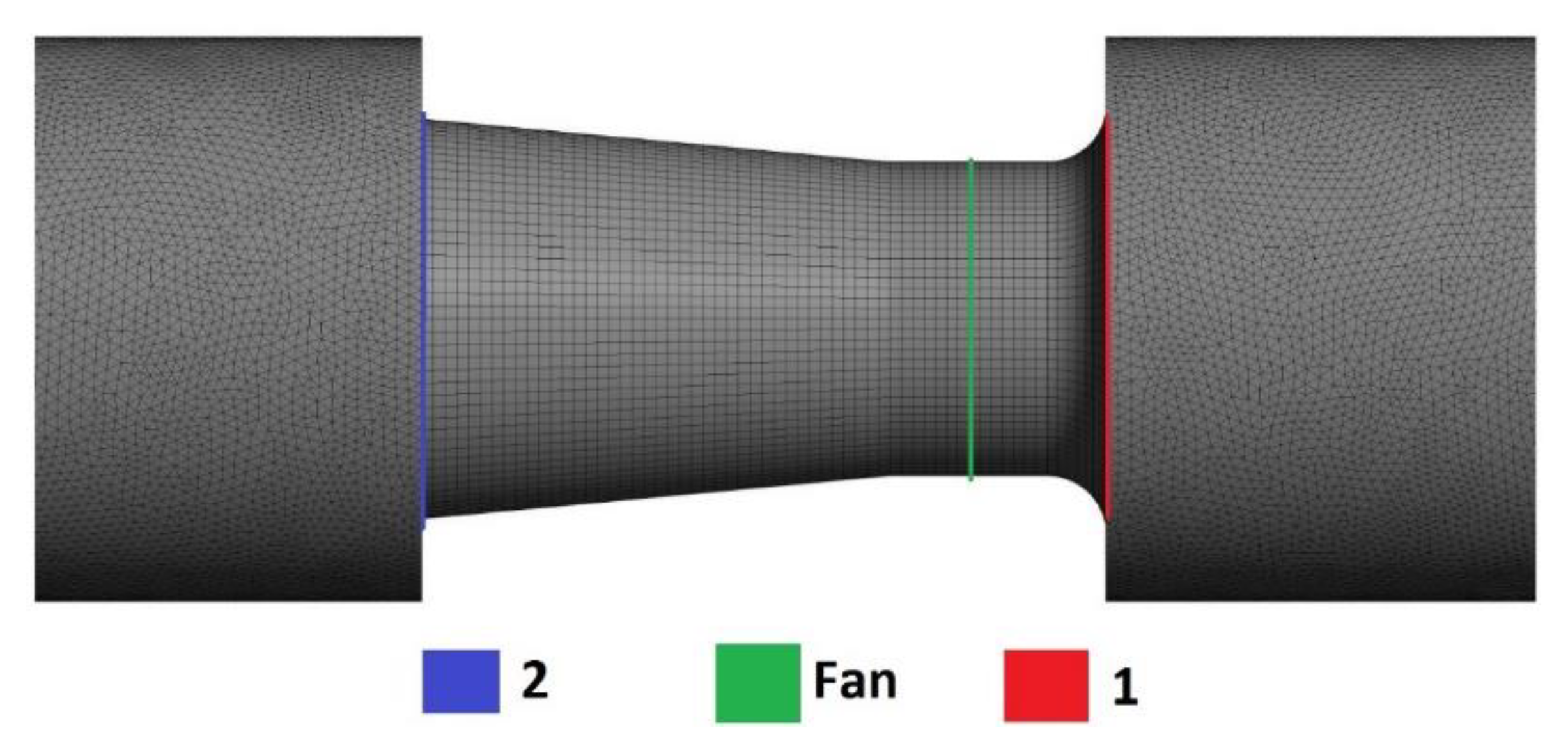
5.2. Mesh
6. Results
6.1. Operational Points
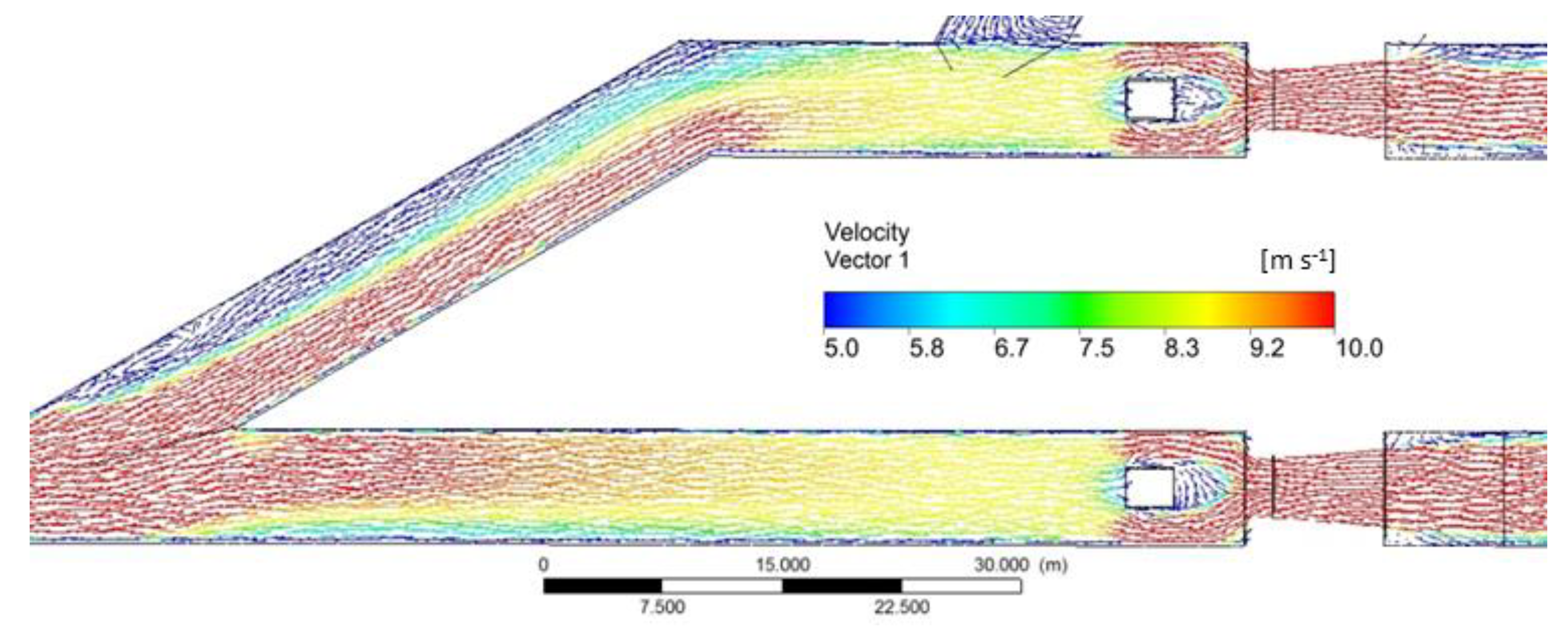
6.2. Computational Fluid Dynamics Analysis
6.3. Energy Consumption Analysis
6.4. Energy and Development Cost Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hartman, H.L.; Mutmansky, J.M.; Ramani, R.V.; Wang, Y.J. Mine Ventilation and Air Conditioning; John Wiley & Sons, Inc.: Toronto, ON, Canada, 1997. [Google Scholar]
- McPherson, M.J. Subsurface Ventilation and Environmental Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Acuña, E.I.; Hurtado, J.P.; Wallace, K. A Summary of Computational Fluid Dynamic Application to the New Level Mine Project of El Teniente. In Proceedings of the 10th International Mine Ventilation Congress, Johannesburg, South Africa, 2–8 August 2014; pp. 91–97. [Google Scholar]
- Versteeg, H.; Malalasereka, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 1st ed.; Longman Scientific & Technical: Essex, UK, 1995. [Google Scholar]
- Diego, I.; Torno, S.; Toraño, J.; Menéndez, M.; Gent, M. A practical use of CFD for ventilation of underground works. Tunn. Undergr. Space Technol. 2011, 26, 189–200. [Google Scholar] [CrossRef]
- Hurtado, J.P.; Acuña, E.I. CFD analysis of 58 adit main fans parallel installation for the 2015–2019 underground developments of the New Level Mine project. Appl. Therm. Eng. 2015, 90, 1109–1118. [Google Scholar] [CrossRef]
- Hurtado, J.P.; Díaz, N.; Acuña, E.I.; Fernández, J. Shock losses characterization of ventilation circuits for block caving production levels. Tunn. Undergr. Space Technol. 2014, 41, 88–94. [Google Scholar] [CrossRef]
- Pan, J. Study on the local ventilation resistance of multistage fan stations. Met. Min. 2001, 9, 49–51. [Google Scholar]
- Gou, Y.; Shi, X.; Zhou, J.; Qiu, X.; Chen, X. Characterization and effects of the shock losses in a parallel fan station in the underground mine. Energies 2017, 10, 785. [Google Scholar] [CrossRef] [Green Version]
- Llanca-Pacheco, J.L. Determinación de la Interferencia en la Incorporación de un Ventilador en Paralelo, Proyecto Nuevo Nivel Mina; Tesis para Optar al Titulo de Ingeniero de Ejecución en Minas; Universidad de Santiago de Chile, Facultad de Ingeniería, Departamento de Ingeniería en Minas: Santiago, Chile, 2013. [Google Scholar]













| Kentry | Koutlet |
|---|---|
| 7.5 | 15 |
| 7.5 | 7 |
| 0 | 6.5 |
| 0 | 3 |
| 0 | 0 |
| Kinlet | Koutlet | QFanA (m3/s) | Ps-FanA (Pa) | QFanB (m3/s) | Ps-FanB (Pa) | QTotal (m3/s) | Ps-Total (Pa) | Hydraulic Power (kW) |
|---|---|---|---|---|---|---|---|---|
| Symmetrical branches (SB) | ||||||||
| 7.5 | 15 | 266 | 1871 | 264 | 1873 | 529 | 1872 | 991 |
| 7.5 | 7 | 309 | 1668 | 310 | 1675 | 619 | 1672 | 1034 |
| 0 | 6.5 | 368 | 1280 | 370 | 1291 | 738 | 1285 | 949 |
| 0 | 3 | 411 | 720 | 412 | 731 | 823 | 726 | 597 |
| 0 | 0 | 439 | 156 | 439 | 166 | 878 | 161 | 141 |
| Overlapped branches (OB) | ||||||||
| 7.5 | 15 | 252 | 1858 | 273 | 1874 | 525 | 1866 | 980 |
| 7.5 | 7 | 305 | 1667 | 308 | 1684 | 613 | 1676 | 1027 |
| 0 | 6.5 | 374 | 1212 | 376 | 1231 | 750 | 1221 | 916 |
| 0 | 3 | 405 | 760 | 408 | 787 | 814 | 773 | 629 |
| 0 | 0 | 434 | 239 | 418 | 242 | 851 | 241 | 205 |
| Run around (RA) | ||||||||
| 7.5 | 15 | 279 | 1856 | 252 | 1880 | 532 | 1868 | 993 |
| 7.5 | 7 | 313 | 1644 | 307 | 1674 | 620 | 1659 | 1029 |
| 0 | 6.5 | 381 | 1148 | 379 | 1177 | 760 | 1162 | 883 |
| 0 | 3 | 415 | 673 | 411 | 726 | 826 | 699 | 577 |
| 0 | 0 | 441 | 98 | 439 | 156 | 880 | 127 | 112 |
| K | SB | OB | RA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kinlet | Koutlet | Q (m3/s) | Ps (Pa) | R (kg s2/m8) | Q (m3/s) | Ps (Pa) | R (kg s2/m8) | Q (m3/s) | Ps (Pa) | R (kg s2/m8) |
| 7.5 | 15 | 529 | 1872 | 0.00668 | 525 | 1866 | 0.00677 | 532 | 1868 | 0.00661 |
| 0 | 6.5 | 738 | 1285 | 0.00236 | 750 | 1221 | 0.00217 | 760 | 1162 | 0.00201 |
| 0 | 0 | 878 | 161 | 0.00021 | 868 | 241 | 0.00032 | 880 | 127 | 0.00016 |
| K | Hydraulic Power (kW) | ∆ (kW) | |||||
|---|---|---|---|---|---|---|---|
| Kinlet | Koutlet | SB | OB | RA | ∆(RA − SB) | ∆(RA − OB) | ∆(SB − OB) |
| 7.5 | 15 | 991 | 980 | 993 | 2 | 14 | 11 |
| 0 | 6.5 | 949 | 916 | 883 | −65 | −32 | 33 |
| 0 | 0 | 141 | 209 | 112 | −30 | −97 | −68 |
| K | Year Consumption (MWh/year) | ∆ (MWh) | |||||
|---|---|---|---|---|---|---|---|
| Kinlet | Koutlet | SB | OB | RA | ∆(RA − SB) | ∆(RA − OB) | ∆(SB − OB) |
| 7.5 | 15 | 8246.1 | 8151.9 | 8265.3 | 19.2 | 113.5 | 94.3 |
| 0 | 6.5 | 7894.3 | 7618.9 | 7350.4 | −543.9 | −268.5 | 275.4 |
| 0 | 0 | 1175.2 | 1737.7 | 928.5 | −246.7 | −809.2 | −562.5 |
| Year | Total Cost (kUSD) | % Difference (RA over OB) | ||
|---|---|---|---|---|
| SB | OB | RA | ||
| 1 | 4457.4 | 3522.2 | 4134.1 | 15% |
| 2 | 5473.0 | 4502.6 | 5079.1 | 11% |
| 3 | 6413.4 | 5410.3 | 5954.1 | 9% |
| 4 | 7284.2 | 6250.7 | 6764.3 | 8% |
| 5 | 8090.4 | 7028.9 | 7514.5 | 6% |
| 6 | 8836.9 | 7749.5 | 8209.1 | 6% |
| 7 | 9528.2 | 8416.7 | 8852.2 | 5% |
| 8 | 10,168.2 | 9034.5 | 9447.7 | 4% |
| 9 | 10,760.8 | 9606.5 | 9999.1 | 4% |
| 10 | 11,309.5 | 10,136.1 | 10,509.7 | 4% |
| 11 | 11,817.6 | 10,626.5 | 10,982.4 | 3% |
| 12 | 12,288.0 | 11,080.6 | 11,420.1 | 3% |
| 13 | 12,723.6 | 11,501.0 | 11,825.4 | 3% |
| 14 | 13,126.9 | 11,890.3 | 12,200.7 | 3% |
| 15 | 13,500.4 | 12,250.8 | 12,548.2 | 2% |
| 16 | 13,846.2 | 12,584.5 | 12,869.9 | 2% |
| 17 | 14,166.3 | 12,893.6 | 13,167.8 | 2% |
| 18 | 14,462.8 | 13,179.7 | 13,443.7 | 2% |
| 19 | 14,737.3 | 13,444.7 | 13,699.1 | 2% |
| 20 | 14,991.4 | 13,690.0 | 13,935.5 | 2% |
| Development Cost of 7.2 m × 7.2 m Cross Section (USD/m) | ||||||
|---|---|---|---|---|---|---|
| Energy Cost (USD/kWh) | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 |
| 75 | - | - | - | - | - | - |
| 100 | - | - | - | - | - | - |
| 125 | 22 | 35 | - | - | - | - |
| 150 | 15 | 20 | 27 | 47 | - | - |
| 175 | 12 | 15 | 18 | 24 | 33 | - |
| 200 | 10 | 12 | 14 | 17 | 21 | 27 |
| 225 | 8 | 10 | 12 | 14 | 17 | 20 |
| 250 | 7 | 9 | 10 | 12 | 14 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hurtado, J.P.; Reyes, G.; Vargas, J.P.; Acuña, E. A Computational Fluid Dynamic Study of Developed Parallel Stations for Primary Fans. Processes 2021, 9, 1607. https://doi.org/10.3390/pr9091607
Hurtado JP, Reyes G, Vargas JP, Acuña E. A Computational Fluid Dynamic Study of Developed Parallel Stations for Primary Fans. Processes. 2021; 9(9):1607. https://doi.org/10.3390/pr9091607
Chicago/Turabian StyleHurtado, Juan Pablo, Gabriel Reyes, Juan Pablo Vargas, and Enrique Acuña. 2021. "A Computational Fluid Dynamic Study of Developed Parallel Stations for Primary Fans" Processes 9, no. 9: 1607. https://doi.org/10.3390/pr9091607
APA StyleHurtado, J. P., Reyes, G., Vargas, J. P., & Acuña, E. (2021). A Computational Fluid Dynamic Study of Developed Parallel Stations for Primary Fans. Processes, 9(9), 1607. https://doi.org/10.3390/pr9091607






